Правата y = 3x + 2 е допирателна към графиката на функцията y = -12x ^ 2 + bx-10. Намерете b, като се има предвид, че абсцисата на точката на допир е по-малка от нула.
Покажете решениеРешение
Нека x_0 е абсцисата на точката от графиката на функцията y = -12x ^ 2 + bx-10, през която минава допирателната към тази графика.
Стойността на производната в точката x_0 е равна на наклона на допирателната, тоест y "(x_0) = - 24x_0 + b = 3. От друга страна, допирателната точка принадлежи и на двете графики на функцията и допирателната, тоест -12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. Получаваме системата от уравнения \ начало (случаи) -24x_0 + b = 3, \\ - 12x_0 ^ 2 + bx_0-10 = 3x_0 + 2. \ край (случаи)
Решавайки тази система, получаваме x_0 ^ 2 = 1, което означава или x_0 = -1, или x_0 = 1. Според условието абсцисата на точката на допир е по-малка от нула, следователно x_0 = -1, след това b = 3 + 24x_0 = -21.
Отговор
състояние
Фигурата показва графиката на функцията y = f (x) (която е начупена линия, съставена от три прави отсечки). Използвайки фигурата, изчислете F (9) -F (5), където F (x) е една от първопроизводните на f (x).
Покажете решениеРешение
Съгласно формулата на Нютон-Лайбниц разликата F (9) -F (5), където F (x) е една от първопроизводните на функцията f (x), е равна на площта на ограничения криволинеен трапец чрез графиката на функцията y = f (x), чрез правите линии y = 0 , x = 9 и x = 5. Според графиката определяме, че посоченият извит трапец е трапец с основи равни на 4 и 3 и височина 3.
Площта му е \ frac (4 + 3) (2) \ cdot 3 = 10,5.
Отговор
Източник: „Математика. Подготовка за изпит-2017. Ниво на профила". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.
състояние
Фигурата показва графиката на y = f "(x) - производната на функцията f (x), дефинирана на интервала (-4; 10). Намерете интервалите на намаляване на функцията f (x). отговор, посочете дължината на най-големия от тях.

Решение
Както знаете, функцията f (x) намалява на онези интервали, във всяка точка на които производната f "(x) е по-малка от нула. Като се има предвид, че е необходимо да се намери дължината на най-големия от тях, три такива интервалите са естествено разграничени от фигурата: (-4; -2) ; (0; 3); (5; 9).
Дължината на най-големия от тях - (5; 9) е равна на 4.
Отговор
Източник: „Математика. Подготовка за изпит-2017. Ниво на профила". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.
състояние
Фигурата показва графиката на y = f "(x) - производната на функцията f (x), дефинирана на интервала (-8; 7). Намерете броя на максималните точки на функцията f (x), принадлежащи на интервалът [-6; -2].
.png)
Решение
Графиката показва, че производната f "(x) на функцията f (x) променя знака от плюс на минус (именно в такива точки ще има максимум) точно в една точка (между -5 и -4) от интервала [-6; -2]. Следователно има точно една максимална точка на интервала [-6; -2].
Отговор
Източник: „Математика. Подготовка за изпит-2017. Ниво на профила". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.
състояние
Фигурата показва графиката на функцията y = f (x), дефинирана на интервала (-2; 8). Определете броя на точките, в които производната на функцията f (x) е 0.

Решение
Равенството на нула на производната в точка означава, че допирателната към графиката на функцията, начертана в тази точка, е успоредна на оста Ox. Следователно намираме точки, в които допирателната към графиката на функцията е успоредна на оста Ox. На тази диаграма такива точки са крайни точки (точки на максимум или минимум). Както можете да видите, има 5 екстремни точки.
Отговор
Източник: „Математика. Подготовка за изпит-2017. Ниво на профила". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.
състояние
Правата y = -3x + 4 е успоредна на допирателната към графиката на функцията y = -x ^ 2 + 5x-7. Намерете абсцисата на точката на допир.
Покажете решениеРешение
Наклонът на правата линия към графиката на функцията y = -x ^ 2 + 5x-7 в произволна точка x_0 е равен на y "(x_0). Но y" = - 2x + 5, така че y "(x_0 ) = - 2x_0 + 5. Ъгловият коефициент на правата y = -3x + 4, посочен в условието, е равен на -3. Успоредните прави имат същия наклон. Следователно намираме такава стойност на x_0, че = -2x_0 + 5 = -3.
Получаваме: x_0 = 4.
Отговор
Източник: „Математика. Подготовка за изпит-2017. Ниво на профила". Изд. Ф. Ф. Лисенко, С. Ю. Кулабухова.
състояние
Фигурата показва графиката на функцията y = f (x) и точките -6, -1, 1, 4 са отбелязани по оста на абсцисата. В коя от тези точки стойността на производната е най-малка? Посочете тази точка в отговора си.
Майсторски клас по математика
в 11 клас
по тази тема
„ПРОИЗВОДНА ФУНКЦИЯ
В ЗАДАЧИТЕ НА ИЗПОЛЗВАНЕТО "
учител по математика
Мартиненко Е.Н.
2017-2018 учебна година
Целта на майсторския клас: развиват уменията на ученицитеприлагане на теоретични знания по темата "Производна на функцията" за решаване на задачите на единния държавен изпит.
Задачи
Образователни:да се обобщят и систематизират знанията на учениците по темата
„Производна на функция“, разгледайте прототипите на задачите на USE по тази тема, предоставят на учениците възможност да тестват знанията си при самостоятелно решаване на задачи.
Разработване: насърчаване на развитието на паметта, вниманието, самочувствието и уменията за самоконтрол; формирането на основни ключови компетенции (сравнение, съпоставяне, класификация на обекти, определяне на адекватни начини за решаване на образователен проблем въз основа на определени алгоритми, способност да действат самостоятелно в ситуация на несигурност, да контролират и оценяват дейността си, да намират и премахване на причините за възникналите трудности).
Образователни: насърчаване на:
Формиране на отговорно отношение към ученето сред учениците;
развиване на устойчив интерес към математиката;
създаване на положителна вътрешна мотивация за изучаване на математика.
Технологии: индивидуално диференцирано обучение, ИКТ.
Методи на преподаване: словесно, визуално, практично, проблематично.
Форми на работа: индивидуално, фронтално, по двойки.
Оборудване и материали за урока:проектор, екран, компютър, симулатор(Приложение 1), презентация за урока(Приложение № 2), индивидуално - диференцирани карти за самостоятелна работа по двойки(Приложение № 3), списък с интернет сайтове, индивидуално диференцирана домашна работа(Приложение № 4).
Обяснение за майсторския клас.
Този майсторски клас се провежда в 11 клас за подготовка за Единния държавен изпит. Цели прилагането на теоретичен материал по темата "Производна на функция" при решаване на изпитни задачи.
Продължителност на майсторския клас- 20 минути.
Структура на майсторски клас
I. Организационен момент -1 мин.
II Комуникация на темата, целите на майсторския клас, мотивация на учебните дейности - 1 мин.
III. Фронтална работа. Обучение „Задачи № 14 БАЗА, № 7 ПРОФИЛ на Единния държавен изпит”. Анализ на работата със симулатора - 7 мин.
IV.Индивидуално - диференцирана работа по двойки. Самостоятелно решаване на задачи No 12. (ПРОФИЛ) Взаимна проверка - 9 мин. Онлайн тестване (БАЗА) Анализ на резултатите от теста - 8 мин
V. Проверка на индивидуална домашна работа. -1 минута.
Vi. Индивидуално - диференцирана домашна работа -1 мин.
VII. КОНТРОЛЕН ТЕСТ 20 МИНУТИ (4 ОПЦИИ)
Напредък на майсторския клас
аз .Организиране на времето.
II Комуникация на темата, целите на майсторския клас, мотивация на учебните дейности.
(Слайдове 1-2, Приложение № 2)
Темата на нашия урок е "Производната на функция в задачите на изпита". Всеки знае поговорката „Малка макара, но скъпа“. Една от такива „шпули“ в математиката е производната. Производната се използва при решаване на много практически задачи по математика, физика, химия, икономика и други дисциплини. Позволява ви да решавате проблемите просто, красиво и интересно.
Темата „Производна” е представена в задача No 14 от основно ниво и в задачите на профилно ниво No 7,12, 18 и единния държавен изпит.
Работихте с документи, регламентиращи структурата и съдържанието на контролно-измервателните материали на единния държавен изпит по математика 2018 г. Направете заключение какви знания и умения са ви необходими, за да решавате успешно задачите за ЕГЭ по темата „Производна“.
(Слайдове 3-4, Приложение № 2)
научихте ли се „Кодификатор на елементите на съдържанието по МАТЕМАТИКА за подготовка на контролно-измерителни материали за единния държавен изпит“,
"Кодификатор на изискванията за нивото на обучение на завършилите", "Спецификация на контролно-измервателните материали", "Демонстрационна версия на контролно-измервателните материали от единния държавен изпит 2018 г." иоткрих какви знания и умения за функцията и нейната производна са необходими за успешно решаване на задачи по темата "Производна".
Необходимо
- ЗНАЯ
правила за изчисление на производни;
производни на основни елементарни функции;
геометричното и физическото значение на производната;
уравнение на допирателната към графиката на функцията;
изследване на функция с помощта на производна.
- ДА МОЖЕТЕ
извършват действия с функции (опишете поведението и свойствата на функция според графиката, намерете нейните най-високи и най-ниски стойности).
- ИЗПОЛЗВАЙТЕ
придобити знания и умения в практиката и ежедневието.
Имате теоретични познания по темата за производните. Днес ще го направимНАУЧЕТЕ СЕ ДА ПРИЛАГАТЕ ЗНАНИЯТА ЗА ПРОИЗВОДНАТА ФУНКЦИЯ ЗА РЕШАВАНЕ НА ПРОБЛЕМИТЕ ЗА ИЗПОЛЗВАНЕ.(Слайд 4, Приложение № 2)
Не е за нищо Това е казал Аристотел„УМЪТ НЕ Е САМО В ЗНАНИЯТА, НО И В СПОСОБНОСТТА ДА ПРИЛАГА ЗНАНИЕТО НА ПРАКТИКА“(Слайд 5, Приложение № 2)
В края на урока ще се върнем към целта на нашия урок и ще разберем дали сме я постигнали?
III ... Фронтална работа.Обучение "Задачи № 14 ОСНОВА № 7 ПРОФИЛ на Единния държавен изпит" (Приложение № 1). Анализ на работата със симулатора.
Изберете верния отговор от четирите предложени.
Каква според вас е трудността при изпълнение на задача № 7?
Какво мислите, какви са типичните грешки, които допускат абитуриентите на изпита при решаването на този проблем?
Когато отговаряте на въпросите на задача № 14 ОСНОВА И № 7 ПРОФИЛ, трябва да можете да опишете поведението и свойствата на функцията от графиката на производната, а от графиката на функцията - поведението и свойствата на производна на функцията. А това изисква добри теоретични познания по следните теми: „Геометричен и механичен смисъл на производната. Допирателна към графиката на функцията. Приложение на производната за изследване на функциите.
Анализирайте какви задачи са ви причинили затруднения?
Какви теоретични въпроси трябва да знаете?
IV. Онлайн тестване по задачи №14 (ОСНОВА)Анализ на резултатите от теста.
Сайт за тестване в урока:http://www.mathb-ege.sdamgia.ru/
Кой не е правил грешки?
Кой изпитва затруднения при тестването? Защо?
В какви задачи са допуснати грешки?
Заключение, какви теоретични въпроси трябва да знаете?
Индивидуално – диференцирана работа по двойки. Самостоятелно решаване на задачи №12. (ПРОФИЛ)Взаимна проверка.(Приложение № 3)
Запомнете алгоритъма за решаване на задачи №12 от изпита за намиране на точки на екстремум, екстремуми на функция, най-голямата и най-малката стойност на функция на интервала с помощта на производната.
Решаване на задачи с производна
Студентите са изправени пред проблем:
„Помислете, възможно ли е да решите някои задачи № 12 по различен начин, без да използвате производна?“
1 чифт
2 чифта
3 чифта
4 чифта
(Учениците защитават своето решение, като пишат основните стъпки за решаване на задачи на дъската. Учениците предлагат два начина за решаване на задача № 2).
Решение на проблем. Заключение за учениците:
„Някои задачи No12 от изпита за намиране на най-малката и най-голямата стойност на функция могат да бъдат решени без да се използва производната, като се разчита на свойствата на функциите.“
Анализирайте каква грешка сте допуснали в задачата?
Какви теоретични въпроси трябва да повторите?
V. Проверка на индивидуална домашна работа. (Слайдове 7-8, Приложение No2)
Вегелман В. получи индивидуална домашна работа: от наръчниците за подготовка за изпит номер 18.
(Студентът дава решението на задачата, разчитайки на функционално-графичния метод, като един от методите за решаване на задачи No 18 от изпита и дава кратко обяснение на този метод).
VII. Индивидуално - диференцирана домашна работа
(Слайд 9, Приложение No2), (Приложение № 4).
Подготвил съм списък с интернет сайтове за подготовка за изпита. Можете също да направите онлайн тестване на тези сайтове. За следващия урок трябва: 1) да прегледате теоретичния материал по темата „Производна на функция“;
2) на сайта „Отворена банка от задачи по математика“ (http://mathege.ru/ ) намерете прототипи на задачи № 14 ОСНОВА И № 7 и 12 ПРОФИЛ и решите поне 10 задачи ПРОФИЛ;
3) В. Вегелман, решаване на задачи с параметри (ПРИЛОЖЕНИЕ 4). задачи 1-8 (вариант 1).ОСНОВНО НИВО НА
VIII. Оценки от урока.
Как бихте оценили себе си за урок?
Мислите ли, че бихте могли да се справите по-добре в урока?
IX. Резюме на урока. Отражение
Нека обобщим нашата работа. Каква беше целта на урока? Смятате ли, че е постигнато?
Погледнете дъската и с едно изречение, като изберете началото на фразата, продължете с изречението, което ви подхожда най-добре.
Почувствах…
Научих…
успях…
Можах да ...
Ще опитам …
Бях изненадан от това …
Исках…
Можете ли да кажете, че по време на урока е имало обогатяване на запаса ви от знания?
И така, повторихте теоретичните въпроси за производната на функцията, приложихте знанията си при решаването на прототипите на задачите USE (№ 14 ОСНОВНО НИВО № 7,12 ПРОФИЛНО НИВО), а В. Вегелман изпълни задача № 18 с параметър, който е задача с повишена степен на трудност.
За мен беше удоволствие да работя с вас и се надявам, че ще можете успешно да приложите знанията, придобити в уроците по математика, не само при полагане на Единния държавен изпит, но и в по-нататъшното си обучение.
Бих искал да завърша урока с думите на италиански философТома Аквински„Знанието е толкова ценно нещо, че не е срамно да се получи от какъвто и да е източник.“(Слайд 10, Приложение № 2).
Желая ти успех в подготовката за изпита!
Визуализация:
За да използвате визуализацията на презентации, създайте си акаунт в Google (акаунт) и влезте в него: https://accounts.google.com
Надписи на слайдове:
Подготовка за изпита СИМУЛАТОР на тема "Производна" Задача номер 14 основно ниво, номер 7, 12 профилно ниво
f (x) f / (x) x Фигурата показва графиката на производната на функцията y = f (x), посочена на интервала (- 8; 8). Нека проучим свойствата на графиката и ще можем да отговорим на много въпроси относно свойствата на функцията, въпреки че графиката на самата функция не е представена! y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 -1 -2 -3 -4 -5 yx 6 3 0 -5 Намерете точки където f / (x) = 0 (това са нулите на функцията). + - - + +
ЗАДАНИЕ № 14 Основно ниво по математика
Фигурата показва графиката на функцията y = f (x) и точките A, B, C и D са отбелязани по оста Ox. С помощта на графиката задайте на всяка точка характеристиките на функцията и нейната производна. ABCD 1) стойността на функцията в точката е отрицателна, а стойността на производната на функцията в точката е положителна 2) стойността на функцията в точката е положителна, а стойността на производната на функцията в точката е отрицателна 3) стойността на функцията в точката е отрицателна, а стойността на производната на функцията в точката е отрицателна 4) стойността на функцията в точката е положителна, а стойността на производната на функцията в точката е положителна
№ 1 Фигурата показва графиката на функцията y = f (x) и маркираните точки A, B, C и D по оста Ox. С помощта на графиката задайте на всяка точка характеристиките на функцията и нейната производна. 1) стойността на функцията в точката е положителна, а стойността на производната на функцията в точката е отрицателна 2) стойността на функцията в точката е отрицателна, а стойността на производната на функцията в точката точката е отрицателна 3) стойността на функцията в точката е положителна, а стойността на производната на функцията в точката е положителна 4) стойността на функцията в точката е отрицателна, а стойността на производната на функцията в точката е положителна ABCD
Фигурата показва графиката на функцията y = f (x). Точки a, b, c, d и e определят интервали по оста Ox. С помощта на графиката задайте на всеки интервал характеристиката на функцията или нейната производна. A) (a; b) B) (b; c) C) (c; d) D) (d; д) 1) стойностите на функцията са положителни във всяка точка от интервала 2) стойностите на производната на функцията са отрицателни във всяка точка от интервала 3) стойностите на производната на функцията са положителни във всяка точка от интервала 4) стойностите на функцията са отрицателни във всяка точка от интервала
Фигурата показва графиката на функцията y = f (x). Числата a, b, c, d и e определят интервалите по оста Ox. С помощта на графиката задайте на всеки интервал характеристиката на функцията или нейната производна. A) (a; b) B) (b; c) C) (c; d) D) (d; д) 1) стойностите на функцията са положителни във всяка точка от интервала 2) стойностите на функцията са отрицателни във всяка точка от интервала 3) стойностите на производните функции са отрицателни във всяка точка от интервала 4) стойностите на производната на функцията са положителни във всяка точка от интервала
Фигурата показва графика на функция и допирателните, начертани към нея в точки с абсциси A, B, C и D. A B C D 1) - 1,5 2) 0,5 3) 2 4) - 0,3
Фигурата показва графика на функция и допирателните, начертани към нея в точки с абсциси A, B, C и D. A B C D 1) 23 2) - 12 3) - 113 4) 123
ЗАДАНИЕ номер 7 Математически профил ниво
Задачи за геометричния смисъл на производната
1) Фигурата показва графиката на функцията y = f (x) и допирателната към нея в точката с абсцисата x 0. Намерете стойността на производната в точката x 0. -2 -0,5 2 0,5 Помислете! Мисля! Точно така! Мисля! x 0 Геометрично значение на производната: k = tg α Ъгълът на наклона на допирателната към оста Ox е тъп, така че k
5 11 8 2) Непрекъснатата функция y = f (x) се задава на интервала (-6; 7). Фигурата показва нейната графика. Намерете броя на точките, в които допирателната към графиката на функцията е успоредна на правата y = 6. Проверка на y = f (x) y x 3 Помислете! Мисля! Мисля! Точно така! - 6 7 у = 6. Точка на пречупване. В този момент производната НЕ съществува! О -4 3 5 1, 5
Задачи за определяне характеристиките на функция от графиката на нейната производна
3) Фигурата показва графиката на производната на функцията y = f / (x), дадена на интервала (- 6; 8). Разгледайте функцията y = f (x) за екстремум и посочете броя на нейните екстремални точки. 2 1 4 5 Грешно! Не е вярно! Точно така! Не е вярно! Проверка (2) f (x) f / (x) -2 + - y = f / (x) 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 4 3 2 1 - 1 -2 -3 -4 -5 yx -5 + min max О
4 -3 -2 -1 1 2 3 4 5 x 5) Фигурата показва графиката на производната на функция, посочена в интервала [-5; 5]. Проверете функцията за монотонност и посочете най-голямата максимална точка. 3 2 4 5 Помислете! Мисля! Точно така! Мисля! y = f / (x) + + + - - О - f / (x) - + - + - + f (x) -4 -2 0 3 4 От двете максимални точки, най-големият x max = 3 max max г
7) Фигурата показва графиката на производната на функцията. Намерете дължината на нарастващия интервал на тази функция. Проверете O -7 -6 -5 -4 -3 -2 -1 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 -7 4 2 3 5 МИСЛЕТЕ! + МИСЛЕТЕ! ТОЧНО! МИСЛЯ! y x 3 y = f / (x)
4 -3 -2 -1 1 2 3 4 5 x 6) Фигурата показва графиката на производната на функция, множество в интервала [-5; 5]. Разгледайте функцията y = f (x) за монотонност и посочете броя на интервалите на намаляване. 3 2 4 1 Помислете! Мисля! Точно така! Мисля! y = f / (x) f (x) -4 -2 0 4 f / (x) - + - + - + + О - - - y
Задачи за определяне характеристиките на графична производна на функция.
Фигурата показва графиката на диференцируемата функция y = f (x). На абсцисата са отбелязани девет точки: x 1, x 2, ..., x 9. Намерете всички маркирани точки, в които производната на функцията f (x) е отрицателна. В отговора посочете броя на тези точки.
Фигурата показва графиката на функцията y = f (x), дефинирана на интервала (a; b). Определете броя на цели точки, в които производната на функцията е положителна. а) б) Решете сами! Решение. ако се увеличи. Цели решения за: x = -2; х = -1; х = 5; х = 6. Броят им е 4. Цели решения за: x = 2; х = 3; х = 4; х = 10; х = 11. Броят им е 5. Отговор: 4. Отговор: 5.
Задачи за физическия смисъл на производната
Отговор: 3 Отговор: 14
ЗАДАНИЕ номер 12 Математически профил ниво
Самостоятелна работа по двойки Задача номер 12 Профилно ниво
Визуализация:
Приложение 3 индивидуални карти No12
1. Намерете максималната точка на функцията1 Намерете минималната точка на функцията
2. Намерете максималната точка на функцията 2 Намерете минималната точка на функцията
2 Намерете минималната точка на функцията
Линик Д. Вовненко И
1. Намерете най-малката стойност на функцията 1. Намерете най-голямата стойност на функцията
1. Намерете най-голямата стойност на функцията на сегмента
на сегмента 
на сегмента 


Вегелман В.
А.
1. Намерете максималната точка на функцията 1. Намерете минималната точка на функцията
1. Намерете минималната точка на функцията
2. Намерете най-малката стойност на функцията 2. Намерете най-голямата стойност на функцията
2. Намерете най-голямата стойност на функцията на сегмента
на сегмента 
На сегмента 
Леонтьева А. Исаенко К.
ПРАКТИКА ИЗВЪН ОДИТ 2
Преобразуване на функционални графики.
Цел
Конструирайте графики на функции, използвайки различни трансформации, отговорете на въпроса на задачата.
Завършване на работата
Методически указания
Работата е предназначена за 10 варианта, номерът на варианта съвпада с последната цифра на серийния номер в списъка. Например, 1, 11, 21, 31 ... изпълнете 1 опция, 2,12, 22 ... - 2 опция и т.н.
Работата се състои от две части: първата част на задачата 1 - 5, това са задачи, които трябва да бъдат изпълнени, за да получите кредит, ако тези задачи са изпълнени с грешка, те трябва да бъдат коригирани и работата трябва да бъде изпратена отново за проверка. Втората част съдържа задачи, изпълнявайки които можете да спечелите допълнителна оценка: основната част +2 задачи - "4", основната част +3 задачи - "5".
Задача 1. Графиката на линейна функция е права линия, две точки са достатъчни, за да се начертае. (взимаме стойностите на аргумента x произволно, а стойността на функцията y броим, като я заместваме във формулата).
За да проверите дали графиката на функцията минава през определената точка, трябва да замените координатите на точката вместо x и y, ако получите правилно равенство, тогава правата линия минава през определената точка, в противен случай не .
Задача 2, 3, 4. Графиките на посочените функции се получават от графиките на функциите , използвайки изместване по оста x или y.
![]() , първо начертаваме функцията или , след това го изместваме с единици "a" надясно или наляво (+ a - наляво, - и надясно), след това го изместваме с "c" единици нагоре или надолу (+ b - нагоре, -b - надолу)
, първо начертаваме функцията или , след това го изместваме с единици "a" надясно или наляво (+ a - наляво, - и надясно), след това го изместваме с "c" единици нагоре или надолу (+ b - нагоре, -b - надолу)
По същия начин и с други функции:
Задача 5 За да начертаете графика на функцията: , трябва да: 1) начертаете функцията , 2) оставят частта от графиката, която е над оста x, непроменена, 3) отразява частта от графиката, която е под оста x.
Задачи за самостоятелно решение.
Задължителна част
Задача 1. Начертайте графика на линейна функция, определете дали графиката на функцията преминава през определената точка:

Задача 2. Начертайте графика на квадратична функция, посочете набора от стойности за тази функция.

Задача 3. Изградете графика на функцията, определете дали посочената функция се увеличава или намалява.

Задача 4. Изградете графика на функцията, отговорете на въпроса на задачата.

Задача 5. Начертайте графиката на функцията, съдържаща знака за модул.

Задачи за допълнителна оценка.
Задача 6. Начертайте графика на дадена функция на парчета, определете дали има точка на прекъсване за тази функция:


Задача 7. Определете колко решения има системата от уравнения, отговорът е да се обоснове. Направете изводи, като отговорите на въпросите.
Какви функции сте начертали в тази работа?
Как се казва графиката на линейна функция?
Как се казва графиката на квадратична функция?
Какви графични трансформации познавате?
Как се намира графиката на четна функция в координатната система? Графика на странна функция?
Производната на функцията $ y = f (x) $ в дадена точка $ x_0 $ е границата на съотношението на увеличението на функцията към съответното увеличение на нейния аргумент, при условие че последният клони към нула:
$ f "(x_0) = (lim) ↙ (△ x → 0) (△ f (x_0)) / (△ x) $
Диференцирането е операцията за намиране на производна.
Таблица с производни на някои елементарни функции
| Функция | Производна |
| $ c $ | $0$ |
| $ x $ | $1$ |
| $ x ^ n $ | $ nx ^ (n-1) $ |
| $ (1) / (x) $ | $ - (1) / (x ^ 2) $ |
| $ √x $ | $ (1) / (2√x) $ |
| $ e ^ x $ | $ e ^ x $ |
| $ lnx $ | $ (1) / (x) $ |
| $ sinx $ | $ cosx $ |
| $ cosx $ | $ -sinx $ |
| $ tgx $ | $ (1) / (cos ^ 2x) $ |
| $ ctgx $ | $ - (1) / (sin ^ 2x) $ |
Основни правила за диференциация
1. Производната на сбора (разликата) е равна на сбора (разликата) на производните
$ (f (x) ± g (x)) "= f" (x) ± g "(x) $
Намерете производната на функцията $ f (x) = 3x ^ 5-cosx + (1) / (x) $
Производната на сбора (разликата) е равна на сбора (разликата) от производните.
$ f "(x) = (3x ^ 5)" - (cos x) "+ ((1) / (x))" = 15x ^ 4 + sinx - (1) / (x ^ 2) $
2. Производна на произведението
$ (f (x) g (x)) "= f" (x) g (x) + f (x) g (x) "$
Намерете производната $ f (x) = 4x cosx $
$ f "(x) = (4x)" cosx + 4x (cosx) "= 4 cosx-4x sinx $
3. Производна на частното
$ ((f (x)) / (g (x))) "= (f" (x) g (x) -f (x) g (x) ") / (g ^ 2 (x)) $
Намерете производната $ f (x) = (5x ^ 5) / (e ^ x) $
$ f "(x) = ((5x ^ 5)" e ^ x-5x ^ 5 (e ^ x) ") / ((e ^ x) ^ 2) = (25x ^ 4 e ^ x- 5x ^ 5 e ^ x) / ((e ^ x) ^ 2) $
4. Производната на сложна функция е равна на произведението на производната на външната функция на производната на вътрешната функция
$ f (g (x)) "= f" (g (x)) g "(x) $
$ f "(x) = cos" (5x) · (5x) "= - sin (5x) · 5 = -5sin (5x) $
Физическото значение на производната
Ако материална точка се движи праволинейно и координатите й се променят в зависимост от времето според закона $ x (t) $, тогава моментната скорост на тази точка е равна на производната на функцията.
Точката се движи по координатната линия по закона $ x (t) = 1,5t ^ 2-3t + 7 $, където $ x (t) $ е координатата в момента $ t $. В кой момент от времето скоростта на точката ще бъде равна на $12 $?
1. Скоростта е производна на $ x (t) $, така че намираме производната на дадената функция
$ v (t) = x "(t) = 1,5 · 2t -3 = 3t -3 $
2. За да намерите в кой момент $ t $ скоростта е била равна на $ 12 $, съставете и решете уравнението:
Геометричното значение на производната
Припомнете си, че уравнението на права линия, която не е успоредна на координатните оси, може да се запише във формата $ y = kx + b $, където $ k $ е наклонът на правата линия. Коефициентът $ k $ е равен на тангенса на ъгъла на наклон между правата линия и положителната посока на оста $ Ox $.
Производната на функцията $ f (x) $ в точката $ x_0 $ е равна на наклона $ k $ на допирателната към графиката в тази точка:
Следователно можем да съставим общо равенство:
$ f "(x_0) = k = tgα $
На фигурата допирателната към функцията $ f (x) $ се увеличава, следователно коефициентът $ k> 0 $. Тъй като $ k> 0 $, то $ f "(x_0) = tgα> 0 $. Ъгълът $ α $ между допирателната и положителната посока $ Ox $ е остър.
На фигурата допирателната към функцията $ f (x) $ намалява, следователно коефициентът $ k< 0$, следовательно, $f"(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
На фигурата допирателната към функцията $ f (x) $ е успоредна на оста $ Ox $, следователно, коефициентът $ k = 0 $, следователно, $ f "(x_0) = tan α = 0 $. точка $ x_0 $, в която $ f "(x_0) = 0 $, извикано екстремни.
Фигурата показва графиката на функцията $ y = f (x) $ и допирателната към тази графика, начертана в точката с абсцисата $ x_0 $. Намерете стойността на производната на функцията $ f (x) $ в точката $ x_0 $.
Допирателната към графиката се увеличава, следователно, $ f "(x_0) = tg α> 0 $
За да намерите $ f "(x_0) $, намерете тангенса на ъгъла на наклон между допирателната и положителната посока на оста $ Ox $. За да направите това, добавете допирателната към триъгълника $ ABC $.
Намерете тангенса на ъгъла $ BAC $. (Тангенсът на остър ъгъл в правоъгълен триъгълник е съотношението на противоположния катет към съседния катет.)
$ tg BAC = (BC) / (AC) = (3) / (12) = (1) / (4) = 0,25 $
$ f "(x_0) = tg BAC = 0,25 $
Отговор: $0,25
Производната се използва и за намиране на интервалите на нарастващи и намаляващи функции:
Ако $ f "(x)> 0 $ в интервала, тогава функцията $ f (x) $ се увеличава в този интервал.
Ако $ f "(x)< 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
Фигурата показва графиката на функцията $ y = f (x) $. Намерете сред точките $ x_1, x_2, x_3… x_7 $ тези точки, в които производната на функцията е отрицателна.
В отговор запишете броя на дадените точки.
В задача номер 13 на USE по математика от основно ниво ще трябва да демонстрирате уменията и знанията за една от концепциите за поведението на функция: производни в точка или скорости на нарастване или намаляване. Теорията ще бъде добавена към тази задача малко по-късно, но това не ни пречи да анализираме подробно няколко типични варианта.
Анализ на типични варианти за задачи № 14 от ЕГЭ по математика от основно ниво
Опция 14MB1
Графиката показва зависимостта на температурата от времето при загряване на двигател на лек автомобил. Хоризонталната ос показва времето в минути, изминало от стартирането на двигателя; вертикалната ос е температурата на двигателя в градуси по Целзий.

С помощта на графиката задайте на всеки интервал от време характеристиката на процеса на загряване на двигателя в този интервал.
В таблицата под всяка буква посочете съответното число.
Алгоритъм за изпълнение:
- Изберете интервала от време, през който температурата пада.
- Нанесете линийка до 30 ° C и определете интервала от време, през който температурата е била под 30 ° C.
Решение:
Нека изберем интервала от време, през който температурата пада. Тази област се вижда с невъоръжено око, започва 8 минути от момента на стартиране на двигателя.
Нанесете линийка до 30 ° C и определете интервала от време, в който температурата е била под 30 ° C.

Под линийката ще има секция, съответстваща на интервала от време 0 - 1 min.
С помощта на молив и линийка ще открием в какъв интервал от време температурата е била в диапазона от 40 ° С до 80 ° С.
Нека пропуснем перпендикулярите от точките, съответстващи на 40°C и 80°C на графиката, а от получените точки ще пропуснем перпендикулярите на оста на времето.

Виждаме, че този температурен интервал съответства на интервал от време от 3 - 6,5 минути. Тоест от дадените в условието 3 - 6 минути.
Използваме метода на елиминиране, за да изберем липсващия отговор.
Опция 14MB2
Решение:
Нека анализираме графиката на функция A. Ако функцията се увеличава, тогава производната е положителна и обратно. Производната на функцията е равна на нула в точките на екстремум.
Първо, функцията А се увеличава, т.е. производната е положителна. Това съответства на графиките на производни 2 и 3. В максималната точка на функцията x = -2, тоест в тази точка производната трябва да е нула. Това условие е изпълнено от графика номер 3.
Първо, функция B намалява, т.е. производната е отрицателна. Това съответства на графиките на производни 1 и 4. Максималната точка на функцията е x = -2, тоест в тази точка производната трябва да е равна на нула. Това условие е изпълнено от графика номер 4.
Първо, функцията B се увеличава, т.е. производната е положителна. Това съответства на графиките на производни 2 и 3. Максималната точка на функцията x = 1, тоест в тази точка производната трябва да е равна на нула. Това условие е изпълнено от графика номер 2.
По метода на елиминиране можем да определим, че графиката на функцията Γ съответства на графиката на производната под номер 1.
Отговор: 3421.
Опция 14MB3
Алгоритъм за изпълнение на всяка от функциите:
- Определете интервалите на нарастващи и намаляващи функции.
- Определете максималната и минималната точка на функциите.
- Направете заключения, съгласувайте предложените графици.
Решение:
Нека анализираме графиката на функцията A.
Ако функцията се увеличава, тогава производната е положителна и обратно. Производната на функцията е равна на нула в точките на екстремум.
Точката на екстремум е точката, в която се достига максималната или минималната стойност на функция.
Първо, функцията А се увеличава, т.е. производната е положителна. Това съответства на графиките на производни 3 и 4. В максималната точка на функцията x = 0, тоест в тази точка производната трябва да е равна на нула. Това условие е изпълнено от графика номер 4.
Нека анализираме графиката на функция B.
Първо, функция B намалява, т.е. производната е отрицателна. Това съответства на графиките на производни 1 и 2. Минималната точка на функцията е x = -1, тоест в тази точка производната трябва да е равна на нула. Това условие е изпълнено от графика номер 2.
Нека анализираме графиката на функция B.
Първо, функция B намалява, т.е. производната е отрицателна. Това съответства на графиките на производни 1 и 2. Минималната точка на функцията x = 0, тоест в тази точка производната трябва да е равна на нула. Това условие е изпълнено от графика номер 1.
По метода на елиминиране можем да определим, че графиката на функцията Γ съответства на графиката на производната под номер 3.
Отговор: 4213.
Опция 14MB4
Фигурата показва графика на функция и допирателните, начертани към нея в точки с абсциси A, B, C и D.Дясната колона показва стойностите на производната в точки A, B, C и D. Използвайки графиката, задайте на всяка точка стойността на производната на функцията в нея.

ТОЧКИ
А
V
С
д
СТОЙНОСТИТЕ НА ПРОИЗВОДНАТА
1) –4
2) 3
3) 2/3
4) -1/2
Нека си припомним какво означава производната, а именно нейната стойност в точката - стойността на производната функция в точка е равна на допирателната на наклона (коефициента) на допирателната.
В отговорите имаме два положителни и два отрицателни варианта. Както си спомняме, ако коефициентът на права линия (графика y = kx + b) положителен, тогава правата се увеличава, ако е отрицателна, тогава правата намалява.
Имаме две възходящи прави линии - в точки A и D. Сега нека си спомним какво означава стойността на коефициента k?
Коефициентът k показва колко бързо се увеличава или намалява функцията (всъщност самият коефициент k е производна на функцията y = kx + b).
Следователно k = 2/3 съответства на по-плоска линия - D, а k = 3 - A.
По същия начин, в случай на отрицателни стойности: точка B съответства на по-стръмна права линия с k = - 4, а точка C - -1/2.
Опция 14MB5
На фигурата точките показват месечните продажби на нагреватели в магазина за домакински уреди. Месеците са показани хоризонтално, а броят на продадените нагреватели – вертикално. За по-голяма яснота точките са свързани с линия.

Използвайки фигурата, съпоставете всеки от посочените периоди от време с характеристика на продажбите на нагревателите.

Алгоритъм за изпълнение
Анализираме частите от графиката, съответстващи на различните сезони. Формулираме ситуациите, показани на графиката. Намираме най-подходящите варианти за отговор за тях.
Решение:
През зимата броят на продажбите надхвърли 120 бр./месец и непрекъснато се увеличаваше. Тази ситуация съответства на отговор номер 3. Тези. получаваме: А – 3.
През пролетта продажбите постепенно паднаха от 120 нагреватели на месец до 50. Вариант 2 е най-близък до тази формулировка. Ние имаме: Б – 2.
През лятото броят на продажбите не се промени и беше минимален. Втората част от тази формулировка не е отразена в отговорите и само #4 е подходяща за първата. Следователно имаме: В 4.
През есента продажбите нараснаха, но броят им в нито един от месеците не надхвърли 100 бройки. Тази ситуация е описана във вариант №1. Получаваме: G – 1.
Опция 14MB6
Графиката показва зависимостта на скоростта на обикновен автобус от времето. По вертикалната ос скоростта на автобуса е отбелязана в km/h, по хоризонталната ос - времето в минути от началото на движението на автобуса.
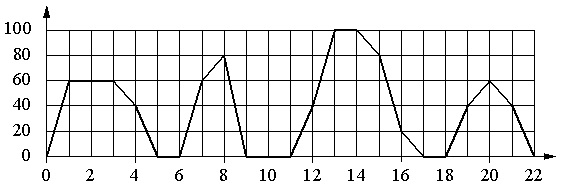
С помощта на графиката задайте на всеки времеви интервал характеристиката на движението на автобуса в този интервал.

Алгоритъм за изпълнение
- Определете цената на разделяне на хоризонталната и вертикалната скала.
- Анализираме на свой ред предложените твърдения 1–4 от дясната колона („Характеристики“). Сравняваме ги с интервалите от време от лявата колона на таблицата, намираме двойките „буква-число“ за отговора.
Решение:
Делението по хоризонталната скала е 1 s, а по вертикалата е 20 km/h.
- Когато автобусът спре, скоростта му е 0. Автобусът имаше нулева скорост за 2 минути подред само от 9-та до 11-та минута. Това време попада в интервала от 8-12 минути. И така, имаме двойка за отговора: Б – 1.
- Автобусът е имал скорост от 20 км/ч и повече за няколко интервала от време. Освен това тук вариант А не е подходящ, защото например на 7-та минута скоростта беше 60 км/ч, вариант Б - защото вече е приложен, вариант D - защото в началото и края на интервала автобусът имаше нулева скорост... В този случай е подходящ вариант Б (12–16 минути); на този интервал автобусът започва да се движи със скорост 40 км/ч, след това ускорява до 100 км/м и след това постепенно намалява скоростта до 20 км/ч. И така, имаме: В 2.
- Ограничението на скоростта е зададено тук. В същото време не разглеждаме варианти B и C. Останалите интервали A и D са подходящи. Следователно би било правилно да разгледаме първо 4-ия вариант и след това отново да се върнем към 3-ия.
- От останалите два интервала само 4–8 минути са подходящи за характеристика № 4, тъй като на този интервал (на 6-та минута) имаше спиране. Нямаше спирания в интервала от 18-22 минути. Получаваме: А – 4... Оттук следва, че за характеристика No3 е необходимо да се вземе интервала Г, т.е. оказва се двойка G – 3.
Опция 14MB7
Цифрата с точка показва увеличението на населението на Китай от 2004 до 2013 г. Хоризонтално показва годината, вертикално - прираст на населението като процент (нарастване на населението спрямо миналата година). За по-голяма яснота точките са свързани с линия.

Използвайки фигурата, съпоставете всеки от посочените периоди от време с характеристиките на растежа на населението на Китай през този период..

Алгоритъм за изпълнение
- Определете цената на разделяне на вертикалния мащаб на картината. Намира се като разлика между двойка съседни стойности на скалата, разделена на 2 (тъй като има 2 деления между две съседни стойности).
- Анализираме последователно характеристиките 1–4, дадени в условието (лява колона на таблицата). Сравняваме всеки от тях с определен период от време (дясна колона на таблицата).
Решение:
Вертикалното деление на скалата е 0,01%.
- Спадът в растежа продължи непрекъснато от 2004 до 2010 г. През 2010–2011 г. растежът е стабилно минимален, а от 2012 г. започва да се увеличава. Тези. растежът спря през 2010 г. Тази година е в периода 2009-2011 г. Съответно имаме: В 1.
- „Най-стръмната“ падаща линия на графиката на фигурата трябва да се счита за най-големия спад в растежа. Той попада в периода 2006-2007 г. и е 0,04% годишно (0,59-0,56 = 0,04% през 2006 г. и 0,56-0,52 = 0,04% през 2007 г.). От тук получаваме: А – 2.
- Ръстът, посочен в характеристика № 3, започва през 2007 г., продължава през 2008 г. и приключва през 2009 г. Това съответства на период от време В, т.е. ние имаме: Б – 3.
- Прирастът на населението започва да нараства след 2011 г., т.е. през 2012–2013 г Следователно получаваме: G-4.
Опция 14MB8
Фигурата показва графика на функция и допирателните, начертани към нея в точки с абсциси A, B, C и D.

Дясната колона показва стойностите на производната на функцията в точки A, B, C и D. Използвайки графиката, задайте на всяка точка стойността на производната на функцията в нея.

Алгоритъм за изпълнение
- Помислете за двойка допирателни, имащи остър ъгъл с положителната посока на оста на абсцисата. Сравняваме ги, намираме съвпадение между двойката съответни стойности на производните.
- Помислете за двойка допирателни, образуващи тъп ъгъл с положителната посока на оста на абсцисата. Сравняваме ги по абсолютна стойност, определяме съответствието им със стойностите на производните сред двете останали в дясната колона.
Решение:
Остър ъгъл с положителна посока на оста на абсцисата се образува от производни в точка B и точка C. Тези производни имат положителни стойности. Следователно, тук трябва да избирате между стойности № 1 и 3. Прилагайки правилото, че ако ъгълът е по-малък от 45 0, тогава производната е по-малка от 1, а ако е повече, тогава повече от 1, заключаваме: в точка B, производната по модул е по-голяма от 1, в точка C - по-малко от 1. Това означава, че можете да съставите двойки за отговора: В 3и С – 1.
Производните в точка A и точка D образуват тъп ъгъл с положителната посока на абсцисата. И тук прилагаме същото правило, като го перифразираме малко: колкото повече допирателната в точката е "притисната" към линията на оста на абсцисата (към нейната отрицателна посока), толкова по-голяма е тя в абсолютна стойност. Тогава получаваме: производната в точка А е по-малка по абсолютна стойност от производната в точка D. Следователно имаме двойки за отговора: А – 2и Г – 4.
Опция 14MB9
На фигурата точките показват средната дневна температура на въздуха в Москва през януари 2011 г. Хоризонтално показва деня от месеца, вертикално - температурата в градуси по Целзий. За по-голяма яснота точките са свързани с линия.

Използвайки фигурата, съпоставете всеки от посочените периоди от време с характеристиката на температурната промяна.

Алгоритъм за изпълнение
Анализираме последователно характеристики 1-4 (дясна колона), като използваме графиката на фигурата. Ние поставяме всеки от тях в съответствие с определен период от време (лява колона).
Решение:
- Повишаване на температурата се наблюдава едва в края на периода 22–28 януари. Тук на 27 и 28 се увеличи съответно с 1 и 2 градуса. В края на периода 1–7 януари температурата беше стабилна (–10 градуса), в края на 8–14 и 15–21 януари тя се понижи (от –1 до –2 и от –11 до – 12 градуса, съответно). Следователно получаваме: G – 1.
- Тъй като всеки период от време обхваща 7 дни, температурата трябва да се анализира от 4-ия ден на всеки период. Температурата остава непроменена за 3-4 дни само от 4 до 7 януари. Следователно получаваме отговора: А – 2.
- Месечната минимална температура се наблюдава на 17 януари. Това число е в периода 15-21 януари. От тук имаме двойка: В 3.
- Температурният максимум падна на 10 януари и достигна +1 градус. Тази дата е между 8-14 януари. Следователно имаме: Б – 4.
Опция 14MB10
Алгоритъм за изпълнение
- Стойността на функцията в точка е положителна, ако тази точка е разположена над оста Ox.
- Производната в точка е по-голяма от нула, ако допирателната към тази точка образува остър ъгъл с положителната посока на оста Ox.
Решение:
Точка А. Намира се под оста Ox, което означава, че стойността на функцията в нея е отрицателна. Ако начертаете допирателна в нея, тогава ъгълът между нея и положителната посока Ox ще бъде около 90 0, т.е. образува остър ъгъл. Така че в този случай е подходяща характеристика номер 3. Тези. ние имаме: А – 3.
Точка Б. Намира се над оста Ox, т.е. точка има положителна стойност на функцията. Допирателната линия в тази точка ще бъде доста близо до оста на абсцисата, образувайки тъп ъгъл (малко по-малко от 180 0) с положителната си посока. Съответно, производната в този момент е отрицателна. Следователно тук е подходяща характеристика 1. Получаваме отговора: В 1.
Точка C. Точката се намира под оста Ox, допирателната в нея образува голям тъп ъгъл с положителната посока на оста на абсцисата. Тези. в точка C стойността както на функцията, така и на производната е отрицателна, което съответства на характеристика No2. Отговор: В – 2.
Точка D. Точката е над оста Ox, а допирателната в нея образува остър ъгъл с положителната посока на оста. Това предполага, че както стойността на функцията, така и стойността на производната тук са по-големи от нула. Отговор: Г – 4.
Опция 14MB11
На фигурата точките показват месечните продажби на хладилници в магазина за домакински уреди. Месеците се показват хоризонтално, а броят на продадените хладилници - вертикално. За по-голяма яснота точките са свързани с линия.
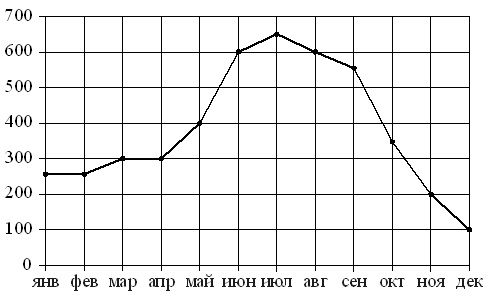
Използвайки фигурата, съпоставете всеки от посочените периоди от време с характеристика на продажбите на хладилниците..

































