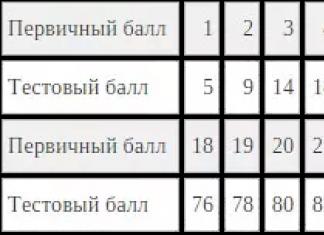
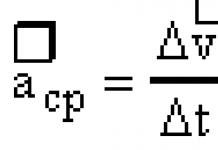цели:

1. Общообразователна: да систематизира, обобщи, разшири знанията и уменията на учениците, свързани с прилагането на методи за решаване на неравенства.
2. Развиващо: да се развие у учениците способността да слушат лекция, като я записват накратко в тетрадка.
3. Образователна: за формиране на познавателна мотивация за изучаване на математика.

По време на занятията

I. Встъпителен разговор:

Приключихме темата „Решаване на ирационални уравнения“ и днес започваме да се учим как да решаваме ирационални неравенства.

Първо, нека си спомним какви видове неравенства можете да решите и с какви методи?

Отговор: Линеен, квадратен, рационален, тригонометричен. Решаваме линейни въз основа на свойствата на неравенствата, свеждаме тригонометричните до най-простите тригонометрични, решени с помощта на тригонометричен кръг, а останалите, главно по метода на интервалите.

Въпрос: На какво твърдение се основава методът на интервалите?

Отговор: На теорема, която гласи, че непрекъсната функция, която не изчезва на някакъв интервал, запазва знака си на този интервал.

II.Нека разгледаме ирационално неравенство като >

Въпрос: Възможно ли е да се приложи интервалният метод за решаването му?

Отговор: Да, тъй като функцията y =- непрекъснато включено D(y).

Решаваме това неравенство интервален метод .

Заключение: ние доста лесно решихме това ирационално неравенство чрез интервалния метод, като всъщност го сведохме до решаване на ирационално уравнение.

Нека се опитаме да решим още едно неравенство с този метод.

3)е (х)непрекъснато включен D(f)

4) Функционални нули:

• Дълго търсене D(f).
• Трудно е да се изчислят точките на прекъсване.

Възниква въпросът: „Има ли други начини за решаване на това неравенство?“.

Очевидно има и сега ще ги опознаем.

III.Така, тема днешната урок: „Методи за решаване на ирационални неравенства“.

Урокът ще се проведе под формата на лекция, тъй като учебникът не съдържа подробен анализ на всички методи. Затова нашата важна задача е да изготвим подробно резюме на тази лекция.

IV.Вече говорихме за първия метод за решаване на ирационални неравенства.

Това - интервален метод , универсален метод за решаване на всички видове неравенства. Но не винаги води до целта по кратък и прост начин.

V.Когато решавате ирационални неравенства, можете да използвате същите идеи като при решаването на ирационални уравнения, но тъй като простата проверка на решенията е невъзможна (в края на краищата решенията на неравенствата най-често са целочислени числови интервали), е необходимо да се използва еквивалентност.

Представяме схеми за решаване на основните видове ирационални неравенства метод на еквивалентни преходиот едно неравенство към система от неравенства.

2. По подобен начин се доказва, че

Нека напишем тези диаграми на референтната дъска. Помислете за доказателствата от тип 3 и 4 у дома, ще ги обсъдим в следващия урок.

Vi.Нека решим неравенството по нов начин.

Първоначалното неравенство е еквивалентно на набор от системи.

VII.И има трети метод, който често помага за решаването на сложни ирационални неравенства. Вече говорихме за него във връзка с неравенствата с модул. Това метод за заместване на функции (заместване с множител). Нека ви напомня, че същността на метода на заместване е, че разликата в стойностите на монотонните функции може да бъде заменена с разликата в стойностите на техните аргументи.

Помислете за ирационално неравенство на формата<,

това е -< 0.

На теория, ако p (x)нараства на някакъв интервал, към който принадлежат аи б, и а>б, след това неравенствата p(a) – p(b) > 0 и a-b> 0 са еквивалентни на Г (п), това е

VIII.Решаваме неравенството по метода на променящите се фактори.

Следователно това неравенство е еквивалентно на системата

По този начин видяхме, че използването на метода за замяна на фактори за намаляване на решението на неравенство до метода на интервалите значително намалява обема на работа.

IX.Сега, след като разгледахме трите основни метода за решаване на уравнения, нека направим самостоятелна работа със самопроверка.

Необходимо е да се изпълнят следните числа (според учебника на А. М. Мордкович): 1790 (а) - решаване_ по метода на_ еквивалентни преходи,_ 1791 (а) - решаване по метода на заместване на фактори. За решаване на ирационални неравенства, предлага се да се използват методите, анализирани преди това при решаване на ирационални уравнения:

• промяна на променливите;
• използване на ОДЗ;
• използване на свойствата на монотонност на функциите.

Завършването на изучаването на темата е тест.

Анализът на контролната работа показва:

• типичните грешки на слабите ученици, освен аритметичните и алгебричните, са неправилни еквивалентни преходи към система от неравенства;
• методът на заместване на фактори се използва успешно само от силни ученици.

Всяко неравенство, което включва функция под корена, се извиква ирационално. Има два вида такива неравенства:

В първия случай коренът е по-малък от функцията g (x), във втория - повече. Ако g(x) - постоянен, неравенството се опростява драстично. Моля, имайте предвид, че външно тези неравенства са много сходни, но техните схеми на решение са коренно различни.

Днес ще научим как да решаваме ирационални неравенства от първия тип - те са най-простите и разбираеми. Знакът за неравенство може да бъде строг или нестриктен. За тях е вярно следното твърдение:

Теорема. Всяко ирационално неравенство на формата

Еквивалентно на системата от неравенства:

Не е слаб? Нека да видим откъде идва такава система:

1. f (x) ≤ g 2 (x) - тук всичко е ясно. Това е първоначалното неравенство на квадрат;
2. f(x) ≥ 0 е ODZ на корена. Нека ви напомня: аритметичният квадратен корен съществува само от неотрицателенчисла;
3. g(x) ≥ 0 е обхватът на корена. Чрез квадратурата на неравенството изгаряме минусите. В резултат на това могат да се появят допълнителни корени. Неравенството g (x) ≥ 0 ги отрязва.

Много ученици "вървят на цикли" по първото неравенство на системата: f (x) ≤ g 2 (x) - и напълно забравят другите две. Резултатът е предвидим: грешно решение, загубени точки.

Тъй като ирационалните неравенства са доста сложна тема, нека анализираме 4 примера наведнъж. От елементарно до наистина сложно. Всички задачи се вземат от приемните изпити на Московския държавен университет. М. В. Ломоносов.

Примери за решаване на проблеми

Задача. Решете неравенството:

Имаме класика ирационално неравенство: f(x) = 2x + 3; g(x) = 2 е константа. Ние имаме:

Само две от трите неравенства остават до края на решението. Тъй като неравенството 2 ≥ 0 винаги важи. Нека пресечем останалите неравенства:

И така, x ∈ [−1,5; 0,5]. Всички точки са засенчени, защото неравенствата не са строги.

Задача. Решете неравенството:

Прилагаме теоремата:

Решаваме първото неравенство. За да направим това, ще отворим квадрата на разликата. Ние имаме:

2x 2 − 18x + 16< (x − 4) 2 ;
2x 2 − 18x + 16< x 2 − 8x + 16:
x 2 − 10x< 0;
x (x − 10)< 0;
x ∈ (0; 10).

Сега нека решим второто неравенство. Там също квадратен трином:

2x 2 − 18x + 16 ≥ 0;
x 2 − 9x + 8 ≥ 0;
(x − 8)(x − 1) ≥ 0;
x ∈ (−∞; 1]∪∪∪∪)