Πρόβλημα νούμερο 1
Η λογική είναι απλή: θα ενεργήσουμε όπως κάναμε πριν, παρά το γεγονός ότι τώρα οι τριγωνομετρικές συναρτήσεις έχουν πιο σύνθετο όρισμα!
Αν λύναμε μια εξίσωση της μορφής:
Έπειτα γράφουμε την εξής απάντηση:
Ή (αφού)
Αλλά τώρα έχουμε την εξής έκφραση στον ρόλο μας:
Τότε μπορείτε να γράψετε:
Στόχος μας μαζί σας είναι να κάνουμε την αριστερή στάση απλά, χωρίς «ακαθαρσίες»!
Ας τα ξεφορτωθούμε σταδιακά!
Αρχικά, αφαιρούμε τον παρονομαστή στο: για αυτό πολλαπλασιάζουμε την ισότητά μας με:
Τώρα ας το ξεφορτωθούμε χωρίζοντας και τα δύο μέρη σε αυτό:
Τώρα ας απαλλαγούμε από τα οκτώ:
Η παράσταση που προκύπτει μπορεί να γραφτεί ως 2 σειρές λύσεων (κατ' αναλογία με μια τετραγωνική εξίσωση, όπου είτε προσθέτουμε είτε αφαιρούμε τη διάκριση)
Πρέπει να βρούμε τη μεγαλύτερη αρνητική ρίζα! Είναι σαφές ότι είναι απαραίτητο να διευθετηθεί.
Εξετάστε πρώτα την πρώτη σειρά:
Είναι σαφές ότι αν πάρουμε, τότε ως αποτέλεσμα θα πάρουμε θετικούς αριθμούς και δεν μας ενδιαφέρουν.
Άρα πρέπει να το πάρεις αρνητικό. Αφήνω.
Όταν η ρίζα είναι ήδη:
Και πρέπει να βρούμε το μεγαλύτερο αρνητικό!! Σημαίνει ότι δεν έχει πλέον νόημα να πηγαίνουμε προς την αρνητική κατεύθυνση. Και η μεγαλύτερη αρνητική ρίζα για αυτή τη σειρά θα είναι.
Ας δούμε τώρα τη δεύτερη σειρά:
Και πάλι αντικαθιστούμε:, τότε:
Δεν ενδιαφέρομαι!
Τότε δεν έχει νόημα να αυξηθεί άλλο! Θα μειώσουμε! Ας, λοιπόν:
Ταιριάζει!
Αφήνω. Τότε
Τότε - η μεγαλύτερη αρνητική ρίζα!
Απάντηση:
Πρόβλημα νούμερο 2
Και πάλι λύνουμε, ανεξάρτητα από το μιγαδικό συνημίτονο:
Τώρα εκφράζουμε πάλι αριστερά:
Πολλαπλασιάζουμε και τις δύο πλευρές
Χωρίζουμε και τις δύο πλευρές
Το μόνο που μένει είναι να το μετακινήσετε προς τα δεξιά, αλλάζοντας το πρόσημά του από μείον σε συν.
Έχουμε πάλι 2 σειρές ρίζες, η μία με και η άλλη με.
Πρέπει να βρούμε τη μεγαλύτερη αρνητική ρίζα. Σκεφτείτε την πρώτη σειρά:
Είναι σαφές ότι θα λάβουμε την πρώτη αρνητική ρίζα στο, θα είναι ίση και θα είναι η μεγαλύτερη αρνητική ρίζα σε 1 σειρά.
Για τη δεύτερη σειρά
Η πρώτη αρνητική ρίζα θα ληφθεί επίσης στο και θα είναι ίση με. Αφού, τότε είναι η μεγαλύτερη αρνητική ρίζα της εξίσωσης.
Απάντηση: .
Πρόβλημα νούμερο 3
Λύστε ανεξάρτητα από το όρισμα μιγαδικής εφαπτομένης.
Δεν φαίνεται να είναι τίποτα περίπλοκο, σωστά;
Όπως και πριν, εκφράζουμε στην αριστερή πλευρά:
Λοιπόν, αυτό είναι υπέροχο, υπάρχει μόνο μία σειρά ριζών εδώ! Βρείτε ξανά το μεγαλύτερο αρνητικό.
Είναι ξεκάθαρο ότι αποδεικνύεται αν βάλουμε. Και αυτή η ρίζα είναι ίση.
Απάντηση:
Τώρα προσπαθήστε να λύσετε μόνοι σας τα παρακάτω προβλήματα.
Εργασίες για το σπίτι ή 3 εργασίες για μια ανεξάρτητη λύση.
- Αποφάσεις-shi-te εξίσωση.
- Αποφάσεις-shi-te εξίσωση.
Στο ot-ve-these na-pi-shi-te, το μικρότερο po-li-tel-root. - Αποφάσεις-shi-te εξίσωση.
Στο ot-ve-these na-pi-shi-te, το μικρότερο po-li-tel-root.
Ετοιμος? Ελεγχος. Δεν θα περιγράψω λεπτομερώς ολόκληρο τον αλγόριθμο λύσης, μου φαίνεται ότι έχει ήδη δοθεί αρκετή προσοχή σε αυτό παραπάνω.
Λοιπόν, είναι όλα σωστά; Ω, αυτά τα άσχημα ιγμόρεια, υπάρχουν πάντα κάποια προβλήματα μαζί τους!
Λοιπόν, τώρα μπορείτε να λύσετε τις πιο απλές τριγωνομετρικές εξισώσεις!
Ελέγξτε τις λύσεις και τις απαντήσεις:
Πρόβλημα νούμερο 1
Ας εκφραστούμε
Η μικρότερη θετική ρίζα προκύπτει αν βάλουμε, από τότε
Απάντηση:
Πρόβλημα νούμερο 2
Η μικρότερη θετική ρίζα λαμβάνεται όταν.
Θα είναι ίσο.
Απάντηση: .
Πρόβλημα νούμερο 3
Πότε παίρνουμε, πότε παίρνουμε.
Απάντηση: .
Αυτή η γνώση θα σας βοηθήσει να λύσετε πολλά από τα προβλήματα που θα αντιμετωπίσετε στις εξετάσεις.
Εάν κάνετε αίτηση για βαθμό "5", τότε απλά πρέπει να πάτε στην ανάγνωση του άρθρου για Μεσαίο επίπεδο,που θα αφιερωθεί στην επίλυση πιο σύνθετων τριγωνομετρικών εξισώσεων (εργασία Γ1).
ΜΕΣΟ ΕΠΙΠΕΔΟ
Σε αυτό το άρθρο θα περιγράψω επίλυση τριγωνομετρικών εξισώσεων πιο σύνθετου τύπουκαι πώς να επιλέξετε τις ρίζες τους. Εδώ θα βασιστώ στα ακόλουθα θέματα:
- Τριγωνομετρικές εξισώσεις για το εισαγωγικό επίπεδο (βλ. παραπάνω).
Πιο πολύπλοκες τριγωνομετρικές εξισώσεις αποτελούν τη βάση πιο πολύπλοκων προβλημάτων. Σε αυτά, απαιτείται τόσο η επίλυση της ίδιας της εξίσωσης σε γενική μορφή, όσο και η εύρεση των ριζών αυτής της εξίσωσης που ανήκουν σε ένα συγκεκριμένο καθορισμένο διάστημα.
Η επίλυση τριγωνομετρικών εξισώσεων καταλήγει σε δύο δευτερεύουσες εργασίες:
- Λύση εξίσωσης
- Επιλογή ριζών
Θα πρέπει να σημειωθεί ότι το τελευταίο δεν απαιτείται πάντα, αλλά εξακολουθεί να απαιτείται επιλογή στα περισσότερα παραδείγματα. Και αν δεν απαιτείται, τότε μπορείτε μάλλον να συμπονέσετε - αυτό σημαίνει ότι η εξίσωση είναι αρκετά περίπλοκη από μόνη της.
Η εμπειρία μου στην ανάλυση εργασιών C1 δείχνει ότι συνήθως χωρίζονται σε αυτές τις κατηγορίες.
Τέσσερις κατηγορίες εργασιών αυξημένης πολυπλοκότητας (πρώην C1)
- Εξισώσεις που ανάγονται σε παραγοντοποίηση.
- Εξισώσεις που ανάγεται στη μορφή.
- Εξισώσεις που λύνονται με μεταβλητή αλλαγή.
- Εξισώσεις που απαιτούν πρόσθετη επιλογή ριζών λόγω παραλογισμού ή παρονομαστή.
Για να το πω απλά: αν συναντήσετε ένας από τους τρεις πρώτους τύπους εξισώσεωντότε θεωρήστε τον εαυτό σας τυχερό. Για αυτούς, κατά κανόνα, πρέπει επιπλέον να μαζέψετε ρίζες που ανήκουν σε ένα συγκεκριμένο διάστημα.
Εάν συναντήσετε μια εξίσωση του τύπου 4, τότε είστε λιγότερο τυχεροί: πρέπει να την ασχοληθείτε λίγο περισσότερο και πιο προσεκτικά, αλλά πολύ συχνά δεν απαιτεί πρόσθετη επιλογή ριζών σε αυτήν. Ωστόσο, θα αναλύσω αυτόν τον τύπο εξισώσεων στο επόμενο άρθρο, και αυτό θα αφιερωθεί στην επίλυση εξισώσεων των τριών πρώτων τύπων.
Εξισώσεις Factoring
Το πιο σημαντικό πράγμα που πρέπει να θυμάστε για να λύσετε εξισώσεις αυτού του τύπου είναι
Όπως δείχνει η πρακτική, κατά κανόνα, αυτή η γνώση είναι επαρκής. Ας δούμε μερικά παραδείγματα:
Παράδειγμα 1. Εξίσωση αναγωγή σε παραγοντοποίηση με χρήση τύπων αναγωγής και ημιτονοειδούς διπλής γωνίας
- Εξίσωση Res-shi-te
- Nay-di-te όλες οι ρίζες αυτής της εξίσωσης
Εδώ, όπως υποσχέθηκα, οι φόρμουλες casting λειτουργούν:
Τότε η εξίσωσή μου θα μοιάζει με αυτό:
Τότε η εξίσωσή μου θα πάρει την ακόλουθη μορφή:
Ένας κοντόφθαλμος μαθητής θα μπορούσε να πει: και τώρα θα συντομεύσω και τα δύο μέρη, θα βρω την πιο απλή εξίσωση και θα απολαύσω τη ζωή! Και θα είναι οικτρά λάθος!
| ΝΑ ΘΥΜΑΣΤΕ: ΠΟΤΕ ΜΗΝ ΜΕΙΩΝΕΤΕ ΚΑΙ ΤΑ ΔΥΟ ΜΕΡΗ ΤΗΣ ΤΡΙΓΩΝΟΜΕΤΡΙΚΗΣ ΕΞΙΣΩΣΗΣ ΑΠΟ ΜΙΑ ΣΥΝΑΡΤΗΣΗ ΠΟΥ ΠΕΡΙΕΧΕΙ ΜΙΑ ΑΓΝΩΣΤΗ! ΕΤΣΙ ΧΑΝΕΙΣ ΡΙΖΕΣ! |
Λοιπόν τι κάνεις? Ναι, όλα είναι απλά, μετακινήστε τα πάντα προς μια κατεύθυνση και αφαιρέστε τον κοινό παράγοντα:
Λοιπόν, το συνυπολογίζουμε σε παράγοντες, γρήγορα! Τώρα αποφασίζουμε:
Η πρώτη εξίσωση έχει ρίζες:
Και το δεύτερο:
Αυτό ολοκληρώνει το πρώτο μέρος του προβλήματος. Τώρα πρέπει να επιλέξουμε τις ρίζες:
Το κενό έχει ως εξής:
Ή μπορεί επίσης να γραφτεί ως εξής:
Λοιπόν, ας πάρουμε τις ρίζες:
Αρχικά, ας δουλέψουμε με την πρώτη σειρά (και είναι πιο εύκολο, τι να πούμε!)
Εφόσον το μεσοδιάστημά μας είναι εντελώς αρνητικό, δεν χρειάζεται να παίρνουμε μη αρνητικές, παρόλα αυτά θα δώσουν μη αρνητικές ρίζες.
Ας πάρουμε, λοιπόν - λίγο πάρα πολύ, δεν ταιριάζει.
Αφήστε, λοιπόν - δεν ξαναχτύπησε.
Μια ακόμη προσπάθεια - λοιπόν - υπάρχει, χτυπήστε! Βρέθηκε η πρώτη ρίζα!
Ξαναπυροβολώ: μετά - το ξαναχτύπησα!
Λοιπόν, άλλη μια φορά:: - αυτή είναι ήδη μια πτήση.
Άρα από την πρώτη σειρά 2 ρίζες ανήκουν στο διάστημα:.
Δουλεύουμε με τη δεύτερη σειρά (χτίζουμε σε βαθμό σύμφωνα με τον κανόνα):
Υποβολή!
Υπερβάζω ξανά!
Και πάλι undershoot!
Το έπιασα!
Πτήση!
Έτσι, οι ακόλουθες ρίζες ανήκουν στο εύρος μου:
Με αυτόν τον αλγόριθμο θα λύσουμε όλα τα άλλα παραδείγματα. Ας εξασκηθούμε μαζί με ένα ακόμη παράδειγμα.
Παράδειγμα 2. Μια εξίσωση που ανάγεται σε παραγοντοποίηση χρησιμοποιώντας τύπους αναγωγής
- Λύστε την εξίσωση
Λύση:
Και πάλι οι περιβόητες φόρμουλες κάστινγκ:
Και πάλι, μην προσπαθήσετε να μειώσετε!
Η πρώτη εξίσωση έχει ρίζες:
Και το δεύτερο:
Τώρα αναζητήστε ξανά τις ρίζες.
Θα ξεκινήσω με τη δεύτερη σειρά, ξέρω ήδη τα πάντα για αυτήν από το προηγούμενο παράδειγμα! Κοιτάξτε και βεβαιωθείτε ότι οι ρίζες που ανήκουν στο κενό είναι οι εξής:
Τώρα το πρώτο επεισόδιο και είναι πιο απλό:
Αν - ταιριάζει
Αν - είναι επίσης καλό
Εάν - ήδη μια πτήση.
Τότε οι ρίζες θα είναι οι εξής:
Ανεξάρτητη εργασία. 3 εξισώσεις.
Λοιπόν, σας είναι ξεκάθαρη η τεχνική; Η επίλυση τριγωνομετρικών εξισώσεων δεν φαίνεται πια τόσο δύσκολη; Στη συνέχεια, λύστε γρήγορα μόνοι σας τα ακόλουθα προβλήματα και, στη συνέχεια, εσείς και εγώ θα λύσουμε άλλα παραδείγματα:
- Λύστε την εξίσωση
Nay-di-these είναι όλες οι ρίζες αυτής της εξίσωσης, που συνδέονται με το διάστημα. - Εξίσωση Res-shi-te
Να αναφέρετε τις ρίζες της εξίσωσης - Εξίσωση Res-shi-te
Ναι-ντι-αυτά είναι όλες οι ρίζες αυτής της εξίσωσης-non-niy, που συνδέονται-πάνω-le-zha-shi-pro-me-zhut-ku.
Εξίσωση 1.
Και πάλι η φόρμουλα casting:
Πρώτη σειρά ριζών:
Δεύτερη σειρά ριζών:
Έναρξη επιλογής για το κενό
Απάντηση: , .
Εξίσωση 2. Έλεγχος ανεξάρτητης εργασίας.
Αρκετά δύσκολη ομαδοποίηση σε παράγοντες (θα χρησιμοποιήσω τον τύπο ημιτόνου διπλής γωνίας):
τότε ή
Αυτή είναι μια γενική λύση. Τώρα πρέπει να επιλέξουμε τις ρίζες. Το πρόβλημα είναι ότι δεν μπορούμε να πούμε την ακριβή τιμή της γωνίας, το συνημίτονο της οποίας είναι ίσο με το ένα τέταρτο. Επομένως, δεν μπορώ απλώς να απαλλαγώ από την αρκοσίνη - είναι τόσο κρίμα!
Αυτό που μπορώ να κάνω είναι να καταλάβω τι και πώς, τότε.
Ας φτιάξουμε έναν πίνακα: interval:
Λοιπόν, μέσα από επίπονες αναζητήσεις, καταλήξαμε στο απογοητευτικό συμπέρασμα ότι η εξίσωσή μας έχει μία ρίζα στο υποδεικνυόμενο διάστημα: \ displaystyle arccos \ frac (1) (4) -5 \ pi
Εξίσωση 3. Έλεγχος ανεξάρτητης εργασίας.
Μια τρομακτική εξίσωση. Ωστόσο, μπορεί να λυθεί πολύ απλά εφαρμόζοντας τον τύπο ημιτόνου διπλής γωνίας:
Μειώστε κατά 2:
Ας ομαδοποιήσουμε τον πρώτο όρο με τον δεύτερο και τον τρίτο με τον τέταρτο και ας βγάλουμε τους κοινούς παράγοντες:
Είναι σαφές ότι η πρώτη εξίσωση δεν έχει ρίζες και τώρα σκεφτείτε τη δεύτερη:
Γενικά, επρόκειτο να σταθώ στη λύση τέτοιων εξισώσεων λίγο αργότερα, αλλά αφού εμφανίστηκε, τότε δεν υπάρχει τίποτα να κάνουμε, είναι απαραίτητο να λυθεί ...
Εξισώσεις της μορφής:
Αυτή η εξίσωση λύνεται διαιρώντας και τα δύο μέρη με:
Έτσι, η εξίσωσή μας έχει μια μοναδική σειρά ριζών:
Είναι απαραίτητο να βρεθούν εκείνα από αυτά που ανήκουν στο διάστημα:.
Ας φτιάξουμε ξανά έναν πίνακα, όπως έκανα νωρίτερα:
Απάντηση: .
Εξισώσεις που ανάγονται στη μορφή:
Λοιπόν, τώρα είναι η ώρα να προχωρήσουμε στη δεύτερη παρτίδα εξισώσεων, ειδικά αφού έχω ήδη πει τι αποτελείται η λύση των τριγωνομετρικών εξισώσεων νέου τύπου. Αλλά δεν θα είναι περιττό να επαναλάβουμε ότι μια εξίσωση της μορφής
Λύνεται διαιρώντας και τα δύο μέρη με το συνημίτονο:
- Εξίσωση Res-shi-te
Υποδείξτε τις ρίζες της εξίσωσης-όχι-νία, όταν-πάνω-πάνω-από-κόψιμο. - Εξίσωση Res-shi-te
Υποδείξτε τις ρίζες της εξίσωσης-not-nia, when-over-le-zha-shi-pro-me-zhut-ku.
Παράδειγμα 1.
Το πρώτο είναι πολύ απλό. Μετακινηθείτε προς τα δεξιά και εφαρμόστε τον τύπο συνημιτόνου διπλής γωνίας:
Αχα! Εξίσωση της μορφής:. Χωρίζω και τα δύο μέρη σε
Κάνουμε το κοσκίνισμα των ριζών:
Χάσμα:
Απάντηση:
Παράδειγμα 2.
Όλα είναι επίσης αρκετά ασήμαντα: ας επεκτείνουμε τις αγκύλες στα δεξιά:
Βασική τριγωνομετρική ταυτότητα:
Ημίτονο διπλής γωνίας:
Τελικά παίρνουμε:
Εγκατάλειψη ρίζας: κενό.
Απάντηση: .
Λοιπόν, πώς σας αρέσει η τεχνική, δεν είναι πολύ περίπλοκη; Ελπίζω όχι. Μπορούμε να κάνουμε αμέσως μια επιφύλαξη: στην καθαρή τους μορφή, οι εξισώσεις, που μειώνονται αμέσως σε εξίσωση για την εφαπτομένη, είναι αρκετά σπάνιες. Τυπικά, αυτή η μετάβαση (διαίρεση με συνημίτονο) είναι μόνο μέρος ενός πιο περίπλοκου προβλήματος. Εδώ είναι ένα παράδειγμα για να εξασκηθείτε:
- Εξίσωση Res-shi-te
- Ναι-ντι-αυτά είναι όλες οι ρίζες αυτής της εξίσωσης-όχι-νία, που συνδέονται-πάνω-λε-ζα-σι-κου.
Ας ελέγξουμε:
Η εξίσωση λύνεται αμέσως, αρκεί να χωρίσουμε και τα δύο μέρη σε:
Εγκατάλειψη ρίζας:
Απάντηση: .
Με τον ένα ή τον άλλο τρόπο, δεν έχουμε ακόμη συναντήσει εξισώσεις του είδους που μόλις αναλύσαμε. Ωστόσο, είναι πολύ νωρίς για να στρογγυλοποιήσουμε: υπάρχει ένα ακόμη «στρώμα» εξισώσεων που δεν έχουμε αναλύσει. Ετσι:
Επίλυση τριγωνομετρικών εξισώσεων αλλάζοντας μια μεταβλητή
Όλα είναι διαφανή εδώ: κοιτάμε προσεκτικά την εξίσωση, την απλοποιούμε όσο το δυνατόν περισσότερο, κάνουμε αντικατάσταση, λύνουμε, κάνουμε αντίστροφη αντικατάσταση! Με λόγια όλα είναι πολύ εύκολα. Ας δούμε στην πράξη:
Παράδειγμα.
- Λύστε την εξίσωση:.
- Ναι-ντι-αυτά είναι όλες οι ρίζες αυτής της εξίσωσης-όχι-νία, που συνδέονται-πάνω-λε-ζα-σι-κου.
Λοιπόν, εδώ η ίδια η αντικατάσταση παρακαλεί να είναι στα χέρια μας!
Τότε η εξίσωσή μας θα μετατραπεί σε αυτό:
Η πρώτη εξίσωση έχει ρίζες:
Και το δεύτερο είναι αυτό:
Τώρα θα βρούμε τις ρίζες που ανήκουν στο διάστημα
Απάντηση: .
Ας δούμε μαζί ένα λίγο πιο περίπλοκο παράδειγμα:
- Εξίσωση Res-shi-te
- Υποδείξτε τις ρίζες της δεδομένης εξίσωσης-non-niy, when-over-le-za-shi-n-e-zhut-ku.
Εδώ η αντικατάσταση δεν είναι άμεσα ορατή, επιπλέον, δεν είναι πολύ εμφανής. Ας σκεφτούμε πρώτα: τι μπορούμε να κάνουμε;
Για παράδειγμα, μπορούμε να φανταστούμε
Και ταυτόχρονα
Τότε η εξίσωσή μου θα πάρει τη μορφή:
Τώρα προσοχή, εστίαση:
Ας διαιρέσουμε και τις δύο πλευρές της εξίσωσης με:
Ξαφνικά εσύ και εγώ πήραμε μια τετραγωνική εξίσωση για! Ας κάνουμε μια αντικατάσταση και μετά παίρνουμε:
Η εξίσωση έχει τις εξής ρίζες:
Άσχημη δεύτερη σειρά ριζών, αλλά δεν γίνεται! Επιλέγουμε τις ρίζες στο διάστημα.
Πρέπει επίσης να το σκεφτούμε
Από τότε και μετά
Απάντηση:
Για να ενοποιήσετε, προτού λύσετε μόνοι σας τα προβλήματα, εδώ είναι μια άλλη άσκηση για εσάς:
- Εξίσωση Res-shi-te
- Ναι-ντι-αυτά είναι όλες οι ρίζες αυτής της εξίσωσης-non-niy, που συνδέονται-πάνω-le-zha-shi-pro-me-zhut-ku.
Εδώ πρέπει να έχετε τα μάτια σας ανοιχτά: τώρα έχουμε παρονομαστές που μπορεί να είναι μηδέν! Επομένως, πρέπει να είστε ιδιαίτερα προσεκτικοί στις ρίζες!
Πρώτα απ 'όλα, πρέπει να μετατρέψω την εξίσωση για να μπορέσω να κάνω μια κατάλληλη αντικατάσταση. Δεν μπορώ να σκεφτώ τίποτα καλύτερο αυτή τη στιγμή από το να ξαναγράψω την εφαπτομένη ως προς το ημίτονο και το συνημίτονο:
Τώρα θα πάω από συνημίτονο σε ημίτονο με βάση τη βασική τριγωνομετρική ταυτότητα:
Και τέλος, θα φέρω τα πάντα σε έναν κοινό παρονομαστή:
Τώρα μπορώ να πάω στην εξίσωση:
Αλλά στο (δηλαδή στο).
Όλα είναι τώρα έτοιμα για αντικατάσταση:
Τότε είτε
Ωστόσο, σημειώστε ότι εάν, τότε ταυτόχρονα!
Ποιος υποφέρει από αυτό; Το πρόβλημα με την εφαπτομένη, είναι απροσδιόριστο όταν το συνημίτονο είναι μηδέν (διαίρεση με μηδέν).
Έτσι, οι ρίζες της εξίσωσης είναι οι εξής:
Τώρα κοσκινίζουμε τις ρίζες στο διάστημα:
| - ταιριάζει | |
| - ωμής βίας |
Έτσι, η εξίσωσή μας έχει μία μόνο ρίζα στο διάστημα, και είναι ίση με.
Βλέπετε: η εμφάνιση του παρονομαστή (όπως και η εφαπτομένη, οδηγεί σε ορισμένες δυσκολίες με τις ρίζες! Εδώ πρέπει να είστε πιο προσεκτικοί!).
Λοιπόν, εσείς και εγώ έχουμε σχεδόν τελειώσει την ανάλυση των τριγωνομετρικών εξισώσεων, απομένουν πολύ λίγα - να λύσουμε ανεξάρτητα δύο προβλήματα. Εδώ είναι.
- Λύστε την εξίσωση
Ναι-ντι-αυτά είναι όλες οι ρίζες αυτής της εξίσωσης-όχι-νία, που συνδέονται-πάνω-λε-ζα-σι-κου. - Εξίσωση Res-shi-te
Υποδείξτε τις ρίζες αυτής της εξίσωσης, που συνδέονται με την τομή.
Αποφασισμένος? Δεν είναι πολύ δύσκολο; Ας ελέγξουμε:
- Εργαζόμαστε σύμφωνα με τους τύπους μείωσης:
Αντικαταστήστε στην εξίσωση:
Ας ξαναγράψουμε τα πάντα με συνημίτονα, ώστε να είναι πιο βολικό να κάνουμε την αντικατάσταση:
Τώρα είναι εύκολο να κάνετε την αντικατάσταση:
Είναι σαφές ότι πρόκειται για μια ξένη ρίζα, αφού η εξίσωση δεν έχει λύσεις. Τότε:
Ψάχνουμε τις ρίζες που χρειαζόμαστε στο μεσοδιάστημα
Απάντηση: .
Εδώ η αντικατάσταση είναι άμεσα ορατή:Τότε είτε
- ταιριάζει! - ταιριάζει! - ταιριάζει! - ταιριάζει! - πολλά! - πολύ επίσης! Απάντηση:
Λοιπόν, τώρα αυτό είναι! Αλλά η λύση των τριγωνομετρικών εξισώσεων δεν τελειώνει εκεί, μας μένουν οι πιο δύσκολες περιπτώσεις: όταν υπάρχει παραλογισμός στις εξισώσεις ή κάθε λογής «σύνθετοι παρονομαστές». Θα εξετάσουμε πώς να επιλύσουμε τέτοιες εργασίες στο άρθρο για προχωρημένο επίπεδο.
ΠΡΟΧΩΡΗΜΕΝΟ ΕΠΙΠΕΔΟ
Εκτός από τις τριγωνομετρικές εξισώσεις που συζητήθηκαν στα δύο προηγούμενα άρθρα, θα εξετάσουμε μια άλλη κατηγορία εξισώσεων που απαιτούν ακόμη πιο προσεκτική ανάλυση. Αυτά τα τριγωνομετρικά παραδείγματα περιέχουν είτε παραλογισμό είτε παρονομαστή, γεγονός που καθιστά πιο δύσκολη την ανάλυσή τους.... Ωστόσο, μπορεί κάλλιστα να συναντήσετε αυτές τις εξισώσεις στο Μέρος Γ του εξεταστικού χαρτιού. Ωστόσο, υπάρχει μια ασημένια επένδυση: για τέτοιες εξισώσεις, κατά κανόνα, δεν τίθεται το ερώτημα ποια από τις ρίζες του ανήκει σε ένα δεδομένο διάστημα. Ας μην χτυπάμε γύρω από τον θάμνο, αλλά μόνο τριγωνομετρικά παραδείγματα.
Παράδειγμα 1.
Λύστε την εξίσωση και βρείτε τις ρίζες που ανήκουν στο τμήμα.
Λύση:
Έχουμε έναν παρονομαστή που δεν πρέπει να είναι μηδέν! Τότε η επίλυση αυτής της εξίσωσης είναι ίδια με την επίλυση του συστήματος
Ας λύσουμε καθεμία από τις εξισώσεις:
Και τώρα το δεύτερο:
Τώρα ας ρίξουμε μια ματιά στη σειρά:
Είναι σαφές ότι η επιλογή δεν μας ταιριάζει, αφού σε αυτήν την περίπτωση ο παρονομαστής μηδενίζεται (δείτε τον τύπο για τις ρίζες της δεύτερης εξίσωσης)
Αν, όμως, τότε όλα είναι εντάξει, και ο παρονομαστής δεν είναι μηδέν! Τότε οι ρίζες της εξίσωσης είναι οι εξής:,.
Τώρα επιλέγουμε τις ρίζες που ανήκουν στο διάστημα.
| - δεν ταιριαζει | - ταιριάζει | |
| - ταιριάζει | - ταιριάζει | |
| ωμής βίας | ωμής βίας |
Τότε οι ρίζες είναι οι εξής:
Βλέπετε, ακόμη και η εμφάνιση ενός μικρού θορύβου με τη μορφή παρονομαστή επηρέασε σημαντικά τη λύση της εξίσωσης: ρίξαμε μια σειρά από ρίζες που μηδενίζουν τον παρονομαστή. Η κατάσταση μπορεί να είναι ακόμα πιο δύσκολη αν συναντήσετε τριγωνομετρικά παραδείγματα που έχουν παραλογισμό.
Παράδειγμα 2.
Λύστε την εξίσωση:
Λύση:
Λοιπόν, τουλάχιστον δεν χρειάζεται να επιλέξετε τις ρίζες και αυτό είναι καλό! Ας λύσουμε πρώτα την εξίσωση, ανεξάρτητα από τον παραλογισμό:
Αυτό είναι όλο? Όχι, δυστυχώς, θα ήταν πολύ εύκολο! Πρέπει να θυμόμαστε ότι μόνο μη αρνητικοί αριθμοί μπορούν να βρίσκονται κάτω από τη ρίζα. Τότε:
Η λύση αυτής της ανισότητας:
Τώρα μένει να μάθουμε αν κάποιες από τις ρίζες της πρώτης εξίσωσης έχουν φτάσει κατά λάθος εκεί όπου η ανισότητα δεν ικανοποιείται.
Για να το κάνετε αυτό, μπορείτε να χρησιμοποιήσετε ξανά τον πίνακα:
| : , αλλά | Δεν! | |
| Ναί! | ||
| Ναί! |
Έτσι, μια από τις ρίζες μου «έπεσε»! Αποδεικνύεται αν το βάλεις. Τότε η απάντηση μπορεί να γραφτεί ως εξής:
Απάντηση:
Βλέπετε, η ρίζα θέλει ακόμη μεγαλύτερη προσοχή! Για να περιπλέκουμε τα πράγματα: τώρα επιτρέψτε μου να έχω μια τριγωνομετρική συνάρτηση κάτω από τη ρίζα.
Παράδειγμα 3.
Όπως και πριν: πρώτα θα λύσουμε το καθένα ξεχωριστά, και μετά θα σκεφτούμε τι κάναμε.
Τώρα η δεύτερη εξίσωση:
Τώρα το πιο δύσκολο πράγμα είναι να μάθουμε αν λαμβάνονται αρνητικές τιμές κάτω από την αριθμητική ρίζα αν αντικαταστήσουμε εκεί τις ρίζες από την πρώτη εξίσωση:
Ο αριθμός πρέπει να γίνει κατανοητός ως ακτίνια. Δεδομένου ότι τα ακτίνια είναι περίπου μοίρες, τα ακτίνια είναι περίπου μοίρες. Αυτή είναι η γωνία του δεύτερου δεκαλέπτου. Ποιο είναι το πρόσημο του συνημιτόνου του δεύτερου τετάρτου; Μείον. Και το ημίτονο; Ενα θετικό. Τι μπορεί να ειπωθεί λοιπόν για την έκφραση:
Είναι λιγότερο από το μηδέν!
Αυτό σημαίνει ότι δεν είναι η ρίζα της εξίσωσης.
Τώρα είναι η σειρά.
Ας συγκρίνουμε αυτόν τον αριθμό με το μηδέν.
Η συνεφαπτομένη είναι μια συνάρτηση που μειώνεται σε 1 τέταρτο (όσο μικρότερο είναι το όρισμα, τόσο μεγαλύτερη είναι η συνεφαπτομένη). τα ακτίνια είναι περίπου μοίρες. Ταυτοχρονα
από τότε και ως εκ τούτου
,
Απάντηση: .
Θα μπορούσε να είναι ακόμα πιο δύσκολο; Παρακαλώ! Θα είναι πιο δύσκολο εάν η τριγωνομετρική συνάρτηση είναι ακόμα κάτω από τη ρίζα, και το δεύτερο μέρος της εξίσωσης είναι και πάλι η τριγωνομετρική συνάρτηση.
Όσο περισσότερα τριγωνομετρικά παραδείγματα τόσο το καλύτερο, δείτε παρακάτω:
Παράδειγμα 4.
Η ρίζα δεν είναι κατάλληλη λόγω του περιορισμένου συνημιτόνου
Τώρα το δεύτερο:
Ταυτόχρονα, εξ ορισμού της ρίζας:
Πρέπει να θυμόμαστε τον μοναδιαίο κύκλο: δηλαδή, εκείνα τα τέταρτα όπου το ημίτονο είναι μικρότερο από το μηδέν. Τι τρίμηνα είναι; Τρίτη και τέταρτη. Τότε θα μας ενδιαφέρουν εκείνες οι λύσεις της πρώτης εξίσωσης που βρίσκονται στο τρίτο ή τέταρτο τρίμηνο.
Η πρώτη σειρά παράγει ρίζες στη διασταύρωση του τρίτου και του τέταρτου τετάρτου. Η δεύτερη σειρά, η οποία είναι διαμετρικά αντίθετη από αυτήν, δημιουργεί ρίζες που βρίσκονται στο όριο του πρώτου και του δεύτερου τετάρτου. Επομένως, αυτή η σειρά δεν μας ταιριάζει.
Απάντηση:,
Και ξανα τριγωνομετρικά παραδείγματα με "δύσκολο παραλογισμό"... Όχι μόνο έχουμε πάλι την τριγωνομετρική συνάρτηση κάτω από τη ρίζα, αλλά τώρα είναι και στον παρονομαστή!
Παράδειγμα 5.
Λοιπόν, τίποτα δεν μπορεί να γίνει - ενεργούμε όπως πριν.
Τώρα εργαζόμαστε με τον παρονομαστή:
Δεν θέλω να λύσω τριγωνομετρική ανισότητα, και ως εκ τούτου θα ενεργήσω πονηρά: θα πάρω και θα αντικαταστήσω τη σειρά των ριζών μου στην ανισότητα:
Αν - ακόμη, τότε έχουμε:
αφού, τότε όλες οι γωνίες θέασης βρίσκονται στο τέταρτο τέταρτο. Και πάλι το ιερό ερώτημα: ποιο είναι το ζώδιο του κόλπου στο τέταρτο τρίμηνο; Αρνητικός. Μετά η ανισότητα
Αν είναι περίεργο, τότε:
Σε ποιο τέταρτο βρίσκεται η γωνία; Αυτή είναι η γωνία του δεύτερου δεκαλέπτου. Τότε όλες οι γωνίες είναι και πάλι οι γωνίες του δεύτερου δεκαλέπτου. Το ιγμόρειο είναι θετικό εκεί. Ακριβώς αυτό που χρειάζεστε! Ως εκ τούτου, η σειρά:
Ταιριάζει!
Αντιμετωπίστε τη δεύτερη σειρά ριζών με τον ίδιο τρόπο:
Αντικαθιστούμε στην ανισότητα μας:
Αν - ακόμη, τότε
Κόρνερ πρώτου δεκαλέπτου. Το ιγμόρειο είναι θετικό εκεί, οπότε η σειρά είναι κατάλληλη. Τώρα αν - περιττό, τότε:
ταιριάζει επίσης!
Λοιπόν, τώρα γράφουμε την απάντηση!
Απάντηση:
Λοιπόν, αυτή ήταν ίσως η πιο χρονοβόρα περίπτωση. Τώρα σας προτείνω προβλήματα για τη δική σας λύση.
Προπόνηση
- Λύστε και βρείτε όλες τις ρίζες της εξίσωσης που ανήκουν στο τμήμα.
Λύσεις:
Πρώτη εξίσωση:
ή
Ρίζα ODZ:Δεύτερη εξίσωση:
Επιλέγοντας ρίζες που ανήκουν στο κενό
Απάντηση:
Ή
ή
Αλλά
Σκεφτείτε:. Αν - ακόμη, τότε
- δεν ταιριαζει!
Εάν - περίεργο,: - ταιριάζει!
Αυτό σημαίνει ότι η εξίσωσή μας έχει την ακόλουθη σειρά ριζών:
ή
Επιλογή ριζών στο διάστημα:
| - δεν ταιριαζει | - ταιριάζει | |
| - ταιριάζει | - παρτίδα | |
| - ταιριάζει | παρτίδα |
Απάντηση: , .
Ή
Αφού, όταν η εφαπτομένη δεν ορίζεται. Αυτή τη σειρά ριζών την απορρίπτουμε αμέσως!
Δεύτερο μέρος:
Παράλληλα, σύμφωνα με την ΟΔΖ, απαιτείται ότι
Ελέγχουμε τις ρίζες που βρέθηκαν στην πρώτη εξίσωση:
Εάν το σημάδι είναι:
Κόρνερ πρώτου τετάρτου όπου η εφαπτομένη είναι θετική. Δεν χωράει!
Εάν το σημάδι είναι:
Γωνία τέταρτου τετάρτου. Εκεί η εφαπτομένη είναι αρνητική. Ταιριάζει. Γράφουμε την απάντηση:
Απάντηση: , .
Καλύψαμε μαζί σύνθετα τριγωνομετρικά παραδείγματα σε αυτό το άρθρο, αλλά θα πρέπει να λύσετε τις εξισώσεις μόνοι σας.
ΣΥΝΟΨΗ ΚΑΙ ΒΑΣΙΚΕΣ ΤΥΠΟΛΟΙ
Τριγωνομετρική εξίσωση είναι μια εξίσωση στην οποία το άγνωστο βρίσκεται αυστηρά κάτω από το πρόσημο της τριγωνομετρικής συνάρτησης.
Υπάρχουν δύο τρόποι επίλυσης τριγωνομετρικών εξισώσεων:
Ο πρώτος τρόπος είναι η χρήση τύπων.
Ο δεύτερος τρόπος είναι μέσω του τριγωνομετρικού κύκλου.
Σας επιτρέπει να μετράτε γωνίες, να βρίσκετε τα ημιτόνια, τα συνημίτονά τους και πολλά άλλα.
Προετοιμασία για το επίπεδο προφίλ της ενιαίας κρατικής εξέτασης στα μαθηματικά. Χρήσιμα υλικά για την τριγωνομετρία, μεγάλες θεωρητικές βιντεοδιαλέξεις, βίντεο αναλύσεις προβλημάτων και επιλογή εργασιών περασμένων ετών.
Χρήσιμα υλικά
Επιλογές βίντεο και διαδικτυακά μαθήματα
Τριγωνομετρικοί τύποι
Γεωμετρική απεικόνιση τριγωνομετρικών τύπων
Λειτουργίες τόξου. Οι απλούστερες τριγωνομετρικές εξισώσεις
Τριγωνομετρικές Εξισώσεις
- Η απαραίτητη θεωρία για την επίλυση προβλημάτων.
- α) Λύστε την εξίσωση $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [- \ dfrac (7 \ pi) (2); - \ dfrac (3 \ pi) (2) \ δεξιά] $. - α) Λύστε την εξίσωση $ \ dfrac (6) (\ cos ^ 2 x) - \ dfrac (7) (\ cos x) + 1 = 0 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [-3 \ pi; - \ pi \ δεξιά] $. - Λύστε την εξίσωση $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $.
- α) Λύστε την εξίσωση $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [- \ pi; \ dfrac (5 \ pi) (2) \ δεξιά] $. - α) Λύστε την εξίσωση $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $.
- Λύστε την εξίσωση $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $.
- Λύστε την εξίσωση $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [- \ dfrac (5 \ pi) (2); - \ pi \ δεξιά) $.- α) Λύστε την εξίσωση $ \ cos 2x = \ sin \ αριστερά (\ dfrac (3 \ pi) (2) - x \ δεξιά) $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [\ dfrac (3 \ pi) (2); \ dfrac (5 \ pi) (2) \ δεξιά] $. - α) Λύστε την εξίσωση $ 2 \ sin ^ 2 \ αριστερά (\ dfrac (3 \ pi) (2) + x \ δεξιά) = \ sqrt3 \ cos x $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [- \ dfrac (7 \ pi) (2); -2 \ pi \ δεξιά] $.
Ανάλυση εργασιών βίντεο
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ sqrt (3); \ sqrt (20) \ δεξιά] $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ dfrac (9 \ pi) (2); -3 \ pi \ δεξιά] $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ sqrt (3); \ sqrt (30) \ δεξιά] $.
α) Λύστε την εξίσωση $ \ cos 2x = 1 - \ cos \ αριστερά (\ dfrac (\ pi) (2) - x \ δεξιά) $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [- \ dfrac (5 \ pi) (2); - \ pi \ δεξιά) $.
α) Λύστε την εξίσωση $ \ cos ^ 2 (\ pi - x) - \ sin \ αριστερά (x + \ dfrac (3 \ pi) (2) \ δεξιά) = 0 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [\ dfrac (5 \ pi) (2); 4 \ pi \ δεξιά] $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [\ log_5 2; \ log_5 20 \ δεξιά] $.
α) Λύστε την εξίσωση $ 8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ αριστερά (\ dfrac (3 \ pi) (2) - x \ δεξιά) = 9 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [- \ dfrac (5 \ pi) (2); - \ pi \ δεξιά] $.
α) Λύστε την εξίσωση $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [\ pi; \ dfrac (5 \ pi) (2) \ δεξιά] $.
α) Λύστε την εξίσωση $ \ αριστερά (\ dfrac (1) (49) \ δεξιά) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [\ dfrac (3 \ pi) (2); 3 \ pi \ δεξιά] $.
α) Λύστε την εξίσωση $ \ sin x + \ αριστερά (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ δεξιά) \ αριστερά (\ cos \ dfrac (x) (2) + \ sin \ dfrac (x) (2) \ δεξιά) = 0 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [\ pi; \ dfrac (5 \ pi) (2) \ δεξιά] $.
α) Λύστε την εξίσωση $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα $ \ αριστερά [-4 \ pi; - \ dfrac (5 \ pi) (2) \ δεξιά] $.
Επιλογή εργασιών προηγούμενων ετών
- α) Λύστε την εξίσωση $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ dfrac (9 \ pi) (2); -3 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2018. Πρώιμο κύμα) - α) Λύστε την εξίσωση $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ sqrt (3); \ sqrt (30) \ δεξιά] $. (ΧΡΗΣΗ-2018. Πρώιμο κύμα, ημέρα επιφύλαξης) - α) Λύστε την εξίσωση $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ αριστερά (x + \ dfrac (\ pi) (4) \ δεξιά) = \ cos x $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-2 \ pi; - \ dfrac (\ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα) - α) Λύστε την εξίσωση $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ αριστερά (x + \ dfrac (\ pi) (6) \ δεξιά) $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [3 \ pi; \ dfrac (9 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα) - α) Λύστε την εξίσωση $ \ sin x + 2 \ sin \ αριστερά (2x + \ dfrac (\ pi) (6) \ δεξιά) = \ sqrt3 \ sin 2x + 1 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ dfrac (7 \ pi) (2); -2 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα) - α) Λύστε την εξίσωση $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ αριστερά (x + \ dfrac (\ pi) (4) \ δεξιά) $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-4 \ pi; - \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα) - α) Λύστε την εξίσωση $ 2 \ sin \ αριστερά (2x + \ dfrac (\ pi) (3) \ δεξιά) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $.
- α) Λύστε την εξίσωση $ 2 \ sqrt3 \ sin \ αριστερά (x + \ dfrac (\ pi) (3) \ δεξιά) - \ cos 2x = 3 \ cos x - 1 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [2 \ pi; \ dfrac (7 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα) - α) Λύστε την εξίσωση $ 2 \ sin \ αριστερά (2x + \ dfrac (\ pi) (6) \ δεξιά) - \ cos x = \ sqrt3 \ sin 2x - 1 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ dfrac (5 \ pi) (2); 4 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα) - α) Λύστε την εξίσωση $ \ sqrt2 \ sin \ αριστερά (\ dfrac (\ pi) (4) + x \ δεξιά) + \ cos 2x = \ sin x - 1 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ dfrac (7 \ pi) (2); 5 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα) - α) Λύστε την εξίσωση $ \ sqrt2 \ sin \ αριστερά (2x + \ dfrac (\ pi) (4) \ δεξιά) + \ sqrt2 \ cos x = \ sin 2x - 1 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ dfrac (5 \ pi) (2); - \ pi \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα) - α) Λύστε την εξίσωση $ 2 \ sin \ αριστερά (x + \ dfrac (\ pi) (3) \ δεξιά) + \ cos 2x = \ sqrt3 \ cos x + 1 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-3 \ pi; - \ dfrac (3 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα)
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ pi; \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα)- α) Λύστε την εξίσωση $ 2 \ sin \ αριστερά (x + \ dfrac (\ pi) (4) \ δεξιά) + \ cos 2x = \ sqrt2 \ cos x + 1 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ pi; \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα, ημέρα επιφύλαξης) - α) Λύστε την εξίσωση $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ dfrac (7 \ pi) (2); -2 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα, ημέρα επιφύλαξης) - α) Λύστε την εξίσωση $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ dfrac (9 \ pi) (2); -3 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα, ημέρα επιφύλαξης) - α) Λύστε την εξίσωση $ 2 \ sqrt2 \ sin \ αριστερά (x + \ dfrac (\ pi) (3) \ δεξιά) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-3 \ pi; - \ dfrac (3 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα, ημέρα επιφύλαξης) - α) Λύστε την εξίσωση $ x - 3 \ sqrt (x - 1) + 1 = 0 $.
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ sqrt (3); \ sqrt (20) \ δεξιά] $. (ΧΡΗΣΗ-2018. Κύριο κύμα, ημέρα επιφύλαξης) - α) Λύστε την εξίσωση $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ dfrac (\ pi) (2), \ \ pi \ δεξιά] $. (ΧΡΗΣΗ-2017, κύριο κύμα, ημέρα κράτησης) - α) Λύστε την εξίσωση $ \ log_3 (x ^ 2 - 2x) = 1 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ log_2 0 (,) 2; \ \ log_2 5 \ δεξιά] $. (ΧΡΗΣΗ-2017, κύριο κύμα, ημέρα κράτησης) - α) Λύστε την εξίσωση $ \ log_3 (x ^ 2 - 24x) = 4 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ log_2 0 (,) 1, \ 12 \ sqrt (5) \ δεξιά] $. (ΧΡΗΣΗ-2017, κύριο κύμα, ημέρα κράτησης) - α) Λύστε την εξίσωση $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [2 \ pi; \ \ dfrac (7 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2017, κύριο κύμα) - α) Λύστε την εξίσωση $ \ log_8 \ αριστερά (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ δεξιά) = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ dfrac (3 \ pi) (2), \ 3 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2017, κύριο κύμα) - α) Λύστε την εξίσωση $ \ log_4 \ αριστερά (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ δεξιά) = x $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ dfrac (5 \ pi) (2), \ 4 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2017, κύριο κύμα) - α) Λύστε την εξίσωση $ 2 \ log_2 ^ 2 \ αριστερά (\ sin x \ δεξιά) - 5 \ log_2 \ αριστερά (\ sin x \ δεξιά) - 3 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- 3 \ pi; \ - \ dfrac (3 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2017, κύριο κύμα) - α) Λύστε την εξίσωση $ 81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- 4 \ pi; \ - \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2017, κύριο κύμα) - α) Λύστε την εξίσωση $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ log_5 2; \ \ log_5 20 \ δεξιά] $. (ΧΡΗΣΗ-2017, πρώιμο κύμα) - α) Λύστε την εξίσωση $ 2 \ log ^ 2_9 x - 3 \ log_9 x + 1 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ sqrt (10)· \ \ sqrt (99) \ δεξιά] $. (ΧΡΗΣΗ-2016, κύριο κύμα, ημέρα κράτησης) - α) Λύστε την εξίσωση $ 6 \ log ^ 2_8 x - 5 \ log_8 x + 1 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [2; \ 2 (,) 5 \ δεξιά] $. (ΧΡΗΣΗ-2016, κύριο κύμα, ημέρα κράτησης) - α) Λύστε την εξίσωση $ \ sin 2x = 2 \ sin x + \ sin \ αριστερά (x + \ dfrac (3 \ pi) (2) \ δεξιά) + 1 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2016, κύριο κύμα, ημέρα κράτησης) - α) Λύστε την εξίσωση $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ αριστερά (\ dfrac (3 \ pi) (2) - x \ δεξιά) $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ dfrac (3 \ pi) (2), \ 3 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2016, κύριο κύμα) - α) Λύστε την εξίσωση $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-2 \ pi; \ - \ dfrac (\ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2016, κύριο κύμα) - α) Λύστε την εξίσωση $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ log_2 5; \ \ log_2 11 \ δεξιά] $. (ΧΡΗΣΗ-2016, πρώιμο κύμα) - α) Λύστε την εξίσωση $ \ cos 2x + \ cos ^ 2 \ αριστερά (\ dfrac (3 \ pi) (2) - x \ δεξιά) = 0,25 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2016, πρώιμο κύμα) - α) Λύστε την εξίσωση $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2016, πρώιμο κύμα) - α) Λύστε την εξίσωση $ \ dfrac (\ sin2x) (\ sin \ αριστερά (\ dfrac (7 \ pi) (2) - x \ δεξιά)) = \ sqrt (2) $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά $. (ΧΡΗΣΗ-2015, κύριο κύμα) - α) Λύστε την εξίσωση $ 4 \ sin ^ 2 x = \ mathrm (tg) x $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ pi; \ 0 \ δεξιά] $. (ΧΡΗΣΗ-2015, κύριο κύμα) - α) Λύστε την εξίσωση $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ pi; \ \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2015, κύριο κύμα) - α) Λύστε την εξίσωση $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2015, κύριο κύμα) - α) Λύστε την εξίσωση $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ pi; \ \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2015, πρώιμο κύμα) - α) Λύστε την εξίσωση $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [2 \ pi; \ \ dfrac (7 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2015, πρώιμο κύμα) - α) Λύστε την εξίσωση $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ dfrac (5 \ pi) (2); \ 4 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2014, κύριο κύμα) - α) Λύστε την εξίσωση $ 2 \ sqrt (3) \ cos ^ 2 \ αριστερά (\ dfrac (3 \ pi) (2) + x \ δεξιά) - \ sin 2x = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ dfrac (3 \ pi) (2); \ 3 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2014, κύριο κύμα) - α) Λύστε την εξίσωση $ \ cos 2x + \ sqrt (2) \ sin \ αριστερά (\ dfrac (\ pi) (2) + x \ δεξιά) + 1 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2014, κύριο κύμα) - α) Λύστε την εξίσωση $ - \ sqrt (2) \ sin \ αριστερά (- \ dfrac (5 \ pi) (2) + x \ δεξιά) \ cdot \ sin x = \ cos x $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [\ dfrac (9 \ pi) (2); \ 6 \ pi \ δεξιά] $. (ΧΡΗΣΗ-2014, πρώιμο κύμα) - α) Λύστε την εξίσωση $ \ sin 2x = \ sin \ αριστερά (\ dfrac (\ pi) (2) + x \ δεξιά) $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [- \ dfrac (7 \ pi) (2); \ - \ dfrac (5 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2013, κύριο κύμα) - α) Λύστε την εξίσωση $ 6 \ sin ^ 2 x + 5 \ sin \ αριστερά (\ dfrac (\ pi) (2) - x \ δεξιά) - 2 = 0 $.
β) Υποδείξτε τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα $ \ αριστερά [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ δεξιά] $. (ΧΡΗΣΗ-2012, δεύτερο κύμα)
Σκοπός του μαθήματος:
ένα) να εμπεδώσει την ικανότητα επίλυσης των απλούστερων τριγωνομετρικών εξισώσεων;
σι) διδάσκουν να επιλέγουν τις ρίζες των τριγωνομετρικών εξισώσεων από ένα δεδομένο διάστημα
Κατά τη διάρκεια των μαθημάτων.
1. Πραγματοποίηση της γνώσης.
α) Έλεγχος της εργασίας: στην τάξη δόθηκε μια προκαταρκτική εργασία για το σπίτι - να λύσει την εξίσωση και να βρει έναν τρόπο να επιλέξει ρίζες από ένα δεδομένο διάστημα.
1) συν Χ= -0,5, όπου xI [-]. Απάντηση:.
2) αμαρτία Χ=, όπου xI. Απάντηση: ; ...
3) co 2 Χ= -, όπου хI. Απάντηση:
Οι μαθητές σημειώνουν τη λύση στον πίνακα, κάποιος χρησιμοποιεί ένα γράφημα, κάποιος χρησιμοποιεί μια μέθοδο επιλογής.
Αυτή τη στιγμή η τάξη λειτουργεί προφορικά.
Βρείτε το νόημα της έκφρασης:
α) tg - αμαρτία + συν + αμαρτία. Απάντηση: 1.
β) 2 τόξο 0 + 3 τόξο 1. Απάντηση: ?
γ) arcsin + arcsin. Απάντηση:.
δ) 5 arctan (-) - arccos (-). Απάντηση:-.
- Ας ελέγξουμε την εργασία σας, ανοίξτε τα τετράδια των εργασιών σας.
Κάποιοι από εσάς βρήκαν τη λύση με τη μέθοδο προσαρμογής και κάποιοι με ένα γράφημα.
2. Συμπέρασμα σχετικά με τον τρόπο επίλυσης αυτών των εργασιών και τη δήλωση του προβλήματος, δηλαδή το μήνυμα του θέματος και τον σκοπό του μαθήματος.
- α) Είναι δύσκολο να λυθεί με τη βοήθεια της επιλογής αν δοθεί μεγάλο διάστημα.
- β) Η γραφική μέθοδος δεν δίνει ακριβή αποτελέσματα, απαιτεί επαλήθευση και απαιτεί πολύ χρόνο.
- Επομένως, πρέπει να υπάρχει τουλάχιστον μια ακόμη μέθοδος, η πιο καθολική - ας προσπαθήσουμε να τη βρούμε. Τι θα κάνουμε λοιπόν σήμερα στην τάξη; (Μάθετε να επιλέγετε τις ρίζες μιας τριγωνομετρικής εξίσωσης σε ένα δεδομένο διάστημα.)
- Παράδειγμα 1 (Ο μαθητής πηγαίνει στον πίνακα)
συν Χ= -0,5, όπου xI [-].
Ερώτηση: Από τι εξαρτάται η απάντηση σε αυτήν την εργασία; (Από τη γενική λύση της εξίσωσης. Ας γράψουμε τη λύση σε γενική μορφή). Η απόφαση γράφεται στον πίνακα
х = + 2; k, όπου k R.
- Ας γράψουμε αυτή τη λύση με τη μορφή ενός συνόλου:

- Πώς πιστεύετε, για ποια εγγραφή της λύσης είναι βολικό να επιλέγετε ρίζες στο διάστημα; (από το δεύτερο λήμμα). Αλλά αυτή είναι και πάλι μια μέθοδος επιλογής. Τι πρέπει να γνωρίζουμε για να λάβουμε τη σωστή απάντηση; (Πρέπει να γνωρίζετε τις τιμές του k).
(Ας φτιάξουμε ένα μαθηματικό μοντέλο για να βρούμε το k).
αφού kI Z, τότε k = 0, επομένως Χ= = |
αυτή η ανισότητα δείχνει ότι δεν υπάρχουν ακέραιες τιμές του k. |
Συμπέρασμα:Για να επιλέξετε ρίζες από ένα δεδομένο διάστημα κατά την επίλυση μιας τριγωνομετρικής εξίσωσης, πρέπει:
- να λύσει μια εξίσωση της μορφής αμαρτία x = α, cos x = αείναι πιο βολικό να γράψουμε τις ρίζες της εξίσωσης ως δύο σειρές ριζών.
- να λύσει εξισώσεις της μορφής tg x = α, ctg x = αγράψτε τον γενικό τύπο για τις ρίζες.
- σχεδιάστε ένα μαθηματικό μοντέλο για κάθε λύση με τη μορφή διπλής ανισότητας και βρείτε την ακέραια τιμή της παραμέτρου k ή n.
- αντικαταστήστε αυτές τις τιμές στον τύπο ρίζας και υπολογίστε τις.
Λύστε τα παραδείγματα 2 και 3 από την εργασία για το σπίτι χρησιμοποιώντας τον αλγόριθμο που προέκυψε. Ταυτόχρονα, δύο μαθητές εργάζονται στον πίνακα και ακολουθούν έλεγχος της εργασίας.
Σε αυτό το άρθρο θα προσπαθήσω να εξηγήσω 2 τρόπους επιλογή ριζών σε τριγωνομετρική εξίσωση: χρησιμοποιώντας ανισώσεις και χρησιμοποιώντας τον τριγωνομετρικό κύκλο. Ας πάμε κατευθείαν σε ένα ενδεικτικό παράδειγμα και ας ασχοληθούμε με την υπόθεση.
Α) Λύστε την εξίσωση sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
β) Βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο διάστημα [-7Pi / 2; -2 Pi]
Ας λύσουμε το σημείο α.
Χρησιμοποιούμε τον τύπο αναγωγής για το sine sin (Pi / 2 + x) = cos (x)
Sqrt (2) cos ^ 2x = cosx
Sqrt (2) cos ^ 2x - cosx = 0
Cosx (sqrt (2) cosx - 1) = 0
X1 = Pi / 2 + Pin, n ∈ Z
Sqrt (2) cosx - 1 = 0
Cosx = 1 / sqrt (2)
Cosx = sqrt (2) / 2
X2 = arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
x3 = -arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
X2 = Pi / 4 + 2Pin, n ∈ Z
x3 = -Pi / 4 + 2Pin, n ∈ Z
Ας λύσουμε το σημείο β.
1) Επιλογή ριζών με χρήση ανισώσεων
Εδώ όλα γίνονται απλά, αντικαθιστούμε τις λαμβανόμενες ρίζες στο δεδομένο διάστημα [-7Pi / 2; -2Pi], βρείτε ακέραιες τιμές για n.
7Pi / 2 μικρότερο ή ίσο του Pi / 2 + Pin μικρότερο ή ίσο με -2Pi
Χωρίστε τα πάντα σε Pi ταυτόχρονα
7/2 είναι μικρότερο ή ίσο με 1/2 + n είναι μικρότερο ή ίσο με -2
7/2 - 1/2 μικρότερο ή ίσο με n μικρότερο ή ίσο με -2 - 1/2
4 μικρότερο ή ίσο με n μικρότερο ή ίσο με -5/2
Το ολόκληρο n σε αυτό το εύρος είναι -4 και -3. Έτσι οι ρίζες που ανήκουν σε αυτό το διάστημα θα είναι Pi / 2 + Pi (-4) = -7Pi / 2, Pi / 2 + Pi (-3) = -5Pi / 2
Ομοίως, κάνουμε δύο ακόμη ανισότητες
7Pi / 2 μικρότερο ή ίσο με Pi / 4 + 2Pin μικρότερο ή ίσο με -2Pi
-15/8 μικρότερο ή ίσο με n μικρότερο ή ίσο με -9/8
Δεν υπάρχουν ακέραιοι ν σε αυτό το διάστημα
7Pi / 2 μικρότερο ή ίσο με -Pi / 4 + 2Pin μικρότερο ή ίσο με -2Pi
-13/8 μικρότερο ή ίσο με n μικρότερο ή ίσο με -7/8
Ένας ακέραιος n σε αυτό το διάστημα είναι -1. Άρα η επιλεγμένη ρίζα σε αυτό το διάστημα είναι -Pi / 4 + 2Pi * (- 1) = -9Pi / 4.
Άρα η απάντηση στο σημείο β: -7Pi / 2, -5Pi / 2, -9Pi / 4
2) Επιλογή ριζών χρησιμοποιώντας τριγωνομετρικό κύκλο
Για να χρησιμοποιήσετε αυτήν τη μέθοδο, πρέπει να κατανοήσετε πώς λειτουργεί αυτός ο κύκλος. Θα προσπαθήσω να εξηγήσω με απλή γλώσσα πώς το καταλαβαίνω αυτό. Νομίζω ότι στα σχολεία στα μαθήματα άλγεβρας αυτό το θέμα εξηγήθηκε πολλές φορές από τα έξυπνα λόγια του δασκάλου, σύνθετες διατυπώσεις στα σχολικά βιβλία. Προσωπικά, το αντιλαμβάνομαι ως κύκλο που μπορεί να διασχιστεί άπειρες φορές, λόγω του ότι οι συναρτήσεις ημιτονοειδούς και συνημιτονοειδούς είναι περιοδικές.
Ας πάμε αριστερόστροφα μια φορά
Ας πάμε γύρω 2 φορές αριστερόστροφα
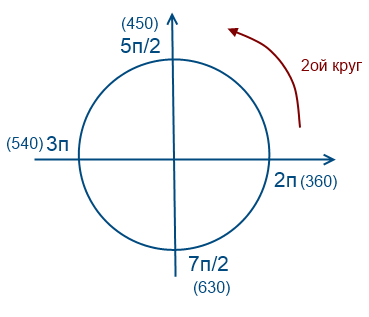
Ας πάμε γύρω 1 φορά δεξιόστροφα (οι τιμές θα είναι αρνητικές)

Ας επιστρέψουμε στην ερώτησή μας, πρέπει να επιλέξουμε ρίζες στο διάστημα [-7Pi / 2; -2 Pi]
Για να φτάσετε στους αριθμούς -7Pi / 2 και -2Pi, πρέπει να περιηγηθείτε στον κύκλο αριστερόστροφα δύο φορές. Για να βρεθούν οι ρίζες της εξίσωσης σε αυτό το διάστημα, είναι απαραίτητο να γίνει εκτίμηση και αντικατάσταση.
Θεωρήστε x = Pi / 2 + Pin. Ποια είναι κατά προσέγγιση η τιμή του n για την τιμή του x να είναι κάπου σε αυτό το διάστημα; Αντικαθιστώντας, ας πούμε -2, παίρνουμε Pi / 2 - 2Pi = -3Pi / 2, προφανώς αυτό δεν περιλαμβάνεται στο μεσοδιάστημά μας, οπότε παίρνουμε λιγότερο από -3, Pi / 2 - 3Pi = -5Pi / 2, ταιριάζει, ας προσπαθήσουμε ξανά -4, Pi / 2 - 4Pi = -7Pi / 2 είναι επίσης κατάλληλο.
Συλλογίζοντας παρόμοια για τα Pi / 4 + 2Pin και -Pi / 4 + 2Pin, βρίσκουμε μια άλλη ρίζα -9Pi / 4.

Σύγκριση των δύο μεθόδων.
Η πρώτη μέθοδος (χρησιμοποιώντας ανισότητες) είναι πολύ πιο αξιόπιστη και πολύ πιο εύκολη στην κατανόηση, αλλά αν ασχολείστε πραγματικά σοβαρά με τον τριγωνομετρικό κύκλο και τη δεύτερη μέθοδο επιλογής, τότε η επιλογή των ριζών θα είναι πολύ πιο γρήγορη, μπορείτε να εξοικονομήσετε περίπου 15 λεπτά το διαγώνισμα.
α) Λύστε την εξίσωση:.
β) Να βρείτε όλες τις ρίζες αυτής της εξίσωσης που ανήκουν στο τμήμα.
Η λύση του προβλήματος

Αυτό το μάθημα εξετάζει ένα παράδειγμα επίλυσης τριγωνομετρικής εξίσωσης, το οποίο μπορεί να χρησιμοποιηθεί ως παράδειγμα για την επίλυση προβλημάτων τύπου C1 κατά την προετοιμασία για την εξέταση στα μαθηματικά.
Πρώτα απ 'όλα, προσδιορίζεται το εύρος της συνάρτησης - όλες οι επιτρεπόμενες τιμές του ορίσματος. Στη συνέχεια, κατά τη διάρκεια της λύσης, η συνάρτηση τριγωνομετρικού ημιτόνου μετατρέπεται σε συνημίτονο χρησιμοποιώντας τον τύπο αναγωγής. Περαιτέρω, όλοι οι όροι της εξίσωσης μεταφέρονται στην αριστερή πλευρά της, όπου ο κοινός παράγοντας αφαιρείται από τις αγκύλες. Κάθε παράγοντας ορίζεται ίσος με το μηδέν, το οποίο σας επιτρέπει να προσδιορίσετε τις ρίζες της εξίσωσης. Στη συνέχεια, οι ρίζες που ανήκουν στο δεδομένο τμήμα προσδιορίζονται με τη μέθοδο των στροφών. Για να γίνει αυτό, σημειώνεται ένας βρόχος στον κατασκευασμένο κύκλο μονάδας από το αριστερό όριο του καθορισμένου τμήματος προς τα δεξιά. Περαιτέρω, οι ρίζες που βρέθηκαν στον μοναδιαίο κύκλο συνδέονται με τμήματα με το κέντρο του και προσδιορίζονται τα σημεία στα οποία αυτά τα τμήματα τέμνουν τον βρόχο. Αυτά τα σημεία τομής είναι η επιθυμητή απάντηση στο δεύτερο μέρος του προβλήματος.

































