Соглашение об использовании материалов сайта

Просим использовать работы, опубликованные на сайте , исключительно в личных целях. Публикация материалов на других сайтах запрещена.
Данная работа (и все другие) доступна для скачивания совершенно бесплатно. Мысленно можете поблагодарить ее автора и коллектив сайта.

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Подобные документы

Сложение и умножение целых p-адических чисел, определяемое как почленное сложение и умножение последовательностей. Кольцо целых p-адических чисел, исследование свойств их деления. Объяснение данных чисел с помощью ввода новых математических объектов.

курсовая работа , добавлен 22.06.2015


Как люди научились считать, возникновение цифр, чисел и систем счисления. Таблица умножения на "пальцах": методика умножения для чисел 9 и 8. Примеры быстрого счета. Способы умножения двузначного числа на 11, 111, 1111 и т.д. и трехзначного числа на 999.

курсовая работа , добавлен 22.10.2011


Новый способ умножения чисел. Схожесть образующейся при вычислении матрицы из цифр, с треугольником относительна, но все же есть, особенно при умножении трехзначных чисел и выше. Треугольная матрица.

статья , добавлен 06.02.2005


реферат , добавлен 13.01.2011


Характеристика истории изучения значения простых чисел в математике путем описания способов их нахождения. Вклад Пьетро Катальди в развитие теории простых чисел. Способ Эратосфена составления таблиц простых чисел. Дружественность натуральных чисел.

контрольная работа , добавлен 24.12.2010


Множество неотрицательных действительных чисел как интерпретируемое подмножество R. Делимость в мультипликативных полугруппах. Строение числовых НОД и НОК полугрупп. Изучение мультипликативных полугрупп неотрицательных действительных чисел с 0 и 1.

дипломная работа , добавлен 27.05.2008


Свойства действительных чисел, их роль в развитии математики. Анализ построения множества действительных чисел в историческом аспекте. Подходы к построению теории действительных чисел по Кантору, Вейерштрассу, Дедекинду. Их изучение в школьном курсе.

презентация , добавлен 09.10.2011


Первоначальные элементы математики. Свойства натуральных чисел. Понятие теории чисел. Общие свойства сравнений и алгебраических уравнений. Арифметические действия со сравнениями. Основные законы арифметики. Проверка результатов арифметических действий.

курсовая работа , добавлен 15.05.2015

В качестве основного понятия при
аксиоматическом построении арифметики
натуральных чисел взято отношение
«непосредственно следовать за», заданное на
непустом множестве N.
Элемент, непосредственно следующий за
элементом а, обозначают а".

Аксиома 1. Во множестве N существует
элемент, непосредственно не следующий ни
за каким элементом этого множества. Будем
называть его единицей.
Аксиома 2. Для каждого элемента а из N
существует единственный элемент а",
непосредственно следующий за а.

Аксиома 3. Для каждого элемента а из N
существует не более одного элемента, за
которым непосредственно следует а.
Аксиома 4. Всякое подмножество М
множества N, обладает свойствами:
1)единица принадлежит множеству М;
2) из того, что а содержится в М, следует,
что и а" содержится в М, то М совпадает со
множеством N.

Определение натурального числа

Множество N, для элементов которого установлено отношение
«непосредственно следовать за», удовлетворяющее аксиомам 1-4,
называется множеством натуральных чисел, а его элементы натуральными числами.

Сложение

Определение. Сложением натуральных чисел называется
алгебраическая операция, обладающим свойствами:
1) (Ɐa ∈ N) a + 1 = a",
2) (Ɐa, b ∈ N) a + b"=(a+b)".
Число a+b называется суммой чисел a и b, а сами числа a и b
слагаемыми.
Условимся о следующих обозначениях:
1" = 2; 2" = 3; 3" = 4; 4" = 5 и т.д.

Свойства сложения

Теорема 3. Сложение натуральных чисел существует и оно
единственно
Теорема 4. (Ɐ a, b, c ∈ N)(а + b) + с = a + (b + c)
Теорема 5. (Ɐ a, b ∈ N) a+b = b+a

Умножение

Умножением натуральных чисел называется алгебраическая
операция, обладающая свойствами:
1)(Ɐ a ∈ N) a·1 =a;
2)(Ɐ a, b ∈ N) a·b" = a·b + a.
Число a·b называется произведением чисел a и b, а сами числа a и
b - множителями

Свойства умножения

Теорема 7. Умножение натуральных чисел существует, и оно
единственно.
Теорема 8. (Ɐ a, b, c ∈ N)(a + b)·c = ac + b·c - дистрибутивность
справа относительно сложения.
Теорема 9. (Ɐ a, b, c ∈ N) а·(b + c) = + a·c - дистрибутивность слева
относительно сложения.
Теорема 10. (Ɐ a, b, c ∈ N) (a·b) ·c = a·(b·с) - ассоциативность
умножения.
Теорема 11. (Ɐ a, b ∈ N) a·b = a·b - коммутативность умножения

Вопросы для самопроверки

1. Можно ли аксиому 3 сформулировать в таком виде: «Для каждого элемента
а из N существует единственный элемент, за которым непосредственно
следует а»?
2. Продолжите определение натурального числа: «Натуральным числом
называется элемент множества ….»
3. Верно ли, что каждое натуральное число получается из предыдущего
прибавлением единицы?
4. Какие свойства умножения могут быть использованы при нахождении
значения выражения:
а) 5·(10 + 4); б) 125·15·6; в) (8·379)·125?

Литература

Стойлова Л. П.
Математика: Учебник для студ. высш. пед. учеб. заведений.
М.: Издательский центр «Академия». 2002. - 424 с.

Требования к системе аксиом, аксиомы Пеано. При аксиоматическом построении какой-либо математической теории соблюдаются определенные правила: 1) некоторые понятия теории выбираются в качестве основных и принимаются без определения; 2) каждому понятию теории, которое не содержится в списке основных, дается определение. В нем разъясняется его смысл с помощью основных и предшествующих данному понятий. 3) формулируется аксиомы, т.е предложения, которое в данной теории принимается без доказательства. В аксиомах раскрываются свойства основных понятий. 4) каждое предложение теории, которое не содержится в списке аксиом должно быть доказано. Такие предложения называются теоремами. Их доказывают на основе аксиом и теорем, предшествующих данной.

Т.О. аксиоматический метод построения математической теории проходит через несколько этапов: 1) введение основных неопределяемых понятий (н-р: множество, элемент множества в теории множеств). 2)введение основных отношений (н-р: отношение принадлежности в теории множеств). 3) через указание основных понятий и основных отношений вводится определение других понятий и отношений (н-р: в теории множеств понятия объединения, пересечения, разности, дополнения).

При аксиоматическом построении теории все утверждения выводятся путем доказательства из аксиом. Основу такой теории составляет система аксиом, и к системе аксиом предъявляются особые требования: 1)система аксиом должна быть непротиворечивой. Систему аксиом называют непротиворечивой, если из нее нельзя логически вывести два взаимоисключающих друг друга предложения. Другими словами, нельзя вывести высказывание и отрицание данного высказывания, так чтобы они одновременно были истинными. Чтобы убедится в непротиворечивости системы аксиом достаточно построить модель этой системы. 2) система аксиом должна быть независимой. Система аксиом называется независимой, если никакие из аксиом этой системы не являются следствием других аксиом. Другими словами каждая аксиома этой системы не может быть выведена из остальных аксиом. Чтобы доказать независимость системы аксиом достаточно построить модель этой системы. 3) система аксиом должна быть полной, т.е. количество аксиом выбранных в данной теории должно быть достаточно для введения новых понятий, отношений, доказательства теорем, для построения всей теории.

При аксиоматическом построении одной и той же теории можно использовать разные системы аксиом, но они должны быть равносильными. В качестве основного понятия при аксиоматическом построении системы натуральных чисел взято отношение «непосредственно следовать за». Известными так же считаются понятия «множество», «элемент множества», правило логики. Элемент, непосредственно следующий за элементом а, обозначается а - штрих.

Суть отношения «непосредственно следовать за» раскрывается в следующих аксиомах: 1) во множестве натуральных чисел существует элемент, непосредственно не следующий ни за каким элементом этого множества, данный элемент 1 (единица). 2) для каждого элемента а из множества натуральных чисел (N) существует единственный элемент а? , не посредственно следующий за а. 3) для каждого элемента а из N, существует не более одного элемента, за которым непосредственно следует а. 4) всякое подмножество М множества N, обладающего свойствами: 1 М, и из того, что а содержится в М что и а? содержится в М, совпадает со множеством N.

Перечисленные системы аксиом называются аксиомами Пеано. Т.О. множество чисел, для которых устанавливается отношение непосредственно следовать за, удовлетворяющее аксиомам Пеано, называется множеством натуральных чисел, а его элемент - натуральным числом. Четвертая аксиома описывает бесконечность натурального ряда чисел и называется аксиомой индукции. На ее основе проводится доказательство различных утверждений методом математической индукции, который заключается в следующем: чтобы доказать, что данное утверждение истинно для любого натурального числа необходимо: 1) доказать, что это утверждение истинно для единицы, 2) из предложения, что утверждение истинно для произвольного числа к, доказать, что оно истинно и для следующего числа к?.

В определении множества N ничего не говорится о природе этого множества, значит оно может быть каким угодно. Выбирая в качестве множества N любое множество, на котором задано отношение непосредственно следовать за и удовлетворяющее аксиомам Пеано получим модель данной системы аксиом. Между всеми такими моделями можно установить взаимно однозначное соответствие. Эти модели будут отличаться только природой элементов, названием и обозначением. Н-р: 1, 2, 3, 4, 5… 0.00,000,0000,00000, … Ѕ, 1/3, ј, 1/5,

При аксиоматическом построении какой-либо теории соблюдаются определенные правила:

некоторые понятия теории выбираются в качестве основных, и принимаются без определения и называется неопределяемыми.

формулируются аксиомы – предложения, которые в данной теории принимаются без доказательства; в них раскрывают свойства основных понятий;

каждому понятию теории, которое не содержится в списке основных, дается определение , в нем разъясняется его смысл помощью основных и предшествующих данному понятий;

каждое предложение теории, которое не содержится в списке аксиом, должно быть доказано; такие предложения называются теоремами и доказывают их на основе аксиом и теорем, предшествующих рассматриваемой.

При аксиоматическом построении теории по существу все утверждения выводятся путем доказательства из аксиом. Поэтому к системе аксиом предъявляются особые требования. Прежде всего, она должна быть непротиворечивой и независимой.

Система аксиом называется непротиворечивой, если из нее нельзя логически вывести два взаимно исключающих друг друга предложения.

Непротиворечивая система аксиом называется независимой, если никакая из аксиом этой системы не является следствием других аксиом этой системы.

Аксиомы, как правило, являются отражением многовековой практической деятельности людей, и этим обусловливается их справедливость.

В качестве основного понятия при аксиоматическом построении арифметики натуральных чисел взято отношение «непосредственно следовать за», заданное на непустом множестве N. Известными также считаются понятия множества, элемента множества и другие теоретико-множественные понятия, а также правила логики.

Элемент, непосредственно следующий за элементом а, обозначают а". Суть отношения «непосредственно следовать за» раскрывается в следующих аксиомах, предложенных итальянским математиком Дж. Пеано в 1891 году.

Аксиома 1. В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Его называют единицей и обозначают символом 1.

Аксиома 2. Для каждого элемента а из N существует единственный элемент а", непосредственно следующий за а.

Аксиома 3. Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а.

Аксиома 4. (Аксиома индукции). Всякое подмножество М множества N совпадает с N, если обладает свойствами: 1) 1 содержится в М; 2) из того, что любой элемент а содержится в М, следует, что и а" содержится в М.

Сформулированные аксиомы часто называют аксиомами Пеано, а аксиому четвертую – аксиомой индукции.

Запишем эти аксиомы в символической форме.

А 1 )( 1  N)( a  N) а "  1;

А 2 )( a  N)( !b  N) а "=b

А 3 ) ( а, b ,с  N )с = а" с = b"  а = b;

A 4) M  N  1  M  (a  M  а "  M)   M=N

Используя отношение «непосредственно следовать за» и аксиомы Пеано 1-4, можно дать следующее определение натурального числа.

Определение 1. Множество N. для элементов которого установлено отношение «непосредственно следовать за», удовлетворяющее аксиомам 1-4, называется множеством натуральных чисел, а его элементы натуральными числами.

___________________________________________________________________

Определение 2 . Если натуральное число b непосредственно следует за числом а, то число а называется непосредственно предшествующим (предшествующим) числу b .

______________________________________________________________________________________________

Теорема 1 . Единица не имеет предшествующего натурального числа (истинность теоремы вытекает сразу из аксиомы А 1 ).

Теорема 2. Каждое натуральное число а, отличное от единицы имеет предшествующее число b, такое, что b" = а.

В определении натурального числа ничего не говорит о природе элементов множества N. Значит, она может быть какой угодно. Стандартной моделью системы аксиом Пеано является возник­ший в процессе исторического развития общества ряд чисел:

1, 2, 3, 4, 5 ,..,

Каждое число этого ряда имеет свое обозначение и название, которые будем считать известными.

Важно заметить, что в определении натурального числа ни одну из аксиом опустить нельзя.

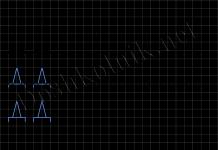
1 a b c d

    …

b

Рис . 16 Рис. 17

Задача 1.

На рисунках каждый элемент соединен стрелкой со следующим за ним элементом.

Установить, какие из множеств, приведенных на рисунках 15 и 16, являются моделями системы аксиом Пеано.

1. На рис. 16 изображено множество, в котором выполняются аксиомы 2 и 3, но не выполняется аксиома 1.

Аксиома 4 не будет иметь смысла, так как в множестве нет элемента, непосредственно не следующего ни за каким другим.

2. На рис. 17 показано множество, в котором выполнены аксиомы 1, 2, 3, но не выполняется аксиома 4 – множество точек, лежащих на луче, содержит 1, и вместе с каждым числом оно содержит непосредственно следующее за ним число, но оно не совпадает со всем множеством точек, показанных на рисунке. Вывод: ни одно из множеств, изображенных на рис. 16 и 17, нельзя считать моделями системы аксиом Пеано.

Задача 2.

Докажем, что всякое натуральное число отлично от непосредственно следующего за ним натурального числа, т.е. ( х  )х  х"

Доказательство

Пользуемся аксиомой индукции – А 4 .

Пусть М= {х/х  , х  х" }, т.к. х   М  N.

Доказательство состоит из двух частей.

Докажем, что 1  М, т.е. 1  1" . Это следует из А 1 .

Докажем, что х  М => х"  М. Пусть  х  М т.е. х  х". Докажем, что х"  М , т.е. х"  (х")". И з аксиомы А 3 следует х"  (х") ". Действительно, по А 3 , если бы х" = (х")" то и х = х", а т.к. по предложению индукции х  М, то х  х", следовательно, приходим к противоречию. Значит, х"  (х") " ,  х"  М.

Здесь применено правило контрапозиции (ПК), широко применяемое в доказательствах «от противного».

Итак, мы получили:

М  N  (1  М  (x М => х"  М))  M = N, т.е. утверждение х  х" верно для любого натурального числа.

Контрольные вопросы

В чем суть аксиоматического построения теории?

Назовите основные понятия школьного курса планиметрии. Вспомните систему аксиом этого курса. Свойства каких понятий в них описываются?

Сформулируйте и запишите в символической форме аксиомы Пеано. "

Сформулируйте аксиоматическое определение натурального числа.

Продолжите определение натурального числа: «Натуральным числом называется элемент множества N ,... ».

Приведите примеры из учебников математики для начальных классов, в которых:

а) новое (для учащихся) число выступает как продолжение полученного отрезка натурального ряда;

б) устанавливается, что за каждым натуральным числом непосредственно следует только одно другое натуральное число.

Упражнения

285. Элементами множества являются группы черточек {I, II, III, IIII,...}. Удовлетворяет ли это множество аксиомам Пеано? Как определено здесь отношение «непосредственно следовать за». Рассмотрите эти же вопросы для множества {0, 00, 000, 0000,...}.

Рис. 17

286. На рисунке 17 а) каждый элемент соединен стрелкой со следую­щим за ним элементом. Можно ли считать множество моделью системы аксиом Пеано? Те же вопросы для множеств на рисунках 17 б), в), г).

287. Удовлетворяет ли аксиомам Пеано множество чисел {1, 2, 3 п, ...}, если отношение следования задано в нем так:

1 3  5 7….

2  4  6 8….

288. Приведите примеры заданий из учебников математики для начальных классов, в которых правильность выполнения заданий объясняется аксиомами Пеано.

Аксиоматический метод в математике.

Основные понятия и отношения аксиоматической теории натурального ряда. Определение натурального числа.

Сложение натуральных чисел.

Умножение натуральных чисел.

Свойства множества натуральных чисел

Вычитание и деление натуральных чисел.

Аксиоматический метод в математике

При аксиоматическом построении какой-либо математической теории соблюдаются определенные правила :

1. Некоторые понятия теории выбираются в качестве основных и принимаются без определения.

2. Формулируются аксиомы , которые в данной теории принимаются без доказательства, в них раскрываются свойства основных понятий.

3. Каждому понятию теории, которое не содержится в списке основных, даётся определение , в нём разъясняется его смысл с помощью основных и предшествующих данному понятию.

4. Каждое предложение теории, которое не содержится в списке аксиом, должно быть доказано. Такие предложения называют теоремами и доказывают их на основе аксиом и теорем, предшествующих рассматриваемой.

Система аксиом должна быть:

а) непротиворечивой: мы должны быть уверены,что, делая всевозможные выводы из данной системы аксиом, никогда не придем к противоречию;

б) независимой : никакая аксиома не должна быть следствием других аксиом этой системы.

в) полной , если в ее рамках всегда можно доказать или данное утверждение, или его отрицание.

Первым опытом аксиоматического построения теории можно считать изложение геометрии Евклидом в его "Началах"(3 в. до н.э.). Значительный вклад в развитие аксиоматического метода построения геометрии и алгебры внесли Н.И. Лобачевский и Э.Галуа. В конце 19 в. итальянским математиком Пеано была разработана система аксиом для арифметики.

Основные понятия и отношения аксиоматической теории натурального числа. Определение натурального числа.

В качестве основного(неопределяемого) понятия в некотором множестве N выбирается отношение , а также используются теоретико-множественные понятия, а также правила логики.

Элемент, непосредственно следующий за элементом а, обозначают а".

Отношения «непосредственно следовать за» удовлетворяет следующим аксиомам:

Аксиомы Пеано :

Аксиома 1 . В множестве N существует элемент, непосредственно не следующий ни за каким элементом этого множества. Будем называть его единицей и обозначать символом 1 .

Аксиома 2 . Для каждого элемента а из N существует единственный элемент а" , непосредственно следующий за а .

Аксиома 3 . Для каждого элемента а из N существует не более одного элемента, за которым непосредственно следует а .

Аксиома 4. Всякое подмножество М множества N совпадает с N , если обладает свойствами: 1) 1 содержится в М ; 2) из того, что а содержится в М , следует, что и а" содержится в М.

Определение 1 . Множество N , для элементов которого установлено отношение «непосредственно следовать за », удовлетворяющее аксиомам 1-4, называется множеством натуральных чисел , а его элементы - натуральными числами .

В данном определении ничего не говорится о природе элементов множества N . Значит, она может быть какой угодно. Выбирая в качестве множества N некоторое конкретное множество, на котором задано конкретное отношение «непосредственно следовать за», удовлетворяющее аксиомам 1-4, мы получим модель данной системы аксиом.

Стандартной моделью системы аксиом Пеано является возникший в процессе исторического развития общества ряд чисел: 1,2,3,4,... Натуральный ряд начинается с числа 1 (аксиома 1); за каждым натуральным числом непосредственно следует единственное натуральное число (аксиома 2); каждое натуральное число непосредственно следует не более чем за одним натуральным числом (аксиома 3); начиная от числа 1 и переходя по порядку к непосредственно следующим друг за другом натуральным числам, получаем все множество этих чисел (аксиома 4).

Итак, мы начали аксиоматическое построение системы натуральных чисел с выбора основного отношения «непосредственно следовать за» и аксиом, в которых описаны его свойства. Дальнейшее построение теории предполагает рассмотрение известных свойств натуральных чисел и операций над ними. Они должны быть раскрыты в определениях и теоремах, т.е. выведены чисто логическим путем из отношения «непосредственно следовать за», и аксиом 1-4.

Первое понятие, которое мы введем после определения натурального числа, - это отношение «непосредственно предшествует» , которое часто используют при рассмотрении свойств натурального ряда.

Определение 2. Если натуральное число b непосредственно следует за натуральным числом а , то число а называется непосредственно предшествующим (или предшествующим) числу b .

Отношение «предшествует» обладает рядом свойств .

Теорема 1. Единица не имеет предшествующего натурального числа.

Теорема 2. Каждое натуральное число а , отличное от 1, имеет единственное предшествующее число b , такое, что b" = а.

Аксиоматическое построение теории натуральных чисел не рас­сматривается ни в начальной, ни в средней школе. Однако те свойства отношения «непосредственно следовать за», которые нашли отражение в аксиомах Пеано, являются предметом изучения в начальном курсе математики. Уже в первом классе при рассмотрении чисел первого десятка выясняется, как может быть получено каждое число. При этом используются понятия «следует» и «предшествует». Каждое новое число выступает как продолжение изученного отрезка натурального ряда чисел. Учащиеся убеждаются в том, что за каждым числом идет следующее, и притом только одно, что натуральный ряд чисел бесконечен.

Сложение натуральных чисел

По правилам построения аксиоматической теории, определение сложения натуральных чисел нужно ввести, используя только отно­шение «непосредственно следовать за» , и понятия «натуральное чис­ло» и «предшествующее число» .

Предварим определение сложения следующими рассуждениями. Если к любому натуральному числу а прибавить 1, то получим число а", непосредственно следующее за а , т.е. а + 1 = а" и, следовательно, мы получим правило прибавления 1 к любому натуральному числу. Но как прибавлять к числу а натуральное число b, отличное от 1? Воспользуемся следующим фактом: если известно, что 2 + 3 = 5, то сумма 2 + 4 = 6, которое непосредственно следует за числом 5. Происходит так потому, что в сумме 2 + 4 второе слагаемое есть число, непосредственно следующее за числом 3. Таким образом, 2 + 4 =2+3" =(2+3)". В общем виде имеем, .

Эти факты положены в основу определения сложения натуральных чисел в аксиоматической теории.

Определение 3 . Сложениемнатуральных чисел называется алгеб­раическая операция, обладающая свойствами:

Число а + b называется суммой чисел а и b , а сами числа а иb - слагаемыми .