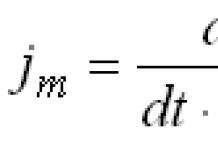Avant de répondre à votre question, permettez-moi d'abord de préciser que je pense qu'il y a une confusion. En mathématiques formelles, $infty$ n'est pas un nombre. La raison pour laquelle les mathématiciens ne traitent pas $infty$ comme un nombre est que si nous le faisions, nous tirerions des conclusions qui sont clairement fausses.

Par exemple, l’une des propriétés des nombres est que vous pouvez soustraire le même nombre des deux côtés d’une équation et l’équation sera toujours vraie. Par exemple, je peux soustraire $1$ des deux côtés de l'équation $x+1=4$ pour obtenir $x=3$ . D'un autre côté, si je traite $infty$ comme un nombre régulier et que je soustrais $infty$ des deux côtés de "l'équation" $infty + 1 = \infty$ , j'obtiens $1=0$ , ce qui est clairement faux.

Au lieu de cela, les mathématiciens considèrent $infty$ comme limite. En gros, cela signifie que si vous voulez "brancher" $infty$ dans une fonction, vous branchez de plus en plus de chiffres et voyez ce qui se passe dans long terme. Par exemple, nous écrivons $lim_(x\to\infty)\frac(1)(x)=0$ pour signifier que "à mesure que vous branchez des nombres de plus en plus grands dans la fonction $f (x) = 1/x$ , la fonction devient arbitrairement proche de zéro. Vous devez vous convaincre que cette limite particulière est correcte. Dans certains cas, la limite est infinie ; tout cela signifie que, à mesure que vous insérez des nombres de plus en plus grands dans la fonction, la fonction devient arbitrairement grande. Par exemple,

• $lim_(x à infty)x = infty$ .
• $lim_(x à infty)x^2 = infty$ .

Pour répondre à votre question, à peu près tout peut arriver lorsque $infty$ est impliqué. Regardons les deux exemples que je viens de donner. Même si les deux fonctions $f (x) = x$ et $g (x) = x^2$ vont à l'infini lorsque $x$ va à l'infini, la seconde grandit beaucoup plus rapide. Exemple concret : $f (100) = 100 $ et $g (100) = 10 000 $. En fait, $g (x)$ croît tellement plus vite que la différence $g (x) - f (x)$ (rappelez-vous qu'il ne s'agit que de $x^2-x$) va également vers l'infini à mesure que $x$ va à l'infini. Vous pouvez vous en convaincre en branchant des valeurs. Dans les symboles, $lim_(x\to\infty)(x^2 - x) = \infty.$ Donc, de manière informelle, il est possible que $infty-infty = infty$ !

Si ce résultat vous semble contre-intuitif, c'est que vous considérez les deux infinis du côté gauche de l'équation $infty-infty = infty$ comme le même $infty$ : en fait, ils sont différents. Le premier $infty$ vient de la fonction $g (x) = x^2$ , et dans un certain sens c'est plus gros que le $infty$ de la fonction $f (x) = x$ puisque $x^2$ grossit beaucoup plus rapidement que $x$.

Dans tous les cas, vous pouvez proposer d'autres fonctions (c'est-à-dire que vous pouvez approcher $infty$ à différentes vitesses) qui rendent les affirmations suivantes vraies :

• $infty- infty$ peut être égal à n'importe quoi entre $- infty$ et $+ infty$ .
• $infty/ infty$ peut être égal à n'importe quoi entre $- infty$ et $+ infty$ .
• $infty^0$ peut être égal à n'importe quoi entre $0$ et $+ infty$ .

Enfin, il peut y avoir des cas où brancher $infty$ ne vous donne aucune réponse. Si vous avez suivi la trigonométrie, vous connaissez probablement la fonction sinusoïdale, dont le graphique oscille d'avant en arrière, comme une onde, entre $- 1$ et $+ 1$ . (J'ai essayé de mettre une image du graphique du sinus ici, mais je n'ai pas réussi à le faire fonctionner car je suis nouveau sur ce site. Recherchez simplement "graphique du sinus" sur Google images et vous verrez ce que je veux dire. .) Si vous branchez des nombres de plus en plus grands dans $sin (x)$ , vous n'approcherez d'aucun nombre fixe. Alors $sin infty$ n'existe pas.

« Ce que nous savons est limité, mais ce que nous ne savons pas est infini. »

Pierre-Simon Laplace (1749-1827), scientifique français

Un amour sans limites, un bonheur immense, un vaste espace, du pergélisol, un océan sans limites et même une leçon sans fin. DANS Vie courante Nous appelons souvent les choses et les phénomènes infinis, mais souvent nous ne pensons même pas au véritable sens de ce concept. Pendant ce temps, depuis l’Antiquité, les théologiens, philosophes et autres plus grands esprits de l’humanité ont essayé d’en comprendre la signification. Et seuls les mathématiciens ont progressé le plus dans la connaissance de ce qu’on appelle l’infini.

Qu'est-ce que l'infini ?

Une grande partie de ce que nous voyons autour de nous est perçue par nous comme l'infini, mais en réalité, il s'avère que ce sont des choses complètement finies. C’est ainsi qu’ils expliquent parfois aux enfants à quel point l’infini est grand : « Si vous collectez un grain de sable tous les cent ans sur une immense plage, alors il faudra une éternité pour collecter tout le sable de la plage. » Mais en réalité, le nombre de grains de sable n’est pas infini. Il est physiquement impossible de les compter, mais on peut affirmer avec certitude que leur nombre ne dépasse pas une valeur égale au rapport de la masse de la Terre à la masse d'un grain de sable.

Ou un autre exemple. Beaucoup de gens pensent que si vous vous tenez entre deux miroirs, le reflet se répétera dans les deux miroirs, s'éloignant, devenant de plus en plus petit, de sorte qu'il est impossible de déterminer où il se termine. Hélas, ce n'est pas l'infini. Que se passe-t-il réellement ? Aucun miroir ne reflète 100 % de la lumière qui lui tombe dessus. Un miroir de très haute qualité peut réfléchir 99 % de la lumière, mais après 70 réflexions il n'en restera que 50 %, après 140 réflexions il ne restera que 25 % de la lumière, etc. jusqu'à ce qu'il y ait trop peu de lumière. De plus, la plupart des miroirs sont incurvés, de sorte que les nombreux reflets que vous voyez se retrouvent « au détour du virage ».

Voyons comment les mathématiques traitent l'infini. Ceci est très différent de tout concept d’infini que vous avez rencontré auparavant et nécessite un peu d’imagination.

L'infini en mathématiques

En mathématiques, il y a une distinction potentiel Et actuel infini.

Lorsqu'ils disent qu'une certaine quantité a un potentiel infini, ils veulent dire qu'elle peut être augmentée indéfiniment, c'est-à-dire qu'il y a toujours un potentiel d'augmentation.

Le concept d’infini réel désigne une valeur infinie qui existe déjà réellement « ici et maintenant ». Expliquons cela en utilisant l'exemple d'une ligne DIRECT ordinaire.

Exemple 1.

L'infini potentiel signifie qu'il existe une ligne droite et qu'elle peut être étendue de manière continue (par exemple, en lui appliquant des segments). Veuillez noter que l'accent n'est pas ici mis sur le fait que la ligne est infinie, mais sur le fait qu'elle peut être continuée indéfiniment.

L’infini réel signifie que la totalité de la ligne droite infinie existe déjà à l’heure actuelle. Mais le problème est que pas une seule personne vivante n’a vu une ligne droite infinie et n’est physiquement incapable de le faire ! C'est une chose de pouvoir étendre une ligne droite à l'infini, et une autre de créer réellement une ligne droite sans fin. Cette différence très subtile distingue l’infini potentiel de l’infini réel. Pouah! Il faut beaucoup d’imagination pour composer avec ces infinis ! Regardons un autre exemple.

Exemple 2.

Supposons que vous décidiez de construire une série de nombres naturels : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10...

À un moment donné, vous atteignez un très grand nombre n et vous pensez que c’est le plus grand nombre. A ce moment, votre ami vous dit que cela ne lui coûte rien d'ajouter 1 (un) à votre nombre n et d'obtenir un nombre encore plus grand k = n + 1. Alors vous, légèrement blessé, comprenez que rien ne peut vous empêcher d'ajouter au numéro k un et obtenez le nombre k+1. Le nombre de ces démarches est-il limité à l’avance ? Non. Bien sûr, vous et votre ami n'aurez peut-être pas assez de force ou de temps à une étape m pour passer à l'étape suivante m + 1, mais potentiellement vous ou quelqu'un d'autre pouvez continuer à construire cette série. Dans ce cas, nous obtenons la notion d’infini potentiel.

Si vous et votre ami parvenez à construire une série infinie de nombres naturels dont les éléments sont présents tous en même temps, ce sera l’infini réel. Mais le fait est que personne ne peut écrire tous les chiffres - c'est un fait incontestable !

Convenez que l'infini potentiel est plus compréhensible pour nous, car il est plus facile à imaginer. Par conséquent, les philosophes et mathématiciens anciens ne reconnaissaient que l’infini potentiel, rejetant résolument la possibilité d’opérer avec l’infini réel.

Le paradoxe de Galilée

En 1638, le grand Galilée posait la question : « L’infini plusieurs est-il toujours également infiniment plusieurs ? Ou peut-il y avoir des infinis plus grands et plus petits ?

Il a formulé un postulat qui reçut plus tard le nom de « paradoxe de Galilée » : il y a autant d'entiers naturels qu'il y a de carrés d'entiers naturels, c'est-à-dire dans l'ensemble 1, 2, 3, 4, 5, 6, 7, 8, 9, 10... il y a le même nombre d'éléments, combien y en a-t-il dans l'ensemble 1, 4, 9, 16, 25, 36, 49, 64, 81, 100...

L'essence du paradoxe est la suivante.

Certains nombres sont des carrés parfaits (c'est-à-dire des carrés d'autres nombres), par exemple : 1, 4, 9... D'autres nombres ne sont pas des carrés parfaits, par exemple 2, 3, 5... Cela signifie qu'il devrait y avoir plus des carrés parfaits et des nombres ordinaires ensemble, plutôt que de simples carrés parfaits. Droite? Droite.

Mais d'un autre côté : pour chaque nombre il y a son carré exact, et vice versa - pour chaque carré exact il y a un tout Racine carrée, il devrait donc y avoir le même nombre de carrés exacts et de nombres naturels. Droite? Droite.

Le raisonnement de Galilée est entré en conflit avec l'axiome indéniable selon lequel le tout est plus grand que chacune de ses parties. Il ne pouvait pas répondre quel infini est le plus grand - le premier ou le second. Galilée croyait que soit il s'était trompé sur quelque chose, soit que de telles comparaisons ne s'appliquaient pas à l'infini. Sur ce dernier point, il avait raison puisque, trois siècles plus tard, Georg Cantor démontra que « l’arithmétique de l’infini est différente de l’arithmétique du fini ».

Infinis dénombrables : la partie est égale au tout

Georg Cantor(1845-1918), le fondateur de la théorie des ensembles, commença à utiliser l’infini réel en mathématiques. Il a admis que l'infini existe d'un seul coup. Et comme il existe une infinité d’ensembles, d’un seul coup, il est possible d’effectuer des manipulations mathématiques avec eux et même de les comparer. Les mots « nombre » et « montant » étant inappropriés dans le cas des infinis, il a introduit le terme « puissance ». Comme norme, Cantor a pris des nombres naturels infinis, qui suffisent pour tout compter, a appelé cet ensemble dénombrable, et sa puissance - la puissance d'un ensemble dénombrable, et a commencé à le comparer avec les puissances d'autres ensembles.

Il a prouvé que l’ensemble des nombres naturels comporte autant d’éléments que l’ensemble des nombres pairs ! En effet, écrivons l’un en dessous de l’autre :

1 2 3 4 5 6 7 8 9 10...

2 4 6 8 10 12 14 16 18 20...

À première vue, il semble évident que la première série contient deux fois plus de nombres que la seconde. Mais, d'un autre côté, il est clair que la deuxième séquence est également dénombrable, puisque n'importe lequel de ses nombres correspond TOUJOURS exactement à un nombre de la première séquence. Et vice versa! La deuxième séquence ne peut donc pas être épuisée avant la première. Par conséquent, ces ensembles sont tout aussi puissants ! Il est également prouvé que l’ensemble des carrés des nombres naturels (du paradoxe de Galilée) est dénombrable et égal à l’ensemble des nombres naturels. Il s’ensuit que tous les infinis dénombrables sont de puissance égale.

Cela s’avère très intéressant : l’ensemble des nombres pairs et l’ensemble des carrés des nombres naturels (du paradoxe de Galilée) font partie de l’ensemble des nombres naturels. Mais en même temps, ils sont tout aussi puissants. Donc LA PARTIE EST ÉGALE AU TOUT !

D'innombrables infinis

Mais tout infini ne peut pas être recalculé de la même manière que nous l’avons fait avec des nombres pairs et des carrés de nombres naturels. Il s'avère qu'on ne peut pas compter les points d'un segment, les nombres réels (exprimés par toutes les fractions décimales finies et infinies), même tous les nombres réels de 0 à 1. En mathématiques, on dit que leur nombre est indénombrable.

Regardons cela en utilisant l'exemple d'une séquence de nombres fractionnaires. Les nombres fractionnaires ont une propriété que les nombres entiers n'ont pas. Il n’y a pas d’autres entiers entre deux entiers consécutifs. Par exemple, aucun autre entier ne « rentrera » entre 8 et 9. Mais si l’on ajoute des nombres fractionnaires à l’ensemble des nombres entiers, cette règle ne tient plus. Oui, le numéro

sera compris entre 8 et 9. De même, vous pouvez trouver un nombre situé entre deux nombres A et B quelconques :

Puisque cette action peut être répétée indéfiniment, on peut affirmer qu’entre deux nombres réels quelconques, il y aura toujours un nombre infini d’autres nombres réels.

Ainsi, l’infinité des nombres réels est indénombrable, et l’infinité des nombres naturels est dénombrable. Ces infinis ne sont pas équivalents, mais à partir d'un ensemble indénombrable de nombres réels, il est toujours possible de sélectionner une partie dénombrable, par exemple des nombres naturels ou pairs. Par conséquent, l’infini indénombrable est plus puissant que l’infini dénombrable.

Tout le monde connaît ce chiffre et l’utilise pour décrire quelque chose d’incompréhensiblement énorme. Cependant, l’infini n’est pas un concept aussi simple qu’il y paraît à première vue.

1. Selon les règles de l’infini, il existe un nombre infini de nombres pairs et impairs. Cependant, les nombres impairs représenteront exactement la moitié du nombre total.

2. L'infini plus un est égal à l'infini, si nous soustrayons un, nous obtenons l'infini, en ajoutant deux infinis, nous obtenons l'infini, l'infini divisé par deux est égal à l'infini, si nous soustrayons l'infini de l'infini, le résultat n'est pas tout à fait clair, mais l'infini divisé par l'infini est le plus probable , est égal à un.

3. Les scientifiques ont déterminé que dans la partie connue de l'Univers, il y a 1080 particules subatomiques - c'est la partie qui a été étudiée. De nombreux scientifiques sont convaincus que l'Univers est infini, et les scientifiques sceptiques quant à l'infinité de l'Univers admettent toujours une telle possibilité dans ce domaine.

4. Si l'Univers est infini, alors d'un point de vue mathématique, il s'avère que quelque part il y a Copie exacte notre planète, car il est possible que les atomes du « jumeau » occupent la même position que sur notre planète. Les chances qu'une telle option existe sont négligeables, mais univers infini cela est non seulement possible, mais doit aussi nécessairement se produire, et au moins un nombre infini de fois, pourvu que l'Univers soit encore infiniment infini.

5. Cependant, tout le monde n’est pas convaincu que l’Univers est infini. Le mathématicien israélien Doron Selberger est convaincu que les nombres ne peuvent pas augmenter indéfiniment, et qu'il existe un nombre si énorme que si vous y ajoutez un, vous obtenez zéro. Cependant, ce nombre et sa signification dépassent de loin la compréhension humaine et il est probable que ce nombre ne sera jamais trouvé ou prouvé. Cette croyance est le principe central de la philosophie mathématique connue sous le nom d’Ultra-Infini.

Comment fonctionne le « brainmail » : transmettre des messages de cerveau à cerveau via Internet

10 mystères du monde que la science a enfin révélés

10 questions principales sur l’Univers auxquelles les scientifiques cherchent actuellement des réponses

Mystère scientifique vieux de 2 500 ans : pourquoi nous bâillons

Atome, lustre, nuctéméron et sept autres unités de temps dont vous n'avez pas entendu parler

Des univers parallèles pourraient réellement exister, selon une nouvelle théorie

L'infini est concept abstrait, utilisé pour décrire ou désigner quelque chose d'infini ou d'illimité. Ce concept est important pour les mathématiques, l'astrophysique, la physique, la philosophie, la logique et l'art.

Voici quelques-uns faits incroyables sur ce concept complexe qui peut époustoufler toute personne peu familiarisée avec les mathématiques.

symbole de l'infini

L'infini a son propre symbole spécial : ∞. Le symbole, ou lemniscate, a été introduit par le pasteur et mathématicien John Wallis en 1655. Le mot « lemniscate » vient de mot latin lemniscus, signifiant « ruban ».

Wallis a peut-être basé le symbole de l'infini sur le chiffre romain 1000, à côté duquel les Romains écrivaient « innombrables », en plus du nombre. Il est également possible que le symbole soit basé sur l'oméga (Ω ou ω), dernière lettre Alphabet grec.

Un fait intéressant est que le concept de l’infini existait et était utilisé bien avant que Wallis ne lui donne le symbole que nous utilisons encore aujourd’hui.

Au quatrième siècle avant JC, un texte mathématique jaïn appelé Surya Prajnapti Sutra divisait tous les nombres en trois catégories, chacune étant à son tour divisée en trois sous-catégories. Ces catégories comprenaient des nombres dénombrables, non dénombrables et infinis.

Aporie de Zénon

Zénon d'Élée, né vers le Ve siècle avant JC. e., était connu pour ses paradoxes, ou apories, y compris le concept d'infini.

De tous les paradoxes de Zénon, le plus célèbre est Achille et la Tortue. En aporie, la tortue défie héros grec Achille, l'invitant à une course. La tortue prétend qu'elle gagnera la course si Achille lui donne une avance de mille pas. Selon le paradoxe, pendant qu'Achille parcourt toute la distance, la tortue fera encore cent pas dans la même direction. Pendant qu'Achille parcourt encore cent pas, la tortue aura le temps d'en faire dix de plus, et ainsi de suite par ordre décroissant.

D'une manière plus simple, le paradoxe s'analyse comme suit : essayez de traverser une pièce si chaque étape suivante est la moitié de la taille de la précédente. Bien que chaque pas vous rapproche du bord de la pièce, vous ne l'atteindrez jamais réellement, ou vous y parviendrez, mais cela prendra un nombre infini de pas.

Selon l’une des interprétations modernes, ce paradoxe repose sur la fausse idée de la divisibilité infinie du temps et de l’espace.

Pi est un exemple de l'infini

Un bon exemple d’infini est le nombre pi. Les mathématiciens utilisent un symbole pour pi car il est impossible d’écrire le nombre entier. Pi est constitué d'un nombre infini de nombres. Il est souvent arrondi à 3,14 ou même à 3,14159, mais le nombre de chiffres écrits après la virgule n'a pas d'importance, car il est impossible d'arriver à la fin du nombre.

Théorème du singe infini

Une autre façon de penser à l’infini est de considérer le théorème du singe infini. Selon le théorème, si vous donnez à un singe une machine à écrire et un temps infini, le singe finira par être capable de taper Hamlet ou toute autre œuvre.

Alors que de nombreuses personnes considèrent un théorème comme une démonstration de la conviction que rien n'est impossible, les mathématiciens le considèrent comme une preuve qu'un certain événement est impossible.

Fractales et infini

Une fractale est un objet mathématique abstrait utilisé en mathématiques et en art, le plus souvent elle modélise phénomène naturel. Une fractale s'écrit sous la forme d'une équation mathématique. En regardant une fractale, vous pouvez remarquer sa structure complexe à n’importe quelle échelle. En d’autres termes, la fractale est extensible à l’infini.

Le flocon de neige de Koch est exemple intéressant fractale Un flocon de neige ressemble à un triangle équilatéral, formant une courbe fermée de longueur infinie. En augmentant la courbe, vous pouvez voir de plus en plus de détails. Le processus d’augmentation de la courbe peut se poursuivre un nombre infini de fois. Bien que le flocon de neige de Koch ait une superficie limitée, elle est limitée par une ligne infiniment longue.

Infinité de différentes tailles

L’infini est illimité, mais il peut être mesuré, quoique de manière relative. Chiffres positifs(supérieurs à 0) et les nombres négatifs (inférieurs à 0) peuvent se vanter d'avoir des ensembles infinis de nombres tailles égales. Que se passe-t-il si vous combinez les deux ensembles ? Donne un ensemble deux fois plus grand. Ou un autre exemple - tous les nombres pairs (il y en a un nombre infini). Et pourtant, ce n’est que la moitié d’un nombre infini de tous les entiers. Autre exemple, ajoutez simplement un à l'infini. Apprenez le chiffre 1 supérieur à l'infini.

Cosmologie et infini

Les cosmologues étudient l’Univers et il n’est pas surprenant que le concept d’infini joue pour eux un rôle important. L'Univers a-t-il des limites ou est-il infini ?

Cette question reste toujours sans réponse. Notre Univers est en expansion, mais où ? Et où est la limite à cette expansion ? Même s’il existe des limites à l’univers physique, nous avons toujours la théorie du multivers, qui considère l’existence d’un nombre infini d’univers, qui peuvent avoir des lois physiques différentes des nôtres.

Division par zéro

Il n'y a pas de division par zéro. C’est impossible, du moins en mathématiques ordinaires. Dans les mathématiques auxquelles nous sommes habitués, un divisé par zéro ne peut pas être défini. C'est une erreur. Cependant, ce n'est pas toujours le cas. Dans la théorie étendue nombres complexes diviser un par zéro ne provoque pas d’effondrement imminent et est déterminé par une certaine forme d’infini. En d’autres termes, les mathématiques sont différentes, et elles ne sont pas toutes limitées par les règles des manuels.

En contact avec

L'infini existe-t-il ?

L’Univers est-il infini, et si c’est le cas, alors « cela ne peut pas être ». Et si non, qu'est-ce qu'il y a de l'autre côté ? Et qui aime les contes de fées sur les limitesdes variétés sans bord, comme une sphère, permettent à la pensée d'être envoyée perpendiculairement au bord.Qu'y a-t-il là? Ou qui. L'infini fictif n'est pas si perçant, mais aussiincompréhensible, par endroits. Georg Cantor. Comparaison des infinis. Continuum. SurIl y a autant de points dans un carré que sur un segment.

La sensation de brûlure flétrie de l’éternité spatiale est choquante tant que les problèmes de l’Empire Céleste sont perçus par l’intestin et non par l’esprit. Puis un appel perçant " inépuisabilité« Petit à petit, ça cale, et, brûlé par la réalité, la personne se cache dans un monde imaginaire. Il n’est toujours pas possible de bien se cacher.

Dans le monde des idées, l’infini apparaît sous une forme différente. Dans quel sens existe-t-il les séries naturelles ? En tant que processus en cours ou en tant que processus achevé ? Entiers Peuvent-ils être construits ou sont-ils déjà disponibles ? Problème au début

des relents de scolastique. Est-ce vraiment important, semble-t-il. Il n'y a aucune conséquence.

Les conséquences sont pourtant énormes. L’alternative est deux mathématiques différentes. L’une est constructive, ne permettant pas la réalisation de l’infini dans toute son immensité. L'autre est un omnivore ordinaire.

Des troubles mineurs dus à la présence de l'infini surviennent déjà dans l'élémentaire

des situations telles que celle où la présence d'une correspondance bijective n ↔ n^2 encourage l'idée qu'il y a autant d'entiers qu'il y a de carrés. L’exemple a longtemps fait grincer des dents, mais il est forme la plus simple indique qu'il y a un problème. Il s’avère que si quelqu’un me prend 10 roubles chaque jour et m’en donne un, alors une fois le processus terminé, nous serons quittes. Car si la série a déjà eu lieu, nième rouble m'a été donné le nième jour. Le paradoxe, bien sûr, n'en vaut pas la peine, car le processus ne se terminera jamais, pense l'élève de cinquième année.

Qu’en est-il des fractions p/q ? Ils sont tous « déjà là » sur le segment. Ils sont là, vous n’avez pas besoin de les ajouter un par un. Donc - " piège de taille finie pour l'infini" Petit

un portefeuille où sont placées toutes les fractions. Et la racine de deux est comme un infini accompli, du fait de l’infinité de la fraction décimale. La théorie des ensembles a donc toutes les raisons de considérer l’infini comme « donné" Une autre chose est que certaines exigences sont imposées à cette donnée afin qu'aucune contradiction ne surgisse.

Cependant, dès que vous admettez quelque chose, les ennuis commencent. Un essaim d'infinis, et avec

ils doivent être gérés d’une manière ou d’une autre. j'ai fait ça Georg Cantor, qui a créé la théorie des ensembles. La révolution qui a eu lieu confirme la thèse bien connue « la vérité naît comme hérésie et meurt comme banalité" Les idées principales sont aujourd’hui accessibles à tous. UN " Alors" impossible

il n'y avait personne pour expliquer. L’intuition était contre. Maintenant que la maladie a pris racine, la perplexité s'est apaisée.

Cantor a utilisé l'outil de correspondance biunivoque comme base pour l'étude des ensembles. Les ensembles X, Y sont équivalents si une correspondance biunivoque peut être établie entre leurs éléments.

Relation d'équivalence par réflexe Et transitivement, ce qui permet de tout casser

ensembles en classes d’équivalence. La classe d'équivalence d'un ensemble X est appelée sa cardinalité et est notée |X|. Les ensembles sont ordonnés par cardinalité en utilisant une astuce naturelle.

Les ensembles équivalents à une série naturelle sont appelés dénombrables. Toute séquence est dénombrable. Considération décimales rencontre un nouveau phénomène. L'ensemble de ces nombres (continuum) s'avère indénombrable.

La tentative historique d'établir qu'un segment et un carré x ont des cardinalités différentes a été très pénible. Il s’est avéré qu’ils étaient identiques. Le monde n'a pas connu un tel bouleversement depuis l'époque de Galilée, lorsqu'on découvrit que tous les corps tombaient de la même manière.

accélération.

Quoi qu’il en soit, l’infini a gagné une place au soleil. Sans cela, tout en mathématiques « resterait immobile ». Oui, c’est le cas – dans les mathématiques constructives, là où les mathématiques ordinaires ne conviennent pas. Les égalités et inégalités des nombres constructifs ne sont le plus souvent pas vérifiées, les séquences n'ont nulle part où converger, les limites n'existent pas, la continuité n'est qu'un rêve, et en général tout s'effondre. Une image terrible. L'ampleur du désastre est même difficile à évaluer. Par conséquent, l’infini est presque aussi utile que « un ». Le revers de la médaille, pour ainsi dire. Une sorte de conteneur pour « ce qui n’arrive pas ».