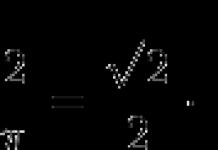Exemples (nombre de racines d'une équation algébrique)
1) X 2 – 4X+ 5 = 0 - équation algébrique du deuxième degré (équation quadratique) 
2 
= 2 je- deux racines ;
2) X 3 + 1 = 0 - équation algébrique du troisième degré (équation binomiale) 
;
3) P. 3 (X) = X 3 + X 2 – X– 1 = 0 – équation algébrique du troisième degré ;
nombre X 1 = 1 est sa racine, puisque P. 3 (1) 
0 donc par le théorème de Bezout 
; diviser le polynôme P. 3 (X) par binôme ( X– 1) « dans une colonne » :
|
|
équation originale P. 3 (X) = X 3 + X 2 – X – 1 = 0 (X – 1)(X 2 + 2X + 1) = 0 (X – 1)(X + 1) 2 = 0 X 1 = 1 - racine simple, X 2 = –1 - racine double. |
|
Propriété 2 (sur les racines complexes d'une équation algébrique à coefficients réels) |
|
Si une équation algébrique à coefficients réels a des racines complexes, alors ces racines sont toujours des paires complexes conjuguées, c'est-à-dire si le nombre |
est la racine de l'équation
, puis le numéro 
est aussi la racine de cette équation. Pour le prouver, vous devez utiliser la définition et les propriétés suivantes facilement vérifiables de l'opération de conjugaison complexe :
Si 
, Que 
et les égalités sont valables :
,
,
,
,
Si 
est un nombre réel, alors 
.
Parce que 
est la racine de l'équation 
, Que 
Où 
-- nombres réels à 
.
Prenons la conjugaison des deux côtés de la dernière égalité et utilisons les propriétés répertoriées de l'opération de conjugaison :
, c'est-à-dire le nombre 
satisfait également l'équation 
, est donc sa racine
Exemples (racines complexes d'équations algébriques à coefficients réels)
Grâce à la propriété prouvée concernant l'appariement des racines complexes d'une équation algébrique avec des coefficients réels, une autre propriété des polynômes est obtenue.
Nous procéderons du développement (6) du polynôme 
aux facteurs linéaires :
Laissez le numéro X 0
= un
+ bi- racine complexe d'un polynôme P. n (X), c'est-à-dire que c'est l'un des nombres 
. Si tous les coefficients de ce polynôme sont des nombres réels, alors le nombre 
est aussi sa racine, c'est-à-dire parmi les nombres 
il y a aussi un numéro 
.
Calculons le produit des binômes 
:
Le résultat est un trinôme quadratique avec de vraies chances
Ainsi, toute paire de binômes avec des racines conjuguées complexes dans la formule (6) conduit à un trinôme quadratique à coefficients réels.
Exemples (factorisation d'un polynôme à coefficients réels)
1)P. 3 (X) = X 3 + 1 = (X + 1)(X 2 – X + 1);
2)P. 4 (X) = X 4 – X 3 + 4X 2 – 4X = X(X –1)(X 2 + 4).
|
Propriété 3 (sur les racines entières et rationnelles d'une équation algébrique à coefficients entiers réels) |
|
Donnons-nous une équation algébrique
 |
, tous les coefficients 
qui sont des entiers réels,1. Que ce soit un entier 
est la racine de l'équation
Puisque le nombre entier 
représenté par le produit d'un nombre entier 
et les expressions qui ont une valeur entière.
2. Laissez l'équation algébrique 
a une racine rationnelle
, de plus, les chiffres p
Et q sont relativement premiers 
.
Cette identité peut s'écrire en deux versions :
De la première version de la notation il résulte que 
, et à partir du second – quoi 
, puisque les chiffres p
Et q sont relativement premiers.
Exemples (sélection de racines entières ou rationnelles d'une équation algébrique à coefficients entiers)
Formules pour les racines d'une équation quadratique. Les cas de racines réelles, multiples et complexes sont considérés. Factoriser un trinôme quadratique. Interprétation géométrique. Exemples de détermination des racines et de factorisation.
ContenuVoir également: Résoudre des équations quadratiques en ligne
Formules de base
Considérons l'équation quadratique :
(1)
.
Racines d'une équation quadratique(1) sont déterminés par les formules :
;
.
Ces formules peuvent être combinées comme ceci :
.
Lorsque les racines d'une équation quadratique sont connues, alors un polynôme du deuxième degré peut être représenté comme un produit de facteurs (factorisé) :
.
Ensuite, nous supposons qu'il s'agit de nombres réels.
Considérons discriminant d'une équation quadratique:
.
Si le discriminant est positif, alors l'équation quadratique (1) a deux racines réelles différentes :
;
.
Alors la factorisation du trinôme quadratique a la forme :
.
Si le discriminant est égal à zéro, alors l'équation quadratique (1) a deux racines réelles multiples (égales) :
.
Factorisation :
.
Si le discriminant est négatif, alors l'équation quadratique (1) a deux racines conjuguées complexes :
;
.
Voici l'unité imaginaire, ;
et sont les parties réelles et imaginaires des racines :
;
.
Alors
.
Interprétation graphique
Si vous tracez la fonction
,
qui est une parabole, alors les points d'intersection du graphique avec l'axe seront les racines de l'équation
.
Lorsque , le graphique coupe l'axe des x (axe) en deux points ().
Lorsque , le graphique touche l'axe des x en un point ().
Lorsque , le graphique ne traverse pas l’axe des x ().
Formules utiles liées à l'équation quadratique
(f.1) ;
(f.2) ;
(f.3) .
Dérivation de la formule des racines d'une équation quadratique
Nous effectuons des transformations et appliquons les formules (f.1) et (f.3) :
,
Où
;
.
Ainsi, nous avons obtenu la formule d'un polynôme du deuxième degré sous la forme :
.
Cela montre que l'équation
effectué à
Et .
Autrement dit, et sont les racines de l'équation quadratique
.
Exemples de détermination des racines d'une équation quadratique
Exemple 1
(1.1)
.
.
En comparant avec notre équation (1.1), on retrouve les valeurs des coefficients :
.
On trouve le discriminant :
.
Puisque le discriminant est positif, l’équation a deux racines réelles :
;
;
.
De là on obtient la factorisation du trinôme quadratique :
.
Graphique de la fonction y = 2 x 2 + 7 x + 3 coupe l'axe des x en deux points.
Traçons la fonction
.
Le graphique de cette fonction est une parabole. Il croise l'axe des abscisses (axis) en deux points :
Et .
Ces points sont les racines de l'équation originale (1.1).
;
;
.
Exemple 2
Trouvez les racines d'une équation quadratique :
(2.1)
.
Écrivons l'équation quadratique sous forme générale :
.
En comparant avec l'équation originale (2.1), on retrouve les valeurs des coefficients :
.
On trouve le discriminant :
.
Puisque le discriminant est nul, l'équation a deux racines multiples (égales) :
;
.
Alors la factorisation du trinôme a la forme :
.
Graphique de la fonction y = x 2 - 4 x + 4 touche l’axe des x à un moment donné.
Traçons la fonction
.
Le graphique de cette fonction est une parabole. Il touche l'axe des x (axe) en un point :
.
Ce point est la racine de l’équation originale (2.1). Car cette racine est factorisée deux fois :
,
alors une telle racine est généralement appelée un multiple. Autrement dit, ils croient qu'il existe deux racines égales :
.
;
.
Exemple 3
Trouvez les racines d'une équation quadratique :
(3.1)
.
Écrivons l'équation quadratique sous forme générale :
(1)
.
Réécrivons l'équation originale (3.1) :
.
En comparant avec (1), on retrouve les valeurs des coefficients :
.
On trouve le discriminant :
.
Le discriminant est négatif, . Il n’y a donc pas de véritables racines.
Vous pouvez trouver des racines complexes :
;
;
.
Alors
.
Le graphique de la fonction ne traverse pas l'axe des x. Il n’y a pas de véritables racines.
Traçons la fonction
.
Le graphique de cette fonction est une parabole. Il ne coupe pas l'axe des x (axe). Il n’y a donc pas de véritables racines.
Il n’y a pas de véritables racines. Racines complexes :
;
;
.
Le projet envisage une méthode permettant de trouver approximativement les racines d'une équation algébrique - la méthode Lobachevsky-Greffe. L'idée de la méthode, son schéma de calcul sont définis dans l'ouvrage et les conditions d'applicabilité de la méthode sont trouvées. Une implémentation de la méthode Lobachevsky-Greffe est présentée.
1 PARTIE THÉORIQUE 6
1.1 Énoncé du problème 6
1.2 Équations algébriques 7
1.2.1 Concepts de base sur l'équation algébrique 7
1.2.2 Racines de l'équation algébrique 7
1.2.3 Nombre de racines réelles du polynôme 9
1.3 Méthode Lobachevsky – Greffe pour la solution approximative d'équations algébriques 11
1.3.1 Idée de méthode 11
1.3.2 Carré des racines 13
2.1 Tâche 1 16
2.2 Tâche 2 18
2.4 Analyse des résultats obtenus 20
LISTE DES RÉFÉRENCES 23
INTRODUCTION
La technologie informatique d’aujourd’hui fournit des outils puissants pour effectuer réellement le travail de comptage. Grâce à cela, dans de nombreux cas, il est devenu possible d'abandonner l'interprétation approximative des problèmes appliqués et de passer à la résolution de problèmes dans une formulation exacte. L’utilisation raisonnable de la technologie informatique moderne est inconcevable sans l’application habile de méthodes d’analyse approximative et numérique.
Les méthodes numériques visent à résoudre des problèmes qui se posent dans la pratique. Résoudre un problème à l'aide de méthodes numériques se résume à des opérations arithmétiques et logiques sur des nombres, ce qui nécessite l'utilisation de technologies informatiques, telles que les tableurs des programmes bureautiques modernes pour ordinateurs personnels.
L'objectif de la discipline « Méthodes numériques » est de trouver la méthode la plus efficace pour résoudre un problème précis.
La résolution d'équations algébriques est l'un des problèmes essentiels de l'analyse appliquée, dont le besoin se fait sentir dans des domaines nombreux et divers de la physique, de la mécanique, de la technologie et des sciences naturelles au sens large du terme.
Ce projet de cours est consacré à l'une des méthodes de résolution d'équations algébriques - la méthode Lobachevsky-Greffe.
Le but de ce travail est d'examiner l'idée de la méthode Lobachevsky-Greffe pour résoudre des problèmes algébriques et de fournir un schéma informatique pour trouver de vraies racines à l'aide de MS Office Excel. Le projet examine les principales questions théoriques liées à la recherche des racines des équations algébriques à l'aide de la méthode Lobachevsky – Greffe. La partie pratique de ce travail présente des solutions aux équations algébriques à l'aide de la méthode Lobachevsky – Greffe.
1 PARTIE THÉORIQUE
1.1 Énoncé du problème
Soit un ensemble X d'éléments x et un ensemble Y avec des éléments y. Supposons également qu'un opérateur soit défini sur l'ensemble X, qui affecte à chaque élément x de X un élément y de Y. Prenons un élément
et nous nous sommes fixé pour objectif de trouver de tels éléments 
, Pour qui 
est une image. Ce problème équivaut à résoudre l'équation
(1.1)
Les problèmes suivants peuvent lui être posés.
Conditions d'existence d'une solution à l'équation.
Condition d'unicité d'une solution de l'équation.
Un algorithme de solution, à la suite duquel il serait possible de trouver, en fonction de l'objectif et des conditions, exactement ou approximativement toutes les solutions de l'équation (1.1), ou n'importe quelle solution spécifiée à l'avance, ou l'une des solutions existantes.
il y aura une certaine fonction. Dans ce cas, l’équation (1.1) peut s’écrire sous la forme 
(1.2)
Dans la théorie des méthodes numériques, on s’efforce de construire un processus informatique à l’aide duquel on peut trouver une solution à l’équation (1.2) avec une précision prédéterminée. Les processus convergents sont particulièrement importants, car ils permettent de résoudre l’équation avec n’importe quelle erreur, aussi petite soit-elle.
Notre tâche est de trouver, d'une manière générale, approximativement, l'élément 
. À cette fin, un algorithme est en cours de développement qui produit une séquence de solutions approximatives 
, et de telle sorte que la relation soit vraie
1.2 Équations algébriques
1.2.1 Concepts de base sur l'équation algébrique
Considérons une équation algébrique de nième degré
où sont les coefficients 
sont des nombres réels, et 
.
Théorème 1.1 (théorème fondamental de l'algèbre). L'équation algébrique du nième degré (1.3) a exactement n racines, réelles et complexes, à condition que chaque racine soit comptée autant de fois que sa multiplicité.
Dans ce cas, ils disent que la racine de l’équation (1.3) a une multiplicité s si
, 
.
Les racines complexes de l’équation (1.3) ont la propriété de conjugaison par paire.
Théorème 1.2. Si les coefficients de l'équation algébrique (1.3) sont réels, alors les racines complexes de cette équation sont des conjuguées complexes par paires, c'est-à-dire Si 
(
sont des nombres réels) est la racine de l'équation (1.3), de multiplicité s, alors le nombre 
est aussi la racine de cette équation et a la même multiplicité s.
Conséquence. Une équation algébrique de degré impair à coefficients réels possède au moins une racine réelle.
1.2.2 Racines d'une équation algébrique
Si
sont les racines de l’équation (1.3), alors le membre de gauche a le développement suivant : . (1.6)
En multipliant les binômes dans la formule (1.6) et en égalisant les coefficients aux mêmes puissances de x aux côtés gauche et droit de l'égalité (1.6), on obtient les relations entre les racines et les coefficients de l'équation algébrique (1.3) :
(1.7)
Si l'on prend en compte les multiplicités des racines, alors le développement (1.6) prend la forme
,
Où
–différentes racines de l'équation (1) et 
– leur multiplicité, et 
.
Dérivé 
s'exprime ainsi :
où Q(x) est un polynôme tel que
à k=1,2,…,m Donc le polynôme
est le plus grand diviseur commun du polynôme
et son dérivé 
, et peut être trouvé en utilisant l'algorithme euclidien. Faisons un quotient 
,
et on obtient un polynôme
avec de vraies chances
, A 1 , A 2 ,…, A m , dont les racines 
sont différents. Ainsi, résoudre une équation algébrique à racines multiples se réduit à résoudre une équation algébrique d’ordre inférieur à racines différentes.
1.2.3 Nombre de racines réelles d'un polynôme
Une idée générale du nombre de racines réelles de l'équation (1.3) sur l'intervalle (a,b) est donnée par le graphique de la fonction
, où les racines 
sont les abscisses des points d'intersection du graphique avec l'axe Ox. Notons quelques propriétés du polynôme P(x) :
Si P(a)P(b)
Si P(a)P(b)>0, alors sur l'intervalle (a, b) il y a un nombre pair ou pas de racines du polynôme P(x).
Définition. Soit un système fini ordonné de nombres réels non nuls :
,
,…,
(1.9)
On dit que pour une paire d'éléments adjacents
, 
système (1.9), il y a un changement de signe si ces éléments ont des signes opposés, c'est-à-dire 
,
et il n'y a pas de changement de signe si leurs signes sont les mêmes, c'est-à-dire
.
Définition. Nombre total de changements de signe de toutes les paires d'éléments adjacents
, 
le système (1.9) est appelé le nombre de changements de signe dans le système (1.9). Définition. Pour un polynôme P(x) donné, le système de Sturm est le système de polynômes
,
, 
, 
,…, 
,
Où 
, – le reste pris de signe opposé lors de la division d'un polynôme par , – le reste pris de signe opposé lors de la division d'un polynôme par, etc.
Remarque 1. Si un polynôme n'a pas de racines multiples, alors le dernier élément du système de Sturm est un nombre réel non nul.
Remarque 2. Les éléments du système Sturm peuvent être calculés jusqu'à un facteur numérique positif près.
Notons N(c) le nombre de changements de signe dans le système de Sturm en x=c, à condition de barrer les éléments zéro de ce système.
Théorème 1.5. (Théorème de Sturm). Si le polynôme P(x) n'a pas plusieurs chevaux et 
, 
, alors le nombre de ses racines réelles 
sur l'intervalle 
exactement égal au nombre de changements de signe perdus dans le système Sturm du polynôme 
en déménageant de 
avant 
, c'est à dire.
.
Corollaire 1. Si
, puis le numéro 
positif et nombre 
les racines négatives du polynôme sont respectivement égales 
,
.
Corollaire 2. Pour que toutes les racines d'un polynôme P(x) de degré n, qui n'a pas de racines multiples, soient réelles, il faut et il suffit que la condition soit satisfaite
.
Ainsi, dans l’équation (1.3) toutes les racines seront valides si et seulement si :
À l'aide du système Sturm, vous pouvez séparer les racines d'une équation algébrique en divisant l'intervalle (a,b), contenant toutes les racines réelles de l'équation, en un nombre fini d'intervalles partiels.
tel que 
.
1.3 Méthode Lobachevsky – Greffe pour la solution approximative d'équations algébriques
1.3.1 Idée de la méthode
Considérons l'équation algébrique (1.3).Faisons comme si
, (1.15)
ceux. les racines ont un module différent et le module de chaque racine précédente est nettement supérieur au module de la suivante. En d’autres termes, supposons que le rapport de deux racines adjacentes quelconques, comptées par ordre décroissant de leurs nombres, est une quantité petite en valeur absolue :
, (1.16)
Où 
Et 
– petite valeur. De telles racines sont appelées séparées.
(1.17)
Où 
, 
,…, 
– des quantités petites en valeur absolue par rapport à l’unité. Négliger dans le système (1.17) les quantités 
, nous aurons des relations approximatives 
(1.18)
Où trouve-t-on les racines ? 
(1.19)
La précision des racines dans le système d'égalités (1.20) dépend de la petite valeur absolue des quantités 
dans les relations (1.16)
Pour réaliser la séparation des racines, sur la base de l'équation (1.3), ils composent l'équation transformée
, (1.20)
dont les racines
, 
,…, 
sont les pouvoirs m-e des racines 
, 
,…, 
équation (1.3). Si toutes les racines de l'équation (1.3) sont différentes et que leurs modules satisfont à la condition (1.17), alors pour un m suffisamment grand les racines , ,..., de l'équation (1.20) seront séparées, car
à 
.
Évidemment, il suffit de construire un algorithme pour trouver une équation dont les racines seront les carrés des racines de l'équation donnée. Il sera alors possible d'obtenir une équation dont les racines seront égales aux racines de l'équation originale à la puissance
.
1.3.2 Carré des racines
On écrit le polynôme (1.3) sous la forme suivanteEt multipliez-le par un polynôme de la forme
Ensuite, nous obtenons
Après avoir effectué un remplacement
et en multipliant par 
, aura . (1.21)
Les racines du polynôme (1.21) sont liées aux racines du polynôme (1.3) par la relation suivante
.
L’équation qui nous intéresse est donc
,
dont les coefficients sont calculés à l'aide de la formule (1.22)
, (1.22)
où l'on suppose que
à 
.
En appliquant successivement k fois le processus de mise au carré des racines au polynôme (1.3), on obtient le polynôme
, (1.23)
dans lequel
, 
, etc. Pour k suffisamment grand, il est possible de s’assurer que les racines de l’équation (1.23) satisfont au système
(1.24)
Déterminons le nombre k pour lequel le système (1.24) est satisfait avec une précision donnée.
Supposons que le k requis ait déjà été atteint et que les égalités (1.24) soient satisfaites avec la précision acceptée. Faisons encore une transformation et trouvons le polynôme
,
pour lequel le système (1.24) est également valable pour
.
Car en vertu de la formule (1.22)
, (1.25)
puis, en substituant (1.25) dans le système (1.24), on obtient que les valeurs absolues des coefficients
doit être égal à la précision acceptée des carrés des coefficients 
. La réalisation de ces égalités indiquera que la valeur requise de k a déjà été atteinte à la kième étape. Ainsi, la mise au carré des racines de l'équation (1.3) doit être arrêtée si, dans la précision acceptée, seuls les coefficients au carré sont conservés du côté droit de la formule (1.24) et que la somme doublée des produits est inférieure à la limite de précision.
Ensuite, les racines réelles de l'équation sont séparées et leurs modules sont trouvés par la formule
(1.26)
Le signe de la racine peut être déterminé par une estimation approximative en substituant les valeurs 
Et 
dans l’équation (1.3).
2 PARTIE PRATIQUE
2.1 Tâche 1
. (2.1)
Tout d'abord, établissons le nombre de racines réelles et complexes dans l'équation (2.1). Pour ce faire, nous utiliserons le théorème de Sturm.
Le système de Sturm pour l’équation (2.1) aura la forme suivante :
D'où le tirons-nous ?
Tableau 2.1.
|
Polynôme |
Points sur l'axe réel |
|
 |
 |
|
 |
+ |
+ |
 |
– |
+ |
 |
– |
– |
 |
– |
+ |
 |
– |
– |
|
Nombre de changements de signe |
1 |
3 |
Ainsi, nous constatons que le nombre de racines réelles dans l’équation (2.1) est égal à
,
ceux. l'équation (2.1) contient 2 racines réelles et deux racines complexes.
Pour trouver les racines de l’équation, nous utilisons la méthode Lobachevsky – Greffe pour une paire de racines conjuguées complexes.
Mettons au carré les racines de l'équation. Les coefficients ont été calculés à l'aide de la formule suivante 
, (2.2)
Où 
, (2.3)
UN 
considéré égal à 0 lorsque 
.
Les résultats des calculs à huit chiffres significatifs sont donnés dans le tableau 2.2.
Tableau 2.2.
|
je |
0 |
1 |
2 |
3 |
4 |
 |
|||||
 |
0 |
-3.8000000E+01 |
3.5400000E+02 |
3.8760000E+03 |
0 |
 |
1 |
4.3000000E+01 |
7.1500000E+02 |
4.8370000E+03 |
1.0404000E+04 |
 |
|||||
 |
0 |
-1.4300000E+03 |
-3.9517400E+05 |
-1.4877720E+07 |
0 |
 |
1 |
4.1900000E+02 |
1.1605100E+05 |
8.5188490E+06 |
1.0824322E+08 |
 |
|||||
 |
0 |
-2.3210200E+05 |
-6.9223090E+09 |
-2.5123467E+13 |
0 |
 |
1 |
-5.6541000E+04 |
6.5455256E+09 |
4.7447321E+13 |
1.1716594E+16 |
 |
|||||
 |
0 |
-1.3091051E+10 |
5.3888712E+18 |
-1.5338253E+26 |
0 |
 |
1 |
-9.8941665E+09 |
4.8232776E+19 |
2.0978658E+27 |
1.3727857E+32 |
 |
|||||
 |
0 |
-9.6465552E+19 |
4.1513541E+37 |
-1.3242653E+52 |
0 |
 |
1 |
1.4289776E+18 |
2.3679142E+39 |
4.3877982E+54 |
1.8845406E+64 |
 |
|||||
 |
0 |
-4.7358285E+39 |
-1.2540130E+73 |
-8.9248610+103 |
0 |
 |
1 |
-4.7337865E+39 |
5.6070053E+78 |
1.9252683+109 |
3.5514932+128 |
 |
|||||
 |
0 |
-1.1214011E+79 |
1.8227619+149 |
-3.9826483+207 |
0 |
 |
1 |
1.1194724E+79 |
3.1438509+157 |
3.7066582+218 |
1.2613104+257 |
Comme le montre le tableau 2.2 à la 7ème étape, les racines 
, 
(en comptant par ordre décroissant des modules) peuvent être considérés comme séparés. On trouve les modules des racines à l'aide de la formule (1.27) et on détermine leur signe à l'aide d'une estimation approximative :
Puisque le coefficient converti à 
change de signe, alors cette équation a des racines complexes, qui sont déterminées à partir de l'équation (1.31) à l'aide des formules (1.29) et (1.30) :
je.
2.2 Tâche 2
À l'aide de la méthode Lobatchevski – Greffe, résolvez l'équation :. (2.4)
Pour commencer, en utilisant le théorème de Sturm, nous déterminons le nombre de racines réelles et complexes dans l’équation (2.2).
Pour cette équation, le système de Sturm a la forme
D'où le tirons-nous ?
Tableau 2.3.
|
Polynôme |
Points sur l'axe réel |
|
|
|
|
|
|
|
+ |
+ |
|
|
– |
+ |
|
|
+ |
+ |
|
|
– |
+ |
|
|
– |
– |
|
Nombre de changements de signe |
3 |
1 |
Ainsi, nous constatons que le nombre de racines réelles dans l’équation (2.2) est égal à
,
ceux. l'équation (2.2) contient 2 racines réelles et deux racines complexes.
Pour trouver approximativement les racines de l’équation, nous utiliserons la méthode Lobachevsky – Greffe pour une paire de racines conjuguées complexes.
Mettons au carré les racines de l'équation. Nous calculerons les coefficients à l'aide des formules (2.2) et (2.3).
Les résultats des calculs à huit chiffres significatifs sont donnés dans le tableau 2.4
Tableau 2.4.
|
je |
0 |
1 |
2 |
3 |
4 |
|
|
|||||
|
|
0 |
-9.2000000E+00 |
-3.3300000E+01 |
1.3800000E+02 |
0 |
.
Et 
dans l’équation (2.4), ce qui entraîne des erreurs d’ordres différents (4,52958089E-11 et 4,22229789E-06, respectivement) pour le même nombre d’itérations.Etc. est de nature pédagogique générale et revêt une grande importance pour l'étude de TOUT le cours de mathématiques supérieures. Aujourd'hui, nous allons répéter les équations « scolaires », mais pas seulement celles « scolaires » - mais celles que l'on retrouve partout dans divers problèmes de vyshmat. Comme d'habitude, l'histoire sera racontée de manière appliquée, c'est-à-dire Je ne me concentrerai pas sur les définitions et les classifications, mais partagerai avec vous mon expérience personnelle pour les résoudre. Les informations s'adressent principalement aux débutants, mais les lecteurs plus avancés trouveront également de nombreux points intéressants. Et bien sûr, il y aura du nouveau matériel qui va au-delà du lycée.
Donc l'équation…. Beaucoup se souviennent de ce mot avec un frisson. Que valent les équations « sophistiquées » avec racines... ... oubliez-les ! Car alors vous rencontrerez les « représentants » les plus inoffensifs de cette espèce. Ou des équations trigonométriques ennuyeuses avec des dizaines de méthodes de résolution. Pour être honnête, je ne les aimais pas vraiment moi-même... Ne pas paniquer! – alors ce sont surtout des « pissenlits » qui vous attendent avec une solution évidente en 1 à 2 étapes. Même si la « bardane » s'accroche certainement, il faut ici être objectif.
Curieusement, en mathématiques supérieures, il est beaucoup plus courant de traiter des équations très primitives comme linéaireéquations
Que signifie résoudre cette équation ? Cela signifie trouver TELLE valeur de « x » (racine) qui en fait une véritable égalité. Jetons le « trois » vers la droite avec un changement de signe :
et déposez le « deux » sur le côté droit (ou, la même chose - multipliez les deux côtés par)
:
Pour vérifier, remplaçons le trophée gagné dans l’équation originale : 
L'égalité correcte est obtenue, ce qui signifie que la valeur trouvée est bien la racine de cette équation. Ou, comme on dit aussi, satisfait à cette équation.
Veuillez noter que la racine peut également s'écrire sous forme de fraction décimale :
Et essayez de ne pas vous en tenir à ce mauvais style ! J'ai répété la raison plus d'une fois, notamment lors de la toute première leçon sur algèbre supérieure.
D’ailleurs, l’équation peut aussi être résolue « en arabe » :
Et ce qui est le plus intéressant, c’est que cet enregistrement est totalement légal ! Mais si vous n'êtes pas enseignant, alors il vaut mieux ne pas faire ça, car ici l'originalité est punissable =)
Et maintenant un peu sur
méthode de solution graphique
L'équation a la forme et sa racine est Coordonnée "X" points d'intersection graphique de fonction linéaire avec le graphique d'une fonction linéaire (axe x):
Il semblerait que l'exemple soit si élémentaire qu'il n'y a plus rien à analyser ici, mais une autre nuance inattendue peut en être « extraite » : présentons la même équation sous la forme et construisons des graphiques des fonctions : 
Où, s'il te plaît, ne confonds pas les deux concepts: une équation est une équation, et fonction– c'est une fonction ! Les fonctions seulement de l'aide trouver les racines de l'équation. Il peut y en avoir deux, trois, quatre, voire une infinité. L'exemple le plus proche en ce sens est le célèbre équation quadratique, l'algorithme de solution pour lequel a reçu un paragraphe séparé des formules scolaires « chaudes ». Et ce n'est pas un hasard ! Si vous pouvez résoudre une équation quadratique et savoir théorème de Pythagore, alors, pourrait-on dire, "la moitié des mathématiques supérieures est déjà dans votre poche" =) Exagéré, bien sûr, mais pas si loin de la vérité !
Par conséquent, ne soyons pas paresseux et résolvons une équation quadratique en utilisant algorithme standard:
, ce qui signifie que l'équation a deux valeurs différentes valide racine: 
Il est facile de vérifier que les deux valeurs trouvées satisfont réellement à cette équation : 
Que faire si vous avez soudainement oublié l'algorithme de solution et qu'il n'y a aucun moyen/coup de main à portée de main ? Cette situation peut survenir, par exemple, lors d'un contrôle ou d'un examen. Nous utilisons la méthode graphique ! Et il y a deux manières : vous pouvez construire point par point parabole 
, découvrant ainsi où il croise l'axe (si ça traverse du tout). Mais il vaut mieux faire quelque chose de plus astucieux : imaginer l'équation sous la forme, dessiner des graphiques de fonctions plus simples - et Coordonnées "X" leurs points d'intersection sont bien visibles ! 
S'il s'avère que la ligne droite touche la parabole, alors l'équation a deux racines correspondantes (plusieurs). S'il s'avère que la ligne droite ne coupe pas la parabole, alors il n'y a pas de véritables racines.
Pour ce faire, bien sûr, vous devez être capable de construire graphiques de fonctions élémentaires, mais d'un autre côté, même un écolier peut acquérir ces compétences.
Et encore une fois - une équation est une équation, et les fonctions sont des fonctions qui seulement aidé résous l'équation!
Et ici, d'ailleurs, il conviendrait de rappeler encore une chose : si tous les coefficients d'une équation sont multipliés par un nombre non nul, alors ses racines ne changeront pas.
Ainsi, par exemple, l'équation 
a les mêmes racines. Comme simple « preuve », je vais retirer la constante entre parenthèses : 
et je l'enlèverai sans douleur (Je diviserai les deux parties par « moins deux »):
MAIS! Si l'on considère la fonction 
, alors vous ne pouvez pas vous débarrasser de la constante ici ! Il est uniquement permis de retirer le multiplicateur entre parenthèses : 
.
Beaucoup de gens sous-estiment la méthode de résolution graphique, la considérant comme « indigne », et certains oublient même complètement cette possibilité. Et c’est fondamentalement faux, car tracer des graphiques sauve parfois la situation !
Autre exemple : supposons que vous ne vous souveniez pas des racines de l’équation trigonométrique la plus simple : . La formule générale se trouve dans les manuels scolaires, dans tous les ouvrages de référence sur les mathématiques élémentaires, mais ils ne sont pas à votre disposition. Cependant, il est essentiel de résoudre l’équation (c’est-à-dire « deux »). Il y a une sortie ! – construire des graphiques de fonctions : 
après quoi on note calmement les coordonnées « X » de leurs points d'intersection : 
Il existe une infinité de racines, et en algèbre leur notation condensée est acceptée :
, Où ( – ensemble d'entiers)
.
Et, sans « s'éloigner », quelques mots sur la méthode graphique de résolution des inégalités à une variable. Le principe est le même. Ainsi, par exemple, la solution de l’inégalité est n’importe quel « x », car La sinusoïde se situe presque entièrement sous la ligne droite. La solution de l'inégalité est l'ensemble des intervalles dans lesquels les morceaux de la sinusoïde se trouvent strictement au-dessus de la droite (axe des x):
ou, en bref :
Mais voici les nombreuses solutions à l’inégalité : vide, puisqu'aucun point de la sinusoïde ne se trouve au-dessus de la droite.
Y a-t-il quelque chose que vous ne comprenez pas ? Étudiez de toute urgence les leçons sur ensembles Et graphiques de fonctions!
Nous allons réchauffer:
Exercice 1
Résolvez graphiquement les équations trigonométriques suivantes :
Réponses à la fin de la leçon
Comme vous pouvez le constater, pour étudier les sciences exactes, il n'est pas du tout nécessaire de fourrer des formules et des ouvrages de référence ! De plus, il s’agit d’une approche fondamentalement erronée.
Comme je vous l'ai déjà rassuré au tout début de la leçon, les équations trigonométriques complexes dans un cours standard de mathématiques supérieures doivent être résolues extrêmement rarement. En règle générale, toute complexité se termine par des équations comme , dont la solution est constituée de deux groupes de racines provenant des équations les plus simples et 
. Ne vous inquiétez pas trop de résoudre ce dernier problème – regardez dans un livre ou trouvez-le sur Internet =)
La méthode de résolution graphique peut également être utile dans des cas moins triviaux. Considérons, par exemple, l’équation « ragtag » suivante :
Les perspectives de sa solution semblent... ne ressemblent à rien du tout, mais il suffit d'imaginer l'équation sous la forme , construire graphiques de fonctions et tout s'avérera incroyablement simple. Il y a un dessin au milieu de l'article sur fonctions infinitésimales (s'ouvrira dans l'onglet suivant).
En utilisant la même méthode graphique, vous pouvez découvrir que l'équation a déjà deux racines, et l'une d'elles est égale à zéro, et l'autre, apparemment, irrationnel et appartient au segment . Cette racine peut être calculée approximativement, par exemple, méthode tangente. D'ailleurs, dans certains problèmes, il arrive que vous n'ayez pas besoin de trouver les racines, mais découvrez est-ce qu'ils existent du tout ?. Et ici aussi, un dessin peut aider - si les graphiques ne se croisent pas, alors il n'y a pas de racines.
Racines rationnelles de polynômes à coefficients entiers.
Schéma Horner
Et maintenant je vous invite à tourner votre regard vers le Moyen Âge et à ressentir l'atmosphère unique de l'algèbre classique. Pour une meilleure compréhension du matériel, je vous recommande de lire au moins un peu nombres complexes.
Ils sont les meilleurs. Polynômes.
L'objet de notre intérêt sera les polynômes les plus courants de la forme avec entier coefficients Un nombre naturel s'appelle degré de polynôme, nombre – coefficient du plus haut degré (ou juste le coefficient le plus élevé), et le coefficient est Membre gratuit.
Je désignerai brièvement ce polynôme par .
Racines d'un polynôme appeler les racines de l'équation
J'adore la logique de fer =)
Pour des exemples, allez au tout début de l'article : 
Il n'y a aucun problème pour trouver les racines des polynômes des 1er et 2e degrés, mais à mesure que vous augmentez, cette tâche devient de plus en plus difficile. Même si d'un autre côté, tout est plus intéressant ! Et c’est exactement à cela que sera consacrée la deuxième partie de la leçon.
Tout d’abord, littéralement la moitié de l’écran de la théorie :
1) D'après le corollaire théorème fondamental de l'algèbre, le polynôme de degré a exactement complexe racines. Certaines racines (voire toutes) peuvent être particulièrement valide. De plus, parmi les racines réelles, il peut y avoir des racines identiques (plusieurs) (minimum deux, maximum pièces).
Si un nombre complexe est la racine d’un polynôme, alors conjuguer son nombre est aussi nécessairement la racine de ce polynôme (les racines complexes conjuguées ont la forme ).
L'exemple le plus simple est une équation quadratique, rencontrée pour la première fois en 8 (comme) classe, et que nous avons finalement « terminé » dans le sujet nombres complexes. Je vous le rappelle : une équation quadratique a soit deux racines réelles différentes, soit des racines multiples, soit des racines complexes conjuguées.
2) De Théorème de Bezout il s'ensuit que si un nombre est la racine d'une équation, alors le polynôme correspondant peut être factorisé :
, où est un polynôme de degré .
Et encore une fois, notre vieil exemple : puisque est la racine de l’équation, alors . Après quoi, il n’est pas difficile d’obtenir la fameuse extension « école ».
Le corollaire du théorème de Bezout a une grande valeur pratique : si l'on connaît la racine d'une équation du 3ème degré, alors on peut la représenter sous la forme 
et à partir de l’équation quadratique, il est facile de découvrir les racines restantes. Si l’on connaît la racine d’une équation du 4ème degré, alors il est possible de développer le côté gauche en un produit, etc.
Et il y a deux questions ici :
Question une. Comment trouver cette racine ? Tout d'abord, définissons sa nature : dans de nombreux problèmes de mathématiques supérieures il faut trouver rationnel, en particulier entier racines des polynômes, et à cet égard, nous nous intéresserons plus loin à elles principalement.... ...ils sont si bons, si moelleux, qu'on a envie de les retrouver ! =)
La première chose qui vient à l’esprit est la méthode de sélection. Considérons, par exemple, l'équation . Le problème ici est dans le terme libre - s'il était égal à zéro, alors tout irait bien - nous retirons le « x » des parenthèses et les racines elles-mêmes « tombent » à la surface : 
Mais notre terme libre est égal à « trois », et nous commençons donc à substituer divers nombres dans l'équation qui prétendent être « racine ». Tout d'abord, la substitution de valeurs uniques s'impose. Remplaçons : 
Reçu Incorrect l’égalité, donc l’unité « ne correspondait pas ». Bon, d'accord, remplaçons : 
Reçu vraiégalité! Autrement dit, la valeur est la racine de cette équation.
Pour trouver les racines d'un polynôme du 3ème degré, il existe une méthode analytique (les formules dites de Cardano), mais maintenant nous nous intéressons à une tâche légèrement différente.
Puisque - est la racine de notre polynôme, le polynôme peut être représenté sous la forme et apparaît Deuxième question: comment trouver un « petit frère » ?
Les considérations algébriques les plus simples suggèrent que pour ce faire, nous devons diviser par . Comment diviser un polynôme par un polynôme ? La même méthode scolaire qui divise les nombres ordinaires - « colonne » ! J'ai discuté de cette méthode en détail dans les premiers exemples de la leçon. Limites complexes, et maintenant nous allons examiner une autre méthode, appelée Schéma Horner.
Nous écrivons d’abord le polynôme « le plus élevé » avec tout le monde
, y compris les coefficients nuls:
, après quoi nous saisissons ces coefficients (strictement dans l'ordre) dans la ligne supérieure du tableau :
On écrit la racine à gauche :
Je ferai immédiatement une réserve sur le fait que le schéma de Horner fonctionne également si le nombre « rouge » Pas est la racine du polynôme. Cependant, ne précipitons pas les choses.
Nous supprimons le coefficient dominant d'en haut :
Le processus de remplissage des cellules inférieures rappelle un peu la broderie, où le « moins un » est une sorte d'« aiguille » qui imprègne les étapes suivantes. Nous multiplions le nombre « reporté » par (–1) et ajoutons le nombre de la cellule supérieure au produit :
Nous multiplions la valeur trouvée par « l'aiguille rouge » et ajoutons le coefficient d'équation suivant au produit :
Et enfin, la valeur résultante est à nouveau « traitée » avec « l'aiguille » et le coefficient supérieur :
Le zéro dans la dernière cellule nous indique que le polynôme est divisé en sans laisser de trace (comme cela devrait être), tandis que les coefficients de dilatation sont « supprimés » directement de la ligne du bas du tableau :
Ainsi, on est passé de l'équation à une équation équivalente et tout est clair avec les deux racines restantes (dans ce cas, nous obtenons des racines complexes conjuguées).
Soit dit en passant, l'équation peut également être résolue graphiquement : tracer "foudre" 
et voyez que le graphique croise l'axe des x ()
au point . Ou la même astuce « rusée » : nous réécrivons l'équation sous la forme , dessinons des graphiques élémentaires et détectons la coordonnée « X » de leur point d'intersection.
À propos, le graphique de tout polynôme de fonction du 3ème degré coupe l'axe au moins une fois, ce qui signifie que l'équation correspondante a au moins un valide racine. Ce fait est vrai pour toute fonction polynomiale de degré impair.
Et ici, je voudrais aussi m'attarder sur point important qui concerne la terminologie : polynôme Et fonction polynomiale – ce n'est pas la même chose! Mais dans la pratique, on parle souvent, par exemple, du « graphique d'un polynôme », ce qui, bien sûr, est de la négligence.
Cependant, revenons au schéma de Horner. Comme je l'ai mentionné récemment, ce système fonctionne pour d'autres numéros, mais si le numéro Pas est la racine de l'équation, alors une addition (reste) non nulle apparaît dans notre formule :
"Exécutons" la valeur "échec" selon le schéma de Horner. Dans ce cas, il est pratique d'utiliser le même tableau - écrivez une nouvelle "aiguille" à gauche, déplacez le coefficient dominant d'en haut (flèche verte gauche), et c'est parti : 
Pour vérifier, ouvrons les parenthèses et présentons des termes similaires :
, D'ACCORD.
Il est facile de remarquer que le reste (« six ») est exactement la valeur du polynôme en . Et en fait, comment ça se passe : 
, et encore plus sympa - comme ceci :
A partir des calculs ci-dessus, il est facile de comprendre que le schéma de Horner permet non seulement de factoriser le polynôme, mais aussi d'effectuer une sélection « civilisée » de la racine. Je vous propose de consolider vous-même l'algorithme de calcul avec une petite tâche :
Tâche 2
À l'aide du schéma de Horner, trouvez la racine entière de l'équation et factorisez le polynôme correspondant
En d'autres termes, vous devez ici vérifier séquentiellement les nombres 1, –1, 2, –2, ... – jusqu'à ce qu'un reste zéro soit « dessiné » dans la dernière colonne. Cela signifiera que « l’aiguille » de cette droite est la racine du polynôme
Il est pratique de regrouper les calculs dans un seul tableau. Solution détaillée et réponse à la fin de la leçon.
La méthode de sélection des racines convient aux cas relativement simples, mais si les coefficients et/ou le degré du polynôme sont grands, le processus peut prendre beaucoup de temps. Ou peut-être qu'il y a des valeurs de la même liste 1, –1, 2, –2 et cela ne sert à rien de les considérer ? Et, en plus, les racines peuvent s'avérer fractionnées, ce qui conduira à un piquage totalement non scientifique.
Heureusement, il existe deux théorèmes puissants qui peuvent réduire considérablement la recherche de valeurs « candidates » pour les racines rationnelles :
Théorème 1 Considérons irréductible fraction , où . Si le nombre est la racine de l'équation, alors le terme libre est divisé par et le coefficient principal est divisé par.
En particulier, si le coefficient dominant est , alors cette racine rationnelle est un entier :
Et nous commençons à exploiter le théorème avec juste ce détail savoureux :
Revenons à l'équation. Puisque son coefficient directeur est , alors les racines rationnelles hypothétiques peuvent être exclusivement entières, et le terme libre doit nécessairement être divisé en ces racines sans reste. Et « trois » ne peut être divisé qu’en 1, –1, 3 et –3. Autrement dit, nous n'avons que 4 « candidats racines ». Et, selon Théorème 1, d'autres nombres rationnels ne peuvent pas être racines de cette équation EN PRINCIPE.
Il y a un peu plus de « prétendants » dans l'équation : le terme libre est divisé en 1, –1, 2, – 2, 4 et –4.
Attention, les chiffres 1, –1 sont des « habitués » de la liste des racines possibles (une conséquence évidente du théorème) et le meilleur choix pour les tests prioritaires.
Passons à des exemples plus significatifs :
Problème 3
Solution: puisque le coefficient dominant est , alors les racines rationnelles hypothétiques ne peuvent être que des nombres entiers, et elles doivent nécessairement être des diviseurs du terme libre. « Moins quarante » est divisé en les paires de nombres suivantes :
– un total de 16 « candidats ».
Et ici apparaît immédiatement une pensée tentante : est-il possible d’éliminer toutes les racines négatives ou toutes les racines positives ? Dans certains cas, c'est possible ! Je formulerai deux signes :
1) Si Tous Si les coefficients du polynôme sont non négatifs ou tous non positifs, alors il ne peut pas avoir de racines positives. Malheureusement, ce n'est pas notre cas (Maintenant, si on nous donnait une équation - alors oui, lors de la substitution d'une valeur du polynôme, la valeur du polynôme est strictement positive, ce qui signifie que tous les nombres positifs (et les irrationnels aussi) ne peuvent pas être les racines de l’équation.
2) Si les coefficients des puissances impaires sont non négatifs, et pour toutes les puissances paires (y compris membre gratuit) sont négatifs, alors le polynôme ne peut pas avoir de racines négatives. Ou « miroir » : les coefficients des puissances impaires sont non positifs, et pour toutes les puissances paires ils sont positifs.
C'est notre cas ! En regardant d’un peu plus près, vous pouvez voir qu’en remplaçant un « X » négatif dans l’équation, le membre de gauche sera strictement négatif, ce qui signifie que les racines négatives disparaissent.
Il reste donc 8 nombres à rechercher :
Nous les « facturons » séquentiellement selon le schéma de Horner. J'espère que vous maîtrisez déjà le calcul mental : 
La chance nous attendait lors du test du « deux ». Ainsi, la racine de l’équation considérée est-elle, et
Reste à étudier l'équation 
. C'est facile à faire grâce au discriminant, mais je vais effectuer un test indicatif en utilisant le même schéma. Notons tout d’abord que le terme libre est égal à 20, ce qui signifie Théorème 1 les nombres 8 et 40 sortent de la liste des racines possibles, laissant les valeurs à la recherche (un a été éliminé selon le schéma de Horner).
Nous écrivons les coefficients du trinôme dans la rangée supérieure du nouveau tableau et On commence à vérifier avec les mêmes "deux". Pourquoi? Et parce que les racines peuvent être multiples, s'il vous plaît : - cette équation a 10 racines identiques. Mais ne nous laissons pas distraire : 
Et là, bien sûr, je mentais un peu, sachant que les racines sont rationnelles. Après tout, s’ils étaient irrationnels ou complexes, je serais alors confronté à une vérification infructueuse de tous les nombres restants. Par conséquent, en pratique, soyez guidé par le discriminant.
Répondre: racines rationnelles : 2, 4, 5
Dans le problème que nous avons analysé, nous avons eu de la chance, car : a) les valeurs négatives sont immédiatement tombées, et b) nous avons trouvé la racine très rapidement (et théoriquement nous pourrions vérifier toute la liste).
Mais en réalité, la situation est bien pire. Je vous invite à regarder un jeu passionnant appelé « The Last Hero » :
Problème 4
Trouver les racines rationnelles de l'équation
Solution: Par Théorème 1 les numérateurs des racines rationnelles hypothétiques doivent satisfaire à la condition (on lit « douze est divisé par el »), et les dénominateurs correspondent à la condition . Sur cette base, nous obtenons deux listes :
"liste des éléments":
et "liste euh": (heureusement, les chiffres ici sont naturels).
Faisons maintenant une liste de toutes les racines possibles. Tout d’abord, nous divisons la « liste el » par . Il est absolument clair que les mêmes chiffres seront obtenus. Pour plus de commodité, mettons-les dans un tableau :
De nombreuses fractions ont été réduites, ce qui a donné lieu à des valeurs qui figurent déjà dans la « liste des héros ». Nous ajoutons uniquement les « débutants » : 
De même, nous divisons la même « liste » par : 
et enfin sur
Ainsi, l'équipe des participants à notre jeu est complétée : 
Malheureusement, le polynôme de ce problème ne satisfait pas au critère « positif » ou « négatif », et nous ne pouvons donc pas écarter la ligne du haut ou du bas. Vous devrez travailler avec tous les chiffres.
Comment te sens-tu? Allez, relevez la tête - il existe un autre théorème que l'on peut appeler au sens figuré le « théorème du tueur »…. ...des « candidats », bien sûr =)
Mais vous devez d'abord faire défiler le diagramme de Horner pendant au moins un la totalité Nombres. Traditionnellement, prenons-en un. Dans la ligne du haut, nous écrivons les coefficients du polynôme et tout se passe comme d'habitude :
Puisque quatre n’est clairement pas zéro, la valeur n’est pas la racine du polynôme en question. Mais elle nous aidera beaucoup.
Théorème 2 Si pour certains en général la valeur du polynôme est non nulle : , alors ses racines rationnelles (si ils sont) satisfaire la condition
Dans notre cas et donc toutes les racines possibles doivent satisfaire la condition (appelons-le Condition n°1). Ce quatre sera le « tueur » de nombreux « candidats ». À titre de démonstration, je vais examiner quelques contrôles :
Vérifions le "candidat". Pour ce faire, représentons-le artificiellement sous la forme d'une fraction, d'où on voit clairement que . Calculons la différence de test : . Quatre est divisé par « moins deux » : , ce qui signifie que la racine possible a réussi le test.
Vérifions la valeur. Ici, la différence de test est : 
. Bien entendu, le deuxième « sujet » reste donc également sur la liste.
Les nombres peuvent être divisés en ensembles, dans l'ordre suivant de puissance croissante :
1. Ensemble - un ensemble de nombres premiers (n'a pas de diviseurs premiers autres que lui-même).
2. Ensemble - un ensemble de nombres naturels.
3. Ensemble - un ensemble d'entiers (ce sont des nombres naturels, zéro et des entiers négatifs).
4. Ensemble - un ensemble de nombres rationnels (ce sont des nombres entiers ou des nombres représentables comme une fraction, dont le numérateur et le dénominateur sont des nombres entiers. La notation décimale des rationnels est soit finie, soit représentable comme une fraction, dans laquelle il y a nécessairement une répétition périodique).
5. Ensemble - un sous-ensemble de nombres réels qui peuvent être représentés sous forme de radicaux sur le champ des nombres réels. Cela inclut tous les rationnels (Q), ainsi que certains irrationnels, par ex. 
. Plus précisément, dans cet ensemble, il y a des nombres qui peuvent être représentés sous la forme d'une notation avec élévation à une puissance, où la puissance sera un nombre rationnel, et tout nombre élevé à une puissance sera un nombre rationnel positif.
6. Ensemble - un sous-ensemble de nombres réels qui peuvent être représentés sous forme de radicaux sur le corps des nombres complexes. Cela inclut tous les rationnels (Q), ainsi que certains irrationnels, par exemple, qui s'avéreront finalement valables. Plus précisément, dans cet ensemble, il y a des nombres qui peuvent être représentés sous la forme d'une notation avec élévation à une puissance, où la puissance est un nombre rationnel, et le nombre qui est élevé à une puissance est rationnel, et peut être négatif .
La différence entre l'ensemble 6 et l'ensemble 5. Par exemple, les racines de l'équation,
, sont égaux.
En même temps, on sait que les équations cubiques soluble dans les radicaux. Cela signifie que ces mêmes racines peuvent être représentées sous la forme d’une notation avec des nombres, des opérations mathématiques et des puissances.
Question. Je suppose que certaines parties de cette entrée seront des nombres complexes, c'est-à-dire vous ne pouvez pas vous en passer. Il y aura certainement des racines issues de nombres négatifs. L'hypothèse est-elle correcte ?
Si l’hypothèse est correcte, alors les racines réelles des équations cubiques appartiennent toujours à l’ensemble, mais elles peuvent ne pas appartenir à l’ensemble. Mais les racines d’une équation quadratique appartiennent toujours à un ensemble de faible puissance.
Question. Le sinus de l'argument (en degrés) présenté comme un nombre rationnel appartient-il toujours à l'ensemble (ou pair), c'est-à-dire peut-il toujours s'exprimer en radicaux ?
Mais passons à un ensemble de chiffres encore plus puissants. Les racines réelles d'une équation du 5ème degré ne peuvent pas toujours être exprimées en radicaux, c'est-à-dire ils ne sont peut-être même pas inclus dans , mais il existe un ensemble dans lequel ils sont inclus -
7. Ensemble - un ensemble de nombres algébriques (un sous-ensemble de nombres réels). Cet ensemble comprend toutes les racines réelles possibles de toutes les équations algébriques possibles, de tout degré et avec tous les coefficients rationnels.
Quels ensembles plus puissants que ceux considérés en mathématiques (sans compter les ensembles les plus larges - réels et complexes) ? Je n'en ai pas rencontré de plus puissants ; généralement, si le nombre n'y est pas inclus, il est simplement appelé transcendantal. Et je présenterais un autre ensemble -
8. Ensemble - un ensemble de nombres qui peuvent être les racines de n'importe quelle équation mathématique (pas nécessairement algébrique), avec toutes les fonctions connues (telles que le sinus, la fonction zêta, le logarithme intégral, etc.), qui peuvent être développées présentées sous la forme d'une série ou de plusieurs lignes. Appelons ces chiffres ANALYTIQUES. En termes simples, vous pouvez spécifier une description des dimensions finales, de telle sorte que, à partir de cette description, vous puissiez trouver n'importe quel chiffre après la virgule décimale d'un nombre donné - à l'infini.
Jusqu'à présent, tous les ensembles considérés étaient des sous-ensembles des éléments suivants, c'est-à-dire : sous-ensemble, etc. - sous-ensemble. L'ensemble suivant est séparé (non inclus), mais le plus puissant.
9. Set - un ensemble de nombres chaotiques. (chaotique est ma définition). Il s'agit de l'ensemble de tous les nombres réels qui ne sont pas inclus dans . Si un nombre est inclus dans , alors ce nombre ne peut être représenté par aucune description mathématique de tailles finies (peu importe - des séries ou des fonctions, etc.), c'est-à-dire si nous donnons une description des dimensions finies, alors nous ne pourrons pas utiliser cette description pour trouver un chiffre après la virgule d'un nombre donné - à l'infini.
10. Ensemble - l'ensemble de TOUS les nombres réels. C'est l'union d'ensembles disjoints et . De plus, un ensemble dans un ensemble a une mesure nulle. Ceux. dans l’ensemble des nombres réels, la majorité des nombres sont chaotiques et la minorité est analytique.
11. Ensemble - l'ensemble de tous les nombres complexes. Il était possible de le diviser en sous-ensembles similaires (algébrique complexe, analytique, chaotique, etc.), mais je pense que ce n'est pas nécessaire.
Mon classement est-il correct ? Quels autres ensembles possèdent les mathématiciens qui sont des sous-ensembles de nombres transcendantaux, mais ne sont pas des nombres algébriques ?
