Solenik Alena Dmitrievna

L'ouvrage examine les problèmes les plus urgents associés aux constructions géométriques au sol - lignes droites suspendues, divisions de segments et d'angles, ainsi que mesure de la hauteur d'un arbre. Le résultat des travaux – les arbres ont été abattus – a été communiqué au nouveau personnel.

Télécharger:

Aperçu:

Ministère de l'Éducation et des Sciences de la République de Khakassie

Établissement d'enseignement municipal

École secondaire Ustino-Kopyevskaya.

Section mathématiques.

TRAVAUX DE MESURES SUR LE TRAVAIL DU TERRITOIRE

VILLAGE USTINKINO

élève de 10ème année

Responsable : Romanova

Elena Alexandrovna,

professeur de mathématiques

Oustinkino, 2010

Page

Introduction………………………………………………………………………………3

1 . L'émergence des mesures dans l'Antiquité

1.1 Unités de mesure des différents peuples…………………………………..4

1.2 Méthodes de mesure dans la Rus antique……………………………………5

1.3 La géométrie dans les problèmes pratiques anciens…………………………..7

1.4 Instruments pour les mesures de terrain……………………………7

2.1 Construction d'une ligne droite au sol (suspendue

Ligne droite)………………………………………………………...8

2.2 Mesure de la longueur moyenne des pas……………………………………..9

2.3 Construction d'angles droits au sol………………………………9

2.4 Construire et mesurer des angles à l'aide d'un astrolabe……………...10

2.5 Construire un cercle au sol……………………………...10

2.6 Mesure de la hauteur des arbres…………………………………………………………......11

3. Résultats des mesures au sol……………………………………………..

Conclusion…………………………………………………………………………………21

Littérature……………………………………………………………………………………….22

Introduction

Pour réaliser la maquette des figurines, j'ai dû réaliser plus de 20 opérations différentes. Et près de la moitié d’entre eux sont liés aux mesures. Je me demande s'il existe des professions dans lesquelles il n'est pas du tout nécessaire de mesurer quoi que ce soit avec des instruments. Je n'en ai trouvé aucun. Je n'ai pas réussi à trouver une matière scolaire dont l'étude ne nécessiterait pas de mesures.

"La science commence quand

Comment commencent-ils à mesurer ?

La science exacte est impensable

sans mesure."

DI. Mendeleïev.

En effet, le rôle des mesures dans la vie de l'homme moderne est très important.

Le dictionnaire encyclopédique populaire définit la mesure. Les mesures sont des actions effectuées dans le but de trouver des valeurs numériques, des quantités quantitatives dans des unités de mesure acceptées. ¹

La valeur peut être mesurée à l'aide d'instruments. Au quotidien, on ne peut plus se passer de montre, de règle, de mètre ruban, de tasse à mesurer, de thermomètre, de compteur électrique. On peut dire que nous rencontrons des appareils à chaque étape.

Objectif : étude des mesures géométriques au sol. Ustinkino.

Tâches:

1. étudier l'historique des mesures;
2. se familiariser et fabriquer des instruments de mesure sur le terrain ;
3. prendre des mesures au sol ;
4. tirer des conclusions et formuler vos propositions.

Hypothèse : actuellement, les travaux de mesure sur le terrain jouent un rôle important, puisque sans prendre de mesures vous pouvez payer de votre vie.

Objet d'étude : mesures au sol.

Sujet de recherche : méthodes de mesures au sol.

___________________________________

21 . Dictionnaire encyclopédique populaire. Maison d'édition scientifique "Grande Encyclopédie russe". Maison d'édition "ONICS 21ème siècle", 2002, p. 485

1. L'émergence des mesures dans l'Antiquité

Dans les temps anciens, une personne devait progressivement comprendre non seulement l'art de compter, mais aussi la mesure. Lorsqu'un homme ancien, déjà réfléchi, essaya de trouver une grotte pour lui-même, il fut obligé de mesurer la longueur, la largeur et la hauteur de sa future maison avec sa propre taille. Mais c’est ça la mesure. Lorsqu'on fabrique les outils les plus simples, qu'on construit des maisons, qu'on se procure de la nourriture, il faut mesurer les distances, puis les surfaces, les conteneurs, la masse, le temps. Notre ancêtre n'avait que sa propre taille, la longueur de ses bras et de ses jambes. Si une personne utilisait ses doigts et ses orteils pour compter, alors pour mesurer les distances, elle utilisait ses bras et ses jambes. Il n'y avait personne qui n'ait inventé ses propres unités de mesure.

1.1 Unités de mesure des différentes nations

Les constructeurs des pyramides égyptiennes considéraient la coudée (la distance entre le coude et l'extrémité du majeur) comme la norme de longueur, les anciens Arabes - les poils du museau d'un âne, les Britanniques utilisent encore le pied royal (en anglais " pied" signifie "jambe"), égale à la longueur du pied du roi. La longueur d'un pied a été clarifiée avec l'introduction d'une unité appelée tige. C’est « la longueur des pieds de 16 personnes quittant le temple après les Matines du dimanche ». En divisant la longueur de la tige en 16 parties égales, nous avons obtenu la longueur moyenne du pied, car des personnes de différentes tailles ont quitté l'église. La longueur d'un pied est devenue 30,48 cm. Le yard anglais est également associé à la taille du corps humain. Cette mesure de longueur a été introduite par le roi Edgar et était égale à la distance entre le bout du nez de Sa Majesté et le bout du majeur de sa main tendue. Dès que le roi changeait, la cour s'allongeait, car le nouveau monarque était plus grand. De tels changements de longueur ont provoqué une grande confusion, c'est pourquoi le roi Henri Ier a légalisé une cour permanente et a ordonné qu'un étendard soit fabriqué en orme. Ce chantier est encore utilisé en Angleterre (sa longueur est de 0,9144 m). Pour mesurer de petites distances, la longueur de l’articulation du pouce a été utilisée (en néerlandais, « pouce » signifie « pouce »). En Angleterre, la longueur d'un pouce a été affinée et est devenue égale à la longueur de trois grains d'orge prélevés dans la partie médiane de l'épi et placés avec leurs extrémités face à face. D'après les romans et les contes anglais, on sait que les paysans déterminaient souvent la hauteur des chevaux avec leurs paumes.

Pour mesurer de grandes distances dans les temps anciens, une mesure appelée champ a été introduite, puis remplacée par un mile. Ce nom vient du mot «tour», qui signifiait d'abord tourner la charrue, puis - un rang, la distance d'un tour à l'autre de la charrue lors du labour. La longueur de la verste variait à différents moments - de 500 à 750 brasses. Oui, et il y avait deux milles : une piste - ils mesuraient la distance du trajet, et une limite - pour les parcelles de terrain.

La distance était mesurée en pas chez presque tous les peuples, mais pour mesurer les champs et autres grandes distances, le pas était une mesure trop petite, c'est pourquoi la canne, ou double pas, puis la double canne, ou persha, ont été introduites. Dans les affaires maritimes, une canne s'appelait une verge. En Angleterre, il existait une mesure telle qu'un bon bâton de laboureur, dont la longueur était de 12 à 16 pieds. À Rome, une mesure égale à mille doubles pas a été introduite, appelée mile (du mot « mille », « milia » - « mille »).

Les Slaves avaient une mesure de longueur telle que "lancer une pierre" - lancer une pierre, "tirer" - la distance parcourue par une flèche tirée depuis un arc. Les distances étaient également mesurées ainsi : « La Petchénégie était à cinq jours des Khazars, à six jours des Alains, à un jour de la Russie, à quatre jours des Magyars et à une demi-journée des Bulgares du Danube. » Dans les anciens documents de concession de terres, on peut lire : « Du cimetière dans toutes les directions jusqu’au rugissement d’un taureau. » Cela signifiait - à une distance à partir de laquelle le rugissement d'un taureau peut encore être entendu. D'autres peuples avaient des mesures similaires - « cri de vache », « cri de coq ». Le temps était également utilisé comme mesure - « jusqu'à ce que la casserole d'eau bout ». Les marins estoniens ont déclaré qu'il y avait encore « trois pipes » jusqu'au rivage (le temps passé à fumer la pipe). Le « coup de canon » est aussi une mesure de distance. Alors qu'au Japon, ils ne connaissaient pas encore les fers à cheval et les chaussaient avec des semelles de paille, une mesure de « fer à paille » est apparue - la distance à laquelle ce fer était usé. En Espagne, on connaît la mesure de la distance « cigare » : la distance qu'une personne peut parcourir en fumant un cigare. En Sibérie, dans les temps anciens, on utilisait la mesure de distance « hêtre » - c'est la distance à laquelle une personne cesse de voir séparément les cornes d'un taureau.

Jusqu'à récemment, l'unité de poids pharmaceutique s'appelait gran, ce qui signifie grain. L'unité de masse des pierres précieuses et des perles est le carat - le poids d'une graine d'un type de haricot, égal à 0,2 g.

Pour les Romains, la mesure des parcelles de terre était le jugement (de « yugum » - « joug »). Il s'agit d'un terrain labouré en une journée par deux bœufs attelés à un joug en bois.

Autrefois, chez de nombreux peuples, la mesure du poids coïncidait souvent avec la mesure de la valeur des marchandises, puisque la monnaie était exprimée en poids d'argent et d'or. Ainsi, à Babylone, l’unité monétaire était le shekel, et à Rome, l’âne était aussi une unité de poids. La même chose est l’origine de la monnaie anglaise, la livre sterling.

1.2 Méthodes de mesure de la Rus antique

La Russie antique avait ses propres dimensions. Les mesures de longueur les plus anciennes sont la coudée et la brasse. La coudée était la longueur allant du coude à l'articulation antérieure du majeur, ce qui était égal à un demi-mètre anglais. Le nom sazhen vient du mot slave « syag » - « étape ». Au début, cela signifiait la distance que l'on pouvait parcourir. Ensuite, ils ont commencé à distinguer les brasses de volant, oblique, de culasse, mesurée, grande, grecque, d'église, royale, de mer et de pipe. Ceci était utilisé uniquement pour mesurer la longueur des tuyaux dans les mines de sel. Le volant d'inertie ou brasse mesurée est la distance entre les doigts tendus des mains tendues (176 cm). Une simple brasse (152 cm) est la distance entre l’envergure des bras tendus d’une personne entre le pouce d’une main et le pouce de l’autre. Fathom oblique (248 cm) - la distance entre la plante du pied gauche et l'extrémité du majeur de la main droite tendue.

Les courtes distances en Russie étaient mesurées en quartiers, travées et archines. Un quart est la distance entre le pouce et l'index écartés, un empan est la distance entre l'extrémité du pouce et l'extrémité du petit doigt à leur plus grand écart possible. Quatre quarts constituaient un archine, qui, à son tour, s'inscrivait trois fois dans une brasse oblique. Une mesure de longueur égale à 0,1 pouce était appelée une ligne (apparemment parce qu'elle pouvait être tracée à l'aide d'une règle). Les plus petites mesures de longueur russes anciennes comprennent un point égal à 0,1 ligne. C’est peut-être de là que vient le mot « précision ».

L’homme n’avait pas seulement besoin de mesurer des distances et des longueurs. Il existait également des mesures de liquides, de solides, d'unités de masse et d'unités monétaires. Parmi les mesures des corps liquides de la Rus antique, on connaît les suivantes : baril, seau, pot, bec, tasse, tasse... La principale mesure de liquide était le seau. Le miel et la cire ont été mesurés à l'aide de pots (12 kg). Buse - 2,5 seaux. Un baril équivalait à 4 buses ou 10 seaux. Un baril peut équivaloir à 40 seaux. Mesures plus petites : shtof - un dixième de seau, un verre - un centième de seau, une balance - deux verres.

Pour mesurer les solides en vrac, un baril et une cuve (fermes) ont été utilisés. Kad était une mesure de céréales pouvant contenir 14 livres de seigle (environ 230 kg). Il était divisé en deux moitiés ou huit octogones (quadrets). Plus tard, des grenats sont apparus, égaux à 1/8 du quadruple. Le nom grenats vient du verbe « ratisser » et désigne un récipient en bois ou en fer pour le grain. Il y avait de nombreuses mesures locales : korobya, ventre, nattes, lukno et autres.

L'unité de masse (poids) la plus ancienne était la hryvnia, ou hryvnia, qui devint plus tard connue sous le nom de livre. La livre russe (400 g) était plus petite que la livre anglaise (454 g). Pound, comme pud, vient d'une racine latine et signifie « poids, lourdeur ». La livre était divisée en 96 bobines et la bobine en 96 actions.

En plus de la livre commerciale, une livre d'apothicaire était utilisée, divisée en 12 onces. Les unités de poids plus grandes étaient le poud, égal à 40 livres, et le berkovets, égal à 10 pouds. Berkovets vient du mot «berkun» - «un grand panier en osier, une boîte pour apporter de la nourriture au bétail, pour transporter du foin et de la paille». Le mot « ton » a une origine similaire : il vient de l'anglais « tun » - « baril ».

La plus ancienne unité de poids et de compte monétaire en Russie était apparemment la hryvnia. Son poids était de 409,5 g. On pense que la hryvnia venait du mot « crinière » : en termes de quantité d'argent, la hryvnia était égale au prix d'un cheval. Il y avait différentes hryvnias : kun, argent et or. Les Kunnies étaient fabriqués à partir d'argent de faible qualité et coûtaient quatre fois moins cher que ceux en argent véritable. La hryvnia en or était 12,5 fois plus chère que la hryvnia en argent. Plus tard, la hryvnia a commencé à être coupée en deux en hryvnias, et une nouvelle barre d'une demi-hryvnia monétaire a été appelée le rouble. Le rouble (évidemment du mot « hacher ») est devenu la principale unité monétaire de la Russie.

Le mot « monnaie » viendrait apparemment du nom de la pièce d’argent indienne « tanka », mentionnée dans les chroniques. Six pièces d'argent constituaient un altyn (du tatar « alty » - « six »). Altyn était égal à trois kopecks. Le nom « kopek » vient de petites pièces de monnaie émises sous Ivan le Terrible, représentant un cavalier armé d'une lance. Sous Pierre Ier, les kryvenniks (pièces de 10 kopecks) et les pièces de cinquante kopecks (pièces de 50 kopecks) sont apparus.

1.3 La géométrie dans les problèmes pratiques anciens.

À ses débuts, la géométrie était un ensemble de règles et de formules utiles mais sans rapport entre elles pour résoudre les problèmes rencontrés dans la vie quotidienne. Quelques siècles plus tard seulement, les scientifiques de la Grèce antique ont créé les bases théoriques de la géométrie.

Dans les temps anciens, les Égyptiens, lorsqu'ils commençaient à construire une pyramide, un palais ou une maison ordinaire, notaient d'abord les directions des côtés de l'horizon (ceci est très important, car l'éclairage du bâtiment dépend de la position de ses fenêtres et de ses portes). par rapport au Soleil). C'est ainsi qu'ils ont agi. Ils plantèrent un bâton verticalement et observaient son ombre. Lorsque cette ombre devenait la plus courte, alors son extrémité pointait dans la direction exacte vers le nord.

Triangle égyptien

Pour mesurer la superficie, les anciens Égyptiens utilisaient un triangle spécial dont les côtés étaient de longueur fixe. Les mesures ont été effectuées par des spécialistes spéciaux appelés « tendeurs de corde » (harpedonaptai). Ils prirent une longue corde, la divisèrent en 12 parties égales avec des nœuds et attachèrent les extrémités de la corde. Dans le sens nord-sud, ils ont installé deux piquets espacés de quatre parties, marqués sur la corde. Ensuite, à l'aide d'un troisième pieu, ils tirèrent sur la corde attachée de manière à former un triangle dont un côté avait trois parties, l'autre quatre et le troisième cinq parties. Le résultat était un triangle rectangle dont l'aire a été prise comme norme.

1.4 Instruments pour les mesures sur le terrain

Autrefois, pour mesurer les distances au sol, on utilisaitboussole d'arpentage.

Éker se compose de deux barres situées à angle droit et montées sur un trépied. Des clous sont enfoncés dans les extrémités des barres de manière à ce que les lignes droites qui les traversent soient mutuellement perpendiculaires.

Astrolabe se compose de deux parties : un disque (limbo), divisé en degrés, et une règle (alidade) tournant autour du centre. Lors de la mesure d'un angle au sol, il vise les objets couchés sur les côtés. Viser l'alidade s'appelle l'observation. Les dioptries sont utilisées pour la visée. Ce sont des plaques métalliques avec des fentes. Il existe deux dioptries : l'une avec une fente en forme de fente étroite, l'autre avec une fente large, au milieu de laquelle est tendu un cheveu. Lors de la visée, l'œil de l'observateur est appliqué sur une fente étroite, c'est pourquoi une dioptrie avec une telle fente est appelée dioptrie oculaire. La dioptrie avec un cheveu est dirigée vers l'objet situé du côté de l'objet à mesurer ; cela s'appelle sujet. Au milieu de l'alidade se trouve une boussole.

2. Travaux de mesures sur le terrain

2.1 Construire une ligne droite au sol (tracer une ligne droite)

Les segments au sol sont marqués à l'aide de jalons. Pour vous assurer que le poteau est droit, utilisez un fil à plomb (une sorte de poids suspendu à un fil). Une série de piquets enfoncés dans le sol marque un segment de ligne droite au sol. Dans la direction choisie, placez deux jalons à distance l'un de l'autre, avec d'autres jalons entre eux, de sorte qu'en regardant à travers l'un, les autres soient recouverts l'un par l'autre.

Travaux pratiques: construire une ligne droite au sol.

Exercice : marquez dessus un segment de 20 m, 36 m, 42 m.

2.2 Mesure de la longueur de foulée moyenne

Un certain nombre de pas est compté (par exemple 50), cette distance est mesurée et la longueur moyenne des pas est calculée. Il est plus pratique de réaliser l'expérience plusieurs fois et de calculer la moyenne arithmétique.

Travaux pratiques: Mesure la longueur de foulée moyenne.

Exercice: Connaissant la longueur moyenne des pas, réservez une section de 20 m au sol et vérifiez-la avec un mètre ruban.

2.3 Construction d'angles droits au sol

Pour construire un angle droit AOB au sol avec un côté OA donné, installez un trépied avec un ecker de manière à ce que le fil à plomb soit situé exactement au-dessus du point O et que la direction d'un bloc coïncide avec la direction du rayon OA. La combinaison de ces directions peut se faire à l'aide d'un poteau placé sur la poutre. Ensuite, une ligne droite est tracée en direction de l'autre bloc (OB).

Travaux pratiques: construction d'un angle droit au sol, d'un rectangle, d'un carré.

Exercice : Mesurez le périmètre et l'aire d'un rectangle ou d'un carré.

2.4 Construire et mesurer des angles à l'aide d'un astrolabe

L'astrolabe est installé au sommet de l'angle de mesure de manière que sa branche soit située dans un plan horizontal, et un fil à plomb suspendu sous le centre de la branche est projeté en un point pris comme sommet de l'angle à la surface de l'angle. Terre. Ensuite, l'alidade est visée dans la direction d'un côté de l'angle mesuré et les divisions en degrés sont comptées sur le cadran par rapport à la marque de la dioptrie sujet. Faites pivoter l'alidade dans le sens des aiguilles d'une montre en direction du deuxième côté de l'angle et comptez une seconde fois. L'angle requis est égal à la différence entre les lectures de la deuxième et de la première lecture.

Travaux pratiques:

1. mesurer des angles spécifiés,
2. construire des angles d'une mesure de degré donnée,
3. construire un triangle en utilisant trois éléments : un côté et deux angles adjacents, deux côtés et l'angle qui les sépare.

Exercice: mesurer les mesures en degrés d'angles donnés.

2.5 Construire un cercle au sol

Un piquet est installé au sol auquel une corde est attachée. En tenant l'extrémité libre de la corde et en vous déplaçant autour du piquet, vous pouvez décrire un cercle.

Travaux pratiques: Dessinez un cercle.

Exercice : mesure du rayon, du diamètre ; calcul de l'aire d'un cercle, circonférence.

2.6 Mesurer la hauteur des arbres

a) À l'aide d'une barre rotative.

Supposons que nous devions déterminer la hauteur d'un objet, par exemple la hauteur du pilier A. 1C1 (tâche n°579). Pour ce faire, placez une perche AC avec une barre rotative à une certaine distance du poteau et dirigez la barre vers le point haut C. 1 pilier Marquons un point B sur la surface de la terre, auquel la droite A 1 A croise la surface de la terre. Triangles rectangles A 1C1 B et ACB sont semblables selon le premier signe de similarité des triangles (angle A 1 = angle A = 90° , angle B – commun). De la similitude des triangles il résulte ;

Où est M.

Distances de mesure VA 1 et BA (la distance du point B à la base du poteau et la distance au poteau avec une barre rotative), connaissant la longueur AC du poteau, en utilisant la formule résultante, nous déterminons la hauteur A 1 À partir de 1 pilier.

b) Utiliser une ombre.

La mesure doit être effectuée par temps ensoleillé. Mesurons la longueur de l'ombre d'un arbre et la longueur de l'ombre d'une personne. Construisons deux triangles rectangles, ils sont semblables. En utilisant la similitude des triangles, nous créons une proportion (le rapport des côtés correspondants), à partir de laquelle nous trouvons la hauteur de l'arbre. Vous pouvez ainsi déterminer la hauteur de l'arbre grâce à la construction de triangles rectangles à une échelle choisie.

c) Utiliser un miroir.

Pour déterminer la hauteur d’un objet, vous pouvez utiliser un miroir posé horizontalement sur le sol. Un rayon de lumière réfléchi par un miroir frappe l’œil d’une personne. En utilisant la similitude des triangles, vous pouvez trouver la hauteur d'un objet, connaître la taille d'une personne (aux yeux), la distance entre les yeux et le sommet de la tête de la personne et mesurer la distance de la personne au miroir, la distance du miroir à l'objet (en tenant compte du fait que l'angle d'incidence du faisceau est égal à l'angle de réflexion).

∆АВD ~∆DFC (2ème signe de similarité

triangles), de la définition on obtient

Ainsi

m.

d) Utiliser un dessin de triangle rectangle.

Nous placerons un triangle rectangle au niveau des yeux, dirigeant une jambe horizontalement vers la surface de la terre et dirigeant l'autre jambe vers l'objet dont nous mesurons la hauteur. On s'éloigne de l'objet à une distance telle que la deuxième patte « recouvre » l'arbre. Si le triangle est également isocèle, alors la hauteur de l’objet est égale à la distance entre la personne et la base de l’objet (en ajoutant la taille de la personne). Si le triangle n'est pas isocèle, alors la similitude des triangles est à nouveau utilisée, en mesurant les jambes du triangle et la distance entre la personne et l'objet (la construction de triangles rectangles à l'échelle sélectionnée est également utilisée). Si un triangle a un angle de 30 0 , alors on utilise la propriété d'un triangle rectangle : contre un angle de 30 0 La jambe fait la moitié de la taille de l'hypoténuse.

e) Pendant le jeu « Zarnitsa »Les étudiants ne sont pas autorisés à utiliser des instruments de mesure, la méthode suivante peut donc être suggérée :

l’un s’allonge sur le sol et dirige son regard vers le sommet de la tête de l’autre, situé à une distance de sa taille de lui, de sorte qu’une ligne droite passe par le sommet de la tête du camarade et le sommet de l’objet. Le triangle s’avère alors isocèle et la hauteur de l’objet est égale à la distance de l’objet posé à la base, qui se mesure en connaissant la longueur moyenne des pas de l’élève. Si le triangle n'est pas isocèle, alors connaissant la longueur moyenne des pas, on mesure la distance de la personne allongée au sol à la personne debout et à l'objet dont la hauteur est connue. Et puis, en fonction de la similitude des triangles, la hauteur de l'objet est calculée (ou la construction de triangles rectangles à une échelle sélectionnée).

Des problèmes avec des données spécifiques sont pris en compte, en les résolvant, vous pouvez voir différentes manières de trouver la hauteur d'un objet et de déterminer la distance jusqu'à un point inaccessible, qui peuvent être appliquées pratiquement à l'avenir.

Supposons que vous deviez déterminer la hauteur AH d'un objet. Pour ce faire, marquez le point B à une certaine distance a de la base H de l'objet et mesurez l'angle ABN. En utilisant ces données du triangle rectangle ANB, on trouve la hauteur de l'objet : AH = HB tgАВН. Si la base de l'objet est inaccessible, alors vous pouvez procéder ainsi : sur une droite passant par la base H de l'objet, marquez deux points B et C à une certaine distance a l'un de l'autre et mesurez les angles ABN et ACB : angle ABN = a, angle ACB = b, angle BAC = a – b . Ces données permettent de déterminer tous les éléments du triangle ABC ; En utilisant la loi des sinus on trouve AB :

AB = péché (a – b ). A partir du triangle rectangle ABH on trouve la hauteur AN de l'objet :

AN = AB péché a.

1) L'observateur se trouve à une distance de 50 m de la tour dont il souhaite déterminer la hauteur. Il voit la base de la tour sous un angle de 10 0 à l'horizon et au sommet - à un angle de 45 0 à l'horizon. Quelle est la hauteur de la tour ?

Solution

Considérons le triangle ABC - rectangulaire et isocèle, car angle CBA = 45 0, alors l'angle BCA = 45 0, ce qui signifie CA = 50m.

Considérons le triangle ABN - rectangle, tg (ABN) = AH/AB, donc

AN = AB tg (AVN), soit AN = 50tg 10 0 , donc AN = 9m. CH = SA + AN = 50 + 9 = 59 (m)

2) Il y a une tour sur la montagne dont la hauteur est de 100 m. Un objet A au pied de la montagne est observé d'abord depuis le sommet B de la tour sous un angle de 60 0 à l'horizon, puis à partir de sa base C sous un angle de 30 0 . Trouvez la hauteur H de la montagne.

Donné:

NE = 100 m

Angle EVA = 60 0

Angle KSA =30 0

Trouvez SR.

Solution:

Angle SVK = 30 0, car angle EBC =90 0 et angle EBA =60 0,

D'où l'angle SKA=60 0, ce qui signifie ∟SKA=180 0 –60 0 = 120 0.

Dans le triangle SKA on voit que l'angle ASK = 30 0 ,

angle SKA = 120 0, alors angle SAC = 30 0 , on trouve que le triangle BCA est isocèle de base AB, car angle SVK = 30 0 et angle BAC = 30 0 , alors AC = 100 m (BC = AC).

Considérons le triangle ACP, un triangle rectangle avec un angle aigu de 30 0 (PAC = ASK, angles transversaux à l'intersection des droites parallèles SC et AR par sécante AC), et contre un angle de 30 0 La jambe mesure la moitié de la taille de l'hypoténuse, donc PC = 50 m.

3. Résultats des mesures au sol

3.1 Planification du site scolaire

3.2 Les arbres constituent une menace pour la vie

3.3 Aide - proposition au Conseil Villageois du village. Oustinkino

Président des SS s. Oustinkino

Volosatov S.I.

élèves de 10e année

Solenik d'Alena

Offre d'aide

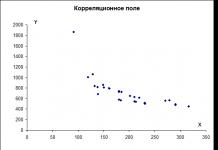
J'ai mesuré la hauteur des poteaux électriques, dont la hauteur est toujours exactement de 17 m. En mesurant la hauteur des arbres, des résultats inattendus ont été obtenus. La hauteur des arbres varie de 19 m à 56 m.

Je pense qu'il faut faire attention à la hauteur des arbres et tailler les arbres à une hauteur de 19 m au printemps.

___________________ __________________

CONCLUSION

Ce résumé aborde les problèmes les plus urgents associés aux constructions géométriques au sol : tracer des lignes droites, diviser des segments et des angles, mesurer la hauteur d'un arbre. Un grand nombre de problèmes sont présentés et leurs solutions sont données. Les problèmes posés présentent un intérêt pratique important, consolident les connaissances acquises en géométrie et peuvent être utilisés pour des travaux pratiques.

Ainsi, je considère que l'objectif du résumé est atteint, les tâches assignées ont été accomplies. J'espère obtenir mon certificat - ils prêteront attention à la proposition et la rempliront comme requis.

Littérature

1. Babansky Yu.K. Optimisation du processus d'apprentissage : Didactique générale
aspect. – M., 1977.
2. Balk M.B., Balk G.D. Mathématiques après les cours, M., Education, 1977.
3. Balk M.B., Balk G.D. Cours de mathématiques au choix hier, aujourd'hui, demain
//Les Mathématiques à l'école - 1987 - N°5.
4. Benbiaminov M.R. Mathématiques et Agriculture, M., 1968.
5. Vilyankin N.Ya., Shibasov L.T., Shibasova Z.F. Derrière les pages d'un manuel
mathématiques : Arithmétique. Algèbre. Géométrie. – M. : Lumières :
JSC "Ucheb. rencontré.", 1996.
6. Ganshin V.N. Les mesures les plus simples au sol, M., 1973 – 126 p.
7. Gilbukh Y., Kondratenko L., Korobko S. Comment ne pas tuer les talents ? //Populaire
éducation. – 1991. - N°4.
8. Géométrie. Manuel pour les 9e et 10e années du secondaire. M., 1979.
9. Depman I. Ya., Vilenkin N. Ya. Derrière les pages d'un manuel de mathématiques. – M.- :
Lumières, 1989.
10. Algèbre divertissante. Géométrie intéressante. / MOI ET. Perlman. –
Rostov n/a : ZAO « Kniga », 2005.
11. Ivankov P.A. Fondements de la géodésie, de la topographie et de la cartographie.-M., 1972
12. Ivanov P.A. Mesures techniques M., 1964
13. Kalmokova Z.I. Principes typologiques du développement des apprentissages.-
M. : Znanie, 1979.
14. Méthodes d'enseignement des mathématiques au secondaire. Méthode privée :
Cahier de texte manuel pour les étudiants en pédagogie. Institut de Physique et Mathématiques spécial/A.Ya.Blokh,
VIRGINIE. Gusev, G.V. Dorofeev et autres ; Comp. DANS ET. Mishin. – M. : Prosvesche-
nié, 1987.
15. Méthodes d'enseignement des mathématiques au secondaire. Technique générale :
Cahier de texte manuel pour les étudiants de physique et de mathématiques. faux. péd. instituts / V.A. Oga-
Nesyan, Yu.M. Kolyaguine, G.L. Loukankine, V.Ya. Sanninski. – 2e éd., re-
esclave. et supplémentaire – M. : Éducation, 1980.
16. Morozova N.G. À l'enseignant sur l'intérêt cognitif. M. : Connaissance, série
"Pédagogie et psychologie", 1979.
17. Encyclopédie pédagogique : en 2 volumes / Ed. I.A. Kairova, F.N. Animal de compagnie-
déplacer. – M. : Encyclopédie soviétique, 1964. – T.1.
18. Encyclopédie pédagogique : en 2 volumes / Ed. I.A. Kairova, F.N. Pet-rova. – M. : Encyclopédie soviétique, 1964. – T.2.
19. Petrov V.A. Enseigner les mathématiques dans les écoles rurales : Livre. pour enseigner-
la. – M..6 Lumières, 1986.
20. Pogorelov A.V. Géométrie. M., 1990.

21. Dictionnaire encyclopédique populaire. Maison d'édition scientifique "Grande Encyclopédie russe". Maison d'édition "ONICS 21ème siècle", 2002, p. 485

22. Sergeev I.N., Olehnik S.N., Gashkov S.B. Appliquez les mathématiques. – M.,
Sciences, 1989.
23. Chichigin V.G. Méthodes d'enseignement de la géométrie : Planimétrie. – M. :
Uchpedgiz, 1959.
24. Chetverukhin N.F. Méthodes de constructions géométriques, M., Uchpedgiz, 1952.

Application:

Envoyer votre bon travail dans la base de connaissances est simple. Utilisez le formulaire ci-dessous

Les étudiants, étudiants diplômés, jeunes scientifiques qui utilisent la base de connaissances dans leurs études et leur travail vous seront très reconnaissants.

Il n'existe pas encore de version HTML de l'œuvre.
Vous pouvez télécharger l'archive de l'œuvre en cliquant sur le lien ci-dessous.

Documents similaires

Concept et classification des angles, angles positifs et négatifs. Mesurer des angles à l'aide d'arcs de cercle. Unités de mesure lors de l'utilisation de mesures en degrés et en radians. Caractéristiques des angles : entre un incliné et un plan, deux plans, dièdre.

résumé, ajouté le 18/08/2011


thèse, ajoutée le 12/01/2007


La figure marquante du Moyen Âge, le scientifique universel et encyclopédiste Abu Rayhan Muhammad ibn Ahmad al-Beruni, dans son ouvrage « Gnomonics », s'attarde en détail sur la mesure des distances sur Terre et des hauteurs des montagnes, des problèmes et donne des moyens de les résoudre.

résumé, ajouté le 25/03/2008


Angles et leur mesure, fonctions trigonométriques d'un angle aigu. Propriétés et signes des fonctions trigonométriques. Fonctions paires et impaires. Fonctions trigonométriques inverses. Résoudre des équations trigonométriques simples et des inégalités à l'aide de formules.

tutoriel, ajouté le 30/12/2009


Utiliser diverses méthodes pour mesurer la distance dans les pays du monde entier. Caractéristiques du système de mesures de la Rus antique : vershok, span, pud, archine, brasse et verste. Développement du système métrique. Mesures de superficie et de longueur en Égypte, en Israël, en Grande-Bretagne et aux États-Unis.

présentation, ajouté le 17/11/2011


Concepts géométriques de point, de rayon et d'angle. Types d'angles : droits, aigus, droits, obtus, adjacents et verticaux. Méthodes de construction d'angles adjacents et verticaux. Égalité des angles verticaux. Tester les connaissances dans un cours de géométrie : déterminer le type d'angles.

présentation, ajouté le 13/03/2010


Le concept de droite numérique. Types d'intervalles numériques. Détermination par coordonnées de la position d'un point sur une droite, sur un plan, dans l'espace, système de coordonnées. Unités pour les axes. Déterminer la distance entre deux points sur un plan et dans l'espace.

Établissement d'enseignement municipal

"L'école secondaire de base Velikodvorskaya"

J'ai fait le travail :

Anfalov Sergueï Vassilievitch, 8 ans

Classe

École secondaire Velikodvorskaya Babushkinsky

Date de naissance : 16/06/1995

Adresse du domicile : 161344, Vologda

région, district de Babushkinsky, village de Velikiy

Dvor, n° 76.

Superviseur:

Belyaeva Elena Vasilievna,

professeur de physique et de mathématiques

Protocole d'entente "Velikodvorskaya principale

école polyvalente"

Adresse de l'école : 161344, Vologda

région du district de Babushkinsky, village de Velikiy

Village de Velikiy Dvor

2009

INTRODUCTION

Le cours de base de géométrie scolaire examine les tâches liées à la mise en pratique des connaissances acquises : mesures des travaux au sol, instruments de mesure. Le travail pratique sur le terrain est l’une des formes les plus actives permettant de relier l’apprentissage à la vie, la théorie à la pratique. Nous apprenons à utiliser des ouvrages de référence, à appliquer les formules nécessaires et à maîtriser les techniques pratiques de mesures et de constructions géométriques. Les travaux pratiques utilisant des instruments de mesure augmentent l'intérêt pour les mathématiques, et résoudre les problèmes de mesure de la largeur d'une rivière, de la hauteur d'un objet et de la détermination de la distance jusqu'à un point inaccessible vous permet de les appliquer dans des activités pratiques et de voir l'échelle d'application des mathématiques dans la vie humaine. Au fur et à mesure que vous étudiez le matériel, les méthodes pour résoudre ces problèmes changent ; le même problème peut être résolu de plusieurs manières. Dans ce cas, les questions de géométrie suivantes sont utilisées : l'égalité et la similitude des triangles, les relations dans un triangle rectangle, le théorème des sinus et le théorème des cosinus (9e année), le théorème de Pythagore, les propriétés des triangles rectangles, etc. À l’école, nous réalisons des constructions géométriques assez détaillées à l’aide de compas et de règles et résolvons de nombreux problèmes. Comment résoudre les mêmes problèmes sur le terrain ? Après tout, il est possible d'imaginer une boussole aussi énorme qui pourrait tracer la circonférence d'un stade scolaire ou une règle pour marquer les allées d'un parc. Dans la pratique, les cartographes doivent utiliser des méthodes spéciales pour dessiner des cartes et des géomètres pour marquer des zones au sol, par exemple pour poser les fondations d'une maison.

Le sujet de notre essai : Travaux de mesure sur site.
Cible: étude de quelques méthodes de résolution de problèmes géométriques sur le terrain.

Pour atteindre cet objectif, nous avons identifié les éléments suivantsTâches:

● Explorer littérature théorique et méthodologique sur cette question.

● Afficher les relations mathématiques et sécurité de base des personnes.

● Appliquer les connaissances théoriques dans la pratique.

Les objets de mes observations étaient :

● Déterminer la hauteur d'un objet.

● Distance à un point inaccessible.

PARTIE PRINCIPALE.

L'une des formes de connexion les plus actives entre l'apprentissage et la vie, la théorie et la pratique est la mise en œuvre de travaux pratiques liés à la mesure, à la construction et à la représentation pendant les cours de géométrie. Les mêmes questions sont abordées dans le cours sur les bases de la sécurité des personnes, mais toutes les mesures sont prises sans instruments spéciaux. Le travail s'effectue à la fois sur le terrain et en résolution de problèmes en classe de différentes manières pour trouver la hauteur d'un objet et déterminer la distance jusqu'à un point inaccessible. Selon le programme, le cours de géométrie aborde les problématiques suivantes :
7e année
● « Tracer une ligne droite au sol » (point 2).
● « Outils de mesure » (article 8).
● « Mesure des angles au sol » (article 10).
● « Construction d'angles droits au sol » (p. 13) ● « Tâches de construction. Cercle" (article 21).
● « Méthodes pratiques pour construire des lignes parallèles » (p. 26).
● « Réflecteur criminel » (article 36).
● « Distance entre lignes droites parallèles » (article 37 – raboteuse).
● « Construction d'un triangle à partir de trois éléments » (p. 38).
8e année
● « Applications pratiques de la similarité des triangles » (point 64 – mesurer la hauteur d'un objet, déterminer la distance jusqu'à un point inaccessible).
9e année
● "Travaux de mesure" (point 100 - mesurer la hauteur d'un objet, déterminer la distance jusqu'à un point inaccessible).

Instruments de mesure utilisés pour les mesures sur le terrain :


● ROULETTE – un ruban sur lequel sont imprimées des divisions, conçu pour construire des angles droits sur le sol.
● EKER – un appareil pour mesurer les angles droits au sol.
● ASTROLABE – un appareil pour mesurer les angles au sol.
● JALONS (VESHKI) – piquets enfoncés dans le sol.
● BOUSSOLE TERRE (BOUSSOLE DE TERRAIN - SAZHEN) - un outil en forme de lettre A, de 1,37 m de haut et 2 m de large, pour mesurer au sol.

ÉKER.

L'ecker est constitué de deux barres situées à angle droit et montées sur un trépied. Des clous sont enfoncés dans les extrémités des barres de manière à ce que les lignes droites qui les traversent soient mutuellement perpendiculaires.


ASTROLABÉ.

L'astrolabe se compose de deux parties : un disque (limbo), divisé en degrés, et une règle tournant autour du centre (alidade). Lors de la mesure d'un angle au sol, il vise les objets couchés sur les côtés. Viser l'alidade s'appelle l'observation. Les dioptries sont utilisées pour la visée. Ce sont des plaques métalliques avec des fentes. Il existe deux dioptries : l'une avec une fente en forme de fente étroite, l'autre avec une fente large, au milieu de laquelle est tendu un cheveu. Lors de la visée, l'œil de l'observateur est appliqué sur une fente étroite, c'est pourquoi une dioptrie avec une telle fente est appelée dioptrie oculaire. La dioptrie avec un cheveu est dirigée vers l'objet situé du côté de l'objet à mesurer ; cela s'appelle sujet. Au milieu de l'alidade se trouve une boussole.


CONSTRUCTION D'UN CERCLE SUR
TERRITOIRES.

Un piquet est installé au sol auquel une corde est attachée. En tenant l'extrémité libre de la corde et en vous déplaçant autour du piquet, vous pouvez décrire un cercle.




TRAVAUX PRATIQUES.


І. Mesurer la hauteur d'un objet.


Méthodes :

1 Mesurer la hauteur d'un pilier à l'aide d'un miroir plat.

D'après les lois de la réflexion (optique, physique), l'angle d'incidence d'un rayon solaire est égal à l'angle de réflexion de ce rayon sur le miroir.



∟3 = ∟4, où DK ┴ d, d – plan horizontal.

S – personne ; b – sujet ; un miroir.

∟ADB=∟FDF, puisque les angles d'incidence et de réflexion du rayon solaire sont égaux, et ∟1 = ∟2 = 90º-∟3, ∟A = ∟E = 90º, ce qui signifie que les triangles ABD et EFD sont similaires en deux angles.

De la similitude des triangles, il résulte AB:AD = FE:DE EF = (AB·DE):AD, où AB est la « taille » d'une personne - la distance du sol aux yeux, EF est la hauteur mesurée, AD et D E sont respectivement les distances entre la personne réfléchie dans le miroir et l'objet mesuré.

2. Mesurer la hauteur d'un objet à l'aide d'une ombre.



VMA




NE est la hauteur du poteau télégraphique.

MN – taille humaine (1,6 m).

AM – ombre humaine (3,35 m).

AB est l'ombre du pilier (15,3 m).

L'homme se tient dans la zone d'ombre du pilier de manière à ce que l'ombre du sommet de sa tête coïncide avec la fin de l'ombre du pilier.

Considérons les triangles ABC et AMN.

∟ABC =∟AMN = 90º. Par deux égaux

∟VOUS – commun. coins.

Les triangles ABC et AMN sont semblables.

Vous pouvez écrire le rapport hauteur/largeur AB:AM = CB:MN

CB = (AB·MN):AM

CB = (15,3 · 1,6) : 3,35

NE = 7,3 m.

3. Mesurer la hauteur d'un objet à l'aide d'une perche.

Nous utilisons une méthode basée sur la mesure de l'ombre projetée par un objet.

● Mesurez la distance entre l’arbre et le point où se termine son ombre.

● Prenez un poteau et, en observant son ombre, revenez vers l'arbre jusqu'à ce que leurs ombres se chevauchent complètement.

● Placez un poteau à cet endroit et mesurez la distance jusqu'à celui-ci.

● De la similitude des triangles, il résulte que la longueur du poteau est liée à la longueur de son ombre de la même manière que la hauteur de l'arbre est à la sienne.

● On détermine la hauteur de l'arbre à l'aide de la formule :

SE :BC = AD:AB, donc AD ​​= (CE·AB):BC.



4. Mesurer la hauteur d'un objet en utilisant l'absence d'ombre.

En l'absence d'ombre, la hauteur des objets verticaux est déterminée comme suit.

Placez un bâton de longueur connue verticalement à côté de l'objet à mesurer et éloignez-vous de 25 à 30 pas. Tenez un crayon ou un bâton droit verticalement devant vos yeux avec une main tendue. Marquez la hauteur du bâton vertical sur un crayon et mesurez cette distance. Multipliez mentalement cette distance par l'objet mesuré. En multipliant le nombre de fois obtenu par la longueur du bâton, vous pouvez obtenir la valeur souhaitée. A partir de cette expérience, nous avons déterminé que la hauteur du pilier est de 6,89 m.







II. Mesurer la distance jusqu'à un point inaccessible.

Méthodes :

1. Mesurer la distance jusqu'à un point inaccessible à l'aide d'un oculaire.

Clairement visible:

● à une distance de 2 à 3 km - les contours de grands arbres ;

● à une distance de 1 km - troncs d'arbres ;

● à une distance de 0,5 km - grosses branches;

● à une distance de 300 m – vous pouvez distinguer les feuilles des arbres.

2. Mesurer la distance jusqu'à un point inaccessible en utilisant la similitude des triangles.

A) Pour mesurer la largeur de la rivière sur la rive, mesurez la distance AC, utilisez un astrolabe pour fixer l'angle A = 90˚ (en pointant l'objet B sur la rive opposée), mesurez l'angle C. Sur une feuille de papier, construisez un triangle similaire à l'échelle 1:1000 et calculez AB (largeur de la rivière).



EN 1

Un 1 C 1

Notons le rapport des côtés AB : A 1 B 1 = CA : A 1 C 1

AB = (AC AB 1) : A 1 C 1

B) La largeur de la rivière peut être déterminée de cette façon : en considérant deux triangles semblables ABC et AB 1C1 . Le point A est sélectionné au bord de la rivière, B 1 et C au bord de la surface de l'eau, BB 1 – largeur de la rivière.

3. Mesurer la distance jusqu'à un point inaccessible en utilisant la méthode du « cap ».

Pour déterminer la largeur d'une rivière (ravin), vous devez vous tenir sur la rive et mettre votre casquette sur votre front de manière à ce que seul le bord de l'eau de la rive opposée soit visible sous la visière. Ensuite, sans changer l'inclinaison de la tête et la position de la casquette, vous devez tourner la tête vers la droite (gauche), remarquer un objet qui se trouve sur la même berge que l'observateur et qui est visible sous le bord de la visière. La distance à cet objet est égale à la largeur de la rivière. Sur la base de notre expérience, nous avons déterminé que la largeur de la rivière est de 6 m.




5. Mesurer la distance jusqu'à un point inaccessible en utilisant l'égalité des triangles.

L'une des façons de déterminer la distance jusqu'à un point inaccessible est liée aux lois de la géométrie et repose sur l'égalité des triangles.

● Placez-vous devant un objet sur la rive opposée de la rivière.

● En tournant à 90˚, longez le rivage sur 20 mètres et placez la borne O.

● Parcourez la même distance dans la même direction.

● En tournant à 90˚, marchez jusqu'à ce que la borne O et l'objet sur la rive opposée soient sur la même ligne.

● La distance CE est égale à la largeur de la rivière ВD.

Le BD est de 5,78 m.










6. Mesurer la distance jusqu'à un point inaccessible selon la méthode du « brin d'herbe ».

L'observateur se place au point A et sélectionne deux objets fixes (repères) sur la rive opposée près de l'eau, puis, tenant dans sa main un brin d'herbe (fil) qui comble l'espace entre les repères, le plie en deux et s'éloigne. de la rivière jusqu'à ce que la distance entre les points de repère ne rentre pas dans un brin d'herbe plié en deux B. La distance de A à B est égale à la largeur de la rivière. AB est égal à 5,96 m.









CONCLUSION.

Ce résumé aborde les problèmes les plus urgents associés aux constructions géométriques au sol : mesurer la hauteur d'un objet, déterminer la distance jusqu'à un point inaccessible. Les problèmes posés présentent un intérêt pratique important, consolident les connaissances acquises en géométrie et peuvent être utilisés pour des travaux pratiques.

Littérature

Atanasyan L.S. Géométrie 7-9. – M. : Éducation, 2003.

Yurchenko O. Méthodes de motivation et de stimulation de l'activité étudiante. // Les mathématiques à l'école, n°1, 2005

AVEC Disque D « École de sécurité ».

La leçon vidéo « Mesurer le travail » démontre la valeur pratique du matériau étudié. La vidéo comprend une démonstration de la façon dont vous pouvez mesurer la hauteur des objets en utilisant vos connaissances existantes sur leur géométrie. De plus, la connaissance de la géométrie vous aidera à trouver la distance jusqu'à un point inaccessible. L’importance pratique de la branche mathématique relative à la résolution de triangles ne peut guère être surestimée. Dans la construction, l'arpentage et d'autres travaux d'ingénierie, les connaissances de ce domaine mathématique sont souvent utilisées.

L'application des connaissances théoriques dans la pratique est démontrée à l'aide d'illustrations qui décrivent facilement un problème pratique réel survenu au cours d'un travail d'ingénierie. Une représentation animée de constructions permet d'identifier des tâches familières lors d'une tâche pratique. À l'aide d'un support sous forme de formules et d'explications vocales, une explication détaillée de la méthode permettant de résoudre de tels problèmes est donnée.



La leçon vidéo commence par l'introduction du sujet. Il est proposé d'appliquer les matériaux étudiés pour résoudre un problème pratique sur le terrain : trouver la hauteur d'un objet. L'illustration montre un grand arbre dont la hauteur doit être mesurée. La base de l'arbre est marquée comme le point H. Il est à noter que lors du marquage d'un certain point A, auquel la hauteur est calculée, et d'un certain point B à une distance b du point H, un triangle ANB se forme, la valeur dont certains éléments sont connus. L'angle droit au sommet du triangle H, l'angle ∠ABN=α au sommet B et le côté a sont connus. Pour trouver la hauteur AN, il faut calculer le produit de la longueur du côté a et de la tangente de l'angle ∠α.

La résolution du problème est possible même dans le cas où il n'est pas possible de mesurer la distance entre la base de l'arbre H et le point B. Dans ce cas, sur la droite à laquelle appartient HB, un autre point C est marqué. la distance a entre les points marqués B et C est mesurée, ainsi que les angles avec eux ∠AVN=∠α et ∠ACV=∠β. Ces éléments sont suffisants pour déterminer les éléments inconnus restants du triangle ABC. Puisque ∠α est l'angle externe du triangle, sa valeur est déterminée par la formule ∠A=α-β. Pour trouver la longueur du côté AB, nous utilisons le théorème du sinus, d'où AB = a·sinβ/sin(α-β). Après avoir calculé le côté AB, vous pouvez déterminer la hauteur AH=AB·sinα. Au lieu de AB, l'expression obtenue ci-dessus est remplacée. On obtient la hauteur AH= a· sinα·sinβ/ sin(α-β).



Un autre type de problème résolu sur le terrain grâce aux connaissances acquises dans cette section est la mesure des distances d'un certain point à un point inaccessible. La figure du problème montre un exemple lorsqu'il est nécessaire de mesurer la distance d'un certain point à un point distant inaccessible. Un certain point A, un point distant C et la distance requise d sont marqués. Il est à noter qu'un problème similaire a déjà été résolu par des étudiants lors d'un cours de mathématiques en utilisant la notion de similarité des triangles. Cette fois, nous montrons comment résoudre un problème en utilisant les méthodes de résolution triangulaire. Pour ce faire, un autre point B est marqué dans cette zone, à partir duquel la distance à A est égale à c. À l'aide d'un astrolabe, vous pouvez mesurer les angles aux sommets du triangle formé ∠A=α et ∠B=β. Les données disponibles sont suffisantes pour déterminer la distance requise d=AC. L'angle inconnu restant ∠С est calculé à l'aide du théorème de la somme triangulaire sinС=sin(180⁰-α-β)= sin(α+β). Ensuite, pour trouver la distance d=AC, on utilise le théorème des sinus, d'où il découle AC/sinB=AB/sinC. En substituant les expressions obtenues à partir du théorème aux inconnues, nous obtenons d=с sinβ/sin(α+β). On note également que, de manière similaire à cette solution, les distances aux corps célestes sont déterminées.



La leçon vidéo « Mesurer le travail » peut être utilisée lors d'un cours de géométrie traditionnel à la place de l'explication de l'enseignant. Ce matériel peut également être recommandé aux étudiants pour un examen indépendant. Cette aide visuelle aidera l'enseignant à présenter la signification pratique de la matière étudiée en enseignement à distance.