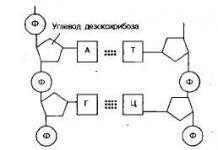
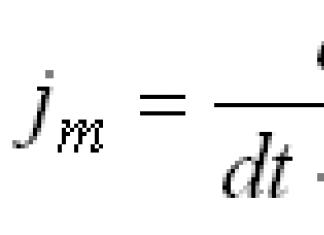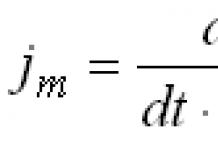Définition 1. Un point x d'une ligne infinie est appelé point limite de la séquence (x n) si dans tout e-voisinage de ce point il y a une infinité d'éléments de la séquence (x n).

Lemme 1. Si x est un point limite de la séquence (x k ), alors à partir de cette séquence on peut sélectionner une sous-séquence (x n k ), convergeant vers le nombre x.

Commentaire. L’affirmation inverse est également vraie. Si à partir de la séquence (x k) il est possible de sélectionner une sous-suite convergeant vers le nombre x, alors le nombre x est le point limite de la séquence (x k). En effet, dans tout e-voisinage du point x il existe une infinité d'éléments de la sous-suite, et donc de la séquence elle-même (x k ).

Du lemme 1, il résulte que nous pouvons donner une autre définition du point limite d'une séquence, équivalente à la définition 1.

Définition 2. Un point x d'une ligne infinie est appelé point limite d'une séquence (x k ), si à partir de cette séquence il est possible de sélectionner une sous-suite convergeant vers x.

Lemme 2. Chaque suite convergente n’a qu’un seul point limite, qui coïncide avec la limite de cette suite.

Commentaire. Si la suite converge, alors d’après le lemme 2 elle n’a qu’un seul point limite. Cependant, si (xn) n’est pas convergent, alors il peut avoir plusieurs points limites (et, en général, une infinité de points limites). Montrons, par exemple, que (1+(-1) n ) a deux points limites.

En effet, (1+(-1) n )=0,2,0,2,0,2,... a deux points limites 0 et 2, car les sous-séquences (0)=0,0,0,... et (2)=2,2,2,... de cette séquence ont respectivement comme limites les nombres 0 et 2. Cette séquence n'a pas d'autres points limites. En effet, soit x n'importe quel point sur l'axe des nombres autre que les points 0 et 2. Prenons e >0 donc

petit pour que les e - voisinages des points 0, x et 2 ne se coupent pas. Le e-voisinage des points 0 et 2 contient tous les éléments de la séquence et donc le e-voisinage du point x ne peut pas contenir une infinité d'éléments (1+(-1) n ) et n'est donc pas un point limite de cette séquence.

Théorème. Chaque séquence bornée a au moins un point limite.

Commentaire. Aucun nombre x dépassant , n'est un point limite de la séquence (x n), c'est-à-dire - le plus grand point limite de la séquence (x n).

Soit x un nombre supérieur à . Choisissons e>0 si petit que

et x 1 О(x), à droite de x 1 il y a un nombre fini d'éléments de la séquence (x n) ou il n'y en a pas du tout, c'est-à-dire x n'est pas un point limite de la séquence (x n ).

Définition. Le plus grand point limite de la séquence (x n) est appelé limite supérieure de la séquence et est désigné par le symbole. Il découle de la remarque que toute séquence bornée a une limite supérieure.

De même, la notion de limite inférieure est introduite (comme le plus petit point limite de la séquence (x n )).

Nous avons donc prouvé l’énoncé suivant. Chaque séquence délimitée a des limites supérieure et inférieure.

Formulons le théorème suivant sans preuve.

Théorème. Pour que la suite (x n) soit convergente, il faut et il suffit qu'elle soit bornée et que ses limites supérieure et inférieure coïncident.

Les résultats de cette section conduisent au théorème principal de Bolzano-Weierstrass suivant.

Théorème de Bolzano-Weierstrass. De n’importe quelle séquence bornée, on peut extraire une sous-séquence convergente.

Preuve. Puisque la suite (x n ) est bornée, elle a au moins un point limite x. Ensuite, à partir de cette séquence, nous pouvons sélectionner une sous-séquence convergeant vers le point x (découle de la définition 2 du point limite).

Commentaire. De toute séquence bornée, on peut isoler une séquence convergente monotone.

Théorème de Bolzano-Weierstrass

Théorème de Bolzano-Weierstrass, ou Lemme de Bolzano-Weierstrass sur le point limite- une proposition d'analyse dont l'une des formulations dit : à partir de toute séquence limitée de points dans l'espace on peut sélectionner une sous-suite convergente. Le théorème de Bolzano-Weierstrass, notamment dans le cas d'une suite de nombres ( n= 1 ), est inclus dans chaque cours d’analyse. Il est utilisé dans la preuve de nombreuses propositions en analyse, par exemple le théorème sur une fonction continue sur un intervalle atteignant ses limites supérieure et inférieure exactes. Le théorème porte les noms du mathématicien tchèque Bolzano et du mathématicien allemand Weierstrass, qui l'ont formulé et prouvé indépendamment.

Formulations

Plusieurs formulations du théorème de Bolzano-Weierstrass sont connues.

Première formule

Soit une séquence de points dans l'espace proposée :

et que cette séquence soit limitée, c'est-à-dire

Où C> 0 - un nombre.

Alors de cette séquence on peut extraire une sous-séquence

qui converge vers un point de l'espace.

Le théorème de Bolzano-Weierstrass dans cette formulation est parfois appelé le principe de compacité d'une suite bornée.

Version étendue de la première formulation

Le théorème de Bolzano-Weierstrass est souvent complété par la phrase suivante.

Si une séquence de points dans l'espace est illimitée, il est alors possible de sélectionner une séquence qui a une limite.

Pour l'occasion n= 1, cette formulation peut être affinée : à partir de toute séquence numérique illimitée on peut sélectionner une sous-suite dont la limite est l'infini d'un certain signe ( ou ).

Ainsi, chaque séquence de nombres contient une sous-séquence qui a une limite dans l’ensemble étendu des nombres réels.

Deuxième formule

La proposition suivante est une formulation alternative du théorème de Bolzano-Weierstrass.

Tout sous-ensemble infini borné E l'espace a au moins un point limite en .

Plus en détail, cela signifie qu'il existe un point dont chaque voisinage contient un nombre infini de points dans l'ensemble E .

Preuve de l'équivalence de deux formulations du théorème de Bolzano-Weierstrass

Laisser E- un sous-ensemble infini et limité de l'espace. Prenons E séquence de différents points

Puisque cette suite est bornée, en vertu de la première formulation du théorème de Bolzano-Weierstrass, on peut en isoler une sous-suite

convergeant vers un certain point. Alors chaque voisinage d'un point X 0 contient un nombre infini de points de l'ensemble E .

Inversement, donnons une séquence arbitrairement limitée de points dans l’espace :

Plusieurs significations E d'une séquence donnée est limitée, mais peut être infinie ou finie. Si E bien sûr, alors l'une des valeurs est répétée dans la séquence un nombre infini de fois. Alors ces termes forment une sous-suite stationnaire convergeant vers le point un .

S'il y en a beaucoup E est infini, alors en vertu de la deuxième formulation du théorème de Bolzano-Weierstrass, il existe un point dans tout voisinage duquel il existe une infinité de termes différents de la séquence.

Nous choisissons séquentiellement pour points , tout en observant la condition des nombres croissants :

Alors la sous-suite converge vers le point X 0 .

Preuve

Le théorème de Bolzano-Weierstrass est dérivé de la propriété d'exhaustivité de l'ensemble des nombres réels. La version la plus célèbre de la preuve utilise la propriété de complétude sous la forme du principe du segment imbriqué.

Cas unidimensionnel

Montrons qu'à partir de n'importe quelle suite de nombres bornée, on peut sélectionner une sous-suite convergente. La méthode de preuve suivante est appelée Méthode Bolzano, ou méthode de réduction de moitié.

Soit une séquence de nombres limitée

Du caractère limité de la séquence, il s'ensuit que tous ses termes se trouvent sur un certain segment de la droite numérique, que nous notons [ un 0 ,b 0 ] .

Divisez le segment [ un 0 ,b 0 ] en deux en deux segments égaux. Au moins un des segments résultants contient un nombre infini de termes de la séquence. Notons-le [ un 1 ,b 1 ] .

Dans l'étape suivante, nous répéterons la procédure avec le segment [ un 1 ,b 1 ] : divisez-la en deux segments égaux et choisissez parmi eux celui sur lequel repose un nombre infini de termes de la suite. Notons-le [ un 2 ,b 2 ] .

En poursuivant le processus, nous obtenons une séquence de segments imbriqués

dans lequel chaque terme suivant est la moitié du précédent et contient un nombre infini de termes de la suite ( X k } .

Les longueurs des segments tendent vers zéro :

En vertu du principe de Cauchy-Cantor des segments imbriqués, il existe un seul point ξ qui appartient à tous les segments :

Par construction sur chaque segment [un m ,b m ] il existe un nombre infini de termes de la suite. Choisissons séquentiellement

tout en observant la condition des nombres croissants :

Alors la sous-suite converge vers le point ξ. Cela découle du fait que la distance de à ξ ne dépasse pas la longueur du segment les contenant [un m ,b m ] , où

Extension au cas d'un espace de dimension arbitraire

Le théorème de Bolzano-Weierstrass se généralise facilement au cas d'un espace de dimension arbitraire.

Soit une séquence de points dans l'espace :

(l'index inférieur est le numéro de membre de séquence, l'index supérieur est le numéro de coordonnée). Si la séquence de points dans l'espace est limitée, alors chacune des séquences numériques de coordonnées :

également limité ( - numéro de coordonnées).

En vertu de la version unidimensionnelle du théorème de Bolzano-Weirstrass de la séquence ( X k) on peut sélectionner une sous-séquence de points dont les premières coordonnées forment une séquence convergente. À partir de la sous-séquence résultante, nous sélectionnons à nouveau une sous-séquence qui converge le long de la deuxième coordonnée. Dans ce cas, la convergence le long de la première coordonnée sera préservée du fait que chaque sous-séquence d’une séquence convergente converge également. Et ainsi de suite.

Après n nous obtenons une certaine séquence d'étapes

qui est une sous-séquence de , et converge le long de chacune des coordonnées. Il s’ensuit que cette sous-suite converge.

Histoire

Théorème de Bolzano-Weierstrass (pour le cas n= 1) a été prouvé pour la première fois par le mathématicien tchèque Bolzano en 1817. Dans les travaux de Bolzano, il servait de lemme dans la preuve du théorème sur les valeurs intermédiaires d'une fonction continue, aujourd'hui connu sous le nom de théorème de Bolzano-Cauchy. Cependant, ces résultats et d’autres, prouvés par Bolzano bien avant Cauchy et Weierstrass, sont passés inaperçus.

Seulement un demi-siècle plus tard, Weierstrass, indépendamment de Bolzano, redécouvrit et démontra ce théorème. Initialement appelé théorème de Weierstrass, avant que les travaux de Bolzano ne soient connus et acceptés.

Ce théorème porte aujourd'hui les noms de Bolzano et Weierstrass. Ce théorème est souvent appelé Lemme de Bolzano-Weierstrass, et parfois lemme du point limite.

Le théorème de Bolzano-Weierstrass et la notion de compacité

Le théorème de Bolzano-Weierstrass établit la propriété intéressante suivante d'un ensemble borné : toute séquence de points M contient une sous-séquence convergente.

Lorsqu'ils prouvent diverses propositions en analyse, ils recourent souvent à la technique suivante : ils déterminent une séquence de points qui possède une propriété souhaitée, puis en sélectionnent une sous-séquence qui la possède également, mais qui est déjà convergente. Par exemple, c’est ainsi que l’on démontre le théorème de Weierstrass selon lequel une fonction continue sur un intervalle est bornée et prend ses plus grandes et ses plus petites valeurs.

L’efficacité d’une telle technique en général, ainsi que la volonté d’étendre le théorème de Weierstrass à des espaces métriques arbitraires, incitent le mathématicien français Maurice Fréchet à introduire le concept en 1906. compacité. La propriété des ensembles bornés dans , établie par le théorème de Bolzano-Weierstrass, est, au sens figuré, que les points de l'ensemble sont situés de manière assez « rapprochée » ou « compacte » : après avoir fait un nombre infini de pas le long de cet ensemble, on va certainement aussi proche que nous le souhaitons d’un certain point dans l’espace.

Fréchet introduit la définition suivante : ensemble M appelé compact, ou compact, si chaque séquence de ses points contient une sous-séquence convergeant vers un point de cet ensemble. On suppose que sur le plateau M la métrique est définie, c'est-à-dire qu'elle est

Définition v.7. Un point x € R sur la droite numérique est appelé point limite d'une suite (xn) si pour tout quartier U (x) et tout entier naturel N il est possible de trouver un élément xn appartenant à ce quartier de nombre supérieur à LG, c'est-à-dire x 6 R - point limite si. En d'autres termes, un point x sera un point limite pour (xn) si l'un de ses voisinages contient des éléments de cette séquence avec des nombres arbitrairement grands, bien que peut-être pas tous les éléments avec des nombres n > N. Par conséquent, l'énoncé suivant est tout à fait évident . Déclaration b.b. Si lim(xn) = 6 6 R, alors b est le seul point limite de la suite (xn). En effet, en vertu de la définition 6.3 de la limite d'une suite, tous ses éléments, à partir d'un certain nombre, tombent dans tout voisinage arbitrairement petit du point 6, et donc les éléments de nombres arbitrairement grands ne peuvent tomber dans le voisinage d'aucun autre point. . Par conséquent, la condition de la définition 6.7 n’est satisfaite que pour un seul point 6. Cependant, tous les points limites (parfois appelés points minces condensés) d’une séquence ne sont pas sa limite. Ainsi, la suite (b.b) n'a pas de limite (voir exemple 6.5), mais a deux points limites x = 1 et x = - 1. La suite ((-1)pp) a deux points infinis +oo et comme points limites - avec la droite numérique étendue, dont l'union est désignée par un symbole oo. C'est pourquoi nous pouvons supposer que les points limites infinis coïncident, et que le point infini oo, d'après (6.29), est la limite de cette séquence. Points limites de la droite des numéros de séquence.Démonstration du test de Weierstrass et du critère de Cauchy. Soit la suite (jn) donnée et les nombres k forment une suite croissante d'entiers positifs. Alors la séquence (Vnb où yn = xkn> est appelée une sous-suite de la séquence originale. Évidemment, si (i„) a le nombre 6 pour limite, alors chacune de ses sous-suites a la même limite, puisqu'à partir d'un certain nombre tous les éléments de la séquence originale et de l'une de ses sous-séquences tombent dans n'importe quel voisinage choisi du point 6. En même temps, tout point limite d'une sous-séquence est également un point limite pour la séquence. Théorème 9. De toute séquence qui a un point limite, on peut choisir une sous-suite qui a ce point limite comme limite. Soit b le point limite de la suite (xn), alors, selon la définition 6. 7 point limite, pour chaque n il existe un élément appartenant au voisinage U (6, 1/n) du point b de rayon 1/n. La sous-suite composée des points ijtj, ...1 ..., où zjfcn€U(6, 1/n) Vn 6 N, a une limite au point 6. En effet, pour un e > 0 arbitraire, on peut choisir N tel que. Alors tous les éléments de la sous-suite, commençant par le nombre km, tomberont dans le ^-voisinage U(6, e) du point 6, ce qui correspond à la condition 6.3 de la définition de la limite de la séquence. Le théorème inverse est également vrai. Points limites de la droite des numéros de séquence.Démonstration du test de Weierstrass et du critère de Cauchy. Théorème 8.10. Si une séquence a une sous-séquence de limite 6, alors b est le point limite de cette séquence. De la définition 6.3 de la limite d'une suite il résulte qu'à partir d'un certain nombre, tous les éléments de la sous-suite de limite b tombent dans un voisinage U(b, ​​​​e) de rayon arbitraire e. Puisque les éléments de la sous-suite sont simultanément des éléments de la suite (xn) > les éléments xn rentrent dans ce voisinage avec autant de nombres arbitrairement grands, et cela, en vertu de la définition 6.7, signifie que b est le point limite de la suite (n). Remarque 0.2. Les théorèmes 6.9 et 6.10 sont également valables dans le cas où le point limite est infini, si, pour prouver le voisinage merto de U(6, 1 /n), on considère le ou les voisinages. peut être isolé d'une suite est établi par le théorème suivant. Théorème 6.11 (Bolzano - Weierstrass). Toute suite bornée contient une sous-suite convergeant vers une limite finie. Soit tous les éléments de la suite (an) compris entre les nombres a et 6. , c'est-à-dire xn € [a, b] Vn € N. Divisez le segment [a , b] en deux. Alors au moins une de ses moitiés contiendra un nombre infini d'éléments de la séquence, car sinon tout le segment [a, b] en contiendrait un nombre fini, ce qui est impossible. Soit ] celui des moitiés du segment [a , 6], qui contient un ensemble infini d'éléments de la séquence (zn) (ou si les deux moitiés sont telles , puis n'importe lequel d'entre eux). De même, à partir du segment contenant un ensemble infini d'éléments de la séquence, etc. En poursuivant ce processus, nous construirons un système de segments imbriqués avec bn - an = (6- a)/2P. Selon le principe des segments imbriqués, il existe un point x qui appartient à tous ces segments. Ce point sera le point limite de la séquence (xn) - En fait, pour tout e-quartier U(x, e) = (xx + e) ​​​​​​point x il existe un segment C U(x, e) (il il suffit de choisir n parmi l'inégalité (, contenant un nombre infini d'éléments de la suite (sn). D'après la définition 6.7, x est le point limite de cette séquence. Alors, d’après le théorème 6.9, il existe une sous-suite convergeant vers le point x. La méthode de raisonnement utilisée dans la preuve de ce théorème (on l'appelle parfois le lemme de Bolzano-Weyer-Strass) et associée à la bissection séquentielle des segments considérés est connue sous le nom de méthode de Bolzano. Ce théorème simplifie grandement la preuve de nombreux théorèmes complexes. Il vous permet de prouver un certain nombre de théorèmes clés d'une manière différente (parfois plus simple). Annexe 6.2. Preuve du test de Weierstrass et du critère de Cauchy Tout d'abord, nous prouvons l'énoncé 6.1 (test de Weierstrass pour la convergence d'une suite monotone bornée). Supposons que la suite (jn) soit non décroissante. Alors l'ensemble de ses valeurs est borné ci-dessus et, d'après le théorème 2.1, a un supremum que l'on note sup(xn) soit R. En raison des propriétés du supremum (voir 2.7) Les points limites de la séquence sont le nombre ligne Démonstration du test de Weierstrass et du critère de Cauchy. D'après la définition 6.1 pour une suite non décroissante on a ou Then > Ny et compte tenu de (6.34) on obtient qui correspond à la définition 6.3 de la limite de la suite, soit 31im(sn) et lim(xn) = 66R. Si la suite (xn) est non croissante, alors le déroulement de la preuve est similaire. Passons maintenant à prouver la suffisance du critère de Kochia pour la convergence d'une suite (voir Énoncé 6.3), puisque la nécessité de la condition critère découle du Théorème 6.7. Soit la séquence (jn) fondamentale. D'après la définition 6.4, étant donné un € > 0 arbitraire, on peut trouver un nombre N(s) tel que m^N et n^N l'impliquent. Alors, en prenant m - N, pour Vn > N on obtient € £ Puisque la suite considérée possède un nombre fini d'éléments dont les nombres ne dépassent pas N, il résulte de (6.35) que la suite fondamentale est bornée (pour comparaison, voir le preuve du théorème 6.2 sur le caractère borné d'une suite convergente ). Pour un ensemble de valeurs d'une séquence bornée, il existe des bornes infimum et supremum (voir Théorème 2.1). Pour l'ensemble des valeurs d'éléments pour n > N, nous désignons ces faces respectivement an = inf xn et bjy = sup xn. À mesure que N augmente, l'infimum exact ne diminue pas et le supremum exact n'augmente pas, c'est-à-dire . Est-ce que je reçois un système de climatisation? segments Selon le principe des segments imbriqués, il existe un point commun qui appartient à tous les segments. Notons-le par b. Ainsi, avec la comparaison From (6. 36) et (6.37) on obtient donc ce qui correspond à la définition 6.3 de la limite de la suite, c'est-à-dire 31im(x„) et lim(sn) = 6 6 R. Bolzano a commencé à étudier les séquences fondamentales. Mais il ne disposait pas d’une théorie rigoureuse des nombres réels et il était donc incapable de prouver la convergence de la séquence fondamentale. Cauchy l'a fait, prenant pour acquis le principe des segments imbriqués, que Cantor a ensuite étayé. Non seulement le critère de convergence d'une séquence est nommé Cauchy, mais la séquence fondamentale est souvent appelée séquence de Cauchy, et le principe des segments imbriqués porte le nom de Cantor. Questions et tâches 8.1. Prouver que : 6.2. Donnez des exemples de séquences non convergentes avec des éléments appartenant aux ensembles Q et R\Q. 0,3. Dans quelles conditions les termes des progressions arithmétiques et géométriques forment-ils des suites décroissantes et croissantes ? 6.4. Démontrer les relations qui découlent du tableau. 6.1. 6.5. Construire des exemples de suites tendant vers les points infinis +oo, -oo, oo, et un exemple de suite convergeant vers le point 6 € R. c.v. Une séquence illimitée peut-elle ne pas être b.b. ? Si oui, donnez un exemple. à 7 heures. Construisez un exemple de séquence divergente composée d’éléments positifs qui n’a ni limite finie ni infinie. 6.8. Prouver la convergence de la suite (jn) donnée par la formule récurrente sn+i = sin(xn/2) sous la condition « 1 = 1. 6.9. Montrer que lim(xn)=09 si sn+i/xn-»g€)