Comment apprendre à résoudre des problèmes de géométrie analytique ?
Problème typique avec un triangle dans un avion

Cette leçon est créée sur l'approche de l'équateur entre la géométrie du plan et la géométrie de l'espace. À l'heure actuelle, il est nécessaire de systématiser les informations accumulées et de répondre à une question très importante : comment apprendre à résoudre des problèmes de géométrie analytique ? La difficulté est que vous pouvez proposer un nombre infini de problèmes de géométrie, et aucun manuel ne contiendra toute la multitude et la variété d'exemples. N'est pas dérivée d'une fonction avec cinq règles de différenciation, un tableau et plusieurs techniques….

Il existe une solution ! Je ne parlerai pas fort du fait que j'ai développé une sorte de technique grandiose, cependant, à mon avis, il existe une approche efficace du problème considéré, qui permet même à un mannequin complet d'obtenir de bons et excellents résultats. Au moins, l'algorithme général de résolution de problèmes géométriques a pris forme très clairement dans ma tête.

CE QUE VOUS DEVEZ SAVOIR ET POUVOIR FAIRE
pour réussir à résoudre des problèmes de géométrie ?

Il n'y a pas d'échappatoire à cela - afin de ne pas appuyer au hasard sur les boutons avec votre nez, vous devez maîtriser les bases de la géométrie analytique. Par conséquent, si vous venez de commencer à étudier la géométrie ou si vous l'avez complètement oublié, veuillez commencer par la leçon Vecteurs pour les nuls. En plus des vecteurs et des actions avec eux, vous devez connaître les concepts de base de la géométrie plane, en particulier, équation d'une droite dans un plan Et . La géométrie de l'espace est présentée dans des articles Équation plane, Équations d'une droite dans l'espace, Problèmes de base sur une ligne droite et un avion et quelques autres leçons. Les lignes courbes et les surfaces spatiales du second ordre se distinguent quelque peu et ne posent pas beaucoup de problèmes spécifiques.

Supposons que l'étudiant possède déjà des connaissances et des compétences de base pour résoudre les problèmes les plus simples de géométrie analytique. Mais cela se passe ainsi : vous lisez l'énoncé du problème, et... vous voulez tout fermer complètement, le jeter au fond et l'oublier, comme un mauvais rêve. De plus, cela ne dépend fondamentalement pas de votre niveau de qualification : de temps en temps, je suis moi-même confronté à des tâches pour lesquelles la solution n'est pas évidente. Que faire dans de tels cas ? Il ne faut pas avoir peur d’une tâche que vous ne comprenez pas !

Premièrement, devrait être installé - Est-ce un problème « plat » ou spatial ? Par exemple, si la condition inclut des vecteurs avec deux coordonnées, il s'agit bien sûr de la géométrie d'un plan. Et si l'enseignant chargeait l'auditeur reconnaissant d'une pyramide, alors il y a clairement la géométrie de l'espace. Les résultats de la première étape sont déjà assez bons, car nous avons réussi à supprimer une énorme quantité d'informations inutiles pour cette tâche !

Deuxième. La condition vous concernera généralement par une figure géométrique. En effet, parcourez les couloirs de votre université natale, et vous verrez de nombreux visages inquiets.

Dans les problèmes « plats », sans parler des points et des lignes évidents, la figure la plus populaire est un triangle. Nous allons l'analyser en détail. Vient ensuite le parallélogramme, et les formes beaucoup moins courantes sont le rectangle, le carré, le losange, le cercle et d'autres formes.

Dans les problèmes spatiaux, les mêmes figures plates + les avions eux-mêmes et les pyramides triangulaires communes à parallélépipèdes peuvent voler.

Deuxième question - Savez-vous tout sur ce chiffre ? Supposons que la condition parle d’un triangle isocèle et que vous vous souveniez très vaguement de quel type de triangle il s’agit. Nous ouvrons un manuel scolaire et lisons un article sur un triangle isocèle. Que faire... le docteur a dit un losange, ça veut dire un losange. La géométrie analytique est une géométrie analytique, mais le problème sera résolu par les propriétés géométriques des figures elles-mêmes, que nous connaissons grâce au programme scolaire. Si vous ne savez pas quelle est la somme des angles d’un triangle, vous pouvez souffrir longtemps.

Troisième. Essayez TOUJOURS de suivre le dessin(sur un brouillon/une copie finale/mentalement), même si cela n'est pas requis par la condition. Dans les problèmes « plats », Euclide lui-même a ordonné de prendre une règle et un crayon - et non seulement pour comprendre l'état, mais aussi à des fins d'auto-test. Dans ce cas, l'échelle la plus pratique est 1 unité = 1 cm (2 cellules de cahier). Ne parlons pas des étudiants et des mathématiciens imprudents qui tournent dans leurs tombes - il est presque impossible de se tromper dans de tels problèmes. Pour les tâches spatiales, nous effectuons un dessin schématique, qui aidera également à analyser l'état.

Un dessin ou un dessin schématique permet souvent de voir immédiatement la manière de résoudre un problème. Bien entendu, pour cela, vous devez connaître les fondements de la géométrie et comprendre les propriétés des formes géométriques (voir le paragraphe précédent).

Quatrième. Développement d'un algorithme de solution. De nombreux problèmes de géométrie comportent plusieurs étapes, la solution et sa conception sont donc très pratiques à décomposer en points. Souvent, l’algorithme vous vient immédiatement à l’esprit après avoir lu la condition ou terminé le dessin. En cas de difficultés, on commence par la QUESTION de la tâche. Par exemple, selon la condition « vous devez construire une ligne droite… ». Ici, la question la plus logique est : « Que faut-il savoir pour construire cette ligne droite ? » Supposons que « nous connaissons le point, nous devons connaître le vecteur de direction ». Nous posons la question suivante : « Comment trouver ce vecteur direction ? Où?" etc.

Parfois, il y a un "bug" - le problème n'est pas résolu et c'est tout. Les raisons de l'arrêt peuvent être les suivantes :

– Grave lacune dans les connaissances de base. En d’autres termes, vous ne savez pas et/ou ne voyez pas une chose très simple.

– Ignorance des propriétés des figures géométriques.

– La tâche était difficile. Oui, ça arrive. Cela ne sert à rien de cuire à la vapeur pendant des heures et de recueillir des larmes dans un mouchoir. Demandez conseil à votre professeur, à vos camarades ou posez une question sur le forum. De plus, il est préférable de concrétiser sa déclaration - sur cette partie de la solution que vous ne comprenez pas. Un cri en forme de « Comment résoudre le problème ? ça n'a pas l'air très bon... et surtout pour votre propre réputation.

Cinquième étape. Nous décidons-vérifions, décidons-vérifions, décidons-vérifions-donnons une réponse. Il est avantageux de vérifier chaque point de la tâche immédiatement après qu'il soit terminé. Cela vous aidera à repérer l'erreur immédiatement. Naturellement, personne n'interdit de résoudre rapidement l'ensemble du problème, mais il existe un risque de tout réécrire (souvent plusieurs pages).

Ce sont peut-être toutes les principales considérations à prendre en compte lors de la résolution de problèmes.

La partie pratique du cours est présentée en géométrie plane. Il n'y aura que deux exemples, mais cela ne semblera pas suffisant =)

Reprenons le fil de l'algorithme que je viens de regarder dans mon petit travail scientifique :

Exemple 1

Trois sommets d'un parallélogramme sont donnés. Trouvez le sommet.

Commençons par comprendre :

La première étape: Il est évident que nous parlons d'un problème « plat ».

Deuxième étape: Le problème concerne un parallélogramme. Est-ce que tout le monde se souvient de cette figure de parallélogramme ? Il n'y a pas lieu de sourire, de nombreuses personnes reçoivent leur éducation entre 30, 40 et 50 ans ou plus, de sorte que même des faits simples peuvent être effacés de la mémoire. La définition d'un parallélogramme se trouve dans l'exemple n°3 de la leçon Dépendance linéaire (non) des vecteurs. Base des vecteurs.

Troisième étape: Faisons un dessin sur lequel on marque trois sommets connus. C'est drôle qu'il ne soit pas difficile de construire immédiatement le point souhaité :

Le construire est certes une bonne chose, mais la solution doit être formulée de manière analytique.

Quatrième étape: Développement d'un algorithme de solution. La première chose qui vient à l’esprit est qu’un point peut être trouvé comme l’intersection de lignes. Nous ne connaissons pas leurs équations, nous devrons donc traiter de cette question :

1) Les côtés opposés sont parallèles. Par points Trouvons le vecteur direction de ces côtés. C’est le problème le plus simple abordé en classe. Vecteurs pour les nuls.

Note: il est plus correct de dire « l'équation d'une droite contenant un côté », mais ici et plus loin, par souci de concision, j'utiliserai les expressions « équation d'un côté », « vecteur directeur d'un côté », etc.

3) Les côtés opposés sont parallèles. A l’aide des points, on trouve le vecteur direction de ces côtés.

4) Créons une équation d’une droite en utilisant un point et un vecteur directeur

Dans les paragraphes 1-2 et 3-4, nous avons en fait résolu deux fois le même problème ; d'ailleurs, il a été discuté dans l'exemple n°3 de la leçon Les problèmes les plus simples avec une ligne droite dans un avion. Il était possible d'emprunter un chemin plus long - trouver d'abord les équations des droites et ensuite seulement « en extraire » les vecteurs directeurs.

5) Les équations des droites sont maintenant connues. Il ne reste plus qu'à composer et résoudre le système d'équations linéaires correspondant (voir exemples n°4, 5 de la même leçon Les problèmes les plus simples avec une ligne droite dans un avion).

Le point est trouvé.

La tâche est assez simple et sa solution est évidente, mais il existe un chemin plus court !

Deuxième solution:

Les diagonales d'un parallélogramme sont divisées en deux par leur point d'intersection. J'ai marqué le point, mais pour ne pas encombrer le dessin, je n'ai pas dessiné les diagonales elles-mêmes.

Composons l'équation du côté point par point :

Pour vérifier, vous devez mentalement ou sur un brouillon remplacer les coordonnées de chaque point dans l'équation résultante. Trouvons maintenant la pente. Pour ce faire, on réécrit l'équation générale sous la forme d'une équation à coefficient de pente :

La pente est donc :

De même, on retrouve les équations des côtés. Je ne vois pas trop l’intérêt de décrire la même chose, je vais donc donner immédiatement le résultat final :

2) Trouvez la longueur du côté. C’est le problème le plus simple abordé en classe. Vecteurs pour les nuls. Pour les points on utilise la formule :

En utilisant la même formule, il est facile de trouver les longueurs des autres côtés. Le contrôle peut être effectué très rapidement avec une règle ordinaire.

Nous utilisons la formule .

Trouvons les vecteurs :

Ainsi:

Au fait, en chemin, nous avons trouvé les longueurs des côtés.

Par conséquent:

Eh bien, cela semble être vrai ; pour être convaincant, vous pouvez attacher un rapporteur au coin.

Attention! Ne confondez pas l'angle d'un triangle avec l'angle entre des lignes droites. L'angle d'un triangle peut être obtus, mais pas l'angle entre des droites (voir le dernier paragraphe de l'article Les problèmes les plus simples avec une ligne droite dans un avion). Cependant, pour trouver l’angle d’un triangle, vous pouvez également utiliser les formules de la leçon ci-dessus, mais le problème est que ces formules donnent toujours un angle aigu. Avec leur aide, j'ai résolu ce problème dans le brouillon et j'ai obtenu le résultat. Et sur la copie finale, je devrais écrire des excuses supplémentaires, ça.

4) Écrivez une équation pour une droite passant par un point parallèle à la droite.

Tâche standard, discutée en détail dans l'exemple n°2 de la leçon Les problèmes les plus simples avec une ligne droite dans un avion. De l'équation générale de la droite Supprimons le vecteur guide. Créons une équation d'une droite en utilisant un point et un vecteur directeur :

Comment trouver la hauteur d'un triangle ?

5) Créons une équation pour la hauteur et trouvons sa longueur.

Il n’y a pas d’échappatoire aux définitions strictes, il faudra donc piocher dans un manuel scolaire :

Hauteur du triangle est appelée la perpendiculaire tirée du sommet du triangle à la ligne contenant le côté opposé.

Autrement dit, il est nécessaire de créer une équation pour une perpendiculaire tracée du sommet vers le côté. Cette tâche est abordée dans les exemples n°6, 7 de la leçon Les problèmes les plus simples avec une ligne droite dans un avion. De l’équation. supprimer le vecteur normal. Composons l'équation de la hauteur à l'aide d'un point et d'un vecteur direction :

Attention, nous ne connaissons pas les coordonnées du point.

Parfois l'équation de la hauteur est trouvée à partir du rapport des coefficients angulaires des droites perpendiculaires : . Dans ce cas, alors : . Composons l'équation de la hauteur à l'aide d'un point et d'un coefficient angulaire (voir le début de la leçon Équation d'une droite sur un plan):

La longueur en hauteur peut être trouvée de deux manières.

Il existe un chemin détourné :

a) trouver – le point d'intersection de la hauteur et du côté ;
b) trouver la longueur du segment en utilisant deux points connus.

Mais en classe Les problèmes les plus simples avec une ligne droite dans un avion une formule pratique pour la distance d'un point à une ligne a été envisagée. Le point est connu : , l'équation de la droite est également connue : , Ainsi:

6) Calculez l'aire du triangle. Dans l'espace, l'aire d'un triangle est traditionnellement calculée à l'aide de produit vectoriel de vecteurs, mais ici on nous donne un triangle sur un plan. Nous utilisons la formule scolaire :
– L’aire d’un triangle est égale à la moitié du produit de sa base par sa hauteur.

Dans ce cas:

Comment trouver la médiane d'un triangle ?

7) Créons une équation pour la médiane.

Médiane d'un triangle appelé segment reliant le sommet d’un triangle au milieu du côté opposé.

a) Trouvez le point - le milieu du côté. Nous utilisons formules pour les coordonnées du milieu d'un segment. Les coordonnées des extrémités du segment sont connues : , puis les coordonnées du milieu :

Ainsi:

Composons l'équation médiane point par point :

Pour vérifier l'équation, vous devez y substituer les coordonnées des points.

8) Trouver le point d'intersection de la hauteur et de la médiane. Je pense que tout le monde a déjà appris à réaliser cet élément du patinage artistique sans tomber :

Dans les problèmes 1 à 20, les sommets du triangle ABC sont donnés.
Trouvez : 1) la longueur du côté AB ; 2) les équations des côtés AB et AC et leurs coefficients angulaires ; 3) Angle interne A en radians avec une précision de 0,01 ; 4) équation pour la hauteur du CD et sa longueur ; 5) l'équation d'un cercle dont la hauteur CD est le diamètre ; 6) un système d'inégalités linéaires définissant le triangle ABC.

Longueur des côtés du triangle :
|AB| = 15
|AC| = 11,18
|C.-B.| = 14,14
Distance d du point M : d = 10
Les coordonnées des sommets du triangle sont données : A(-5,2), B(7,-7), C(5,7).
2) Longueur des côtés du triangle
La distance d entre les points M 1 (x 1 ; y 1) et M 2 (x 2 ; y 2) est déterminée par la formule :

8) Équation d'une droite
Une droite passant par les points A 1 (x 1 ; y 1) et A 2 (x 2 ; y 2) est représentée par les équations :

Équation de la droite AB


ou

ou
y = -3 / 4 x -7 / 4 ou 4y + 3x +7 = 0
Équation de la droite AC
Équation canonique de la droite :

ou

ou
y = 1 / 2 x + 9 / 2 ou 2y -x - 9 = 0
Équation de la droite BC
Équation canonique de la droite :

ou

ou
y = -7x + 42 ou y + 7x - 42 = 0
3) Angle entre les lignes droites
Équation de la droite AB:y = -3 / 4 x -7 / 4
Équation de droite AC : y = 1 / 2 x + 9 / 2
L'angle φ entre deux droites, donné par des équations à coefficients angulaires y = k 1 x + b 1 et y 2 = k 2 x + b 2, est calculé par la formule :

Les pentes de ces lignes sont de -3/4 et 1/2. Utilisons la formule, et prenons son membre de droite modulo :

tg φ = 2
φ = arctan(2) = 63,44 0 ou 1,107 rad.
9) Équation de la hauteur passant par le sommet C
La droite passant par le point N 0 (x 0 ;y 0) et perpendiculaire à la droite Ax + By + C = 0 a un vecteur directeur (A;B) et est donc représentée par les équations :



Cette équation peut être trouvée d'une autre manière. Pour ce faire, trouvons la pente k 1 de la droite AB.
Équation AB : y = -3 / 4 x -7 / 4, soit k 1 = -3 / 4
Trouvons le coefficient angulaire k de la perpendiculaire à partir de la condition de perpendiculaire de deux droites : k 1 *k = -1.
En substituant la pente de cette droite au lieu de k 1, on obtient :
-3 / 4 k = -1, d'où k = 4 / 3
Puisque la perpendiculaire passe par le point C(5,7) et a k = 4 / 3, nous chercherons son équation sous la forme : y-y 0 = k(x-x 0).
En remplaçant x 0 = 5, k = 4/3, y 0 = 7, nous obtenons :
y-7 = 4/3 (x-5)
ou
y = 4 / 3 x + 1 / 3 ou 3y -4x - 1 = 0
Trouvons le point d'intersection avec la droite AB :
Nous avons un système de deux équations :
4 ans + 3x +7 = 0
3 ans -4x - 1 = 0
À partir de la première équation, nous exprimons y et le substituons dans la deuxième équation.
On a:
x = -1
y=-1
D(-1;-1)
9) Longueur de l'altitude du triangle tiré du sommet C
La distance d du point M 1 (x 1 ;y 1) à la droite Ax + By + C = 0 est égale à la valeur absolue de la grandeur :

Trouver la distance entre le point C(5;7) et la ligne AB (4y + 3x +7 = 0)


La longueur de la hauteur peut être calculée à l'aide d'une autre formule, comme la distance entre le point C(5;7) et le point D(-1;-1).
La distance entre deux points est exprimée en coordonnées par la formule :

5) l'équation d'un cercle dont la hauteur CD est le diamètre ;
L'équation d'un cercle de rayon R de centre au point E(a;b) a la forme :
(x-a) 2 + (y-b) 2 = R 2
Puisque CD est le diamètre du cercle souhaité, son centre E est le milieu du segment CD. En utilisant les formules pour diviser un segment en deux, on obtient :


Donc E(2;3) et R = CD / 2 = 5. En utilisant la formule, on obtient l'équation du cercle recherché : (x-2) 2 + (y-3) 2 = 25

6) un système d'inégalités linéaires définissant le triangle ABC.
Équation de la droite AB : y = -3 / 4 x -7 / 4
Équation de la droite AC : y = 1 / 2 x + 9 / 2
Équation de la droite BC : y = -7x + 42

Problème 1. Les coordonnées des sommets du triangle ABC sont données : A(4 ; 3), B(16 ;-6), C(20 ; 16). Trouvez : 1) la longueur du côté AB ; 2) les équations des côtés AB et BC et leurs coefficients angulaires ; 3) angle B en radians avec une précision de deux chiffres ; 4) équation de la hauteur CD et de sa longueur ; 5) l'équation de la médiane AE et les coordonnées du point K de l'intersection de cette médiane avec la hauteur CD ; 6) l'équation d'une droite passant par le point K parallèle au côté AB ; 7) coordonnées du point M, situé symétriquement au point A par rapport à la droite CD.

Solution:

1. La distance d entre les points A(x 1 ,y 1) et B(x 2 ,y 2) est déterminée par la formule

En appliquant (1), on trouve la longueur du côté AB :

2. L'équation de la droite passant par les points A(x 1 ,y 1) et B(x 2 ,y 2) a la forme

(2)

En substituant les coordonnées des points A et B dans (2), on obtient l'équation du côté AB :

Après avoir résolu la dernière équation pour y, on retrouve l'équation du côté AB sous la forme d'une droite à coefficient angulaire :

où

En substituant les coordonnées des points B et C dans (2), on obtient l'équation de la droite BC :

Ou

3. On sait que la tangente de l'angle entre deux droites dont les coefficients angulaires sont respectivement égaux est calculée par la formule

(3)

L'angle B recherché est formé par les droites AB et BC dont on trouve les coefficients angulaires : En appliquant (3), on obtient

Ou content.

4. L'équation d'une droite passant par un point donné dans une direction donnée a la forme

(4)

La hauteur CD est perpendiculaire au côté AB. Pour trouver la pente de la hauteur CD, on utilise la condition de perpendiculaire des droites. Depuis lors En substituant dans (4) les coordonnées du point C et le coefficient angulaire de hauteur trouvé, on obtient

Pour trouver la longueur de la hauteur CD, nous déterminons d'abord les coordonnées du point D - le point d'intersection des droites AB et CD. Résoudre le système ensemble :

nous trouvons c'est-à-dire D(8;0).

En utilisant la formule (1), nous trouvons la longueur de la hauteur CD :

5. Pour trouver l'équation de la médiane AE, on détermine d'abord les coordonnées du point E, qui est le milieu du côté BC, en utilisant les formules pour diviser un segment en deux parties égales :

(5)

Ainsi,

En substituant les coordonnées des points A et E dans (2), on trouve l'équation de la médiane :

Pour trouver les coordonnées du point d'intersection de la hauteur CD et de la médiane AE, on résout ensemble le système d'équations

Nous trouvons.

6. Puisque la droite souhaitée est parallèle au côté AB, son coefficient angulaire sera égal au coefficient angulaire de la droite AB. En substituant dans (4) les coordonnées du point K trouvé et le coefficient angulaire on obtient

3x + 4a – 49 = 0 (KF)

7. Puisque la droite AB est perpendiculaire à la droite CD, le point recherché M, situé symétriquement au point A par rapport à la droite CD, se trouve sur la droite AB. De plus, le point D est le milieu du segment AM. A l'aide des formules (5), on trouve les coordonnées du point M recherché :

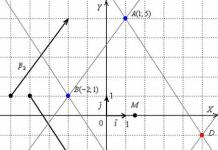
Le triangle ABC, la hauteur CD, la médiane AE, la droite KF et le point M sont construits dans le système de coordonnées xOy de la Fig. 1.

Tâche 2. Créez une équation pour le lieu des points dont les distances à un point donné A(4; 0) et à une ligne donnée x=1 sont égales à 2.

Solution:

Dans le système de coordonnées xOy, nous construisons le point A(4;0) et la droite x = 1. Soit M(x;y) un point arbitraire de l'emplacement géométrique souhaité des points. Abaissons la perpendiculaire MB à la droite donnée x = 1 et déterminons les coordonnées du point B. Puisque le point B se trouve sur la droite donnée, son abscisse est égale à 1. L'ordonnée du point B est égale à l'ordonnée du point M Par conséquent, B(1;y) (Fig. 2).

Selon les conditions du problème |MA| : |MV| = 2. Distances |MA| et |Mo| on trouve à partir de la formule (1) du problème 1 :

En mettant au carré les côtés gauche et droit, on obtient

L'équation résultante est une hyperbole dans laquelle le demi-axe réel est a = 2 et le demi-axe imaginaire est

Définissons les foyers d'une hyperbole. Pour une hyperbole, l’égalité est satisfaite. Par conséquent, et – astuces hyperboles. Comme vous pouvez le voir, le point donné A(4;0) est le bon foyer de l'hyperbole.

Déterminons l'excentricité de l'hyperbole résultante :

Les équations des asymptotes de l'hyperbole ont la forme et . Par conséquent, ou et sont des asymptotes d’une hyperbole. Avant de construire une hyperbole, on construit ses asymptotes.

Problème 3. Créez une équation pour le lieu des points équidistants du point A(4; 3) et de la droite y = 1. Réduisez l'équation résultante à sa forme la plus simple.

Solution: Soit M(x; y) l'un des points du lieu géométrique des points souhaité. Déposons la perpendiculaire MB du point M à cette droite y = 1 (Fig. 3). Déterminons les coordonnées du point B. Évidemment, l'abscisse du point B est égale à l'abscisse du point M, et l'ordonnée du point B est égale à 1, c'est-à-dire B(x; 1). Selon les conditions du problème |MA|=|MV|. Par conséquent, pour tout point M(x;y) appartenant au lieu géométrique des points souhaité, l'égalité suivante est vraie :

L'équation résultante définit une parabole avec un sommet au point. Pour amener l'équation de la parabole à sa forme la plus simple, posons et y + 2 = Y, alors l'équation de la parabole prend la forme :

Instructions

Vous recevez trois points. Notons-les comme (x1, y1), (x2, y2), (x3, y3). On suppose que ces points sont les sommets de certains Triangle. La tâche est de créer des équations de ses côtés - plus précisément, des équations des lignes sur lesquelles se trouvent ces côtés. Ces équations devraient ressembler à :
y = k1*x + b1 ;
y = k2*x + b2;
y = k3*x + b3. Il faut donc trouver les valeurs angulaires k1, k2, k3 et les déplacements b1, b2, b3.

Trouvez une droite passant par les points (x1, y1), (x2, y2). Si x1 = x2, alors la droite souhaitée est verticale et son équation est x = x1. Si y1 = y2, alors la droite est horizontale et son équation est y = y1. En général, ces coordonnées ne se correspondent pas.

En remplaçant les coordonnées (x1, y1), (x2, y2) dans l'équation générale de la droite, vous obtenez un système de deux équations linéaires : k1*x1 + b1 = y1 ;
k1*x2 + b1 = y2. Soustrayez une équation de l'autre et résolvez l'équation résultante pour k1 : k1*(x2 - x1) = y2 - y1, donc k1 = (y2 - y1)/(x2 - x1).

En remplaçant ce que vous avez trouvé dans l'une des équations originales, trouvez l'expression de b1 :((y2 - y1)/(x2 - x1))*x1 + b1 = y1 ;
b1 = y1 - ((y2 - y1)/(x2 - x1))*x1. Puisque nous savons déjà que x2 ≠ x1, nous pouvons simplifier l'expression en multipliant y1 par (x2 - x1)/(x2 - x1). Ensuite pour b1 vous obtiendrez l'expression suivante : b1 = (x1*y2 - x2*y1)/(x2 - x1).

Vérifiez si le tiers des points donnés se trouve sur la ligne trouvée. Pour ce faire, remplacez (x3, y3) dans l’équation résultante et voyez si l’égalité est vraie. Si on l’observe, les trois points se trouvent donc sur la même ligne et le triangle dégénère en segment.

De la même manière que décrit ci-dessus, dérivez les équations pour les droites passant par les points (x2, y2), (x3, y3) et (x1, y1), (x3, y3).

La forme finale des équations pour les côtés d'un triangle donnée par les coordonnées des sommets est : (1) y = ((y2 - y1)*x + (x1*y2 - x2*y1))/(x2 - x1 );
(2) y = ((y3 - y2)*x + (x2*y3 - x3*y2))/(x3 - x2) ;
(3) y = ((y3 - y1)*x + (x1*y3 - x3*y1))/(x3 - x1).

Trouver équations des soirées Triangle, tout d'abord, il faut essayer de résoudre la question de savoir comment trouver l'équation d'une droite sur un plan si son vecteur directeur s(m, n) et un point M0(x0, y0) appartenant à la droite sont connus.

Instructions

Prenez un point arbitraire (variable, flottant) М(x, y) et construisez un vecteur М0M =(x-x0, y-y0) (écrivez aussi М0M(x-x0, y-y0)), qui sera évidemment colinéaire (parallèle) par k s. Ensuite, nous pouvons conclure que les coordonnées de ces vecteurs sont proportionnelles, nous pouvons donc créer une droite canonique : (x-x0)/m = (y-y0)/n. C'est ce rapport qui sera utilisé pour résoudre le problème.

Toutes les autres actions sont déterminées sur la base de la méthode .1ère méthode. Un triangle est donné par les coordonnées de ses trois sommets, ce qui, en géométrie scolaire, est donné par les longueurs de ses trois sommets. des soirées(voir fig. 1). Autrement dit, la condition contient les points M1(x1, y1), M2(x2, y2), M3(x3, y3). Ils correspondent à leurs rayons vecteurs) OM1, 0M2 et OM3 de mêmes coordonnées que les points. Pour obtenir équations des soirées s M1M2 nécessite son vecteur directeur M1M2=OM2 – OM1=M1M2(x2-x1, y2-y1) et l'un des points M1 ou M2 (ici le point d'indice le plus bas est pris).

Donc pour des soirées y M1M2 équation canonique de la droite (x-x1)/(x2-x1)=(y-y1)/(y2-y1). En agissant de manière purement inductive, nous pouvons écrire équations le reste des soirées.Pour des soirées s М2М3 : (x-x2)/(x3-x2)=(y-y2)/(y3-y2). Pour des soirées s М1М3 : (x-x1)/(x3-x1)=(y-y1)/(y3-y1).

2ème méthode. Le triangle est défini par deux points (les mêmes qu'avant M1(x1, y1) et M2(x2, y2)), ainsi que les vecteurs unitaires des directions des deux autres des soirées. Pour des soirées s М2М3 : p^0(m1, n1). Pour M1M3 : q^0(m2, n2). Donc pour des soirées s M1M2 sera le même que dans la première méthode : (x-x1)/(x2-x1)=(y-y1)/(y2-y1).

Pour des soirées s М2М3 comme point (x0, y0) du repère canonique équations(x1, y1), et le vecteur directeur est p^0(m1, n1). Pour des soirées s M1M3, (x2, y2) est pris comme point (x0, y0), le vecteur directeur est q^0(m2, n2). Ainsi, pour M2M3 : équation (x-x1)/m1=(y-y1)/n1. Pour M1M3 : (x-x2)/m2=(y-y2)/n2.

Vidéo sur le sujet

Astuce 3 : Comment trouver la hauteur d'un triangle si les coordonnées des points sont données

La hauteur est le segment de droite reliant le haut de la figure au côté opposé. Ce segment doit être perpendiculaire au côté, donc un seul peut être dessiné à partir de chaque sommet hauteur. Puisqu’il y a trois sommets sur cette figure, il y a le même nombre de hauteurs. Si un triangle est donné par les coordonnées de ses sommets, la longueur de chacune des hauteurs peut être calculée, par exemple, en utilisant la formule pour trouver l'aire et calculer les longueurs des côtés.

Instructions

Commencez par calculer les longueurs des côtés Triangle. Désigner coordonnées des chiffres comme celui-ci : A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) et C(X₃,Y₃,Z₃). Ensuite, vous pouvez calculer la longueur du côté AB en utilisant la formule AB = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²). Pour les deux autres côtés, cela ressemblera à ceci : BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) et AC = √((X₁-X₃)² + (Y₁ -Y₃ )² + (Z₁-Z₃)²). Par exemple, pour Triangle de coordonnées A(3,5,7), B(16,14,19) et C(1,2,13) ​​​​​​la longueur du côté AB sera √((3-16)² + (5-14 )² + (7 -19)²) = √(-13² + (-9²) + (-12²)) = √(169 + 81 + 144) = √394 ≈ 19,85. Les longueurs des côtés BC et AC, calculées de la même manière, seront √(15² + 12² + 6²) = √405 ≈ 20,12 et √(2² + 3² + (-6²)) = √49 = 7.

Connaître les longueurs des trois côtés obtenus à l'étape précédente suffit pour calculer l'aire Triangle(S) selon la formule de Héron : S = ¼ * √((AB+BC+CA) * (BC+CA-AB) * (AB+CA-BC) * (AB+BC-CA)). Par exemple, en substituant dans cette formule les valeurs obtenues à partir des coordonnées Triangle-échantillon de l'étape précédente, cela donnera la valeur : S = ¼*√((19.85+20.12+7) * (20.12+7-19.85) * (19.85+7-20.12 ) * (19.85+20.12-7) ) = ¼*√(46,97 * 7,27 * 6,73 * 32,97) ≈ ¼*√75768,55 ≈ ¼*275,26 = 68,815 .

Basé sur la zone Triangle, calculées à l'étape précédente, et les longueurs des côtés obtenues à la deuxième étape, calculent les hauteurs de chacun des côtés. Puisque l'aire est égale à la moitié du produit de la hauteur et de la longueur du côté vers lequel elle est dessinée, pour trouver la hauteur, divisez l'aire doublée par la longueur du côté souhaité : H = 2*S/a. Pour l'exemple utilisé ci-dessus, la hauteur descendue du côté AB sera 2*68,815/16,09 ≈ 8,55, la hauteur du côté BC aura une longueur de 2*68,815/20,12 ≈ 6,84, et pour le côté AC cette valeur sera égale à 2 *68,815/7 ≈ 19,66.

Sources:

• points donnés trouver l'aire du triangle

Astuce 4 : Comment utiliser les coordonnées des sommets d'un triangle pour trouver les équations de ses côtés

En géométrie analytique, un triangle sur un plan peut être défini dans un système de coordonnées cartésiennes. Connaissant les coordonnées des sommets, vous pouvez créer des équations pour les côtés du triangle. Ce seront les équations de trois droites qui, se coupant, forment une figure.