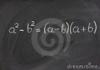Opérations sur des nombres complexes écrits sous forme algébrique

Forme algébrique d'un nombre complexe z =(un,b).est appelée une expression algébrique de la forme

z = un + bi.

Opérations arithmétiques sur des nombres complexes z 1 = un 1 +b 1 je Et z 2 = un 2 +b 2 je, écrits sous forme algébrique, s'effectuent comme suit.

1. Somme (différence) de nombres complexes

z 1 ±z 2 = (un 1 ±a 2) + (b 1 ±b 2)∙je,

ceux. l'addition (soustraction) est effectuée selon la règle d'addition de polynômes avec réduction de termes similaires.

2. Produit de nombres complexes

z 1 ∙z 2 = (un 1 ∙une 2 -b 1 ∙b 2) + (un 1 ∙b 2 + un 2 ∙b 1)∙je,

ceux. la multiplication s'effectue selon la règle habituelle de multiplication des polynômes, en tenant compte du fait que je 2 = 1.

3. La division de deux nombres complexes s'effectue selon la règle suivante :

, (z 2 ≠ 0),

ceux. la division s'effectue en multipliant le dividende et le diviseur par le nombre conjugué du diviseur.

L'exponentiation des nombres complexes est définie comme suit :

Il est facile de montrer que

Exemples.

1. Trouvez la somme des nombres complexes z 1 = 2 – je Et z 2 = – 4 + 3je.

z 1 + z 2 = (2 + (–1)∙je)+ (–4 + 3je) = (2 + (–4)) + ((–1) + 3) je = –2+2je.

2. Trouver le produit de nombres complexes z 1 = 2 – 3je Et z 2 = –4 + 5je.

= (2 – 3je) ∙ (–4 + 5je) = 2 ∙(–4) + (-4) ∙(–3je)+ 2∙5je– 3je∙ 5je = 7+22je.

3. Trouvez le quotient z de la division z 1 = 3 – 2na z 2 = 3 – je.

z = .

4. Résolvez l'équation : , X Et oui Î R..

(2x+y) + (x+y)je = 2 + 3je.

Grâce à l'égalité des nombres complexes, nous avons :

où X =–1 , oui= 4.

5. Calculez : je 2 ,je 3 ,je 4 ,je 5 ,je 6 ,je -1 , je -2 .

6. Calculez si .

.

7. Calculer l'inverse d'un nombre z=3-je.

Nombres complexes sous forme trigonométrique

Plan complexe appelé plan de coordonnées cartésiennes ( x, y), si chaque point de coordonnées ( un B) est associé à un nombre complexe z = a + bi. Dans ce cas, l’axe des abscisses est appelé axe réel, et l'axe des ordonnées est imaginaire. Alors tout nombre complexe a+bi représenté géométriquement sur un plan comme un point UNE (une, b) ou vecteur.

Par conséquent, la position du point UN(et donc un nombre complexe z) peut être spécifié par la longueur du vecteur | | = r et angle j, formé par le vecteur | | avec la direction positive de l’axe réel. La longueur du vecteur s'appelle module d'un nombre complexe et est noté | z |=r, et l'angle j appelé argument de nombre complexe et est désigné j = argument z.

Il est clair que | z| ³ 0 et | z | = 0 Û z = 0.

De la fig. 2 il est clair que .

L'argument d'un nombre complexe est déterminé de manière ambiguë, mais avec une précision de 2 pk,kÎ Z.

De la fig. 2, il est également clair que si z=a+bi Et j = argument z, Que

parce que j =,péché j =, tg j = .

Si zÎR. Et z> 0, alors argument z = 0 +2pk;

Si z ОR. Et z< 0, alors argument z = p + 2pk;

Si z = 0,argument z indéfini.

La valeur principale de l'argument est déterminée sur l'intervalle 0 £ arg z 2 £ p,

ou -p£ arg z £ p.

Exemples:

1. Trouver le module des nombres complexes z 1 = 4 – 3je Et z 2 = –2–2je.

2. Définir des zones sur le plan complexe défini par les conditions :

1) | z | = 5; 2) | z| 6 £ ; 3) | z – (2+je) | 3 £ ; 4) 6 £ | z – je| 7 £.

Solutions et réponses :

1) | z| = 5 Û Û - équation d'un cercle de rayon 5 et de centre à l'origine.

2) Un cercle de rayon 6 et de centre à l'origine.

3) Cercle de rayon 3 avec centre au point z 0 = 2 + je.

4) Un anneau délimité par des cercles de rayons 6 et 7 avec un centre en un point z 0 = je.

3. Trouvez le module et l'argument des nombres : 1) ; 2) .

1) ; UN = 1, b = Þ ,

Þ j 1 = .

2) z 2 = –2 – 2je; une =–2, b =-2Þ ,

.

Astuce : Lorsque vous déterminez l'argument principal, utilisez le plan complexe.

Ainsi: z 1 = .

2) , r 2 = 1, j 2 = , .

3) , r 3 = 1, j 3 = , .

4) , r 4 = 1, j 4 = , .

Conférence

Forme trigonométrique d'un nombre complexe

Plan

1. Représentation géométrique des nombres complexes.

2. Notation trigonométrique des nombres complexes.

3. Actions sur des nombres complexes sous forme trigonométrique.

Représentation géométrique de nombres complexes.

a) Les nombres complexes sont représentés par des points sur un plan selon la règle suivante : un + bi = M ( un ; b ) (Fig. 1).

Image 1

b) Un nombre complexe peut être représenté par un vecteur qui commence au pointÀ PROPOS et la fin en un point donné (Fig. 2).

Figure 2

Exemple 7. Construire des points représentant des nombres complexes :1; - je ; - 1 + je ; 2 – 3 je (Fig. 3).

figure 3

Notation trigonométrique des nombres complexes.

Nombre complexez = un + bi peut être spécifié en utilisant le vecteur rayon avec coordonnées( un ; b ) (Fig. 4).

Figure 4

Définition . Longueur du vecteur , représentant un nombre complexez , est appelé module de ce nombre et est noté our .

Pour tout nombre complexez son moduler = | z | est déterminé uniquement par la formule .

Définition . La grandeur de l'angle entre la direction positive de l'axe réel et le vecteur , représentant un nombre complexe, est appelé l'argument de ce nombre complexe et est notéUN rg z ouφ .

Argument de nombre complexez = 0 indéfini. Argument de nombre complexez≠ 0 – une quantité à plusieurs valeurs et est déterminée à l'intérieur d'un terme2πk (k = 0 ; - 1 ; 1 ; - 2 ; 2 ; …) : Arg z = argument z + 2πk , Oùargument z – la valeur principale de l'argument contenu dans l'intervalle(-π; π] , c'est-π < argument z ≤ π (parfois une valeur appartenant à l'intervalle est prise comme valeur principale de l'argument .

Cette formule quandr =1 souvent appelée formule de Moivre :

(cos φ + je péché φ) n = cos (nφ) + i sin (nφ), n  N .

Exemple 11 : Calculer(1 + je ) 100 .

Écrivons un nombre complexe1 + je sous forme trigonométrique.

une = 1, b = 1 .

cos φ = , péché φ = , φ = .

(1+je) 100 = [ (parce que + je pèche )] 100 = ( ) 100 (parce que 100 + je pèche ·100) = = 2 50 (cos 25π + je sin 25π) = 2 50 (cos π + je péché π) = - 2 50 .

4) Extraction racine carréeà partir d'un nombre complexe.

En prenant la racine carrée d'un nombre complexeun + bi nous avons deux cas :

Sib >o , Que ;

NUMÉROS COMPLEXES XI

§ 256. Forme trigonométrique des nombres complexes

Soit un nombre complexe a + bi correspond au vecteur O.A.> avec les coordonnées ( un B ) (voir fig. 332).

Notons la longueur de ce vecteur par r , et l'angle qu'il fait avec l'axe X , à travers φ . Par définition du sinus et du cosinus :

un / r =cos φ , b / r = péché φ .

C'est pourquoi UN = r parce que φ , b = r péché φ . Mais dans ce cas le nombre complexe a + bi peut s'écrire sous la forme :

a + bi = r parce que φ + ir péché φ = r (parce que φ + je péché φ ).

Comme vous le savez, le carré de la longueur de tout vecteur est égal à la somme des carrés de ses coordonnées. C'est pourquoi r 2 = un 2 + b 2, d'où r = √un 2 + b 2

Donc, n'importe quel nombre complexe a + bi peut être représenté sous la forme :

a + bi = r (parce que φ + je péché φ ), (1)

où r = √un 2 + b 2 et l'angle φ est déterminé à partir de la condition :

Cette forme d'écriture des nombres complexes s'appelle trigonométrique.

Nombre r dans la formule (1) est appelé module, et l'angle φ - argument, nombre complexe a + bi .

Si un nombre complexe a + bi n'est pas égal à zéro, alors son module est positif ; si a + bi = 0, alors une = b = 0 et alors r = 0.

Le module de tout nombre complexe est déterminé de manière unique.

Si un nombre complexe a + bi n'est pas égal à zéro, alors son argument est déterminé par les formules (2) certainement précis à un angle divisible par 2 π . Si a + bi = 0, alors une = b = 0. Dans ce cas r = 0. À partir de la formule (1), il est facile de comprendre que comme argument φ dans ce cas, vous pouvez choisir n'importe quel angle : après tout, pour n'importe quel φ

0 (cos φ + je péché φ ) = 0.

Par conséquent, l’argument nul n’est pas défini.

Module d'un nombre complexe r parfois noté | z |, et l'argument argument z . Examinons quelques exemples de représentation de nombres complexes sous forme trigonométrique.

Exemple. 1. 1 + je .

Trouvons le module r et argumentation φ Ce nombre.

r = √ 1 2 + 1 2 = √ 2 .

Donc le péché φ = 1 / √ 2, cos φ = 1 / √ 2, d'où φ = π / 4 + 2nπ .

Ainsi,

1 + je = √ 2 ,

Où P. - n'importe quel entier. Habituellement, parmi l'ensemble infini de valeurs de l'argument d'un nombre complexe, on en choisit une qui est comprise entre 0 et 2. π . Dans ce cas, cette valeur est π / 4 . C'est pourquoi

1 + je = √ 2 (car π / 4 + je péché π / 4)

Exemple 2.Écrire un nombre complexe sous forme trigonométrique √ 3 - je . Nous avons:

r = √ 3+1 = 2, car φ = √ 3 / 2, péché φ = - 1 / 2

Donc, jusqu'à un angle divisible par 2 π , φ = 11 / 6 π ; ainsi,

√ 3 - je = 2(cos 11 / 6 π + je péché 11 / 6 π ).

Exemple 3Écrire un nombre complexe sous forme trigonométrique je.

Nombre complexe je correspond au vecteur O.A.> , se terminant au point A de l'axe à d'ordonnée 1 (Fig. 333). La longueur d'un tel vecteur est 1 et l'angle qu'il fait avec l'axe des x est égal à π / 2. C'est pourquoi

je =cos π / 2 + je péché π / 2 .

Exemple 4.Écrivez le nombre complexe 3 sous forme trigonométrique.

Le nombre complexe 3 correspond au vecteur O.A. > X abscisse 3 (Fig. 334).

La longueur d'un tel vecteur est 3 et l'angle qu'il fait avec l'axe des x est 0. Par conséquent

3 = 3 (cos 0 + je péché 0),

Exemple 5.Écrivez le nombre complexe -5 sous forme trigonométrique.

Le nombre complexe -5 correspond à un vecteur O.A.> se terminant à un point de l'axe X en abscisse -5 (Fig. 335). La longueur d'un tel vecteur est 5 et l'angle qu'il forme avec l'axe des x est égal à π . C'est pourquoi

5 = 5(cos π + je péché π ).

Des exercices

2047. Écrivez ces nombres complexes sous forme trigonométrique, en définissant leurs modules et arguments :

1) 2 + 2√3 je , 4) 12je - 5; 7).3je ;

2) √3 + je ; 5) 25; 8) -2je ;

3) 6 - 6je ; 6) - 4; 9) 3je - 4.

2048. Indiquer sur le plan un ensemble de points représentant des nombres complexes dont les modules r et les arguments φ satisfont aux conditions :

1) r = 1, φ = π / 4 ; 4) r < 3; 7) 0 < φ < π / 6 ;

2) r =2; 5) 2 < r <3; 8) 0 < φ < я;

3) r < 3; 6) φ = π / 3 ; 9) 1 < r < 2,

10) 0 < φ < π / 2 .

2049. Les nombres peuvent-ils être simultanément le module d'un nombre complexe ? r Et - r ?

2050. L'argument d'un nombre complexe peut-il être simultanément des angles ? φ Et - φ ?

Présentez ces nombres complexes sous forme trigonométrique, en définissant leurs modules et arguments :

2051*. 1 + parce que α + je péché α . 2054*. 2(cos 20° - je péché 20°).

2052*. péché φ + je parce que φ . 2055*. 3(- cos 15° - je péché 15°).

Pour déterminer la position d'un point sur un plan, vous pouvez utiliser les coordonnées polaires [g, (r), Où g est la distance du point à l'origine, et (R.- l'angle que fait le rayon - le vecteur de ce point avec la direction positive de l'axe Oh. Direction positive du changement d'angle (R. Le sens considéré est le sens inverse des aiguilles d'une montre. Profitant de la connexion entre les coordonnées cartésiennes et polaires : x = g cos moyenne, y = g sin (p,

on obtient la forme trigonométrique d'écriture d'un nombre complexe

z - r(péché (p + i péché

Où g

Xi + y2, (p est l'argument d'un nombre complexe, qui se trouve à partir de

lX . ouais

formules cos(p --, sin^9 ​​​​= - ou du fait que tg(p--, (p-arctg

Notez que lors du choix des valeurs Épouser de la dernière équation il faut prendre en compte les signes x et y.

Exemple 47. Écrire un nombre complexe sous forme trigonométrique 2 = -1 + l/Z / .

Solution. Trouvons le module et l'argument d'un nombre complexe :

= yj 1 + 3 = 2 . Coin Épouser on trouve à partir des relations cos(p = -, péché(p = - . Alors

on a cos(p = -, suup

u/z g~

• - -. Évidemment, le point z = -1 + V3-/ se situe
• 2 À 3

au deuxième trimestre : (R.= 120°

Remplacement

2k.. matraque; péché

dans la formule (1) trouvée 27Г L

Commentaire. L’argument d’un nombre complexe n’est pas défini de manière unique, mais à un terme qui est un multiple de 14h. Puis à travers sp ^ g dénoter

valeur de l'argument entourée (p 0 %2 Alors

A)^r = + 2kk.

En utilisant la célèbre formule d'Euler e, on obtient la forme exponentielle d’écriture d’un nombre complexe.

Nous avons r = g(co^(p + i?,p(p)=ge,

Opérations sur les nombres complexes

• 1. La somme de deux nombres complexes r, = X] + oui x/ et g 2 -x 2 +y 2/ est déterminé selon la formule r ! +2 2 = (x, +^2) + (^1 + ^2)'r
• 2. L'opération de soustraction de nombres complexes est définie comme l'opération inverse de l'addition. Nombre complexe g = g x - g 2, Si g 2 + g = g x,

est la différence des nombres complexes 2, et g2. Alors r = (x, - x2) + (oui, - à 2) /.

• 3. Produit de deux nombres complexes g x= x, +y, -z et 2 2 = x2+ U2‘ r est déterminé par la formule
• *1*2 =(* +U"0(X2+ T2 -0= X 1 X 2 Oui 1 2 -1 +x Y2 " * + U1 U2 " ^ =

= (хх 2 ~УУ 2)+(Х У2 + Х 2У)-"-

En particulier, o-o= (x + y-y)(x-y /)= x 2 + y 2.

Vous pouvez obtenir des formules pour multiplier des nombres complexes sous des formes exponentielles et trigonométriques. Nous avons:

• 1^ 2 - G x e 1 = )G 2 e > = G]G 2 cOs((P + moyenne 2) + isine
• 4. La division des nombres complexes est définie comme l'opération inverse

multiplication, c'est-à-dire nombre G-- appelé le quotient de division r ! sur g 2,

Si g x -1 2 ? 2 . Alors

X +Ti_ (*і + UI 2 ~ 1 U2 ) x2 + ІУ2 ( 2 + ^У 2)( 2 ~ 1 У 2)

x, x 2 + /y, x 2 -ix x y 2 - je 2 y x y 2 (x x x 2 + y x y 2)+ /(- x,y 2 + X 2 Y])

2 2 x 2 + Oui 2

1 e

je (r g

• - 1U e "(1 Fg) - I.сОї((Р -ср 1)+ І- (R.-,)] >2 >2
• 5. Il est préférable d'élever un nombre complexe à une puissance entière positive si le nombre est écrit sous forme exponentielle ou trigonométrique.

En effet, si g = ge 1 alors

=(ge,) = g p e t = G"(co8 psr+іт gkr).

Formule g" =r n (cosn(p+est n(p) appelée formule de Moivre.

6. Extraction des racines P- La puissance d'un nombre complexe est définie comme l'opération inverse d'élévation à une puissance p, p- 1,2,3,... c'est-à-dire nombre complexe = y[g appelé racine P- la puissance d'un nombre complexe

g, si g = g x. De cette définition il résulte que g-g", UN g x= l/g. (r-psr x, UN sr^-sr/p, qui découle de la formule de Moivre écrite pour le nombre = r/*+ іьіпп(р).

Comme indiqué ci-dessus, l'argument d'un nombre complexe n'est pas défini de manière unique, mais jusqu'à un terme multiple de 2 et. C'est pourquoi = (p + 2pqt, et l'argument du nombre r, en fonction de À, désignons (rk et bouh

ils calculent en utilisant la formule (rk= - + . Il est clair qu'il y a P. com-

nombres complexes, P.-ième puissance dont est égale au nombre 2. Ces nombres ont un

et le même module égal y[g, et les arguments de ces nombres sont obtenus par À = 0, 1, P- 1. Ainsi, sous forme trigonométrique, la ième racine est calculée à l'aide de la formule :

(p + 2kp . . Mer + 2kp

, À = 0, 1, 77-1,

.(p+2kg

et sous forme exponentielle - selon la formule l[g - y[ge p

Exemple 48. Effectuer des opérations sur des nombres complexes sous forme algébrique :

a) (1-/H/2) 3 (3 + /)

• (1 - /l/2) 3 (z + /) = (1 - zl/2/ + 6/ 2 - 2 l/2 / ? 3)(3 + /) =
• (1 - Zl/2/ - 6 + 2l/2/DZ + /)=(- 5 - l/2/DZ + /) =

15-Zl/2/-5/-l/2/ 2 = -15 - Zl/2/-5/+ l/2 = (-15 +l/2)-(5 +Zl/2)/;

Exemple 49. Élevez le nombre r = Uz - / à la puissance cinquième.

Solution. On obtient la forme trigonométrique de l'écriture du nombre r.

G = l/3 + 1 =2, C08 (p --, 5ІІ7 (R. =

• (1 - 2/X2 + /)
• (z-,)

O - 2.-X2 + o

• 12+ 4/-9/
• 2 +і - 4/ - 2/ 2 2 - 3/ + 2 4 - 3/ 3 + і
• (z-O " (z-O

Z/ 2 12-51 + 3 15 - 5/

• (3-i) ’з+/
• 9 + 1 z_±.
• 5 2 1 "

D'ici O--, UN r = 2

On obtient Moivre : je -2

/ ^ _ 7G, . ?G

• -SS-- ІБІП -

• --b / -

= -(l/w + g)= -2 .

Exemple 50 : Trouver toutes les valeurs

Solution, r = 2, une Épouser on trouve à partir de l'équation sanglot(p = -,zt--.

Ce point 1 - /d/z se situe au quatrième trimestre, c'est à dire f =--. Alors

• 1 - 2
• ( ( UG L

On retrouve les valeurs racines de l'expression

V1 - /l/z = l/2

• ---+ 2А:/г ---ь 2 kk
• 3 . . 3

S08--1- et 81P-

À À - 0 nous avons 2 0 = l/2

Vous pouvez retrouver les valeurs de la racine du nombre 2 en représentant le nombre à l'écran

-* À/ 3 + 2 cl

À À= 1 nous avons une autre valeur racine :

• 7G. 7G_
• ---ь27г ---ь2;г
• 3. . h

7G . . 7GL-С05- + 181П - 6 6

• --N-

co? -7G + /5SH-I"

l/3__t_

forme téliale. Parce que r= 2, un Épouser= , alors g = 2e 3 , une y[g = y/2e 2

2.3. Forme trigonométrique des nombres complexes

Soit le vecteur spécifié sur le plan complexe par le nombre .

Notons φ l'angle entre le demi-axe positif Ox et le vecteur (l'angle φ est considéré comme positif s'il est mesuré dans le sens inverse des aiguilles d'une montre, et négatif sinon).

Notons la longueur du vecteur par r. Alors . On note également

Écrire un nombre complexe z non nul sous la forme

est appelé la forme trigonométrique du nombre complexe z. Le nombre r est appelé module du nombre complexe z, et le nombre φ est appelé argument de ce nombre complexe et est noté Arg z.

Forme trigonométrique d'écriture d'un nombre complexe - (formule d'Euler) - forme exponentielle d'écriture d'un nombre complexe :

Le nombre complexe z a une infinité d'arguments : si φ0 est un argument du nombre z, alors tous les autres peuvent être trouvés à l'aide de la formule

Pour un nombre complexe, l'argument et la forme trigonométrique ne sont pas définis.

Ainsi, l'argument d'un nombre complexe non nul est toute solution du système d'équations :

(3)

La valeur φ de l'argument d'un nombre complexe z, satisfaisant les inégalités, est appelée valeur principale et est notée arg z.

Les arguments Arg z et arg z sont liés par

, (4)

La formule (5) est une conséquence du système (3), donc tous les arguments d'un nombre complexe satisfont à l'égalité (5), mais toutes les solutions φ de l'équation (5) ne sont pas des arguments du nombre z.

La valeur principale de l'argument d'un nombre complexe non nul se trouve selon les formules :

Les formules pour multiplier et diviser des nombres complexes sous forme trigonométrique sont les suivantes :

. (7)

Lorsqu'il est érigé en diplôme naturel nombre complexe, utilisez la formule de Moivre :

Lors de l'extraction de la racine d'un nombre complexe, la formule est utilisée :

, (9)

où k=0, 1, 2, …, n-1.

Problème 54. Calculez où .

Présentons la solution de cette expression sous forme exponentielle d'écriture d'un nombre complexe : .

Si donc.

Alors , . Par conséquent, alors Et , Où .

Répondre: , à .

Problème 55. Écrivez des nombres complexes sous forme trigonométrique :

UN) ; b) ; V) ; G) ; d) ; e) ; et) .

Puisque la forme trigonométrique d’un nombre complexe est , alors :

a) Dans un nombre complexe : .

,

C'est pourquoi

b) , Où ,

G) , Où ,

e) .

et) , UN , Que .

C'est pourquoi

Répondre: ; 4; ; ; ; ; .

Problème 56. Trouver la forme trigonométrique d'un nombre complexe

.

Laisser , .

Alors , , .

Depuis et , , alors , et

Par conséquent, donc

Répondre: , Où .

Problème 57. En utilisant la forme trigonométrique d'un nombre complexe, effectuez les actions suivantes : .

Imaginons les chiffres et sous forme trigonométrique.

1) , où Alors

Trouvez la valeur de l'argument principal :

Remplaçons les valeurs et dans l'expression, on obtient

2) , Où alors

Alors

3) Trouvons le quotient

En supposant k=0, 1, 2, nous obtenons trois différentes significations la racine souhaitée :

Si donc

si donc

si donc .

Répondre: :

:

: .

Problème 58. Soient , , , des nombres complexes différents et . Prouve-le

un numéro est valable nombre positif;

b) l'égalité est vraie :

a) Représentons ces nombres complexes sous forme trigonométrique :

Parce que .

Faisons semblant. Alors

.

La dernière expression est un nombre positif, puisque les signes sinusoïdaux contiennent des nombres de l'intervalle.

depuis le numéro réel et positif. En effet, si a et b sont des nombres complexes, réels et supérieurs à zéro, alors .

En plus,

par conséquent, l’égalité requise est prouvée.

Problème 59. Écrivez le nombre sous forme algébrique .

Représentons le nombre sous forme trigonométrique puis trouvons sa forme algébrique. Nous avons . Pour on obtient le système :

Cela implique l'égalité : .

Application de la formule de Moivre : ,

on a

La forme trigonométrique du nombre donné est trouvée.

Écrivons maintenant ce nombre sous forme algébrique :

.

Répondre: .

Problème 60. Trouver la somme , ,

Considérons le montant

En appliquant la formule de Moivre, on trouve

Cette somme est la somme de n termes d'une progression géométrique de dénominateur et le premier membre .

En appliquant la formule de la somme des termes d'une telle progression, on a

En isolant la partie imaginaire dans la dernière expression, on trouve

En isolant la partie réelle, on obtient également la formule suivante : , , .

Problème 61. Trouvez la somme :

UN) ; b) .

D’après la formule d’exponentiation de Newton, nous avons

En utilisant la formule de Moivre on trouve :

En égalisant les parties réelles et imaginaires des expressions résultantes pour , nous avons :

Et .

Ces formules peuvent être écrites sous forme compacte comme suit :

,

, Où - partie entière les chiffres a.

Problème 62. Trouver tout , pour lequel .

Parce que le , alors, en utilisant la formule

, Pour extraire les racines, on obtient ,

Ainsi, , ,

, .

Les points correspondant aux nombres sont situés aux sommets d'un carré inscrit dans un cercle de rayon 2 dont le centre est le point (0;0) (Fig. 30).

Répondre: , ,

, .

Problème 63. Résoudre l'équation , .

Par état ; par conséquent, cette équation n’a pas de racine et est donc équivalente à l’équation.

Pour que le nombre z soit la racine d’une équation donnée, il doit être la racine nième degré du numéro 1.

De là, nous concluons que l'équation originale a des racines déterminées à partir des égalités

,

Ainsi,

,

c'est à dire. ,

Répondre: .

Problème 64. Résolvez l'équation dans l'ensemble des nombres complexes.

Puisque le nombre n'est pas la racine de cette équation, alors pour cette équation est équivalent à l'équation

Autrement dit, l'équation.

Toutes les racines de cette équation sont obtenues à partir de la formule (voir problème 62) :

; ; ; ; .

Problème 65. Dessinez sur le plan complexe un ensemble de points qui satisfont aux inégalités : . (2ème façon de résoudre le problème 45)

Laisser .

Les nombres complexes ayant des modules identiques correspondent à des points du plan situés sur un cercle centré à l'origine, donc l'inégalité satisfaire tous les points d'un anneau ouvert délimité par des cercles avec un centre commun à l'origine et aux rayons et (Fig. 31). Soit un point du plan complexe correspondant au nombre w0. Nombre , a un module plusieurs fois plus petit que le module w0, et un argument supérieur à l'argument w0. D'un point de vue géométrique, le point correspondant à w1 peut être obtenu à l'aide d'une homothétie avec un centre à l'origine et un coefficient, ainsi qu'une rotation par rapport à l'origine d'un angle dans le sens antihoraire. Suite à l'application de ces deux transformations aux pointes de l'anneau (Fig. 31), celui-ci se transformera en un anneau délimité par des cercles de même centre et de mêmes rayons 1 et 2 (Fig. 32).

Conversion implémenté en utilisant un transfert parallèle vers un vecteur. En transférant l'anneau avec le centre au point sur le vecteur indiqué, on obtient un anneau de même taille avec le centre au point (Fig. 22).

La méthode proposée, qui utilise l'idée de transformations géométriques d'un plan, est sans doute moins commode à décrire, mais est très élégante et efficace.

Problème 66. Trouver si .

Soit , alors et . L'égalité initiale prendra la forme . De la condition d'égalité de deux nombres complexes on obtient , , d'où , . Ainsi, .

Écrivons le nombre z sous forme trigonométrique :

, Où , . D'après la formule de Moivre, on trouve .

Réponse : – 64.

Problème 67. Pour un nombre complexe, trouvez tous les nombres complexes tels que , et .

Représentons le nombre sous forme trigonométrique :

. D'ici, . Pour le nombre que nous obtenons , peut être égal à ou .

Dans le premier cas , dans la seconde

.

Répondre: , .

Problème 68. Trouvez la somme de nombres tels que . Veuillez indiquer l'un de ces numéros.

Notez qu'à partir de la formulation même du problème, on peut comprendre que la somme des racines de l'équation peut être trouvée sans calculer les racines elles-mêmes. En effet, la somme des racines de l'équation est le coefficient pour , pris avec le signe opposé (théorème de Vieta généralisé), c'est-à-dire

Les étudiants, la documentation scolaire, tirent des conclusions sur le degré de maîtrise ce concept. Résumer l'étude des caractéristiques de la pensée mathématique et du processus de formation du concept de nombre complexe. Description des méthodes. Diagnostic : Stade I. La conversation a eu lieu avec un professeur de mathématiques qui enseigne l'algèbre et la géométrie en 10e année. La conversation a eu lieu après un certain temps depuis le début...

Résonance" (!)), qui comprend également une évaluation de son propre comportement. 4. Évaluation critique de sa compréhension de la situation (doutes). 5. Enfin, le recours aux recommandations de la psychologie juridique (prise en compte par un avocat aspects psychologiques actions professionnelles réalisées - préparation professionnelle et psychologique). Considérons maintenant analyse psychologique faits juridiques. ...

Mathématiques de substitution trigonométrique et test de l'efficacité de la méthodologie pédagogique développée. Étapes de travail : 1. Élaboration d'un cours optionnel sur le thème : « Application de la substitution trigonométrique pour résoudre des problèmes algébriques » avec des élèves des classes de mathématiques avancées. 2. Diriger le cours au choix développé. 3. Réaliser un test de diagnostic...

Les tâches cognitives sont uniquement destinées à compléter les supports pédagogiques existants et doivent être en combinaison appropriée avec tous les moyens et éléments traditionnels du processus éducatif. Différence tâches éducatives dans l'enseignement sciences humaines des problèmes exacts, mathématiques, c'est seulement que dans les problèmes historiques, il n'y a pas de formules, d'algorithmes stricts, etc., ce qui complique leur solution. ...