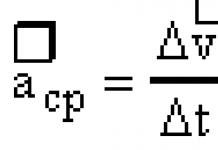Les fonctions trigonométriques inverses sont des fonctions mathématiques qui sont des fonctions trigonométriques inverses.

Fonction y = arcsin (x)

L'arc sinus d'un nombre α est tel un nombre α de l'intervalle [-π / 2; π / 2], dont le sinus est égal à α.
Graphique de fonction
La fonction у = sin⁡ (x) sur le segment [-π / 2; π / 2] est strictement croissante et continue ; par conséquent, il a une fonction inverse, strictement croissante et continue.
La fonction inverse pour la fonction y = sin⁡ (x), où х ∈ [-π / 2; π / 2], est appelée arc sinus et est notée y = arcsin (x), où х∈ [-1; 1].
Ainsi, d'après la définition de la fonction inverse, le domaine de définition de l'arc sinus est le segment [-1 ; 1], et l'ensemble des valeurs est le segment [-π/2 ; π/2].
Notez que le graphe de la fonction y = arcsin (x), où x [-1; 1].Est symétrique au graphe de la fonction y = sin (⁡x), où x [-π / 2; π / 2], par rapport à la bissectrice des angles de coordonnées premier et troisième quarts.

Plage de fonction y = arcsin (x).

Exemple 1.

Trouver arcsin (1/2) ?

Etant donné que la plage de valeurs de la fonction arcsin (x) appartient à l'intervalle [-π / 2; π / 2], seule la valeur de π / 6 convient. Par conséquent, arcsin (1/2) = π / 6.
Réponse : π / 6

Exemple n°2.
Trouver arcsin (- (√3) / 2) ?

Étant donné que la plage de valeurs arcsin (x) х ∈ [-π / 2; π / 2], seule la valeur -π / 3 convient. Par conséquent, arcsin (- (√3) / 2) = - π / 3.

Fonction y = arccos (x)

Le cosinus inverse d'un nombre α est un nombre α de l'intervalle dont le cosinus est égal à α.

Graphique de fonction

La fonction y = cos (⁡x) sur un segment est strictement décroissante et continue ; il a donc une fonction inverse, strictement décroissante et continue.
La fonction inverse pour la fonction y = cos⁡x, où x ∈, est appelée arccosinus et est noté y = arccos (x), où х ∈ [-1; 1].
Ainsi, selon la définition de la fonction inverse, le domaine de définition de l'arccosinus est le segment [-1; 1], et l'ensemble des valeurs est le segment.
Notons que le graphe de la fonction y = arccos (x), où x [-1; 1], est symétrique au graphe de la fonction y = cos (⁡x), où x ∈, par rapport à la bissectrice de la coordonnées des angles des premier et troisième quarts.

Plage de fonction y = arccos (x).

Exemple n°3.

Trouver des arccos (1/2) ?

Étant donné que la plage de valeurs est arccos (x) х∈, seule la valeur π / 3 convient ; par conséquent, arccos (1/2) = π / 3.
Exemple n° 4.
Trouver arccos (- (√2) / 2) ?

Etant donné que la plage de valeurs de la fonction arccos (x) appartient à l'intervalle, seule la valeur 3π/4 convient ; par conséquent, arccos (- (√2) / 2) = 3π/4.

Réponse : 3π / 4

Fonction y = arctan (x)

L'arc tangente d'un nombre α est un nombre α de l'intervalle [-π / 2; π / 2], dont la tangente est égale à α.

Graphique de fonction

La fonction tangente est continue et strictement croissante sur l'intervalle (-π/2; π/2); par conséquent, il a une fonction inverse, qui est continue et strictement croissante.
La fonction inverse pour la fonction y = tg⁡ (x), où х∈ (-π / 2; π / 2); est appelée l'arctangente et est notée y = arctan (x), où х∈R.
Ainsi, selon la définition de la fonction inverse, le domaine de définition de l'arctangente est l'intervalle (-∞; + ∞), et l'ensemble des valeurs est l'intervalle
(-π/2; π/2).
Notons que le graphe de la fonction y = arctan (x), où х∈R, est symétrique du graphe de la fonction y = tg⁡x, où х ∈ (-π / 2; π / 2), par rapport au bissectrice des angles de coordonnées des premier et troisième quarts.

Plage de fonction y = arctan (x).

Exemple #5 ?

Trouvez l'arctan ((√3) / 3).

Étant donné que la plage de valeurs arctan (x) х ∈ (-π / 2; π / 2), seule la valeur π / 6 convient. Par conséquent, arctg ((√3) / 3) = π / 6.
Exemple # 6.
Trouver arctg (-1) ?

Étant donné que la plage de valeurs arctan (x) х ∈ (-π / 2; π / 2), seule la valeur -π / 4 convient. Par conséquent, arctg (-1) = - π / 4.

Fonction y = arcctg (x)

L'arccotangente d'un nombre α est un nombre de l'intervalle (0 ; π), dont la cotangente est égale à α.

Graphique de fonction

Sur l'intervalle (0 ; ), la fonction cotangente est strictement décroissante ; de plus, elle est continue en tout point de cet intervalle ; donc, sur l'intervalle (0 ; ), cette fonction a une fonction inverse, strictement décroissante et continue.
La fonction inverse pour la fonction y = ctg (x), où ∈ (0; π), est appelée arc cotangente et est notée y = arcctg (x), où х∈R.
Ainsi, d'après la définition de la fonction inverse, le domaine de définition de l'arc cotangente est R, et l'ensemble des valeurs est l'intervalle (0 ; ).Le graphe de la fonction y = arcctg (x), où х∈R est symétrique au graphique de la fonction y = ctg (x) х∈ (0 ; π), par rapport à la bissectrice des angles de coordonnées des premier et troisième quarts.

Plage de fonctions y = arcctg (x).

Exemple # 7.
Trouver arcctg ((√3) / 3) ?

Étant donné que la plage de valeurs est arcctg (x) х ∈ (0; π), seule la valeur π / 3 convient; par conséquent, arccos ((√3) / 3) = π / 3.

Exemple # 8.
Trouver arcctg (- (√3) / 3) ?

Puisque la plage de valeurs est arcctg (x) х∈ (0; π), seule la valeur 2π / 3 convient ; par conséquent, arccos (- (√3) / 3) = 2π / 3.

Rédacteurs : Ageeva Lyubov Alexandrovna, Gavrilina Anna Viktorovna

Dans un certain nombre de problèmes de mathématiques et de ses applications, il est demandé, à partir de la valeur connue de la fonction trigonométrique, de trouver la valeur correspondante de l'angle, exprimée en degré ou en radian. On sait qu'un ensemble infini d'angles correspond à la même valeur de sinus, par exemple, si $ \ sin = 1/2, $ alors l'angle $ α $ peut être égal à la fois à $ 30 ° $ et $ 150 °, $ ou en radian mesure $ π / 6 $ et $ 5π / 6, $ et l'un des angles obtenus à partir de ceux-ci en ajoutant un terme de la forme $ 360 ° ⋅k, $ ou, respectivement, $ 2πk, $ où $ k $ est un entier quelconque. Cela devient également clair en considérant le graphique de la fonction $ y = \ sin x $ sur toute la droite numérique (voir Fig. $ 1 $) : si sur l'axe $ Oy $ nous retirons un segment de longueur $ 1/2 $ et tracez une droite parallèle à l'axe $ Ox, $ alors elle coupera une sinusoïde en un nombre infini de points. Pour éviter la variété possible de réponses, des fonctions trigonométriques inverses sont introduites, autrement appelées fonctions circulaires ou en arc (du mot latin arcus - "arc").

Les quatre fonctions trigonométriques de base $ \ sin x, $ $ \ cos x, $ $ \ mathrm (tg) \, x $ et $ \ mathrm (ctg) \, x $ correspondent à quatre fonctions d'arc $ \ arcsin x, $ $ \ arccos x , $ $ \ mathrm (arctg) \, x $ et $ \ mathrm (arcctg) \, x $ (lire : arcsinus, arccosinus, arctangent, arccotangent). Considérons les fonctions \ arcsin x et \ mathrm (arctg) \, x, puisque les deux autres sont exprimées en fonction d'elles par les formules :

$ \ arccos x = \ frac (π) (2) - \ arcsin x, $ $ \ mathrm (arcctg) \, x = \ frac (π) (2) - \ mathrm (arctg) \, x. $

L'égalité $ y = \ arcsin x $ signifie par définition un tel angle $ y, $ exprimé en radian et compris dans l'intervalle de $ - \ frac (π) (2) $ à $ \ frac (π) (2), $ sinus qui est égal à $ x, soit $ \ sin y = x. $ La fonction $ \ arcsin x $ est la fonction inverse de la fonction $ \ sin x $ considérée sur le segment $ \ left [- \ frac (π) (2 ), + \ frac (π) (2) \ right], $ où cette fonction augmente de façon monotone et prend toutes les valeurs de $ -1 $ à $ + 1. $ Évidemment, l'argument $ y $ de la fonction $\arcsin x $ ne peut prendre des valeurs que du segment $\left [−1, + 1\right].$ Ainsi, la fonction $y = \arcsin x $ est définie sur le segment $\ left [−1, + 1 \ right], $ augmente de façon monotone, et ses valeurs remplissent le segment $ \ left [- \ frac (π) (2), + \ frac (π) (2) \ right] $ Le graphique de la fonction est représenté sur la fig. $ 2. $

Sous la condition $ −1 ≤ a ≤ 1 $, toutes les solutions de l'équation $ \ sin x = a $ peuvent être représentées par $ x = (- 1) ^ n \ arcsin a + πn, $ $ n = 0, ± 1, ± 2, …. $ Par exemple, si

$ \ sin x = \ frac (\ sqrt (2)) (2) $ alors $ x = (−1) ^ n \ frac (π) (4) + πn, $ $ n = 0, ± 1, ± 2 ,…. $

La relation $ y = \ mathrm (arcctg) \, x $ est définie pour toutes les valeurs de $ x $ et signifie par définition que l'angle $ y, $, exprimé en radian, est dans les limites

$ - \ frac (π) (2)

et la tangente de cet angle est x, c'est-à-dire $ \ mathrm (tg) \, y = x. $ La fonction $ \ mathrm (arctg) \, x $ est définie sur toute la droite numérique, est une fonction inverse de la fonction $ \ mathrm ( tg) \, x $, qui n'est considérée que sur l'intervalle

$ - \ frac (π) (2)

La fonction $ y = \ mathrm (arctg) \, x $ augmente de façon monotone, son graphique est illustré à la Fig. $ 3. $

Toutes les solutions de l'équation $ \ mathrm (tg) \, x = a $ peuvent s'écrire sous la forme $ x = \ mathrm (arctg) \, a + πn, $ $ n = 0, ± 1, ± 2,…. $

Notez que les fonctions trigonométriques inverses sont largement utilisées en analyse mathématique. Par exemple, l'une des premières fonctions pour lesquelles une représentation d'une série infinie de puissances a été obtenue était la fonction $ \ mathrm (arctg) \, x. $ De cette série, G. Leibniz, pour une valeur fixe de l'argument $ x = 1 $, obtenu la fameuse représentation du nombre k près

Fonction cosinus inverse

La plage de valeurs de la fonction y = cos x (voir Fig. 2) est un segment. Sur un segment, la fonction est continue et décroît de façon monotone.

Riz. 2

Cela signifie que la fonction inverse de la fonction y = cos x est définie sur le segment. Cette fonction inverse est appelée cosinus inverse et est notée y = arccos x.

Définition

L'arcosinus du nombre a, si | a | 1, est l'angle dont le cosinus appartient au segment ; il est noté arccos a.

Ainsi, arccos a est un angle qui satisfait aux deux conditions suivantes : cos (arccos a) = a, | a | 1; 0 ? arccos a?p.

Par exemple, arccos, puisque cos et ; arccos depuis cosi.

La fonction y = arccos x (Fig. 3) est définie sur un segment, la plage de ses valeurs est un segment. Sur le segment, la fonction y = arccos x est continue et décroît de façon monotone de p à 0 (puisque y = cos x est une fonction continue et décroissante monotone sur le segment) ; aux extrémités du segment il atteint ses valeurs extrêmes : arccos (-1) = p, arccos 1 = 0. Notez que arccos 0 =. Le graphe de la fonction y = arccos x (voir Fig. 3) est symétrique du graphe de la fonction y = cos x par rapport à la droite y = x.

Riz. 3

Montrons que l'égalité arccos (-x) = р-arccos x est vérifiée.

En effet, par définition, 0? arccos x? R. En multipliant par (-1) toutes les parties de la dernière double inégalité, on obtient - p? arccos x? 0. En ajoutant p à toutes les parties de la dernière inégalité, nous trouvons que 0? p-arccos x ? R.

Ainsi, les valeurs des angles arccos (-x) et p - arccos x appartiennent au même segment. Puisque le cosinus diminue de façon monotone sur un segment, il ne peut pas y avoir deux angles différents avec des cosinus égaux sur celui-ci. Trouvez les cosinus des angles arccos (-x) et p-arccos x. Par définition, cos (arccos x) = - x, par les formules de réduction et par définition, on a : cos (p - - arccos x) = - cos (arccos x) = - x. Ainsi, les cosinus des angles sont égaux, ce qui signifie que les angles eux-mêmes sont égaux.

Fonction sinus inverse

Considérons la fonction y = sin x (Fig. 6), qui sur le segment [-p/2;p/2] est croissante, continue et prend les valeurs du segment [-1; un]. Ainsi, sur le segment [- p/2 ; р / 2], une fonction est définie qui est l'inverse de la fonction y = sin x.

Riz. 6

Cette fonction inverse est appelée arcsinus et est notée y = arcsin x. Introduisons la définition du sinus inverse d'un nombre.

L'arc sinus du nombre a, si l'on appelle l'angle (ou arc), dont le sinus est égal au nombre a et qui appartient au segment [-p/2 ; p/2] ; il est noté arcsin a.

Ainsi, arcsin a est un angle satisfaisant aux conditions suivantes : sin (arcsin a) = a, |a | ?un; -p/2 ? arcsin hein? p/2. Par exemple, puisque sin et [- p/2; p/2] ; arcsin, puisque sin = et [- p / 2; p / 2].

La fonction y = arcsin х (Fig. 7) est définie sur le segment [-1 ; 1], la plage de ses valeurs est le segment [-p/2;p/2]. Sur le segment [- 1; 1] la fonction y = arcsin x est continue et croît de façon monotone de -p/2 à p/2 (cela découle du fait que la fonction y = sin x sur le segment [-p/2; p/2] est continue et monotone croissante). Il prend la plus grande valeur à x = 1 : arcsin 1 = p/2, et la plus petite à x = -1 : arcsin (-1) = -p/2. Pour x = 0, la fonction est nulle : arcsin 0 = 0.

Montrons que la fonction y = arcsin x est impaire, c'est-à-dire arcsin (-x) = - arcsin x pour tout x [ - 1; 1].

En effet, par définition, si |x| ?1, on a : - p/2 ? arcsin x ? ? p/2. Ainsi, les angles arcsin (-x) et - arcsin x appartiennent au même segment [ - p/2 ; p / 2].

Trouvez les sinus de ces angles : sin (arcsin (-x)) = - x (par définition) ; puisque la fonction y = sin x est impaire, alors sin (-arcsin x) = - sin (arcsin x) = - x. Ainsi, les sinus des angles appartenant au même intervalle [-p/2; р / 2], sont égaux, ce qui signifie que les angles eux-mêmes sont également égaux, c'est-à-dire arcsin (-x) = - arcsin x. Par conséquent, la fonction y = arcsin x est impaire. Le tracé de la fonction y = arcsin x est symétrique par rapport à l'origine.

Montrons que arcsin (sin x) = x pour tout x [-p / 2; p / 2].

En effet, par définition -p/2 ? arcsin (péché x) ? p/2, et par condition -p/2? X? p/2. Cela signifie que les angles x et arcsin (sin x) appartiennent au même intervalle de monotonie de la fonction y = sin x. Si les sinus de ces angles sont égaux, alors les angles eux-mêmes sont égaux. Trouvons les sinus de ces angles : pour l'angle x on a sin x, pour l'angle arcsin (sin x) on a sin (arcsin (sin x)) = sin x. Nous avons obtenu que les sinus des angles sont égaux, par conséquent, les angles sont égaux, c'est-à-dire arcsin (sin x) = x. ...

Riz. 7

Riz. 8

Le graphe de la fonction arcsin (sin | x |) est obtenu par les transformations usuelles associées au module du graphe y = arcsin (sin x) (représenté par la ligne pointillée sur la figure 8). Le graphe souhaité y = arcsin (sin | x- / 4 |) est obtenu à partir de celui-ci en décalant / 4 vers la droite le long de l'axe des abscisses (représenté par le trait plein sur la Fig. 8)

Fonction tangente inverse

La fonction y = tg x sur l'intervalle prend toutes les valeurs numériques : E (tg x) =. Sur cet intervalle, il est continu et augmente de façon monotone. Par conséquent, sur l'intervalle, une fonction est définie qui est inverse à la fonction y = tg x. Cette fonction inverse est appelée l'arctangente et est notée y = arctan x.

L'arc tangente du nombre a est l'angle de l'intervalle dont la tangente est égale à a. Ainsi, arctan a est un angle satisfaisant aux conditions suivantes : tg (arctan a) = a et 0 ? arctg un? R.

Ainsi, tout nombre x correspond toujours à une seule valeur de la fonction y = arctan x (Fig. 9).

Évidemment, D (arctan x) =, E (arctan x) =.

La fonction y = arctan x augmente car la fonction y = tan x augmente dans l'intervalle. Il n'est pas difficile de prouver que arctg (-x) = - arctgx, c'est-à-dire que l'arctangente est une fonction impaire.

Riz. 9

Le graphique de la fonction y = arctan x est symétrique au graphique de la fonction y = tg x par rapport à la droite y = x, le graphique de y = arctan x passe par l'origine (car arctan 0 = 0) et est symétrique par rapport à l'origine (comme le graphique d'une fonction impaire).

On peut prouver que arctan (tg x) = x si x.

Fonction cotangente inverse

La fonction y = ctg x sur l'intervalle prend toutes les valeurs numériques de l'intervalle. Sa plage de valeurs coïncide avec l'ensemble de tous les nombres réels. Dans l'intervalle, la fonction y = ctg x est continue et monotone croissante. Ainsi, sur cet intervalle, une fonction est définie qui est inverse à la fonction y = ctg x. La fonction inverse de la cotangente est appelée arc cotangente et est notée y = arcctg x.

L'arc cotangente du nombre a est l'angle appartenant à l'intervalle dont la cotangente est égale à a.

Ainsi, arcctg a est un angle satisfaisant aux conditions suivantes : ctg (arcctg a) = a et 0 ? arcctg un? R.

De la définition de la fonction inverse et de la définition de l'arctangente, il résulte que D (arcctg x) =, E (arcctg x) =. L'arc cotangente est une fonction décroissante, puisque la fonction y = ctg x décroît dans l'intervalle.

Le graphe de la fonction y = arcctg x ne coupe pas l'axe Ox, puisque y> 0 R. A x = 0 y = arcctg 0 =.

Le graphique de la fonction y = arcctg x est illustré à la figure 11.

Riz. 11

Notez que pour toutes les valeurs réelles de x l'identité est vraie : arcctg (-x) = p-arcctg x.

Leçons 32-33. Fonctions trigonométriques inverses

09.07.2015 8936 0

Cibler: considérer les fonctions trigonométriques inverses, leur utilisation pour écrire des solutions d'équations trigonométriques.

I. Communication du sujet et du but des cours

II. Apprendre du nouveau matériel

1. Fonctions trigonométriques inverses

Commençons notre discussion sur ce sujet avec l'exemple suivant.

Exemple 1

Résolvons l'équation : a) sin x = 1/2 ; b) sin x = a.

a) En ordonnée, on reporte la valeur 1/2 et on trace les angles x 1 et x2, pour lequel péché x = 1/2. De plus, x1 + x2 = , d'où x2 = π - x 1 ... D'après le tableau des valeurs des fonctions trigonométriques, on trouve la valeur x1 = π/6, alorsPrenons en compte la périodicité de la fonction sinus et notons les solutions de cette équation :où k Z.

b) Évidemment, l'algorithme pour résoudre l'équation péché x = a est le même que dans le paragraphe précédent. Bien sûr, maintenant la valeur a est tracée le long de l'ordonnée. Il devient nécessaire de désigner en quelque sorte l'angle x1. Nous avons convenu de désigner un tel angle par le symbole arcsin une. Alors les solutions de cette équation peuvent s'écrire sous la formeCes deux formules peuvent être combinées en une seule : où

Les autres fonctions trigonométriques inverses sont introduites de manière similaire.

Très souvent, il est nécessaire de déterminer la valeur de l'angle à partir de la valeur connue de sa fonction trigonométrique. Ce problème est multivalué - il existe d'innombrables angles dont les fonctions trigonométriques sont égales à la même valeur. Par conséquent, partant de la monotonie des fonctions trigonométriques, les fonctions trigonométriques inverses suivantes sont introduites pour déterminer de manière unique les angles.

Arcsinus de nombre a (arcsin , dont le sinus est égal à a, c'est-à-dire

Arc cosinus d'un nombre a (arccos a) est un tel angle a à partir de l'intervalle dont le cosinus est égal à a, c'est-à-dire

Arc tangente d'un nombre a (arctg a) - un tel angle a à partir de l'intervalledont la tangente est égale à a, c'est-à-diretg a = a.

Arccotangente du nombre a (arcctg a) est un tel angle a à partir de l'intervalle (0; π), dont la cotangente est égale à a, c'est-à-dire ctg a = a.

Exemple 2

Allons trouver:

En tenant compte des définitions des fonctions trigonométriques inverses, on obtient :

Exemple 3

Calculons

Soit l'angle a = arcsin 3/5, alors par définition sin a = 3/5 et ... Il faut donc trouver car une. En utilisant l'identité trigonométrique de base, on obtient :Il a été pris en compte que cos a 0. Donc,

Propriétés de la fonction	Une fonction
	y = arc sinus x	y = arccos x	y = arctan x	y = arcctg x
Domaine	x [-1; un]	x [-1; un]	х ∈ (-∞; + ∞)	x (-∞ + ∞)
Plage de valeurs	y [-π / 2; / 2]	oui	y ∈ (-π / 2; π / 2)	y (0; π)
Parité	Impair	Ni pair ni impair	Impair	Ni pair ni impair
Zéros de fonction (y = 0)	Pour x = 0	Pour x = 1	Pour x = 0	y ≠ 0
Intervalles de constance	y> 0 pour x (0; 1], à< 0 при х ∈ [-1; 0)	y> 0 pour x [-1; un)	y> 0 pour х ∈ (0; + ∞), à< 0 при х ∈ (-∞; 0)	y> 0 pour x (-∞; + ∞)
Monotone	En augmentant	Diminue	En augmentant	Diminue
Relation avec la fonction trigonométrique	sin y = x	cos y = x	tg y = x	ctg y = x
Programme

Voici quelques exemples plus typiques liés aux définitions et aux propriétés de base des fonctions trigonométriques inverses.

Exemple 4

Trouver le domaine de la fonction

Pour que la fonction y soit définie, il faut satisfaire l'inégalitéce qui équivaut au système d'inégalitésLa solution de la première inégalité est l'intervalle x∈ (-∞; + ∞), le second - Cet écart et est une solution du système d'inégalités, et, par conséquent, le domaine de définition de la fonction

Exemple 5

Trouver la zone de changement de la fonction

Considérez le comportement de la fonction z = 2x - x2 (voir figure).

On voit que z ∈ (-∞; 1]. Considérant que l'argument z la fonction arc cotangente varie dans les limites spécifiées, à partir des données du tableau, nous obtenons queDonc la zone de changement

Exemple 6

Montrons que la fonction y = arctg x est impair. LaisserAlors tan a = -x ou x = - tan a = tan (- a), et Par conséquent, - a = arctan x ou a = - arctan X. Ainsi, nous voyons quec'est-à-dire que y (x) est une fonction impaire.

Exemple 7

Exprimons en fonction de toutes les fonctions trigonométriques inverses

Laisser Il est évident que puis depuis

Introduisons un angle Parce que ensuite

De même, donc et

Alors,

Exemple 8

Construisons un graphe de la fonction y = cos (arcsin x).

On note a = arcsin x, alors Nous prenons en compte que x = sin a et y = cos a, c'est-à-dire x 2 + y2 = 1, et restrictions sur x (x∈ [-un; 1]) et y (y 0). Alors le graphique de la fonction y = cos (arcsin x) est un demi-cercle.

Exemple 9

Construisons un graphe de la fonction y = arccos (cos x).

Puisque la fonction cos x change sur le segment [-1; 1], alors la fonction y est définie sur tout l'axe numérique et change sur le segment. On gardera à l'esprit que y = arccos (cos x) = x sur le segment ; la fonction y est paire et périodique de période 2π. Compte tenu du fait que ces propriétés sont possédées par la fonction cos x, il est maintenant facile à tracer.

Notons quelques égalités utiles :

Exemple 10

Trouver les valeurs les plus petites et les plus grandes de la fonction Nous désignons ensuite On obtient la fonction Cette fonction a un minimum au point z = π / 4, et il est égal à La plus grande valeur de la fonction est atteinte au point z = -π / 2, et il est égal à Ainsi, et

Exemple 11

Résolvons l'équation

Prenons en compte que Alors l'équation a la forme :ou où Par définition de l'arctangente, on obtient :

2. Solution des équations trigonométriques les plus simples

Comme dans l'exemple 1, vous pouvez obtenir des solutions aux équations trigonométriques les plus simples.

L'équation	Solution
tgx = un
ctg x = un

Exemple 12

Résolvons l'équation

Puisque la fonction sinus est impaire, nous écrivons l'équation sous la formeSolutions de cette équation :où trouve-t-on

Exemple 13

Résolvons l'équation

En utilisant la formule ci-dessus, nous écrivons les solutions de l'équation:et trouve

A noter que dans des cas particuliers (a = 0 ; ± 1), lors de la résolution des équations sin x = a et cos x = et il est plus facile et plus pratique d'utiliser non pas des formules générales, mais d'écrire des solutions basées sur le cercle unité :

pour l'équation sin = 1 solutions

pour l'équation sin = 0 solutions х = π k;

pour l'équation sin x = -1 solutions

pour l'équation cos x = 1 solution x = 2π k ;

pour l'équation cos = 0 solutions

pour l'équation cos x = -1 solutions

Exemple 14

Résolvons l'équation

Étant donné que dans cet exemple, il existe un cas particulier de l'équation, nous écrivons la solution à l'aide de la formule correspondante :où trouverons-nous

III. Questions de test (enquête frontale)

1. Donnez une définition et listez les principales propriétés des fonctions trigonométriques inverses.

2. Donner les graphiques des fonctions trigonométriques inverses.

3. Solution des équations trigonométriques les plus simples.

IV. Devoir en classe

§ 15, n° 3 (a, b) ; 4 (c, d) ; 7 (a); 8 (a); 12 (b) ; 13 (a) ; 15 (c) ; 16 (a) ; 18 (a, b) ; 19 (c) ; 21 ;

§ 16, n° 4 (a, b) ; 7 (a); 8 (b); 16 (a, b) ; 18 (a) ; 19 (c, d) ;

§ 17, n° 3 (a, b) ; 4 (c, d) ; 5 (a, b) ; 7 (c, d) ; 9 (b) ; 10 (a, c).

V. Affectation à domicile

§ 15, n° 3 (c, d) ; 4 (a, b) ; 7 (c); 8 (b); 12 (a); 13 (b) ; 15 (d) ; 16 (b) ; 18 (c, d) ; 19 (d) ; 22 ;

§ 16, n° 4 (c, d) ; 7 (b) ; 8 (a); 16 (c, d) ; 18 (b) ; 19 (a, b) ;

§ 17, n° 3 (c, d) ; 4 (a, b) ; 5 (c, d) ; 7 (a, b) ; 9 (d) ; 10 (b, d).

Vi. Tâches créatives

1. Trouvez le domaine de la fonction :

Réponses:

2. Trouvez la plage de valeurs de la fonction :

Réponses:

3. Tracez la fonction :

VII. Résumer les leçons

Les fonctions trigonométriques étant périodiques, leurs fonctions inverses ne sont pas à valeur unique. Ainsi, l'équation y = péché x, pour un donné, a une infinité de racines. En effet, du fait de la périodicité du sinus, si x est une telle racine, alors x + 2πn(où n est un entier) sera également la racine de l'équation. De cette façon, les fonctions trigonométriques inverses sont multivaluées... Pour faciliter le travail avec eux, ils introduisent le concept de leurs significations principales. Considérons, par exemple, sinus : y = péché x... Si nous restreignons l'argument x par un intervalle, alors sur lui la fonction y = péché x augmente de façon monotone. Par conséquent, il a une fonction inverse à valeur unique, qui s'appelle l'arc sinus : x = arcsin y.

Sauf indication contraire, les fonctions trigonométriques inverses signifient leurs significations principales, qui sont déterminées par les définitions suivantes.

Arcsin ( y = arcsin x) est la fonction sinus inverse ( x = péché y
Arccosinus ( y = arccos x) est la fonction inverse du cosinus ( x = confortable), qui a un domaine et de nombreuses valeurs.
Arc tangente ( y = arctg x) est la fonction inverse de la tangente ( x = tg y), qui a un domaine et de nombreuses valeurs.
Arccotangente ( y = arcctg x) est la fonction inverse de la cotangente ( x = ctg y), qui a un domaine et de nombreuses valeurs.

Graphiques de fonctions trigonométriques inverses

Les graphiques des fonctions trigonométriques inverses sont obtenus à partir des graphiques des fonctions trigonométriques en les reflétant par rapport à la droite y = x. Voir les sections Sinus, Cosinus, Tangente, Cotangente.

y = arcsin x

y = arccos x

y = arctg x

y = arcctg x

Formules de base

Ici, vous devez porter une attention particulière aux intervalles pour lesquels les formules sont valables.

arcsin (sin x) = xà
sin (arcsin x) = x
arccos (cos x) = xà
cos (arccos x) = x

arctan (tg x) = xà
tg (arctan x) = x
arcctg (ctg x) = xà
ctg (arcctg x) = x

Formules relatives aux fonctions trigonométriques inverses

Voir également: Dérivation de formules pour les fonctions trigonométriques inverses

Formules de somme et de différence

à ou

à et

à et

à ou

à et

à et

à

à

à

à

à

à

à

à

à

à

Les références:
DANS. Bronstein, K.A. Semendyaev, Manuel de mathématiques pour les ingénieurs et les étudiants des établissements techniques, "Lan", 2009.