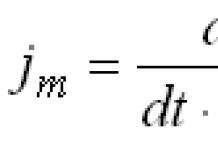Séquence de Fibonacci, connu de tous grâce au film "Le Da Vinci Code" - une série de nombres décrits sous forme d'énigme par le mathématicien italien Léonard de Pise, plus connu sous le surnom de Fibonacci, au XIIIe siècle. En bref l'essence de l'énigme :

Quelqu'un a placé un couple de lapins dans un certain espace clos pour savoir combien de couples de lapins naîtraient au cours de l'année, si la nature des lapins est telle que chaque mois un couple de lapins donne naissance à un autre couple, et ils deviennent capables de produire une progéniture lorsqu'ils atteignent l'âge de deux mois.

Le résultat est une série de nombres comme ceci : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 , où est indiqué le nombre de couples de lapins dans chacun des douze mois, séparés par des virgules. Cela peut être poursuivi indéfiniment. Son essence est que chaque nombre suivant est la somme des deux précédents.

Cette série comporte plusieurs caractéristiques mathématiques, qu'il faut absolument toucher. Il tend asymptotiquement (en s'approchant de plus en plus lentement) vers un rapport constant. Cependant, ce rapport est irrationnel, c'est-à-dire qu'il s'agit d'un nombre avec une séquence infinie et imprévisible de chiffres décimaux dans la partie fractionnaire. Il est impossible de l'exprimer avec précision.

Ainsi, le rapport d'un membre d'une série à celui qui le précède fluctue autour du nombre 1,618 , parfois le dépassant, parfois ne l'atteignant pas. Le rapport avec ce qui suit se rapproche également du nombre 0,618 , ce qui est inversement proportionnel 1,618 . Si on divise les éléments par un, on obtient des nombres 2,618 Et 0,382 , qui sont également inversement proportionnels. Ce sont ce qu’on appelle les ratios de Fibonacci.

A quoi ça sert tout ça ? C’est ainsi que nous abordons l’un des phénomènes naturels les plus mystérieux. Le sage Leonardo n'a essentiellement rien découvert de nouveau, il a simplement rappelé au monde un phénomène tel que Nombre d'or, qui n'est pas inférieur en importance au théorème de Pythagore.

Nous distinguons tous les objets qui nous entourent par leur forme. On en aime plus, d'autres moins, d'autres sont complètement rebutants. Parfois, l’intérêt peut être dicté situation de vie, et parfois la beauté de l'objet observé. La forme symétrique et proportionnelle favorise la meilleure perception visuelle et évoque une sensation de beauté et d'harmonie. Une image complète est toujours constituée de parties de tailles différentes qui entretiennent une certaine relation les unes avec les autres et avec l'ensemble. nombre d'or - la plus haute manifestation de la perfection de l'ensemble et de ses parties dans la science, l'art et la nature.

Si allumé exemple simple, alors le nombre d'or est la division d'un segment en deux parties dans un rapport dans lequel la plus grande partie est liée à la plus petite, comme leur somme (le segment entier) est à la plus grande.

Si nous prenons tout le segment c derrière 1 , puis le segment un sera égal 0,618 , segment de ligne b - 0,382 , ce n'est qu'ainsi que la condition du nombre d'or sera remplie (0,618/0,382=1,618 ; 1/0,618=1,618 ) . Attitude c À un équivaut à 1,618 , UN Avec À b 2,618 . Ce sont les mêmes ratios de Fibonacci qui nous sont déjà familiers.

Bien sûr, il existe un rectangle doré, un triangle doré et même un cuboïde doré. Les proportions du corps humain sont à bien des égards proches du nombre d’or.

Image: marcus-frings.de

Mais le plaisir commence lorsque nous combinons les connaissances que nous avons acquises. La figure montre clairement la relation entre la séquence de Fibonacci et le nombre d'or. On commence avec deux carrés de la première taille. Ajoutez un carré de la deuxième taille par-dessus. Dessinez un carré à côté avec un côté égal à la somme des côtés des deux précédents, troisième taille. Par analogie, un carré de taille cinq apparaît. Et ainsi de suite jusqu'à ce que vous soyez fatigué, l'essentiel est que la longueur du côté de chaque carré suivant soit égale à la somme des longueurs des côtés des deux précédents. Nous voyons une série de rectangles dont les côtés sont des nombres de Fibonacci et, curieusement, ils sont appelés rectangles de Fibonacci.

Si nous traçons des lignes douces passant par les coins de nos carrés, nous n'obtiendrons rien de plus qu'une spirale d'Archimède dont l'incrément est toujours uniforme.

Cela ne vous rappelle rien ?

Photo: éthanhéine sur Flickr

Et non seulement dans la coquille d’un mollusque, vous pouvez trouver des spirales d’Archimède, mais dans de nombreuses fleurs et plantes, elles ne sont tout simplement pas si évidentes.

Aloès multifolia :

Photo: livres de bière sur Flickr

Photo: beart.org.uk
Photo: esdrascalderan sur Flickr
Photo: manj98 sur Flickr

Et maintenant, il est temps de se souvenir du nombre d’or ! Certaines des créations les plus belles et les plus harmonieuses de la nature sont-elles représentées dans ces photographies ? Et ce n'est pas tout. Si vous regardez attentivement, vous pouvez trouver des modèles similaires sous de nombreuses formes.

Bien sûr, l’affirmation selon laquelle tous ces phénomènes sont basés sur la séquence de Fibonacci semble trop forte, mais la tendance est évidente. Et d’ailleurs, elle-même est loin d’être parfaite, comme tout dans ce monde.

On suppose que la série de Fibonacci est par nature une tentative de s'adapter à une séquence logarithmique du nombre d'or plus fondamentale et plus parfaite, qui est presque la même, sauf qu'elle commence de nulle part et ne mène nulle part. La nature a certainement besoin d’une sorte de commencement à partir duquel elle peut partir ; elle ne peut pas créer quelque chose à partir de rien. Les rapports des premiers termes de la suite de Fibonacci sont loin du nombre d'or. Mais plus on avance, plus ces écarts s’estompent. Pour définir une série quelconque, il suffit de connaître ses trois termes qui se succèdent. Mais pas pour la séquence dorée, deux lui suffisent, c'est géométrique et progression arithmétique simultanément. On pourrait penser qu’elle constitue la base de toutes les autres séquences.

Chaque terme de la séquence logarithmique dorée est une puissance du nombre d'or ( z). Une partie de la série ressemble à ceci : ... z -5 ; z-4 ; z-3 ; z-2 ; z-1 ; z 0 ; z 1 ; z 2 ; z 3 ; z 4 ; z 5... Si nous arrondissons la valeur du nombre d’or à trois décimales, nous obtenons z=1,618, alors la série ressemble à ceci : ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Chaque terme suivant peut être obtenu non seulement en multipliant le précédent par 1,618 , mais aussi en ajoutant les deux précédents. Ainsi, une croissance exponentielle est obtenue en ajoutant simplement deux éléments adjacents. C'est une série sans début ni fin, et c'est à cela que tente de ressembler la séquence de Fibonacci. Ayant un début très précis, elle s'efforce d'atteindre l'idéal, sans jamais l'atteindre. C'est la vie.

Et pourtant, à propos de tout ce que nous avons vu et lu, des questions assez logiques se posent :
D'où viennent ces chiffres ? Qui est cet architecte de l’univers qui a tenté de le rendre idéal ? Est-ce que tout s'est toujours passé comme il le souhaitait ? Et si oui, pourquoi cela a-t-il mal tourné ? Des mutations ? Choix libre? Quelle sera la prochaine étape ? La spirale s’enroule-t-elle ou se déroule-t-elle ?

Après avoir trouvé la réponse à une question, vous obtiendrez la suivante. Si vous le résolvez, vous en obtiendrez deux nouveaux. Une fois que vous les aurez traités, trois autres apparaîtront. Après les avoir résolus également, vous en aurez cinq non résolus. Puis huit, puis treize, 21, 34, 55...

Sources: ; ; ;

À propos des nombres et des formules qui apparaissent dans la nature. Eh bien, quelques mots sur ces mêmes nombres et formules.

Les nombres et les formules dans la nature constituent une pierre d'achoppement entre ceux qui croient en la création de l'univers par quelqu'un et ceux qui croient en la création de l'univers lui-même. Car la question est : « Si l’univers était apparu tout seul, alors presque tous les objets vivants et inanimés ne seraient-ils pas construits selon le même schéma, selon les mêmes formules ?

Eh bien, sur celui-ci question philosophique Nous ne répondrons pas ici (le format du site n’est pas le même 🙂), mais nous exprimerons les formules. Et commençons par les nombres de Fibonacci et de la Spirale d'Or.

Ainsi, les nombres de Fibonacci sont les éléments séquence de nombres, dans lequel chaque nombre suivant est égal à la somme des deux nombres précédents. Autrement dit, 0 +1=1, 1+1=2, 2+1=3, 3+2=5 et ainsi de suite.

Au total, on obtient la série : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946

Autre exemple de la série de Fibonacci : 0, 2, 2, 4, 6, 10, 16, 26, 42, 68, 110, 178 et ainsi de suite. Vous pouvez expérimenter vous-même :)

Comment les nombres de Fibonacci apparaissent-ils dans la nature ? Très simple:

1. La disposition des feuilles des plantes est décrite par la séquence de Fibonacci. Les graines de tournesol, les pommes de pin, les pétales de fleurs et les cellules d'ananas sont également disposés selon la séquence de Fibonacci.
2. La longueur des phalanges des doigts humains est approximativement la même que celle des nombres de Fibonacci.
3. La molécule d’ADN est constituée de deux hélices entrelacées verticalement, mesurant 34 angströms de long et 21 angströms de large. Les nombres 21 et 34 se succèdent dans la séquence de Fibonacci.

En utilisant les nombres de Fibonacci, vous pouvez construire une spirale dorée. Alors, dessinons un petit carré dont le côté est, disons, 1. Ensuite, souvenons-nous de l'école. Qu'est-ce que 1 2 ? Ce sera 1. Dessinons donc un autre carré à côté du premier, proches les uns des autres. Ensuite, le prochain nombre de Fibonacci est 2 (1+1). Qu'est-ce que 2 2 ? Ce sera 4. Dessinons un autre carré proche des deux premiers carrés, mais maintenant avec un côté de 2 et une aire de 4. Le nombre suivant est le nombre 3 (1+2). Le carré du chiffre 3 est 9. Dessinez un carré de côté 3 et d'aire 9 à côté de ceux déjà dessinés. Ensuite, nous avons un carré de côté 5 et d'aire 25, un carré de côté 8 et d'aire 64 - et ainsi de suite, à l'infini.

C'est l'heure de la spirale dorée. Relions les points frontaliers entre les carrés avec une ligne courbe lisse. Et nous obtiendrons cette même spirale dorée, sur la base de laquelle de nombreux objets vivants et inanimés dans la nature sont construits.

Et avant de passer au nombre d’or, réfléchissons. Ici, nous avons construit une spirale basée sur les carrés de la séquence de Fibonacci (séquence 1, 1, 2, 3, 5, 8 et carrés 1, 1, 4, 9, 25, 64). Mais que se passe-t-il si nous utilisons non pas les carrés des nombres, mais leurs cubes ? Les cubes ressembleront à ceci vu du centre :

Et à côté :

Eh bien, lors de la construction d'une spirale, il s'avérera spirale dorée volumétrique:

Voici à quoi ressemble cette volumineuse spirale dorée vue de côté :

Mais que se passerait-il si nous ne prenions pas des cubes de nombres de Fibonacci, mais passions à la quatrième dimension ?... C'est un casse-tête, n'est-ce pas ?

Cependant, je n'ai aucune idée de la manière dont le nombre d'or volumétrique se manifeste dans la nature à partir des cubes de nombres de Fibonacci, et encore moins de nombres à la puissance quatre. Revenons donc au nombre d'or dans l'avion. Alors, regardons à nouveau nos carrés. Mathématiquement parlant, voici l'image que nous obtenons :

C'est-à-dire que nous obtenons le nombre d'or - où un côté est divisé en deux parties dans un rapport tel que la plus petite partie est liée à la plus grande comme la plus grande l'est à la valeur entière.

Autrement dit, a : b = b : c ou c : b = b : a.

Sur la base de ce rapport de grandeurs, on construit entre autres un pentagone régulier et un pentagramme :

Pour référence : pour construire un pentagramme, vous devez construire un pentagone régulier. La méthode de construction a été développée par le peintre et graphiste allemand Albrecht Dürer (1471...1528). Soit O le centre du cercle, A un point du cercle et E le milieu du segment OA. La perpendiculaire au rayon OA, restituée au point O, coupe le cercle au point D. A l'aide d'un compas, tracez le segment CE = ED sur le diamètre. Longueur d'un côté inscrit dans un cercle pentagone régulierégal à DC. Nous traçons les segments DC sur le cercle et obtenons cinq points pour dessiner un pentagone régulier. Nous connectons les coins du pentagone les uns aux autres avec des diagonales et obtenons un pentagramme. Toutes les diagonales du pentagone se divisent en segments reliés par le nombre d'or.

En général, ce sont les modèles. De plus, il existe des modèles beaucoup plus diversifiés que ceux décrits. Et maintenant, après tous ces chiffres ennuyeux, voici la vidéo promise où tout est simple et clair :

Comme vous pouvez le constater, les mathématiques sont bel et bien présentes dans la nature. Et pas seulement dans les objets répertoriés dans la vidéo, mais aussi dans bien d’autres domaines. Par exemple, lorsqu’une vague frappe le rivage et tourne, elle tourne le long de la Spirale Dorée. Et ainsi de suite :)

Découvrons ce que les pyramides égyptiennes antiques, la Joconde de Léonard de Vinci, un tournesol, un escargot, une pomme de pin et des doigts humains ont en commun ?

La réponse à cette question se cache dans les chiffres étonnants qui ont été découverts Mathématicien médiéval italien Léonard de Pise, plus connu sous le nom de Fibonacci (né vers 1170 - décédé après 1228), mathématicien italien . En voyageant à travers l'Orient, il se familiarise avec les réalisations des mathématiques arabes ; ont contribué à leur transfert vers l’Ouest.

Après sa découverte, ces chiffres ont commencé à porter le nom du célèbre mathématicien. L’essence étonnante de la suite de nombres de Fibonacci est que que chaque nombre de cette séquence est obtenu à partir de la somme des deux nombres précédents.

Ainsi, les nombres formant la séquence :

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …

sont appelés « nombres de Fibonacci », et la séquence elle-même est appelée la séquence de Fibonacci.

Dans les nombres de Fibonacci, il y en a un très fonctionnalité intéressante. Lorsque vous divisez un nombre dans une séquence par le nombre qui le précède dans la série, le résultat sera toujours une valeur qui fluctue autour de sens irrationnel 1,61803398875... et une fois sur deux, soit il le dépasse, soit il ne l'atteint pas. (Nombre approximatif irrationnel, c'est-à-dire un nombre dont la représentation décimale est infinie et non périodique)

De plus, après le 13ème nombre de la suite, ce résultat de division devient constant jusqu'à l'infini de la série... C'est ce nombre constant de divisions au Moyen Âge qui était appelé la proportion divine, et maintenant, de nos jours, on l'appelle le nombre d'or, le juste milieu ou nombre d'or . En algèbre, ce nombre est désigné par la lettre grecque phi (Ф)

Donc, nombre d'or = 1:1,618

233 / 144 = 1,618

377 / 233 = 1,618

610 / 377 = 1,618

987 / 610 = 1,618

1597 / 987 = 1,618

2584 / 1597 = 1,618

Le corps humain et le nombre d'or

Artistes, scientifiques, créateurs de mode, designers réalisent leurs calculs, dessins ou croquis sur la base du rapport du nombre d'or. Ils utilisent des mesures du corps humain, qui a également été créé selon le principe du nombre d'or. Avant de créer leurs chefs-d'œuvre, Léonard de Vinci et Le Corbusier ont pris les paramètres du corps humain, créé selon la loi de la proportion d'or.

Le plus livre principal Pour tous les architectes modernes, l'ouvrage de référence « Building Design » d'E. Neufert contient des calculs de base des paramètres du torse humain, qui contiennent la proportion d'or.

Proportions diverses pièces notre corps est un nombre très proche du nombre d’or. Si ces proportions coïncident avec la formule du nombre d’or, alors l’apparence ou le corps de la personne est considéré comme idéalement proportionné. Le principe de calcul de la mesure d'or sur le corps humain peut être représenté sous la forme d'un schéma :

M/m=1,618

Le premier exemple du nombre d'or dans la structure du corps humain :
Si nous prenons le nombril comme centre du corps humain et la distance entre le pied d’une personne et le nombril comme unité de mesure, alors la taille d’une personne équivaut au nombre 1,618.

En plus de cela, il existe plusieurs proportions dorées plus fondamentales de notre corps :

* la distance entre le bout des doigts, le poignet et le coude est de 1 : 1,618 ;

* la distance entre le niveau des épaules et le sommet de la tête et la taille de la tête est de 1 : 1,618 ;

* la distance entre la pointe du nombril et le sommet de la tête et entre le niveau des épaules et le sommet de la tête est de 1:1,618 ;

* la distance du nombril aux genoux et des genoux aux pieds est de 1:1,618 ;

* la distance entre la pointe du menton et la pointe de la lèvre supérieure et entre la pointe de la lèvre supérieure et les narines est de 1 : 1,618 ;

* la distance entre la pointe du menton et la ligne supérieure des sourcils et entre la ligne supérieure des sourcils et la couronne est de 1:1,618 ;

* la distance entre la pointe du menton et la ligne supérieure des sourcils et entre la ligne supérieure des sourcils et la couronne est de 1:1,618 :

Le nombre d'or dans les traits du visage humain comme critère de beauté parfaite.

Dans la structure des traits du visage humain, il existe également de nombreux exemples dont la valeur est proche de la formule du nombre d'or. Cependant, ne vous précipitez pas immédiatement pour qu'un dirigeant mesure les visages de tous. Car les correspondances exactes au nombre d'or, selon les scientifiques et les artistes, artistes et sculpteurs, n'existent que chez les personnes d'une beauté parfaite. En fait, la présence exacte de la proportion dorée sur le visage d’une personne constitue l’idéal de beauté pour le regard humain.

Par exemple, si nous additionnons la largeur des deux dents supérieures de devant et divisons cette somme par la hauteur des dents, alors, ayant obtenu le nombre d'or, nous pouvons dire que la structure de ces dents est idéale.

Il existe d'autres incarnations de la règle du nombre d'or sur le visage humain. Voici quelques-unes de ces relations :

*Hauteur du visage/largeur du visage ;

* Point central de liaison des lèvres à la base du nez/longueur du nez ;

* Hauteur du visage/distance entre la pointe du menton et le point central où les lèvres se rejoignent ;

*Largeur de la bouche/largeur du nez ;

* Largeur du nez / distance entre les narines ;

* Distance entre pupilles / distance entre sourcils.

Main humaine

Il suffit de rapprocher votre paume de vous et de regarder attentivement votre index, et vous y trouverez immédiatement la formule du nombre d'or. Chaque doigt de notre main est constitué de trois phalanges.

* La somme des deux premières phalanges du doigt par rapport à toute la longueur du doigt donne le numéro du nombre d'or (à l'exception du pouce) ;

* De plus, le rapport entre le majeur et l'auriculaire est également égal au nombre d'or ;

* Une personne a 2 mains, les doigts de chaque main sont constitués de 3 phalanges (sauf le pouce). Il y a 5 doigts sur chaque main, soit 10 au total, mais à l'exception de deux pouces à deux phalanges, seuls 8 doigts sont créés selon le principe du nombre d'or. Alors que tous ces nombres 2, 3, 5 et 8 sont les nombres de la suite de Fibonacci :

Le nombre d'or dans la structure des poumons humains

Le physicien américain B.D. West et le Dr A.L. Goldberger, au cours d'études physiques et anatomiques, a établi que le nombre d'or existe également dans la structure des poumons humains.

La particularité des bronches qui composent les poumons humains réside dans leur asymétrie. Les bronches sont constituées de deux voies respiratoires principales, dont l’une (la gauche) est plus longue et l’autre (la droite) est plus courte.

* On a constaté que cette asymétrie se poursuit dans les branches des bronches, dans toutes les petites voies respiratoires. De plus, le rapport entre les longueurs des bronches courtes et longues est également le nombre d’or et est égal à 1 : 1,618.

Structure du quadrilatère orthogonal doré et de la spirale

Le nombre d'or est une telle division proportionnelle d'un segment en parties inégales, dans laquelle le segment entier est lié à la plus grande partie comme la plus grande partie elle-même est liée à la plus petite ; ou en d’autres termes, le plus petit segment est au plus grand comme le plus grand l’est au tout.

En géométrie, un rectangle avec ce rapport hauteur/largeur est devenu appelé le rectangle d'or. Ses longs côtés correspondent à côtés courtsà un rapport de 1,168:1.

Le rectangle d’or possède également de nombreuses propriétés étonnantes. Le rectangle d’or possède de nombreuses propriétés inhabituelles. En découpant dans le rectangle d'or un carré dont le côté est égal au plus petit côté du rectangle, on obtient à nouveau un rectangle d'or de dimensions plus petites. Ce processus peut être poursuivi indéfiniment. Au fur et à mesure que nous continuons à découper des carrés, nous obtiendrons des rectangles dorés de plus en plus petits. De plus, ils seront situés dans une spirale logarithmique, ce qui est important dans les modèles mathématiques d'objets naturels (par exemple, des coquilles d'escargots).

Le pôle de la spirale se situe à l'intersection des diagonales du rectangle initial et de la première verticale à couper. De plus, les diagonales de tous les rectangles dorés décroissants suivants se trouvent sur ces diagonales. Bien sûr, il y a aussi le triangle d’or.

Le designer et esthéticien anglais William Charlton a déclaré que les gens trouvent les formes en spirale agréables à l'œil et les utilisent depuis des milliers d'années, l'expliquant ainsi :

"Nous aimons l'apparence d'une spirale car visuellement nous pouvons facilement la regarder."

Dans la nature

* La règle du nombre d'or, qui sous-tend la structure de la spirale, se retrouve très souvent dans la nature dans des créations d'une beauté inégalée. Le plus exemples illustratifs— la forme en spirale se retrouve dans la disposition des graines de tournesol, des pommes de pin, des ananas, des cactus, dans la structure des pétales de roses, etc. ;

* Les botanistes ont découvert que dans la disposition des feuilles sur une branche, des graines de tournesol ou des pommes de pin, la série de Fibonacci se manifeste clairement, et donc la loi du nombre d'or se manifeste ;

Le Seigneur Tout-Puissant a établi une mesure spéciale pour chacune de ses créations et lui a donné une proportionnalité, ce qui est confirmé par des exemples trouvés dans la nature. On peut donner de nombreux exemples où le processus de croissance d'organismes vivants se déroule en stricte conformité avec la forme d'une spirale logarithmique.

Tous les ressorts de la spirale ont même forme. Les mathématiciens ont découvert que même avec une augmentation de la taille des ressorts, la forme de la spirale reste inchangée. Il n’existe aucune autre forme en mathématiques qui possède les mêmes propriétés uniques que la spirale.

La structure des coquillages

Les scientifiques qui ont étudié l'intérieur et structure externe coquilles de mollusques au corps mou vivant au fond des mers, il a été déclaré :

« La surface intérieure des coques est impeccablement lisse, tandis que la surface extérieure est entièrement recouverte de rugosités et d'irrégularités. Le mollusque était dans une coquille et pour cela la surface intérieure de la coquille devait être parfaitement lisse. Les coins-courbes externes de la coque augmentent sa résistance, sa dureté et augmentent ainsi sa résistance. La perfection et l'intelligence étonnante de la structure de la coquille (escargot) sont étonnantes. L'idée en spirale des coquillages est une forme géométrique parfaite et est étonnante par sa beauté aiguisée.

Chez la plupart des escargots qui ont une coquille, celle-ci se développe sous la forme d’une spirale logarithmique. Cependant, il ne fait aucun doute que ces créatures déraisonnables non seulement n'ont aucune idée de la spirale logarithmique, mais n'ont même pas les connaissances mathématiques les plus simples pour se créer une coquille en forme de spirale.

Mais alors, comment ces créatures déraisonnables ont-elles pu déterminer et choisir elles-mêmes la forme idéale de croissance et d’existence sous la forme d’une coquille en spirale ? Ces êtres vivants, que monde des scientifiques appelle des formes de vie primitives, calcule que la forme logarithmique d'une coquille serait idéale pour leur existence ?

Bien sûr que non, car un tel projet ne peut se réaliser sans intelligence et sans connaissances. Mais ni les mollusques primitifs ni la nature inconsciente ne possèdent une telle intelligence, que certains scientifiques appellent pourtant le créateur de la vie sur terre (?!)

Essayer d’expliquer l’origine d’une forme de vie, même la plus primitive, par une combinaison aléatoire de certaines circonstances naturelles est pour le moins absurde. Il est clair que ce projet est une création consciente.

Le biologiste Sir D'arky Thompson appelle ce type de croissance des coquillages "forme de croissance des nains."

Sir Thompson fait ce commentaire :

« Il n’existe pas de système plus simple que la croissance des coquillages, qui grandissent et se dilatent proportionnellement, tout en conservant la même forme. Le plus étonnant, c’est que la coquille grandit, mais ne change jamais de forme.

Le Nautilus, mesurant plusieurs centimètres de diamètre, est l'exemple le plus frappant de l'habitude de croissance des gnomes. S. Morrison décrit ainsi ce processus de croissance du nautile, qui semble assez difficile à planifier même avec l'esprit humain :

«À l'intérieur de la coquille du nautile, il y a de nombreux compartiments-pièces avec des cloisons en nacre, et la coquille elle-même à l'intérieur est une spirale qui s'étend à partir du centre. Au fur et à mesure que le nautile grandit, une autre pièce se développe dans la partie avant de la coquille, mais cette fois plus grande que la précédente, et les cloisons de la pièce laissée derrière sont recouvertes d'une couche de nacre. Ainsi, la spirale s’étend proportionnellement tout le temps.

Voici quelques types de coquilles en spirale avec un modèle de croissance logarithmique conformément à leurs noms scientifiques :
Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, Solarium Trochleare.

Tous les restes fossiles de coquilles découverts avaient également une forme de spirale développée.

Cependant, la forme de croissance logarithmique se retrouve dans le monde animal et pas seulement chez les mollusques. Les cornes des antilopes, des chèvres sauvages, des béliers et autres animaux similaires se développent également sous la forme d'une spirale selon les lois du nombre d'or.

Nombre d'or dans l'oreille humaine

Dans l’oreille interne humaine se trouve un organe appelé Cochlée (« Escargot »), qui remplit la fonction de transmission des vibrations sonores.. Cette structure osseuse est remplie de liquide et a également la forme d'un escargot, contenant une forme de spirale logarithmique stable = 73º 43'.

Cornes et défenses d'animaux se développant en forme de spirale

Les défenses des éléphants et des mammouths disparus, les griffes des lions et les becs des perroquets sont de forme logarithmique et ressemblent à la forme d'un axe qui tend à se transformer en spirale. Les araignées tissent toujours leurs toiles sous la forme d'une spirale logarithmique. La structure des micro-organismes tels que le plancton (espèces globigerinae, planorbis, vortex, terebra, turitellae et trochida) a également une forme en spirale.

Nombre d'or dans la structure des microcosmes

Les formes géométriques ne se limitent pas à un triangle, un carré, un pentagone ou un hexagone. Si nous connectons ces figures de différentes manières entre elles, nous obtenons de nouveaux éléments tridimensionnels. figures géométriques. Des exemples en sont des figures telles qu'un cube ou une pyramide. Cependant, à côté d'eux, il existe également d'autres figures tridimensionnelles que nous n'avons pas rencontrées dans Vie courante, et dont nous entendons peut-être les noms pour la première fois. Parmi ces figures tridimensionnelles figurent le tétraèdre (figure régulière à quatre côtés), l'octaèdre, le dodécaèdre, l'icosaèdre, etc. Le dodécaèdre est constitué de 13 pentagones, l'icosaèdre de 20 triangles. Les mathématiciens notent que ces chiffres se transforment mathématiquement très facilement et que leur transformation se produit conformément à la formule de la spirale logarithmique du nombre d'or.

Dans le microcosme, les formes logarithmiques tridimensionnelles construites selon des proportions dorées sont omniprésentes. . Par exemple, de nombreux virus ont la forme géométrique tridimensionnelle d’un icosaèdre. Le virus Adeno est peut-être le plus célèbre de ces virus. L'enveloppe protéique de l'Adenovirus est formée de 252 unités de cellules protéiques disposées dans un certain ordre. À chaque coin de l’icosaèdre se trouvent 12 unités de cellules protéiques en forme de prisme pentagonal et des structures en forme de pointes s’étendent à partir de ces coins.

Le nombre d’or dans la structure des virus a été découvert pour la première fois dans les années 1950. scientifiques du Birkbeck College de Londres A. Klug et D. Kaspar. 13 Le virus Polyo a été le premier à présenter une forme logarithmique. La forme de ce virus s’est avérée similaire à celle du virus Rhino 14.

La question se pose de savoir comment les virus forment des formes tridimensionnelles aussi complexes, dont la structure contient le nombre d'or, qui sont assez difficiles à construire même avec notre esprit humain ? Le découvreur de ces formes de virus, le virologue A. Klug, fait le commentaire suivant :

« Le Dr Kaspar et moi avons montré que pour la coque sphérique du virus, la forme la plus optimale est une symétrie telle que la forme de l'icosaèdre. Cet ordre minimise le nombre d'éléments de connexion... La plupart des cubes hémisphériques géodésiques de Buckminster Fuller sont construits sur un principe géométrique similaire. 14 L'installation de tels cubes nécessite un schéma explicatif extrêmement précis et détaillé. Alors que les virus inconscients construisent eux-mêmes une enveloppe si complexe à partir d’unités cellulaires protéiques élastiques et flexibles.

Gymnase GOU n°1505

"Gymnase-Laboratoire Pédagogique de la Ville de Moscou"

Essai

Nombres de Fibonacci et nombre d'or

Azov Nikita

Superviseur: Shalimova M.N.

Introduction ………………………………………………….……………2

Chapitre 1

Histoire des nombres de Fibonacci………………………………..……..5

Chapitre 2

Les nombres de Fibonacci comme progression réciproque………...…...………………………………………………………..….....12

chapitre 3

Nombres de Fibonacci et nombre d'or………………………

Conclusion …………………………………………………...…...16

Bibliographie ………………………………………………………………….……..20

Introduction.

La pertinence de la recherche. À mon avis, on accorde peu d’attention de nos jours aux théorèmes mathématiques et aux faits connus de l’histoire du développement de la science. En utilisant l'exemple des nombres de Fibonacci, je voudrais montrer à quel point ils peuvent être globaux et à quel point ils sont largement applicables non seulement en mathématiques, mais aussi dans la vie quotidienne.

Le but de mon travail est d'étudier l'histoire, les propriétés, les applications et les connexions des nombres de Fibonacci avec le nombre d'or.

Chapitre 1. Les nombres de Fibonacci et leur histoire.

Léonard (1170-1250) est né à Pise. Il reçut plus tard le surnom de Fibonacci, qui signifie « fils bien né ». Son père faisait du commerce dans les pays arabes d'Afrique du Nord. Là, Léonard a étudié les mathématiques avec des professeurs arabes et s'est également familiarisé avec les réalisations des scientifiques indiens et grecs anciens grâce à des traités sur Traduction arabe. Après avoir maîtrisé tout le matériel étudié, il a créé son propre livre - "Le Livre du Boulier" (la première édition a été écrite en 1202, mais seule la réimpression de 1228 nous a survécu). Ainsi, il devint le premier mathématicien médiéval de premier plan et initia également l'Europe aux chiffres arabes et aux chiffres arabes. système décimal calculs que nous utilisons quotidiennement avec premières années et jusqu'à la vieillesse.

Le Livre du Boulier peut être divisé en cinq parties selon son contenu. Les cinq premiers chapitres du livre sont consacrés à l'arithmétique des nombres entiers basée sur la numérotation décimale. Les chapitres 6 et 7 décrivent les opérations sur les fractions ordinaires. Les chapitres 8 à 10 décrivent les techniques permettant de résoudre des problèmes en utilisant des proportions. Le chapitre 11 traite des problèmes de mélange ; le chapitre 12 traite des nombres dits de Fibonacci. Ci-dessous, nous décrivons d'autres techniques avec des nombres et donnons des problèmes sur divers sujets.

Le principal problème expliquant l’origine de la série de nombres de Fibonacci est le problème du lapin. La question du problème est la suivante : « Combien de couples de lapins naissent d’un même couple en un an ? » Une explication est donnée pour le problème selon lequel un couple de lapins donne naissance à un autre couple un mois plus tard et, par nature, les lapins commencent à donner naissance à une progéniture au cours du deuxième mois après leur naissance. L'auteur nous donne une solution au problème. Il s'avère qu'au cours du premier mois, le premier couple donnera naissance à un autre. Dans le second, le premier couple donnera naissance à un autre – il y aura trois couples. Au 3ème mois, deux couples accoucheront : celui initialement donné et celui né au cours du premier mois. Donne 5 paires. Et ainsi de suite, en utilisant la même logique de raisonnement, nous obtenons qu'au quatrième mois il y aura 8 paires, au cinquième 13, au sixième 21, au septième 34, au huitième 55, au neuvième 89, en le dixième 144, le onzième 233, le douzième 377.

Nous pouvons désigner le nombre de lapins au cours d’une période de douze mois par un. On obtient une série de nombres :

Dans une série de ces nombres, chaque terme est égal à la somme des deux précédents. Il s'avère que n'importe quel terme de l'équation peut être déterminé par l'équation :

Considérons un cas particulier important pour cette équation, lorsque u 1 et u 2 =1. Nous obtiendrons une séquence de nombres 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377... Nous avons reçu la même séquence de nombres dans le problème des lapins. Ces nombres sont appelés nombres de Fibonacci en l’honneur de l’auteur.

Ces nombres ainsi que l'équation (2) ont de nombreuses propriétés qui seront prises en compte dans mon travail.

Chapitre 2. Relation entre la série de nombres de Fibonacci et les progressions. Propriétés de base de la série.

Afin de déduire les propriétés de base de la série, prenons comme exemple les cinq premiers nombres : 1, 1, 2, 3, 5, 8. On voit que chaque nouveau nombre est égal à la somme des deux précédents. De là, nous pouvons dériver une formule pour obtenir n’importe quel nombre dans une série, ainsi qu’une formule pour la somme de n’importe quel nombre de nombres dans une série.

On voit que les formules sont radicalement différentes des formules caractéristiques des progressions arithmétiques et géométriques. Et on peut aussi dire que seuls les deux premiers numéros de la série peuvent se rapporter à des progressions éventuelles.

Les progressions arithmétiques et géométriques n'ont que deux formules mentionnées précédemment, et pour calculer, par exemple, la somme des nombres pairs, impairs ou la somme des carrés de nombres, vous devez à chaque fois résoudre le problème pour une série distincte. Mais comme la série de nombres de Fibonacci est immuable (elle n'a pas d'étapes, de dénominateurs et de divers premiers termes de progression), cela signifie qu'il est possible d'en dériver une formule pour obtenir les sommes des éléments individuels de la série. Voici un exemple de formule pour obtenir la somme des nombres dans une série de nombres pairs :

Il existe une formule similaire pour les nombres impairs :

Il existe également une formule pour obtenir la somme des nombres d'une série au carré :

Les nombres de Fibonacci ont une autre propriété unique qui n'est pas typique des progressions arithmétiques et géométriques. Le rapport d'une série de nombres (précédent au suivant) tend constamment vers la valeur 0,618, une situation similaire se produit lors de la division de F n par F n +2 (le rapport tend vers 0,382), lors de la division de F n par F n +3 ( le rapport tend vers 0,236) et ainsi de suite. En conséquence, nous avons obtenu un ensemble de relations. L'ensemble de leurs valeurs et de leurs valeurs inverses sont appelés ratios de Fibonacci. Et la valeur inverse 0,618 – 1,618 est un nombre

("Fi") Il fait également partie d'une paire de racines du polynôme x 2 -x-1 caractéristique de la série.

Chapitre 3. Nombre d'or et nombres de Fibonacci.

Nombre d'or (nombre d'or, division en rapport extrême et moyen) - division valeur continue en deux parties dans un rapport tel que la plus petite partie soit liée à la plus grande comme la plus grande l'est à la grandeur entière.

Essayons d'expliquer cela en utilisant l'exemple d'une droite infinie. Prenons la droite entière c comme une seule. Divisons-la en deux parties a et b, qui divisent la ligne en segments égaux à 1, comme 0,618 et 0,382, respectivement. Et ces nombres sont l'un des coefficients de la série de nombres de Fibonacci. Nous constatons que le rapport des grandes parties de cette droite aux plus petites se rapproche asymptotiquement du nombre

.

Il existe deux chiffres principaux qui reflètent le principe du nombre d'or.

Le nombre d’or était connu des anciens Grecs. Archimède est considéré comme le découvreur de la spirale d'Archimède. Sa signification est que chaque nouvelle boucle augmente d'un certain nombre et que le rapport de ces boucles est égal au nombre

.

Le deuxième chiffre est un triangle d'or. Il s'agit d'un triangle isocèle dans lequel le rapport des côtés à la base est égal à

Séquence de Fibonacci en mathématiques et dans la nature

Séquence de Fibonacci, connu de tous grâce au film "Le Da Vinci Code" - une série de nombres décrits sous forme d'énigme par le mathématicien italien Léonard de Pise, plus connu sous le surnom de Fibonacci, au XIIIe siècle. En bref l'essence de l'énigme :

Quelqu'un a placé un couple de lapins dans un certain espace clos pour savoir combien de couples de lapins naîtraient au cours de l'année, si la nature des lapins est telle que chaque mois un couple de lapins donne naissance à un autre couple, et ils deviennent capables de produire une progéniture lorsqu'ils atteignent l'âge de deux mois.

Le résultat est la séquence suivante : 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 , où est indiqué le nombre de couples de lapins dans chacun des douze mois, séparés par des virgules.

Cette séquence peut être poursuivie indéfiniment. Son essence est que chaque nombre suivant est la somme des deux précédents.

Cette séquence présente un certain nombre de caractéristiques mathématiques qui doivent absolument être abordées. Cette séquence tend asymptotiquement (s'approchant de plus en plus lentement) vers une certaine constante rapport. Cependant, ce rapport est irrationnel, c'est-à-dire qu'il s'agit d'un nombre avec une séquence infinie et imprévisible de chiffres décimaux dans la partie fractionnaire. Il est impossible de l'exprimer avec précision.

Ainsi, le rapport de n'importe quel membre de la séquence à celui qui le précède fluctue autour du nombre 1,618 , parfois le dépassant, parfois ne l'atteignant pas. Le rapport avec ce qui suit se rapproche également du nombre 0,618 , ce qui est inversement proportionnel 1,618 . Si nous divisons les éléments de la séquence par un, nous obtenons des nombres 2,618 Et 0,382 , qui sont également inversement proportionnels. Ce sont ce qu’on appelle les ratios de Fibonacci.

A quoi ça sert tout ça ? C’est ainsi que nous abordons l’un des phénomènes naturels les plus mystérieux. Fibonacci n'a essentiellement rien découvert de nouveau, il a simplement rappelé au monde un phénomène tel que Nombre d'or, qui n'est pas inférieur en importance au théorème de Pythagore

Nous distinguons tous les objets qui nous entourent par leur forme. On en aime plus, d'autres moins, d'autres sont complètement rebutants. Parfois, l’intérêt peut être dicté par la situation de la vie, parfois par la beauté de l’objet observé. La forme symétrique et proportionnelle favorise la meilleure perception visuelle et évoque une sensation de beauté et d'harmonie. Une image complète est toujours constituée de parties de tailles différentes qui entretiennent une certaine relation les unes avec les autres et avec l'ensemble.

nombre d'or- la plus haute manifestation de la perfection de l'ensemble et de ses parties dans la science, l'art et la nature.

Pour prendre un exemple simple, le nombre d'or est la division d'un segment en deux parties dans un rapport tel que la plus grande partie est liée à la plus petite, comme leur somme (le segment entier) est à la plus grande.

Si nous prenons tout le segment c derrière 1 , puis le segment un sera égal 0,618 , segment de ligne b - 0,382 , ce n'est qu'ainsi que la condition du nombre d'or sera remplie (0,618/0,382= 1,618 ; 1/0,618=1,618 ). Attitude cÀ unéquivaut à 1,618 , UN AvecÀ b2.618. Ce sont les mêmes ratios de Fibonacci qui nous sont déjà familiers.

Bien sûr, il existe un rectangle doré, un triangle doré et même un cuboïde doré. Les proportions du corps humain sont à bien des égards proches du nombre d’or.

Image: marcus-frings.de

Mais le plaisir commence lorsque nous combinons les connaissances que nous avons acquises. La figure montre clairement la relation entre la séquence de Fibonacci et le nombre d'or. On commence avec deux carrés de la première taille. Ajoutez un carré de la deuxième taille par-dessus. Dessinez un carré à côté avec un côté égal à la somme des côtés des deux précédents, troisième taille. Par analogie, un carré de taille cinq apparaît. Et ainsi de suite jusqu'à ce que vous soyez fatigué, l'essentiel est que la longueur du côté de chaque carré suivant soit égale à la somme des longueurs des côtés des deux précédents. Nous voyons une série de rectangles dont les côtés sont des nombres de Fibonacci et, curieusement, ils sont appelés rectangles de Fibonacci.

Si nous traçons des lignes douces passant par les coins de nos carrés, nous n'obtiendrons rien de plus qu'une spirale d'Archimède dont l'incrément est toujours uniforme.

Cela ne vous rappelle rien ?

Photo: éthanhéine sur Flickr

Et non seulement dans la coquille d’un mollusque, vous pouvez trouver des spirales d’Archimède, mais dans de nombreuses fleurs et plantes, elles ne sont tout simplement pas si évidentes.

Aloès multifolia :

Photo: livres de bière sur Flickr

Photo: beart.org.uk

Photo: esdrascalderan sur Flickr

Photo: manj98 sur Flickr

Et maintenant, il est temps de se souvenir du nombre d’or ! Certaines des créations les plus belles et les plus harmonieuses de la nature sont-elles représentées dans ces photographies ? Et ce n'est pas tout. Si vous regardez attentivement, vous pouvez trouver des modèles similaires sous de nombreuses formes.

Bien sûr, l’affirmation selon laquelle tous ces phénomènes sont basés sur la séquence de Fibonacci semble trop forte, mais la tendance est évidente. Et d’ailleurs, la séquence elle-même est loin d’être parfaite, comme tout dans ce monde.

On suppose que la séquence de Fibonacci est par nature une tentative de s'adapter à une séquence logarithmique du nombre d'or plus fondamentale et plus parfaite, qui est presque la même, sauf qu'elle part de nulle part et ne mène nulle part. La nature a certainement besoin d’une sorte de commencement à partir duquel elle peut partir ; elle ne peut pas créer quelque chose à partir de rien. Les rapports des premiers termes de la suite de Fibonacci sont loin du nombre d'or. Mais plus on avance, plus ces écarts s’estompent. Pour définir n'importe quelle séquence, il suffit de connaître ses trois termes, qui se succèdent. Mais pas pour la séquence d'or, deux lui suffisent, c'est une progression géométrique et arithmétique à la fois. On pourrait penser qu’elle constitue la base de toutes les autres séquences.

Chaque terme de la séquence logarithmique dorée est une puissance du nombre d'or ( z). Une partie de la série ressemble à ceci : ... z -5 ; z-4 ; z-3 ; z-2 ; z-1 ; z 0 ; z 1 ; z 2 ; z 3 ; z 4 ; z 5... Si nous arrondissons la valeur du nombre d’or à trois décimales, nous obtenons z=1,618, alors la série ressemble à ceci : ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Chaque terme suivant peut être obtenu non seulement en multipliant le précédent par 1,618 , mais aussi en ajoutant les deux précédents. Ainsi, la croissance exponentielle d’une séquence est obtenue en ajoutant simplement deux éléments adjacents. C'est une série sans début ni fin, et c'est à cela que tente de ressembler la séquence de Fibonacci. Ayant un début très précis, elle s'efforce d'atteindre l'idéal, sans jamais l'atteindre. C'est la vie.

Et pourtant, à propos de tout ce que nous avons vu et lu, des questions assez logiques se posent :
D'où viennent ces chiffres ? Qui est cet architecte de l’univers qui a tenté de le rendre idéal ? Est-ce que tout s'est toujours passé comme il le souhaitait ? Et si oui, pourquoi cela a-t-il mal tourné ? Des mutations ? Choix libre? Quelle sera la prochaine étape ? La spirale s’enroule-t-elle ou se déroule-t-elle ?

Après avoir trouvé la réponse à une question, vous obtiendrez la suivante. Si vous le résolvez, vous en obtiendrez deux nouveaux. Une fois que vous les aurez traités, trois autres apparaîtront. Après les avoir résolus également, vous en aurez cinq non résolus. Puis huit, puis treize, 21, 34, 55...