Le texte de l'ouvrage est affiché sans images ni formules.
La version complète de l'ouvrage est disponible dans l'onglet "Fichiers de travail" au format PDF

INTRODUCTION

PL. Chebyshev, le plus grand mathématicien et mécanicien russe, fondateur de l'école mathématique de Saint-Pétersbourg, originaire de la province de Kaluga, a écrit dans l'article «Sur le deuxième volume de l'histoire de Polevoy» à propos des personnes capables de deviner et de saisir l'essence de phénomènes :

« L’esprit humain, selon l’expression populaire, n’est pas un prophète, mais un devin ; il voit le cours général des choses et peut en déduire des hypothèses profondes, souvent justifiées par le temps… »

En 1838, alors qu'il participait à un concours étudiant, P.L. Chebyshev a reçu une médaille d'argent pour ses travaux visant à trouver les racines d'une équation du nième degré. Le travail original avait déjà été achevé en 1838 et était basé sur l'algorithme de Newton.

Hypothèse : la solution d'une équation incomplète du troisième degré, dont les racines ne sont pas entières, est résolue à l'aide de la formule de P.L. Chebyshev de manière rationnelle.

Objectif de l'étude : résoudre une équation incomplète du troisième degré en utilisant plusieurs méthodes et déterminer la plus rationnelle d'entre elles.

Objectifs de recherche:

Familiarisez-vous avec la définition des dérivées du premier et du second ordre ;

Apprenez à construire des graphiques de fonctions polynomiales du troisième degré ;

Appliquez la formule de P.L. à la solution d’une équation incomplète du troisième degré. Tchebycheva ;

Appliquer les méthodes connues pour résoudre une équation incomplète du troisième degré ;

Appliquer un algorithme pour affiner les racines d'un polynôme si deux valeurs de sa racine sont connues approximativement ;

Parmi les méthodes de résolution obtenues, choisissez la plus rationnelle.

REVUE DE LITTÉRATURE

Dérivée d'une fonction

La limite d'une fonction en un point donné, limitant le domaine de définition de la fonction, est la valeur vers laquelle tend la valeur de la fonction considérée lorsque son argument tend vers un point donné.

La dérivée d'une fonction est un concept du calcul différentiel qui caractérise le taux de variation d'une fonction en un point donné. Elle est définie comme la limite du rapport entre l'incrément d'une fonction et l'incrément de son argument lorsque l'incrément de l'argument tend vers zéro, si une telle limite existe. Une fonction qui a une dérivée finie (à un moment donné) est appelée différentiable (à ce stade).

Déterminer la dérivée d'une fonction par une limite.

Laissez dans un certain voisinage du point (displaystyle x_(0)in mathbb (R) ) la fonction (displaystyle fcolon U(x_(0))subset mathbb (R) to mathbb (R) .) être définie. La dérivée du fonction (style d'affichage f) Fà ce point (style d'affichage x_(0)) la limite est appelée si elle existe,

La dérivée de la dérivée première est appelée dérivée du second ordre ou dérivée seconde.

Formule P.L. Tchebycheva

Méthodes de résolution d'équations algébriques de degrés supérieurs

Les équations du troisième degré (et supérieur) peuvent être résolues des manières suivantes :

Graphique, qui devient d'autant plus difficile que le degré du polynôme est élevé, puisque construire un graphe est parfois plus difficile que trouver les racines correspondantes ;

Opérationnel, souvent approximatif, mais permettant de retrouver des racines avec une grande précision. La méthode graphique est auxiliaire de la méthode opérationnelle.

Théorème 1. S'il existe une racine entière d'un polynôme à coefficients entiers, lorsque le terme principal a un coefficient un, alors c'est un diviseur du terme libre.

Théorème 2. Tout polynôme de degré impair sur l’ensemble des nombres réels a au moins une racine réelle.

Nomogrammes

Le nomogramme (grec νομοσ - loi) est une représentation graphique d'une fonction de plusieurs variables, qui permet d'utiliser des opérations géométriques simples (par exemple, appliquer une règle) pour étudier les dépendances fonctionnelles sans calculs. Par exemple, résolvez une équation quadratique sans utiliser de formules. Nomographie (du grec nómos - droit et...graphie), une branche des mathématiques qui combine théorie et méthodes pratiques pour construire des nomogrammes - des dessins spéciaux qui sont des images de dépendances fonctionnelles. La particularité des nomogrammes est que chaque dessin représente une zone donnée de changement de variables et chacune des valeurs des variables dans cette zone est représentée sur le nomogramme par un certain élément géométrique (point ou ligne) ; les images des valeurs des variables liées par dépendance fonctionnelle se trouvent sur le nomogramme dans une certaine correspondance, commune aux nomogrammes du même type.

Nomogrammes pour résoudre des équations. Pour résoudre les équations X α +p 0 X ß +q 0 = 0 nomogrammes de points alignés sont utilisés. Vous pouvez obtenir un tel nomogramme comme ceci : Traçons deux lignes droites parallèles verticales - l'axe R. avec le début du compte à rebours UN et axe q avec le début du compte à rebours DANS(Fig. 1); sur cette figure il y a un segment UN B perpendiculaire aux axes p,q, mais ce n'est pas du tout nécessaire).

Prenons des nombres arbitraires α, ß et un nombre positif UN. Sur l'axe R. prenons un point AVEC avec coordonnées - UN α-ß sur l'axe R.- indiquer D avec coordonnées -UN α . Laisser ANNONCE∩AVANT JC.=E. Laissez-vous guider E une ligne droite arbitraire, non parallèle aux axes R., q. Notons la coordonnée d'intersection M c'est une ligne droite avec un axe R.à travers R. 0 , intersections de N avec l'axe q- à travers q. Alors UN α + R. 0 α ß + q 0 = 0 (1), c'est-à-dire nombre UN est la racine de l'équation X α + R. 0 X ß + q 0 = 0 (2). Droit MN peut croiser des axes R., q de l'une des trois manières suivantes : R. 0 < 0, q 0 > 0 (Fig.1) ; R. 0 > 0, q 0 < 0 (рис. 2); R. 0 < 0, q 0 < 0 (рис.3).

Riz. 2 Fig. 3

Prouvons l'égalité (1) pour le cas illustré à la Fig. 1 (les deux autres cas sont traités de la même manière). De la similitude des triangles A.E.C. Et LIT nous avons

ce qui donne (1). Fixons α, ß arbitraires et considérons toutes les équations possibles X α + px ß + q= 0 . Un nomogramme pour trouver les racines positives de telles équations est dessiné comme suit : 1) paramètre UN différentes valeurs positives sont données et un point est construit pour chacune d'elles E comme décrit ci-dessus; 2) les points résultants, marqués des valeurs des paramètres correspondants, sont reliés par une courbe lisse g(Fig. 4).

Maintenant, en utilisant ce nomogramme, vous pouvez trouver approximativement les racines positives d'une équation spécifique X α + R. 0 X ß + q 0 = 0, pour cela il faut prendre un point sur l'axe p M avec coordonnées R. 0 , sur l'axe q- point N avec coordonnée q 0 et faire un direct MN. Chaque point d'intersection d'une ligne MN avec une courbe g donne, grâce à (1), une racine positive de l'équation (2). Points correspondant à p coefficients qéquations et points correspondant aux racines positives souhaitées de l'équation X α + px ß + q=0, se situe sur la même ligne droite.

Un algorithme pour affiner les racines d'un polynôme si deux valeurs de sa racine sont connues approximativement

Théorème. Connaissant deux valeurs approchées et polynômes, on peut obtenir des valeurs approchées améliorées en utilisant la formule récurrente :

SOLUTION D'UNE ÉQUATION INCOMPLÈTE DU TROISIÈME DEGRÉ

Un exemple de résolution d'une équation du troisième degré

Soit l'équation

Solution 1.

Puisque le côté gauche de l’équation est un polynôme du troisième degré (impair), il a au moins une racine réelle sur l’ensemble des nombres réels, c’est-à-dire ces nombres sont des diviseurs du terme libre 1.

Nous avons 1 3 -5 1+1=-3 et cela signifie qu’il n’y a pas de racines entières.

Peut-être une racine rationnelle ? Non, puisqu'un polynôme avec un coefficient du terme principal 1 n'a pas de racines entières.

Cela signifie que l'hypothèse est incorrecte - la racine est irrationnelle, nous la trouverons approximativement en établissant l'intervalle dans lequel elle se trouve.

Faisons le tableau 1, donnant les valeurs de la variable X et calculer les valeurs de fonction à:

Tableau 1

L'intervalle a déjà été trouvé, nous avons une racine négative contenue dans les limites :

Deuxième intervalle, nous avons une racine positive contenue dans les limites

Le troisième intervalle, nous avons une racine positive contenue dans les limites

Il n’est pas nécessaire de trouver d’autres racines, puisqu’une équation du troisième degré ne peut pas avoir plus de trois racines.

La fonction est continue pendant R. et différentiable sur R..

Le graphique d'une fonction coupe l'axe UOà ce point.

La dérivée de la fonction est égale à

Points critiques de 1ère espèce :

Examinons la fonction de monotonie :

Nous avons appliqué la formule de Bernoulli pour calculer la valeur approximative

Donnons une représentation graphique de la fonction (Fig. 6) qui clarifie quelque peu la signification des racines irrationnelles, donnant des approximations rationnelles :

Solution 2.

Transformons l'équation originale sous la forme :

Résolvons cette équation graphiquement.

Introduisons deux fonctions :

Construisons des graphiques de données pour ces fonctions (Fig. 7) :

Solution 3.

Appliquons la formule de P.L. Tchebycheva

Nous utilisons le graphe de fonctions (Fig. 6)

On voit que l’une des racines de l’équation est située près de

Trouvons les dérivées du premier et du second ordre de cette fonction :

Faisons les calculs :

Appliquons la formule :

Les racines restantes sont plus faciles à trouver en utilisant les propriétés des polynômes :

1). Si la racine d'un polynôme est divisible par.

2). Lorsqu'un polynôme est divisé par, le reste est égal à la valeur de ce polynôme à.

3). Schéma Horner, où (tableau 2) :

Tableau 2

Nous avons obtenu un reste de division de 0,008.

Nous assimilons le diviseur à zéro :

Réponse : -2,33 ; 0,2 ; 2.13.

Solution 4.

Résolvons cette équation à l'aide de ce nomogramme (Fig. 8), en effectuant les calculs appropriés :

Construisons un segment. Il coupera le graphique résultant aux points avec des coordonnées.

Pour obtenir la troisième racine, changez le signe X sur - X, on a

Trouvons la racine négative de l'équation en construisant un segment ; il coupe le graphique de la fonction en un point.

Réponse : -2,3 ; 0,25 ; 2.2.

Vérifions les racines obtenues à l'aide de ressources Internet : site Internet

Résoudre des équations gratuitement - Calculateur en ligne Équations régulières

Les réponses sont présentées dans la Fig. 9 et fig. dix:

Réponse : 0,2 ; 2.13 ; -2.33.

Affinons l'une des racines du polynôme obtenu dans la solution 4 à l'aide de l'algorithme d'affinement des racines d'un polynôme si deux valeurs de sa racine sont connues approximativement.

Prenons .

On peut continuer à affiner la valeur approximative de la racine. Prenons le nombre comme valeur approximative de la racine.

CONCLUSION

Analysons les méthodes utilisées pour résoudre l'équation (tableau 3) :

Solution	Défauts	Avantages
Tracer un graphique d'une fonction et déterminer la valeur approximative des zéros de la fonction à l'aide d'une table de dépendance X depuis à.	Longue, se pose le problème de l'estimation de la valeur d'un nombre irrationnel. Erreur dans la recherche d'une des trois racines.	Visuel : Il est intéressant d'estimer des racines en utilisant les propriétés des fonctions continues (signe constant et zéros de la fonction). Peut être appliqué à la plupart des équations algébriques.
Manière graphique de résoudre l'équation	Inexacte. Erreur dans la recherche d'une des trois racines.	Visuel, donne le droit de choisir l'introduction de fonctions auxiliaires.
Application de la formule P.L. Tchebycheva	Des calculs fastidieux, pour les éviter, ont eu recours à la théorie des polynômes pour trouver deux racines.
Application du nomogramme	Prend du temps, nécessite de la précision dans la construction d'un graphique de fonction, d'une échelle et d'une précision.	Les racines ont été trouvées avec assez de précision.

Tableau 3

Ainsi, la méthode la plus rationnelle s’est avérée être l’utilisation de la formule de Chebyshev.

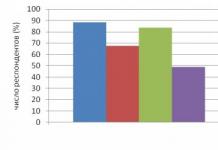
D'après une enquête menée en 11e année, il a été constaté que la formule et le nomogramme de Chebyshev sont des concepts peu familiers aux diplômés en physique et en mathématiques. Estimer les racines d'une équation à l'aide d'un tableau utilisant la propriété de continuité d'une fonction s'est avéré une nouveauté pour 80 % des étudiants.

Ainsi, la capacité de résoudre une équation algébrique incomplète ayant des racines non rationnelles est pertinente et, comme la pratique l'a montré, problématique.

LISTE DES SOURCES ET RÉFÉRENCES UTILISÉES

1. Limite de fonction — Mode d'accès : Wikipedia ru.wikipedia.org (date d'accès 20/07/2018)

Dérivée d'une fonction - Mode d'accès : Wikipediaru.wikipedia.org (date d'accès 20/07/2018)

2. Leçon-jeu "Vainqueur des nombres premiers - P.L. Chebyshev... - Mode d'accès : ouvert lesson.rf (date d'accès 21/07/2018)
3. Akiri I., Garit V. et al. Mathématiques. Manuel pour la 11e année - Chisinau : PrutInternatijnal, 2004, 120-121 p.

I. Klumova « Nomogrammes de points alignés ». Revue scientifique populaire "Quantum", n° 9 1978

Résolution d'équations gratuitement - Calculatrice en ligne Équations ordinaires Expressions simplifiantes - Mode d'accès : kontrolnaya-rabota.ru (date d'accès 19/07/2018)

Explique comment résoudre des équations cubiques. Le cas où une racine est connue est considéré. Méthodes pour trouver des racines entières et rationnelles. Application des formules de Cardano et Vieta pour résoudre n'importe quelle équation cubique.

Contenu

Nous considérons ici la résolution d'équations cubiques de la forme
(1) .
Ensuite, nous supposons qu’il s’agit de nombres réels.

(2) ,
puis en le divisant par , on obtient une équation de la forme (1) à coefficients
.

L'équation (1) a trois racines : , et . L'une des racines est toujours réelle. Nous désignons la vraie racine par . Les racines peuvent être réelles ou complexes conjuguées. Les vraies racines peuvent être multiples. Par exemple, si , alors et sont des racines doubles (ou des racines multiples de 2), et est une racine simple.

Si une racine est connue

Connaissons une racine de l’équation cubique (1). Désignons la racine connue par . En divisant ensuite l’équation (1) par , nous obtenons une équation quadratique. En résolvant l'équation quadratique, nous trouvons deux autres racines et .

Pour le prouver, nous utilisons le fait qu’un polynôme cubique peut être représenté comme suit :
.
Ensuite, en divisant (1) par , nous obtenons une équation quadratique.

Des exemples de polynômes diviseurs sont présentés sur la page
"Division et multiplication d'un polynôme par un polynôme avec un coin et une colonne."
La résolution d'équations quadratiques est discutée sur la page
"Racines d'une équation quadratique."

Si une des racines est entière

Si l'équation d'origine est :
(2) ,
et ses coefficients , , , sont des entiers, alors vous pouvez essayer de trouver la racine entière. Si cette équation a une racine entière, alors c'est un diviseur du coefficient. La méthode pour trouver des racines entières consiste à trouver tous les diviseurs du nombre et à vérifier si l'équation (2) est satisfaite pour eux. Si l’équation (2) est satisfaite, alors nous avons trouvé sa racine. Notons-le comme . Ensuite, nous divisons l'équation (2) par . Nous obtenons une équation quadratique. En le résolvant, nous trouvons deux autres racines.

Des exemples de définition de racines entières sont donnés sur la page
Exemples de factorisation de polynômes > > > .

Trouver des racines rationnelles

Si dans l'équation (2) , , , sont des nombres entiers et qu'il n'y a pas de racines entières, alors vous pouvez essayer de trouver des racines rationnelles, c'est-à-dire des racines de la forme , où et sont des nombres entiers.

Pour ce faire, multipliez l'équation (2) par et effectuez la substitution :
;
(3) .
Ensuite, nous recherchons les racines entières de l’équation (3) parmi les diviseurs du terme libre.

Si nous avons trouvé la racine entière de l'équation (3), alors, en revenant à la variable, nous obtenons la racine rationnelle de l'équation (2) :
.

Formules de Cardano et Vieta pour résoudre l'équation cubique

Si nous ne connaissons pas une seule racine et qu’il n’y a pas de racines entières, nous pouvons alors trouver les racines de l’équation cubique à l’aide des formules de Cardano.

Considérons l'équation cubique :
(1) .
Faisons une substitution :
.
Après cela, l'équation est réduite à une forme incomplète ou réduite :
(4) ,
Où
(5) ; .

Les références:
DANS. Bronstein, KA (2004). Semendyaev, Manuel de mathématiques pour ingénieurs et étudiants, « Lan », 2009.
G. Korn, Manuel de mathématiques pour les scientifiques et les ingénieurs, 2012.

L'utilisation d'équations est répandue dans nos vies. Ils sont utilisés dans de nombreux calculs, construction de structures et même dans le sport. L’homme utilisait des équations dans l’Antiquité et depuis lors, leur utilisation n’a fait que croître. L'équation cubique est une équation du troisième ordre et a la forme suivante :

\ où \ Nombre \ est appelé la racine d'une équation cubique si, en la substituant, l'équation se transforme en une vraie égalité.

Ce type d'équation a toujours 3 racines. Les racines peuvent être réelles ou complexes. Si les données initiales vous permettent de sélectionner l'une des racines de l'équation cubique \ alors vous pouvez diviser le polynôme cubique par \[(x - x1)\] et résoudre l'équation quadratique résultante.

Supposons qu’on nous donne une équation de la forme :

Pour résoudre, regroupons :

Après avoir analysé l'équation, il est clair que \ est la racine de l'équation

Trouvons les racines du trinôme quadratique résultant \

Nous obtenons la réponse : \

Où puis-je résoudre une équation du 3ème degré à l’aide d’un solveur en ligne ?

Vous pouvez résoudre l’équation sur notre site https://site. Le solveur en ligne gratuit vous permettra de résoudre des équations en ligne de toute complexité en quelques secondes. Tout ce que vous avez à faire est simplement de saisir vos données dans le solveur. Vous pouvez également regarder des instructions vidéo et apprendre à résoudre l'équation sur notre site Web. Et si vous avez encore des questions, vous pouvez les poser dans notre groupe VKontakte http://vk.com/pocketteacher. Rejoignez notre groupe, nous sommes toujours heureux de vous aider.

Dans une équation cubique, l'exposant le plus élevé est 3, une telle équation a 3 racines (solutions) et a la forme . Certaines équations cubiques ne sont pas si faciles à résoudre, mais si vous utilisez la bonne méthode (avec une bonne base théorique), vous pouvez trouver les racines même de l'équation cubique la plus complexe - pour ce faire, utilisez la formule de résolution d'une équation quadratique, trouver des racines entières ou calculer le discriminant.

Pas

Comment résoudre une équation cubique sans terme libre

Découvrez si une équation cubique a un terme explicatif d (style d'affichage d) . L'équation cubique a la forme a x 3 + b x 2 + c x + d = 0 (\displaystyle ax^(3)+bx^(2)+cx+d=0). Pour qu'une équation soit considérée comme cubique, il suffit qu'elle contienne uniquement le terme x 3 (\style d'affichage x^(3))(c'est-à-dire qu'il se peut qu'il n'y ait aucun autre membre).

Sortie du support X (style d'affichage x) . Puisqu'il n'y a pas de terme libre dans l'équation, chaque terme de l'équation comprend une variable x (style d'affichage x). Cela signifie que l'un x (style d'affichage x) peut être retiré des parenthèses pour simplifier l’équation. Ainsi, l’équation s’écrira ainsi : x (a x 2 + b x + c) (\displaystyle x(ax^(2)+bx+c)).

Factorisez (le produit de deux binômes) l'équation quadratique (si possible). De nombreuses équations quadratiques de la forme a x 2 + b x + c = 0 (\displaystyle ax^(2)+bx+c=0) peut être factorisé. Cette équation sera obtenue si l'on retire x (style d'affichage x) hors parenthèses. Dans notre exemple :

Résolvez une équation quadratique en utilisant une formule spéciale. Faites cela si l'équation quadratique ne peut pas être prise en compte. Pour trouver deux racines d'une équation, les valeurs des coefficients une (\style d'affichage a), b (style d'affichage b), c (style d'affichage c) remplacer dans la formule.

• Dans notre exemple, substituez les valeurs des coefficients une (\style d'affichage a), b (style d'affichage b), c (style d'affichage c) (3 (style d'affichage 3), − 2 (\style d'affichage -2), 14 (style d'affichage 14)) dans la formule : − b ± b 2 − 4 une c 2 une (\displaystyle (\frac (-b\pm (\sqrt (b^(2)-4ac)))(2a))) − (− 2) ± ((− 2) 2 − 4 (3) (14) 2 (3) (\displaystyle (\frac (-(-2)\pm (\sqrt (((-2)^(2 )-4(3)(14))))(2(3)))) 2 ± 4 − (12) (14) 6 (\displaystyle (\frac (2\pm (\sqrt (4-(12)(14))))(6))) 2 ± (4 − 168 6 (\displaystyle (\frac (2\pm (\sqrt ((4-168)))(6))) 2 ± − 164 6 (\displaystyle (\frac (2\pm (\sqrt (-164)))(6)))
• Première racine : 2 + − 164 6 (\displaystyle (\frac (2+(\sqrt (-164)))(6))) 2 + 12 , 8 je 6 (\displaystyle (\frac (2+12,8i)(6)))
• Deuxième racine : 2 − 12 , 8 je 6 (\displaystyle (\frac (2-12,8i)(6)))

1. Utilisez le zéro et les racines d'une équation quadratique comme solutions à une équation cubique. Les équations quadratiques ont deux racines, tandis que les équations cubiques en ont trois. Vous avez déjà trouvé deux solutions : ce sont les racines de l’équation quadratique. Si vous retiriez « x » entre parenthèses, la troisième solution serait .

   Comment trouver des racines entières à l'aide de facteurs

   1. Assurez-vous qu'il y a une intersection dans l'équation cubique d (style d'affichage d) . Si dans une équation de la forme a x 3 + b x 2 + c x + d = 0 (\displaystyle ax^(3)+bx^(2)+cx+d=0) avoir un membre gratuit ré (style d'affichage d)(qui n’est pas zéro), mettre « x » entre parenthèses ne fonctionnera pas. Dans ce cas, utilisez la méthode décrite dans cette section.

      Notez les facteurs de coefficient un (style d'affichage a) et membre gratuit d (style d'affichage d) . Autrement dit, trouvez les facteurs du nombre lorsque x 3 (\style d'affichage x^(3)) et les nombres avant le signe égal. Rappelez-vous que les facteurs d’un nombre sont les nombres qui, une fois multipliés, produisent ce nombre.

      Divisez chaque facteur un (style d'affichage a) pour chaque multiplicateur d (style d'affichage d) . Le résultat final est un grand nombre de fractions et quelques nombres entiers ; Les racines d’une équation cubique seront l’un des nombres entiers ou la valeur négative de l’un des nombres entiers.

      • Dans notre exemple, divisez les facteurs une (\style d'affichage a) (1 Et 2 ) par facteurs ré (style d'affichage d) (1 , 2 , 3 Et 6 ). Tu auras: 1 (style d'affichage 1), , , , 2 (style d'affichage 2) Et . Ajoutez maintenant les valeurs négatives des fractions et des nombres résultants à cette liste : 1 (style d'affichage 1), − 1 (\style d'affichage -1), 1 2 (\displaystyle (\frac (1)(2))), − 1 2 (\displaystyle -(\frac (1)(2))), 1 3 (\displaystyle (\frac (1)(3))), − 1 3 (\displaystyle -(\frac (1)(3))), 1 6 (\displaystyle (\frac (1)(6))), − 1 6 (\displaystyle -(\frac (1)(6))), 2 (style d'affichage 2), − 2 (\style d'affichage -2), 2 3 (\displaystyle (\frac (2)(3))) Et − 2 3 (\displaystyle -(\frac (2)(3))). Les racines entières d'une équation cubique sont quelques nombres de cette liste.

   2. Remplacez les entiers dans l’équation cubique. Si l'égalité est satisfaite, le nombre substitué est la racine de l'équation. Par exemple, remplacez dans l'équation 1 (style d'affichage 1):

      Utilisez la méthode de division des polynômes par Le plan de Horner pour trouver rapidement les racines de l’équation. Faites cela si vous ne souhaitez pas insérer manuellement des nombres dans l'équation. Dans le schéma de Horner, les nombres entiers sont divisés par les valeurs des coefficients de l'équation une (\style d'affichage a), b (style d'affichage b), c (style d'affichage c) Et ré (style d'affichage d). Si les nombres sont divisibles par un nombre entier (c'est-à-dire que le reste l'est), le nombre entier est la racine de l'équation.

Sans l'aide d'un script, vous devrez effectuer des calculs assez complexes grâce à la méthode Cardano, qui comprend au moins 6 étapes. Le calcul commence par réduire l'équation d'origine à la forme y³ + py + q = 0, etc.

Le calcul d'équations du troisième degré est demandé pour résoudre de nombreux problèmes mathématiques, physiques, statistiques, de recherche et d'ingénierie fondamentaux et appliqués.

Équation du troisième degré en ligne

L'équation cubique ressemble à :

$$ x^3 + a \cdot x^2 + b \cdot x +c =0 $$

où a, b, c sont des coefficients numériques pour x.

x est une variable dont la valeur, transformant le polynôme cubique en identité, sera la racine de l'équation cubique.

Afin de résoudre une équation cubique en ligne, vous devez définir les coefficients de l'équation un par un.

Une équation cubique peut avoir trois racines réelles, ou une (ou deux pour le cas dégénéré) et deux racines conjuguées complexes.

L'équation a trois racines réelles si $$R^2< Q^3$$

$$ R $$ se trouve à l'aide de la formule suivante :

$$ Q $$ peut être trouvé en utilisant la formule :

Si $$R^2< Q^3 $$ , то уравнение имеет три действительных корня:

Si $$ R^2 >= Q^3 $$ , alors l'équation a une racine réelle (ou deux, pour les cas dégénérés) et deux conjugués complexes :

Fonction y = x³ et son graphique

Faisons un tableau des valeurs de la fonction y = x 3 : On voit que pour x > 0 et y > 0 (le cube d'un nombre positif est positif), et pour x< 0 и y < 0 (куб отрицательного числа отрицателен). Следовательно, график расположится на координатной плоскости в I и III четвертях. Заменим значение аргумента x противоположным значением –x , тогда и функция примет противоположное значение; так как если y = x 3 , то

Cela signifie que chaque point (x; y) du graphe correspond à un point (–x; –y) du même graphe, situé symétriquement par rapport à l'origine.

Ainsi, l’origine est le centre de symétrie du graphique.

Le graphique de la fonction y = x 3 est représenté sur la figure 81. Cette ligne est appelée parabole cubique.

Au premier trimestre, la parabole cubique (à x > 0) monte « fortement » vers le haut (la valeur y augmente « rapidement » à mesure que x augmente, voir tableau) ; à de petites valeurs de x, la ligne se rapproche « de près » de la axe des x (aux valeurs « petites » x, la valeur y est « très petite », voir tableau). Le côté gauche de la parabole cubique (au troisième quart) est symétrique au côté droit par rapport à l'origine.

Un graphique bien dessiné peut servir à approximer des cubes de nombres. Ainsi, par exemple, en mettant x = 1,6, on trouve sur le graphique y ≈ 4,1.

Pour le calcul approximatif des cubes, des tableaux spéciaux ont été établis.

Un tel tableau est également disponible dans le manuel de V. M. Bradis « Tableaux mathématiques à quatre chiffres ».

Ce tableau contient des cubes approximatifs de nombres de 1 à 10, arrondis à 4 chiffres significatifs.

La structure de la table cubique et les règles d'utilisation sont les mêmes que celles de la table carrée. Cependant, lorsqu'un nombre augmente (ou diminue) de 10, 100, etc. fois, son cube augmente (ou diminue) de 1000, etc. Cela signifie que lorsque vous utilisez une table de cubes, vous devez garder à l'esprit la règle suivante de retour à la ligne par des virgules :

Si dans un nombre vous déplacez la virgule de plusieurs chiffres, alors dans le cube de ce nombre, vous devez déplacer la virgule dans la même direction du triple du nombre de chiffres.

Expliquons cela avec des exemples :

1) Calculez 2,2353. D'après le tableau, nous trouvons : 2,233 ≈ 11,09 ; on ajoute au dernier chiffre une correction de 8 pour le dernier chiffre : 2,2353 ≈ 11,17.

2) Calculer (–179,8) 3 . Puisque (–a) 3 = –a 3, on trouve (179,8) 3.

En utilisant le tableau, on trouve 1,798 3 ≈ 5,813, en déplaçant la virgule décimale, on obtient 179,8 3 ≈.

Cela signifie (–179,8) 3 ≈ –.

Formules approximatives. Si en identité

(1 ± α)³ ≈ 1 ± 3α ± 3α² ± α³

le nombre α est petit par rapport à l'unité, alors en écartant les termes avec α² et α³, on obtient des formules approximatives :

En utilisant ces formules, il est facile de trouver des cubes approximatifs de nombres proches de un, par exemple :

1,02³ ≈ 1 + 3 * 0,02 = 1,06 ; cube exact : 1,061208 ;

1,03³ ≈ 1 + 3 * 0,03 = 1,09 ; cube exact : 1,092727 ;

0,98³ ≈ 1 – 3 * 0,02 = 0,94 ; cube exact : 0,941192 ;

0,97³ ≈ 1 – 3 * 0,03 = 0,91 ; cube exact : 0,912673.

Numéros de cube sur une règle. Pour les nombres cubiques, il y a une échelle cubique K sur le corps de la règle. L'échelle du cube se compose de trois parties : gauche, milieu et droite (voir dessin 82) ; chacune de ces parties représente l'échelle D principale, mais réduite d'un facteur trois.

Nous marquons la valeur du nombre au cube avec un viseur sur l'échelle principale D et lisons le résultat sur l'échelle du cube K.

Par exemple, 2³ = 8 (voir schéma 39).

Plusieurs exemples de nombres au cube sont donnés dans le tableau suivant. A titre de comparaison, les valeurs des cubes des mêmes nombres, calculées à partir de tableaux à quatre chiffres, sont données.

Résolution d'équations cubiques.

Toute équation cubique à coefficients réels a au moins une racine réelle, les deux autres sont également réelles ou constituent une paire conjuguée complexe.

Commençons l'examen par les cas les plus simples - binôme Et consignééquations. Ensuite, nous passons à la recherche de racines rationnelles (le cas échéant). Terminons par un exemple de recherche des racines d'une équation cubique en utilisant La formule de Cardano pour le cas général.

Navigation dans les pages.

Résoudre une équation cubique à deux termes.

L'équation cubique binomiale a la forme.

Cette équation est réduite à la forme en divisant par un coefficient A non nul. Ensuite, appliquez la formule de multiplication abrégée de la somme des cubes :

À partir de la première parenthèse, nous trouvons que le trinôme carré n'a que des racines complexes.

Trouvez les vraies racines de l’équation cubique.

Nous appliquons la formule de multiplication abrégée de la différence de cubes :

À partir de la première parenthèse, nous constatons que le trinôme carré de la deuxième parenthèse n’a pas de racines réelles, puisque son discriminant est négatif.

Résoudre l'équation cubique réciproque.

L'équation cubique réciproque a la forme où A et B sont des coefficients.

Évidemment, x = -1 est la racine d'une telle équation, et les racines du trinôme quadratique résultant peuvent facilement être trouvées grâce au discriminant.

Résolvez l’équation cubique.

Il s'agit d'une équation réciproque. Regroupons :

Évidemment, x = -1 est la racine de l'équation.

Trouver les racines du trinôme quadratique :

Résoudre des équations cubiques avec des racines rationnelles.

Commençons par le cas le plus simple, lorsque x=0 est la racine de l'équation cubique.

Dans ce cas, le terme libre D est égal à zéro, c'est-à-dire que l'équation a la forme.

Si nous retirons x des parenthèses, alors un trinôme carré restera entre parenthèses, dont les racines peuvent être facilement trouvées soit par le discriminant, soit par le théorème de Vieta.

Trouvez les vraies racines de l’équation.

x=0 est la racine de l'équation. Trouvons les racines du trinôme quadratique.

Puisque son discriminant est inférieur à zéro, le trinôme n’a pas de véritables racines.

Si les coefficients d’une équation cubique sont des nombres entiers, alors l’équation peut avoir des racines rationnelles.

Quand, multipliez les deux côtés de l'équation par et changez les variables y = Ax :

Nous sommes arrivés à l’équation cubique donnée. Il peut avoir des racines entières, qui sont des diviseurs du terme libre. Nous notons donc tous les diviseurs et commençons à les substituer dans l’équation résultante jusqu’à obtenir une égalité identique. Le diviseur auquel l'identité est obtenue est la racine de l'équation. La racine de l’équation originale est donc.

Trouvez les racines de l'équation cubique.

Transformons l'équation comme ci-dessus : multipliez par les deux côtés et changez la variable y = 2x.

La durée libre est de 36 ans. Notons tous ses diviseurs : .

On les substitue tour à tour en égalité jusqu'à obtenir une identité :

Donc y = -1 est la racine. Cela lui va bien.

Il ne reste plus qu'à trouver les racines du trinôme quadratique.

Évidemment, sa racine multiple est x=3.

Cet algorithme peut être utilisé pour résoudre des équations réciproques. Puisque -1 est la racine de toute équation cubique réciproque, nous pouvons diviser le côté gauche de l’équation originale par x+1 et trouver les racines du trinôme quadratique résultant.

Dans le cas où l'équation cubique n'a pas de racines rationnelles, d'autres méthodes de résolution sont utilisées, par exemple des méthodes spécifiques de factorisation du polynôme.

Résoudre des équations cubiques à l'aide de la formule de Cardano.

En général, les racines d’une équation cubique se trouvent à l’aide de la formule de Cardano.

Trouvez les valeurs de l'équation cubique. Ensuite, nous trouvons et.

Nous substituons les p et q résultants dans la formule de Cardano :

Les valeurs des racines cubiques doivent être prises telles que leur produit soit égal. En conséquence, nous trouvons les racines de l'équation originale à l'aide de la formule.

Résolvons l'exemple précédent en utilisant la formule de Cardano.

Comment résoudre des équations cubiques

Les équations cubiques ont la forme hache 3 + bx 2 + CX + d= 0. La méthode pour résoudre de telles équations est connue depuis plusieurs siècles (elle a été découverte au XVIe siècle par des mathématiciens italiens). Certaines équations cubiques sont assez difficiles à résoudre, mais avec la bonne approche (et un bon niveau de connaissances théoriques), vous pouvez résoudre même les équations cubiques les plus difficiles.

Étapes Modifier

Méthode 1 sur 3 :

Solution utilisant la formule pour résoudre une équation quadratique Modifier

Méthode 2 sur 3 :

Trouver des solutions entières à l'aide de la factorisation Modifier

Équations cubiques

où \(a\ne 0,\ b,\ c,\ d\) sont des nombres.

Une équation cubique a toujours au moins une racine \(x_1\) .

Cela signifie que ce qui suit est toujours satisfait : \(ax^3+bx^2+cx+d=a(x-x_1)(x^2+mx+n)\) , où \(m, n\) sont quelques chiffres.

pour tout nombre \(a\) avoir une seule racine

La solution de l'équation \(x^3=-8\) est \(x=\sqrt=-2\) .

\(>\) Les équations cubiques de la forme \(ax^3+bx^2+cx+d=0\) peuvent dans certains cas être résolues en factorisant le côté gauche.

Résolvez l'équation \(5x^3-x^2-20x+4=0\) .

Regroupons les termes sur le côté gauche et factorisons-les : \[(5x^3-20x)-(x^2-4)=0 \quad \Leftrightarrow \quad 5x(x^2-4)-(x^2 - 4)=0 \quad \Leftrightarrow \quad (x^2-4)(5x-1)=0\]

Alors les racines de cette équation sont \(x_1=-2, x_2=2, x_3=\frac15\) .

Dans certains problèmes, des formules de multiplication abrégées peuvent être utiles :

\(>\) Les équations cubiques de la forme \(ax^3+bx^2+cx+d=0\) dans lesquelles il n'est pas possible de factoriser le côté gauche peuvent être résolues d'une autre manière : sélectionner un rationnel racine, le cas échéant.

Pour ce faire, vous pouvez utiliser les instructions suivantes :

\(\blacktriangleright\) Si la somme est \(a+b+c+d=0\) , alors la racine de l'équation est le nombre \(1\) .

\(\blacktriangleright\) Si \(b+d=a+c\) , alors la racine de l'équation est le nombre \(-1\) .

\(\blacktriangleright\) Soit \(a,b,c,d\) des nombres \(>>\). Ensuite, si l'équation a une racine rationnelle \(\large >\) , alors ce qui suit sera vrai pour elle :

\(d\) est divisible par \(p\) ; \(a\) est divisible par \(q\) .

1. L'équation \(7x^3+3x^2-x-9=0\) a une somme de coefficients égale à \(7+3-1-9=0\), ce qui signifie \(x=1\ ) est la racine (pas nécessairement la seule) de cette équation.

2. L'équation \(4,5x^3-3x^2-0,5x+7=0\) est vraie : \(4,5-0,5=-3+7\), ce qui signifie que \(x= -1\) est le racine de cette équation.

3. L'équation \(2x^3+5x^2+3x-3=0\) a des coefficients qui sont des entiers, vous pouvez donc sélectionner la racine : diviseurs du terme libre \(-3\) : \(\pm 1, \pm 3 \) ; diviseurs du coefficient dominant \(2\) : \(\pm1, \pm2\) . Cela signifie que les combinaisons possibles de racines rationnelles sont : \[\pm 1, \ \pm \dfrac12, \ \pm 3, \ \pm \dfrac32\]

En substituant tour à tour chaque nombre dans l'équation, on s'assure que \(x=\frac12\) est une racine (puisqu'après avoir substitué ce nombre dans l'équation, il se transforme en une vraie égalité) :

Notez que si les coefficients d'une équation sont des nombres rationnels, alors en multipliant l'équation par leur dénominateur commun, nous pouvons obtenir une équation équivalente à coefficients entiers. Par exemple, l'équation \(\frac12x^3+\frac16x+2=0\) après multiplication par \(6\) se réduit à une équation à coefficients entiers : \(3x^3+x+12=0\) .

Trouvez la racine de l'équation \((2x + 1)^3 = 27\) . Si une équation a plus d’une racine, notez la plus grande dans votre réponse.

L'équation originale \((2x + 1)^3 = 3^3\) est de forme standard, elle est équivalente à l'équation \(2x + 1 = 3\), d'où on conclut que \(x = 1\ ) convient selon l'ODZ.

Trouvez la racine de l'équation \((2x + 1)^3 = -27\) . Si une équation a plus d’une racine, notez la plus grande dans votre réponse.

ODZ : \(x\) – arbitraire. Décidons d'ODZ :

L'équation originale \((2x + 1)^3 = (-3)^3\) est de forme standard, elle est équivalente à l'équation \(2x + 1 = -3\), de laquelle on conclut que \( x = -2\) – Convient pour ODZ.

Trouvez la racine de l'équation \((3x + 2)^3 = -64\) . Si une équation a plus d’une racine, notez la plus grande dans votre réponse.

ODZ : \(x\) – arbitraire. Décidons d'ODZ :

L'équation originale \((3x + 2)^3 = (-4)^3\) est de forme standard, elle est équivalente à l'équation \(3x + 2 = -4\), de laquelle on conclut que \( x = -2\) – Convient pour ODZ.

Trouvez la racine de l'équation \((7x + 11)^3 = 64\) . Si une équation a plus d’une racine, notez la plus grande dans votre réponse.

ODZ : \(x\) – arbitraire. Décidons d'ODZ :

L'équation originale \((7x + 11)^3 = 4^3\) est de forme standard, elle est équivalente à l'équation \(7x + 11 = 4\), d'où on conclut que \(x = -1 \) convient selon l'ODZ.

Trouvez la racine de l'équation \((-x - 11)^3 = 216\) . Si une équation a plus d’une racine, notez la plus grande dans votre réponse.

ODZ : \(x\) – arbitraire. Décidons d'ODZ :

L'équation originale \((-x - 11)^3 = 6^3\) est de forme standard, elle est équivalente à l'équation \(-x - 11 = 6\), dont on conclut que \(x = -17\) convient à ODZ.

Résolvez l'équation \(8x^3-36x^2+54x-27=0\) .

Notez que le côté gauche est un cube de la différence : \[(2x)^3-3\cdot (2x)^2\cdot 3+3\cdot (2x)\cdot3^2-3^3=0\quad \ Leftrightarrow\quad (2x-3)^3=0\quad\Leftrightarrow\quad x=\frac32.\]

Trouvez la plus grande racine de l'équation \(8x^3+12x^2+6x+1=0\) .

Notez que le côté gauche est le cube de la somme : \[(2x)^3+3\cdot (2x)^2\cdot 1+3\cdot (2x)\cdot1^2+1^3=0\quad \ Leftrightarrow\quad (2x+1)^3=0\quad\Leftrightarrow\quad x=-\frac12.\]

Dans l'examen d'État unifié, les équations cubiques se retrouvent à la fois au niveau du profil et au niveau de base. Cela signifie que chaque étudiant doit être capable de résoudre correctement ces tâches. Certains diront peut-être que le nombre de points à l'examen d'État unifié pour résoudre des équations du troisième degré est faible et que cela ne vaut pas la peine d'y consacrer du temps. Il est difficile d'être d'accord avec cela. Premièrement, chaque point de l'examen d'État unifié est extrêmement important, et deuxièmement, les équations du troisième degré ne sont pas si compliquées si vous y prêtez toute l'attention nécessaire lors de la préparation. Pour que l'étudiant puisse accomplir rapidement et, surtout, correctement ces tâches, il vaut la peine d'utiliser notre ressource pédagogique.

"Shkolkovo" est une plate-forme unique qui permet aux diplômés de Moscou et d'autres régions ayant n'importe quel niveau de connaissances mathématiques d'apprendre à résoudre des équations cubiques et de se préparer efficacement à l'examen d'État unifié. Tout d'abord, nous vous recommandons de commencer par réviser ou étudier du matériel théorique sur ce sujet. "Shkolkovo" présente à l'attention des étudiants de Moscou et d'autres villes qui se préparent à l'examen d'État unifié, en fait, le manuel de l'auteur, qui présente de manière claire et accessible des documents sur le thème "Équations cubiques".

En plus de présenter des définitions et des formules de base, vous pourrez vous familiariser avec des exemples sur le sujet et apprendre à les résoudre. A noter que nos spécialistes ont sélectionné des options très intéressantes. Pour que vous appreniez à résoudre les problèmes d’examen en toute confiance, vous avez besoin d’une formation. Par conséquent, nous vous recommandons d’aller ensuite dans la section « Catalogue » et de commencer à travailler de manière indépendante avec des équations du troisième degré.

X à la troisième puissance

La fonction est égale à x au cube

Propriétés de la fonction i est égale à x au cube

La fonction égale à x au cube a les propriétés suivantes :

2. La fonction y est égale à x augmente au cube sur toute la droite numérique ;

3. Le domaine de définition de la fonction y = x 3 est la droite numérique entière ;

4. L'ensemble des valeurs de la fonction y = x 3 est la droite numérique entière.

Le graphique de la fonction i est égal à x au cube

Le graphique de la fonction y = x 3 est appelé une parabole cubique :

Vous pouvez construire vous-même un graphique de la fonction y = x 3 dès maintenant à l'aide d'un générateur de graphiques. Dans celui-ci, sélectionnez le type de fonction « Puissance : y = k * x n + b », précisez la valeur « n » égale à trois et cliquez sur le bouton « Construire un graphique ».

La fonction y = x 3 est un cas particulier de fonction puissance.

Ce sont les propriétés et le graphique de la fonction i est égal à x au cube.

Équation cubique

Résoudre une équation cubique en utilisant la formule de Vieta. Créé à la demande de l'utilisateur.

Forme canonique de l'équation cubique :

Nous allons résoudre l'équation cubique en utilisant la formule de Vieta.

La formule de Vieta est une méthode pour résoudre une équation cubique de la forme

La calculatrice est ci-dessous et la description de la formule de Vieta est en dessous

Équation cubique

À propos, pour une raison quelconque, d'autres sites utilisent la formule de Cardano pour résoudre des équations cubiques, mais je suis d'accord avec Wikipédia sur le fait que la formule de Vieta est plus pratique pour une utilisation pratique. Alors pourquoi la formule de Cardano est partout n'est pas clair, à moins que les gens ne soient trop paresseux pour implémenter des fonctions hyperboliques et des fonctions hyperboliques inverses. Eh bien, je n'étais pas paresseux.

Donc, la formule de Vieta (de Wikipédia)

Veuillez noter que selon la représentation de la formule Vieta, a est le deuxième coefficient, et le coefficient avant x3 est toujours considéré comme égal à 1. La calculatrice vous permet de saisir a comme coefficient avant x3, mais divise immédiatement l'équation par celui-ci. pour en avoir 1

Si S > 0, alors on calcule :

Si S< 0, то заменяем тригонометрические функции гиперболическими. Здесь возможны два случая в зависимости от знака Q

(paire de racines complexes)

(paire de racines complexes)

Si S = 0, alors l'équation est dégénérée et a moins de 3 solutions différentes (racine seconde de multiplicité 2) :

La calculatrice fonctionne en utilisant ces formules. Cela semble se résoudre correctement, même si je n’ai pas vérifié les solutions avec la partie imaginaire. Si quoi que ce soit, écrivez.

Racines et degrés

Degré

Un diplôme est une expression de la forme : , où :

Définissons la notion de degré dont l'exposant est un nombre naturel (c'est-à-dire entier et positif).

1. A-prieuré : .
2. Mettre un nombre au carré signifie le multiplier par lui-même :
3. Cuber un nombre signifie le multiplier par lui-même trois fois : .

Élever un nombre à une puissance naturelle signifie multiplier le nombre par lui-même par :

Diplôme avec un exposant entier

Si l'exposant est un entier positif :

Montée à la puissance zéro :

Si l'exposant est un entier négatif :

Remarque : l'expression n'est pas définie dans le cas de n ≤ 0. Si n > 0, alors

Puissance avec exposant rationnel

Propriétés des diplômes

Racine

L'équation a deux solutions : x=2 et x=-2. Ce sont des nombres dont le carré est 4.

Considérez l'équation. Traçons un graphique de la fonction et voyons que cette équation a également deux solutions, l'une positive, l'autre négative.

Mais dans ce cas, les solutions ne sont pas des nombres entiers. De plus, ils ne sont pas rationnels. Afin d’écrire ces décisions irrationnelles, nous introduisons un symbole spécial de racine carrée.

Une racine carrée arithmétique est un nombre non négatif dont le carré est égal à a ≥ 0. Lorsqu'un< 0 - выражение не определено, т.к. нет такого действительного числа, квадрат которого равен отрицательному числу.

Racine carrée

Par exemple, . Et les solutions de l'équation, respectivement, et

racine cubique

La racine cubique d'un nombre est le nombre dont le cube est égal. La racine cubique est définie pour tout le monde. Il peut être extrait de n'importe quel nombre : .

nième racine

La racine ième d’un nombre est le nombre dont la puissance ième est égale.

• Alors si un< 0 корень n-ой степени из a не определен.
• Ou si a ≥ 0, alors la racine non négative de l'équation est appelée la nième racine arithmétique de a et est notée

• L’équation a alors une racine unique pour chaque équation.

Racines et degrés

Un diplôme est une expression de la forme.

Ici - la base du degré, - l'exposant.

Diplôme avec indicateur naturel

Le moyen le plus simple de déterminer un degré consiste à utiliser un exposant naturel (c'est-à-dire un entier positif).

Les expressions « carré » et « cube » nous sont familières depuis longtemps.

Mettre un nombre au carré signifie le multiplier par lui-même.

Cuber un nombre signifie le multiplier par lui-même trois fois.

Élever un nombre à une puissance naturelle revient à le multiplier par lui-même par :

Diplôme avec un exposant entier

L'exposant peut être non seulement un nombre naturel (c'est-à-dire un entier positif), mais également égal à zéro, ainsi qu'un entier négatif.

C'est vrai pour. L'expression n'est pas définie.

Définissons également ce qu'est un degré avec un exposant entier négatif.

Bien sûr, tout cela est vrai, puisqu’on ne peut pas diviser par zéro.

Notez que lorsqu’elle est élevée à la puissance première négative, la fraction est inversée.

L'exposant peut être non seulement un nombre entier, mais aussi une fraction, c'est-à-dire un nombre rationnel. Dans l'article « Ensembles numériques », nous avons expliqué ce que sont les nombres rationnels. Ce sont des nombres qui peuvent être écrits sous forme de fraction, où - est un nombre entier - est un nombre naturel.

Ici, nous avons besoin d’un nouveau concept : la racine du diplôme. Les racines et les diplômes sont deux sujets interdépendants. Commençons par la racine carrée arithmétique déjà familière.

Racine carrée arithmétique

L'équation a deux solutions : et.

Ce sont des nombres dont le carré est égal à.

Comment résoudre l'équation ?

Si nous dessinons un graphique de la fonction, nous verrons que cette équation a également deux solutions, dont l’une est positive et l’autre négative.

Mais ces solutions ne sont pas des nombres entiers. De plus, ils ne sont pas rationnels. Pour écrire ces solutions, nous introduisons un symbole spécial de racine carrée.

La racine carrée arithmétique d'un nombre est un nombre non négatif dont le carré est égal à.

Rappelez-vous cette définition.

La racine carrée arithmétique est notée.

1) La racine carrée ne peut être extraite que de nombres non négatifs

2) L'expression est toujours non négative. Par exemple, .

Listons les propriétés de la racine carrée arithmétique :

N'oubliez pas que l'expression n'est pas égale. Facile à vérifier :

J'ai eu une réponse différente.

racine cubique

De même, la racine cubique de est un nombre qui, élevé à la puissance trois, donne un nombre.

Par exemple, depuis ;

Notez que la troisième racine peut être extraite de nombres positifs et négatifs.

Nous pouvons maintenant définir le degré racine de n’importe quel entier.

Racine du nième degré

La racine ième d’un nombre est le nombre qui, lorsqu’il est élevé à la puissance ième, produit un nombre.

Notez que la racine troisième, cinquième, neuvième - en un mot, n'importe quel degré impair - peut être extraite à la fois de nombres positifs et négatifs.

La racine carrée, ainsi que la quatrième, la dixième et en général toute puissance paire, ne peuvent être extraites qu'à partir de nombres non négatifs.

Donc, - un tel nombre. Il s’avère que les racines peuvent être écrites sous forme de puissances avec un exposant rationnel. C'est confortable.

Convenons tout de suite que la base du diplôme est plus grande.

Une expression par définition est égale.

Dans ce cas, la condition la plus élevée est également satisfaite.

Rappelons les règles de gestion des diplômes :

En multipliant les degrés, les exposants s'additionnent

Lors de la division par degré, les exposants sont soustraits

Lorsqu'on élève une puissance à une puissance, les exposants sont multipliés

Montrons comment ces formules sont utilisées dans les tâches de l'examen d'État unifié en mathématiques :

Nous avons tout mis sous la racine commune, l'avons factorisé, réduit la fraction et extrait la racine.

Ici, nous avons écrit les racines sous forme de puissances et utilisé des formules pour les opérations avec puissances.

Appelez-nous : (appel gratuit en Russie) (appel gratuit à Moscou)

Ou cliquez sur le bouton « En savoir plus » pour remplir le formulaire de contact. Nous vous rappellerons certainement.

Appelez maintenant et nous vous offrirons une réduction de 25 % sur votre premier mois de cours ! Appel:

Pour un fonctionnement normal et votre commodité, le site utilise des cookies. Il s'agit d'une pratique tout à fait normale. En continuant à utiliser le portail, vous acceptez notre politique de confidentialité.