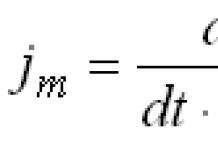Loi normale La distribution (souvent appelée loi de Gauss) joue un rôle extrêmement important dans la théorie des probabilités et occupe une position particulière parmi les autres lois de distribution. Il s’agit de la loi de répartition la plus fréquemment rencontrée en pratique. La principale caractéristique qui distingue la loi normale des autres lois est qu'il s'agit d'une loi limitative, à laquelle se rapprochent d'autres lois de distribution dans des conditions typiques très courantes.

On peut prouver que la somme d'un nombre suffisamment grand de variables aléatoires indépendantes (ou faiblement dépendantes), soumises à des lois de distribution (sous réserve de certaines restrictions très lâches), obéit approximativement à la loi normale, et cela est vrai d'autant plus précisément que grande quantité les variables aléatoires sont résumées. La plupart des variables aléatoires rencontrées dans la pratique, comme par exemple les erreurs de mesure, les erreurs de tir, etc., peuvent être représentées comme la somme d'un très grand nombre de termes relativement petits - erreurs élémentaires, dont chacune est provoquée par un cause distincte, indépendante des autres. Quelles que soient les lois de distribution auxquelles sont soumises les erreurs élémentaires individuelles, les caractéristiques de ces distributions dans la somme d'un grand nombre de termes sont nivelées, et la somme s'avère soumise à une loi proche de la normale. La principale limite imposée aux erreurs totalisables est qu’elles jouent toutes un rôle relativement faible dans le total. Si cette condition n'est pas remplie et, par exemple, l'une des erreurs aléatoires s'avère fortement dominante dans son influence sur le montant sur toutes les autres, alors la loi de distribution de cette erreur dominante imposera son influence sur le montant et déterminera son principales caractéristiques du droit de la distribution.

Les théorèmes établissant la loi normale comme limite pour la somme de termes aléatoires indépendants uniformément petits seront discutés plus en détail au chapitre 13.

La loi de distribution normale est caractérisée par une densité de probabilité de la forme :

La courbe de distribution normale a une apparence symétrique en forme de colline (Fig. 6.1.1). L'ordonnée maximale de la courbe, égale à , correspond au point ; À mesure que l'on s'éloigne du point, la densité de distribution diminue, et à , la courbe se rapproche asymptotiquement de l'abscisse.

Découvrons la signification des paramètres numériques et inclus dans l'expression de la loi normale (6.1.1) ; Montrons que la valeur n'est rien de plus qu'une espérance mathématique et que la valeur est l'écart type de la valeur. Pour ce faire, nous calculons les principales caractéristiques numériques de la quantité - espérance mathématique et dispersion.

Utiliser le changement de variable

Il est facile de vérifier que le premier des deux intervalles de la formule (6.1.2) égal à zéro; la seconde est la fameuse intégrale d'Euler-Poisson :

Ainsi,

ceux. le paramètre représente l'espérance mathématique de la valeur. Ce paramètre, notamment dans les problèmes de tir, est souvent appelé centre de dispersion (en abrégé c.r.).

Calculons la variance de la quantité :

.

Appliquer à nouveau le changement de variable

En intégrant par parties, on obtient :

Le premier terme entre accolades est égal à zéro (puisque à diminue plus vite que toute puissance augmente), le deuxième terme selon la formule (6.1.3) est égal à , d'où

Par conséquent, le paramètre de la formule (6.1.1) n’est rien de plus que l’écart type de la valeur.

Découvrons la signification des paramètres et de la distribution normale. Il ressort immédiatement de la formule (6.1.1) que le centre de symétrie de la distribution est le centre de dispersion. Cela ressort clairement du fait que lorsque le signe de la différence est inversé, l’expression (6.1.1) ne change pas. Si vous modifiez le centre de dispersion, la courbe de distribution se déplacera le long de l'axe des abscisses sans changer de forme (Fig. 6.1.2). Le centre de dispersion caractérise la position de la distribution sur l'axe des abscisses.

La dimension du centre de diffusion est la même que la dimension de la variable aléatoire.

Le paramètre caractérise non pas la position, mais la forme même de la courbe de distribution. C'est la caractéristique de la dispersion. La plus grande ordonnée de la courbe de distribution est inversement proportionnelle à : à mesure que vous augmentez, l'ordonnée maximale diminue. Puisque l'aire de la courbe de distribution doit toujours rester égale à l'unité, lorsqu'elle augmente, la courbe de distribution devient plus plate, s'étirant le long de l'axe des x ; au contraire, avec une diminution, la courbe de distribution s'étire vers le haut, se comprimant simultanément sur les côtés, et prend davantage la forme d'une aiguille. En figue. 6.1.3 montre trois courbes normales (I, II, III) en ; parmi celles-ci, la courbe I correspond à la plus grande valeur et la courbe III à la plus petite valeur. Changer le paramètre équivaut à changer l'échelle de la courbe de distribution - augmenter l'échelle le long d'un axe et la même diminuer le long de l'autre.

La théorie des probabilités considère un assez grand nombre de lois de distribution différentes. Pour résoudre des problèmes liés à la construction de cartes de contrôle, seuls quelques-uns d’entre eux sont intéressants. Le plus important d'entre eux est loi de distribution normale, qui est utilisé pour construire les cartes de contrôle utilisées dans contrôle quantitatif, c'est à dire. lorsqu'il s'agit d'une variable aléatoire continue. La loi de distribution normale occupe une place particulière parmi les autres lois de distribution. Cela s'explique par le fait que, d'une part, elle est le plus souvent rencontrée dans la pratique, et, d'autre part, il s'agit d'une loi limitante, à laquelle se rapprochent d'autres lois de distribution dans des conditions typiques très courantes. Quant à la deuxième circonstance, il a été prouvé en théorie des probabilités que la somme d'un nombre suffisamment grand de variables aléatoires indépendantes (ou faiblement dépendantes), soumises à des lois de distribution (sous réserve de certaines restrictions très lâches), obéit approximativement à la loi normale. , et cela est d’autant plus vrai que l’on ajoute davantage de variables aléatoires. La plupart des variables aléatoires rencontrées dans la pratique, comme par exemple les erreurs de mesure, peuvent être représentées comme la somme d'un très grand nombre de termes relativement petits - des erreurs élémentaires, dont chacune est causée par une cause distincte, indépendante de la autres. La loi normale apparaît dans les cas où une variable aléatoire X est le résultat d’un grand nombre de facteurs différents. Chaque facteur séparément vaut X influence légèrement, et il est impossible d’indiquer lequel influence plus que les autres.

Distribution normale(Distribution Laplace – Gaussienne) – distribution de probabilité de continu Variable aléatoire X telle que la densité de distribution de probabilité pour - ¥<х< + ¥ принимает действительное значение:

Exp. (3)

Autrement dit, la distribution normale est caractérisée par deux paramètres m et s, où m est l'espérance mathématique ; s est l'écart type de la distribution normale.

Valeurs 2 est la variance de la distribution normale.

L'espérance mathématique m caractérise la position du centre de distribution et l'écart type s (SD) est une caractéristique de dispersion (Fig. 3).

f(x) f(x)

Figure 3 – Fonctions de densité de distribution normale avec :

a) différentes attentes mathématiques m ; b) différents écarts types s.

Ainsi, la valeur μ déterminé par la position de la courbe de répartition sur l'axe des abscisses. Dimension μ - la même que la dimension de la variable aléatoire X. À mesure que l’espérance mathématique m augmente, les deux fonctions se déplacent parallèlement vers la droite. Avec variance décroissante s 2 la densité se concentre de plus en plus autour de m, tandis que la fonction de distribution devient de plus en plus raide.

La valeur de σ détermine la forme de la courbe de distribution. Puisque l’aire sous la courbe de distribution doit toujours rester égale à l’unité, à mesure que σ augmente, la courbe de distribution devient plus plate. En figue. La figure 3.1 montre trois courbes pour différents σ : σ1 = 0,5 ; σ2 = 1,0 ; σ3 = 2,0.

Figure 3.1 – Fonctions de densité de distribution normale avec différents écarts types s.

La fonction de distribution (fonction intégrale) a la forme (Fig. 4) :

(4)

Figure 4 – Fonctions de distribution normale intégrale (a) et différentielle (b)

La transformation linéaire d'une variable aléatoire normalement distribuée est particulièrement importante. X, après quoi une variable aléatoire est obtenue Z avec une espérance mathématique 0 et une variance 1. Cette transformation est appelée normalisation :

Elle peut être réalisée pour chaque variable aléatoire. La normalisation permet de réduire toutes les variantes possibles de la distribution normale à un seul cas : m = 0, s = 1.

La distribution normale avec m = 0, s = 1 est appelée distribution normale normalisée (standardisée).

Distribution normale standard(distribution Laplace – Gaussienne standard ou distribution normale normalisée) est la distribution de probabilité d'une variable aléatoire normale standardisée Z, dont la densité de répartition est égale à :

à - ¥<z< + ¥

Valeurs de fonction Ф(z) déterminé par la formule :

(7)

Valeurs de fonction Ф(z) et la densité f(z) la distribution normale normalisée est calculée et tabulée. Le tableau est compilé uniquement pour les valeurs positives z C'est pourquoi:

F (–z) = 1–Ф(z) (8)

À l'aide de ces tableaux, vous pouvez déterminer non seulement les valeurs de la fonction et la densité de la distribution normale normalisée pour un z, mais aussi les valeurs de la fonction de distribution normale générale, puisque :

; (9)

. 10)

Dans de nombreux problèmes impliquant des variables aléatoires normalement distribuées, il est nécessaire de déterminer la probabilité d'apparition d'une variable aléatoire. X, soumis à la loi normale avec les paramètres m et s, pour une certaine zone. Une telle section pourrait être, par exemple, le champ de tolérance d'un paramètre à partir de la valeur supérieure U vers le bas L.

Probabilité de se situer dans l'intervalle de X 1 à X 2 peut être déterminé par la formule :

Ainsi, la probabilité de toucher une variable aléatoire (valeur du paramètre) X dans le champ de tolérance est déterminé par la formule

Vous pouvez trouver la probabilité qu'une variable aléatoire X sera dans μ k s . Les valeurs obtenues pour k=1,2 et 3 sont les suivants (voir également Fig. 5) :

Ainsi, si une valeur apparaît en dehors de la région des trois sigma, qui contient 99,73 % de toutes les valeurs possibles, et que la probabilité qu'un tel événement se produise est très faible (1:270), il faut considérer que la valeur en question était trop petit ou trop grand, non pas à cause d'une variation aléatoire, mais à cause d'une perturbation importante dans le processus lui-même, qui peut entraîner des changements dans la nature de la distribution.

La zone située à l’intérieur des limites des trois sigmas est également appelée zone de tolérance statistique machine ou processus concerné.

(réel, strictement positif)

Distribution normale, aussi appelé Distribution gaussienne ou Gauss-Laplace- la distribution de probabilité, qui dans le cas unidimensionnel est spécifiée par la fonction de densité de probabilité coïncidant avec la fonction gaussienne :

où le paramètre μ est l'espérance (valeur moyenne), la médiane et le mode de la distribution, et le paramètre σ est l'écart type (σ² est la dispersion) de la distribution.

Ainsi, la distribution normale unidimensionnelle est une famille de distributions à deux paramètres. Le cas multivarié est décrit dans l'article « Distribution multivariée normale  ».

Distribution normale standard est appelée une distribution normale avec une espérance mathématique μ = 0 et un écart type σ = 1.

YouTube encyclopédique

• 1 / 5

  L'importance de la distribution normale dans de nombreux domaines scientifiques (par exemple, les statistiques mathématiques et la physique statistique) découle du théorème central limite de la théorie des probabilités. Si le résultat d'une observation est la somme de nombreuses quantités aléatoires faiblement interdépendantes, dont chacune apporte une petite contribution par rapport à la somme totale, alors à mesure que le nombre de termes augmente, la distribution du résultat centré et normalisé tend à être normale. Cette loi de la théorie des probabilités aboutit à une distribution généralisée de la distribution normale, ce qui explique en partie son nom.

  Propriétés

  Des moments

  Si des variables aléatoires X 1 (\style d'affichage X_(1)) Et X 2 (\style d'affichage X_(2)) sont indépendants et ont une distribution normale avec des attentes mathématiques μ 1 (\displaystyle \mu _(1)) Et μ 2 (\displaystyle \mu _(2)) et les écarts σ 1 2 (\displaystyle \sigma _(1)^(2)) Et σ 2 2 (\displaystyle \sigma _(2)^(2)) en conséquence, alors X 1 + X 2 (\displaystyle X_(1)+X_(2)) a également une distribution normale avec une espérance mathématique μ 1 + μ 2 (\displaystyle \mu _(1)+\mu _(2)) et écart σ 1 2 + σ 2 2 . (\displaystyle \sigma _(1)^(2)+\sigma _(2)^(2).) Il s’ensuit qu’une variable aléatoire normale peut être représentée comme la somme d’un nombre arbitraire de variables aléatoires normales indépendantes.

  Entropie maximale

  La distribution normale a l'entropie différentielle maximale parmi toutes les distributions continues dont la variance ne dépasse pas une valeur donnée.

  Modélisation de variables pseudo-aléatoires normales

  Les méthodes de modélisation approchée les plus simples sont basées sur le théorème central limite. À savoir, si vous ajoutez plusieurs quantités indépendantes distribuées de manière identique avec une variance finie, alors la somme sera distribuée environ Bien. Par exemple, si vous ajoutez 100 indépendants en standard uniformément variables aléatoires distribuées, alors la distribution de la somme sera approximativement normale.

  Pour la génération programmatique de variables pseudo-aléatoires normalement distribuées, il est préférable d'utiliser la transformation de Box-Muller. Il vous permet de générer une valeur normalement distribuée basée sur une valeur uniformément distribuée.

  Distribution normale dans la nature et les applications

  La distribution normale se retrouve souvent dans la nature. Par exemple, les variables aléatoires suivantes sont bien modélisées par la distribution normale :

  • déviation lors de la prise de vue.
  • erreurs de mesure (cependant, les erreurs de certains instruments de mesure n'ont pas de distribution normale).
  • certaines caractéristiques des organismes vivants dans une population.

  Cette distribution est si répandue car il s’agit d’une distribution continue infiniment divisible à variance finie. Par conséquent, d'autres l'approchent à la limite, par exemple le binôme et Poisson. Cette distribution modélise de nombreux processus physiques non déterministes.

  Relation avec d'autres distributions

  • La distribution normale est une distribution Pearson de type XI.
  • Le rapport d'une paire de variables aléatoires standard indépendantes normalement distribuées a une distribution de Cauchy. Autrement dit, si la variable aléatoire X (style d'affichage X) représente la relation X = Y / Z (\displaystyle X=Y/Z)(Où Oui (\style d'affichage Y) Et Z (style d'affichage Z)- variables aléatoires normales standard indépendantes), alors il aura une distribution de Cauchy.
  • Si z 1 , … , z k (\displaystyle z_(1),\ldots,z_(k))- des variables aléatoires normales standards conjointement indépendantes, c'est-à-dire z je ∼ N (0, 1) (\displaystyle z_(i)\sim N\left(0,1\right)), alors la variable aléatoire x = z 1 2 + … + z k 2 (\displaystyle x=z_(1)^(2)+\ldots +z_(k)^(2)) a une distribution du chi carré avec k degrés de liberté.
  • Si la variable aléatoire X (style d'affichage X) est soumis à une distribution lognormale, alors son logarithme népérien a une distribution normale. Autrement dit, si X ∼ L o g N (μ , σ 2) (\displaystyle X\sim \mathrm (LogN) \left(\mu,\sigma ^(2)\right)), Que Y = ln ⁡ (X) ∼ N (μ , σ 2) (\displaystyle Y=\ln \left(X\right)\sim \mathrm (N) \left(\mu,\sigma ^(2)\right )). Et vice versa, si Oui ∼ N (μ , σ 2) (\displaystyle Y\sim \mathrm (N) \left(\mu,\sigma ^(2)\right)), Que X = exp ⁡ (Y) ∼ L o g N (μ , σ 2) (\displaystyle X=\exp \left(Y\right)\sim \mathrm (LogN) \left(\mu,\sigma ^(2) \droite)).
  • Le rapport des carrés de deux variables aléatoires normales standard a

  Les variables aléatoires sont associées à des événements aléatoires. On parle d'événements aléatoires lorsqu'il s'avère impossible de prédire sans ambiguïté le résultat qui peut être obtenu dans certaines conditions.

  Supposons que nous lançons une pièce de monnaie ordinaire. Habituellement, le résultat de cette procédure n’est pas clairement défini. Nous pouvons seulement dire avec certitude que l’une des deux choses suivantes se produira : soit « pile » soit « face » apparaîtra. Chacun de ces événements sera aléatoire. Vous pouvez introduire une variable qui décrira le résultat de cet événement aléatoire. Évidemment, cette variable prendra deux valeurs discrètes : « pile » et « face ». Puisque nous ne pouvons pas prédire avec précision à l'avance laquelle des deux valeurs possibles cette variable prendra, nous pouvons affirmer que dans ce cas, nous avons affaire à des variables aléatoires.

  Supposons maintenant que, dans une expérience, nous évaluions le temps de réaction d'un sujet lorsqu'il présente un stimulus. En règle générale, il s'avère que même lorsque l'expérimentateur prend toutes les mesures pour normaliser les conditions expérimentales, minimisant ou même éliminant les variations possibles dans la présentation du stimulus, les temps de réaction mesurés du sujet seront toujours différents. Dans ce cas, on dit que le temps de réaction du sujet est décrit par une variable aléatoire. Puisque, en principe, dans une expérience, nous pouvons obtenir n'importe quelle valeur du temps de réaction - l'ensemble des valeurs possibles du temps de réaction qui peuvent être obtenues à la suite de mesures s'avère être infini - nous parlons de continuité cette variable aléatoire.

  La question se pose : existe-t-il des modèles dans le comportement des variables aléatoires ? La réponse à cette question s'avère affirmative.

  Ainsi, si vous lancez un nombre infini de lancers de la même pièce, vous constaterez que le nombre de fois où chacune des deux faces de la pièce apparaît est approximativement le même, à moins, bien sûr, que la pièce ne soit contrefaite ou pliée. Pour souligner ce schéma, le concept de probabilité d’un événement aléatoire est introduit. Il est clair que dans le cas d'un tirage au sort, l'un des deux événements possibles se produira certainement. En effet, la probabilité totale de ces deux événements, autrement appelée probabilité totale, est de 100 %. Si nous supposons que les deux événements associés au test de la pièce se produisent avec des parts de probabilité égales, alors la probabilité de chaque résultat séparément est évidemment égale à 50 %. Ainsi, les réflexions théoriques permettent de décrire le comportement d'une variable aléatoire donnée. Une telle description en statistique mathématique est désignée par le terme "distribution d'une variable aléatoire".

  La situation est plus compliquée avec une variable aléatoire qui n'a pas d'ensemble de valeurs clairement défini, c'est-à-dire s'avère être continue. Mais même dans ce cas, certains modèles importants de son comportement peuvent être notés. Ainsi, lors d’une expérience de mesure du temps de réaction d’un sujet, on peut noter que différents intervalles de la durée de la réaction du sujet sont estimés avec différents degrés de probabilité. Il sera probablement rare qu’un sujet réponde trop rapidement. Par exemple, dans les tâches de décision sémantique, il est pratiquement impossible pour les sujets de répondre plus ou moins précisément à une vitesse inférieure à 500 ms (1/2 s). De même, il est peu probable qu'un sujet qui suit fidèlement les instructions de l'expérimentateur retarde trop sa réponse. Dans les tâches de décision sémantique, par exemple, les réponses dont l’évaluation prend plus de 5 secondes sont généralement considérées comme peu fiables. Néanmoins, nous pouvons supposer avec 100 % de confiance que le temps de réaction du sujet sera compris entre O et +co. Mais cette probabilité est la somme des probabilités de chaque valeur individuelle de la variable aléatoire. Par conséquent, la distribution d’une variable aléatoire continue peut être décrite comme une fonction continue y = f (X ).

  Si nous avons affaire à une variable aléatoire discrète, lorsque toutes ses valeurs possibles sont connues à l'avance, comme dans l'exemple d'une pièce de monnaie, construire un modèle de sa distribution, en règle générale, n'est pas très difficile. Il suffit d'introduire seulement quelques hypothèses raisonnables, comme nous l'avons fait dans l'exemple considéré. La situation est plus compliquée avec la distribution de valeurs continues qui prennent un nombre de valeurs jusqu'alors inconnu. Bien entendu, si nous avions, par exemple, développé un modèle théorique décrivant le comportement d'un sujet dans une expérience de mesure du temps de réaction lors de la résolution d'une tâche de décision sémantique, nous pourrions essayer, sur la base de ce modèle, de décrire la distribution théorique de valeurs de temps de réaction spécifiques pour le même sujet lorsqu'il est présenté avec le même stimulus. Cependant, ce n'est pas toujours possible. Par conséquent, l'expérimentateur est obligé de supposer que la distribution de la variable aléatoire qui l'intéresse est décrite par une loi déjà étudiée à l'avance. Le plus souvent, bien que cela ne soit pas toujours tout à fait correct, on utilise à ces fins la distribution dite normale, qui sert de norme pour la distribution de toute variable aléatoire, quelle que soit sa nature. Cette distribution a été décrite mathématiquement pour la première fois dans la première moitié du XVIIIe siècle. de Moivre.

  Distribution normale se produit lorsque le phénomène qui nous intéresse est influencé par un nombre infini de facteurs aléatoires qui s'équilibrent. Formellement, la distribution normale, comme le montre de Moivre, peut être décrite par la relation suivante :

  Où X représente une variable aléatoire qui nous intéresse et dont nous étudions le comportement ; R. – la valeur de probabilité associée à cette variable aléatoire ; π et e – des constantes mathématiques bien connues qui décrivent respectivement le rapport de la circonférence au diamètre et la base du logarithme népérien ; μ et σ2 – paramètres de la distribution normale d'une variable aléatoire – espérance mathématique et dispersion d'une variable aléatoire, respectivement X.

  Pour décrire la distribution normale, il s'avère qu'il est nécessaire et suffisant de déterminer uniquement les paramètres μ et σ2.

  Par conséquent, si nous avons une variable aléatoire dont le comportement est décrit par l'équation (1.1) avec des valeurs arbitraires de μ et σ2, alors nous pouvons la noter Ν (μ, σ2), sans garder à l’esprit tous les détails de cette équation.

  

  Riz. 1.1.

  Toute distribution peut être visualisée sous forme de graphique. Graphiquement, la distribution normale ressemble à une courbe en forme de cloche dont la forme exacte est déterminée par les paramètres de distribution, c'est-à-dire espérance mathématique et variance. Les paramètres d'une distribution normale peuvent prendre presque n'importe quelle valeur, qui s'avère limitée uniquement par l'échelle de mesure utilisée par l'expérimentateur. En théorie, la valeur de l'espérance mathématique peut être égale à n'importe quel nombre compris dans la plage de nombres allant de -∞ à +∞, et la variance peut être égale à n'importe quel nombre non négatif. Il existe donc un nombre infini de types différents de distribution normale et, par conséquent, un nombre infini de courbes qui la représentent (qui ont cependant une forme similaire en forme de cloche). Il est clair qu’il est impossible de tous les décrire. Cependant, si les paramètres d'une distribution normale particulière sont connus, elle peut être convertie en ce qu'on appelle distribution normale unitaire, dont l'espérance mathématique est égale à zéro et la variance est égale à un. Cette distribution normale est également appelée standard ou distribution z. Le graphique d’une distribution normale unitaire est présenté sur la Fig. 1.1, d'où il ressort clairement que le sommet de la courbe en cloche de la distribution normale caractérise la valeur de l'espérance mathématique. Un autre paramètre de la distribution normale – la dispersion – caractérise le degré de « planéité » de la courbe en cloche par rapport à l'horizontale (axe des x).

  Aléatoire si, à la suite d'une expérimentation, il peut prendre des valeurs réelles avec certaines probabilités. La caractéristique la plus complète et la plus complète d'une variable aléatoire est la loi de distribution. La loi de distribution est une fonction (tableau, graphique, formule) qui permet de déterminer la probabilité qu'une variable aléatoire X prenne une certaine valeur xi ou tombe dans un certain intervalle. Si une variable aléatoire a une loi de distribution donnée, alors on dit qu'elle est distribuée selon cette loi ou obéit à cette loi de distribution.

  Chaque droit de la distribution est une fonction qui décrit complètement une variable aléatoire d'un point de vue probabiliste. En pratique, la distribution de probabilité d’une variable aléatoire X doit souvent être jugée uniquement à partir des résultats de tests.

  Distribution normale

  Distribution normale, également appelée distribution gaussienne, est une distribution de probabilité qui joue un rôle essentiel dans de nombreux domaines de la connaissance, notamment en physique. Une grandeur physique suit une distribution normale lorsqu’elle est soumise à l’influence d’un très grand nombre de bruits aléatoires. Il est clair que cette situation est extrêmement courante, on peut donc dire que de toutes les distributions, la distribution normale est la plus courante par nature - d'où l'un de ses noms.

  La distribution normale dépend de deux paramètres - le déplacement et l'échelle, c'est-à-dire que d'un point de vue mathématique, il ne s'agit pas d'une distribution, mais de toute une famille d'entre elles. Les valeurs des paramètres correspondent aux valeurs de la moyenne (espérance mathématique) et de l'étalement (écart type).

  

  

  La distribution normale standard est une distribution normale avec une espérance mathématique de 0 et un écart type de 1.

  

  

  Coefficient d'asymétrie

  

  Le coefficient d'asymétrie est positif si la queue droite de la distribution est plus longue que la gauche, et négatif dans le cas contraire.

  Si la distribution est symétrique par rapport à l'espérance mathématique, alors son coefficient d'asymétrie est nul.

  

  Le coefficient d'asymétrie de l'échantillon est utilisé pour tester la symétrie de la distribution ainsi qu'un test préliminaire approximatif de normalité. Cela permet de rejeter, mais ne permet pas d’accepter, l’hypothèse de normalité.

  Coefficient d'aplatissement

  

  Le coefficient d'aplatissement (coefficient de pic) est une mesure de la netteté du pic de la distribution d'une variable aléatoire.

  «Moins trois» à la fin de la formule est introduit de sorte que le coefficient d'aplatissement de la distribution normale soit égal à zéro. Il est positif si le pic de la distribution autour de l’espérance mathématique est net, et négatif s’il est lisse.

  

  Moments d'une variable aléatoire

  Le moment d'une variable aléatoire est une caractéristique numérique de la distribution d'une variable aléatoire donnée.