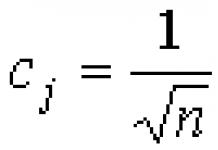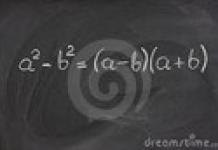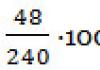Toute équation quadratique complète hache 2 + bx + c = 0 peut être rappelé x 2 + (b/a)x + (c/a) = 0, si vous divisez d'abord chaque terme par le coefficient a avant x2. Et si on introduit de nouvelles notations (b/a) = p Et (c/a) = q, alors nous aurons l'équation x 2 + px + q = 0, qui en mathématiques s'appelle équation quadratique donnée.
Racines de l'équation quadratique réduite et coefficients p Et q connectés les uns aux autres. C'est confirmé Théorème de Vieta, du nom du mathématicien français François Vieta, qui vécut à la fin du XVIe siècle.
Théorème. Somme des racines de l'équation quadratique réduite x 2 + px + q = 0égal au deuxième coefficient p, pris avec le signe opposé, et le produit des racines - au terme libre q.
Écrivons ces relations sous la forme suivante :
Laisser x1 Et x2 différentes racines de l'équation donnée x 2 + px + q = 0. D'après le théorème de Vieta x1 + x2 = -p Et x 1 x 2 = q.
Pour le prouver, substituons chacune des racines x 1 et x 2 dans l'équation. On obtient deux vraies égalités :
x 1 2 + px 1 + q = 0
x 2 2 + px 2 + q = 0
Soustrayons la seconde de la première égalité. On a: 
x 1 2 – x 2 2 + p(x 1 – x 2) = 0
Nous développons les deux premiers termes en utilisant la formule de la différence des carrés :
(x 1 – x 2)(x 1 – x 2) + p(x 1 – x 2) = 0
Par condition, les racines x 1 et x 2 sont différentes. Par conséquent, nous pouvons réduire l’égalité à (x 1 – x 2) ≠ 0 et exprimer p.
(x 1 + x 2) + p = 0 ;
(x 1 + x 2) = -p.
La première égalité est prouvée.
Pour prouver la deuxième égalité, on substitue dans la première équation
x 1 2 + px 1 + q = 0 au lieu du coefficient p, un nombre égal est (x 1 + x 2) :
x 1 2 – (x 1 + x 2) x 1 + q = 0
En transformant le côté gauche de l’équation, on obtient :
x 1 2 – x 2 2 – x 1 x 2 + q = 0 ;
x 1 x 2 = q, c'est ce qu'il fallait prouver.
Le théorème de Vieta est bon parce que Même sans connaître les racines d'une équation quadratique, on peut calculer leur somme et leur produit .
Le théorème de Vieta aide à déterminer les racines entières d'une équation quadratique donnée. Mais pour de nombreux étudiants, cela pose des difficultés du fait qu'ils ne connaissent pas un algorithme d'action clair, surtout si les racines de l'équation ont des signes différents.
Ainsi, l'équation quadratique ci-dessus a la forme x 2 + px + q = 0, où x 1 et x 2 sont ses racines. D'après le théorème de Vieta, x 1 + x 2 = -p et x 1 · x 2 = q.
On peut tirer la conclusion suivante.
Si le dernier terme de l'équation est précédé d'un signe moins, alors les racines x 1 et x 2 ont des signes différents. De plus, le signe de la racine la plus petite coïncide avec le signe du deuxième coefficient de l’équation.
Partant du fait que lors de l'addition de nombres avec des signes différents, leurs modules sont soustraits et le résultat obtenu est précédé du signe du plus grand nombre en valeur absolue, vous devez procéder comme suit :
- déterminer les facteurs du nombre q tels que leur différence soit égale au nombre p ;
- placez le signe du deuxième coefficient de l'équation devant le plus petit des nombres résultants ; la deuxième racine aura le signe opposé.
Regardons quelques exemples.
Exemple 1.
Résolvez l'équation x 2 – 2x – 15 = 0.
Solution.
Essayons de résoudre cette équation en utilisant les règles proposées ci-dessus. On peut alors dire avec certitude que cette équation aura deux racines différentes, car D = b 2 – 4ac = 4 – 4 · (-15) = 64 > 0.
Maintenant, parmi tous les facteurs du nombre 15 (1 et 15, 3 et 5), on sélectionne ceux dont la différence est 2. Ce seront les nombres 3 et 5. On met un signe moins devant le plus petit nombre, c'est-à-dire signe du deuxième coefficient de l'équation. Ainsi, on obtient les racines de l'équation x 1 = -3 et x 2 = 5.
Répondre. x 1 = -3 et x 2 = 5.
Exemple 2.
Résolvez l'équation x 2 + 5x – 6 = 0.
Solution.
Vérifions si cette équation a des racines. Pour ce faire, on trouve un discriminant :
D = b 2 – 4ac = 25 + 24 = 49 > 0. L'équation a deux racines différentes.
Les facteurs possibles du nombre 6 sont 2 et 3, 6 et 1. La différence est de 5 pour la paire 6 et 1. Dans cet exemple, le coefficient du deuxième terme a un signe plus, donc le plus petit nombre aura le même signe . Mais avant le deuxième chiffre, il y aura un signe moins.
Réponse : x 1 = -6 et x 2 = 1.
Le théorème de Vieta peut également être écrit pour une équation quadratique complète. Donc, si l'équation quadratique hache 2 + bx + c = 0 a des racines x 1 et x 2, alors les égalités sont valables pour eux
x 1 + x 2 = -(b/a) Et x 1 x 2 = (c/a). Cependant, l’application de ce théorème dans une équation quadratique complète est assez problématique, car s’il y a des racines, au moins l’une d’elles est un nombre fractionnaire. Et travailler avec la sélection de fractions est assez difficile. Mais il existe encore une issue.
Considérons l'équation quadratique complète ax 2 + bx + c = 0. Multipliez ses côtés gauche et droit par le coefficient a. L'équation prendra la forme (ax) 2 + b(ax) + ac = 0. Introduisons maintenant une nouvelle variable, par exemple t = ax.
Dans ce cas, l'équation résultante se transformera en une équation quadratique réduite de la forme t 2 + bt + ac = 0, dont les racines t 1 et t 2 (le cas échéant) peuvent être déterminées par le théorème de Vieta.
Dans ce cas, les racines de l’équation quadratique originale seront
x 1 = (t 1 / a) et x 2 = (t 2 / a).
Exemple 3.
Résolvez l'équation 15x 2 – 11x + 2 = 0.
Solution.
Créons une équation auxiliaire. Multiplions chaque terme de l'équation par 15 :
15 2 x 2 – 11 15x + 15 2 = 0.
On fait le remplacement t = 15x. Nous avons:
t2 – 11t + 30 = 0.
Selon le théorème de Vieta, les racines de cette équation seront t 1 = 5 et t 2 = 6.
On revient au remplacement t = 15x :
5 = 15x ou 6 = 15x. Donc x 1 = 5/15 et x 2 = 6/15. On réduit et obtenons la réponse finale : x 1 = 1/3 et x 2 = 2/5.
Répondre. x1 = 1/3 et x2 = 2/5.
Pour maîtriser la résolution d'équations quadratiques à l'aide du théorème de Vieta, les étudiants doivent s'entraîner autant que possible. C’est précisément le secret du succès.
site Web, lors de la copie du matériel en totalité ou en partie, un lien vers la source est requis.
Avant de passer au théorème de Vieta, nous introduisons une définition. Équation quadratique de la forme X² + px + q= 0 est dit réduit. Dans cette équation, le coefficient dominant est égal à un. Par exemple, l'équation X² - 3 X- 4 = 0 est réduit. Toute équation quadratique de la forme hache² + b X + c= 0 peut être réduit en divisant les deux côtés de l'équation par UN≠ 0. Par exemple, équation 4 X² + 4 X— 3 = 0 en divisant par 4 se réduit à la forme : X² + X— 3/4 = 0. Dérivons la formule des racines de l'équation quadratique réduite, pour cela nous utilisons la formule des racines d'une équation quadratique générale : hache² + bx + c = 0
Équation réduite X² + px + q= 0 coïncide avec une équation générale dans laquelle UN = 1, b = p, c = q. Par conséquent, pour l’équation quadratique donnée, la formule prend la forme : 

la dernière expression est appelée la formule des racines de l'équation quadratique réduite ; il est particulièrement pratique d'utiliser cette formule lorsque R.- nombre pair. Par exemple, résolvons l'équation X² — 14 X — 15 = 0
![]()
En réponse, nous écrivons que l’équation a deux racines.
![]()
Pour l’équation quadratique réduite avec positif, le théorème suivant est valable.
Théorème de Vieta
Si X 1 et X 2 - racines de l'équation X² + px + q= 0, alors les formules sont valides :
X 1 + X 2 = — R.
x 1 * x 2 = q, c'est-à-dire que la somme des racines de l'équation quadratique réduite est égale au deuxième coefficient pris avec le signe opposé, et le produit des racines est égal au terme libre.
Sur la base de la formule des racines de l’équation quadratique ci-dessus, nous avons :

En additionnant ces égalités, on obtient : X 1 + X 2 = —R.
En multipliant ces égalités, en utilisant la formule de la différence des carrés, on obtient :

A noter que le théorème de Vieta est également valable lorsque le discriminant est égal à zéro, si l'on suppose que dans ce cas l'équation quadratique a deux racines identiques : X 1 = X 2 = — R./2.
Sans résoudre les équations X² — 13 X+ 30 = 0 trouver la somme et le produit de ses racines X 1 et X 2. cette équation D= 169 – 120 = 49 > 0, donc le théorème de Vieta peut être appliqué : X 1 + X 2 = 13, x 1 * x 2 = 30. Examinons quelques exemples supplémentaires. Une des racines de l'équation X² — px- 12 = 0 est égal X 1 = 4. Trouver le coefficient R. et la deuxième racine X 2 de cette équation. Par le théorème de Vieta x 1 * x 2 =— 12, X 1 + X 2 = — R. Parce que X 1 = 4, puis 4 X 2 = - 12, d'où X 2 = — 3, R. = — (X 1 + X 2) = - (4 - 3) = - 1. En réponse, nous écrivons la deuxième racine X 2 = - 3, coefficient p = — 1.
Sans résoudre les équations X² + 2 X- 4 = 0 trouvons la somme des carrés de ses racines. Laisser X 1 et X 2 - racines de l'équation. Par le théorème de Vieta X 1 + X 2 = — 2, x1 * x2 = — 4. Parce que X 1²+ X 2² = ( X 1 + X 2)² - 2 X 1 X 2 alors X 1²+ X 2² =(- 2)² -2 (- 4) = 12.
Trouvons la somme et le produit des racines de l'équation 3 X² + 4 X- 5 = 0. Cette équation a deux racines différentes, puisque le discriminant D= 16 + 4*3*5 > 0. Pour résoudre l’équation, nous utilisons le théorème de Vieta. Ce théorème a été prouvé pour l'équation quadratique donnée. Divisons donc cette équation par 3.

Par conséquent, la somme des racines est égale à -4/3 et leur produit est égal à -5/3.
En général, les racines de l'équation hache² + b X + c= 0 sont liés par les égalités suivantes : X 1 + X 2 = — b/une, x 1 * x 2 = c/une, Pour obtenir ces formules, il suffit de diviser les deux côtés de cette équation quadratique par UN ≠ 0 et appliquez le théorème de Vieta à l’équation quadratique réduite résultante. Prenons un exemple : vous devez créer une équation quadratique réduite dont les racines X 1 = 3, X 2 = 4. Parce que X 1 = 3, X 2 = 4 - racines de l'équation quadratique X² + px + q= 0, alors par le théorème de Vieta R. = — (X 1 + X 2) = — 7, q = X 1 X 2 = 12. Nous écrivons la réponse sous la forme X² — 7 X+ 12 = 0. Lors de la résolution de certains problèmes, le théorème suivant est utilisé.
Théorème inverse du théorème de Vieta
Si les chiffres R., q, X 1 , X 2 sont tels que X 1 + X 2 = — p, x 1 * x 2 = q, Que x1 Et x2- racines de l'équation X² + px + q= 0. Remplacer par le côté gauche X² + px + q au lieu de R. expression - ( X 1 + X 2), et à la place q- travail x1 * x2 . On a: X² + px + q = X² — ( X 1 + X 2) x + x 1 x 2 = x² - x 1 x - x 2 x + x 1 x 2 = (x - x 1) (x - x 2). Ainsi, si les chiffres R., q, X 1 et X 2 sont reliés par ces relations, alors pour tout X l'égalité est vraie X² + px + q = (x - x 1) (x - x 2), d'où il résulte que X 1 et X 2 - racines de l'équation X² + px + q= 0. En utilisant le théorème inverse du théorème de Vieta, on peut parfois trouver les racines d’une équation quadratique par sélection. Regardons un exemple, X² — 5 X+ 6 = 0. Ici R. = — 5, q= 6. Choisissons deux nombres X 1 et X 2 pour que X 1 + X 2 = 5, x 1 * x 2 = 6. En remarquant que 6 = 2 * 3, et 2 + 3 = 5, par le théorème inverse du théorème de Vieta, on obtient que X 1 = 2, X 2 = 3 - racines de l'équation X² — 5 X + 6 = 0.
Le théorème de Vieta est souvent utilisé pour vérifier les racines déjà trouvées. Si vous avez trouvé les racines, vous pouvez utiliser les formules \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) pour calculer les valeurs de \(p \) et \(q\ ). Et s’ils s’avèrent être les mêmes que dans l’équation originale, alors les racines sont trouvées correctement.
Par exemple, en utilisant , résolvons l'équation \(x^2+x-56=0\) et obtenons les racines : \(x_1=7\), \(x_2=-8\). Vérifions si nous avons commis une erreur dans le processus de résolution. Dans notre cas, \(p=1\), et \(q=-56\). D'après le théorème de Vieta, nous avons :
\(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)7+(-8)=-1 \\7\cdot(-8)=-56\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)-1=-1\\-56=-56\end(cases)\ )
Les deux affirmations ont convergé, ce qui signifie que nous avons résolu l’équation correctement.
Cette vérification peut être effectuée oralement. Cela prendra 5 secondes et vous évitera des erreurs stupides.
Théorème inverse de Vieta
Si \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\end(cases)\), alors \(x_1\) et \(x_2\) sont les racines de l'équation quadratique \ (x^ 2+px+q=0\).
Ou de manière simple : si vous avez une équation de la forme \(x^2+px+q=0\), alors résoudre le système \(\begin(cases)x_1+x_2=-p \\x_1 \cdot x_2=q\ end(cases)\) vous trouverez ses racines.
Grâce à ce théorème, on peut trouver rapidement les racines d'une équation quadratique, surtout si ces racines sont . Cette compétence est importante car elle permet de gagner beaucoup de temps.
Exemple . Résolvez l'équation \(x^2-5x+6=0\).
Solution
: En utilisant le théorème inverse de Vieta, nous constatons que les racines satisfont aux conditions : \(\begin(cases)x_1+x_2=5 \\x_1 \cdot x_2=6\end(cases)\).
Regardez la deuxième équation du système \(x_1 \cdot x_2=6\). En quels deux le nombre \(6\) peut-il être décomposé ? Sur \(2\) et \(3\), \(6\) et \(1\) ou \(-2\) et \(-3\), et \(-6\) et \(- 1\). La première équation du système vous indiquera quelle paire choisir : \(x_1+x_2=5\). \(2\) et \(3\) sont similaires, puisque \(2+3=5\).
Répondre
: \(x_1=2\), \(x_2=3\).
Exemples
. En utilisant l'inverse du théorème de Vieta, trouvez les racines de l'équation quadratique :
une) \(x^2-15x+14=0\); b) \(x^2+3x-4=0\); c) \(x^2+9x+20=0\); d) \(x^2-88x+780=0\).
Solution
:
a) \(x^2-15x+14=0\) – en quels facteurs \(14\) se décompose-t-il ? \(2\) et \(7\), \(-2\) et \(-7\), \(-1\) et \(-14\), \(1\) et \(14\ ). Quelles paires de nombres totalisent \(15\) ? Réponse : \(1\) et \(14\).
b) \(x^2+3x-4=0\) – en quels facteurs \(-4\) se décompose-t-il ? \(-2\) et \(2\), \(4\) et \(-1\), \(1\) et \(-4\). Quelles paires de nombres totalisent \(-3\) ? Réponse : \(1\) et \(-4\).
c) \(x^2+9x+20=0\) – en quels facteurs \(20\) se décompose-t-il ? \(4\) et \(5\), \(-4\) et \(-5\), \(2\) et \(10\), \(-2\) et \(-10\ ), \(-20\) et \(-1\), \(20\) et \(1\). Quelles paires de nombres totalisent \(-9\) ? Réponse : \(-4\) et \(-5\).
d) \(x^2-88x+780=0\) – en quels facteurs \(780\) se décompose-t-il ? \(390\) et \(2\). Vont-ils totaliser \(88\) ? Non. Quels autres multiplicateurs possède \(780\) ? \(78\) et \(10\). Vont-ils totaliser \(88\) ? Oui. Réponse : \(78\) et \(10\).
Il n’est pas nécessaire d’étendre le dernier terme à tous les facteurs possibles (comme dans le dernier exemple). Vous pouvez immédiatement vérifier si leur somme donne \(-p\).
Important! Le théorème de Vieta et le théorème inverse ne fonctionnent qu'avec , c'est-à-dire celui pour lequel le coefficient de \(x^2\) est égal à un. Si on nous donnait initialement une équation non réduite, alors nous pouvons la réduire en divisant simplement par le coefficient devant \(x^2\).
Par exemple, donnons l’équation \(2x^2-4x-6=0\) et nous voulons utiliser l’un des théorèmes de Vieta. Mais nous ne pouvons pas, puisque le coefficient de \(x^2\) est égal à \(2\). Débarrassons-nous-en en divisant l'équation entière par \(2\).
\(2x^2-4x-6=0\) \(|:2\)
\(x^2-2x-3=0\)
Prêt. Vous pouvez maintenant utiliser les deux théorèmes.
Réponses aux questions fréquemment posées
Question:
En utilisant le théorème de Vieta, vous pouvez résoudre n'importe quel ?
Répondre:
Malheureusement non. Si l’équation ne contient pas d’entiers ou si l’équation n’a aucune racine, alors le théorème de Vieta ne sera d’aucune aide. Dans ce cas, vous devez utiliser discriminant
. Heureusement, 80 % des équations mathématiques scolaires ont des solutions entières.
Tout d'abord, formulons le théorème lui-même : Ayons une équation quadratique réduite de la forme x^2+b*x + c = 0. Disons que cette équation contient les racines x1 et x2. Alors, d’après le théorème, les affirmations suivantes sont valides :
1) La somme des racines x1 et x2 sera égale à la valeur négative du coefficient b.
2) Le produit de ces mêmes racines nous donnera le coefficient c.
Mais quelle est l’équation donnée ?
Une équation quadratique réduite est une équation quadratique dont le coefficient du plus haut degré est égal à un, c'est-à-dire il s'agit d'une équation de la forme x^2 + b*x + c = 0. (et l'équation a*x^2 + b*x + c = 0 n'est pas réduite). En d’autres termes, pour amener l’équation à la forme donnée, il faut diviser cette équation par le coefficient de puissance la plus élevée (a). La tâche consiste à amener cette équation sous la forme suivante :
3*x^2 12*x + 18 = 0 ;
−4*x^2 + 32*x + 16 = 0 ;
1,5*x^2 + 7,5*x + 3 = 0 ; 2*x^2 + 7*x − 11 = 0.
En divisant chaque équation par le coefficient du degré le plus élevé, on obtient :
X^2 4*x + 6 = 0 ; X^2 8*x − 4 = 0 ; X^2 + 5*x + 2 = 0 ;
X^2 + 3,5*x − 5,5 = 0.
Comme vous pouvez le voir dans les exemples, même les équations contenant des fractions peuvent être réduites à la forme donnée.
Utiliser le théorème de Vieta
X^2 5*x + 6 = 0 ⇒ x1 + x2 = − (−5) = 5 ; x1*x2 = 6 ;
on obtient les racines : x1 = 2 ; x2 = 3 ;
X^2 + 6*x + 8 = 0 ⇒ x1 + x2 = −6 ; x1*x2 = 8 ;
on obtient ainsi les racines : x1 = -2 ; x2 = -4 ;
X^2 + 5*x + 4 = 0 ⇒ x1 + x2 = −5 ; x1*x2 = 4 ;
on obtient les racines : x1 = −1 ; x2 = −4.
La signification du théorème de Vieta
Le théorème de Vieta nous permet de résoudre n'importe quelle équation quadratique réduite en presque quelques secondes. À première vue, cela semble être une tâche assez difficile, mais après 5 à 10 équations, vous pouvez immédiatement apprendre à voir les racines.
À partir des exemples donnés et en utilisant le théorème, il est clair comment vous pouvez simplifier considérablement la solution des équations quadratiques, car en utilisant ce théorème, vous pouvez résoudre une équation quadratique pratiquement sans calculs complexes ni calcul du discriminant, et comme vous le savez, le moins de calculs, plus il est difficile de se tromper, ce qui est important.
Dans tous les exemples, nous avons utilisé cette règle sur la base de deux hypothèses importantes :
L'équation donnée, c'est-à-dire le coefficient du degré le plus élevé est égal à un (cette condition est facile à éviter. Vous pouvez utiliser la forme non réduite de l'équation, alors les affirmations suivantes seront valides x1+x2=-b/a; x1*x2=c/ a, mais c'est généralement plus difficile à résoudre :))
Lorsqu'une équation a deux racines différentes. Nous supposons que l’inégalité est vraie et que le discriminant est strictement supérieur à zéro.
Par conséquent, nous pouvons créer un algorithme de solution général en utilisant le théorème de Vieta.
Algorithme de solution générale utilisant le théorème de Vieta
Nous réduisons une équation quadratique à une forme réduite si l’équation nous est donnée sous forme non réduite. Lorsque les coefficients de l'équation quadratique, que nous avons présentée précédemment comme donnée, s'avèrent être fractionnaires (et non décimaux), alors dans ce cas, notre équation doit être résolue par le discriminant.
Il existe également des cas où le retour à l'équation initiale permet de travailler avec des nombres « pratiques ».
I. Théorème de Vieta pour l'équation quadratique réduite.
Somme des racines de l'équation quadratique réduite x 2 +px+q=0 est égal au deuxième coefficient pris de signe opposé, et le produit des racines est égal au terme libre :
x 1 + x 2 = -p ; x1 ∙x2 =q.
Trouvez les racines de l'équation quadratique donnée en utilisant le théorème de Vieta.
Exemple 1) x 2 -x-30=0. C'est l'équation quadratique réduite ( x2 +px+q=0), deuxième coefficient p=-1, et le membre gratuit q=-30. Tout d’abord, assurons-nous que cette équation a des racines et que les racines (le cas échéant) seront exprimées en nombres entiers. Pour ce faire, il suffit que le discriminant soit le carré parfait d’un nombre entier.
Trouver le discriminant D=b 2 — 4ac=(-1) 2 -4∙1∙(-30)=1+120=121= 11 2 .
Or, selon le théorème de Vieta, la somme des racines doit être égale au deuxième coefficient pris de signe opposé, c'est-à-dire ( -p), et le produit est égal au terme libre, c'est-à-dire ( q). Alors:
x1 +x2 =1 ; x1 ∙x2 =-30. Il faut choisir deux nombres tels que leur produit soit égal à -30 , et le montant est unité. Ce sont des chiffres -5 Et 6 . Réponse : -5 ; 6.
Exemple 2) x 2 +6x+8=0. On a l'équation quadratique réduite avec le deuxième coefficient p=6 et membre gratuit q=8. Assurons-nous qu'il existe des racines entières. Trouvons le discriminant J 1 J 1=3 2 -1∙8=9-8=1=1 2 . Le discriminant D 1 est le carré parfait du nombre 1 , ce qui signifie que les racines de cette équation sont des nombres entiers. Sélectionnons les racines à l'aide du théorème de Vieta : la somme des racines est égale à –р=-6, et le produit des racines est égal à q=8. Ce sont des chiffres -4 Et -2 .
En fait : -4-2=-6=-р ; -4∙(-2)=8=q. Réponse : -4 ; -2.
Exemple 3) x 2 +2x-4=0. Dans cette équation quadratique réduite, le deuxième coefficient p=2, et le membre gratuit q=-4. Trouvons le discriminant J 1, puisque le deuxième coefficient est un nombre pair. J 1=1 2 -1∙(-4)=1+4=5. Le discriminant n'est pas un carré parfait du nombre, donc nous le faisons conclusion: Les racines de cette équation ne sont pas des nombres entiers et ne peuvent être trouvées à l’aide du théorème de Vieta. Cela signifie que nous résolvons cette équation, comme d'habitude, en utilisant les formules (dans ce cas, en utilisant les formules). On a:
Exemple 4).Écrivez une équation quadratique en utilisant ses racines si x1 =-7, x2 =4.
Solution. L'équation recherchée s'écrira sous la forme : x 2 +px+q=0, et, basé sur le théorème de Vieta –p=x 1 +x 2=-7+4=-3 →p=3 ; q=x 1 ∙x 2=-7∙4=-28 . L’équation prendra alors la forme : x2 +3x-28=0.
Exemple 5).Écrivez une équation quadratique en utilisant ses racines si :

II. Théorème de Vieta pour une équation quadratique complète hache 2 +bx+c=0.
La somme des racines est moins b, divisé par UN, le produit des racines est égal à Avec, divisé par