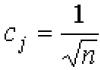Objectifs de la leçon:

Les étudiants doivent savoir :

• ce qu'on appelle la pente d'une droite ;
• l'angle entre la droite et l'axe Ox ;
• quelle est la signification géométrique de la dérivée ;
• équation de la tangente au graphique d'une fonction ;
• un procédé pour construire une tangente à une parabole ;
• être capable d'appliquer les connaissances théoriques dans la pratique.

Objectifs de la leçon:

Pédagogique : créer les conditions permettant aux étudiants de maîtriser un système de connaissances, de compétences et d'aptitudes avec les concepts de signification mécanique et géométrique d'une dérivée.

Pédagogique : former une vision scientifique du monde chez les étudiants.

Développemental : développer l’intérêt cognitif, la créativité, la volonté, la mémoire, la parole, l’attention, l’imagination, la perception des élèves.

Modalités d'organisation des activités éducatives et cognitives :

• visuel;
• pratique;
• par activité mentale : inductive ;
• selon l'assimilation du matériel : partiellement recherché, reproductif ;
• par degré d'indépendance : travaux de laboratoire ;
• stimulant : encouragement ;
• contrôle : examen oral frontal.

Plan de cours

1. Exercices oraux (trouver la dérivée)
2. Message de l'étudiant sur le thème « Raisons de l'émergence de l'analyse mathématique ».
3. Apprendre du nouveau matériel
4. Phys. Juste une minute.
5. Résoudre des tâches.
6. Travaux de laboratoire.
7. Résumer la leçon.
8. Commenter les devoirs.

Équipement : projecteur multimédia (présentation), fiches (travaux de laboratoire).

Pendant les cours

"Une personne ne réalise quelque chose que lorsqu'elle croit en sa propre force"

L. Feuerbach

I. Moment organisationnel.

Organisation de la classe tout au long du cours, préparation des élèves au cours, ordre et discipline.

Fixer des objectifs d'apprentissage pour les étudiants, à la fois pour l'ensemble de la leçon et pour ses étapes individuelles.

Déterminez l'importance du matériel étudié à la fois dans ce sujet et dans l'ensemble du cours.

Comptage verbal

1. Trouver des dérivés :

" , ()" , (4sin x)", (cos2x)", (tg x)", "

2. Test de logique.

a) Insérez l'expression manquante.

5x3-6x	15x2-6	30x
2sinx	2cosx…
cos2x	… …

II. Message de l'étudiant sur le thème « Raisons de l'émergence de l'analyse mathématique ».

L'orientation générale du développement de la science est finalement déterminée par les exigences de la pratique de l'activité humaine. L'existence d'États anciens dotés d'un système de gestion hiérarchique complexe aurait été impossible sans le développement suffisant de l'arithmétique et de l'algèbre, car la collecte des impôts, l'organisation du ravitaillement militaire, la construction de palais et de pyramides et la création de systèmes d'irrigation nécessitaient des calculs complexes. À la Renaissance, les liens entre les différentes parties du monde médiéval se sont développés, le commerce et l'artisanat se sont développés. Une augmentation rapide du niveau technique de production commence et de nouvelles sources d'énergie, non associées aux efforts musculaires de l'homme ou des animaux, sont utilisées industriellement. Aux XI-XII siècles, des machines à foulon et à tisser sont apparues, et au milieu du XV - une presse à imprimer. En raison de la nécessité d'un développement rapide de la production sociale au cours de cette période, l'essence des sciences naturelles, descriptives depuis l'Antiquité, a changé. Le but des sciences naturelles est une étude approfondie des processus naturels et non des objets. Les mathématiques, qui fonctionnaient avec des quantités constantes, correspondaient aux sciences naturelles descriptives de l'Antiquité. Il était nécessaire de créer un appareil mathématique qui décrirait non pas le résultat du processus, mais la nature de son déroulement et ses schémas inhérents. En conséquence, à la fin du XIIe siècle, Newton en Angleterre et Leibniz en Allemagne ont achevé la première étape de la création de l'analyse mathématique. Qu’est-ce que « l’analyse mathématique » ? Comment caractériser et prédire les caractéristiques d’un processus ? Utiliser ces fonctionnalités ? Pénétrer plus profondément dans l’essence d’un phénomène particulier ?

III. Apprendre du nouveau matériel.

Suivons le chemin de Newton et de Leibniz et voyons comment analyser le processus en le considérant en fonction du temps.

Introduisons plusieurs concepts qui nous aideront davantage.

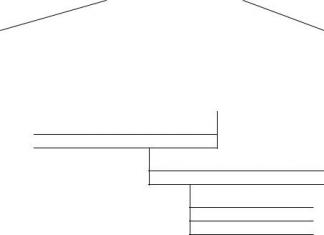
Le graphique de la fonction linéaire y=kx+ b est une droite, le nombre k s'appelle la pente de la droite. k=tg, où est l'angle de la droite, c'est-à-dire l'angle entre cette droite et la direction positive de l'axe Ox.

Image 1

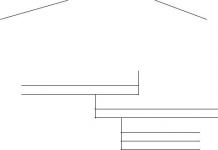
Considérons le graphique de la fonction y=f(x). Traçons une sécante passant par deux points quelconques, par exemple, sécante AM. (Fig.2)

Coefficient angulaire de la sécante k=tg. Dans un triangle rectangle AMC<МАС = (объясните почему?). Тогда tg = = , что с точки зрения физики есть величина средней скорости протекания любого процесса на данном промежутке времени, например, скорости изменения расстояния в механике.

Figure 2

figure 3

Le terme « vitesse » lui-même caractérise la dépendance d’un changement d’une quantité par rapport à un changement d’une autre, et cette dernière ne doit pas nécessairement être le temps.

Ainsi, la tangente de l'angle d'inclinaison de la sécante tg = .

Nous nous intéressons à la dépendance des changements de quantités sur une période de temps plus courte. Dirigons l'incrément de l'argument vers zéro. Ensuite, le côté droit de la formule est la dérivée de la fonction au point A (expliquez pourquoi). Si x -> 0, alors le point M se déplace le long du graphique jusqu'au point A, ce qui signifie que la droite AM s'approche d'une droite AB, qui est tangente au graphique de la fonction y = f(x) au point A. (Fig.3)

L'angle d'inclinaison de la sécante tend vers l'angle d'inclinaison de la tangente.

La signification géométrique de la dérivée est que la valeur de la dérivée en un point est égale à la pente de la tangente au graphique de la fonction en ce point.

Signification mécanique du dérivé.

La tangente de l'angle tangent est une valeur montrant le taux de changement instantané de la fonction en un point donné, c'est-à-dire une nouvelle caractéristique du processus étudié. Leibniz a appelé cette quantité dérivé, et Newton a dit que la dérivée elle-même est appelée l'instantané vitesse.

IV. Minute d'éducation physique.

V. Résoudre des problèmes.

N° 91(1) page 91 – afficher au tableau.

Le coefficient angulaire de la tangente à la courbe f(x) = x 3 au point x 0 – 1 est la valeur de la dérivée de cette fonction en x = 1. f’(1) = 3x 2 ; f'(1) = 3.

N° 91 (3.5) – dictée.

N° 92(1) – au tableau si vous le souhaitez.

N° 92 (3) – indépendamment avec des tests oraux.

N° 92 (5) – au conseil d’administration.

Réponses : 45 0, 135 0, 1,5 e 2.

VI. Travaux de laboratoire.

Objectif : développer le concept de « signification mécanique d’une dérivée ».

Applications des dérivés à la mécanique.

La loi du mouvement rectiligne du point x = x(t), t est donnée.

1. Vitesse moyenne de déplacement sur une période de temps déterminée ;
2. Vitesse et accélération au temps t 04
3. Moments d'arrêt ; si le point après le moment de l'arrêt continue de se déplacer dans la même direction ou commence à se déplacer dans la direction opposée ;
4. La vitesse de déplacement la plus élevée sur une période de temps spécifiée.

Le travail est réalisé selon 12 options, les tâches sont différenciées par niveau de difficulté (la première option est le niveau de difficulté le plus bas).

Avant de commencer le travail, une conversation sur les questions suivantes :

1. Quelle est la signification physique de la dérivée du déplacement ? (Vitesse).
2. Est-il possible de trouver la dérivée de la vitesse ? Cette quantité est-elle utilisée en physique ? Comment appelle-t-on ceci? (Accélération).
3. La vitesse instantanée est nulle. Que peut-on dire du mouvement du corps à ce moment-là ? (C'est le moment de s'arrêter).
4. Quelle est la signification physique des énoncés suivants : la dérivée du mouvement est égale à zéro au point t 0 ; la dérivée change-t-elle de signe en passant par le point t 0 ? (Le corps s'arrête ; la direction du mouvement change dans le sens opposé).

Un échantillon de travaux d'étudiants.

x(t)= t 3 -2 t 2 +1, t 0 = 2.

Figure 4

Dans la direction opposée.

Dessinons un diagramme schématique de la vitesse. La vitesse la plus élevée est atteinte au point

t=10, v (10) =3· 10 2 -4· 10 =300-40=260

Figure 5

VII. Résumer la leçon

1) Quelle est la signification géométrique de la dérivée ?
2) Quelle est la signification mécanique d’une dérivée ?
3) Tirez une conclusion sur votre travail.

VIII. Commenter les devoirs.

Page 90. N° 91(2,4,6), n°92(2,4,6,), page 92 n°112.

Livres d'occasion

• Manuel d'algèbre et débuts de l'analyse.
  Auteurs : Yu.M. Kolyaguine, M.V. Tkacheva, N.E. Fedorova, M.I. Chabounine.
  Edité par A. B. Zhizhchenko.
• Algèbre 11e année. Plans de cours basés sur le manuel de Sh. A. Alimov, Yu. M. Kolyagin, Yu. V. Sidorov. Partie 1.
• Ressources Internet : http://orags.narod.ru/manuals/html/gre/12.jpg

Pour connaître la valeur géométrique de la dérivée, considérons le graphique de la fonction y = f(x). Prenons un point arbitraire M de coordonnées (x, y) et un point N proche de lui (x + $\Delta $x, y + $\Delta $y). Traçons les ordonnées $\overline(M_(1) M)$ et $\overline(N_(1) N)$, et à partir du point M - une ligne droite parallèle à l'axe OX.

Le rapport $\frac(\Delta y)(\Delta x) $ est la tangente de l'angle $\alpha $1 formé par la sécante MN avec la direction positive de l'axe OX. Comme $\Delta $x tend vers zéro, le point N se rapprochera de M, et la position limite de la sécante MN sera la tangente MT à la courbe au point M. Ainsi, la dérivée f`(x) est égale à la tangente de l'angle $\alpha $ formé par la tangente à la courbe au point M (x, y) avec une direction positive par rapport à l'axe OX - la pente de la tangente (Fig. 1).

Figure 1. Graphique de fonction

Lors du calcul des valeurs à l'aide des formules (1), il est important de ne pas se tromper dans les signes, car l'incrément peut également être négatif.

Le point N situé sur une courbe peut tendre vers M de n'importe quel côté. Ainsi, si sur la figure 1 la tangente est donnée dans la direction opposée, l'angle $\alpha $ changera du montant $\pi $, ce qui affectera considérablement la tangente de l'angle et, par conséquent, le coefficient angulaire.

Conclusion

Il s'ensuit que l'existence d'une dérivée est associée à l'existence d'une tangente à la courbe y = f(x), et le coefficient angulaire - tg $\alpha $ = f`(x) est fini. Par conséquent, la tangente ne doit pas être parallèle à l'axe OY, sinon $\alpha $ = $\pi $/2, et la tangente de l'angle sera infinie.

À certains endroits, une courbe continue peut ne pas avoir de tangente ou avoir une tangente parallèle à l'axe OY (Fig. 2). Alors la fonction ne peut pas avoir de dérivée dans ces valeurs. Il peut y avoir n’importe quel nombre de points similaires sur la courbe de fonction.

Figure 2. Points exceptionnels de la courbe

Considérez la figure 2. Laissez $\Delta $x tendre vers zéro à partir de valeurs négatives ou positives :

\[\Delta x\to -0\begin(array)(cc) () & (\Delta x\to +0) \end(array)\]

Si dans ce cas les relations (1) ont une limite finale, celle-ci est notée :

Dans le premier cas, la dérivée est à gauche, dans le second, la dérivée est à droite.

L'existence d'une limite indique l'équivalence et l'égalité des dérivées gauche et droite :

Si les dérivées gauche et droite sont inégales, alors en un point donné il existe des tangentes qui ne sont pas parallèles à OY (point M1, Fig. 2). Aux points M2, M3 les relations (1) tendent vers l'infini.

Pour les points N situés à gauche de M2, $\Delta $x $

À droite de $M_2$, $\Delta $x $>$ 0, mais l'expression est aussi f(x + $\Delta $x) -- f(x) $

Pour le point $M_3$ à gauche, $\Delta $x $$ 0 et f(x + $\Delta $x) -- f(x) $>$ 0, soit les expressions (1) à gauche et à droite sont positives et tendent vers +$\infty $ à mesure que $\Delta $x s'approche de -0 et +0.

Le cas de l'absence de dérivée en des points précis de la droite (x = c) est présenté à la figure 3.

Figure 3. Aucun dérivé

Exemple 1

La figure 4 montre un graphique de la fonction et la tangente au graphique au point abscisse $x_0$. Trouver la valeur de la dérivée de la fonction en abscisse.

Solution. La dérivée en un point est égale au rapport de l'incrément de la fonction à l'incrément de l'argument. Sélectionnons deux points sur la tangente de coordonnées entières. Soit par exemple les points F (-3,2) et C (-2,4).

Dérivée d'une fonction.

1. Définition d'une dérivée, sa signification géométrique.

2. Dérivée d'une fonction complexe.

3. Dérivée de la fonction inverse.

4. Dérivés d'ordre supérieur.

5. Fonctions définies paramétriquement et implicitement.

6. Différenciation des fonctions spécifiées paramétriquement et implicitement.

Introduction.

Les origines du calcul différentiel sont deux questions soulevées par les exigences de la science et de la technologie au XVIIe siècle.

1) Question sur le calcul de la vitesse pour une loi du mouvement arbitrairement donnée.

2) La question de trouver (par des calculs) une tangente à une courbe arbitrairement donnée.

Le problème du dessin d'une tangente à certaines courbes a été résolu par l'ancien scientifique grec Archimède (287-212 avant JC), en utilisant la méthode du dessin.

Mais ce n'est qu'aux XVIIe et XVIIIe siècles, en lien avec les progrès des sciences naturelles et de la technologie, que ces questions ont reçu le développement qui leur était dû.

L’une des questions importantes lors de l’étude de tout phénomène physique est généralement la question de la vitesse, de la vitesse à laquelle le phénomène se produit.

La vitesse à laquelle un avion ou une voiture se déplace est toujours l'indicateur le plus important de ses performances. Le taux de croissance démographique d'un État particulier est l'une des principales caractéristiques de son développement social.

L'idée originale de la vitesse est claire pour tout le monde. Toutefois, cette idée générale ne suffit pas à résoudre la plupart des problèmes pratiques. Il est nécessaire d'avoir une telle définition quantitative de cette quantité, que nous appelons vitesse. La nécessité d’une détermination quantitative aussi précise a toujours été l’une des principales incitations à la création d’une analyse mathématique. Une section entière d’analyse mathématique est consacrée à résoudre ce problème fondamental et à tirer des conclusions de cette solution. Nous passons à l'étude de cette section.

Définition de dérivée, sa signification géométrique.

Soit une fonction définie dans un certain intervalle (une,c) et continu en lui.

1. Donnons l'argument X incrément, alors la fonction obtiendra

incrément:

2. Créons une relation .

3. Passage à la limite en et, en supposant que la limite

existe, on obtient une quantité appelée

dérivée d'une fonction par rapport à l'argument X.

Définition. La dérivée d'une fonction en un point est la limite du rapport de l'incrément de la fonction à l'incrément de l'argument lorsque →0.

La valeur de la dérivée dépend évidemment du point X, dans lequel on le trouve, donc la dérivée de la fonction est, à son tour, une fonction de X. Noté par .

Par définition nous avons

ou (3)

Exemple. Trouvez la dérivée de la fonction.

1. ;

Nous commençons cet article par un aperçu des définitions et des concepts nécessaires.

Après cela, nous passerons à l’écriture de l’équation d’une ligne tangente et fournirons des solutions détaillées aux exemples et problèmes les plus typiques.

En conclusion, nous nous concentrerons sur la recherche de l’équation de la tangente aux courbes du second ordre, c’est-à-dire au cercle, à l’ellipse, à l’hyperbole et à la parabole.

Navigation dans les pages.

Définitions et concepts.

Définition.

Angle d'une droite y=kx+b est l'angle mesuré entre la direction positive de l'axe des x et la ligne droite y=kx+b dans la direction positive (c'est-à-dire dans le sens inverse des aiguilles d'une montre).

Sur la figure, la direction positive de l'axe des x est indiquée par une flèche verte horizontale, la direction positive de l'angle est indiquée par un arc vert, la ligne droite est indiquée par une ligne bleue et l'angle d'inclinaison de la droite La ligne est représentée par un arc rouge.

Définition.

Pente d'une droite y=kx+b est appelé coefficient numérique k.

La pente d'une droite est égale à la tangente de l'angle d'inclinaison de la droite, c'est, .

Définition.

Direct AB tracé par deux points sur le graphique de la fonction y=f(x) est appelé sécante. Autrement dit, sécante est une droite passant par deux points du graphique d’une fonction.

Sur la figure, la ligne sécante AB est représentée par une ligne bleue, le graphique de la fonction y=f(x) est représenté par une courbe noire et l'angle d'inclinaison de la ligne sécante est représenté par un arc rouge.

Si l'on tient compte du fait que le coefficient angulaire d'une droite est égal à la tangente de l'angle d'inclinaison (cela a été discuté ci-dessus), et que la tangente de l'angle dans un triangle rectangle ABC est le rapport de la jambe opposée au adjacent (c'est la définition de la tangente de l'angle), alors une série d'égalités sera vraie pour notre sécante , où sont les abscisses des points A et B, - les valeurs des fonctions correspondantes.

C'est, angle sécant est déterminé par l'égalité ou , UN équation sécanteécrit sous la forme ou (si nécessaire, se référer à la rubrique).

Une ligne sécante divise le graphique d'une fonction en trois parties : à gauche du point A, de A à B et à droite du point B, bien qu'elle puisse avoir plus de deux points communs avec le graphique de la fonction.

La figure ci-dessous montre trois sécantes réellement différentes (les points A et B sont différents), mais elles coïncident et sont données par une seule équation.

Nous n'avons jamais entendu parler d'une ligne sécante pour une ligne droite. Mais quand même, si l'on part de la définition, alors la droite et sa ligne sécante coïncident.

Dans certains cas, une sécante peut avoir un nombre infini de points d'intersection avec le graphique d'une fonction. Par exemple, la sécante définie par l'équation y=0 possède une infinité de points communs avec la sinusoïde.

Définition.

Tangente au graphique de la fonction y=f(x) au point appelé une droite passant par un point, avec un segment dont le graphique d'une fonction se confond pratiquement pour des valeurs de x arbitrairement proches de .

Expliquons cette définition avec un exemple. Montrons que la droite y = x+1 est tangente au graphique de la fonction au point (1 ; 2). Pour ce faire, nous montrerons des graphiques de ces fonctions à mesure que nous nous approchons du point de tangence (1 ; 2). Le graphique de la fonction est affiché en noir, la ligne tangente est représentée par une ligne bleue et le point de tangence est représenté par un point rouge.

Chaque dessin suivant est une zone agrandie du précédent (ces zones sont mises en évidence par des carrés rouges).

On voit clairement que près du point de tangence, le graphique de la fonction se confond pratiquement avec la tangente y=x+1.

Passons maintenant à la définition plus significative d'une tangente.

Pour ce faire, nous allons montrer ce qui arrivera à la sécante AB si le point B est infiniment plus proche du point A.

La figure ci-dessous illustre ce processus.

La sécante AB (représentée par une ligne pointillée bleue) aura tendance à prendre la position de la tangente à la droite (représentée par une ligne continue bleue), l'angle d'inclinaison de la sécante (représentée par un arc pointillé rouge) aura tendance à l'angle d'inclinaison de la tangente (représenté par un arc plein rouge).

Définition.

Ainsi, tangente au graphique de la fonction y=f(x) au point A est la position limite de la sécante AB en .

Nous pouvons maintenant passer à la description de la signification géométrique de la dérivée d’une fonction en un point.

Signification géométrique de la dérivée d'une fonction en un point.

Considérons la sécante AB du graphe de la fonction y=f(x) telle que les points A et B ont respectivement pour coordonnées et , où est l'incrément de l'argument. Notons par l'incrément de la fonction. Marquons tout sur le dessin :

Du triangle rectangle ABC nous avons . Puisque, par définition, une tangente est la position limite d'une sécante, alors .

Rappelons la définition de la dérivée d'une fonction en un point : la dérivée d'une fonction y=f(x) en un point est la limite du rapport de l'incrément de la fonction à l'incrément de l'argument en , noté .

Ainsi, , où est la pente de la tangente.

Ainsi, l'existence d'une dérivée de la fonction y=f(x) en un point équivaut à l'existence d'une tangente au graphe de la fonction y=f(x) au point de tangence, et la pente de la tangente est égale à la valeur de la dérivée au point, c'est .

Nous concluons: signification géométrique de la dérivée d'une fonction en un point consiste en l’existence d’une tangente au graphe de la fonction en ce point.

Équation d'une ligne tangente.

Pour écrire l'équation d'une droite quelconque sur un plan, il suffit de connaître son coefficient angulaire et le point par lequel elle passe. La tangente passe par le point de tangence et son coefficient angulaire pour la fonction différentiable est égal à la valeur de la dérivée au point. Autrement dit, à partir du moment où nous pouvons prendre toutes les données pour écrire l’équation de la tangente.

Équation de la tangente au graphique de la fonction y = f(x) en un point ressemble à .

On suppose qu'il existe une valeur finie de la dérivée, sinon la tangente est droite ou verticale (si Et ), ou n'existe pas (si ).

Selon le coefficient angulaire, la tangente peut être parallèle à l'axe des abscisses (), parallèle à l'axe des ordonnées (dans ce cas, l'équation de la tangente aura la forme), augmentation () ou diminution ().

Il est temps de donner quelques exemples pour clarifier.

Exemple.

Écrire une équation pour la tangente au graphique de la fonction au point (-1;-3) et déterminer l'angle d'inclinaison.

Solution.

La fonction est définie pour tous les nombres réels (se référer à l'article si nécessaire). Puisque (-1;-3) est un point de tangence, alors .

Nous trouvons la dérivée (pour cela, le matériel de l'article différenciant une fonction, trouver la dérivée peut être utile) et calculons sa valeur au point :

Puisque la valeur de la dérivée au point de tangence est la pente de la tangente et qu'elle est égale à la tangente de l'angle d'inclinaison, alors .

L’angle d’inclinaison de la tangente est donc égal à , et l'équation de la tangente a la forme

Illustration graphique.

Le graphique de la fonction d'origine est affiché en noir, la ligne tangente est représentée par une ligne bleue et le point de tangence est représenté par un point rouge. L'image de droite est une vue agrandie de la zone indiquée par le carré en pointillé rouge dans l'image de gauche.

Exemple.

Découvrez s'il existe une tangente au graphique d'une fonction au point (1 ; 1), si oui, alors composez son équation et déterminez son angle d'inclinaison.

Solution.

Le domaine d’une fonction est l’ensemble des nombres réels.

Trouver la dérivée :

Lorsque la dérivée n'est pas définie, mais Et donc, au point (1;1) il y a une tangente verticale, son équation est x = 1 et l'angle d'inclinaison est égal à .

Illustration graphique.

Exemple.

Trouvez tous les points sur le graphique de la fonction auxquels :
a) la tangente n'existe pas ; b) la tangente est parallèle à l'axe des x ; c) la tangente est parallèle à la droite.

Solution.

Comme toujours, nous commençons par le domaine de définition de la fonction. Dans notre exemple, la fonction est définie sur l’ensemble des nombres réels. Développons le signe du module ; pour cela, considérons deux intervalles et :

Différencions la fonction :

À La dérivée x=-2 n'existe pas, puisque les limites unilatérales à ce stade ne sont pas égales :

Ainsi, après avoir calculé la valeur de la fonction en x=-2, on peut donner la réponse au point a) : la tangente au graphe de la fonction n'existe pas au point (-2;-2).

b) Une tangente est parallèle à l'axe des x si sa pente est nulle (la tangente de l'angle d'inclinaison est nulle). Parce que , alors nous devons trouver toutes les valeurs de x auxquelles la dérivée de la fonction disparaît. Ces valeurs seront les abscisses des points tangents auxquels la tangente est parallèle à l'axe Ox.

Quand on résout l'équation , et quand est l'équation :

Il reste à calculer les valeurs correspondantes de la fonction :

C'est pourquoi, - les points requis du graphe de fonction.

Illustration graphique.

Le graphique de la fonction originale est représenté par une ligne noire ; des points rouges marquent les points trouvés auxquels les tangentes sont parallèles à l'axe des abscisses.

c) Si deux droites sur un plan sont parallèles, alors leurs coefficients angulaires sont égaux (c'est écrit dans l'article). Sur la base de cette affirmation, nous devons trouver tous les points sur le graphique de la fonction auxquels la pente de la tangente est égale à huit cinquièmes. Autrement dit, nous devons résoudre l'équation. Ainsi, quand on résout l’équation , et quand est l'équation .

Le discriminant de la première équation est négatif, il n’a donc pas de vraies racines :

La deuxième équation a deux racines réelles :

On retrouve les valeurs de fonction correspondantes :

Aux points les tangentes au graphique d'une fonction sont parallèles à la droite.

Illustration graphique.

Le graphique de la fonction est représenté par une ligne noire, la ligne rouge montre le graphique de la droite, les lignes bleues montrent les tangentes au graphique de la fonction aux points .

Pour les fonctions trigonométriques, du fait de leur périodicité, il peut y avoir un nombre infini de droites tangentes ayant la même pente (la même pente).

Exemple.

Écrire les équations de toutes les tangentes au graphique de la fonction qui sont perpendiculaires à la ligne.

Solution.

Pour créer une équation pour une tangente au graphique d’une fonction, il suffit de connaître sa pente et les coordonnées du point de tangence.

On trouve le coefficient angulaire des tangentes à partir de : le produit des coefficients angulaires des droites perpendiculaires est égal à moins un, c'est-à-dire. Puisque, par condition, le coefficient angulaire d'une droite perpendiculaire est égal à , alors .

Commençons par trouver les coordonnées des points tangents. Commençons par trouver les abscisses, puis calculons les valeurs correspondantes de la fonction - ce seront les ordonnées des points tangents.

En décrivant la signification géométrique de la dérivée d'une fonction en un point, nous l'avons noté. De cette égalité on retrouve l'abscisse des points tangents.

Nous sommes arrivés à une équation trigonométrique. Veuillez y prêter attention, car nous l'utiliserons plus tard pour calculer les ordonnées des points tangents. Nous le résolvons (si vous rencontrez des difficultés, veuillez vous référer à la section résoudre des équations trigonométriques):

Les abscisses des points tangents ont été trouvées, calculons les ordonnées correspondantes (on utilise ici l'égalité à laquelle nous vous avons demandé de faire attention juste au dessus) :

Ainsi, tous les points de contact. Par conséquent, les équations tangentes requises ont la forme :

Illustration graphique.

La figure de la courbe noire montre le graphique de la fonction d'origine sur le segment [-10;10], les lignes bleues représentent les lignes tangentes. On voit bien qu'ils sont perpendiculaires à la ligne rouge. Les points de contact sont marqués de points rouges.

Tangente à un cercle, une ellipse, une hyperbole, une parabole.

Jusqu’à présent, nous avons été occupés à trouver des équations pour les tangentes aux graphiques de fonctions à valeur unique de la forme y = f(x) en différents points. Les équations canoniques des courbes du second ordre ne sont pas des fonctions à valeur unique. Mais nous pouvons représenter un cercle, une ellipse, une hyperbole et une parabole par une combinaison de deux fonctions à valeur unique et ensuite composer des équations tangentes selon un schéma bien connu.

Tangente à un cercle.

Cercle avec le centre en un point et le rayon R est donné par .

Écrivons cette égalité comme une union de deux fonctions :

Ici, la première fonction correspond au demi-cercle supérieur, la seconde au demi-cercle inférieur.

Ainsi, afin de construire l'équation de la tangente au cercle en un point appartenant au demi-cercle supérieur (ou inférieur), on retrouve l'équation de la tangente au graphique de la fonction (ou) au point spécifié.

Il est facile de montrer qu'aux points d'un cercle de coordonnées Et les tangentes sont parallèles à l'axe des x et sont données par les équations et respectivement (dans la figure ci-dessous elles sont représentées par des points bleus et des lignes droites bleues), et aux points Et - sont parallèles à l'axe des ordonnées et ont des équations et, respectivement (dans la figure ci-dessous, elles sont marquées de points rouges et de lignes rouges).

Tangente à une ellipse.

Ellipse centrée en un point avec les demi-axes a et b est donné par l'équation .

Une ellipse, tout comme un cercle, peut être définie en combinant deux fonctions : la demi-ellipse supérieure et inférieure :

Les tangentes aux sommets de l'ellipse sont parallèles soit à l'axe des abscisses (représenté par des lignes droites bleues dans la figure ci-dessous), soit à l'axe des ordonnées (représenté par des lignes droites rouges dans la figure ci-dessous).

Autrement dit, la demi-ellipse supérieure est donnée par la fonction , et celui du bas - .

Nous pouvons maintenant utiliser l’algorithme standard pour construire une équation pour une tangente au graphique d’une fonction en un point.

Première tangente au point :

Deuxième tangente en un point :

Illustration graphique.

Tangente à l'hyperbole.

Hyperbole centrée en un point et des sommets Et est donnée par l'égalité (image en bas à gauche), et avec des sommets Et - l'égalité (photo en bas à droite).

Comme combinaison de deux fonctions, une hyperbole peut être représentée comme

ou .

Aux sommets de l'hyperbole, les tangentes sont parallèles à l'axe Oy pour le premier cas et parallèles à l'axe Ox pour le second.

Ainsi, pour trouver l'équation de la tangente à l'hyperbole, on recherche à quelle fonction appartient le point de tangence et on procède de la manière habituelle.

Une question logique se pose : comment déterminer à quelle fonction appartient un point. Pour y répondre, nous substituons les coordonnées dans chaque équation et voyons laquelle des égalités se transforme en identité. Regardons cela avec un exemple.

Exemple.

Écrire une équation pour la tangente à l'hyperbole au point .

Solution.

Écrivons l'hyperbole sous la forme de deux fonctions :

Voyons à quelle fonction appartient le point tangent.

Pour la première fonction donc, le point n’appartient pas au graphe de cette fonction.

Pour la deuxième fonction, le point appartient donc au graphe de cette fonction.

Trouver le coefficient angulaire de la tangente :

Ainsi, l'équation tangente a la forme .

Illustration graphique.

Tangente à une parabole.

Pour créer une équation pour une tangente à une parabole de la forme à un moment donné, nous utilisons le schéma standard et écrivons l'équation de la tangente sous la forme . La tangente au graphique d'une telle parabole au sommet est parallèle à l'axe Ox.

Parabole Nous le définissons d’abord en combinant deux fonctions. Pour ce faire, résolvons cette équation pour y :

Nous découvrons maintenant à quelle fonction appartient le point tangent et procédons selon le schéma standard.

La tangente au graphique d'une telle parabole au sommet est parallèle à l'axe Oy.

Pour la deuxième fonction :

Obtenir le point de contact .

Ainsi, l'équation de la tangente recherchée a la forme .

Sujet. Dérivé. Signification géométrique et mécanique de la dérivée

Si cette limite existe, alors la fonction est dite dérivable en un point. La dérivée d'une fonction est notée (formule 2).

1. Signification géométrique de la dérivée. Regardons le graphique de la fonction. D'après la figure 1, il est clair que pour deux points A et B quelconques du graphique de la fonction, la formule 3 peut être écrite). Il contient l'angle d'inclinaison de la sécante AB.

Ainsi, le rapport de différence est égal à la pente de la sécante. Si vous fixez le point A et déplacez le point B vers lui, alors il diminue sans limite et se rapproche de 0, et la sécante AB se rapproche de la tangente AC. Par conséquent, la limite du rapport de différence est égale à la pente de la tangente au point A. Cela conduit à la conclusion.

La dérivée d'une fonction en un point est la pente de la tangente au graphique de cette fonction en ce point. C'est la signification géométrique de la dérivée.

1. Équation tangente . Dérivons l'équation de la tangente au graphique de la fonction en un point. Dans le cas général, l'équation d'une droite à coefficient angulaire a la forme : . Pour trouver b, on profite du fait que la tangente passe par le point A : . Cela implique: . En substituant cette expression au lieu de b, on obtient l'équation tangente (formule 4).