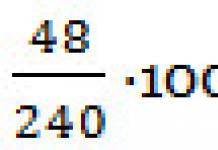7.5. Le principe de superposition des champs électrostatiques

7.5.2 Principe de superposition des potentiels

Principe de superposition du potentiel permet de calculer le potentiel de champ formé par plusieurs objets chargés.

Le potentiel φ du champ électrostatique résultant formé par plusieurs charges en un point donné de l'espace est calculé comme la somme des potentiels de champ formés par chacune des charges séparément :

φ = φ 1 + φ 2 + … + φn,

où φ 1 est le potentiel du champ formé par la première charge ; φ 2 - potentiel du champ formé par la deuxième charge ; ... ; φ n est le potentiel du champ formé par la nième charge.

Afin de calculer le potentiel de champ créé par plusieurs charges Q 1, Q 2, ..., Q n en un point donné de l'espace, utilisez l'algorithme suivant :

1) enregistrer les potentiels des champs formés par chacune des charges Q 1, Q 2, ..., Q n (séparément) en tenant compte du signe des charges :

φ 1, φ 2, …, φ n,

où φ 1 est le potentiel du champ formé par la première charge ; φ 2 - potentiel du champ formé par la deuxième charge ; ... ; φ n est le potentiel du champ formé par la nième charge ;

2) calculer le potentiel du champ résultant comme la somme algébrique des potentiels écrits ci-dessus :

φ = φ 1 + φ 2 + … + φ n.

Exemple 12. Deux charges ponctuelles q 1 = 5 µC et q 2 = −2 µC sont situées aux points (5 ; 0) et (0 ; 2) du système de coordonnées rectangulaires xOy, où les coordonnées x, y sont exprimées en mètres. Calculez le potentiel du champ résultant à l'origine du système de coordonnées si la constante diélectrique du milieu est égale à l'unité.

Solution . La figure montre le système de coordonnées et les charges situées en des points avec des coordonnées données. Le potentiel du champ électrostatique résultant à l'origine du système de coordonnées est une somme algébrique

= φ 1 + φ 2,

où φ 1 est le potentiel du champ formé par la première charge ; φ 2 est le potentiel du champ formé par la deuxième charge.

Calculons le potentiel du champ résultant à l'origine du système de coordonnées à l'aide de l'algorithme :

1) les potentiels des champs créés par chacune des charges séparément sont déterminés par les formules suivantes :

φ 1 = k q 1 r 1 ,

où k est le coefficient de proportionnalité, k = 9,0 ⋅ 10 9 N ⋅ m 2 / Cl 2 ; q 1 - charge située en un point de coordonnées (5 ; 0) ; r 1 - distance de la charge q 1 à l'origine du système de coordonnées, r 1 = 5 m ;

φ 2 = k q 2 r 2,

où q 2 est la charge (en tenant compte du signe) située au point de coordonnées (0 ; 2) ; r 2 - distance de la charge q 2 à l'origine du système de coordonnées, r 2 = 2 m ;

φ = φ 1 + φ 2 = φ 1 − | φ2 | = k q 1 r 1 - k | q2 | r2.

Le calcul donne la valeur potentielle souhaitée :

φ = 9 ⋅ 10 9 ⋅ 5 ⋅ 10 − 6 5 − 9 ⋅ 10 9 ⋅ 2 ⋅ 10 − 6 2 = 0 V.

A l'origine, le potentiel du champ résultant est nul.

Exemple 13. Aux trois sommets d'un carré de 60 cm de côté se trouvent des charges positives de 0,30 µC chacune. Trouvez le potentiel du champ résultant au quatrième sommet du carré. La constante diélectrique du milieu dans lequel se trouve le système de charges est égale à l'unité.

Solution . La figure montre un carré aux trois sommets duquel se trouvent des charges positives identiques. Le potentiel du champ résultant doit être déterminé au sommet A.

Calculons le potentiel du champ résultant au quatrième sommet du carré à l'aide de l'algorithme :

1) les potentiels des champs formés au point A par les charges q 1, q 2 et q 3 séparément sont déterminés par les formules suivantes :

• champ formé par la charge q 1, -

φ 1 = k q 1 r 1 = k q une ,

où k est le coefficient de proportionnalité, k = 9,0 ⋅ 10 9 N ⋅ m 2 / Cl 2 ; q 1 = q ; r 1 - distance de q 1 au point A, r 1 = a ;

• champ formé par la charge q 2 -

φ 2 = k q 2 r 2 = k q une 2,

où q 2 = q ; r 2 - distance de q 2 au point A, r 2 = a 2 ;

• champ formé par la charge q 3, -

φ 3 = k q 3 r 3 = k q a,

où q 3 = q ; r 3 - distance de q 3 au point A, r 3 = a ;

2) le potentiel du champ résultant est la somme algébrique des potentiels écrits ci-dessus

φ = φ 1 + φ 2 + φ 3 = k q a + k q a 2 + k q a = k q a (2 + 1 2) = k q a ⋅ 4 + 2 2.

Calculons :

φ = 9,0 ⋅ 10 9 ⋅ 0,30 ⋅ 10 − 6 60 ⋅ 10 − 2 ⋅ 4 + 2 2 = 12 ⋅ 10 3 V = 12 kV.

Le potentiel du champ électrostatique au quatrième sommet du carré est de 12 kV.

Exemple 14. Deux sphères concentriques de rayons 0,25 et 0,50 m sont uniformément chargées de charges de –0,80 et 0,50 µC, respectivement. Trouvez le potentiel d'un point de champ situé à une distance de 1,0 m du centre des sphères. Le système de tarification est en vase clos.

Solution . Illustrons l'énoncé du problème. Les sphères concentriques ont un centre commun, la sphère de plus petit rayon 1 est chargée d'une charge négative et la sphère de plus grand rayon 2 est chargée d'une charge positive.

Le potentiel du champ électrostatique au point M est la somme algébrique des potentiels des champs formés par la première φ 1 et la seconde φ 2 :

= φ 1 + φ 2.

Calculons le potentiel du champ résultant à l'aide de l'algorithme :

1) les potentiels des champs formés au point M par les charges q 1 et q 2 réparties respectivement sur la surface des sphères intérieure et extérieure sont déterminés séparément par les formules suivantes :

• champ formé par la charge q 1, -

φ 1 = k q 1 r 1 = k q 1 l,

où k est le coefficient de proportionnalité, k ≈ 9 ⋅ 10 9 N ⋅ m 2 /Cl 2 ; q 1 - charge répartie sur la surface de la sphère intérieure, q 1 = −|q 1 |; r 1 - distance du centre des sphères au point M, r 1 = l ;

• champ formé par la charge q 2 -

φ 2 = k q 2 r 2 = k q 2 l,

où q 2 est la charge répartie sur la surface de la sphère extérieure ; r 2 - distance du centre de la sphère au point M, r 2 = r 1 = l ;

2) le potentiel du champ résultant est la somme algébrique des potentiels écrits ci-dessus

φ = φ 1 + φ 2 = k q 1 l + k q 2 l = k l (q 1 + q 2) = k l (− | q 1 | + q 2) .

Calculons :

φ = 9 ⋅ 10 9 1,0 (− 0,80 + 0,50) ⋅ 10 − 6 = − 2,7 ⋅ 10 3 V = − 2,7 kV.

Le potentiel du champ électrostatique résultant au point M est de −2,7 kV. Le résultat ne dépend pas des rayons des sphères.

Théorème de Gauss pour le vecteur

peut être utilisé avec succès comme un outil efficace pour calculer l'intensité et le potentiel du champ électrique d'une certaine distribution de charge, lorsque l'intégrale de gauche peut être transformée en produit de la surface sur laquelle l'intégration est effectuée et de la valeur de la composante vectorielle normale à la surface, c'est-à-dire lorsque

.

Il est bien évident que pour calculer vecteur cela suffira, d'abord, lorsque vecteur perpendiculaire à la surface. La surface d’intégration doit donc être surface équipotentielle champ calculé. Sa forme il faut savoir à l'avance. Enfin, deuxièmement, en tous points de cette surface - équipotentielle - la composante qui lui est normale doit avoir la même valeur, sinon elle ne pourra pas être retirée sous le signe intégral et il ne sera possible de trouver que la valeur moyenne sur l'équipotentielle surface. Nous soulignons que du fait de l'équipotentialité de la surface, c'est-à-dire du fait que

ça ne suit pas du tout ça

en certains points de cette surface. Pour l'avenir, nous soulignons que, par exemple, la surface d'un conducteur chargé, à condition qu'il y ait une répartition des charges d'équilibre sur elle, est toujours équipotentielle, mais s'il ne s'agit pas d'une sphère, mais d'un corps de forme complexe, alors dans le à proximité des saillies (points), l'intensité du champ peut être de plusieurs ordres de grandeur supérieure à celle à proximité des dépressions de la surface. L’exigence de permanence est une exigence distincte.

De ce qui précède, il s'ensuit que le théorème de Gauss ne peut conduire rapidement et simplement au résultat (vecteur ) que dans le cas où la distribution de charges créant le champ a un degré élevé de symétrie ; en conséquence, la forme des surfaces équipotentielles du champ est connue à l'avance et on est sûr que sur ces surfaces. Si tout cela se produit, alors la solution ressemble à ceci :

Reste à choisir la surface en fonction de la symétrie de la répartition des charges et à calculer la charge à l'intérieur.

Symétrie sphérique

Avec une distribution de charge à symétrie sphérique, le champ créé par celle-ci est également à symétrie sphérique. Les champs vectoriels (et scalaires) présentant une telle symétrie sont également appelés champs centraux. Dans le cas général, un corps à symétrie centrale peut s'écrire sous la forme

Ici - rayon vecteur commençant au centre de symétrie du champ r est son module, est la composante radiale de l'intensité du champ, en fonction seulement de la distance à son centre de symétrie. Le potentiel d'un tel domaine dépend uniquement de et

Et, de plus, comme il s'ensuit, avec une normalisation arbitraire, le potentiel de champ a la forme

Ainsi, les conditions d’applicabilité sont satisfaites et nous pouvons utiliser cette relation.

Prenons comme surface sphérique équipotentielle d'un certain rayon actuel r, sa zone. Compte tenu de la continuité supposée de la distribution des charges, nous utilisons l'expression :

.

où est la densité de charge volumétrique. Encore une fois, compte tenu de la symétrie sphérique de la distribution des charges - cela ne dépend que de , il est naturel de prendre une couche sphérique infiniment mince avec un rayon interne et un rayon externe comme élément de volume. Le volume d'une telle couche, on obtient ainsi

.

Enfin, pour toute distribution de charge à symétrie sphérique, lorsque , on obtient

La poursuite des calculs nécessite de préciser la forme de la dépendance de la densité de charge sur la valeur absolue du rayon vecteur.

Le champ est uniforme dans tout le volume de la balle chargée

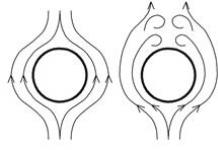
Une répartition uniforme des charges sur le volume d'une boule de rayon (Fig. 1.41) signifie que sa densité de charge a la forme

Riz. 1.41. Lignes de champ électrique d'une balle uniformément chargée

Il ne faut pas oublier que, par condition, il n'y a pas de charges en dehors du ballon.

Puisqu'à un moment donné la densité de charge change brusquement : la limite « à gauche » est différente de zéro , et la limite « à droite » est nulle , le calcul devra être effectué en deux étapes : d'abord pour une surface sphérique de rayon (elle se trouve à l'intérieur de la balle), puis pour une surface sphérique de rayon (elle recouvre la balle). Dans le premier cas

.

En conséquence, le domaine

augmente linéairement avec l'augmentation de la distance jusqu'au centre de la balle, ce qui s'explique simplement : la surface et la charge à l'intérieur

Dans le deuxième cas, l’intégrale est « coupée par le haut » en :

La dernière expression prend en compte que , où est la charge totale de la balle. Ainsi, à l'extérieur de la balle, son champ est le champ d'une charge ponctuelle égale à la charge totale de la balle et placée au centre de cette balle :

.

Les deux expressions peuvent être combinées en une seule formule. Si on utilise la pleine charge de la balle, on obtient :

Si au lieu de la charge totale de la balle on utilise la densité de charge comme paramètre, ces formules prendront la forme suivante (Fig. 1.42) :

Riz. 1.42. Distribution de l'intensité du champ électrique d'une balle uniformément chargée

Les formules et expriment la même dépendance, leur commodité est déterminée par les paramètres spécifiés : ou . Ces formules montrent clairement qu’à la surface de la balle, l’intensité du champ est continue, c’est-à-dire qu’elle ne présente aucune discontinuité. Cela est dû au fait que dans ce cas, l'écart de densité de charge à la surface de la balle du premier type est de grandeur finie : de à zéro. Par conséquent, tant dans les formules supérieures que inférieures, il existe des signes de faibles inégalités. Les cas dans lesquels l'intensité du champ peut subir une discontinuité ressortent clairement de l'exemple suivant.

Le potentiel du champ peut être facilement trouvé en remplaçant, par exemple, de à et en effectuant une intégration. On a:

où et sont des constantes d’intégration, qui ressortent des considérations suivantes. La constante est déterminée à partir de la condition de normalisation, par exemple, jusqu'à zéro à l'infini

Où . La constante est déterminée à partir de la condition de continuité du potentiel à la surface de la balle, c'est-à-dire lorsque :

A noter que l’exigence de continuité potentielle est souvent appelée « assemblage » de deux solutions à l’interface. Dans ce cas, il s'agit de l'interface entre deux régions : la région où il y a une charge (à l'intérieur de la balle), et la région où il n'y en a pas (à l'extérieur de la balle). On peut déjà constater que le potentiel est continu dans tous les cas sauf un : ce qu'on appelle la « double couche ». Imaginez une surface d'un côté de laquelle une charge positive est distribuée avec densité, et de l'autre côté de laquelle une charge négative est distribuée avec densité. Une telle surface est appelée double couche ; sur cette surface le potentiel subit une rupture. Une telle surface (plate) peut être obtenue en rapprochant indéfiniment deux plaques d’un condensateur plat. La même chose peut être faite pour un condensateur de forme quelconque, par exemple sphérique ou cylindrique. Dans tous les autres cas, le potentiel est continu.

En remplaçant les valeurs obtenues des constantes d'intégration, nous écrivons le résultat final sous la forme

Avec cette normalisation, le potentiel au centre de la balle est non nul et égal à

.

Les résultats obtenus sont illustrés dans la figure 1.43 ci-dessous.

Riz. 1.43. Force (1) et potentiel (2) du champ électrique d'une boule uniformément chargée de rayon R en unités de force et de potentiel à sa surface (r = R)

Champ d'une surface sphérique uniformément chargée

Dans ce cas de répartition uniforme des charges sur une surface sphérique, comme dans le précédent, une symétrie sphérique a lieu, donc les formules générales obtenues ci-dessus sont également applicables ici. Cependant, ils doivent être traités avec une certaine prudence pour la raison suivante. La densité de charge volumique incluse sur le côté droit se comporte dans ce cas de la manière intéressante suivante :

Riz. 1.44. Intensité du champ électrique d'une sphère uniformément chargée

En effet, il n'y a de frais que sur surface, c'est-à-dire à , partout à l'intérieur, c'est-à-dire à et partout à l'extérieur, c'est-à-dire à il n'y a pas de frais. Quoi volumétrique La densité de charge en points de la surface va vers l'infini (+∞ dans le cas d'une charge positive et –∞ dans le cas d'une charge négative) peut être représentée comme suit. La figure à côté montre une coupe d'une surface le long de laquelle superficiel la densité de charge est distribuée. Pour déterminer la valeur volumétrique densité de charge en un certain point de la surface, considérons un cylindre (Fig. 1.45) dont la base supérieure est au-dessus de la surface et la base inférieure est sous la surface. L'aire de la base du cylindre est , la hauteur est , et le volume est . La charge à l'intérieur du cylindre, la densité volumétrique de charge, par définition, est égale à la limite du rapport de la charge située à l'intérieur d'un certain volume à la valeur de ce volume lorsque cette dernière tend vers zéro (avec toutes les réserves concernant le volume de « physiquement infinitésimal »). On a

Riz. 1h45. Densité de charge de surface

Il est important que la densité à la surface soit infinie. Les fonctions de ce type (partout sauf un point - zéro, et en ce point unique - l'infini) appartiennent à la classe des fonctions dites généralisées, appelées fonctions de Dirac en l'honneur du physicien Dirac, qui fut le premier à introduire une telle fonction en physique pour répondre aux besoins de la mécanique quantique. Nous n'étudierons pas en détail ici et n'utiliserons pas de telles fonctions dans les calculs. Notre objectif est de montrer que la prise en compte de surfaces chargées formellement infiniment minces conduit à l'apparition de discontinuités (infinies) dans la densité de charge volumétrique, qui, à leur tour, donnent lieu à des discontinuités infinies sur une telle surface chargée dans l'intensité du champ électrique. Nous soulignons que le potentiel du champ reste continu.

La sortie est simple. Pour tout, on utilise la première des formules avec , on constate qu'il n'y a pas de champ partout à l'intérieur d'une coque sphérique uniformément chargée : . Pour tous, la deuxième formule de est valable. Comme dans le cas d'une balle uniformément chargée, en dehors d'une coque sphérique uniformément chargée, son champ est le champ d'une charge ponctuelle placée au centre de cette coque et égal à sa charge totale. Dans ce cas, bien sûr.

Le résultat final est le suivant :

Sur la surface sphérique elle-même, l'intensité du champ souffre dans ce cas d'une discontinuité. La dépendance de la composante du champ radial sur la distance au centre de la surface sphérique est représentée sur la Fig. 1.46.

Riz. 1.46. Dépendance du champ à la distance au centre de la coque sphérique

La dépendance du potentiel sur la distance au centre de la coque sphérique peut être obtenue par intégration. Lorsqu'il est normalisé à zéro à l'infini, le résultat ressemble à ceci :

La dépendance est représentée sur la Fig. 1.47.

Riz. 1.47. Potentiel d'une sphère uniformément chargée

Une distribution de charge homogène (uniforme) sur une surface cylindrique infiniment longue (Fig. 1.48) a une symétrie cylindrique, translationnelle et miroir. Cela signifie ce qui suit. Lorsqu'une telle distribution de charge tourne autour de l'axe d'une surface cylindrique sous n'importe quel angle, elle coïncide avec elle-même. Lorsqu'une telle distribution de charges est décalée (transférée) à n'importe quelle distance le long de l'axe de symétrie, elle coïncide également avec elle-même. Et, enfin, si par n'importe quel point de l'axe de symétrie nous traçons un plan perpendiculaire à l'axe et réfléchissons dans ce plan, comme dans un miroir, la partie « supérieure » de la répartition des charges, alors la réflexion de la partie « supérieure » " La partie "inférieure" coïncidera avec la partie "inférieure" et vice versa, le reflet du "inférieur" coïncidera avec le "haut". En d’autres termes, cette distribution de charges est invariante sous les transformations indiquées. Par conséquent, le champ électrique créé par cette distribution de charge doit être invariant (coïncider avec lui-même) sous les transformations indiquées.

Riz. 1.48. Surface cylindrique infiniment longue

Introduisons un système de coordonnées cylindriques : l'axe est dirigé selon l'axe de symétrie, - la distance à l'axe de symétrie, - l'angle azimutal, l'angle de rotation autour de l'axe de symétrie, - comme précédemment, le potentiel de champ.

Il résulte des propriétés de symétrie que le potentiel de champ ne peut dépendre ni de la coordonnée - la symétrie de translation est rompue, ni de la coordonnée - la symétrie axiale (cylindrique) est rompue. Il ne reste plus que la dépendance à l'égard de la distance par rapport à l'axe du cylindre. Ainsi:

Respectivement

le vecteur d'intensité du champ électrique est dirigé le long de lignes radiales perpendiculaires à l'axe de symétrie (Fig. 1.49) et sa valeur ne dépend que de la distance à l'axe. Les surfaces potentielles sont des cylindres coaxiaux à une surface cylindrique chargée.

Riz. 1.49. Le vecteur d’intensité du champ électrique est dirigé le long de lignes droites radiales

En utilisant ces circonstances, nous intégrerons le côté gauche du théorème de Gauss sur la surface fermée d'un cylindre de rayon de base et de hauteur coaxiale à la surface cylindrique chargée de rayon . Le débit à travers les bases du cylindre est nul du fait que sur les bases, et le débit à travers sa surface latérale est égal au produit de sa surface : . En conséquence, le flux vectoriel total (à travers toute la surface fermée du cylindre considéré) est égal à

En , la charge située à l’intérieur du cylindre est égale à

où est la densité de charge linéaire numériquement égale à la charge par unité de longueur de la surface cylindrique. D'après le théorème de Gauss

d'où nous obtenons

À l'intérieur du cylindre, à travers la surface duquel le flux vectoriel est calculé, il n'y a pas de charges et donc le champ est nul. En combinant ces deux résultats, on obtient finalement (Fig. 1.50) :

En raison de la nature superficielle de la répartition des charges (voir le calcul précédent plus en détail), la surface la plus chargée, c'est-à-dire la composante radiale du champ, subit une discontinuité.

Riz. 1h50. Intensité du champ électrique d'une surface cylindrique uniformément chargée

L'intégration (1.51) (voir aussi (1.49)), l'exigence de continuité de potentiel en , et la normalisation conduisent à la dépendance suivante du potentiel sur la distance à l'axe de la surface cylindrique :

Dans ce cas, lorsqu'une charge de module infiniment grand est distribuée sur un cylindre infiniment long, cela fait référence aux cas où la normalisation à zéro à l'infini n'a aucun sens. Comme le montre (1.52), la dépendance du potentiel sur la distance à l'axe est logarithmique, la normalisation à zéro à l'infini, dans le langage des formules (1.52), signifie que , mais, alors le potentiel sera infiniment grand en valeur absolue à tout moment final distance de l'axe de la surface chargée, ce qui n'a aucun sens. Le choix de cette distance finie par rapport à l'axe de symétrie à laquelle il convient de considérer le potentiel égal à zéro ne pose pas de difficultés et est déterminé par les spécificités du problème. Par exemple, rien ne vous empêche de mettre , alors le potentiel partout à l'intérieur et sur la surface la plus chargée sera nul.

Champ infini uniformément avion chargé

Soit la densité de charge de surface . Cette répartition de charge sur un plan infini se caractérise par le fait que son apparition ne dépend pas : a) d'une rotation d'un angle quelconque autour d'un axe d'un plan perpendiculaire, b) d'un déplacement d'une distance quelconque le long d'une ligne droite située dans le plan et N'importe quelle direction. Enfin, c) la réflexion d'une distribution de charges donnée dans un miroir coïncidant avec le plan lui-même la laissera inchangée.

De l'analyse de la symétrie, il est tout à fait évident que le potentiel en tout point extérieur au plan ne peut dépendre que de la distance de ce point au plan. Dirigons l'axe du système de coordonnées cartésiennes perpendiculairement au plan, et laissons les axes et appartenir au plan lui-même, alors

De plus, en raison de la symétrie miroir, le champ « devant » l’avion diffère du champ « derrière » l’avion. seulement direction du vecteur. Cela signifie que la dépendance de doit être impaire et la dépendance du potentiel doit être paire.

Grâce à ces considérations, nous prenons une surface fermée - celle pour laquelle nous écrirons le théorème de Gauss - de la forme suivante (Figure 1.51).

Riz. 1.51. Champ électrique d'un avion chargé

Il s'agit d'un cylindre avec une surface latérale perpendiculaire au plan et des bases parallèles au plan. Hauteur du cylindre, surface de la base. Compte tenu de l'étrangeté de la dépendance, il convient de placer les bases du cylindre à la même distance du plan, la contribution des bases à l'écoulement sera alors la même. L'intensité du champ sur les bases, d'une part, leur est perpendiculaire, d'autre part, elle est co-dirigée avec la normale externe, et troisièmement, elle est la même en tous leurs points en valeur absolue

La contribution au flux vectoriel de la surface latérale est nulle, puisque sur la surface latérale .

Par conséquent, le flux total à travers toute la surface cylindrique fermée est

A l'intérieur de la surface cylindrique considérée se trouve une charge

où est la densité de charge dans l'avion. Par le théorème de Gauss

d'où le module intensité de champ de l'avion chargééquivaut à

Soulignons que le résultat ne dépend évidemment pas de la distance au plan où se trouvent les bases du cylindre considéré. Il s'ensuit que de chaque côté du plan le champ électrique créé par celui-ci est uniforme.

En utilisant l'axe perpendiculaire au plan chargé précédemment introduit, le champ des deux côtés du plan peut être décrit par une formule, adaptée à tout signe de charge sur le plan

Voici le vecteur unitaire de l’axe.

Intégration avec

pour la dépendance au potentiel de champ de l'avion il est facile d'obtenir :

Le potentiel in est normalisé par la condition . Ici, comme dans l'exemple d'une surface cylindrique chargée infiniment longue, le potentiel augmente avec la distance jusqu'à l'infini, donc la normalisation à zéro à l'infini n'a aucun sens.

Les lignes de champ du plan chargé sont représentées sur la Fig. 1,52 et 1,53.

Riz. 1.52. Champ d'un avion chargé positivement

Riz. 1.53. Champ d'un avion chargé négativement

Champ d'un condensateur à plaques parallèles

Déterminons l'intensité du champ créé par deux plans parallèles infinis chargés uniformément et différemment. Les densités de charge sur les plans sont identiques en module et égales respectivement : et (condensateur plat idéal). En utilisant la fig. 1.54, il n'est pas difficile de comprendre que dans l'espace entre les plans, les champs qu'ils créent sont dirigés dans une direction, donc à l'intérieur le champ total est deux fois plus grand que le champ de chacun des plans. En dehors des plans, les champs qu'ils créent sont dirigés dans des directions opposées : par conséquent, le champ total des deux plans est nul (Fig. 1.55).

Riz. 1.54. Champ électrique d'un condensateur à plaques parallèles

Riz. 1,55. Champ électrique de plans de charges opposées

L'annexe 6 présente un exemple de mouvement d'une particule chargée dans un champ électrique constant.

Potentiel de champ d'un disque chargé

Comme cela a été noté à plusieurs reprises, connaissant le potentiel de champ d'une charge ponctuelle et utilisant le principe de superposition, il est en principe toujours possible de calculer le potentiel de champ créé par n'importe quelle distribution de charge.

Trouvons par exemple le potentiel du champ électrique créé sur l'axe d'un disque mince de rayon R., uniformément chargé de la densité de charge de surface (Fig. 1.57). En raison de la symétrie axiale, en des points sur l'axe, deux composantes de l'intensité du champ perpendiculaire à l'axe sont égales à zéro : , il reste à trouver - la composante du champ dirigée le long de l'axe.

Peut être étendu en série, limité aux deux premiers termes de l'extension

La loi de Coulomb et la dimension de l'espace

L'espace dans lequel nous vivons a trois dimensions. En d'autres termes, trois coordonnées sont nécessaires (par exemple, dans les systèmes cartésiens ou sphériques) pour spécifier la position d'un point. UN(Fig. 1.58). Il s'avère que le nombre 3 est étroitement lié à la forme de la loi de Coulomb. Nous avons vu que le théorème d'Ostrogradsky-Gauss découle de la loi de Coulomb. L'inverse est également vrai : la loi de Coulomb peut être dérivée du théorème d'Ostrogradsky-Gauss. Mais ce théorème est plus général que la loi de Coulomb. En particulier, cela s'applique aux espaces de dimension , où il ne doit pas nécessairement être égal à trois.

Ainsi, dans un espace à deux dimensions, le rôle de volume est joué par notre zone. En effet, une sphère est le lieu de points dans l’espace équidistants du centre. Selon cette définition, une sphère bidimensionnelle est un cercle dont le rayon dans le monde dimensionnel est proportionnel au monde dimensionnel.

Quand on obtient d’ici la loi du carré inverse (loi de Coulomb). Quand on trouve En fait, nous connaissons déjà ce comportement du champ électrique. C'est précisément cette loi (10.17) que nous avons dérivée pour le champ d'un cylindre chargé infini. Si vous réfléchissez bien et rappelez-vous l'emplacement des lignes de force du cylindre, vous comprendrez que rien ne dépend des coordonnées le long de l'axe du cylindre. Ainsi, ce système simule un champ électrique dans un monde bidimensionnel. Il est désormais plus facile de comprendre qu'un avion chargé imite une charge ponctuelle dans un monde unidimensionnel : tout dépend d'une seule coordonnée : la distance au plan. Mais nous avons constaté plus haut que le champ électrique ne dépend pas de cette distance. Et de la formule (10.49) il s'ensuit également que le degré d'intensité ) devrait donner une expression de l'intensité du champ électrique.

Cela conduit à des conclusions intéressantes. Puisque dans les mondes à une et deux dimensions, les potentiels croissent à l’infini, une quantité de travail infiniment grande est nécessaire pour séparer deux charges attractives. Cela signifie que dans les mondes de petite dimension, seul le mouvement fini de deux corps attracteurs (charges, masses) est possible. Rappelez-vous que le mouvement dans une région limitée de l’espace est appelé fini. Par conséquent, dans des mondes où il est impossible d’ioniser un atome, il est impossible de lancer un satellite au-delà du système solaire, etc. Dans un tel monde, il n’y aurait pas de réactions chimiques, les galaxies et les étoiles ne pourraient pas évoluer. En un mot, la vie là-bas serait ennuyeuse.

On pourrait s’attendre à des moments plus agréables dans des mondes multidimensionnels. Hélas, cela s'avère être une illusion. Etude de l'équation du mouvement

conduit à la conclusion qu'en substance il n'y a pas de mouvement fini : il n'est réalisé que pour des orbites circulaires, et même dans ce cas, il est instable - la moindre perturbation conduit l'électron (planète) à tomber sur le centre d'attraction ou à s'échapper vers une distance infiniment grande. Il s’avère que dans un tel monde, les atomes, les systèmes planétaires et tout le reste n’auraient pas pu se former du tout. Pas de stabilité dans les mondes de dimension supérieure – c’est une alternative aux mondes « stagnants » de basse dimension. Ce n’est qu’avec cela qu’un mouvement stable, fini et infini, est possible. Il s'avère que l'espace tridimensionnel est la seule forme pratique d'existence et de mouvement de la matière, du moins les types que nous connaissons et que nous étudions en physique.

Informations Complémentaires

http://hea.iki.rssi.ru/~nik/astro/spher.htm - système de coordonnées sphériques ;

http://edu.ioffe.ru/register/?doc=physica/lect3.ch2.tex - mouvement fini, problème de Kepler.

Le champ électrostatique a deux caractéristiques : la force (tension) et l'énergie (potentiel). La tension et le potentiel sont des caractéristiques différentes d’un même point du champ, il doit donc y avoir une connexion entre eux.

Le travail de déplacement d'une charge positive ponctuelle d'un point à un autre le long de l'axe x, à condition que les points soient situés infiniment proches les uns des autres et que x 1 – x 2 = dx, est égal à qE x dx. Le même travail est égal à q(φ 1 - φ 2)= -dφq. En égalisant les deux expressions, nous pouvons écrire

En répétant un raisonnement similaire pour les axes y et z, nous pouvons trouver le vecteur :

où sont les vecteurs unitaires des axes de coordonnées x, y, z.

De la définition du gradient, il résulte que

Ou (12.31)

ceux. l'intensité de champ E est égale au gradient de potentiel avec un signe moins. Le signe moins est déterminé par le fait que vecteur de tension E le champ est orienté vers un potentiel décroissant.

La connexion établie entre tension et potentiel nous permet de trouver la différence de potentiel entre deux points arbitraires de ce champ en utilisant une intensité de champ connue.

Ø Champ d'une sphère uniformément chargée rayon R

L'intensité du champ en dehors de la sphère est déterminée par la formule

La différence de potentiel entre les points r 1 et r 2 (r 1 >R ; r 2 >R) est déterminée à l'aide de la relation

On obtient le potentiel de la sphère si r 1 = R, r 2 → ∞ :

Ø Champ d'un cylindre infiniment long chargé uniformément

L'intensité du champ à l'extérieur du cylindre (r >R) est déterminée par la formule

(τ – densité linéaire).

La différence de potentiel entre deux points situés à une distance r 1 et r 2 (r 1 >R ; r 2 >R) de l'axe du cylindre est égale à

(12.32)

Ø Champ d'un plan infini uniformément chargé

L'intensité du champ de ce plan est déterminée par la formule

(σ - densité surfacique).

La différence de potentiel entre les points situés à une distance x 1 et x 2 du plan est égale à

(12.33)

Ø Champ de deux plans parallèles infinis de charges opposées

L'intensité du champ de ces avions est déterminée par la formule

La différence de potentiel entre les plans est

(12.34)

(d – distance entre les plans).

Exemples de résolution de problèmes

Exemple 12.1. Les charges à trois points Q 1 =2nC, Q 2 =3nC et Q 3 =-4nC sont situées aux sommets d'un triangle équilatéral de longueur de côté un=10cm. Déterminez l’énergie potentielle de ce système.

Donné: Q 1 =2nC=2∙10 -9 C ; Q 2 =3nC=3∙10 -9 C ; et Q 3 =-4nC=4∙10 -9 C ; un=10cm=0,1m.

Trouver : U.

Solution: L'énergie potentielle d'un système de charges est égale à la somme algébrique des énergies d'interaction de chacune des paires de charges en interaction, c'est-à-dire

U=U 12 +U 13 +U 23

où, respectivement, les énergies potentielles d'une des charges situées dans le champ d'une autre charge à distance UN de lui sont égaux

; ; (2)

Remplaçons les formules (2) dans l'expression (1) et trouvons l'énergie potentielle souhaitée du système de charges

Répondre: U = -0,126 µJ.

Exemple 12.2. Déterminez le potentiel au centre d'un anneau de rayon interne R 1 = 30 cm et de rayon externe R 2 = 60 cm, si une charge q = 5 nC y est uniformément répartie.

Donné: R1 = 30 cm = 0,3 m ; R2 = 60 cm = 0,6 m ; q=5nC=5∙10 -9C

Trouver : φ.

Solution: Divisons l'anneau en anneaux concentriques infiniment minces de rayon intérieur r et de rayon extérieur (r+dr).

L'aire de l'anneau mince considéré (voir figure) dS=2πrdr.

Le potentiel au centre de l'anneau, créé par un anneau infiniment fin,

où est la densité de charge de surface.

Pour déterminer le potentiel au centre de l’anneau, il faut additionner arithmétiquement dφ de tous les anneaux infiniment minces. Alors

Considérant que la charge de l'anneau Q=σS, où S= π(R 2 2 -R 1 2) est l'aire de l'anneau, on obtient le potentiel souhaité au centre de l'anneau

Répondre: φ=25V

Exemple 12.3.Deux charges ponctuelles du même nom (q 1 = 2 nC et q 2 = 5 nC) sont dans le vide à une distance r 1 = 20 cm. Déterminez le travail A qu'il faut effectuer pour les rapprocher d'une distance r 2 = 5 cm.

Donné: q 1 =2nCl=2∙10-9Cl ; q 2 =5nCl=5∙10-9Cl ; r1 = 20 cm = 0,2 m ; r2 = 5 cm = 0,05 m.

Trouver un.

Solution: Le travail effectué par les forces d'un champ électrostatique lorsqu'une charge Q se déplace d'un point de champ de potentiel φ 1 à un point de potentiel φ 2.

UNE 12 = q(φ 1 - φ 2)

Lorsque des charges du même nom se réunissent, le travail est effectué par des forces extérieures, donc le travail de ces forces est égal en grandeur, mais de signe opposé au travail des forces coulombiennes :

UNE= -q(φ 1 - φ 2)= q(φ 2 - φ 1). (1)

Potentiels des points 1 et 2 du champ électrostatique

En substituant les formules (2) dans l'expression (1), on trouve le travail nécessaire qui doit être fait pour rapprocher les charges,

Répondre: A = 1,35 µJ.

Exemple 12.4.Un champ électrostatique est créé par un fil sans fin chargé positivement. Le proton, se déplaçant sous l'influence d'un champ électrostatique le long de la ligne de tension partant du fil d'une distance r 1 = 2 cm à r 2 = 10 cm, a changé sa vitesse de υ 1 = 1 mm/s à υ 2 = 5 mm /s. Déterminez la densité de charge linéaire τ du fil.

Donné: q=1,6∙10 -19 °C ; m=1,67∙10 -27 kg ; r 1 =2 cm = 2∙10 -2 m ; r2 = 10 cm = 0,1 m ; r2 = 5 cm = 0,05 m ; υ 1 = 1 Mm/s = 1∙10 6 m/s ; jusqu'à υ 2 =5Mm/s=5∙10 6 m/s.

Trouver:τ .

Solution: Le travail effectué par les forces du champ électrostatique lors du déplacement d'un proton d'un point de champ de potentiel φ 1 à un point de potentiel φ 2 va augmenter l'énergie cinétique du proton

q(φ 1 - φ 2)=ΔT (1)

Dans le cas d'un filetage, le champ électrostatique présente une symétrie axiale, donc

Ou dφ=-Edr,

puis la différence de potentiel entre deux points situés à une distance r 1 et r 2 du fil,

(tenez compte du fait que l'intensité du champ créé par un fil sans fin uniformément chargé est de ).

En remplaçant l'expression (2) dans la formule (1) et en tenant compte du fait que , on a

D'où vient la densité de charge linéaire souhaitée pour le fil ?

Répondre: τ = 4,33 µC/m.

Exemple 12.5.Un champ électrostatique est créé dans le vide par une boule de rayon R = 8 cm, uniformément chargée d'une densité volumique ρ = 10 nC/m 3. Déterminer la différence de potentiel entre deux points de ce champ situés à partir du centre de la balle aux distances : 1) r 1 = 10 cm et r 2 = 15 cm ; 2) r 3 = 2 cm et r 4 = 5 cm.

Donné: R=8cm=8∙10 -2m; ρ=10nC/m 3 =10∙10 -9 nC/m3; r 1 =10 cm = 10∙10 -2 m ;

r 2 =15 cm = 15∙10 -2 m ; r 3 = 2 cm = 2∙10 -2 m ; r 4 =5cm=5∙10 -2 m.

Trouver:1) 1 - 2 ; 2) 3 - 4.

Solution: 1) La différence de potentiel entre deux points situés à une distance r 1 et r 2 du centre de la balle.

(1)

où est l'intensité du champ créé par une balle uniformément chargée avec une densité volumétrique ρ en tout point situé à l'extérieur de la balle à une distance r de son centre.

En substituant cette expression dans la formule (1) et en intégrant, on obtient la différence de potentiel souhaitée

2) La différence de potentiel entre deux points situés à une distance r 3 et r 4 du centre de la balle,

(2)

où est l'intensité du champ créé par une balle uniformément chargée avec une densité volumique ρ en tout point situé à l'intérieur de la balle à une distance r de son centre.

En substituant cette expression dans la formule (2) et en intégrant, on obtient la différence de potentiel souhaitée

Répondre: 1) φ 1 - φ 2 =0,643 V ; 2) φ 3 - φ 4 =0,395 V

Formule

peut être utilisé pour trouver la fonction potentielle d'un champ potentiel donné

une(x, y, z)=P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k.

Pour ce faire, on fixe le point de départ M 0 (x 0 , y 0 , z 0) et on le relie au point courant M (x, y, z) de la ligne brisée M 0 ABM dont les maillons sont parallèles aux axes de coordonnées, à savoir M 0 A?Ox , АВ?Оу, ВМ?Оz (Fig. 6.2). Alors la formule (6.6) prendra la forme

où x, y, z sont les coordonnées du point courant sur les segments de la ligne brisée le long desquels l'intégration est effectuée.

Exemple 6.7. Montrer que le champ vectoriel

une = (e + z)i + (x + z)j + (x + y)k

est potentiel, et trouver son potentiel.

Solution. 1ère méthode. Une condition nécessaire et suffisante pour la virtualité du champ a(M) est que rot a(M) soit égal à zéro. Dans notre cas

c'est-à-dire que le champ est potentiel. On trouve le potentiel de ce champ à l'aide de la formule (6.10). Prenons l'origine des coordonnées O(0, 0, 0) comme point fixe initial. Ensuite, nous obtenons

où C est une constante arbitraire.

2ème méthode. Par définition, le potentiel est une fonction scalaire pour laquelle grad φ=a. Cette égalité vectorielle équivaut à trois égalités scalaires :

En intégrant (6.12) sur x, on obtient

où f(y, z) est une fonction arbitrairement différentiable de y et z. En différenciant les deux côtés de (6.12) par rapport à y et en tenant compte de (6.11), nous obtenons une relation pour trouver la fonction encore indéfinie f(y, z). Nous avons

Ayant intégré (6.16) sur y, on a

où F(z) est une fonction encore indéfinie de z. En remplaçant (6.17) dans (6.11) on obtient

En différenciant la dernière égalité par rapport à z et en tenant compte de la relation (6.12), on obtient une équation pour trouver F(z) :

A partir de là, donc.

3ème méthode. Par définition de la différentielle totale d'une fonction on a

En substituant ici aux dérivées partielles , , leurs expressions de (6.10), (6.11), (6.12), on obtient

dφ =(y + z)dx + (x + z)dy + (x + y)dz

ou, après de simples transformations,

réφ=(ydx+xdy)+(zdx+xdz)+(ydz+zdy)=d(xy)+d(xz)+d(yz)=d(xy +xz +yz).

réφ = ré (xy + yz + zx).

Il s'ensuit que

Dans le cas où la région Ω est stellaire de centre à l'origine O(0, 0, 0), le potentiel φ(M) du champ vectoriel a=a(M) au point M(x, y, z ) peut être trouvé par la formule

où r(M)=xi + yj + zk est le rayon vecteur du point M(x, y, z), et le point (tx,ty,tz) quand parcourt un segment OM de droite passant par les points O et M.

Exemple 6.8. Trouver le potentiel du champ vectoriel

une= yzi + xzj + xyk.

Solution. Il est facile de voir que pourrir est égal à 0, c'est-à-dire que ce champ de vecteurs est potentiel. Ce champ est défini dans tout l'espace tridimensionnel, qui est stellaire avec un centre à l'origine des coordonnées O(0, 0, 0), donc pour trouver son potentiel on utilise la formule (6.12). Puisque dans ce cas

un( )=une(tx, ty, tz)= t 2 yzi + t 2 xzj + t 2 xyk,

alors le produit scalaire des vecteurs un() Et r(M)équivaut à

(un( ), r(M))=t 2 (xyz+xyz+xyz)=3t 2 xyz.

À la recherche de potentiel

Le potentiel φ en tout point du champ électrostatique est une grandeur physique déterminée par l'énergie potentielle d'une charge unitaire positive placée en ce point. Le potentiel de champ créé par une charge ponctuelle Q est égal à

Le potentiel est une quantité physique déterminée par le travail effectué pour déplacer une charge électrique positive unitaire lorsqu'elle est retirée d'un point donné du champ vers l'infini. Ce travail est numériquement égal au travail effectué par des forces externes (contre les forces du champ électrostatique) pour déplacer une charge positive unitaire de l'infini vers un point donné du champ.

L'unité de potentiel est le volt (V) : 1 V est égal au potentiel d'un point du champ auquel une charge de 1 C a une énergie potentielle de 1 J (1 V = 1 J/C). En prenant en compte la dimension du volt, on peut montrer que l'unité d'intensité de champ électrostatique introduite précédemment est bien égale à 1 V/m : 1 N/C=1 N m/(C m)=1 J/(C m) = 1 V/m.

Des formules (3) et (4) il résulte que si un champ est créé par plusieurs charges, alors le potentiel d'un champ donné d'un système de charges est égal à la somme algébrique des potentiels des champs de toutes ces charges :

L'intensité en tout point du champ électrique est égale au gradient de potentiel en ce point, pris avec le signe opposé. Le signe moins indique que la tension E est dirigée dans le sens d'un potentiel décroissant.

E = - grade phi = - N phi.

Pour établir un lien entre la force caractéristique du champ électrique - intensité et sa caractéristique énergétique - potentiel, considérons le travail élémentaire des forces du champ électrique sur un déplacement infinitésimal d'une charge ponctuelle q : dA = q E dl, le même travail est égal à la diminution de l'énergie potentielle de la charge q : dA = - dWп = - q dphi, où dphi est la variation du potentiel du champ électrique sur la longueur de déplacement dl. En égalisant les côtés droits des expressions, on obtient : E dl = -d phi ou dans le système de coordonnées cartésiennes

Ex dx + Ey dy + Ez dz = -d fi

où Ex, Ey, Ez sont des projections du vecteur tension sur les axes du repère. Puisque l'expression est une différentielle totale, alors pour les projections du vecteur d'intensité nous avons

L'expression entre parenthèses est le gradient du potentiel phi.

Le principe de superposition comme propriété fondamentale des champs. Expressions générales de la force et du potentiel du champ créé en un point avec un rayon vecteur par un système de charges ponctuelles situées en des points avec des coordonnées (voir paragraphe 4)

Si nous considérons le principe de superposition au sens le plus général, alors selon lui, la somme de l'influence des forces externes agissant sur une particule sera la somme des valeurs individuelles de chacune d'elles. Ce principe s'applique à divers systèmes linéaires, c'est-à-dire systèmes dont le comportement peut être décrit par des relations linéaires. Un exemple serait une situation simple dans laquelle une onde linéaire se propage dans un milieu spécifique, auquel cas ses propriétés seraient préservées même sous l'influence de perturbations provenant de l'onde elle-même. Ces propriétés sont définies comme une somme spécifique des effets de chacune des composantes harmonieuses.

Le principe de superposition peut prendre d'autres formulations tout à fait équivalentes à celles ci-dessus :

· L'interaction entre deux particules ne change pas lorsqu'une troisième particule est introduite, qui interagit également avec les deux premières.

· L'énergie d'interaction de toutes les particules dans un système à plusieurs particules est simplement la somme des énergies d'interactions par paires entre toutes les paires possibles de particules. Il n’y a pas d’interactions à plusieurs particules dans le système.

· Les équations décrivant le comportement d'un système à plusieurs particules sont linéaires en nombre de particules.

6 La circulation du vecteur tension est le travail effectué par les forces électriques lors du déplacement d'une seule charge positive le long d'un chemin fermé L

Puisque le travail des forces du champ électrostatique le long d’une boucle fermée est nul (le travail des forces du champ potentiel), la circulation de l’intensité du champ électrostatique le long d’une boucle fermée est nulle.

Potentiel de terrain. Le travail de tout champ électrostatique lors du déplacement d'un corps chargé d'un point à un autre ne dépend pas non plus de la forme de la trajectoire, tout comme le travail d'un champ uniforme. Sur une trajectoire fermée, le travail du champ électrostatique est toujours nul. Les champs possédant cette propriété sont appelés potentiels. En particulier, le champ électrostatique d'une charge ponctuelle a un caractère potentiel.
Le travail d'un champ potentiel peut être exprimé en termes de changement d'énergie potentielle. La formule est valable pour tout champ électrostatique.

7-11Si les lignes de champ d'un champ électrique uniforme d'intensité pénètrent dans une certaine zone S, alors le flux du vecteur d'intensité (auparavant nous appelions le nombre de lignes de champ à travers la zone) sera déterminé par la formule :

où En est le produit du vecteur et de la normale à une zone donnée (Fig. 2.5).

Riz. 2.5

Le nombre total de lignes de force traversant la surface S est appelé flux du vecteur intensité FU à travers cette surface.

Sous forme vectorielle, on peut écrire le produit scalaire de deux vecteurs, où vecteur .

Ainsi, le flux vectoriel est un scalaire qui, selon la valeur de l'angle α, peut être soit positif, soit négatif.

Regardons les exemples présentés dans les figures 2.6 et 2.7.

	Riz. 2.6	Riz. 2.7

Pour la figure 2.6, la surface A1 est entourée d'une charge positive et le flux est ici dirigé vers l'extérieur, c'est-à-dire La surface A2– est entourée d’une charge négative, ici elle est dirigée vers l’intérieur. Le flux total à travers la surface A est nul.

Pour la figure 2.7, le flux ne sera pas nul si la charge totale à l’intérieur de la surface n’est pas nulle. Pour cette configuration, le flux traversant la surface A est négatif (comptez le nombre de lignes de champ).

Ainsi, le flux du vecteur tension dépend de la charge. C'est le sens du théorème d'Ostrogradsky-Gauss.

Théorème de Gauss

La loi de Coulomb établie expérimentalement et le principe de superposition permettent de décrire pleinement le champ électrostatique d'un système de charges donné dans le vide. Cependant, les propriétés du champ électrostatique peuvent être exprimées sous une autre forme, plus générale, sans recourir à l'idée d'un champ coulombien de charge ponctuelle.

Introduisons une nouvelle grandeur physique caractérisant le champ électrique – le flux Φ du vecteur intensité du champ électrique. Supposons qu'il y ait une zone ΔS assez petite située dans l'espace où le champ électrique est créé. Le produit du module vectoriel par l'aire ΔS et le cosinus de l'angle α entre le vecteur et la normale au site est appelé flux élémentaire du vecteur intensité à travers le site ΔS (Fig. 1.3.1) :

Considérons maintenant une surface fermée arbitraire S. Si nous divisons cette surface en petites zones ΔSi, déterminons les flux élémentaires ΔΦi du champ à travers ces petites zones, puis les résumons, alors nous obtenons le flux Φ du vecteur passant par la surface fermée S (Fig. 1.3.2 ) :

Le théorème de Gauss énonce :

Le flux du vecteur d'intensité du champ électrostatique à travers une surface fermée arbitraire est égal à la somme algébrique des charges situées à l'intérieur de cette surface, divisée par la constante électrique ε0.

où R est le rayon de la sphère. Le flux Φ à travers une surface sphérique sera égal au produit de E et l'aire de la sphère 4πR2. Ainsi,

Entourons maintenant la charge ponctuelle d'une surface fermée arbitraire S et considérons une sphère auxiliaire de rayon R0 (Fig. 1.3.3).

Considérons un cône avec un petit angle solide ΔΩ au sommet. Ce cône mettra en évidence une petite aire ΔS0 sur la sphère, et une aire ΔS sur la surface S. Les flux élémentaires ΔΦ0 et ΔΦ traversant ces zones sont les mêmes. Vraiment,

De la même manière, on peut montrer que si une surface fermée S ne couvre pas une charge ponctuelle q, alors le flux Φ = 0. Un tel cas est représenté sur la Fig. 1.3.2. Toutes les lignes de force du champ électrique d'une charge ponctuelle pénètrent de part en part dans la surface fermée S. Il n’y a aucune charge à l’intérieur de la surface S, donc dans cette région les lignes de champ ne se rompent pas et ne se forment pas.

Une généralisation du théorème de Gauss au cas d'une distribution de charges arbitraire découle du principe de superposition. Le champ de toute distribution de charges peut être représenté comme une somme vectorielle des champs électriques de charges ponctuelles. Le flux Φ d'un système de charges à travers une surface fermée arbitraire S sera la somme des flux Φi des champs électriques de charges individuelles. Si la charge qi se trouve à l’intérieur de la surface S, alors sa contribution au flux est égale à si cette charge est à l’extérieur de la surface, alors la contribution de son champ électrique au flux sera égale à zéro.

Ainsi, le théorème de Gauss est prouvé.

Le théorème de Gauss est une conséquence de la loi de Coulomb et du principe de superposition. Mais si nous prenons l’énoncé contenu dans ce théorème comme axiome initial, alors sa conséquence sera la loi de Coulomb. Par conséquent, le théorème de Gauss est parfois appelé une formulation alternative de la loi de Coulomb.

En utilisant le théorème de Gauss, dans certains cas, il est possible de calculer facilement l'intensité du champ électrique autour d'un corps chargé si la distribution de charge donnée présente une certaine symétrie et si la structure générale du champ peut être devinée à l'avance.

Un exemple est le problème du calcul du champ d'un long cylindre à paroi mince, creux et uniformément chargé de rayon R. Ce problème a une symétrie axiale. Pour des raisons de symétrie, le champ électrique doit être dirigé selon le rayon. Par conséquent, pour appliquer le théorème de Gauss, il convient de choisir une surface fermée S en forme de cylindre coaxial d'un certain rayon r et longueur l, fermé aux deux extrémités (Fig. 1.3.4).

Pour r ≥ R, tout le flux du vecteur intensité traversera la surface latérale du cylindre dont l'aire est égale à 2πrl, puisque le flux passant par les deux bases est nul. L'application du théorème de Gauss donne :

Ce résultat ne dépend pas du rayon R du cylindre chargé, il s'applique donc également au domaine d'un long filament uniformément chargé.

Pour déterminer l'intensité du champ à l'intérieur d'un cylindre chargé, il est nécessaire de construire une surface fermée pour le cas r< R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.

De la même manière, on peut appliquer le théorème de Gauss pour déterminer le champ électrique dans un certain nombre d'autres cas où la distribution des charges présente une sorte de symétrie, par exemple une symétrie par rapport au centre, au plan ou à l'axe. Dans chacun de ces cas, il faut choisir une surface gaussienne fermée de forme appropriée. Par exemple, dans le cas d'une symétrie centrale, il convient de choisir une surface gaussienne en forme de sphère dont le centre est le point de symétrie. Avec une symétrie axiale, la surface fermée doit être choisie sous la forme d'un cylindre coaxial, fermé aux deux extrémités (comme dans l'exemple évoqué ci-dessus). Si la répartition des charges n'a aucune symétrie et que la structure générale du champ électrique ne peut être devinée, l'application du théorème de Gauss ne peut pas simplifier le problème de la détermination de l'intensité du champ.

Considérons un autre exemple de distribution de charge symétrique : déterminer le champ d'un plan uniformément chargé (Fig. 1.3.5).

Dans ce cas, il convient de choisir la surface gaussienne S sous la forme d'un cylindre d'une certaine longueur, fermé aux deux extrémités. L'axe du cylindre est dirigé perpendiculairement au plan chargé et ses extrémités sont situées à la même distance de celui-ci. En raison de la symétrie, le champ d’un plan uniformément chargé doit être partout dirigé le long de la normale. L'application du théorème de Gauss donne :

où σ est la densité de charge de surface, c'est-à-dire la charge par unité de surface.

L'expression résultante pour le champ électrique d'un plan uniformément chargé est également applicable dans le cas de zones chargées plates de taille finie. Dans ce cas, la distance entre le point auquel l'intensité du champ est déterminée et la zone chargée doit être nettement inférieure à la taille de la zone.

Et les horaires de 7h à 11h

1. L'intensité du champ électrostatique créé par une surface sphérique uniformément chargée.

Supposons qu'une surface sphérique de rayon R (Fig. 13.7) porte une charge q uniformément répartie, c'est-à-dire la densité de charge de surface en tout point de la sphère sera la même.

un. Entourons notre surface sphérique dans une surface symétrique S de rayon r>R. Le flux du vecteur tension à travers la surface S sera égal à

Par le théorème de Gauss

Ainsi

c. Traçons par le point B, situé à l'intérieur d'une surface sphérique chargée, une sphère S de rayon r

2. Champ électrostatique du ballon.

Disons une boule de rayon R, uniformément chargée de densité volumique.

En tout point A situé à l'extérieur du ballon à une distance r de son centre (r>R), son champ est similaire au champ d'une charge ponctuelle située au centre du ballon. Puis hors du ballon

(13.10)

et à sa surface (r=R)

(13.11)

Au point B, situé à l'intérieur de la balle à une distance r de son centre (r>R), le champ est déterminé uniquement par la charge enfermée à l'intérieur de la sphère de rayon r. Le flux du vecteur tension à travers cette sphère est égal à

d'autre part, conformément au théorème de Gauss

D'une comparaison des dernières expressions, il résulte

(13.12)

où est la constante diélectrique à l’intérieur de la balle. La dépendance de l'intensité du champ créé par une sphère chargée sur la distance jusqu'au centre de la balle est illustrée dans (Fig. 13.10)

Soit le plan ayant une étendue infinie et la charge par unité de surface égale à σ. Des lois de symétrie, il s'ensuit que le champ est dirigé partout perpendiculairement au plan, et s'il n'y a pas d'autres charges externes, alors les champs des deux côtés du plan doivent être les mêmes. Limitons une partie du plan chargé à une boîte cylindrique imaginaire, de sorte que la boîte soit coupée en deux et que ses constituants soient perpendiculaires, et que les deux bases, ayant chacune une aire S, soient parallèles au plan chargé (Figure 1.10).

Flux vectoriel total ; la tension est égale au vecteur multiplié par l'aire S de la première base, plus le flux du vecteur passant par la base opposée. Le flux de tension à travers la surface latérale du cylindre est nul, car les lignes de tension ne les coupent pas. Ainsi, Par contre, d'après le théorème de Gauss

Ainsi,

(13.15)

À l’extérieur de la plaque, les vecteurs de chacun d’eux sont dirigés dans des directions opposées et s’annulent. Par conséquent, l’intensité du champ dans l’espace entourant les plaques sera nulle E=0.

12. Champ d'une sphère uniformément chargée.

Laissez le champ électrique être créé par la charge Q, uniformément réparti sur la surface d'une sphère de rayon R.(Fig. 190). Pour calculer le potentiel de champ en un point arbitraire situé à distance rà partir du centre de la sphère, il faut calculer le travail effectué par le champ lors du déplacement d'une charge unitaire positive d'un point donné vers l'infini. Précédemment, nous avons prouvé que l’intensité du champ d’une sphère uniformément chargée à l’extérieur de celle-ci est équivalente au champ d’une charge ponctuelle située au centre de la sphère. Par conséquent, en dehors de la sphère, le potentiel de champ de la sphère coïncidera avec le potentiel de champ d'une charge ponctuelle.

φ (r)=Q 4πε 0r . (1)

En particulier, à la surface de la sphère le potentiel est égal à φ 0=Q 4πε 0R.. Il n'y a pas de champ électrostatique à l'intérieur de la sphère, donc le travail effectué pour déplacer une charge d'un point arbitraire situé à l'intérieur de la sphère jusqu'à sa surface est nul. UN= 0, donc la différence de potentiel entre ces points est également nulle Δ φ = -UN= 0. Par conséquent, tous les points à l'intérieur de la sphère ont le même potentiel, coïncidant avec le potentiel de sa surface φ 0=Q 4πε 0R. .

Ainsi, la distribution du potentiel de champ d'une sphère uniformément chargée a la forme (Fig. 191)

φ (r)=⎧⎩⎨Q 4πε 0R., npu r<QR 4πε 0r, npu r>R. . (2)

Attention, il n’y a pas de champ à l’intérieur de la sphère, et le potentiel est non nul ! Cet exemple illustre clairement le fait que le potentiel est déterminé par la valeur du champ d'un point donné jusqu'à l'infini.