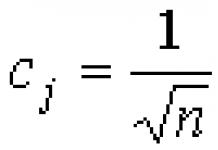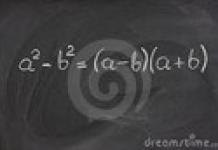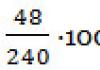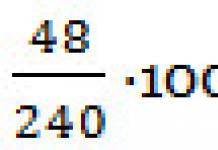Les solitons sont des ondes qui stockent des informations. Des ondes de choc. Ondes solitaires Que sont les solitons

annotation. Le rapport est consacré aux possibilités de l'approche soliton en biologie supramoléculaire, principalement pour modéliser une large classe de mouvements ondulatoires et oscillatoires naturels dans les organismes vivants. L'auteur a identifié de nombreux exemples de l'existence de processus supramoléculaires de type soliton (« biosolitons ») dans des phénomènes locomoteurs, métaboliques et autres de biomorphologie dynamique à diverses lignes et niveaux d'évolution biologique. Les biosolitons sont avant tout compris comme des déformations locales caractéristiques à bosse unique (unipolaires) se déplaçant le long d'un biocorps tout en conservant leur forme et leur vitesse.

Les solitons, parfois appelés « atomes d’onde », sont dotés de propriétés inhabituelles d’un point de vue classique (linéaire). Ils sont capables d’actes d’auto-organisation et d’auto-développement : autolocalisation ; captage d'énergie; reproduction et mort; formation d'ensembles avec une dynamique de nature palpitante et autre. Les solitons étaient connus dans le plasma, les cristaux liquides et solides, les liquides classiques, les réseaux non linéaires, les milieux magnétiques et autres milieux multidomaines, etc. La découverte des biosolitons indique qu'en raison de sa mécanochimie, la matière vivante est un milieu soliton avec une variété de propriétés physiologiques. utilisations des mécanismes solitons. Une chasse à la recherche en biologie est possible pour de nouveaux types de solitons - respirateurs, wobblers, pulsons, etc., déduits par les mathématiciens au « bout d'un stylo » et découverts ensuite seulement par les physiciens dans la nature. Le rapport est basé sur les monographies : S.V. Petukhov « Biosolitons. Fondamentaux de la biologie des solitons", 1999 ; S.V.Petukhov « Tableau bipériodique code génétique et le nombre de protons", 2001.

Les solitons sont un objet important de la physique moderne. Le développement intensif de leur théorie et de leurs applications a commencé après la publication en 1955 des travaux de Fermi, Paste et Ulam sur le calcul informatique des oscillations dans un système non linéaire simple d'une chaîne de poids reliés par des ressorts non linéaires. Bientôt le nécessaire méthodes mathématiques, vous permettant de résoudre des équations solitons, qui sont des équations aux dérivées partielles non linéaires. Les solitons, parfois appelés « atomes d’ondes », possèdent à la fois les propriétés d’ondes et de particules, mais ne sont au sens plein ni l’un ni l’autre, mais constituent un nouvel objet de la science mathématique. Ils sont dotés de propriétés inhabituelles d'un point de vue classique (linéaire). Les solitons sont capables d'actes d'auto-organisation et d'auto-développement : autolocalisation ; capter l'énergie venant de l'extérieur dans le milieu « soliton » ; reproduction et mort; la formation d'ensembles avec une morphologie non triviale et une dynamique de nature pulsée et autre ; auto-complication de ces ensembles lorsqu'une énergie supplémentaire pénètre dans l'environnement ; surmonter la tendance au désordre dans les milieux solitons les contenant ; etc. Elles peuvent être interprétées comme une forme spécifique d'organisation de l'énergie physique dans la matière, et on peut donc parler d'« énergie soliton » par analogie avec les expressions bien connues « énergie ondulatoire » ou « énergie vibratoire ». Les solitons sont réalisés comme des états de milieux (systèmes) non linéaires spéciaux et présentent des différences fondamentales par rapport aux ondes ordinaires. En particulier, les solitons sont souvent des caillots d'énergie stables et autolocalisés ayant la forme caractéristique d'une onde à bosse unique, se déplaçant en conservant leur forme et leur vitesse sans dissipation de leur énergie. Les solitons sont capables de collisions non destructives, c'est-à-dire sont capables de se traverser lors de leur rencontre sans se déformer. Ils ont de nombreuses applications technologiques.

Un soliton est généralement compris comme un objet semblable à une onde solitaire (une solution localisée d'une équation aux dérivées partielles non linéaire appartenant à une certaine classe d'équations dites solitons), qui est capable d'exister sans dissiper son énergie et, lorsqu'il interagit avec d'autres perturbations locales, retrouve toujours sa forme originale, c'est-à-dire . capable de collisions non destructives. Comme on le sait, les équations du soliton « apparaissent de la manière la plus naturelle lors de l'étude de systèmes de dispersion faiblement non linéaires de divers types à diverses échelles spatiales et temporelles. L'universalité de ces équations s'avère si étonnante que beaucoup étaient enclins à y voir quelque chose de magique... Mais il n'en est rien : les systèmes non linéaires dispersifs, faiblement amortis ou non, se comportent de la même manière, qu'ils soient rencontrés ou non dans le description de plasmas, de liquides classiques, de lasers ou de réseaux non linéaires". En conséquence, les solitons sont connus dans le plasma, les cristaux liquides et solides, les liquides classiques, les réseaux non linéaires, les milieux magnétiques et autres milieux multidomaines, etc. (Le mouvement des solitons dans les milieux réels n'est souvent pas de nature absolument non dissipative, accompagné de petits pertes d'énergie, que les théoriciens prennent en compte en ajoutant de petits termes dissipatifs dans les équations du soliton).

Notez que la matière vivante est pénétrée par de nombreux réseaux non linéaires : des réseaux de polymères moléculaires aux cytosquelettes supramoléculaires et à la matrice organique. Les réarrangements de ces réseaux ont une signification biologique importante et pourraient très bien se comporter à la manière d'un soliton. De plus, les solitons sont connus comme formes de mouvement des fronts de réarrangements de phase, par exemple dans cristaux liquides(voir, par exemple). Étant donné que de nombreux systèmes d'organismes vivants (y compris ceux à cristaux liquides) existent au bord de transitions de phase, il est naturel de croire que les fronts de leurs réarrangements de phases dans les organismes se déplaceront également souvent sous forme de solitons.

Même le découvreur des solitons, Scott Russell, a montré expérimentalement au siècle dernier qu'un soliton agit comme un concentrateur, un piège et un transporteur d'énergie et de matière, capable de collisions non destructives avec d'autres solitons et de perturbations locales. Il est évident que ces caractéristiques des solitons peuvent être bénéfiques pour les organismes vivants et que les mécanismes des biosolitons peuvent donc être spécialement cultivés dans la nature vivante par des mécanismes. sélection naturelle. Énumérons quelques-uns de ces avantages :

- 1) la capture spontanée de l'énergie, de la matière, etc., ainsi que leur concentration locale spontanée (autolocalisation) et leur transport soigné et sans perte sous forme galénique au sein de l'organisme ;
- 2) facilité de contrôle des flux d'énergie, de matière, etc. (lorsqu'ils sont organisés sous forme soliton) du fait de la commutation locale possible des caractéristiques de non-linéarité de l'environnement biologique du type soliton au type non-linéarité non-soliton et vice versa ;
- 3) découplage pour beaucoup de ceux qui se produisent simultanément et en un seul endroit du corps, c'est-à-dire processus qui se chevauchent (locomoteur, vascularisation, métabolique, croissance, morphogénétique, etc.), qui nécessitent une relative indépendance de leur évolution. Ce découplage peut être assuré précisément par la capacité des solitons à subir des collisions non destructives.

Notre première étude des processus coopératifs supramoléculaires dans les organismes vivants du point de vue des solitons a révélé la présence en eux de nombreux processus macroscopiques de type soliton. Le sujet d’étude était avant tout les mouvements locomoteurs et autres mouvements biologiques directement observés, dont les biologistes ont longtemps supposé la haute efficacité énergétique. Lors de la première étape de l'étude, nous avons découvert que chez de nombreux organismes vivants, les macromouvements biologiques ont souvent l'apparence d'un soliton, une onde caractéristique de déformation locale à bosse unique, se déplaçant le long d'un corps vivant tout en conservant sa forme et sa vitesse et démontrant parfois la capacité de collisions non destructives. Ces « biosolitons » sont réalisés à diverses branches et niveaux d’évolution biologique dans des organismes dont la taille diffère de plusieurs ordres de grandeur.

Le rapport présente de nombreux exemples de tels biosolitons. En particulier, un exemple de rampement de l'escargot Helix est considéré, qui se produit en raison d'une déformation en forme de vague à bosse unique traversant son corps tout en conservant sa forme et sa vitesse. Des enregistrements détaillés de ce type de mouvement biologique sont tirés du livre. Dans une version de ramper (avec une « démarche »), l’escargot subit des déformations de traction locales le long de la surface d’appui de son corps d’avant en arrière. Dans une autre version plus lente de l'exploration, des déformations de compression locales se produisent le long de la même surface du corps, allant dans la direction opposée de la queue à la tête. Ces deux types de déformations du soliton, directes et rétrogrades, peuvent se produire simultanément dans la cochlée avec des contre-collisions entre elles. Nous soulignons que leur collision est non destructive, caractéristique des solitons. En d’autres termes, après une collision, elles conservent leur forme et leur vitesse, c’est-à-dire leur individualité : « la présence de grandes ondes rétrogrades n’affecte pas la propagation des ondes normales et de nombreuses ondes directes plus courtes ; les deux types d’ondes se propageaient sans aucun signe d’interférence mutuelle. » Ce fait biologique est connu depuis le début du siècle, même si les chercheurs n'ont jamais été associés aux solitons auparavant.

Comme l’ont souligné Gray et d’autres classiques de l’étude de la locomotion (mouvements spatiaux des organismes), ces derniers sont des processus très économes en énergie. Ceci est essentiel à la capacité vitale du corps à se déplacer sans fatigue. longues distancesà la recherche de nourriture, pour échapper au danger, etc. (les organismes manipulent généralement l'énergie avec une extrême prudence, ce qui n'est pas du tout facile pour eux de la stocker). Ainsi, dans une cochlée, la déformation locale soliton du corps, grâce à laquelle son corps se déplace dans l'espace, ne se produit que dans la zone de séparation du corps de la surface d'appui. Ainsi toute la partie du corps en contact avec le support n'est pas déformée et est au repos par rapport au support. En conséquence, pendant toute la période de déformation de type soliton traversant le corps de la cochlée, une telle locomotion ondulatoire (ou processus de transfert de masse) ne nécessite pas de dépense d'énergie pour vaincre les forces de frottement de la cochlée sur le support, étant à cet égard aussi économique que possible. Bien entendu, on peut supposer qu’une partie de l’énergie lors de la locomotion est encore dissipée par le frottement mutuel des tissus à l’intérieur du corps de la cochlée. Mais si cette onde locomotrice ressemble à un soliton, elle assure également une minimisation des pertes par frottement à l’intérieur du corps. (À notre connaissance, la question des pertes d'énergie dues aux frottements intracorporels lors de la locomotion n'a pas été suffisamment étudiée expérimentalement, cependant, il est peu probable que le corps ait manqué l'occasion de les minimiser). Avec l'organisation de la locomotion considérée ci-dessus, tous (ou presque tous) les coûts énergétiques sont réduits aux coûts de création initiale de chacune de ces déformations locales de type soliton. C’est la physique des solitons qui offre des possibilités de gestion de l’énergie extrêmement économes en énergie. Et son utilisation par les organismes vivants semble logique, d'autant plus que le monde saturé de milieux solitons et de solitons.

Il convient de noter que, au moins depuis le début du siècle, les chercheurs ont représenté la locomotion ondulatoire comme une sorte de processus de relais. À cette époque de la « physique pré-solitonique », l’analogie physique naturelle d’un tel processus de relais était le processus de combustion, dans lequel la déformation corporelle locale était transférée d’un point à l’autre comme une inflammation. Cette idée de processus dissipatifs en relais tels que la combustion, appelés processus à ondes automatiques de nos jours, était la meilleure possible à l'époque et elle est depuis longtemps devenue familière à beaucoup. Cependant, la physique elle-même n’est pas restée immobile. Et au cours des dernières décennies, il a développé l'idée des solitons en tant que nouveau type de processus de relais non dissipatifs de la plus haute efficacité énergétique avec des propriétés paradoxales auparavant inimaginables, qui constituent la base d'une nouvelle classe de modèles non linéaires de processus de relais. .

L'un des avantages importants de l'approche soliton par rapport à l'approche traditionnelle des ondes automatiques lors de la modélisation des processus dans un organisme vivant est déterminé par la capacité des solitons à subir des collisions non destructives. En effet, les auto-ondes (décrivant par exemple le mouvement d'une zone de combustion le long d'un cordon brûlant) se caractérisent par le fait que derrière elles subsiste une zone d'inexcitabilité (un cordon brûlé), et donc deux auto-ondes, lorsqu'elles entrent en collision. , cessent d'exister, ne pouvant plus se déplacer dans la zone déjà « incendiée ». Mais dans les zones d'un organisme vivant, de nombreux processus biomécaniques se produisent simultanément - locomoteurs, sanguins, métaboliques, de croissance, morphogénétiques, etc., et donc, en les modélisant avec des ondes automatiques, le théoricien est confronté au problème suivant de destruction mutuelle des ondes automatiques. Un processus d'auto-ondes, se déplaçant à travers la zone du corps considérée en raison de la combustion continue des réserves d'énergie sur celle-ci, rend cet environnement inexcitable pour d'autres auto-ondes pendant un certain temps jusqu'à ce que les réserves d'énergie pour leur existence soient restaurées dans cette zone. Dans la matière vivante, ce problème est particulièrement pertinent également parce que les types de réserves énergétiques et chimiques qu'elle contient sont hautement unifiés (les organismes ont une monnaie énergétique universelle - ATP). Par conséquent, il est difficile de croire que l'existence simultanée de nombreux processus dans une zone du corps soit assurée par le fait que chaque processus d'auto-onde dans le corps se déplace en brûlant son type d'énergie spécifique, sans brûler d'énergie pendant autres. Pour les modèles de solitons, ce problème de destruction mutuelle de processus biomécaniques entrant en collision en un seul endroit n'existe en principe pas, puisque les solitons, en raison de leur capacité à des collisions non destructives, se croisent calmement et dans une zone en même temps leur nombre peut être aussi grand que désiré. D'après nos données, l'équation sinus-Gordon du soliton et ses généralisations revêtent une importance particulière pour la modélisation des phénomènes biosoliton de la matière vivante.

Comme on le sait, dans les milieux multidomaines (aimants, ferroélectriques, supraconducteurs, etc.), les solitons agissent comme des parois interdomaines. Dans la matière vivante, le phénomène de polydomaine joue un rôle important dans les processus morphogénétiques. Comme dans d'autres milieux multidomaines, dans les milieux biologiques multidomaines, il est associé au principe classique de Landau-Lifshitz de minimisation de l'énergie dans le milieu. Dans ces cas, les parois interdomaines des solitons s'avèrent être des lieux de concentration énergétique accrue, dans lesquels les réactions biochimiques se produisent souvent particulièrement activement.

La capacité des solitons à jouer le rôle de locomotives transportant des portions de matière vers l'endroit souhaité au sein d'un environnement soliton (organisme) selon les lois de la dynamique non linéaire mérite également toute l'attention en lien avec les problèmes bioévolutifs et physiologiques. Ajoutons que l'énergie physique du biosoliton est capable de coexister harmonieusement dans un organisme vivant avec les types chimiques connus de son énergie. Le développement du concept de biosolitons permet notamment d’ouvrir une « chasse » de recherche en biologie aux analogues différents types solitons - respirateurs, wobblers, pulsons, etc., dérivés par les mathématiciens « du bout de leur plume » lors de l'analyse des équations des solitons et ensuite découverts par les physiciens dans la nature. De nombreux processus physiologiques oscillatoires et ondulatoires peuvent éventuellement recevoir des modèles solitons significatifs pour leur description, associés à la nature soliton non linéaire de la matière vivante biopolymère.

Par exemple, cela s’applique aux mouvements physiologiques de base d’une substance biopolymère vivante, comme les battements cardiaques, etc. Rappelons que embryon humainà l'âge de trois semaines, alors qu'il ne mesure que quatre millimètres, le cœur est le premier à bouger. Le début de l'activité cardiaque est dû à certains mécanismes énergétiques internes, car à ce moment-là, le cœur ne dispose pas encore de connexions nerveuses pour contrôler ces contractions et il commence à se contracter lorsqu'il n'y a toujours pas de sang à pomper. À ce stade, l’embryon lui-même est essentiellement un morceau de mucus polymère dans lequel l’énergie interne s’auto-organise en pulsations économes en énergie. Une chose similaire peut être dite à propos de l'apparition de battements cardiaques dans les œufs et les œufs d'animaux, où l'apport d'énergie de l'extérieur est minimisé par l'existence de la coquille et d'autres enveloppes isolantes. Des formes similaires d'auto-organisation et d'autolocalisation énergétiques sont connues dans les milieux polymères, y compris les types non biologiques et idées modernes ont une nature de soliton, puisque les solitons sont les structures auto-organisatrices les plus économes en énergie (non dissipatives ou peu dissipatives) de nature pulsée et autre. Les solitons sont réalisés dans une variété de milieux naturels entourant les organismes vivants : cristaux solides et liquides, liquides classiques, aimants, structures en treillis, plasma, etc. L'évolution de la matière vivante avec ses mécanismes de sélection naturelle n'est pas passée par les propriétés uniques des solitons. et leurs ensembles.

Ces matériaux ont-ils quelque chose à voir avec une synergie ? Oui définitivement. Comme défini dans la monographie de Hagen /6, p.4/, « dans le cadre de la synergie, une telle action conjointe de parties individuelles de tout système désordonné est étudiée, à la suite de laquelle se produit une auto-organisation - macroscopique spatiale, temporelle ou spatio-temporelle. des structures apparaissent et sont considérées comme des processus déterministes et stochastiques. Il existe de nombreux types de processus et de systèmes non linéaires étudiés dans le cadre de la synergie. Kurdyumov et Knyazeva /7, p.15/, énumérant un certain nombre de ces types, notent spécifiquement que parmi eux, l'un des plus importants et des plus étudiés est celui des solitons. DANS dernières années a commencé à publier revue internationale"Chaos, solitons et fractales". Les solitons observés dans une grande variété de milieux naturels sont exemple brillant comportement coopératif non linéaire de nombreux éléments du système, conduisant à la formation de structures spatiales, temporelles et spatio-temporelles spécifiques. Le plus célèbre, bien que loin d'être le seul type de telles structures solitons, est la déformation locale auto-localisée à bosse unique du milieu décrit ci-dessus, de forme stable, fonctionnant à une vitesse constante. Les solitons sont activement utilisés et étudiés dans physique moderne. Depuis 1973, depuis les travaux de Davydov /8/, les solitons sont également utilisés en biologie pour modéliser des processus de biologie moléculaire. Il existe actuellement de nombreuses publications dans le monde entier sur l’utilisation de tels « solitons moléculaires » en biologie moléculaire, en particulier pour comprendre les processus dans les protéines et l’ADN. Nos travaux /3, 9/ ont été les premières publications dans la littérature mondiale sur le thème des « solitons supramoléculaires » dans les phénomènes biologiques au niveau supramoléculaire. Nous soulignons que l'existence de biosolitons moléculaires (qui, selon de nombreux auteurs, reste encore à prouver) n'implique en aucun cas l'existence de solitons dans des processus biologiques supramoléculaires coopératifs qui unissent des myriades de molécules.

LITTÉRATURE:

Dodd R. et al. Solitons et équations d'ondes non linéaires. M., 1988, 694 p.
Kamenski V.G. JETP, 1984, v. 87, numéro. 4(10), p. 1262-1277.
Petoukhov S.V. Biosolitons. Fondamentaux de la biologie des solitons. – M., 1999, 288 p.
Gray J. Locomotion animale. Londres, 1968.
Petoukhov S.V. Tableau bipériodique du code génétique et du nombre de protons. – M., 2001, 258 p.
Hagen G. Synergique. – M., Mir, 1980, 404 p.
Knyazeva E.N., Kurdyumov S.P. Lois d'évolution et d'auto-organisation des systèmes complexes. M., Nauka, 1994, 220 p.
Davydov A.S. Solitons en biologie. – Kyiv, Naukova Dumka, 1979.
Petoukhov S.V. Solitons en biomécanique. Déposé chez VINITI RAS le 12 février 1999, n° 471-B99. (Index de VINITI « Travaux scientifiques déposés », n°4, 1999)

Résumé . Le rapport discute des opportunités ouvertes par une approche solitonique de la biologie supramoléculaire, tout d'abord pour modéliser une large classe de mouvements naturels d'ondes dans les organismes vivants. Les résultats des recherches de l’auteur démontrent l’existence de processus supramoléculaires de type soliton dans les manifestations locomotrices, métaboliques et autres de la biomorphologie dynamique sur une grande variété de branches et de niveaux d’évolution biologique.

Les solitons, parfois appelés « atomes d'onde », ont des propriétés inhabituelles du point de vue classique (linéaire). Ils ont la capacité de s’auto-organiser : auto-localisations ; captage d'énergie; formation d'ensembles avec une dynamique de pulsations et d'autres personnages. Les solitons étaient connus dans le plasma, les cristaux liquides et fermes, les liquides classiques, les réseaux non linéaires, les matières magnétiques et autres poly-domaines, etc. La découverte des biosolitons souligne que la mécanochimie biologique fait de la matière vivante un environnement solitonique offrant des possibilités d'utilisations physiologiques diverses des mécanismes solitoniques. Le rapport est basé sur les livres : S.V. Petoukhov « Biosolitons. Bases de la biologie solitonique", Moscou, 1999 (en russe).

Petukhov S.V., Solitons dans les processus biologiques coopératifs au niveau supramoléculaire // "Académie du Trinitarisme", M., El n° 77-6567, pub. 13240, 21/04/2006

), qui à chaque instant est localisée dans une région finie de l’espace et change relativement lentement de structure au fur et à mesure de sa propagation.

Exemples d'ondes solitaires : a - élévation stationnaire (soliton) en eau peu profonde ; h - déplacement de la surface du liquide ; b - petite amplitude dans le gaz ; p - changement de pression ; c - excitations dans l'axone nerveux ; et - les membranes. La variable est tracée le long de l'axe des abscisses

Typique U.v. a la forme d'une seule impulsion ou d'une goutte (Fig.), mais les U.V. peut avoir une structure plus complexe.

Dans un sens plus étroit, sous U. siècle. comprendre une onde non linéaire stationnaire localisée, se propageant sans changer de forme à une vitesse constante et décrite par des équations en dérivées ordinaires. Dans l'espace des phases des UV. réponses, reliant deux points d’équilibre différents ou revenant au même point. À U. c. inclure, par exemple, des types d'ondes non linéaires telles que les ondes de choc dans un milieu dissipatif, les ondes d'excitation pulsées stationnaires dans un milieu actif (par exemple) et dans un milieu sans perte.

Physique Dictionnaire encyclopédique. - M. : Encyclopédie soviétique. . 1983 .

VAGUE DE SOLITUDE

Mouvement des vagues (voir Vagues), qui à chaque instant du temps est localisé dans une région finie de l'espace et diminue assez rapidement avec l'éloignement de cette région. Typique U.v. a la forme d'une seule impulsion ou d'une goutte (Fig.), mais les U.V. peut avoir une structure plus complexe.

Dans un sens plus étroit, sous U. siècle. comprendre une onde non linéaire stationnaire localisée qui se propage sans changer de forme depuis le poteau. vitesse et décrit par des équations en dérivées ordinaires. DANS espace des phases U.V. correspond à la trajectoire reliant les deux différents. point d’équilibre ou retour au même point. À U. c. inclure, par exemple, des types d'ondes non linéaires telles que des ondes de choc dans un milieu dissipatif, des ondes d'excitation pulsées stationnaires dans un milieu actif (par exemple, un influx nerveux) et un soliton dans un milieu sans perte. Allumé. voir sous l'art. Soliton. L.A. Ostrovsky.

Exemples de vagues solitaires : UN -élévation stationnaire (solitone) en eau peu profonde ; h- déplacement de la surface du liquide ; b- onde de choc de faible amplitude dans le gaz ; p- changement de pression; V- impulsion d'excitation dans l'axone nerveux; Et - potentiel membranaire. La variable est tracée le long de l'axe des abscisses Où t- temps, X-coordonner, tu- vitesse des vagues solitaires.

Encyclopédie physique. En 5 tomes. - M. : Encyclopédie soviétique. Rédacteur en chef A. M. Prokhorov. 1988 .

Voyez ce qu'est « SOLINET WAVE » dans d'autres dictionnaires :

- (onde solitaire), une onde solitaire structurellement stable, qui, en se propageant, ne se dilate pas et conserve sa forme et sa vitesse. Les solitons se comportent comme des particules. Ils sont importants dans de nombreux domaines de la MÉCANIQUE DES FLUIDES, ainsi que de la PHYSIQUE DES SOLIDES... ... Dictionnaire encyclopédique scientifique et technique

Onde solitaire structurellement stable se propageant dans un milieu non linéaire. Les solitons se comportent comme des particules (onde de type particule) : lorsqu'ils interagissent entre eux ou avec d'autres perturbations, ils ne s'effondrent pas, mais divergent,... ... Dictionnaire encyclopédique

Soliton- une onde solitaire structurellement stable se propageant dans un milieu non linéaire, qui peut être caractérisée comme une onde de type particule, particule... Les débuts des sciences naturelles modernes

1) L. t. en théorie descriptive des ensembles : topologique. une application entre deux ensembles in peut être étendue à un homéomorphisme de certains ensembles de types les contenant. Une conséquence de cette théorie linéaire est topologique. Invariance de type Hausdorff... Encyclopédie mathématique

Les ondes suivantes sont décrites ici : a) les vagues d'eau, b) les ondes sonores de l'air, c) les ondes lumineuses, d) les ondes électriques et e) la théorie mathématique. A) Les vagues dans l'eau sont généralement le résultat d'un impact indirect du vent sur l'eau. Cela rend la surface de l'eau concave, mais... ... Dictionnaire encyclopédique F.A. Brockhaus et I.A. Éfron

Après calculs et recherche d'analogies, ces scientifiques ont établi que l'équation utilisée par Fermi, Pasta et Ulam, avec une diminution de la distance entre les poids et avec une augmentation illimitée de leur nombre, se transforme en équation de Korteweg-de Vries. Autrement dit, le problème proposé par Fermi était réduit à la solution numérique de l'équation de Korteweg-de Vries, proposée en 1895 pour décrire l'onde solitaire de Russell. Vers les mêmes années, il a été démontré que l'équation de Korteweg-de Vries est également utilisée pour décrire les ondes acoustiques ioniques dans le plasma. Il est alors devenu clair que cette équation se produit dans de nombreux domaines de la physique et que, par conséquent, l’onde solitaire décrite par cette équation est un phénomène largement répandu.

Poursuivant leurs expériences informatiques pour simuler la propagation de telles ondes, Kruskal et Zabuski ont envisagé leur collision. Arrêtons-nous plus en détail sur la discussion de ce fait remarquable. Supposons qu'il y ait deux ondes solitaires décrites par l'équation de Korteweg-de Vries, qui diffèrent en amplitude et se déplacent l'une après l'autre dans la même direction (Fig. 2). De la formule des ondes solitaires (8), il résulte que la vitesse de déplacement de ces ondes est d'autant plus élevée que leur amplitude est grande et que la largeur du pic diminue avec l'augmentation de l'amplitude. Ainsi, les hautes vagues solitaires se déplacent plus rapidement. Une vague de plus grande amplitude rattrapera une vague de plus petite amplitude qui avance. Puis, pendant un certain temps, les deux vagues se déplaceront ensemble comme un tout, interagissant l’une avec l’autre, puis se sépareront. Une propriété remarquable de ces ondes est qu'après leur interaction, la forme et

Riz. 2. Deux solitons décrits par l'équation de Korteweg-de Vries,

avant l'interaction (en haut) et après (en bas)

la vitesse de ces ondes est restaurée. Après la collision, les deux vagues ne se déplacent que sur une certaine distance par rapport à la façon dont elles se seraient déplacées sans interaction.

Le processus dans lequel la forme et la vitesse sont préservées après l'interaction des ondes ressemble à une collision élastique de deux particules. Par conséquent, Kruskal et Zabuski ont appelé ces ondes solitaires solitons (de l'anglais solitaire - solitaire). C'est un nom spécial pour les ondes solitaires, en accord avec l'électron, le proton et bien d'autres. particules élémentaires, est désormais généralement accepté.

Les ondes solitaires découvertes par Russell se comportent en réalité comme des particules. La grande vague ne traverse pas la petite lorsqu’elles interagissent. Lorsque des ondes solitaires entrent en contact, la grande vague ralentit et diminue, et la vague qui était petite, au contraire, accélère et grandit. Et quand petite vague grandit jusqu'à la taille d'un grand, et le grand diminue jusqu'à la taille d'un petit, les solitons se séparent et le plus grand avance. Ainsi, les solitons se comportent comme des balles de tennis élastiques.

Définissons un soliton. Soliton est appelée une onde solitaire non linéaire, qui conserve sa forme et sa vitesse lors de son propre mouvement et de sa collision avec des ondes solitaires similaires, c'est-à-dire qu'il s'agit d'une formation stable. Le seul résultat de l’interaction des solitons peut être un déphasage.

Les découvertes associées à l'équation de Korteweg-de Vries ne se sont pas arrêtées à la découverte du soliton. La prochaine étape importante liée à cette équation remarquable a été la création d’une nouvelle méthode de résolution d’équations aux dérivées partielles non linéaires. Il est bien connu qu’il est très difficile de trouver des solutions aux équations non linéaires. Jusque dans les années 60 de notre siècle, on croyait que de telles équations ne pouvaient avoir que certaines solutions partielles satisfaisant des conditions initiales spécialement spécifiées. Cependant, l’équation de Korteweg-de Vries s’est également révélée dans une position exceptionnelle dans ce cas.

En 1967, les physiciens américains K.S. Gardner, J.M. Green, M. Kruskal et R. Miura ont montré qu'une solution de l'équation de Korteweg-de Vries peut en principe être obtenue pour toutes les conditions initiales, qui d'une certaine manière disparaissent lorsque la coordonnée tend vers l'infini. Ils ont utilisé une transformation de l'équation de Korteweg-de Vries en un système de deux équations, désormais appelé paire de Lax (en hommage au mathématicien américain Peter Lax, qui a apporté une contribution majeure au développement de la théorie des solitons), et ont découvert une nouvelle méthode pour résoudre un certain nombre d'équations aux dérivées partielles non linéaires très importantes. Cette méthode est appelée méthode du problème de diffusion inverse, car elle utilise essentiellement la solution du problème de mécanique quantique consistant à reconstruire le potentiel à partir de données de diffusion.

2.2. Soliton de groupe

Nous avons dit plus haut que dans la pratique, les vagues se propagent généralement en groupes. Les gens ont observé des groupes de vagues similaires sur l’eau depuis des temps immémoriaux. La question de savoir pourquoi les « groupes » de vagues sont si typiques des vagues sur l'eau n'a été résolue que par T. Benjamin et J. Feyer en 1967. À l'aide de calculs théoriques, ils ont montré qu'une simple vague périodique en eau profonde est instable (ce phénomène est maintenant appelé instabilité de Benjamin-Feuer) et que les vagues d'eau sont donc divisées en groupes en raison de l'instabilité. L'équation qui décrit la propagation des groupes d'ondes sur l'eau a été obtenue par V.E. Zakharov en 1968. À cette époque, cette équation était déjà connue en physique et s’appelait l’équation non linéaire de Schrödinger. En 1971, V.E. Zakharov et A.B. Shabat a montré que cette équation non linéaire a également des solutions sous forme de solitons ; de plus, l'équation non linéaire de Schrödinger, ainsi que l'équation de Korteweg-de Vries, peuvent être intégrées par la méthode du problème de diffusion inverse. Les solitons de l'équation non linéaire de Schrödinger diffèrent des solitons de Korteweg-de Vries évoqués ci-dessus en ce qu'ils correspondent à la forme de l'enveloppe d'un groupe d'ondes. Extérieurement, ils ressemblent à des ondes radio modulées. Ces solitons sont appelés solitons de groupe, et parfois solitons d'enveloppe. Ce nom reflète la persistance de l'enveloppe du paquet d'ondes lors de l'interaction (analogue à la ligne pointillée présentée sur la Fig. 3), bien que les ondes elles-mêmes sous l'enveloppe se déplacent à une vitesse différente de celle du groupe. Dans ce cas, la forme de l'enveloppe est décrite

Riz. 3. Exemple de soliton de groupe (ligne pointillée)

dépendance

a(x,t)=a 0 cosh -1 ( )

Où un un - l'amplitude, et je- la moitié de la taille du soliton. Il y a généralement entre 14 et 20 ondes sous l’enveloppe du soliton, l’onde médiane étant la plus grande. À cela s’ajoute le fait bien connu que la vague la plus élevée d’un groupe sur l’eau se situe entre la septième et la dixième (neuvième vague). Si un groupe de vagues s'est formé grande quantité vagues, puis il se désintégrera en plusieurs groupes.

L'équation non linéaire de Schrödinger, comme l'équation de Korteweg-de Vries, est également largement utilisée pour décrire les ondes dans divers domaines de la physique. Cette équation a été proposée en 1926 par l'éminent physicien autrichien E. Schrödinger pour l'analyse propriétés fondamentales systèmes quantiques et était à l'origine utilisé pour décrire l'interaction des particules intraatomiques. L'équation de Schrödinger généralisée ou non linéaire décrit un ensemble de phénomènes dans la physique des processus ondulatoires. Par exemple, il est utilisé pour décrire l'effet d'autofocalisation lorsqu'il est exposé à un faisceau laser de haute puissance sur un milieu diélectrique non linéaire et pour décrire la propagation d'ondes non linéaires dans un plasma.

3. Énoncé du problème

3.1. Description du modèle. Actuellement, l’étude des processus ondulatoires non linéaires suscite un intérêt croissant. divers domaines physique (par exemple optique, physique des plasmas, radiophysique, hydrodynamique, etc.). Pour étudier les ondes d'amplitude petite mais finie dans les milieux dispersifs, l'équation de Korteweg-de Vries (KdV) est souvent utilisée comme équation modèle :

toit+ ii x +bet xxx = 0(3.1)

L'équation KdV a été utilisée pour décrire les ondes magnétosoniques se propageant strictement à travers champ magnétique ou à des angles proches de

Les principales hypothèses faites lors de l'élaboration de l'équation sont : 1) une amplitude petite mais finie, 2) la longueur d'onde est grande par rapport à la longueur de dispersion.

En compensant l'effet de non-linéarité, la dispersion permet à des ondes stationnaires d'amplitude finie - solitaires et périodiques - de se former dans un milieu dispersif. Les ondes solitaires pour l'équation KdV après le début des travaux ont commencé à être appelées solitons. Les ondes périodiques sont appelées ondes cnoïdales. Les formules correspondantes pour leur description sont données dans.

3.2. Énoncé du problème différentiel. L'ouvrage examine la solution numérique du problème de Cauchy pour l'équation de Korteweg-de Vries avec des conditions périodiques dans l'espace dans un rectangle. QT={(t, X):0< t< T, XÎ [0, je].

toit+ ii x +bet xxx = 0(3.2)

u(x,t)| x=0 =u(x,t)| x=l(3.3)

avec condition initiale

u(x,t)| t=0 =u 0 (x) (3.4)

4. Propriétés de l'équation de Korteweg-de Vries

4.1. Bref aperçu résultats pour l’équation KdV. Problème de Cauchy pour l’équation KdV sous diverses hypothèses concernant toi 0 (X) a été envisagée dans de nombreux travaux. Le problème de l'existence et de l'unicité d'une solution avec des conditions de périodicité comme conditions aux limites a été résolu dans le travail utilisant la méthode des différences finies. Plus tard, sous des hypothèses moins fortes, l'existence et l'unicité ont été prouvées dans l'article dans l'espace L ¥ (0,T,H s (R 1)), où s>3/2, et dans le cas d'un problème périodique - dans l'espace L ¥ (0 ,T,H ¥ (C))où C est un cercle de longueur égale à la période, en russe ces résultats sont présentés dans le livre.

Dans le cours actuel, les séminaires ont commencé à consister non pas à résoudre des problèmes, mais à rédiger des rapports sur divers sujets. Je pense qu'il serait correct de les laisser ici sous une forme plus ou moins populaire.

Le mot « soliton » vient de l’anglais solitaire wave et désigne précisément une onde solitaire (ou, dans le langage de la physique, une certaine excitation).

Soliton près de l'île de Molokai (archipel hawaïen)

Un tsunami est aussi un soliton, mais beaucoup plus gros. La solitude ne signifie pas qu’il n’y aura qu’une seule vague pour le monde entier. Les solitons se présentent parfois en groupes, comme près de la Birmanie.

Solitons dans la mer d'Andaman, baignant les côtes de la Birmanie, du Bengale et de la Thaïlande.

Au sens mathématique, un soliton est une solution à une équation aux dérivées partielles non linéaire. Cela signifie ce qui suit. L'humanité est capable de résoudre des équations linéaires, à la fois ordinaires et différentielles, depuis longtemps. Mais dès qu'un carré, un cube ou une dépendance encore plus astucieuse apparaît dans une équation différentielle sur une quantité inconnue, l'appareil mathématique développé au cours de tous les siècles échoue - une personne n'a pas encore appris à les résoudre et les solutions sont le plus souvent devinées ou sélectionnées. à partir de diverses considérations. Mais ce sont eux qui décrivent la Nature. Ainsi, les dépendances non linéaires donnent naissance à presque tous les phénomènes qui captivent l'œil, et permettent également à la vie d'exister. Un arc-en-ciel dans sa profondeur mathématique est décrit par la fonction Airy (n'est-ce pas un nom révélateur pour un scientifique dont les recherches parlent d'arcs-en-ciel ?)

Les contractions du cœur humain en sont un exemple typique processus biochimiques, appelés autocatalytiques - ceux qui soutiennent leur propre existence. Toutes les dépendances linéaires et la proportionnalité directe, bien que simples à analyser, sont ennuyeuses : rien n'y change, car la droite reste la même à l'origine et jusqu'à l'infini. Plus fonctions complexes ont des points particuliers : minimums, maximums, défauts, etc., qui, une fois dans l'équation, créent d'innombrables variations pour le développement des systèmes.

Les fonctions, objets ou phénomènes appelés solitons ont deux propriétés importantes : ils sont stables dans le temps et conservent leur forme. Bien sûr, dans la vie, personne ni rien ne les satisfera indéfiniment, il faut donc les comparer avec des phénomènes similaires. De retour à la surface de la mer, des ondulations apparaissent et disparaissent en une fraction de seconde, de grosses vagues, ballottées par le vent, décollent et se dispersent en éclaboussures. Mais le tsunami se déplace comme un mur blanc sur des centaines de kilomètres sans perdre sensiblement la hauteur et la force des vagues.

Il existe plusieurs types d'équations conduisant aux solitons. C’est d’abord le problème Sturm-Liouville

En théorie quantique, cette équation est connue sous le nom d’équation de Schrödinger non linéaire si la fonction a une forme arbitraire. Dans cette notation, le nombre est appelé nombre propre. Il est si spécial qu'on le retrouve également lors de la résolution d'un problème, car toutes ses valeurs ne peuvent pas apporter une solution. Le rôle des valeurs propres en physique est très important. Par exemple, l’énergie est une valeur propre dans mécanique quantique, les transitions entre différents systèmes de coordonnées ne peuvent pas non plus se faire sans eux. Si vous souhaitez qu'un paramètre change t in n'a pas changé les valeurs propres (et t peut être le temps, par exemple, ou une influence externe sur le système physique), alors nous arrivons à l'équation de Korteweg-de Vries :

Il existe d’autres équations, mais elles ne sont plus si importantes actuellement.

En optique, le phénomène de dispersion joue un rôle fondamental - la dépendance de la fréquence d'une onde sur sa longueur, ou plutôt ce qu'on appelle le nombre d'onde :

Dans le cas le plus simple, elle peut être linéaire (où est la vitesse de la lumière). Dans la vie, nous obtenons souvent le nombre d’onde carré, ou même quelque chose de plus délicat. En pratique, la dispersion limite la bande passante de la fibre optique sur laquelle ces mots viennent de parvenir à votre FAI depuis les serveurs WordPress. Mais il permet également de transmettre non pas un seul faisceau, mais plusieurs, via une seule fibre optique. Et en termes d'optique, les équations ci-dessus considèrent les cas de dispersion les plus simples.

Les solitons peuvent être classés de différentes manières. Par exemple, les solitons qui apparaissent comme une sorte d'abstraction mathématique dans des systèmes sans frottement ni autres pertes d'énergie sont appelés conservateurs. Si nous considérons le même tsunami sur une période pas très longue (et cela devrait être plus sain pour la santé), alors ce sera un soliton conservateur. D'autres solitons n'existent que grâce aux flux de matière et d'énergie. Ils sont généralement appelés autosolitons, et nous parlerons plus loin des autosolitons.

En optique, on parle aussi de solitons temporels et spatiaux. D'après le nom, il devient clair si nous observerons un soliton comme une sorte d'onde dans l'espace ou s'il s'agira d'une explosion dans le temps. Les temporaires surviennent en raison de l'équilibrage des effets non linéaires par diffraction - la déviation des rayons de la propagation rectiligne. Par exemple, nous avons projeté un laser sur du verre (fibre optique), et à l'intérieur du faisceau laser, l'indice de réfraction a commencé à dépendre de la puissance du laser. Les solitons spatiaux apparaissent en raison de l'équilibrage des non-linéarités par dispersion.

Soliton fondamental

Comme nous l'avons déjà mentionné, le haut débit (c'est-à-dire la capacité de transmettre de nombreuses fréquences, et donc informations utiles) des lignes de communication à fibre optique est limité par des effets non linéaires et une dispersion qui modifient l'amplitude des signaux et leur fréquence. Mais d’un autre côté, la même non-linéarité et la même dispersion peuvent conduire à la création de solitons qui conservent leur forme et d’autres paramètres beaucoup plus longtemps qu’autre chose. Une conclusion naturelle d'ici est le désir d'utiliser le soliton lui-même comme signal d'information (il y a un flash de soliton à l'extrémité de la fibre - ils ont transmis un un, non - ils ont transmis un zéro).

L'exemple d'un laser qui modifie l'indice de réfraction à l'intérieur d'une fibre optique au fur et à mesure de sa propagation est tout à fait viable, surtout si une impulsion de plusieurs watts est « bourrée » dans une fibre plus fine qu'un cheveu humain. À titre de comparaison, que ce soit beaucoup ou non, une ampoule à économie d'énergie typique de 9 watts éclaire un bureau, mais elle n'a que la taille d'une paume. En général, on ne s'éloignera pas loin de la réalité en supposant que la dépendance de l'indice de réfraction sur la puissance d'impulsion à l'intérieur de la fibre ressemblera à ceci :

Après des considérations physiques et des transformations mathématiques plus ou moins complexes sur l'amplitude du champ électrique à l'intérieur de la fibre, on peut obtenir une équation de la forme

où est la coordonnée le long de la propagation du faisceau et transversalement à celle-ci. Le coefficient joue un rôle important. Il définit la relation entre dispersion et non-linéarité. S'il est très petit, le dernier terme de la formule peut être supprimé en raison de la faiblesse des non-linéarités. S'il est très grand, les non-linéarités, supprimant la diffraction, détermineront à elles seules les caractéristiques de propagation du signal. Jusqu’à présent, des tentatives ont été faites pour résoudre cette équation uniquement pour des valeurs entières. Le résultat est donc particulièrement simple :
.
Bien que la fonction sécante hyperbolique ait un nom long, elle ressemble à une cloche ordinaire

Répartition de l'intensité dans la section transversale d'un faisceau laser sous forme d'un soliton fondamental.

C'est cette solution que l'on appelle le soliton fondamental. L'exponentielle imaginaire détermine la propagation du soliton le long de l'axe de la fibre. En pratique, tout cela signifie que si nous éclairions le mur, nous verrions un point lumineux au centre, dont l’intensité diminuerait rapidement sur les bords.

Le soliton fondamental, comme tous les solitons produits à l'aide de lasers, présente certaines caractéristiques. Premièrement, si la puissance du laser est insuffisante, il n’apparaîtra pas. Deuxièmement, même si quelque part un mécanicien plie excessivement la fibre, fait couler de l'huile dessus ou fait un autre sale tour, le soliton traversant la zone endommagée s'indignera (au sens physique et figuré), mais reviendra rapidement à ses paramètres d'origine. Les personnes et autres êtres vivants relèvent également de la définition d'un autosoliton, et cette capacité à revenir à un état calme est très importante dans la vie 😉

Les flux d’énergie à l’intérieur du soliton fondamental ressemblent à ceci :

Direction des flux d'énergie à l'intérieur du soliton fondamental.

Ici, les zones avec des directions d'écoulement différentes sont séparées par un cercle et la direction est indiquée par des flèches.

En pratique, il est possible d'obtenir plusieurs solitons si le laser possède plusieurs canaux laser parallèles à son axe. Ensuite, l'interaction des solitons sera déterminée par le degré de chevauchement de leurs « jupes ». Si la dissipation d’énergie n’est pas très importante, on peut supposer que les flux d’énergie à l’intérieur de chaque soliton se conservent dans le temps. Ensuite, les solitons commencent à tourbillonner et à s'accrocher les uns aux autres. La figure suivante montre une simulation de la collision de deux triplets de solitons.

Simulation de collisions de solitons. Les amplitudes sont représentées sur fond gris (comme un relief) et la distribution de phase est représentée sur fond noir.

Des groupes de solitons se rencontrent, s'accrochent et forment une structure en forme de Z et commencent à tourner. Des résultats encore plus intéressants peuvent être obtenus en brisant la symétrie. Si vous disposez les solitons laser en damier et que vous en jetez un, la structure commencera à tourner.

La rupture de symétrie dans un groupe de solitons entraîne une rotation du centre d'inertie de la structure dans le sens de la flèche de la figure. vers la droite et rotation autour de la position instantanée du centre d'inertie

Il y aura deux rotations. Le centre d'inertie tournera dans le sens inverse des aiguilles d'une montre et la structure elle-même tournera autour de sa position à chaque instant. De plus, les périodes de rotation seront égales, par exemple, comme la Terre et la Lune, qui sont tournées vers notre planète d'un seul côté.

Expériences

Ces propriétés inhabituelles des solitons ont attiré l’attention et nous ont fait réfléchir à des applications pratiques depuis environ 40 ans. On peut immédiatement dire que les solitons peuvent être utilisés pour compresser des impulsions. Aujourd'hui, vous pouvez ainsi obtenir une durée d'impulsion allant jusqu'à 6 femtosecondes (les secondes ou deux prennent un millionième de seconde et divisent le résultat par mille). Les lignes de communication solitons, dont le développement dure depuis un certain temps, sont particulièrement intéressantes. Hasegawa a donc proposé le schéma suivant en 1983.

Ligne de communication Soliton.

La ligne de communication est constituée de tronçons d'environ 50 km de long. La longueur totale de la ligne était de 600 km. Chaque section est constituée d'un récepteur avec un laser qui transmet un signal amplifié au guide d'ondes suivant, ce qui a permis d'atteindre une vitesse de 160 Gbit/s.

Présentation

Littérature

J.Lem. Introduction à la théorie des solitons. Par. de l'anglais M. : Mir, - 1983. -294 p.
J. Whitham Ondes linéaires et non linéaires. - M. : Mir, 1977. - 624 p.
I.R. Shen. Principes de l'optique non linéaire : Trad. de l'anglais/Ed. S.A. Akhmanova. - M. : Nauka., 1989. - 560 p.
S.A. Boulgakova, A.L. Dmitriev. Dispositifs de traitement de l'information optique non linéaire// Didacticiel. - Saint-Pétersbourg : SPbGUITMO, 2009. - 56 p.
Werner Alpers et. Al. Observation des ondes internes dans la mer d'Andaman par ERS SAR // Earthnet Online
A. I. Latkin, A. V. Yakasov. Modes autosolitons de propagation d'impulsions dans une ligne de communication à fibre optique avec miroirs annulaires non linéaires // Autométrie, 4 (2004), vol. 40.
N.N. Rozanov. Le monde des solitons laser // Nature, 6 (2006). p. 51-60.
O.A. Tatarkina. Quelques aspects de la conception de systèmes de transmission à fibre optique soliton // Recherche basique, 1 (2006), pages 83-84.

P.S. À propos des diagrammes dans .

SOLITON

Onde solitaire structurellement stable dans un milieu dispersif non linéaire. Les S. se comportent comme des noirs : lorsqu'ils interagissent entre eux ou avec certaines autres perturbations, les S. ne sont pas détruits, mais divergent à nouveau, gardant leur structure inchangée. La structure de la forme d'onde est maintenue stationnaire en raison de l'équilibre entre les effets de non-linéarité du milieu (voir SYSTÈMES NON LINÉAIRES) et de dispersion (voir DISPERSION DES ONDES). Par exemple, dans le cas de la gravité ondes à la surface d'un liquide pour un plat suffisamment long (l->2pH, où H est la profondeur du réservoir) il n'y a pas de dispersion, les ondes se propagent avec une vitesse de phase v=?(g(H+h)) , où g-, h est l'élévation de la surface de l'eau en un point donné du profil des vagues. Le sommet de la vague se déplace plus rapidement que sa base (non-linéarité), donc l'inclinaison du front d'onde augmente jusqu'à ce que la longueur du front devienne proportionnelle à la valeur de 2pH, après quoi v dépendra de l'inclinaison du front (dispersion). . En conséquence, des vagues apparaissent sur le profil (Fig. 1), dont le développement conduit à la formation de S.

Riz. 1. Evolution du profil des vagues à la surface d'un réservoir de profondeur N.

Riz. 5. Paire de solitons liés.

Dans les systèmes à forte dispersion, si le profil d'onde stationnaire est proche de la sinusoïdale, l'existence d'une modulation est également possible. ondes sous forme d'ondes localisées. les paquets avec une enveloppe mobile stationnaire, qui présentent également un comportement « semblable à celui d'une particule » lors du déplacement (C. « enveloppe »). De tels signaux sont possibles pour les ondes à la surface d'un réservoir profond, les ondes de Langmuir dans un plasma, les impulsions lumineuses puissantes et courtes (picosecondes) dans l'environnement de travail d'un laser, etc.

S. jouent un rôle important dans la théorie du condenseur. États dans les îles, en particulier dans le quantum. statistiques, théorie des transitions de phase. Les solutions Soliton ont certaines équations proposées pour les décrire. tsk. L'étude des ondes solaires en tant qu'ondes « de type particule », y compris d'éventuelles ondes tridimensionnelles, dans lesquelles elles diminuent dans toutes les directions dans un espace tridimensionnel (et pas seulement le long d'une coordonnée, comme dans les exemples ci-dessus), a conduit à tente d'utiliser S. dans la construction du quantum. théorie des champs non linéaires.

Dictionnaire encyclopédique physique. - M. : Encyclopédie soviétique. Rédacteur en chef A. M. Prokhorov. 1983 .

SOLITON

(du latin solus - un) - perturbation localisée stationnaire ou stationnaire moyenne d'une perturbation homogène ou spatialement périodique. S. se caractérise par les propriétés suivantes : localisée dans une région finie ; se propage sans déformation, transférant de l'énergie et du moment cinétique ; conserve sa structure lors de l'interaction avec d'autres S. similaires ; peut former des états liés, des ensembles. Le profil (forme) de l'onde est déterminé dans un milieu non linéaire par deux processus concurrents : la propagation de l'onde due à la dispersion du milieu et le « renversement » du front d'onde croissant dû à la non-linéarité.

Jusqu'au début années 1960 S. s'appelait une vague solitaire - une forme inchangée, se propageant depuis le poteau. vitesse à la surface d’un liquide lourd de profondeur finie et dans le plasma. De nos jours, diverses substances physiques relèvent de la définition de S. objets. La première classification des systèmes peut être faite selon le nombre de dimensions spatiales le long desquelles se produit la localisation d'une perturbation stationnaire d'un milieu non linéaire. S. unidimensionnel inclut le classique. Impulsions 2p et enveloppes en optique non linéaire (voir. Solitons optique), localisation. conductivité collective dans les molécules organiques. semi-conducteurs et dans les métaux unidimensionnels (voir ondes de densité de charge), S. (quanta de flux magnétique) dans les supraconducteurs à jonctions Josephson (voir. effet Josephson) etc. Aux dislocations S. bidimensionnelles dans le cristallin. treillis, déclinaisons en les cristaux liquides, structures vortex dans une fine couche de liquide superfluide, Superfluidité), mag. tubes (vortex d'Abrikosov) dans les supraconducteurs de type 2 (voir. Supraconductivité), zones anticycloniques en géophysique. l'hydrodynamique, y compris la « Grande Tache Rouge » sur Jupiter, les canaux autofocus en optique non linéaire. Soliton en théorie quantique des champs), trous noirs théorie de la gravité. Dans la théorie quantique des champs, les particules localisées dans l'espace-temps à quatre dimensions sont considérées - instantons.

Mathématiquement, les systèmes représentent des solutions stationnaires localisées de problèmes non linéaires. équations différentielles aux dérivées partielles ou à leurs généralisations (équations différentielles-différences, intégro-différentielles, etc.). cas diff. physique les situations et les phénomènes sont décrits par les mêmes équations, par exemple. Korteweg - équation de Vries, équation sinus-Gordon, - Équation de Petviashvili. Les équations linéaires (à l'exception de l'équation d'onde unidimensionnelle) n'ont pas de solutions stationnaires localisées. S. sont des objets essentiellement non linéaires avec une charge topologique, c'est-à-dire si la configuration du champ d'ondes en présence d'énergie solaire est topologiquement différente de la configuration de l'état non perturbé. Moyens. une partie des équations, la méthode du problème de diffusion inverse, la plupart d'entre elles sont des systèmes hamiltoniens intégrables.

Solitons unidimensionnels. Une onde solitaire à la surface d'un liquide de profondeur finie a été observée pour la première fois en 1834 par J. S. Russell. Mathématiques.

Ici N- profondeur non perturbée du liquide, - la vitesse des ondes longues de faible amplitude, x 0 - la position du centre du système solaire, les ondes de choc sans collision dans le plasma qui surviennent, modélisant le comportement d'une chaîne d'atomes reliés par des forces élastiques non linéaires et décrits par les équations du mouvement

où l est le numéro de l'atome dans la chaîne, E. Fermi, J. Pasta et S. Ulam (S. Ulam) a découvert en 1954 une stochastisation anormalement lente dans ce système. Le système n'était pas thermalisé (les conditions thermodynamiques n'y étaient pas établies).

dérivé en 1895 pour décrire l'évolution d'un paquet d'ondes à la surface d'un liquide peu profond. L'équation KdV est une équation universelle qui décrit des milieux unidimensionnels ou quasi-unidimensionnels, dans lesquels entre en compétition une faible non-linéarité quadratique [terme 6 et eux vur-nii (3)] et faible dispersion linéaire [terme et xxx dans l’équation (3)]. Il s’est avéré qu’il décrit également des oscillations. comportement d'une chaîne d'atomes,

En fonction du rapport des deux facteurs ci-dessus, le système passe d'un état à un autre, et dans le cas de leur compensation mutuelle, C apparaît.

À partir de la solution numérique de l’équation (3) [N. Zabusky (N. Zabusky) et M. Kruskal (M. Kruskal), 1964] il s'ensuit que S. a des moyens. stabilité et collisions, ils se dissipent élastiquement, conservant leur forme et leur amplitude. Analysant ce phénomène, M. Kruskal, J. Green (G. Green), C. Gardner (S. Gardner) et R. Miura (R. Miura) a été ouverte en 1967 par le fonds. méthode du problème de diffusion inverse :

L'équation (5) est une équation de Schrödinger stationnaire avec un potentiel u(x,t). S'il satisfait à l'équation KdV (3), alors propriétés discrètes. les valeurs de l'équation de Schrödinger ne dépendent pas du temps et sont directement liées à C. Si l'équation (5) a N propriétés discrètes valeurs, alors at sera présent N S. type (4) avec paramètres. Dans le cas général, la solution contient également une « partie non soliton » oscillante. La solution de l'équation (5), déterminée par la méthode du problème de diffusion inverse, a la forme :

Dans le cas purement soliton

La solution N-soliton décrit la diffusion N S. les uns sur les autres. collision appariée de S. avec des amplitudes S. acquérir des quarts de travail

c'est-à-dire que S. rapide acquiert des changements positifs et lents - négatifs. Lors de l'interaction N C. complet de chaque C. est égal à algébrique. interaction de particules non relativistes, entre lesquelles agissent des forces répulsives appariées. Par exemple, pour deux S. (4) d'amplitudes identiques séparées d'une distance L, beaucoup plus grand que la taille caractéristique de S., le potentiel de la force répulsive

Une image typique de l'émergence de l'énergie solaire dans l'océan, photographiée depuis l'espace, est présentée sur la figure : cinq bandes (solitons) sont clairement visibles en se déplaçant du bas à droite vers le haut à gauche.

Équation non linéaire de Schrödinger pour une fonction complexe u(x,t)

est l'un des principaux équations de physique non linéaire qui décrivent l'évolution de l'optique. ondes dans les cristaux non linéaires, ondes de Langmuir dans le plasma, ondes thermiques dans les solides, etc. Lors de la propagation d'ondes quasi-harmoniques unidimensionnelles. et xx) et une automodulation à dispersion linéaire (terme ) se produit - des ondes d'enveloppe apparaissent. Dans le cas d'un équilibre d'autocompression non linéaire et d'étalement de dispersion, des paramètres d'enveloppe apparaissent.

Ici et v- amplitude et vitesse de S. [contrairement à S. (4), ces paramètres sont mutuellement indépendants], Ф 0 et X 0 décrire la phase et la position de S. au début. moment.

V. E. Zakharov et A. B. Shabat ont montré (1971) que l'équation (7) est également exactement intégrable dans le cadre de la méthode du problème de diffusion inverse à l'aide d'un auxiliaire. un système surdéterminé d'équations linéaires de type (5), (6) pour une fonction (vecteur) à plusieurs composantes. Une conséquence de l'intégrabilité exacte est la présence de solutions multisolitons exactes. Comme dans le cas de l'équation KdV, ces solutions décrivent des collisions purement élastiques avec préservation de la forme, de l'amplitude et de la vitesse. Unité la conséquence de la collision est des déphasages - des changements dans les paramètres Ф 0 et x0.

Équation sinusoïdale unidimensionnelle de Gordon. Intégré avec précision à l'aide d'auxiliaires

Cette équation apparaît au pluriel. physique problèmes dans lesquels anharmonique l'auto-action potentielle non linéaire du champ d'onde est périodique dans la variable de champ Ф(х,t). Les exemples sont dans les jonctions Josephson, ondes de densité de charge dans métaux unidimensionnels, ondes de magnétisation non linéaires dans des ferromagnétiques facilement plans et faibles, etc.

L'équation (9) contient des solutions solitons de deux types différents. types: soi-disant ibreezers pervers. K i n k

est une onde solitaire avec une topologie charge , se déplaçant à grande vitesse v(v2< 1). Kink a du sens. n. fluxona - mag quantique. flux dans la théorie des jonctions Josephson longues, x 0, caractérisant la position des plis au début. v1 ,v 2 (v1v 2) les déphasages sont égaux :

On voit que les déphasages ne dépendent pas de facteurs topologiques. frais de pliage.

Comme pour les synchrotrons décrits par les équations (3) et (7), le déphasage total de tout coude lorsqu'il est diffusé sur un ensemble d'autres plis est exactement égal à la somme des décalages générés par ses collisions avec chacun des autres plis séparément.

Visuellement, deux plis, séparés par une distance L, bien supérieure à leurs tailles caractéristiques ~ (1 - v 2) -1/2, peuvent être représentés comme des particules relativistes de porte interagissant avec le potentiel

Ainsi, les plis avec des charges identiques se repoussent, avec des charges opposées - sont attirés.

Une paire de coudes avec des charges opposées peut former un état oscillant couplé - ce qu'on appelle. reniflard, représentant le 2ème type de solution soliton exacte de l'équation (9) :

[Un respirateur en mouvement peut être obtenu à partir de (11) par la transformation de Lorentz]. Le paramètre varie dans , caractérise l'énergie de liaison du respirateur, une certaine différence dans les énergies d'une paire de repos lointains ( v= 0) plis (10) et énergie de respiration (11) :. Les collisions des reniflards entre eux et avec les plis sont également purement élastiques et s'accompagnent de déphasages additifs. Dans les systèmes réels, le reniflard n'est pas observé en raison de la dissipation.

Dans la limite Ф 2 1 substitution

transforme l'équation (9) en équation de Schrödinger non linéaire (7) (avec signe supérieur). Dans ce cas, le reniflard (11) (à ) est transformé en un S stationnaire. (8) d'amplitude

Solitons multidimensionnels. S. bidimensionnel est une solution de l'équation de Kadomtsev-Petviashvili exactement intégrable

décrivant les ondes acoustiques ioniques dans le plasma, à la surface d'un liquide « peu profond », etc. Solution exacte de l'équation (12)

contenant un paramètre complexe arbitraire v, décrit un système bidimensionnel stable (appelé lampe) se déplaçant avec vitesse et = (v x ,Vy),,. Au moment de décider. (13) diminue à mesure que ( x2 + et 2) -1, t. Autrement dit, contrairement à S. (4), (8), (10), (11) unidimensionnel, caractérisé par une décroissance exponentielle du profil en , S. (13) bidimensionnel a une loi de puissance comportement asymptotique. Les collisions d'un nombre quelconque de lampes (13) sont purement élastiques et, contrairement aux collisions unidimensionnelles, les déphasages sont identiques à zéro.

La notion de signal peut être généralisée au cas de niveaux d'ondes non linéaires non intégrables. Cela inclut les systèmes presque intégrables qui diffèrent des équations universelles intégrables par de petits termes perturbateurs, ce qui se produit dans les sciences physiques réelles. systèmes. La théorie des perturbations pour les systèmes presque intégrables est également basée sur la méthode du problème de diffusion inverse [D. Kaup (D. Le Caire), 1976 ; V.I. Karpman et E.M. Maslov, 1977]. Dans les systèmes presque intégrables, S. est plus riche ; en particulier, de petites perturbations peuvent donner lieu à des interactions inélastiques de particules et à des effets multisolitons absents dans le cas exactement intégrable.

Dans les systèmes qui sont loin d’être exactement intégrables, les interactions du système s’avèrent profondément inélastiques. Ainsi, le niveau d’onde non intégrable et relativiste

décrivant, par exemple, la dynamique du paramètre d'ordre lors des transitions de phase de type déplacement dans les ferroélectriques, a une solution de type coude stable et exacte :