La résolution de la plupart des problèmes de mathématiques au secondaire nécessite la connaissance de la formulation de proportions. Cette compétence simple vous aidera non seulement à effectuer des exercices complexes du manuel, mais également à approfondir l'essence même de la science mathématique. Comment faire une proportion ? Voyons cela maintenant.

L’exemple le plus simple est un problème où trois paramètres sont connus et où le quatrième doit être trouvé. Les proportions sont bien sûr différentes, mais vous devez souvent trouver un nombre à l'aide de pourcentages. Par exemple, le garçon avait dix pommes au total. Il a donné la quatrième partie à sa mère. Combien de pommes reste-t-il au garçon ? C'est l'exemple le plus simple qui vous permettra de créer une proportion. L'essentiel est de le faire. Au départ, il y avait dix pommes. Que ce soit 100%. Nous avons marqué toutes ses pommes. Il en a donné un quart. 1/4=25/100. Cela signifie qu'il lui reste : 100 % (c'était à l'origine) - 25 % (il a donné) = 75 %. Ce chiffre montre le pourcentage de la quantité de fruits restant par rapport à la quantité initialement disponible. Nous avons maintenant trois nombres grâce auxquels nous pouvons déjà résoudre la proportion. 10 pommes - 100%, X pommes - 75%, où x est la quantité de fruits requise. Comment faire une proportion ? Vous devez comprendre ce que c'est. Mathématiquement, cela ressemble à ceci. Le signe égal est placé pour votre compréhension.

10 pommes = 100 % ;

x pommes = 75%.

Il s'avère que 10/x = 100 %/75. C'est la propriété principale des proportions. Après tout, plus x est grand, plus le pourcentage de ce nombre par rapport à l'original est élevé. Nous résolvons cette proportion et trouvons que x = 7,5 pommes. Nous ne savons pas pourquoi le garçon a décidé de donner une somme entière. Vous savez maintenant comment faire une proportion. L'essentiel est de trouver deux relations, dont l'une contient l'inconnu.

Résoudre une proportion se résume souvent à une simple multiplication puis à une division. Les écoles n'expliquent pas aux enfants pourquoi il en est ainsi. Bien qu’il soit important de comprendre que les relations proportionnelles sont des classiques mathématiques, l’essence même de la science. Pour résoudre des proportions, vous devez être capable de gérer des fractions. Par exemple, vous devez souvent convertir des pourcentages en fractions. Autrement dit, enregistrer 95% ne fonctionnera pas. Et si vous écrivez immédiatement 95/100, vous pouvez alors effectuer des réductions significatives sans lancer le calcul principal. Il faut dire tout de suite que si votre proportion s'avère être à deux inconnues, alors elle ne peut pas être résolue. Aucun professeur ne vous aidera ici. Et votre tâche comporte probablement un algorithme plus complexe pour les actions correctes.

Regardons un autre exemple où il n'y a pas de pourcentages. Un automobiliste a acheté 5 litres d'essence pour 150 roubles. Il a pensé à combien il paierait pour 30 litres de carburant. Pour résoudre ce problème, notons x la somme d'argent requise. Vous pouvez résoudre ce problème vous-même, puis vérifier la réponse. Si vous n'avez pas encore compris comment établir une proportion, jetez-y un œil. 5 litres d'essence équivalent à 150 roubles. Comme dans le premier exemple, nous notons 5l - 150r. Trouvons maintenant le troisième nombre. Bien sûr, cela fait 30 litres. Convenez qu'une paire de 30 l - x roubles est appropriée dans cette situation. Passons au langage mathématique.

5 litres - 150 roubles;

30 litres - x roubles;

Résolvons cette proportion :

x = 900 roubles.

Nous avons donc décidé. Dans votre tâche, n'oubliez pas de vérifier l'adéquation de la réponse. Il arrive qu'avec une mauvaise décision, les voitures atteignent des vitesses irréalistes de 5 000 kilomètres par heure, etc. Vous savez maintenant comment faire une proportion. Vous pouvez également le résoudre. Comme vous pouvez le constater, cela n’a rien de compliqué.

L'utilisation d'équations est répandue dans nos vies. Ils sont utilisés dans de nombreux calculs, construction de structures et même dans le sport. L’homme utilisait des équations dans l’Antiquité et depuis lors, leur utilisation n’a fait que croître. Si vous voyez une expression avec des fractions avec une variable au numérateur/dénominateur, alors vous avez une expression appelée équation rationnelle en mathématiques. En général, toutes les équations contenant une expression rationnelle peuvent être appelées équations rationnelles. Quant aux solutions des équations rationnelles, elles se résolvent comme suit : les opérations sont effectuées sur les côtés gauche et droit jusqu'au moment où la variable n'est pas isolée d'un côté. Il existe deux manières de résoudre de telles équations :

Multiplication croisée ;

LCD (plus petit dénominateur commun).

La première méthode est utilisée si, après réécriture de l'équation, une fraction est formée de chaque côté. Par exemple:

\[\frac (x+3)(4)- \frac(x)(2)= 0\]

Pour utiliser la méthode de multiplication croisée, vous devez convertir les équations sous la forme :

\[\frac (x+3)(4)= \frac (x)(-2)\]

La deuxième méthode peut être utilisée lorsque vous avez une équation avec 3 fractions ou plus. Par exemple:

\[\frac (x)(3)+ \frac (1)(2)=\frac(3x+1)(6) \]

Pour cette équation, le plus petit commun multiple est 6, ce qui facilite la résolution de cette équation.

Où puis-je résoudre gratuitement des équations rationnelles en ligne ?

Vous pouvez résoudre une équation rationnelle en ligne avec une solution sur notre site https://site. Le solveur en ligne gratuit vous permettra de résoudre des équations en ligne de toute complexité en quelques secondes. Tout ce que vous avez à faire est simplement de saisir vos données dans le solveur. Vous pouvez également regarder des instructions vidéo et apprendre à résoudre l'équation sur notre site Web. Et si vous avez encore des questions, vous pouvez les poser dans notre groupe VKontakte http://vk.com/pocketteacher. Rejoignez notre groupe, nous sommes toujours heureux de vous aider.

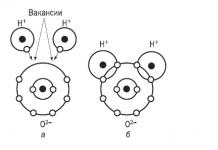
Il s’agit du schéma de différence homogène le plus simple et le plus précis pour calculer la dynamique des gaz. Son modèle est présenté sur la Fig. 98 ; les valeurs de rayon sont attribuées aux nœuds de la grille, les valeurs de vitesse sont attribuées aux limites des intervalles spatiaux sur des couches à moitié entières et les valeurs de densité, de pression et d'énergie interne sont attribuées aux milieux d'intervalles sur des couches entières.

La construction du circuit ressemble à une « croix » acoustique. Pour simplifier la notation, nous choisissons des pas et t qui sont uniformes en masse et en temps et nous approximons le système avec les équations aux différences suivantes :

Ces équations sont écrites dans l’ordre qui convient aux calculs.

Discutons de l'expression différentielle de la pression visqueuse (65). Pour effectuer le passage limite du schéma de différence aux équations de la dynamique des gaz, il faut d'abord tendre vers zéro à un coefficient de viscosité fixe, puis construire une série de telles solutions limites pour des valeurs infiniment décroissantes de . Mais cela demande beaucoup de travail. Par conséquent, dans la pratique, ces transitions limites sont combinées en une seule commune, bien que la légalité d'une telle procédure n'ait pas été prouvée (la densité est introduite dans la formule pour que les coefficients soient sans dimension).

Ainsi, la pression visqueuse (65) prend la forme

où est la vitesse du son. L'expression (67) est écrite pour le cas plan ; mais il est généralement utilisé pour toute symétrie du problème.

Approximation. À partir de la vue modèle de la Fig. 98 et l'écriture symétrique du schéma (66), il est facile de remarquer que dans les écoulements sans compression, lorsque la pseudoviscosité (67) devient nulle, le schéma « croisé » a une approximation locale

Dans les écoulements avec compression (y compris les ondes de choc), la pseudoviscosité est non nulle. Certes, le terme quadratique dans (67a) a une grandeur, mais le terme linéaire a une grandeur et, par conséquent, aggrave l'ordre d'approximation. De plus, les termes visqueux ne s’écrivent pas de manière complètement symétrique dans le temps. En conséquence, l’approximation se détériore jusqu’à

Trouver une solution différente. Le schéma (66) est explicite ; les calculs dessus sont effectués comme suit. Que toutes les quantités sur le calque d'origine soient connues. Ensuite, à partir de l'équation différentielle de la quantité de mouvement (66a), nous trouvons dans tous les intervalles ; puis à partir de la deuxième équation (66b) nous déterminons et à partir de l'équation (66c) - .

L'équation énergétique (66d) est résolue en dernier. Formellement, il s'agit d'une équation algébrique implicite pour la définition dans un intervalle donné. Mais pour chaque valeur de l'indice, les équations (66d) sont résolues indépendamment, sans former de système d'équations couplé, de sorte que le schéma de différence reste essentiellement explicite.

Remarque 1. L'équation énergétique de (66) peut être rendue explicite en utilisant uniquement la valeur de la couche d'origine :

Cela simplifie quelque peu le calcul et n'affecte pas la stabilité, mais détériore sensiblement la précision, car l'erreur d'approximation devient même dans des écoulements fluides. Cette option est rarement utilisée.

La stabilité du circuit peut être étudiée par la méthode de séparation des variables, linéarisation du circuit et gel des coefficients. Des calculs fastidieux conduisent à une condition de stabilité de type Courant.

Par exemple, dans des écoulements réguliers avec une viscosité nulle, le schéma est stable à

Pour un gaz parfait, la condition (69) prend la forme où est la vitesse adiabatique du son. Pour les écoulements avec une viscosité non nulle, la limitation du pas est un peu plus forte ; à viscosité quadratique, la condition de stabilité prend la forme

où est le saut de vitesse sur l’onde de choc. Bien que cette étude ne soit pas rigoureuse, cette condition de stabilité est néanmoins bien confirmée en pratique.

Ainsi, la « croix » est un schéma conditionnellement stable. Notons une circonstance intéressante. Pour calculer des écoulements réguliers, la viscosité n'est pas nécessaire. Et si nous calculons l’onde de choc sans viscosité (en choisissant une petite qui satisfait à la condition (70)), nous obtenons le « relâchement » illustré à la Fig. 99. Ce calcul est stable car l'amplitude des oscillations n'augmente pas avec le temps. Mais il n’y a pas de convergence vers une solution physiquement correcte, puisque l’approximation est perdue au niveau de la discontinuité.

La convergence du schéma « croisé » gaz-dynamique n’a pas été prouvée. Cependant, ce schéma a été utilisé avec succès dans les calculs depuis 1950 environ et a été testé sur de nombreux problèmes difficiles avec des solutions exactes connues. Comme les pas tendaient vers zéro, une convergence vers la solution correcte a été observée si les pas satisfaisaient à la condition de stabilité.

Remarque 2. Le schéma (66) n'est pas conservateur ; cependant, son déséquilibre tend vers zéro lorsque

Remarque 3. Les problèmes de dynamique des gaz avec des couches très minces sont particulièrement difficiles à calculer. En fait, si , alors pour calculer avec une précision satisfaisante à l'aide de la formule (66c), il faut connaître les rayons avec une très grande précision, comparable aux erreurs d'arrondi sur un ordinateur. Dans de tels problèmes, il est parfois nécessaire d'effectuer des calculs avec un nombre double de chiffres ou de modifier spécialement le schéma de différence.

Aujourd'hui, nous poursuivons une série de leçons vidéo dédiées aux problèmes impliquant des pourcentages de l'examen d'État unifié en mathématiques. En particulier, nous analyserons deux problèmes très réels de l'examen d'État unifié et verrons une fois de plus combien il est important de lire attentivement les conditions du problème et de l'interpréter correctement.

Donc, la première tâche :

Tâche. Seuls 95 % et 37 500 diplômés de la ville ont résolu correctement le problème B1. Combien de personnes ont résolu correctement le problème B1 ?

À première vue, il semble que ce soit une sorte de tâche pour les casquettes. Comme:

Tâche. Il y avait 7 oiseaux assis sur un arbre. 3 d’entre eux se sont envolés. Combien d’oiseaux se sont envolés ?

Néanmoins, comptons quand même. Nous résoudrons en utilisant la méthode des proportions. Nous avons donc 37 500 étudiants, soit 100 %. Et il y a aussi un certain nombre x d'étudiants, qui représentent 95 % des chanceux qui ont correctement résolu le problème B1. Écrivons ceci :

37 500 — 100%
X-95%

Vous devez faire une proportion et trouver x. On a:

Nous avons devant nous une proportion classique, mais avant d'utiliser la propriété principale et de la multiplier transversalement, je propose de diviser les deux côtés de l'équation par 100. Autrement dit, barrons deux zéros au numérateur de chaque fraction. Réécrivons l'équation résultante :

Selon la propriété fondamentale de proportion, le produit des termes extrêmes est égal au produit des termes moyens. Autrement dit:

x = 375 95

Ce sont des nombres assez grands, vous devrez donc les multiplier dans une colonne. Permettez-moi de vous rappeler qu'il est strictement interdit d'utiliser une calculatrice à l'examen d'État unifié de mathématiques. On a:

x = 35 625

Réponse totale : 35 625. C’est exactement le nombre de personnes sur les 37 500 initiales qui ont résolu correctement le problème B1. Comme vous pouvez le constater, ces chiffres sont assez proches, ce qui est logique car 95 % est également très proche de 100 %. En général, le premier problème a été résolu. Passons au deuxième.

Problème d'intérêt n°2

Tâche. Seuls 80 % des 45 000 diplômés de la ville ont résolu correctement le problème B9. Combien de personnes ont mal résolu le problème B9 ?

Nous résolvons selon le même schéma. Au départ, il y avait 45 000 diplômés, soit 100 %. Ensuite, à partir de ce nombre, vous devez sélectionner x diplômés, qui doivent représenter 80 % du nombre initial. On fait une proportion et on résout :

45 000 — 100%
x — 80 %

Réduisons un zéro chacun au numérateur et au dénominateur de la 2ème fraction. Réécrivons à nouveau la construction résultante :

La propriété principale de la proportion : le produit des termes extrêmes est égal au produit des termes moyens. On a:

45 000 8 = x 10

C'est l'équation linéaire la plus simple. Exprimons-en la variable x :

x = 45 000 8:10

On réduit 45 000 et 10 d'un zéro, le dénominateur reste un, il suffit donc de trouver la valeur de l'expression :

x = 4500 8

Vous pouvez bien sûr faire la même chose que la dernière fois et multiplier ces nombres dans une colonne. Mais ne nous compliquons pas la vie, et au lieu de multiplier dans une colonne, factorisons les huit en facteurs :

x = 4 500 2 2 2 = 9 000 2 2 = 36 000

Et maintenant, c'est la chose la plus importante dont j'ai parlé au tout début de la leçon. Vous devez lire attentivement les conditions de la tâche !

Qu'est-ce qu'on a besoin de savoir? Combien de personnes ont résolu le problème B9 faux. Et nous venons de trouver ces personnes qui ont pris la bonne décision. Il s'est avéré qu'ils représentaient 80 % du nombre initial, c'est-à-dire 36 000. Cela signifie que pour obtenir la réponse finale, nous devons soustraire nos 80 % du nombre initial d’étudiants. On a:

45 000 − 36 000 = 9000

Le nombre résultant 9000 est la réponse au problème. Au total, dans cette ville, sur 45 000 diplômés, 9 000 personnes ont mal résolu le problème B9. Voilà, problème résolu.

J'espère que cette vidéo aidera ceux qui se préparent de manière indépendante à l'examen d'État unifié en mathématiques. Et c'est tout pour moi. Pavel Berdov était avec vous. À la prochaine! :)

Méthodologie de résolution de problèmes
pour les solutions utilisant
règles de la croix

De nombreuses questions importantes liées à l'étude d'un cours de chimie sont exclues du programme scolaire pour plusieurs raisons. Parmi eux figurent la loi des équivalents, les différentes manières d'exprimer la concentration des solutions, la règle de la croix et bien d'autres. Cependant, dans les classes périscolaires, lors de la préparation des enfants aux Olympiades, on ne peut pas s'en passer. Et ils seront utiles aux enfants dans la vie, notamment à ceux qui relieront leur futur métier à la chimie (laboratoires d'usine, pharmacies, travaux de recherche, et juste la chimie au quotidien).
C'est particulièrement difficile à cet égard pour les jeunes enseignants - ils ne disposent pas de la masse de littérature supplémentaire que les anciens enseignants ont accumulée au fil des décennies de travail à l'école, et tout le monde sait ce que publie l'industrie moderne de l'imprimerie. Par conséquent, il semble que la méthode proposée pour résoudre des problèmes impliquant des solutions utilisant la règle de la croix aidera au moins dans une certaine mesure les jeunes collègues dans ce domaine.

"L'enveloppe de Pearson"

Très souvent, dans la pratique de laboratoire et lors de la résolution de problèmes d'Olympiade, on rencontre des cas de préparation de solutions avec une certaine fraction massique d'une substance dissoute, de mélange de deux solutions de concentrations différentes ou de dilution d'une solution forte avec de l'eau. Dans certains cas, il est possible d'effectuer des calculs arithmétiques assez complexes. Cependant, cela est improductif. Le plus souvent, pour cela il vaut mieux appliquer la règle du mélange (le modèle diagonal de « l'enveloppe Pearson », ou, ce qui revient au même, la règle de la croix).
Disons que nous devons préparer une solution d'une certaine concentration, en ayant à notre disposition deux solutions avec une concentration supérieure et inférieure à celle dont nous avons besoin. Alors, si on note la masse de la première solution par m 1, et le second – à travers m 2, alors lors du mélange, la masse totale du mélange sera la somme de ces masses. Soit la fraction massique de la substance dissoute dans la première solution soit 1, dans la seconde – 2 et dans leur mélange – 3. Ensuite, la masse totale de la substance dissoute dans le mélange sera composée des masses de la substance dissoute dans les solutions originales :

m 1 1 +m 2 2 = 3 (m 1 + m 2) .

D'ici

m 1 ( 1 – 3) = m 2 ( 3 – 2),

m 1 /m 2 = ( 3 – 2)/( 1 – 3).

On peut voir que le rapport de la masse de la première solution à la masse de la deuxième solution est le rapport de la différence des fractions massiques de la substance dissoute dans le mélange et dans la deuxième solution à la différence des valeurs correspondantes ​​dans la première solution et dans le mélange.

Lors de la résolution de problèmes impliquant des solutions avec des concentrations différentes, le schéma diagonal de la règle de mélange est le plus souvent utilisé. Lors du calcul, notez les fractions massiques de la substance dissoute dans les solutions originales les unes au-dessus des autres, à droite entre elles - sa fraction massique dans la solution à préparer, et soustrayez la plus petite valeur en diagonale de la plus grande. Les différences dans leurs soustractions montrent les fractions massiques des première et deuxième solutions nécessaires pour préparer la solution souhaitée.

Pour expliquer cette règle, nous résolvons d’abord le problème le plus simple.

TACHE 1

Déterminez la concentration de la solution obtenue en combinant 150 g de solutions à 30 % et 250 g de solutions à 10 % de n'importe quel sel.

Donné:

m 1 = 150 g,
m 2 = 250g,
1 = 30%,
2 = 10%.

Trouver:

Solution

1ère méthode (méthode des proportions).

Masse totale de solution :

m 3 = m 1 + m 2 = 150 + 250 = 400 g.

Nous trouvons la masse de la substance dans la première solution en utilisant la méthode des proportions, basée sur la définition : le pourcentage de concentration de la solution indique combien de grammes de substance dissoute il y a dans 100 g de solution :

100 g de solution à 30% – 30 g de liquide,

150 g de solution à 30% – X ville,

X= 150 30/100 = 45g.

Pour la deuxième solution on fait une proportion similaire :

100 g de solution à 10% - 10 g de liquide,

250 g de solution à 10% – oui ville,

oui= 250 10/100 = 25 g.

Ainsi, 400 g de nouvelle solution contiennent 45 + 25 = 70 g de soluté.

Vous pouvez maintenant déterminer la concentration de la nouvelle solution :

400 g de solution - 70 g de liquide,

100 g de solution – z ville,

z= 100 70/400 = 17,5 g, soit 17,5 %.

2ème méthode (algébrique).

m 1 1 + m 2 2 = 3 (m 1 + m 2).

3 = (m 1 1 + m 2 2)/(m 1 + m 2).

En conséquence nous trouvons :

3 = (150 30 + 250 10)/(150 + 250) = 17,5%.

3ème méthode (règle de la croix).

( 3 – 10)/(30 – 3) = 150/250.

(30 – 3) 150 = ( 3 – 10) 250,

4500 – 150 3 = 250 3 – 2500,

4500 – 2500 = 250 3 – 150 3 ,

7000 = 400 3 , 3 = 7000/400 = 17,5%.

Répondre. Lorsque les solutions prises sont combinées, une nouvelle solution avec une concentration de 3 = 17,5 % sera obtenue.

Résolvons maintenant des problèmes plus difficiles.

TÂCHE 2

Déterminez la quantité dont vous avez besoin pour prendre une solution de sel à 10 % et une solution à 30 % du même sel pour préparer 500 g d'une solution à 20 %.

Donné:

1 = 10%,
2 = 30%,
3 = 20%,
m 3 = 500g.

Trouver:

m 1 , m 2 .

Solution

Nous utilisons la règle de la croix.

Pour préparer 500 g d'une solution saline à 20 %, vous devez prendre 10 parties de solutions aux concentrations d'origine.
Vérifions l'exactitude de notre solution, en tenant compte du fait que 1 partie est égale à 500/(10 + 10) = 25 g.

250 g de solution à 10% – X g de sel,

X= 250 10/100 = 25 g.

250 g de solution à 30% – oui g de sel,

100 g de solution à 30% – 30 g de sel,

oui= 250 30/100 = 75 g.

m(solution) = 250 + 250 = 500 g.

m(sel) = 25 + 75 = 100 g.

De là, nous en trouvons 3 :

500 g de solution – 100 g de sel,

100 g de solution – 3 g de sel,

3 = 100 100/500 = 20 g, soit 20 %.

Répondre. Pour préparer 500 g d'une solution à 20 %, il faut prélever 250 g de solutions initiales
(m 1 = 250g, m 2 = 250g).

TÂCHE 3

Déterminez combien de solutions salines à 60 % et 10 % de concentration doivent être prises pour préparer 300 g d'une solution à 25 % de concentration.

Donné:

1 = 60%,
2 = 10%,
3 = 25%,
3 = 300g.

Trouver:

m 1 , m 2 .

Solution

Poids d'une pièce : 300/50 = 6 g.

m 1 = 6 15 = 90 g, m 2 = 6 35 = 210 g.

100 g de solution à 60% – 60 g de sel,

90 g de solution à 60% – X g de sel,

X= 54g.

100 g de solution à 10% – 10 g de sel,

210 g de solution à 30% – oui g de sel,

oui= 21 ans

m(sel) = 54 + 21 = 75 g.

Trouvez la concentration de la nouvelle solution :

300 g de solution – 75 g de sel,

100 g de solution – z g de sel,

z= 100 75/300 = 25 g, soit 25 %.

Répondre. m 1 = 90g, m 2 = 210g.

Passons maintenant à des tâches encore plus complexes.

TÂCHE 4

Déterminer la masse de la solution Na2CO3 10% de concentration et poids d'hydrate cristallin sec Na 2 CO 3 10H 2 O que vous devez prendre pour préparer 540 g d'une solution à 15% de concentration.

Donné:

1 = 10%,
3 = 15%,
m 3 = 540g.

Trouver:

m 1 , m 2 .

Solution

1ère méthode (par un système d'équations à deux inconnues).

Déterminer la masse de sel Na 2 CO 3 dans 540 g de solution à 15 % :

100 g de solution à 15% – 15 g de sel,

540 g de solution à 15% – z g de sel,

z= 540 15/100 = 81 g.

Créons un système d'équations :

Trouver la masse molaire :

Se débarrasser des inconnues inutiles :

m 2 = 286oui/106;

100 g de solution à 10% – 10 g de sel,

m 1 g de solution à 10% – X g de sel,

m 1 = 100X/10 = 10X.

Remplaçons m 2 et m 1 au système d'équations :

Étant donné que X = 81 – oui, on se débarrasse de la deuxième inconnue :

10(81 – oui) + 286oui/106 = 540.

oui= 270/7,3 = 37 g.

Alors m 2 = 286oui/106 = 2,7 37 100 g est la masse de la quantité requise d'hydrate cristallin Na 2 CO 3 10H 2 O.
On retrouve ensuite : X = 81 – oui= 81 – 37 = 44 g – c'est la masse de sel d'une solution à 10 %.
Trouver la masse d'une solution à 10 % :

100 g de solution à 10% – 10 g de sel,

m 1 g de solution à 10% – 44 g de sel,

m 1 = 100 44/10 = 440 g.

Il est clair que ce problème peut être résolu de cette manière - une méthode fiable, mais malheureusement assez longue, lourde et complexe. Il peut être utilisé avec succès par des étudiants ayant une pensée logique suffisamment développée. Pour d’autres, ce sera difficile.

2ème méthode (règle de la croix).

Supposons que Na 2 CO 3 10H 2 O soit une « solution sèche » (après tout, elle contient de l'eau). On retrouve ensuite sa « concentration » :

286 g – 106 g de sel,

100g - X g de sel,

X= 100 106/286 = 37 g, soit 37 %.

Nous appliquons la règle de la croix.

Trouvez la masse d'une pièce et la masse des substances :

m 1 = 20 22 = 440 g, m 2 = 20 5 = 100 g.

Répondre. Pour préparer 540 g de solution de Na 2 CO 3 à 15 %, il faut prendre 440 g d'une solution à 10 % et 100 g d'hydrate cristallin.
Ainsi, appliquer la règle de la croix est plus pratique et plus simple pour résoudre de tels problèmes. Cette méthode permet de gagner du temps et demande moins de travail.
La règle du croisement peut également être appliquée dans les cas où il est nécessaire d'obtenir une solution de concentration plus faible en diluant une solution plus concentrée avec de l'eau, ou d'obtenir une solution plus concentrée en ajoutant un mélange sec à la solution d'origine. Regardons cela avec des exemples.

TÂCHE 5

Quelle quantité d'eau faut-il ajouter à 250 g de solution saline pour réduire sa concentration de 45 % à 10 % ?

Donné:

1 = 45%,
3 = 10%,
m 1 = 250g.

Trouver:

Solution

Nous supposons que la concentration de l'eau ajoutée est de 2 = 0 %. Nous utilisons la règle de la croix.

On détermine la masse d'une pièce grâce à la première solution : 250/10 = 25 g.
La masse d’eau nécessaire est alors :

m 2 = 25 35 = 875 g.

Vérifions l'exactitude de la solution.
Poids de la nouvelle solution :

m 3 = 250 + 875 = 1125 g.

250 g de solution à 45% – X g de sel,

100 g de solution à 45% – 45 g de sel,

X= 250 45/100 = 112,5 g.

On en retrouve 3 :

1125 g de solution – 112,5 g de sel,

100 g de solution – oui g de sel,

oui= 100 112,5/1125 = 10 g, soit 10 %.

Répondre. m 2 = 875g.

TÂCHE 6

Quelle quantité de sel sec faut-il ajouter à 250 g d'une solution concentrée à 10 % pour l'augmenter à 45 % ?

Donné:

1 = 10%,
m 1 = 250g,
3 = 45%.

Trouver:

m(s.s.).

Solution

Nous supposons que le sel sec est une solution avec 2 = 100 %. Nous utilisons la règle de la croix.

On détermine la masse d'une pièce grâce à la première solution : 250/55 = 4,5 g.
Déterminer la masse de sel sec :

m(s.s.) = 4,5 35 = 158 g.

Nous vérifions l'exactitude de la solution.
Poids de la nouvelle solution :

m 3 = 250 + 158 = 408 g.

Masse de sel dans la solution originale :

100 g de solution à 10% – 10 g de sel,

250 g de solution à 10% – X g de sel,

X= 250 10/100 = 25 g.

Masse totale de sel dans la nouvelle solution :

25 + 158 = 183 g.

Concentration de la nouvelle solution :

408 g de solution – 183 g de sel,

100 g de solution – oui g de sel,

oui= 100 183/408 = 45 g, soit 45 %.

Répondre. m(s.s.) = 158 g.

Il semble qu’un enseignant expérimenté trouvera toujours plusieurs façons de résoudre n’importe quel problème. Mais comme ma première professeure de chimie Klavdia Makarovna me l'a enseigné à l'école n°17 ​​d'Irkoutsk, j'essaie d'enseigner à mes élèves : toujours réfléchir profondément et comprendre l'essence chimique du problème et trouver la manière la plus rationnelle de le résoudre, et pas seulement ajuster à la réponse à la fin du manuel.