Atstumo tarp: 1 - taško ir plokštumos nustatymas; 2 - tiesus ir plokščias; 3 - plokštumos; 4 - kertančios tiesės nagrinėjamos kartu, nes visų šių problemų sprendimo algoritmas iš esmės yra tas pats ir susideda iš geometrinių konstrukcijų, kurias reikia atlikti norint nustatyti atstumą tarp tam tikro taško A ir plokštumos α. Jei yra koks nors skirtumas, jis susideda tik iš to, kad 2 ir 3 atvejais, prieš pradedant spręsti problemą, reikia pažymėti savavališką tašką A tiesėje m (2 atvejis) arba plokštumoje β (3 atvejis). atstumai tarp susikirtimo linijų, pirmiausia jas įtraukiame į lygiagrečias plokštumas α ir β ir tada nustatome atstumą tarp šių plokštumų.

Panagrinėkime kiekvieną iš nurodytų problemų sprendimo atvejų.

1. Atstumo tarp taško ir plokštumos nustatymas.

Atstumas nuo taško iki plokštumos nustatomas pagal statmenos atkarpos, nubrėžtos nuo taško iki plokštumos, ilgį.

Todėl šios problemos sprendimas susideda iš nuoseklaus šių grafinių operacijų atlikimo:

1) nuo taško A nuleidžiame statmeną plokštumai α (269 pav.);

2) raskite šio statmens susikirtimo su plokštuma M = a ∩ α tašką M;

3) nustatyti atkarpos ilgį.

Jei plokštuma α yra bendroje padėtyje, tai norint nuleisti statmeną į šią plokštumą, pirmiausia reikia nustatyti šios plokštumos horizontalios ir priekinės projekcijos kryptį. Norint rasti šio statmens susitikimo tašką su plokštuma, reikia ir papildomų geometrinių konstrukcijų.

Problemos sprendimas supaprastinamas, jei plokštuma α užima tam tikrą padėtį projekcinių plokštumų atžvilgiu. Šiuo atveju tiek statmeno projekcija, tiek jo susitikimo su plokštuma taško suradimas atliekamas be jokių papildomų pagalbinių konstrukcijų.

PAVYZDYS 1. Nustatykite atstumą nuo taško A iki frontaliai išsikišančios plokštumos α (270 pav.).

SPRENDIMAS. Per A" braižome horizontaliąją statmens projekciją l" ⊥ h 0α, o per A" - jos frontalinę projekciją l" ⊥ f 0α. Pažymime tašką M" = l" ∩ f 0α . Nuo AM || π 2, tada [A" M"] == |AM| = d.

Iš nagrinėjamo pavyzdžio matyti, kaip paprastai problema išsprendžiama, kai lėktuvas užima išsikišimo padėtį. Todėl, jei šaltinio duomenyse nurodyta bendrosios padėties plokštuma, prieš tęsiant sprendimą, plokštuma turi būti perkelta į padėtį, statmeną bet kuriai projekcijos plokštumai.

PAVYZDYS 2. Nustatykite atstumą nuo taško K iki plokštumos, nurodytos ΔАВС (271 pav.).

1. Plokštumą ΔАВС perkeliame į išsikišimo padėtį *. Norėdami tai padaryti, iš sistemos xπ 2 /π 1 pereiname prie x 1 π 3 /π 1: naujos x 1 ašies kryptis pasirenkama statmena trikampio horizontaliosios plokštumos horizontaliai projekcijai.

2. Projektuokite ΔABC į naują plokštumą π 3 (ΔABC plokštuma projektuojama į π 3, [ C " 1 B " 1 ]).

3. Projektuokite tašką K į tą pačią plokštumą (K" → K" 1).

4. Per tašką K" 1 brėžiame (K" 1 M" 1)⊥ atkarpą [C" 1 B" 1 ]. Reikiamas atstumas d = |K" 1 M" 1 |

Problemos sprendimas supaprastinamas, jei plokštuma apibrėžiama pėdsakais, nes nereikia braižyti lygių linijų projekcijų.

PAVYZDYS 3. Nustatykite atstumą nuo taško K iki plokštumos α, nurodytą takeliais (272 pav.).

* Racionaliausias būdas trikampio plokštumą perkelti į projektavimo padėtį yra pakeisti projekcijų plokštumas, nes tokiu atveju pakanka sukonstruoti tik vieną pagalbinę projekciją.

SPRENDIMAS. Plokštumą π 1 pakeičiame plokštuma π 3, tam nubrėžiame naują ašį x 1 ⊥ f 0α. Ant h 0α pažymime savavališką tašką 1" ir nustatome jo naują horizontalią projekciją plokštumoje π 3 (1" 1). Per taškus X α 1 (X α 1 = h 0α 1 ∩ x 1) ir 1" 1 nubrėžiame h 0α 1. Nustatome naują taško K → K" 1 horizontaliąją projekciją. Iš taško K" 1 nuleidžiame statmeną iki h 0α 1 ir pažymime jo sankirtos tašką su h 0α 1 - M" 1. Atkarpos ilgis K" 1 M" 1 parodys reikiamą atstumą.

2. Atstumo tarp tiesės ir plokštumos nustatymas.

Atstumas tarp tiesės ir plokštumos nustatomas pagal statmenos atkarpos, nukritusios iš savavališko tiesės taško į plokštumą, ilgį (žr. 248 pav.).

Todėl atstumo tarp tiesės m ir plokštumos α nustatymo problemos sprendimas niekuo nesiskiria nuo 1 pastraipoje aptartų atstumo tarp taško ir plokštumos nustatymo pavyzdžių (žr. 270 ... 272 ​​pav.). Kaip tašką galite paimti bet kurį tašką, priklausantį tiesei m.

3. Atstumo tarp plokštumų nustatymas.

Atstumas tarp plokštumų nustatomas pagal statmenos atkarpos, nukritusios iš taško vienoje plokštumoje į kitą plokštumą, dydį.

Iš šio apibrėžimo matyti, kad atstumo tarp plokštumų α ir β nustatymo problemos sprendimo algoritmas skiriasi nuo panašaus atstumo tarp tiesės m ir plokštumos α nustatymo uždavinio sprendimo tik tuo, kad tiesė m turi priklausyti plokštumai α t.y., norint nustatyti atstumą tarp plokštumų α ir β:

1) α plokštumoje paimkite tiesę m;

2) pasirinkite savavališką tašką A tiesėje m;

3) nuo taško A statmeną l nuleisti plokštumai β;

4) nustatyti tašką M - statmens l susitikimo tašką su plokštuma β;

5) nustatyti atkarpos dydį.

Praktikoje patartina naudoti kitokį sprendimo algoritmą, kuris nuo pateiktojo skirsis tik tuo, kad prieš pradedant pirmąjį žingsnį plokštumas reikia perkelti į projekcijos padėtį.

Šios papildomos operacijos įtraukimas į algoritmą supaprastina visų kitų be išimties taškų vykdymą, o tai galiausiai lemia paprastesnį sprendimą.

PAVYZDYS 1. Nustatykite atstumą tarp plokštumų α ir β (273 pav.).

SPRENDIMAS. Iš sistemos xπ 2 /π 1 pereiname į x 1 π 1 /π 3. Naujos plokštumos π 3 atžvilgiu plokštumos α ir β užima išsikišimo padėtį, todėl atstumas tarp naujų frontalinių pėdsakų f 0α 1 ir f 0β 1 yra pageidaujamas.

Inžinerinėje praktikoje dažnai reikia išspręsti plokštumos, lygiagrečios tam tikrai plokštumai ir pašalinimo iš jos tam tikru atstumu, problemą. 2 pavyzdys iliustruoja tokios problemos sprendimą.

PAVYZDYS 2. Reikia sudaryti plokštumos β projekcijas, lygiagrečias duotai plokštumai α (m || n), jei žinoma, kad atstumas tarp jų yra d (274 pav.).

1. α plokštumoje nubrėžiame savavališkas horizontalias linijas h (1, 3) ir priekines linijas f (1,2).

2. Iš taško 1 atstatome statmeną l plokštumai α(l" ⊥ h", l" ⊥ f").

3. Ant statmeno l pažymime savavališką tašką A.

4. Nustatykite atkarpos ilgį - (padėtis diagramoje nurodo metrinę tiesės l kryptį).

5. Ištieskite atkarpą = d tiesėje (1"A 0) nuo 1 taško".

6. Ant projekcijų l" ir l" pažymėkite taškus B" ir B", atitinkančius tašką B 0.

7. Per tašką B nubrėžiame plokštumą β (h 1 ∩ f 1). Į β || α, būtina laikytis sąlygos h 1 || h ir f 1 || f.

4. Atstumo tarp susikertančių tiesių nustatymas.

Atstumas tarp susikertančių tiesių nustatomas pagal statmens, esančio tarp lygiagrečių plokštumų, kurioms priklauso susikertančios tiesės, ilgį.

Norint nubrėžti viena kitai lygiagrečias plokštumas α ir β per susikertančias tieses m ir f, pakanka per tašką A (A ∈ m) nubrėžti tiesę p, lygiagrečią tiesei f, o per tašką B (B ∈ f) tiesė k lygiagreti tiesei m . Susikertančios tiesės m ir p, f ir k apibrėžia tarpusavyje lygiagrečias plokštumas α ir β (žr. 248 pav., e). Atstumas tarp plokštumų α ir β lygus reikiamam atstumui tarp susikirtimo tiesių m ir f.

Galima pasiūlyti kitą atstumo tarp susikertančių tiesių nustatymo būdą, kuris susideda iš to, kad naudojant tam tikrą stačiakampių projekcijų transformavimo būdą viena iš susikertančių tiesių perkeliama į projektavimo padėtį. Šiuo atveju viena tiesės projekcija išsigimsta į tašką. Atstumas tarp naujų susikertančių linijų projekcijų (taškas A" 2 ir atkarpa C" 2 D" 2) yra reikiamas.

Fig. 275 parodytas atstumo tarp susikertančių tiesių a ir b nustatymo problemos sprendimas, duotos atkarpos [AB] ir [CD]. Sprendimas atliekamas tokia seka:

1. Vieną iš susikirtimo tiesių (a) perkelkite į lygiagrečią plokštumai π 3 padėtį; Norėdami tai padaryti, iš projekcijų plokštumų sistemos xπ 2 /π 1 pereikite prie naujos x 1 π 1 /π 3, x 1 ašis lygiagreti horizontaliai tiesės a projekcijai. Nustatykite a" 1 [A" 1 B" 1 ] ir b" 1.

2. Pakeitę plokštumą π 1 plokštuma π 4, išverčiame tiesę

ir į padėtį a" 2, statmenai plokštumai π 4 (nauja x 2 ašis nubrėžta statmenai a" 1).

3. Sukurkite naują horizontalią tiesės b" 2 - [ C" 2 D" 2 ] projekciją.

4. Atstumas nuo taško A" 2 iki tiesės C" 2 D" 2 (atkarpa (A" 2 M" 2 ]) (reikia.

Reikėtų nepamiršti, kad vienos iš kryžminių tiesių perkėlimas į išsikišimo padėtį yra ne kas kita, kaip lygiagretumo plokštumų, kuriose gali būti uždengtos tiesės a ir b, perkėlimas taip pat į projektavimo padėtį.

Tiesą sakant, perkeldami tiesę a į plokštumai π 4 statmeną padėtį, užtikriname, kad bet kuri plokštuma, kurioje yra linija a, yra statmena plokštumai π 4, įskaitant plokštumą α, apibrėžtą tiesėmis a ir m (a ∩ m, m | |. b ). Jei dabar nubrėžtume tiesę n, lygiagrečią su a ir susikertančią tiesę b, tai gautume plokštumą β, kuri yra antroji lygiagretumo plokštuma, kurioje yra susikertančios tiesės a ir b. Kadangi β || α, tada β ⊥ π 4 .

Atstumo nuo taško iki plokštumos radimas yra dažna problema, kylanti sprendžiant įvairius analitinės geometrijos uždavinius, pavyzdžiui, šią problemą galima sumažinti iki atstumo tarp dviejų susikertančių tiesių arba tarp tiesės ir lygiagrečios plokštumos; tai.

Apsvarstykite plokštumą $β$ ir tašką $M_0$ su koordinatėmis $(x_0;y_0; z_0)$, kuris nepriklauso plokštumai $β$.

1 apibrėžimas

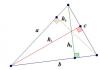
Trumpiausias atstumas tarp taško ir plokštumos bus statmenas, nubrėžtas nuo taško $M_0$ iki plokštumos $β$.

1 pav. Atstumas nuo taško iki plokštumos. Avtor24 – internetinis keitimasis studentų darbais

Žemiau aptariame, kaip koordinačių metodu rasti atstumą nuo taško iki plokštumos.

Atstumo nuo taško iki plokštumos erdvėje nustatymo koordinačių metodo formulės išvedimas

Statmenas iš taško $M_0$, kertantis plokštumą $β$ taške $M_1$ su koordinatėmis $(x_1;y_1; z_1)$, yra tiesėje, kurios krypties vektorius yra normalusis plokštumos $β$ vektorius. Šiuo atveju vieneto vektoriaus $n$ ilgis lygus vienetui. Atitinkamai, atstumas nuo $β$ iki taško $M_0$ bus:

$ρ= |\vec(n) \cdot \vec(M_1M_0)|\left(1\right)$, kur $\vec(M_1M_0)$ yra normalus $β$ plokštumos vektorius, o $\vec( n)$ yra nagrinėjamos plokštumos vienetinis normalusis vektorius.

Tuo atveju, kai plokštumos lygtis pateikiama bendra forma $Ax+ By + Cz + D=0$, plokštumos normaliojo vektoriaus koordinatės yra lygties $\(A;B;C\) koeficientai )$, o vieneto normalusis vektorius šiuo atveju turi koordinates, apskaičiuotas naudojant šią lygtį:

$\vec(n)= \frac(\(A;B;C\))(\sqrt(A^2 + B^2 + C^2))\left(2\right)$.

Dabar galime rasti normalaus vektoriaus $\vec(M_1M_0)$ koordinates:

$\vec(M_0M_1)= \(x_0 – x_1;y_0-y_1;z_0-z_1\)\left(3\right)$.

Taip pat išreiškiame koeficientą $D$ naudodami $β$ plokštumoje esančio taško koordinates:

$D = Ax_1+By_1+Cz_1$

Vienetinio normaliojo vektoriaus koordinates iš lygybės $(2)$ galima pakeisti $β$ plokštumos lygtimi, tada turime:

$ρ= \frac(|A(x_0 -x_1) + B(y_0-y_1)+C(z_0-z_1)|)(\sqrt(A^2+B^2+C^2))= \frac( |Ax_0+ By_0 + Cz_0-(Ax_1+By_1+Cz_1)|)(\sqrt(A^2+B^2+C^2)) = \frac(Ax_0+ By_0 + Cz_0 + D)(\sqrt(A^2) +B^2+C^2))\left(4\right)$

Lygybė $(4)$ yra atstumo nuo taško iki plokštumos erdvėje nustatymo formulė.

Bendras atstumo nuo taško $M_0$ iki plokštumos nustatymo algoritmas

1. Jei plokštumos lygtis nėra pateikta bendra forma, pirmiausia reikia ją redukuoti į bendrą formą.
2. Po to iš bendrosios plokštumos lygties reikia išreikšti tam tikros plokštumos normalųjį vektorių per tašką $M_0$ ir tašką, priklausantį duotai plokštumai, tam reikia panaudoti lygybę $(3)$ .
3. Kitas etapas – plokštumos vienetinio normaliojo vektoriaus koordinačių paieška naudojant formulę $(2)$.
4. Galiausiai galite pradėti ieškoti atstumo nuo taško iki plokštumos, tai daroma apskaičiuojant vektorių $\vec(n)$ ir $\vec(M_1M_0)$ skaliarinę sandaugą.

Tegul būna lėktuvas .
Nupieškime normalų
per koordinačių pradžią O. Tegu duota – normalaus suformuoti kampai
su koordinačių ašimis. . Leiskite
– normalaus segmento ilgis kol susikirs su plokštuma. Darant prielaidą, kad normalaus krypties kosinusai yra žinomi .

, išvedame plokštumos lygtį
Leiskite
) yra savavališkas taškas plokštumoje. Vieneto normalusis vektorius turi koordinates. Raskime vektoriaus projekciją

į normalią. Nuo taško M

.

tada priklauso lėktuvui Tai duotosios plokštumos lygtis, vadinama .

normalus

Atstumas nuo taško iki plokštumos ,Nuo taško*
Tegu duotas lėktuvas - taškas erdvėje, d

– jo atstumas nuo lėktuvo. Apibrėžimas. Nukrypimas taškų M* + - taškas erdvėje,), iš lėktuvo vadinamas numeriu ( Jeigu* M yra kitoje plokštumos pusėje, kur rodo teigiama normaliosios krypties kryptis - taškas erdvėje,, ir numeris (-

.

), jei taškas yra kitoje plokštumos pusėje:. Teorema Leisk lėktuvui su normaliu vienetu

, išvedame plokštumos lygtį Nuo taško*
pateikiama normalia lygtimi: Jeigu– taškas erdvėje Nuokrypis t.

* iš plokštumos pateikiama išraiškaĮrodymas.
Projekcija t. * žymime normaliu. K taškų Taško nuokrypis

.

iš plokštumos yra lygus Taisyklė. Norėdami rasti nukrypimas Jeigu T. Jeigu* * iš plokštumos reikia pakeisti koordinates t į normalią plokštumos lygtį. .

. Atstumas nuo taško iki plokštumos yra

Bendrosios plokštumos lygties redukavimas į normaliąją formą

Tegul ta pati plokštuma apibrėžiama dviem lygtimis:

Bendroji lygtis

Normali lygtis.

Kadangi abi lygtys apibrėžia tą pačią plokštumą, jų koeficientai yra proporcingi:

Padėkime pirmąsias tris lygybes kvadratu ir sudėkime jas: Iš čia rasime

. (10)

Normalizuojantis faktorius:

Bendrąją plokštumos lygtį padauginę iš normalizuojančio koeficiento, gauname normaliąją plokštumos lygtį:

Problemų pavyzdžiai tema „Lėktuvas“. 1 pavyzdys. Sukurkite plokštumos lygtį
einantis per tam tikrą tašką

(2,1,-1) ir lygiagrečiai plokštumai. Sprendimas :
. Normalus lėktuvui . Kadangi plokštumos lygiagrečios, tai normalioji taip pat yra normalus norimai plokštumai . Naudodami plokštumos, einančios per nurodytą tašką (3), lygtį, gauname plokštumą

lygtis:

Atsakymas: Statmens pagrindas nukrito nuo pradžios iki plokštumos , yra esmė
. Raskite plokštumos lygtį .

(2,1,-1) ir lygiagrečiai plokštumai.. Vektorius
yra normalu lėktuvui . Taškas Nuo taško 0 priklauso lėktuvui. Galite naudoti plokštumos, einančios per nurodytą tašką, lygtį (3):

lygtis:

3 pavyzdys. Sukonstruoti plokštumą , einantis per taškus

ir statmenai plokštumai :.

Todėl tam tikru momentu Nuo taško (x, y, z) priklausė lėktuvui , būtina, kad trys vektoriai
buvo lygiagrečiai:

=0.

Belieka atskleisti determinantą ir gautą išraišką paversti bendrosios lygties (1) forma.

4 pavyzdys. Lėktuvas pateikiama pagal bendrąją lygtį:

Raskite taško nuokrypį
iš nurodytos plokštumos.

(2,1,-1) ir lygiagrečiai plokštumai.. Perkelkime plokštumos lygtį į normaliąją formą.

,

.

Į gautą normaliąją lygtį pakeisime taško koordinates taškų.

.

lygtis:
.

5 pavyzdys. Ar plokštuma kerta atkarpą?

(2,1,-1) ir lygiagrečiai plokštumai.. Pjaustyti AB kirto lėktuvą, nukrypimai Ir iš lėktuvo turi turėti skirtingus ženklus:

.

6 pavyzdys. Trijų plokštumų susikirtimas viename taške.

.

Sistema turi unikalų sprendimą, todėl visos trys plokštumos turi vieną bendrą tašką.

7 pavyzdys. Dviejų duotųjų plokštumų sudaryto dvikampio kampo pusiausvyros radimas.

, išvedame plokštumos lygtį Ir - tam tikro taško nukrypimas
iš pirmos ir antros plokštumos.

Vienoje iš bisektoriaus plokštumų (atitinkančio kampą, kuriame yra koordinačių pradžia) šie nuokrypiai yra vienodi dydžiu ir ženklu, o kitoje jie yra vienodi pagal dydį ir priešingi pagal ženklą.

Tai pirmosios pusiausvyros plokštumos lygtis.

Tai antrosios pusiausvyros plokštumos lygtis.

8 pavyzdys. Dviejų nurodytų taškų vietos nustatymas Ir šių plokštumų suformuotų dvikampių kampų atžvilgiu.

, išvedame plokštumos lygtį
. Nustatykite: viename, gretimuose arba vertikaliuose kampuose yra taškai Ir .

A). Jeigu Ir gulėti ant vienos pusės ir iš , tada jie yra tame pačiame dvikampyje.

b). Jeigu Ir gulėti ant vienos pusės ir skiriasi nuo , tada jie guli gretimuose kampuose.

V). Jeigu Ir gulėti priešingose ​​pusėse Ir , tada jie guli vertikaliuose kampuose.

3 koordinačių sistemos

Linijos plokštumoje 8

Pirmojo užsakymo eilutės. Tiesiai lėktuve. 10

Kampas tarp tiesių 12

Bendroji 13 eilutės lygtis

Nepilna pirmojo laipsnio lygtis 14

Tiesės lygtis „atkarpomis“ 14

Bendras dviejų eilučių lygčių tyrimas 15

Įprasta 15 eilutei

Kampas tarp dviejų tiesių 16

Kanoninė 16 eilutės lygtis

Parametrinės tiesės lygtys 17

Normalioji (normalizuota) tiesės lygtis 18

Atstumas nuo taško iki 19 linijos

20 eilučių pieštuko lygtis

Užduočių pavyzdžiai tema „linija plokštumoje“ 22

Vektorių sandauga 24

Kryžminio produkto savybės 24

Geometrinės savybės 24

Algebrinės savybės 25

Vektorinės sandaugos išreiškimas per faktorių koordinates 26

Mišrus trijų vektorių sandauga 28

Geometrinė mišraus produkto reikšmė 28

Mišrios sandaugos išreiškimas vektorinėmis koordinatėmis 29

Problemų sprendimo pavyzdžiai

Mums svarbu išlaikyti jūsų privatumą. Dėl šios priežasties sukūrėme Privatumo politiką, kurioje aprašoma, kaip naudojame ir saugome jūsų informaciją. Peržiūrėkite mūsų privatumo praktiką ir praneškite mums, jei turite klausimų.

Asmeninės informacijos rinkimas ir naudojimas

Asmeninė informacija reiškia duomenis, kurie gali būti naudojami konkretaus asmens tapatybei nustatyti arba susisiekti su juo.

Jūsų gali būti paprašyta pateikti savo asmeninę informaciją bet kuriuo metu, kai susisiekiate su mumis.

Toliau pateikiami keli pavyzdžiai, kokios rūšies asmeninės informacijos galime rinkti ir kaip galime tokią informaciją naudoti.

Kokią asmeninę informaciją renkame:

• Kai pateikiate paraišką svetainėje, galime rinkti įvairią informaciją, įskaitant jūsų vardą, telefono numerį, el. pašto adresą ir kt.

Kaip naudojame jūsų asmeninę informaciją:

• Mūsų renkama asmeninė informacija leidžia mums susisiekti su jumis dėl unikalių pasiūlymų, akcijų ir kitų renginių bei būsimų renginių.
• Retkarčiais galime naudoti jūsų asmeninę informaciją svarbiems pranešimams ir pranešimams siųsti.
• Mes taip pat galime naudoti asmeninę informaciją vidiniais tikslais, pavyzdžiui, atlikti auditą, duomenų analizę ir įvairius tyrimus, siekdami tobulinti teikiamas paslaugas ir teikti rekomendacijas dėl mūsų paslaugų.
• Jei dalyvaujate prizų traukime, konkurse ar panašioje akcijoje, mes galime naudoti jūsų pateiktą informaciją tokioms programoms administruoti.

Informacijos atskleidimas trečiosioms šalims

Mes neatskleidžiame iš jūsų gautos informacijos trečiosioms šalims.

Išimtys:

• Jei reikia – įstatymų nustatyta tvarka, teismine tvarka, teismo procese ir (arba) remiantis viešais prašymais arba Rusijos Federacijos valdžios institucijų prašymais – atskleisti savo asmeninę informaciją. Taip pat galime atskleisti informaciją apie jus, jei nuspręsime, kad toks atskleidimas yra būtinas arba tinkamas saugumo, teisėsaugos ar kitais visuomenei svarbiais tikslais.
• Reorganizavimo, susijungimo ar pardavimo atveju surinktą asmeninę informaciją galime perduoti atitinkamai trečiajai šaliai.

Asmeninės informacijos apsauga

Mes imamės atsargumo priemonių, įskaitant administracines, technines ir fizines, siekdami apsaugoti jūsų asmeninę informaciją nuo praradimo, vagystės ir netinkamo naudojimo, taip pat nuo neteisėtos prieigos, atskleidimo, pakeitimo ir sunaikinimo.

Jūsų privatumo gerbimas įmonės lygiu

Siekdami užtikrinti, kad jūsų asmeninė informacija būtų saugi, savo darbuotojams pranešame apie privatumo ir saugumo standartus ir griežtai vykdome privatumo praktiką.

Šiame straipsnyje kalbama apie atstumo nuo taško iki plokštumos nustatymą. Išanalizuokime tai koordinačių metodu, kuris leis rasti atstumą nuo duoto taško trimatėje erdvėje. Norėdami tai sustiprinti, pažvelkime į kelių užduočių pavyzdžius.

Atstumas nuo taško iki plokštumos randamas naudojant žinomą atstumą nuo taško iki taško, kur vienas iš jų yra duotas, o kitas yra projekcija į tam tikrą plokštumą.

Kai erdvėje nurodytas taškas M 1 su plokštuma χ, tai per tašką galima nubrėžti plokštumai statmeną tiesę. H 1 yra jų bendras susikirtimo taškas. Iš to gauname, kad atkarpa M 1 H 1 yra statmena, nubrėžta iš taško M 1 į plokštumą χ, kur taškas H 1 yra statmens pagrindas.

1 apibrėžimas

Atstumas nuo tam tikro taško iki statmens, nubrėžto iš tam tikro taško į tam tikrą plokštumą, pagrindo vadinamas.

Apibrėžimas gali būti parašytas įvairiomis formuluotėmis.

2 apibrėžimas

Atstumas nuo taško iki plokštumos yra statmens, nubrėžto iš tam tikro taško į tam tikrą plokštumą, ilgis.

Atstumas nuo taško M 1 iki χ plokštumos nustatomas taip: atstumas nuo taško M 1 iki χ plokštumos bus mažiausias nuo nurodyto taško iki bet kurio plokštumos taško. Jei taškas H 2 yra χ plokštumoje ir nėra lygus taškui H 2, tai gauname M 2 H 1 H 2 formos statųjį trikampį , kuris yra stačiakampis, kur yra kojelė M 2 H 1, M 2 H 2 – hipotenuzė. Tai reiškia, kad M 1 H 1< M 1 H 2 . Тогда отрезок М 2 H 1 laikomas pasvirusiu, kuris nubrėžtas iš taško M 1 į plokštumą χ. Turime, kad statmenas, nubrėžtas iš tam tikro taško į plokštumą, yra mažesnis nei pasviręs, nubrėžtas iš taško į nurodytą plokštumą. Pažiūrėkime į šį atvejį žemiau esančiame paveikslėlyje.

Atstumas nuo taško iki plokštumos – teorija, pavyzdžiai, sprendimai

Yra keletas geometrinių uždavinių, kurių sprendimuose turi būti nurodytas atstumas nuo taško iki plokštumos. Gali būti įvairių būdų tai nustatyti. Norėdami išspręsti, naudokite Pitagoro teoremą arba trikampių panašumą. Kai pagal sąlygą reikia apskaičiuoti atstumą nuo taško iki plokštumos, pateiktą trimatės erdvės stačiakampėje koordinačių sistemoje, tai sprendžiama koordinačių metodu. Šioje pastraipoje aptariamas šis metodas.

Pagal uždavinio sąlygas turime, kad trimatėje erdvėje taškas su koordinatėmis M 1 (x 1, y 1, z 1) su plokštuma χ reikia nustatyti atstumą nuo M 1 iki plokštuma χ. Šiai problemai išspręsti naudojami keli sprendimo būdai.

Pirmas būdas

Šis metodas pagrįstas atstumo nuo taško iki plokštumos nustatymu naudojant taško H 1 koordinates, kurios yra statmens nuo taško M 1 iki plokštumos χ pagrindas. Tada turite apskaičiuoti atstumą tarp M 1 ir H 1.

Norėdami išspręsti problemą antruoju būdu, naudokite normaliąją tam tikros plokštumos lygtį.

Antras būdas

Pagal sąlygą turime, kad H 1 yra statmens, kuris buvo nuleistas iš taško M 1 į plokštumą χ, pagrindas. Tada nustatome taško H 1 koordinates (x 2, y 2, z 2). Reikiamas atstumas nuo M 1 iki χ plokštumos randamas pagal formulę M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + (z 2 - z 1) 2, kur M 1 (x 1, y 1, z 1) ir H 1 (x 2, y 2, z 2). Norėdami išspręsti, turite žinoti taško H 1 koordinates.

Turime, kad H 1 yra χ plokštumos susikirtimo taškas su tiese a, kuri eina per tašką M 1, esantį statmenai χ plokštumai. Iš to išplaukia, kad būtina sudaryti tiesės, einančios per tam tikrą tašką, statmeną tam tikrai plokštumai, lygtį. Būtent tada galėsime nustatyti taško H 1 koordinates. Būtina apskaičiuoti tiesės ir plokštumos susikirtimo taško koordinates.

Algoritmas atstumo nuo taško su koordinatėmis M 1 (x 1, y 1, z 1) iki χ plokštumos nustatymo:

3 apibrėžimas

• nubrėžkite tiesės a, einančios per tašką M 1, lygtį ir tuo pačiu
• statmena χ plokštumai;
• suraskite ir apskaičiuokite taško H 1 koordinates (x 2 , y 2 , z 2), kurios yra taškai
• tiesės a susikirtimas su plokštuma χ ;
• apskaičiuokite atstumą nuo M 1 iki χ pagal formulę M 1 H 1 = (x 2 - x 1) 2 + (y 2 - y 1) 2 + z 2 - z 1 2.

Trečias būdas

Duotoje stačiakampėje koordinačių sistemoje O x y z yra plokštuma χ, tada gauname normaliąją lygtį plokštumos formos cos α · x + cos β · y + cos γ · z - p = 0. Iš čia gauname, kad atstumas M 1 H 1 su tašku M 1 (x 1 , y 1 , z 1), nubrėžtas iki plokštumos χ, apskaičiuojamas pagal formulę M 1 H 1 = cos α x + cos β y + cos γ z - p . Ši formulė galioja, nes buvo nustatyta teoremos dėka.

), jei taškas yra kitoje plokštumos pusėje:

Jei trimatėje erdvėje pateiktas taškas M 1 (x 1, y 1, z 1), turintis normaliąją plokštumos χ lygtį, kurios forma yra cos α x + cos β y + cos γ z - p = 0, tada apskaičiuojant atstumą nuo taško iki plokštumos M 1 H 1 gaunamas pagal formulę M 1 H 1 = cos α · x + cos β · y + cos γ · z - p, nes x = x 1, y = y 1 , z = z 1.

Įrodymas

Teoremos įrodymas yra atstumas nuo taško iki tiesės. Iš to gauname, kad atstumas nuo M 1 iki χ plokštumos yra skirtumo tarp spindulio vektoriaus M 1 skaitinės projekcijos ir atstumo nuo pradžios iki χ plokštumos modulis. Tada gauname išraišką M 1 H 1 = n p n → O M → - p. Plokštumos χ normalusis vektorius turi formą n → = cos α, cos β, cos γ, o jo ilgis lygus vienetui, n p n → O M → yra vektoriaus O M → = (x 1, y 1) skaitmeninė projekcija. , z 1) vektoriaus n → nustatyta kryptimi.

Taikykime skaliarinių vektorių skaičiavimo formulę. Tada gauname išraišką n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → formos vektoriaus radimui, nes n → = cos α , cos β , cos γ · z ir O M → = (x 1 , y 1 , z 1) . Įrašo koordinačių forma bus n → , O M → = cos α · x 1 + cos β · y 1 + cos γ · z 1 , tada M 1 H 1 = n p n → O M → - p = cos α · x 1 + cos β · y 1 + cos γ · z 1 - p . Teorema įrodyta.

Iš čia gauname, kad atstumas nuo taško M 1 (x 1, y 1, z 1) iki plokštumos χ apskaičiuojamas cos α · x + cos β · y + cos γ · z - p = 0 į kairioji normaliosios plokštumos lygties pusė vietoj x, y, z koordinačių x 1, y 1 ir z 1, susijęs su tašku M 1, imant absoliučią gautos vertės vertę.

Pažvelkime į atstumo nuo taško su koordinatėmis iki nurodytos plokštumos pavyzdžius.

1 pavyzdys

Apskaičiuokite atstumą nuo taško su koordinatėmis M 1 (5, - 3, 10) iki plokštumos 2 x - y + 5 z - 3 = 0.

(2,1,-1) ir lygiagrečiai plokštumai.

Išspręskime problemą dviem būdais.

Pirmasis metodas prasideda tiesės a krypties vektoriaus apskaičiavimu. Pagal sąlygą gauname, kad duotoji lygtis 2 x - y + 5 z - 3 = 0 yra bendroji plokštumos lygtis, o n → = (2, - 1, 5) yra duotosios plokštumos normalusis vektorius. Jis naudojamas kaip tiesės a, kuri yra statmena nurodytai plokštumai, krypties vektorius. Būtina užrašyti kanoninę tiesės erdvėje, einančios per M 1 (5, - 3, 10), lygtį krypties vektoriumi, kurio koordinatės yra 2, - 1, 5.

Lygtis taps x - 5 2 = y - (- 3) - 1 = z - 10 5 ⇔ x - 5 2 = y + 3 - 1 = z - 10 5.

Turi būti nustatyti susikirtimo taškai. Norėdami tai padaryti, švelniai sujunkite lygtis į sistemą, kad pereitumėte nuo kanoninės prie dviejų susikertančių tiesių lygčių. Paimkime šį tašką kaip H 1. Mes tai gauname

x - 5 2 = y + 3 - 1 = z - 10 5 ⇔ - 1 (x - 5) = 2 (y + 3) 5 (x - 5) = 2 (z - 10) 5 ( y + 3) = - 1 · (z - 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 = 0 5 x - 2 z - 5 = 0

Po to turite įjungti sistemą

x + 2 y + 1 = 0 5 x - 2 z - 5 = 0 2 x - y + 5 z - 3 = 0 ⇔ x + 2 y = 1 5 x - 2 z = 5 2 x - y + 5 z = 3

Pereikime prie Gauso sistemos sprendimo taisyklės:

1 2 0 - 1 5 0 - 2 5 2 - 1 5 3 ~ 1 2 0 - 1 0 - 10 - 2 10 0 - 5 5 5 ~ 1 2 0 - 1 0 - 10 - 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0, y = - 1 10 10 + 2 z = - 1, x = - 1 - 2 y = 1

Gauname H 1 (1, - 1, 0).

Apskaičiuojame atstumą nuo nurodyto taško iki plokštumos. Mes paimame taškus M 1 (5, - 3, 10) ir H 1 (1, - 1, 0) ir gauname

M 1 H 1 = (1 - 5) 2 + ( - 1 - ( - 3)) 2 + (0 - 10) 2 = 2 30

Antrasis sprendimas yra pirmiausia pateikti pateiktą lygtį 2 x - y + 5 z - 3 = 0 į normalią formą. Nustatome normalizavimo koeficientą ir gauname 1 2 2 + (- 1) 2 + 5 2 = 1 30. Iš čia gauname plokštumos lygtį 2 30 · x - 1 30 · y + 5 30 · z - 3 30 = 0. Kairioji lygties pusė apskaičiuojama pakeičiant x = 5, y = - 3, z = 10, ir reikia paimti atstumą nuo M 1 (5, - 3, 10) iki 2 x - y + 5 z - 3 = 0 modulio. Gauname išraišką:

M 1 H 1 = 2 30 5 - 1 30 - 3 + 5 30 10 - 3 30 = 60 30 = 2 30

Atsakymas: 230.

Kai χ plokštuma nurodoma vienu iš metodų skyriuje apie plokštumos nurodymo metodus, pirmiausia turite gauti χ plokštumos lygtį ir bet kuriuo metodu apskaičiuoti reikiamą atstumą.

2 pavyzdys

Trimatėje erdvėje nurodomi taškai, kurių koordinatės M 1 (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, - 1). Apskaičiuokite atstumą nuo M 1 iki plokštumos A B C.

(2,1,-1) ir lygiagrečiai plokštumai.

Pirmiausia reikia užrašyti plokštumos, einančios per nurodytus tris taškus, lygtį su koordinatėmis M 1 (5, - 3, 10), A (0, 2, 1), B (2, 6, 1), C ( 4, 0, - 1) .

x - 0 y - 2 z - 1 2 - 0 6 - 2 1 - 1 4 - 0 0 - 2 - 1 - 1 = 0 ⇔ x y - 2 z - 1 2 4 0 4 - 2 - 2 = 0 ⇔ ⇔ - 8 x + 4 y - 20 z + 12 = 0 ⇔ 2 x - y + 5 z - 3 = 0

Iš to išplaukia, kad problemos sprendimas yra panašus į ankstesnį. Tai reiškia, kad atstumas nuo taško M 1 iki plokštumos A B C yra 2 30.

Atsakymas: 230.

Atstumą nuo nurodyto taško plokštumoje arba iki plokštumos, kuriai jie yra lygiagretūs, rasti patogiau taikant formulę M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 - p . Iš to gauname, kad normaliosios plokštumų lygtys gaunamos keliais etapais.

3 pavyzdys

Raskite atstumą nuo nurodyto taško koordinatėmis M 1 (- 3, 2, - 7) iki koordinačių plokštumos O x y z ir plokštumos, pateiktos lygtimi 2 y - 5 = 0.

(2,1,-1) ir lygiagrečiai plokštumai.

Koordinačių plokštuma O y z atitinka x = 0 formos lygtį. O y z plokštumai tai normalu. Todėl reikia pakeisti reikšmes x = - 3 į kairę išraiškos pusę ir paimti absoliučią atstumo nuo taško su koordinatėmis M 1 (- 3, 2, - 7) reikšmę iki plokštumos. Gauname vertę, lygią - 3 = 3.

Po transformacijos plokštumos 2 y - 5 = 0 normalioji lygtis įgis formą y - 5 2 = 0. Tada galite rasti reikiamą atstumą nuo taško su koordinatėmis M 1 (- 3, 2, - 7) iki plokštumos 2 y - 5 = 0. Pakeitę ir apskaičiavę, gauname 2 - 5 2 = 5 2 - 2.

lygtis: Reikalingas atstumas nuo M 1 (- 3, 2, - 7) iki O y z yra 3, o iki 2 y - 5 = 0 yra 5 2 - 2.

Jei tekste pastebėjote klaidą, pažymėkite ją ir paspauskite Ctrl+Enter