§ 1 Lygties šaknų pasirinkimas realiose situacijose

Panagrinėkime šią realią situaciją:

Meistras ir mokinys kartu pagamino 400 nestandartinių dalių. Be to, meistras dirbo 3 dienas, o studentas - 2 dienas. Kiek dalių padarė kiekvienas žmogus?

Sukurkime šios situacijos algebrinį modelį. Leiskite meistrui pagaminti dalis per 1 dieną. O mokinys yra ties detalėmis. Tada meistras per 3 dienas pagamins 3 dalis, o mokinys – per 2 dienas. Kartu jie pagamins 3 + 2 dalis. Kadangi pagal būklę iš viso buvo pagaminta 400 dalių, gauname lygtį:

Gauta lygtis vadinama tiesine lygtimi iš dviejų kintamųjų. Čia turime rasti skaičių x ir y porą, kuriai lygtis bus tikrosios skaitinės lygybės forma. Atkreipkite dėmesį, kad jei x = 90, y = 65, tada gauname lygybę:

3 ∙ 90 + 65 ∙ 2 = 400

Kadangi buvo gauta teisinga skaitinė lygybė, skaičių 90 ir 65 pora bus šios lygties sprendimas. Tačiau rastas sprendimas nėra vienintelis. Jei x = 96 ir y = 56, tada gauname lygybę:

96 ∙ 3 + 56 ∙ 2 = 400

Tai taip pat yra tikra skaitinė lygybė, o tai reiškia, kad skaičių 96 ir 56 pora taip pat yra šios lygties sprendimas. Tačiau skaičių pora x = 73 ir y = 23 nebus šios lygties sprendimas. Tiesą sakant, 3 ∙ 73 + 2 ∙ 23 = 400 duos neteisingą skaitinę lygybę 265 = 400. Reikėtų pažymėti, kad jei nagrinėsime lygtį šios realios situacijos atžvilgiu, tada bus skaičių poros, kurios, būdamos šios lygties sprendimas nebus problemos sprendimas. Pavyzdžiui, pora skaičių:

x = 200 ir y = -100

yra lygties sprendimas, tačiau mokinys negali sudaryti -100 dalių, todėl tokia skaičių pora negali būti atsakymas į uždavinio klausimą. Taigi kiekvienoje konkrečioje realioje situacijoje reikia priimti pagrįstą požiūrį į lygties šaknų pasirinkimą.

Apibendrinkime pirmuosius rezultatus:

Ax + bу + c = 0 formos lygtis, kur a, b, c yra bet kokie skaičiai, vadinama tiesine lygtimi su dviem kintamaisiais.

Dviejų kintamųjų tiesinės lygties sprendimas yra skaičių pora, atitinkanti x ir y, kuriai lygtis virsta tikrąja skaitine lygybe.

§ 2 Tiesinės lygties grafikas

Jau pats poros (x;y) įrašymas verčia susimąstyti apie galimybę pavaizduoti ją kaip tašką su koordinatėmis xy y plokštumoje. Tai reiškia, kad galime gauti konkrečios situacijos geometrinį modelį. Pavyzdžiui, apsvarstykite lygtį:

2x + y - 4 = 0

Išsirinkime kelias skaičių poras, kurios bus šios lygties sprendiniai, ir su rastomis koordinatėmis sukonstruokime taškus. Tegul tai yra taškai:

A(0; 4), B(2; 0), C(1; 2), D(-2; 8), E(- 1; 6).

Atkreipkite dėmesį, kad visi taškai yra toje pačioje linijoje. Ši linija vadinama dviejų kintamųjų tiesinės lygties grafiku. Tai grafinis (arba geometrinis) tam tikros lygties modelis.

Jei skaičių pora (x;y) yra lygties sprendimas

ax + vy + c = 0, tai taškas M(x;y) priklauso lygties grafikui. Galima sakyti ir atvirkščiai: jei taškas M(x;y) priklauso lygties ax + y + c = 0 grafikui, tai skaičių pora (x;y) yra šios lygties sprendinys.

Iš geometrijos kurso žinome:

Norint nubraižyti tiesę, reikia 2 taškų, taigi norint nubraižyti tiesinės lygties grafiką su dviem kintamaisiais, pakanka žinoti tik 2 poras sprendinių. Tačiau atspėti šaknis ne visada yra patogi ar racionali procedūra. Galite elgtis pagal kitą taisyklę. Kadangi taško abscisė (kintamasis x) yra nepriklausomas kintamasis, galite suteikti jam bet kokią patogią reikšmę. Pakeitę šį skaičių į lygtį, randame kintamojo y reikšmę.

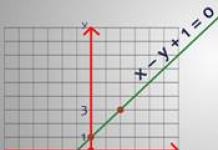
Pavyzdžiui, leiskite pateikti lygtį:

Tegu x = 0, tada gauname 0 - y + 1 = 0 arba y = 1. Tai reiškia, kad jei x = 0, tai y = 1. Skaičių pora (0;1) yra šios lygties sprendimas. Nustatykime kitą kintamojo x reikšmę: x = 2. Tada gausime 2 - y + 1 = 0 arba y = 3. Skaičių pora (2;3) taip pat yra šios lygties sprendimas. Naudojant du rastus taškus, jau galima sudaryti lygties x - y + 1 = 0 grafiką.

Galite padaryti taip: pirmiausia kintamajam y priskirkite tam tikrą konkrečią reikšmę, o tik tada apskaičiuokite x reikšmę.

§ 3 Lygčių sistema

Raskite du natūraliuosius skaičius, kurių suma yra 11, o skirtumas yra 1.

Norėdami išspręsti šią problemą, pirmiausia sukuriame matematinį modelį (būtent algebrinį). Tegul pirmasis skaičius yra x, o antrasis skaičius y. Tada skaičių suma x + y = 11 ir skaičių skirtumas x - y = 1. Kadangi abi lygtys susijusios su tais pačiais skaičiais, šios sąlygos turi būti įvykdytos vienu metu. Paprastai tokiais atvejais naudojamas specialus įrašas. Lygtys parašytos viena po kitos ir sujungtos su garbanotu skliaustu.

Toks įrašas vadinamas lygčių sistema.

Dabar sukonstruokime kiekvienos lygties sprendinių aibes, t.y. kiekvienos lygties grafikai. Paimkime pirmąją lygtį:

Jei x = 4, tai y = 7. Jei x = 9, tai y = 2.

Per taškus (4;7) ir (9;2) nubrėžkime tiesę.

Paimkime antrą lygtį x - y = 1. Jei x = 5, tai y = 4. Jei x = 7, tai y = 6. Taip pat brėžiame tiesę per taškus (5;4) ir (7;6) ). Gavome geometrinį problemos modelį. Mus dominanti skaičių pora (x;y) turi būti abiejų lygčių sprendimas. Paveiksle matome vieną tašką, esantį ant abiejų tiesių, tai yra linijų susikirtimo taškas.

Jo koordinatės yra (6;5). Todėl problemos sprendimas bus toks: pirmasis reikalingas skaičius yra 6, antrasis - 5.

Naudotos literatūros sąrašas:

1. Mordkovich A.G., Algebra 7 klasė iš 2 dalių, 1 dalis, Vadovėlis bendrojo ugdymo įstaigoms / A.G. Mordkovičius. – 10 leid., pataisyta – Maskva, „Mnemosyne“, 2007 m
2. Mordkovich A.G., Algebra 7 klasė iš 2 dalių, 2 dalis, Užduočių knygelė ugdymo įstaigoms / [A.G. Mordkovičius ir kiti]; redagavo A.G. Mordkovičius - 10-asis leidimas, pataisytas - Maskva, „Mnemosyne“, 2007 m.
3. JOS. Tulčinskaja, Algebra 7 klasė. „Blitz“ apklausa: vadovas bendrojo ugdymo įstaigų mokiniams, 4 leidimas, pataisytas ir išplėstas, Maskva, „Mnemosyne“, 2008 m.
4. Aleksandrova L.A., Algebra 7 klasė. Naujos formos teminiai kontroliniai darbai bendrojo ugdymo įstaigų mokiniams, redagavo A.G. Mordkovičius, Maskva, „Mnemosyne“, 2011 m
5. Aleksandrova L.A. Algebra 7 klasė. Savarankiški darbai bendrojo ugdymo įstaigų mokiniams, redagavo A.G. Mordkovičius - 6-asis leidimas, stereotipinis, Maskva, „Mnemosyne“, 2010 m.

Tema:Linijinė funkcija

Pamoka:Tiesinė lygtis dviejuose kintamuosiuose ir jos grafikas

Susipažinome su koordinačių ašies ir koordinačių plokštumos sąvokomis. Žinome, kad kiekvienas plokštumos taškas vienareikšmiškai apibrėžia skaičių porą (x; y), pirmasis skaičius yra taško abscisė, o antrasis – ordinatė.

Labai dažnai susidursime su tiesine lygtimi dviejuose kintamuosiuose, kurių sprendimas yra skaičių pora, kurią galima pavaizduoti koordinačių plokštumoje.

Formos lygtis:

Kur a, b, c yra skaičiai ir

Ji vadinama tiesine lygtimi su dviem kintamaisiais x ir y. Tokios lygties sprendimas bus bet kuri tokia skaičių pora x ir y, kurią pakeitę į lygtį gausime teisingą skaitinę lygybę.

Skaičių pora koordinačių plokštumoje bus pavaizduota kaip taškas.

Tokioms lygtims matysime daug sprendinių, tai yra daug skaičių porų, o visi atitinkami taškai bus toje pačioje tiesėje.

Pažiūrėkime į pavyzdį:

Norėdami rasti šios lygties sprendimus, turite pasirinkti atitinkamas skaičių x ir y poras:

Leiskite , tada pradinė lygtis virsta lygtimi su vienu nežinomu:

,

Tai yra pirmoji skaičių pora, kuri yra duotosios lygties (0; 3) sprendimas. Gavome tašką A(0; 3)

Tegul . Gauname pradinę lygtį su vienu kintamuoju: , iš čia gauname tašką B(3; 0)

Sudėkime skaičių poras į lentelę:

Nubraižykime taškus grafike ir nubrėžkime tiesią liniją:

Atkreipkite dėmesį, kad bet kuris tam tikros linijos taškas bus duotosios lygties sprendimas. Patikrinkime – paimkime tašką su koordinate ir grafike suraskime jo antrąją koordinatę. Akivaizdu, kad šiuo metu. Pakeiskime šią skaičių porą į lygtį. Gauname 0=0 – teisingą skaitinę lygybę, o tai reiškia, kad taškas, esantis tiesėje, yra sprendimas.

Kol kas negalime įrodyti, kad bet kuris taškas, esantis sukonstruotoje tiesėje, yra lygties sprendimas, todėl priimame tai kaip teisingą ir įrodysime vėliau.

2 pavyzdys – nubraižykite lygtį:

Padarykime lentelę, kad nubrėžtume tiesią liniją, bet paimsime trečią.

Pirmajame stulpelyje paėmėme patogų, jį rasime iš:

, ,

Antrame stulpelyje paėmėme patogų, suraskime x:

, , ,

Patikrinkime ir surasime:

, ,

Sukurkime grafiką:

Pateiktą lygtį padauginkime iš dviejų:

Nuo tokios transformacijos sprendinių aibė nepasikeis, o grafikas išliks toks pat.

Išvada: išmokome spręsti lygtis su dviem kintamaisiais ir sudaryti jų grafikus, sužinojome, kad tokios lygties grafikas yra tiesė ir bet kuris šios tiesės taškas yra lygties sprendimas

1. Dorofejevas G.V., Suvorova S.B., Bunimovičius E.A. ir kt. Algebra 7. 6-asis leidimas. M.: Nušvitimas. 2010 m

2. Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7. M.: VENTANA-GRAF

3. Kolyagin Yu.M., Tkacheva M.V., Fedorova N.E. ir kt. Algebra 7.M.: Apšvietos. 2006 m

2. Portalas šeimos apžiūrai ().

1 užduotis: Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7, Nr.960, 210 str.

2 užduotis: Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7, Nr.961, 210 str.

3 užduotis: Merzlyak A.G., Polonsky V.B., Yakir M.S. Algebra 7, Nr.962, 210 str.

Tiesinė lygtis yra algebrinė lygtis. Šioje lygtyje bendras ją sudarančių daugianario laipsnis yra lygus vienetui.

Tiesinės lygtys pateikiamos taip:

Bendra forma: a 1 x 1 + a 2 x 2 + … + a n x n + b = 0

Kanonine forma: a 1 x 1 + a 2 x 2 + … + a n x n = b.

Tiesinė lygtis su vienu kintamuoju.

Tiesinė lygtis su 1 kintamuoju redukuojama į formą:

kirvis+ b=0.

Pavyzdžiui:

2x + 7 = 0. Kur a = 2, b = 7;

0,1 x 2,3 = 0. Kur a = 0,1, b = -2,3;

12x + 1/2 = 0. Kur a = 12, b = 1/2.

Šaknų skaičius priklauso nuo a Ir b:

Kada a= b=0 , o tai reiškia, kad lygtis turi neribotą skaičių sprendinių, nes .

Kada a=0 , b≠ 0 , o tai reiškia, kad lygtis neturi šaknų, nes .

Kada a ≠ 0 , o tai reiškia, kad lygtis turi tik vieną šaknį.

Tiesinė lygtis su dviem kintamaisiais.

Lygtis su kintamuoju x yra tipo lygybė A(x) = B(x), Kur A(x) Ir B(x)- posakiai iš x. Keičiant rinkinį T vertybes xį lygtį gauname tikrąją skaitinę lygybę, kuri vadinama tiesos rinkinysši lygtis taip pat duotosios lygties sprendimas, ir visos tokios kintamojo reikšmės yra lygties šaknis.

2 kintamųjų tiesinės lygtys pateikiamos tokia forma:

Bendra forma: ax + by + c = 0,

Kanonine forma: ax + by = -c,

Tiesinės funkcijos forma: y = kx + m, Kur .

Šios lygties sprendimas arba šaknys yra tokia kintamųjų reikšmių pora (x;y), kuris paverčia jį tapatybe. Tiesinė lygtis su 2 kintamaisiais turi neribotą šių sprendinių (šaknių) skaičių. Šios lygties geometrinis modelis (grafas) yra tiesi linija y=kx+m.

Jei lygtyje yra x kvadratas, tada lygtis vadinama

Ir pan., logiška susipažinti su kitų tipų lygtimis. Toliau eilėje tiesines lygtis, kurio kryptingas mokymasis prasideda algebros pamokose 7 klasėje.

Aišku, kad pirmiausia reikia paaiškinti, kas yra tiesinė lygtis, pateikti tiesinės lygties apibrėžimą, jos koeficientus ir parodyti bendrą jos formą. Tada galite išsiaiškinti, kiek sprendinių turi tiesinė lygtis, priklausomai nuo koeficientų verčių ir kaip randamos šaknys. Tai leis jums pereiti prie pavyzdžių sprendimo ir taip įtvirtinti išmoktą teoriją. Šiame straipsnyje mes tai padarysime: išsamiai aptarsime visus teorinius ir praktinius dalykus, susijusius su tiesinėmis lygtimis ir jų sprendimais.

Iš karto pasakykime, kad čia nagrinėsime tik tiesines lygtis su vienu kintamuoju, o atskirame straipsnyje išnagrinėsime sprendimo principus tiesinės lygtys su dviem kintamaisiais.

Puslapio naršymas.

Kas yra tiesinė lygtis?

Tiesinės lygties apibrėžimas pateikiamas pagal jos parašymo būdą. Be to, skirtinguose matematikos ir algebros vadovėliuose tiesinių lygčių apibrėžimų formuluotės turi tam tikrų skirtumų, kurie neturi įtakos klausimo esmei.

Pavyzdžiui, Yu N. Makarychev ir kt. algebros vadovėlyje 7 klasei tiesinė lygtis apibrėžiama taip:

Apibrėžimas.

Formos lygtis a x=b, kur x yra kintamasis, a ir b yra kai kurie skaičiai, vadinamas tiesinė lygtis su vienu kintamuoju.

Pateiksime tiesinių lygčių, atitinkančių pateiktą apibrėžimą, pavyzdžių. Pavyzdžiui, 5 x = 10 yra tiesinė lygtis su vienu kintamuoju x, čia koeficientas a yra 5, o skaičius b yra 10. Kitas pavyzdys: −2.3·y=0 taip pat yra tiesinė lygtis, bet su kintamuoju y, kurioje a=−2.3 ir b=0. O tiesinėse lygtyse x=−2 ir −x=3,33 a nėra aiškiai ir yra atitinkamai lygios 1 ir −1, o pirmoje lygtyje b=−2, o antroje – b=3,33.

O metais anksčiau N. Ya matematikos vadovėlyje tiesinės lygtys su vienu nežinomu, be a x = b lygčių, taip pat buvo svarstomos lygtys, kurias galima perkelti į šią formą perkeliant terminus iš vienos dalies. lygties į kitą su priešingu ženklu, taip pat sumažinant panašius terminus. Pagal šį apibrėžimą 5 x = 2 x + 6 formos lygtys ir kt. taip pat linijinis.

Savo ruožtu A. G. Mordkovičiaus 7 klasės algebros vadovėlyje pateikiamas toks apibrėžimas:

Apibrėžimas.

Tiesinė lygtis su vienu kintamuoju x yra a·x+b=0 formos lygtis, kur a ir b yra kai kurie skaičiai, vadinami tiesinės lygties koeficientais.

Pavyzdžiui, tokio tipo tiesinės lygtys yra 2 x−12=0, čia koeficientas a yra 2, o b lygus –12 ir 0,2 y+4,6=0, kai koeficientai a=0,2 ir b =4,6. Tačiau tuo pat metu yra tiesinių lygčių pavyzdžių, kurių forma yra ne a·x+b=0, o a·x=b, pavyzdžiui, 3·x=12.

Kad ateityje neturėtume neatitikimų, tiesine lygtimi su vienu kintamuoju x ir koeficientais a ir b suprasime a x + b = 0 formos lygtį. Šio tipo tiesinė lygtis atrodo labiausiai pagrįsta, nes tiesinės lygtys yra tokios algebrines lygtis pirmas laipsnis. Ir visas kitas aukščiau nurodytas lygtis, taip pat lygtis, kurios, naudojant ekvivalentines transformacijas, redukuojamos į formą a x + b = 0, vadinsime lygtys, kurios redukuoja į tiesines lygtis. Taikant šį metodą, lygtis 2 x+6=0 yra tiesinė lygtis, o 2 x=−6, 4+25 y=6+24 y, 4 (x+5)=12 ir t.t. – Tai lygtys, kurios redukuojasi į tiesines.

Kaip išspręsti tiesines lygtis?

Dabar atėjo laikas išsiaiškinti, kaip išsprendžiamos tiesinės lygtys a·x+b=0. Kitaip tariant, laikas išsiaiškinti, ar tiesinė lygtis turi šaknis ir, jei taip, kiek jų ir kaip jas rasti.

Tiesinės lygties šaknų buvimas priklauso nuo koeficientų a ir b verčių. Šiuo atveju tiesinė lygtis a x+b=0 turi

• vienintelė šaknis a≠0,
• neturi a=0 ir b≠0 šaknų,
• turi be galo daug šaknų a=0 ir b=0, tokiu atveju bet kuris skaičius yra tiesinės lygties šaknis.

Paaiškinkime, kaip buvo gauti šie rezultatai.

Žinome, kad norėdami išspręsti lygtis, galime pereiti nuo pradinės lygties prie lygiaverčių lygčių, tai yra, prie lygčių su tomis pačiomis šaknimis arba, kaip ir pradinė, be šaknų. Norėdami tai padaryti, galite naudoti šias lygiavertes transformacijas:

• perkeliant terminą iš vienos lygties dalies į kitą su priešingu ženklu,
• taip pat padauginti arba padalyti abi lygties puses iš to paties skaičiaus, kuris skiriasi nuo nulio.

Taigi tiesinėje lygtyje su vienu a·x+b=0 formos kintamuoju terminą b galime perkelti iš kairės pusės į dešinę su priešingu ženklu. Šiuo atveju lygtis bus tokia: a·x=−b.

Ir tada kyla klausimas, kaip padalyti abi lygties puses iš skaičiaus a. Tačiau yra vienas dalykas: skaičius a gali būti lygus nuliui, tokiu atveju toks padalijimas neįmanomas. Norėdami išspręsti šią problemą, pirmiausia darysime prielaidą, kad skaičius a yra ne nulis, o atvejį, kai būtis lygi nuliui, nagrinėsime atskirai kiek vėliau.

Taigi, kai a nelygus nuliui, tai abi lygties a·x=−b puses galime padalinti iš a, po to ji transformuosis į formą x=(−b):a, šį rezultatą galima parašyti naudojant trupmeninį pasvirąjį brūkšnį kaip.

Taigi a≠0 tiesinė lygtis a·x+b=0 yra lygiavertė lygčiai, iš kurios matoma jos šaknis.

Nesunku parodyti, kad ši šaknis yra unikali, tai yra, tiesinė lygtis neturi kitų šaknų. Tai leidžia atlikti priešingą metodą.

Pažymėkime šaknį x 1. Tarkime, kad yra kita tiesinės lygties šaknis, kurią žymime x 2 ir x 2 ≠x 1, kuri dėl vienodų skaičių nustatymas per skirtumą yra lygiavertis sąlygai x 1 −x 2 ≠0. Kadangi x 1 ir x 2 yra tiesinės lygties a·x+b=0 šaknys, tai galioja skaitinės lygybės a·x 1 +b=0 ir a·x 2 +b=0. Galime atimti atitinkamas šių lygybių dalis, kurias leidžia padaryti skaitinių lygybių savybės, gauname a·x 1 +b−(a·x 2 +b)=0−0, iš kurios a·(x 1 −x 2)+(b−b)=0 ir tada a·(x 1 −x 2)=0 . Tačiau ši lygybė neįmanoma, nes ir a≠0, ir x 1 − x 2 ≠0. Taigi priėjome prie prieštaravimo, kuris įrodo tiesinės lygties a·x+b=0 šaknies unikalumą, kai a≠0.

Taigi išsprendėme tiesinę lygtį a·x+b=0, kai a≠0. Pirmasis šios pastraipos pradžioje pateiktas rezultatas yra pagrįstas. Liko dar du, atitinkantys sąlygą a=0.

Kai a=0, tiesinė lygtis a·x+b=0 įgauna formą 0·x+b=0. Iš šios lygties ir skaičių padauginti iš nulio išplaukia, kad nesvarbu, kokį skaičių laikytume x, jį pakeitus į lygtį 0 x + b=0, bus gauta skaitinė lygybė b=0. Ši lygybė yra teisinga, kai b=0, o kitais atvejais, kai b≠0 ši lygybė yra klaidinga.

Todėl, kai a=0 ir b=0, bet koks skaičius yra tiesinės lygties a·x+b=0 šaknis, nes tokiomis sąlygomis pakeitus bet kurį skaičių x, gaunama teisinga skaitinė lygybė 0=0. Ir kai a=0 ir b≠0, tiesinė lygtis a·x+b=0 neturi šaknų, nes tokiomis sąlygomis pakeitus x bet kokiu skaičiumi, gaunama neteisinga skaitinė lygybė b=0.

Pateikti pagrindimai leidžia suformuluoti veiksmų seką, leidžiančią išspręsti bet kurią tiesinę lygtį. Taigi, tiesinės lygties sprendimo algoritmas yra:

• Pirma, parašydami tiesinę lygtį, randame koeficientų a ir b reikšmes.
• Jei a=0 ir b=0, tai ši lygtis turi be galo daug šaknų, būtent bet kuris skaičius yra šios tiesinės lygties šaknis.
• Jei a yra ne nulis, tada
• koeficientas b perkeliamas į dešinę pusę su priešingu ženklu, o tiesinė lygtis transformuojama į formą a·x=-b,
• po to abi gautos lygties pusės dalijamos iš nulinio skaičiaus a, kuris suteikia norimą pradinės tiesinės lygties šaknį.

Parašytas algoritmas yra išsamus atsakymas į klausimą, kaip išspręsti tiesines lygtis.

Apibendrinant šį punktą, verta pasakyti, kad panašus algoritmas naudojamas sprendžiant a·x=b formos lygtis. Jo skirtumas tas, kad kai a≠0, iš šio skaičiaus iš karto padalytos abi lygties pusės, čia b jau yra reikiamoje lygties dalyje ir jos perkelti nereikia.

Formos a x = b lygtims išspręsti naudojamas toks algoritmas:

• Jei a=0 ir b=0, tai lygtis turi be galo daug šaknų, kurios yra bet kokie skaičiai.
• Jei a=0 ir b≠0, tai pradinė lygtis neturi šaknų.
• Jei a yra ne nulis, tai abi lygties pusės dalijamos iš ne nulio skaičiaus a, iš kurio randama vienintelė lygties šaknis, lygi b/a.

Tiesinių lygčių sprendimo pavyzdžiai

Pereikime prie praktikos. Pažiūrėkime, kaip naudojamas tiesinių lygčių sprendimo algoritmas. Pateiksime tipinių pavyzdžių, atitinkančių skirtingas tiesinių lygčių koeficientų reikšmes, sprendimus.

Pavyzdys.

Išspręskite tiesinę lygtį 0·x−0=0.

Sprendimas.

Šioje tiesinėje lygtyje a=0 ir b=−0 , kuri yra tokia pati kaip b=0 . Todėl ši lygtis turi be galo daug šaknų, bet koks skaičius yra šios lygties šaknis.

Atsakymas:

x – bet koks skaičius.

Pavyzdys.

Ar tiesinė lygtis 0 x + 2,7 = 0 turi sprendinių?

Sprendimas.

Šiuo atveju koeficientas a yra lygus nuliui, o šios tiesinės lygties koeficientas b yra lygus 2,7, tai yra, skiriasi nuo nulio. Todėl tiesinė lygtis neturi šaknų.

Autoriaus požiūris į šią temą nėra atsitiktinis. Su lygtimis su dviem kintamaisiais pirmą kartą susiduriama 7 klasės kursuose. Viena lygtis su dviem kintamaisiais turi begalinį sprendinių skaičių. Tai aiškiai parodo tiesinės funkcijos grafikas, pateiktas kaip ax + by=c. Mokykliniame kurse mokiniai mokosi dviejų lygčių su dviem kintamaisiais sistemas. Dėl to iš mokytojo, taigi ir mokinio, akiračio iškrenta visa eilė problemų, turinčių ribotas lygties koeficiento sąlygas, taip pat jų sprendimo būdus.

Mes kalbame apie lygties su dviem nežinomaisiais sveikaisiais arba natūraliaisiais skaičiais sprendimą.

Mokykloje natūralieji skaičiai ir sveikieji skaičiai mokomi 4-6 klasėse. Kai baigia mokyklą, ne visi mokiniai prisimena šių skaičių aibių skirtumus.

Tačiau tokia problema kaip „išspręskite lygtį, kurios forma ax + by=c sveikaisiais skaičiais“ vis dažniau aptinkama stojant į universitetus ir vieningų valstybinių egzaminų medžiagoje.

Neaiškių lygčių sprendimas ugdo loginį mąstymą, intelektą ir dėmesį analizei.

Siūlau parengti keletą pamokų šia tema. Neturiu aiškių rekomendacijų dėl šių pamokų laiko. Kai kurie elementai gali būti naudojami ir 7 klasėje (stipriai klasei). Šiomis pamokomis galima remtis ir parengti nedidelį pasirenkamąjį ikiprofesinio mokymo kursą 9 klasėje. Ir, žinoma, ši medžiaga gali būti naudojama 10-11 klasėse ruošiantis egzaminams.

Pamokos tikslas:

• žinių kartojimas ir apibendrinimas tema „Pirmos ir antros eilės lygtys“
• ugdyti pažintinį susidomėjimą dalyku
• ugdyti gebėjimą analizuoti, daryti apibendrinimus, perkelti žinias į naują situaciją

1 pamoka.

Pamokos eiga.

1) Org. akimirka.

2) Pagrindinių žinių atnaujinimas.

Apibrėžimas. Dviejų kintamųjų tiesinė lygtis yra formos lygtis

mx + ny = k, kur m, n, k yra skaičiai, x, y yra kintamieji.

Pavyzdys: 5x+2y=10

Apibrėžimas. Lygties su dviem kintamaisiais sprendimas yra kintamųjų reikšmių pora, kuri lygtį paverčia tikrąja lygybe.

Lygtys su dviem kintamaisiais, turinčios tuos pačius sprendinius, vadinamos ekvivalentinėmis.

1. 5x+2y=12 (2)y = -2,5x+6

Ši lygtis gali turėti bet kokį sprendinių skaičių. Norėdami tai padaryti, pakanka paimti bet kurią x reikšmę ir rasti atitinkamą y reikšmę.

Tegu x = 2, y = -2,5 2+6 = 1

x = 4, y = -2,5 4+6 =- 4

Skaičių poros (2;1); (4;-4) – (1) lygties sprendiniai.

Ši lygtis turi be galo daug sprendinių.

3) Istorinis fonas

Neapibrėžtos (diofantinės) lygtys yra lygtys, kuriose yra daugiau nei vienas kintamasis.

III amžiuje. AD – Diofantas Aleksandrietis parašė „Aritmetiką“, kurioje išplėtė skaičių aibę iki racionaliųjų ir įvedė algebrinę simboliką.

Diofantas taip pat nagrinėjo neapibrėžtų lygčių sprendimo problemas ir pateikė metodus antrojo ir trečiojo laipsnio neapibrėžtoms lygtims spręsti.

4) Naujos medžiagos studijavimas.

Apibrėžimas: pirmos eilės nehomogeninė diofantino lygtis su dviem nežinomaisiais x, y yra lygtis, kurios formos mx + ny = k, kur m, n, k, x, y Z k0

1 teiginys.

Jei (1) lygties laisvasis narys k nesidalija iš didžiausio skaičių m ir n bendro daliklio (GCD), tai (1) lygtis neturi sveikųjų skaičių sprendinių.

Pavyzdys: 34x – 17m = 3.

GCD (34; 17) = 17, 3 nesidalija tolygiai iš 17, sveikaisiais skaičiais sprendinio nėra.

Tegu k dalijasi iš gcd (m, n). Padalinę visus koeficientus, galime užtikrinti, kad m ir n taptų santykinai pirminiais.

2 teiginys.

Jei (1) lygties m ir n yra santykinai pirminiai skaičiai, tai ši lygtis turi bent vieną sprendinį.

3 teiginys.

Jei (1) lygties koeficientai m ir n yra pirminiai skaičiai, tai ši lygtis turi be galo daug sprendinių:

Kur (; ) yra bet koks (1) lygties sprendinys, t Z

Apibrėžimas. Pirmos eilės vienalytė Diofantono lygtis su dviem nežinomaisiais x, y yra lygtis, kurios formos mx + ny = 0, kur (2)

4 teiginys.

Jei m ir n yra pirminiai skaičiai, tai bet koks (2) lygties sprendinys turi formą

5) Namų darbai. Išspręskite lygtį sveikais skaičiais:

1. 9x – 18m = 5
2. x + y= xy
3. Keli vaikai rinko obuolius. Kiekvienas berniukas surinko po 21 kg, o mergina – 15 kg. Iš viso jie surinko 174 kg. Kiek berniukų ir kiek mergaičių rinko obuolius?

komentuoti. Šioje pamokoje nepateikiami sveikųjų skaičių lygčių sprendimo pavyzdžiai. Todėl vaikai namų darbus sprendžia vadovaudamiesi 1 teiginiu ir atranka.

2 pamoka.

1) Organizacinis momentas

2) Namų darbų tikrinimas

1) 9x – 18y = 5

5 nesidalija iš 9; sveikųjų skaičių sprendinių nėra.

Naudodami atrankos metodą galite rasti sprendimą

Atsakymas: (0;0), (2;2)

3) Sudarykite lygtį:

Tegul berniukai yra x, x Z, o mergaitės y, y Z, tada galime sukurti lygtį 21x + 15y = 174

Daugelis studentų, parašę lygtį, nesugebės jos išspręsti.

Atsakymas: 4 berniukai, 6 mergaitės.

3) Naujos medžiagos mokymasis

Susidūrę su sunkumais atliekant namų darbus, mokiniai įsitikino, kad reikia išmokti jų neapibrėžtų lygčių sprendimo metodus. Pažvelkime į kai kuriuos iš jų.

I. Padalijimo liekanų svarstymo metodas.

Pavyzdys. Išspręskite lygtį sveikais skaičiais 3x – 4y = 1.

Kairioji lygties pusė dalijasi iš 3, todėl dešinioji turi dalytis. Panagrinėkime tris atvejus.

Atsakymas: kur m Z.

Aprašytą metodą patogu naudoti, jei skaičiai m ir n nėra maži, bet gali būti skaidomi į paprastus veiksnius.

Pavyzdys: išspręskite lygtis sveikais skaičiais.

Tegul y = 4n, tada 16 - 7y = 16 - 7 4n = 16 - 28n = 4*(4-7n) dalijamas iš 4.

y = 4n+1, tada 16 – 7y = 16 – 7 (4n + 1) = 16 – 28n – 7 = 9 – 28n nesidalija iš 4.

y = 4n+2, tada 16 – 7y = 16 – 7 (4n + 2) = 16 – 28n – 14 = 2 – 28n nesidalija iš 4.

y = 4n+3, tada 16 – 7y = 16 – 7 (4n + 3) = 16 – 28n – 21 = -5 – 28n nesidalija iš 4.

Todėl y = 4n, tada

4x = 16-7 4n = 16-28n, x = 4-7n

Atsakymas: , kur n Z.

II. Neaiškios 2-ojo laipsnio lygtys

Šiandien pamokoje paliesime tik antros eilės Diofanto lygčių sprendimą.

O iš visų lygčių tipų nagrinėsime atvejį, kai galime pritaikyti kvadratų skirtumo formulę ar kitą faktorizavimo metodą.

Pavyzdys: išspręskite lygtį sveikaisiais skaičiais.

13 yra pirminis skaičius, todėl jį galima apskaičiuoti tik keturiais būdais: 13 = 13 1 = 1 13 = (-1) (-13) = (-13) (-1)

Panagrinėkime šiuos atvejus

Atsakymas: (7;-3), (7;3), (-7;3), (-7;-3).

4) Namų darbai.

Pavyzdžiai. Išspręskite lygtį sveikais skaičiais:

(x - y) (x + y) = 4

2x = 4	2x = 5	2x = 5
x = 2	x = 5/2	x = 5/2
y = 0	netinka	netinka
2x = -4	netinka	netinka
x = -2
y = 0

Atsakymas: (-2;0), (2;0).

Atsakymai: (-10;9), (-5;3), (-2;-3), (-1;-9), (1;9), (2;3), (5;-3) , (10;-9).

V)

Atsakymas: (2;-3), (-1;-1), (-4;0), (2;2), (-1;3), (-4;5).

Rezultatai. Ką reiškia lygtį išspręsti sveikais skaičiais?

Kokius žinote neapibrėžtų lygčių sprendimo būdus?

Taikymas:

Pratimai treniruotėms.

1) Išspręskite sveikais skaičiais.

a) 8x + 12y = 32	x = 1 + 3n, y = 2 - 2n, n Z
b) 7x + 5y = 29	x = 2 + 5n, y = 3 - 7n, n Z
c) 4x + 7y = 75	x = 3 + 7n, y = 9 - 4n, n Z
d) 9x – 2y = 1	x = 1–2 m, y = 4 + 9 m, m Z
e) 9x – 11y = 36	x = 4 + 11n, y = 9n, n Z
e) 7x – 4y = 29	x = 3 + 4n, y = -2 + 7n, n Z
g) 19x – 5y = 119	x = 1 + 5p, y = -20 + 19p, p Z
h) 28x – 40y = 60	x = 45 + 10 t, y = 30 + 7 t, t Z

2) Raskite sveikųjų skaičių neneigiamus lygties sprendinius:

Sprendimas: Z (2; -1)

Literatūra.

1. Vaikų enciklopedija „Pedagogika“, Maskva, 1972 m.
2. Algebra-8, N.Ya. Vilenkin, VO „Mokslas“, Novosibirskas, 1992 m
3. Skaičių teorija pagrįstos konkurencijos problemos.
4. V.Ya. Galkinas, D. Yu. Sičugovas. MSU, VMK, Maskva, 2005 m.
5. Padidinto sunkumo problemos 7-9 klasių algebros kurse. N.P. Kosrykina. „Švietimas“, Maskva, 1991 m