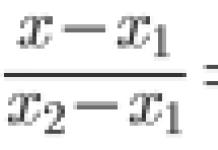Skaičius, padalintas iš 0, yra begalybė. L'Hopital taisyklė: teorija ir sprendimų pavyzdžiai. Ribų sprendimo būdai. Funkcijos augimo tvarka. Pakeitimo būdas

Labai dažnai daugelis žmonių stebisi, kodėl negalima naudoti dalybos iš nulio? Šiame straipsnyje mes labai išsamiai kalbėsime apie tai, iš kur kilo ši taisyklė, taip pat kokius veiksmus galima atlikti su nuliu.

Susisiekus su

Nulį galima vadinti vienu įdomiausių skaičių. Šis skaičius neturi reikšmės, tai reiškia tuštumą tikrąja to žodžio prasme. Tačiau jei prie bet kurio skaičiaus dedamas nulis, šio skaičiaus reikšmė padidės kelis kartus.

Pats skaičius labai paslaptingas. Jį naudojo senovės majų žmonės. Majams nulis reiškė „pradžia“, o kalendorinės dienos taip pat prasidėdavo nuo nulio.

Labai įdomus faktas yra tai, kad nulio ženklas ir neapibrėžtumo ženklas buvo panašūs. Tuo majai norėjo parodyti, kad nulis yra tas pats ženklas kaip ir neapibrėžtumas. Europoje pavadinimas nulis pasirodė palyginti neseniai.

Daugelis žmonių taip pat žino draudimą, susijusį su nuliu. Bet kuris žmogus tai pasakys negalima dalyti iš nulio. Mokykloje tai sako mokytojai, o vaikai dažniausiai laikosi žodžio. Paprastai vaikams tai tiesiog neįdomu, arba jie žino, kas nutiks, jei išgirdę svarbų draudimą iškart paklaus: „Kodėl negalima dalyti iš nulio? Tačiau kai senstate, jūsų susidomėjimas pabunda ir norite daugiau sužinoti apie šio draudimo priežastis. Tačiau yra pagrįstų įrodymų.

Veiksmai su nuliu

Pirmiausia turite nustatyti, kokius veiksmus galima atlikti su nuliu. Egzistuoja kelių rūšių veiksmai:

Papildymas;
Daugyba;
Atimtis;
Padalinys (nulis pagal skaičių);
Eksponentiškumas.

Svarbu! Jei pridėdami prie bet kurio skaičiaus pridėsite nulį, šis skaičius išliks toks pat ir nepakeis jo skaitinės reikšmės. Tas pats atsitinka, jei iš bet kurio skaičiaus atimate nulį.

Dauginant ir dalijant viskas šiek tiek skiriasi. Jeigu bet kurį skaičių padauginkite iš nulio, tada produktas taip pat taps nuliu.

Pažiūrėkime į pavyzdį:

Parašykime tai kaip priedą:

Iš viso yra penki nuliai, taigi taip ir išeina

Pabandykime padauginti vieną iš nulio. Rezultatas taip pat bus lygus nuliui.

Nulis taip pat gali būti padalintas iš bet kurio kito skaičiaus, kuris jam nėra lygus. Tokiu atveju rezultatas bus , kurio reikšmė taip pat bus lygi nuliui. Ta pati taisyklė galioja ir neigiamiems skaičiams. Jei nulis yra padalintas iš neigiamo skaičiaus, rezultatas yra nulis.

Taip pat galite sukurti bet kokį skaičių iki nulio laipsnio. Šiuo atveju rezultatas bus 1. Svarbu atsiminti, kad posakis „nulis iki nulio laipsnio“ yra visiškai beprasmis. Jei bandysite pakelti nulį iki bet kokios galios, gausite nulį. Pavyzdys:

Mes naudojame daugybos taisyklę ir gauname 0.

Taigi ar galima dalyti iš nulio?

Taigi, mes priėjome prie pagrindinio klausimo. Ar galima padalyti iš nulio? iš viso? Ir kodėl mes negalime padalyti skaičiaus iš nulio, turint omenyje, kad visi kiti veiksmai su nuliu egzistuoja ir yra taikomi? Norint atsakyti į šį klausimą, būtina atsigręžti į aukštąją matematiką.

Pradėkime nuo sąvokos apibrėžimo, kas yra nulis? Mokyklos mokytojai sako, kad nulis yra niekas. Tuštuma. Tai yra, kai sakote, kad turite 0 rankenų, tai reiškia, kad neturite jokių rankenų.

Aukštojoje matematikoje „nulio“ sąvoka yra platesnė. Tai visai nereiškia tuštumos. Čia nulis vadinamas neapibrėžtumu, nes jei atliksime nedidelį tyrimą, paaiškėja, kad padalijus nulį iš nulio, galime gauti bet kokį kitą skaičių, kuris nebūtinai yra nulis.

Ar žinojote, kad tie paprasti aritmetiniai veiksmai, kurių mokėtės mokykloje, nėra tokie lygūs? Pagrindiniai veiksmai yra sudėjimas ir daugyba.

Matematikams sąvokos „“ ir „atimtis“ neegzistuoja. Tarkime: jei iš penkių atimsi tris, liks du. Taip atrodo atimtis. Tačiau matematikai tai parašytų taip:

Taigi, paaiškėja, kad nežinomas skirtumas yra tam tikras skaičius, kurį reikia pridėti prie 3, kad gautumėte 5. Tai yra, jums nereikia nieko atimti, tereikia rasti tinkamą skaičių. Ši taisyklė taikoma papildymui.

Viskas yra šiek tiek kitaip su daugybos ir dalybos taisyklės. Yra žinoma, kad padauginus iš nulio gaunamas nulis. Pavyzdžiui, jei 3:0=x, tada, jei įvedimą apverčiate, gausite 3*x=0. O skaičius, padaugintas iš 0, sandaugoje bus nulis. Pasirodo, produkte su nuliu nėra skaičiaus, kuris suteiktų kitokią reikšmę nei nulis. Tai reiškia, kad dalyba iš nulio yra beprasmė, tai yra, tai atitinka mūsų taisyklę.

Bet kas atsitiks, jei bandysite padalyti nulį iš savęs? Paimkime neapibrėžtą skaičių kaip x. Gauta lygtis yra 0*x=0. Tai galima išspręsti.

Jei bandysime vietoj x imti nulį, gausime 0:0=0. Atrodytų logiška? Bet jei bandysime paimti bet kokį kitą skaičių, pavyzdžiui, 1, o ne x, gausime 0:0=1. Ta pati situacija atsitiks, jei imsime bet kokį kitą skaičių ir prijunkite jį prie lygties.

Šiuo atveju paaiškėja, kad veiksniu galime paimti bet kurį kitą skaičių. Rezultatas bus begalinis skirtingų skaičių skaičius. Kartais aukštojoje matematikoje dalyba iš 0 dar turi prasmę, bet tada dažniausiai atsiranda tam tikra sąlyga, kurios dėka vis tiek galime pasirinkti vieną tinkamą skaičių. Šis veiksmas vadinamas „neapibrėžtumo atskleidimu“. Įprastoje aritmetikoje dalyba iš nulio vėl neteks prasmės, nes negalėsime pasirinkti vieno skaičiaus iš aibės.

Svarbu! Negalite padalyti nulio iš nulio.

Nulis ir begalybė

Begalybę labai dažnai galima rasti aukštojoje matematikoje. Kadangi moksleiviams tiesiog nėra svarbu žinoti, kad yra ir matematinių veiksmų su begalybe, mokytojai negali tinkamai paaiškinti vaikams, kodėl negalima dalyti iš nulio.

Pagrindinių matematikos paslapčių studentai pradeda mokytis tik pirmaisiais instituto metais. Aukštoji matematika pateikia didelį problemų, kurios neturi sprendimo, kompleksą. Garsiausios problemos yra problemos su begalybe. Jas galima išspręsti naudojant matematinė analizė.

Galima pritaikyti ir iki begalybės elementarios matematinės operacijos: sudėjimas, daugyba iš skaičiaus. Paprastai jie taip pat naudoja atimtį ir padalijimą, tačiau galiausiai jie vis tiek susideda į dvi paprastas operacijas.

Bet kas bus jei pabandysi:

Begalybė padauginta iš nulio. Teoriškai, jei bandysime bet kurį skaičių padauginti iš nulio, gausime nulį. Tačiau begalybė yra neapibrėžtas skaičių rinkinys. Kadangi negalime pasirinkti vieno skaičiaus iš šios aibės, išraiška ∞*0 neturi sprendimo ir yra visiškai beprasmė.
Nulis padalintas iš begalybės. Čia vyksta ta pati istorija, kaip ir aukščiau. Negalime pasirinkti vieno skaičiaus, vadinasi, nežinome, iš ko padalyti. Išraiška neturi reikšmės.

Svarbu! Begalybė šiek tiek skiriasi nuo netikrumo! Begalybė yra viena iš neapibrėžtumo rūšių.

Dabar pabandykime padalyti begalybę iš nulio. Atrodytų, turėtų būti netikrumo. Bet jei bandytume dalybą pakeisti daugyba, gautume labai aiškų atsakymą.

Pavyzdžiui: ∞/0=∞*1/0= ∞*∞ = ∞.

Pasirodo taip matematinis paradoksas.

Atsakymas į klausimą, kodėl negalima dalyti iš nulio

Mintinis eksperimentas, bandymas padalyti iš nulio

Išvada

Taigi, dabar žinome, kad nuliui taikomos beveik visos operacijos, su kuriomis atliekamos, išskyrus vieną. Negalite padalyti iš nulio vien todėl, kad rezultatas yra neapibrėžtumas. Taip pat išmokome atlikti operacijas su nuliu ir begalybe. Tokių veiksmų rezultatas bus netikrumas.

Ribų sprendimo būdai. Neaiškumai.
Funkcijos augimo tvarka. Pakeitimo būdas

4 pavyzdys

Raskite ribą

Tai paprastesnis pavyzdys, kurį galite išspręsti patys. Siūlomame pavyzdyje vėl yra neapibrėžtumas (aukštesnio augimo nei šaknis).

Jei "x" linkęs į "minus begalybę"

„Minuso begalybės“ šmėkla šiame straipsnyje sklando ilgą laiką. Panagrinėkime ribas su polinomais, kuriuose . Sprendimo principai ir metodai bus lygiai tokie patys kaip ir pirmoje pamokos dalyje, išskyrus kai kuriuos niuansus.

Pažvelkime į 4 gudrybes, kurių prireiks sprendžiant praktines užduotis:

1) Apskaičiuokite ribą

Ribos reikšmė priklauso tik nuo termino, nes ji turi didžiausią augimo eilę. Jei tada be galo didelis modulis neigiamas skaičius iki LYGINIO laipsnio, šiuo atveju – ketvirtoje, yra lygus „plius begalybė“: . Pastovus („du“) teigiamas, Štai kodėl:

2) Apskaičiuokite ribą

Čia vėl aukštasis laipsnis net, Štai kodėl: . Bet prieš jį yra „minusas“ ( neigiamas konstanta –1), todėl:

3) Apskaičiuokite ribą

Ribinė vertė priklauso tik nuo . Kaip prisimenate iš mokyklos laikų, „minusas“ „iššoka“ iš po nelyginio laipsnio, taigi be galo didelis modulis neigiamas skaičius iki ODD laipsnio lygus „minus begalybei“, šiuo atveju: .
Pastovus („keturi“) teigiamas, Reiškia:

4) Apskaičiuokite ribą

Pirmasis vaikinas kaime vėl turi nelyginis laipsnis, be to, krūtinėje neigiamas konstanta, o tai reiškia: Taigi:
.

5 pavyzdys

Raskite ribą

Remdamiesi aukščiau pateiktais punktais, darome išvadą, kad čia yra neapibrėžtumo. Skaitiklis ir vardiklis yra tos pačios augimo eilės, o tai reiškia, kad riboje rezultatas bus baigtinis skaičius. Išsiaiškinkime atsakymą išmesdami visus kepinius:

Sprendimas yra trivialus:

6 pavyzdys

Raskite ribą

Tai pavyzdys, kurį galite išspręsti patys. Visas sprendimas ir atsakymas pamokos pabaigoje.

O dabar, ko gero, patys subtiliausi atvejai:

7 pavyzdys

Raskite ribą

Atsižvelgdami į pagrindinius terminus, darome išvadą, kad čia yra neapibrėžtumo. Skaitiklis yra aukštesnės eilės augimo nei vardiklis, todėl iš karto galime pasakyti, kad riba lygi begalybei. Bet kokia begalybė, „pliusas“ ar „minusas“? Technika ta pati – atsikratykime smulkmenų skaitiklyje ir vardiklyje:

Mes nusprendžiame:

Padalinkite skaitiklį ir vardiklį iš

15 pavyzdys

Raskite ribą

Tai pavyzdys, kurį galite išspręsti patys. Apytikslis galutinio dizaino pavyzdys pamokos pabaigoje.

Dar keli įdomūs pavyzdžiai kintamųjų pakeitimo tema:

16 pavyzdys

Raskite ribą

Vienybę pakeičiant riba, gaunamas neapibrėžtumas. Kintamojo keitimas jau siūlo save, bet pirmiausia mes transformuojame liestinę naudodami formulę. Iš tiesų, kam mums reikia liestinės?

Atkreipkite dėmesį, kad todėl . Jei tai nėra visiškai aišku, pažiūrėkite į sinuso reikšmes trigonometrinė lentelė. Taip iš karto atsikratome daugiklio, be to, gauname labiau pažįstamą neapibrėžtumą 0:0. Būtų gerai, jei mūsų limitas būtų lygus nuliui.

Pakeiskime:

Jei tada

Po kosinusu turime „x“, kurį taip pat reikia išreikšti per „te“.
Iš pakeitimo išreiškiame: .

Mes užbaigiame sprendimą:

(1) Mes atliekame pakeitimą

(2) Atidarykite skliaustus po kosinusu.

(4) Organizuoti pirmoji nuostabi riba, dirbtinai padauginkite skaitiklį iš ir grįžtamojo skaičiaus.

Užduotis savarankiškam sprendimui:

17 pavyzdys

Raskite ribą

Visas sprendimas ir atsakymas pamokos pabaigoje.

Tai buvo paprastos užduotys jų klasėje, praktiškai viskas gali būti blogiau, be to redukcijos formules, turite naudoti įvairius trigonometrines formules, taip pat kitų gudrybių. Straipsnyje „Sudėtingos ribos“ pažvelgiau į keletą realių pavyzdžių =)

Šventės išvakarėse situaciją pagaliau išsiaiškinsime su dar vienu dažnu neaiškumu:

Neapibrėžtumo pašalinimas „vienas iki begalybės galios“

Šis netikrumas yra „aptarnaujamas“ antra nuostabi riba, o antroje tos pamokos dalyje labai išsamiai išnagrinėjome standartinius sprendimų pavyzdžius, kurie dažniausiai randami praktikoje. Dabar paveikslėlis su eksponentais bus baigtas, be to, paskutinės pamokos užduotys bus skirtos „netikroms“ riboms, kuriose ATRODO, kad reikia taikyti 2-ąją nuostabią ribą, nors tai visai ne atvejis.

Dviejų darbinių formulių, skirtų 2-ajai nepaprastai ribai, trūkumas yra tas, kad argumentas turi būti linkęs į „plius begalybę“ arba į nulį. Bet kas, jei argumentas linkęs į kitą skaičių?

Į pagalbą ateina universali formulė (kuri iš tikrųjų yra antrosios nepaprastos ribos pasekmė):

Neapibrėžtumą galima pašalinti naudojant formulę:

Kažkur manau, kad jau paaiškinau, ką reiškia laužtiniai skliaustai. Nieko ypatingo, skliausteliuose yra tik skliausteliuose. Paprastai jie naudojami matematiniam užrašymui aiškiau paryškinti.

Pabrėžkime esminius formulės punktus:

1) Tai apie tik apie netikrumą ir nieko daugiau.

2) Argumentas „x“ gali būti linkęs savavališka vertė(ir ne tik iki nulio ar), ypač iki „minuso begalybės“ arba iki bet kas baigtinis skaičius.

Naudodami šią formulę galite išspręsti visus pamokoje pateiktus pavyzdžius. Nuostabios ribos, kurie priklauso 2-ajai reikšmingai ribai. Pavyzdžiui, apskaičiuokime ribą:

Tokiu atveju , ir pagal formulę :

Tiesa, to daryti nerekomenduoju, kad vis dar būtų naudojamas „įprastas“ sprendimo dizainas, jei jį galima pritaikyti. Tačiau naudojant formulę labai patogu patikrinti„klasikiniai“ pavyzdžiai iki 2-os nepaprastos ribos.

Skaičius 0 gali būti įsivaizduojamas kaip tam tikra riba, skirianti realiųjų skaičių pasaulį nuo menamų ar neigiamų. Dėl dviprasmiškos padėties daugelis operacijų su šia skaitine reikšme nepaklūsta matematinei logikai. Puikus to pavyzdys yra tai, kad neįmanoma padalyti iš nulio. Ir leidžiamos aritmetinės operacijos su nuliu gali būti atliekamos naudojant visuotinai priimtus apibrėžimus.

Nulio istorija

Nulis yra atskaitos taškas visose standartinėse skaičių sistemose. Europiečiai šį skaičių pradėjo naudoti palyginti neseniai, tačiau senovės Indijos išminčiai naudojo nulį tūkstantį metų prieš tai, kai Europos matematikai reguliariai naudojo tuščią skaičių. Dar prieš indėnus majų skaitinėje sistemoje nulis buvo privaloma reikšmė. Šie amerikiečiai naudojo dvyliktainę skaičių sistemą, o pirmoji kiekvieno mėnesio diena prasidėdavo nuliu. Įdomu tai, kad tarp majų ženklas, reiškiantis „nulis“, visiškai sutapo su ženklu, reiškiančiu „begalybę“. Taigi senovės majai padarė išvadą, kad šie kiekiai yra identiški ir nežinomi.

Matematiniai veiksmai su nuliu

Standartinės matematinės operacijos su nuliu gali būti sumažintos iki kelių taisyklių.

Papildymas: jei prie savavališko skaičiaus pridėsite nulį, jis nepakeis jo reikšmės (0+x=x).

Atimtis: iš bet kurio skaičiaus atimant nulį, atimties reikšmė lieka nepakitusi (x-0=x).

Daugyba: bet koks skaičius, padaugintas iš 0, gauna 0 (a*0=0).

Padalijimas: Nulį galima padalyti iš bet kurio skaičiaus, kuris nėra lygus nuliui. Tokiu atveju tokios trupmenos reikšmė bus 0. O dalyti iš nulio draudžiama.

Eksponentiškumas. Šį veiksmą galima atlikti su bet kokiu numeriu. Savavališkas skaičius, padidintas iki nulio laipsnio, duos 1 (x 0 =1).

Nulis bet kokiam laipsniui yra lygus 0 (0 a = 0).

Tokiu atveju iš karto iškyla prieštaravimas: išraiška 0 0 neturi prasmės.

Matematikos paradoksai

Daugelis žmonių iš mokyklos žino, kad dalyti iš nulio neįmanoma. Tačiau paaiškinti tokio draudimo priežasties kažkodėl neįmanoma. Tiesą sakant, kodėl dalybos iš nulio formulės neegzistuoja, bet kiti veiksmai su šiuo skaičiumi yra gana pagrįsti ir įmanomi? Atsakymą į šį klausimą pateikia matematikai.

Reikalas tas, kad įprasti aritmetiniai veiksmai, kurių mokiniai mokosi pradinėje mokykloje, iš tikrųjų nėra tokie lygūs, kaip mes manome. Visas paprastas skaičių operacijas galima sumažinti iki dviejų: sudėties ir daugybos. Šie veiksmai sudaro pačios skaičiaus sąvokos esmę, o kitos operacijos yra pagrįstos šių dviejų vartojimu.

Sudėjimas ir daugyba

Paimkime standartinį atimties pavyzdį: 10-2=8. Mokykloje jie svarsto paprastai: iš dešimties dalykų atėmus du, lieka aštuoni. Tačiau matematikai į šią operaciją žiūri visiškai kitaip. Juk tokia operacija kaip atimtis jiems neegzistuoja. Šį pavyzdį galima parašyti ir kitaip: x+2=10. Matematikams nežinomas skirtumas yra tiesiog skaičius, kurį reikia pridėti prie dviejų, kad būtų aštuoni. Ir čia nereikia atimti, tereikia rasti atitinkamą skaitinę reikšmę.

Daugyba ir dalyba traktuojami vienodai. Pavyzdyje 12:4=3 galite suprasti, kad mes kalbame apie aštuonių objektų padalijimą į dvi lygias krūvas. Tačiau iš tikrųjų tai tik apversta formulė rašant 3x4 = 12. Tokių padalijimo pavyzdžių galima pateikti be galo.

Padalinimo iš 0 pavyzdžiai

Čia tampa šiek tiek aišku, kodėl negalite padalyti iš nulio. Daugyba ir padalijimas iš nulio laikosi savo taisyklių. Visi šio dydžio padalijimo pavyzdžiai gali būti suformuluoti kaip 6:0 = x. Bet tai yra atvirkštinis išraiškos 6 * x = 0 žymėjimas. Bet, kaip žinote, bet koks skaičius, padaugintas iš 0, duoda tik 0. Ši savybė būdinga pačiai nulinės vertės sąvokai.

Pasirodo, nėra tokio skaičiaus, kuris, padaugintas iš 0, gautų kokią nors apčiuopiamą reikšmę, tai yra, ši problema neturi sprendimo. Jūs neturėtumėte bijoti šio atsakymo, tai yra natūralus atsakymas į tokio tipo problemas. Tiesiog rekordas 6:0 neturi jokios prasmės ir nieko negali paaiškinti. Trumpai tariant, šią išraišką galima paaiškinti nemirtingu žodžiu „dalyti iš nulio neįmanoma“.

Ar yra 0:0 operacija? Iš tiesų, jei daugybos iš 0 operacija yra teisėta, ar nulį galima padalyti iš nulio? Juk 0x 5=0 formos lygtis yra gana teisėta. Vietoj skaičiaus 5 galite įdėti 0, produktas nepasikeis.

Iš tiesų, 0x0 = 0. Bet jūs vis tiek negalite padalyti iš 0. Kaip minėta, padalijimas yra tiesiog atvirkštinė daugyba. Taigi, jei pavyzdyje 0x5=0, reikia nustatyti antrąjį faktorių, gauname 0x0=5. Arba 10. Arba begalybė. Begalybės dalijimas iš nulio – kaip tau tai patinka?

Bet jei koks nors skaičius telpa į išraišką, tai nėra prasmės pasirinkti tik vieną iš begalinio skaičiaus. Ir jei taip, tai reiškia, kad išraiška 0:0 neturi prasmės. Pasirodo, net paties nulio negalima padalyti iš nulio.

Aukštoji matematika

Dalyba iš nulio – vidurinės mokyklos matematikos galvos skausmas. Technikos universitetuose studijuojama matematinė analizė šiek tiek praplečia problemų, kurios neturi sprendimo, sampratą. Pavyzdžiui, prie jau žinomos išraiškos 0:0 pridedami nauji, kurie mokykliniuose matematikos kursuose neturi sprendimų:

begalybė padalinta iš begalybės: ∞:∞;
begalybė minus begalybė: ∞−∞;
vienetas pakeltas iki begalinės galios: 1 ∞ ;
begalybė padauginta iš 0: ∞*0;
kai kurie kiti.

Elementariais metodais tokių išraiškų išspręsti neįmanoma. Tačiau aukštoji matematika, dėl papildomų galimybių daugeliui panašių pavyzdžių, pateikia galutinius sprendimus. Tai ypač akivaizdu nagrinėjant problemas iš ribų teorijos.

Netikrumo atrakinimas

Ribų teorijoje reikšmė 0 pakeičiama sąlyginiu be galo mažu kintamuoju. O išraiškos, kuriose, pakeitus norimą reikšmę, gaunamas dalijimas iš nulio, yra transformuojamos. Žemiau pateikiamas standartinis ribos atskleidimo, naudojant įprastas algebrines transformacijas, pavyzdys:

Kaip matote pavyzdyje, paprasčiausiai sumažinus trupmeną, jos vertė yra visiškai racionali.

Nagrinėjant trigonometrinių funkcijų ribas, jų išraiškos linkusios sumažinti iki pirmosios reikšmingos ribos. Nagrinėjant ribas, kuriose vardiklis tampa 0, kai riba pakeičiama, naudojama antra reikšminga riba.

L'Hopital metodas

Kai kuriais atvejais išraiškų ribos gali būti pakeistos jų išvestinių ribomis. Guillaume'as L'Hopitalis – prancūzų matematikas, prancūzų matematinės analizės mokyklos įkūrėjas. Jis įrodė, kad posakių ribos yra lygios šių posakių išvestinių riboms. Matematiniu žymėjimu jo taisyklė atrodo taip.

Jei skaičius padalytas iš begalybės, ar koeficientas bus linkęs į nulį? Tęsė viduje ir gavo geriausią atsakymą

Atsakymas iš Olenka[naujokas]
visi 0
Krab Вark
Orakulas
(56636)
Nr. Tikslus nulis. Kadangi daliklis linkęs į begalybę, koeficientas bus linkęs į nulį. Ir, jei dalijame ne iš skaičiaus, linkusio į begalybę, o iš pačios begalybės (beje, tiksliau, oficialiai jis visai nelaikomas skaičiumi, o laikomas specialiu simboliu, papildančiu skaičių žymėjimą) - lygiai nulis.

Atsakymas iš Jugejus Vladimiras[guru]
Net jei padalysite nulį, net jei padauginsite jį iš bet kurio skaičiaus, jis vis tiek bus nulis!

Atsakymas iš 1 23 [guru]
jei kažkoks šūdas linkęs į nulį, tai padauginti iš kažko baigtinio (skaičiaus ar ribotos funkcijos) yra nenaudinga, nes viskas linksta į nulį.
bet jei padauginsite jį iš kažkokio daikto, kuris linkęs į begalybę, gali būti variantų.

Atsakymas iš Krab Вark[guru]
Kai bet kuris skaičius yra padalintas iš begalybės, rezultatas yra nulis. Tikslus nulis, jokio „siekimo nulio link“. Ir tada, nesvarbu, iš kokio skaičiaus jį padauginsite, nulį. O rezultatas padalijus nulį iš bet kurio kito skaičiaus nei nulis bus lygus nuliui, tik dalijant nulį iš nulio rezultatas nenustatomas, nes daliniui tiks bet koks skaičius.

Funkcijos išvestinė toli nenukrenta, o L'Hopital taisyklių atveju ji patenka tiksliai į tą pačią vietą, kur patenka pradinė funkcija. Ši aplinkybė padeda atskleisti 0/0 arba ∞/∞ formos neapibrėžtumus ir kai kuriuos kitus neapibrėžtumus, atsirandančius skaičiuojant riba dviejų be galo mažų arba be galo didelių funkcijų ryšys. Skaičiavimas labai supaprastinamas naudojant šią taisyklę (iš tikrųjų dvi taisyklės ir pastabos joms):

Kaip rodo aukščiau pateikta formulė, skaičiuojant dviejų be galo mažų arba be galo didelių funkcijų santykio ribą, dviejų funkcijų santykio ribą galima pakeisti jų santykio riba. dariniai ir taip gauti tam tikrą rezultatą.

Pereikime prie tikslesnių L'Hopital taisyklių formuluočių.

L'Hopital taisyklė dviejų be galo mažų dydžių ribos atveju. Tegul funkcijos f(x) Ir g(x a. Ir pačiame taške a a funkcijos išvestinė g(x) nėra nulis ( g"(x a yra lygūs vienas kitam ir lygūs nuliui:

L'Hopital taisyklė dviejų be galo didelių kiekių ribos atveju. Tegul funkcijos f(x) Ir g(x) turi išvestinių (ty diferencijuojamų) tam tikroje taško kaimynystėje a. Ir pačiame taške a jie gali neturėti darinių. Be to, netoli taško a funkcijos išvestinė g(x) nėra nulis ( g"(x)≠0) ir šių funkcijų ribos, nes x yra linkusi į funkcijos reikšmę taške a yra lygūs vienas kitam ir lygūs begalybei:

Tada šių funkcijų santykio riba yra lygi jų išvestinių santykio ribai:

Kitaip tariant, 0/0 arba ∞/∞ formos neapibrėžčių atveju dviejų funkcijų santykio riba yra lygi jų išvestinių santykio ribai, jei pastaroji egzistuoja (baigtinė, tai yra lygi a tam tikras skaičius arba begalinis, tai yra lygus begalybei).

Pastabos.

1. L'Hopital taisyklės taip pat taikomos, kai funkcijos f(x) Ir g(x) nėra apibrėžti, kada x = a.

2. Jei, skaičiuojant funkcijų išvestinių santykio ribą f(x) Ir g(x) vėl gauname 0/0 arba ∞/∞ formos neapibrėžtį, tada L'Hopital taisyklės turėtų būti taikomos pakartotinai (bent du kartus).

3. L'Hopital taisyklės taip pat taikomos, kai funkcijų argumentas (x) nėra linkęs į baigtinį skaičių a, ir iki begalybės ( x → ∞).

Kitų tipų neapibrėžtis taip pat gali būti sumažinta iki 0/0 ir ∞/∞ tipų neapibrėžčių.

„nulis padalintas iš nulio“ ir „begalybė padalytas iš begalybės“ tipų neapibrėžčių atskleidimas

1 pavyzdys.

x=2 lemia 0/0 formos neapibrėžtumą. Todėl gaunama kiekvienos funkcijos išvestinė

Daugiano išvestinė buvo apskaičiuota skaitiklyje, o vardiklyje - sudėtingos logaritminės funkcijos išvestinė. Prieš paskutinį lygybės ženklą, įprastas riba, vietoj X pakeičiant du.

2 pavyzdys. Apskaičiuokite dviejų funkcijų santykio ribą naudodami L'Hopital taisyklę:

Sprendimas. Reikšmės pakeitimas tam tikra funkcija x

3 pavyzdys. Apskaičiuokite dviejų funkcijų santykio ribą naudodami L'Hopital taisyklę:

Sprendimas. Reikšmės pakeitimas tam tikra funkcija x=0 lemia 0/0 formos neapibrėžtumą. Todėl apskaičiuojame skaitiklio ir vardiklio funkcijų išvestines ir gauname:

4 pavyzdys. Apskaičiuoti

Sprendimas. Reikšmę x, lygią plius begalybei, pakeitus duotoje funkcijoje, susidaro ∞/∞ formos neapibrėžtis. Todėl taikome L'Hopital taisyklę:

komentuoti. Pereikime prie pavyzdžių, kuriuose L'Hopital taisyklė turi būti taikoma du kartus, tai yra prieiti prie antrųjų išvestinių santykio ribos, nes pirmųjų išvestinių santykio riba yra 0 formos neapibrėžtis. /0 arba ∞/∞.