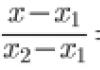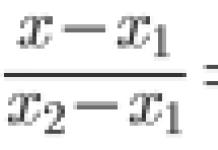40 pamoka. Proporcingos stačiojo trikampio atkarpos. C. b. a. h. S. bc. N. ac. A. B. Stačiojo trikampio aukštinė, nubrėžta iš viršūnės stačiu kampu, padalija trikampį į 2 panašius stačiuosius trikampius, kurių kiekvienas yra panašus šis trikampis. Stačiųjų trikampių panašumo testas. Du stačiakampiai trikampiai yra panašūs, jei kiekvienas turi vienodą smailųjį kampą. Atkarpa XY vadinama atkarpų AB ir CD proporcingu vidurkiu (geometriniu vidurkiu), jei savybė 1. Stačiojo trikampio, nubrėžto iš stačiojo kampo viršūnės, aukštis yra proporcingas vidurkis tarp kojų projekcijų į hipotenuzą. Savybė 2. Stačiojo trikampio kojelė yra proporcingas vidurkis tarp hipotenuzės ir šios kojos projekcijos į hipotenuzę.
28 skaidrė iš pristatymo „Geometrija „Panašūs trikampiai“. Archyvo su pristatymu dydis yra 232 KB.Geometrija 8 klasė
santrauka kiti pristatymai„Uždavinių sprendimas pagal Pitagoro teoremą“ - trikampis ABC yra lygiašonis. Praktinis naudojimas Pitagoro teorema. ABCD yra keturkampis. Kvadrato plotas. Surask saulę. Įrodymas. Lygiašonės trapecijos pagrindai. Apsvarstykite Pitagoro teoremą. Keturkampio plotas. Stačiakampiai trikampiai. Pitagoro teorema. Hipotenuzės kvadratas yra lygus kojų kvadratų sumai.
„Lygiagretainio ploto radimas“ - Pagrindas. Aukštis. Lygiagretainio aukščio nustatymas. Stačiųjų trikampių lygybės ženklai. Lygiagretainio plotas. Raskite trikampio plotą. Teritorijų savybės. Burnos pratimai. Raskite lygiagretainio plotą. Lygiagretainio aukščiai. Raskite kvadrato perimetrą. Trikampio plotas. Raskite aikštės plotą. Raskite stačiakampio plotą. Kvadrato plotas.
""Kvadratas" 8 klasė" - Juodasis kvadratas. Žodinio darbo užduotys aikštės perimetru. Kvadrato plotas. Kvadrato ženklai. Aikštė yra tarp mūsų. Kvadratas yra stačiakampis, kurio visos kraštinės lygios. Kvadratas. Krepšys kvadratiniu pagrindu. Užduotys žodžiu. Kiek kvadratų pavaizduota paveikslėlyje? Kvadrato savybės. Turtingas pirklys. Žodinio darbo užduotys aikštės plote. Kvadrato perimetras.
„Ašinės simetrijos apibrėžimas“ – taškai, esantys tame pačiame statmenyje. Nubrėžkite dvi tiesias linijas. Statyba. Nubraižykite taškus. Užuomina. Figūros, kurių nėra ašinė simetrija. Linijos segmentas. Trūksta koordinačių. Paveikslas. Figūros, turinčios daugiau nei dvi simetrijos ašis. Simetrija. Simetrija poezijoje. Sukonstruoti trikampius. Simetrijos ašys. Segmento konstravimas. Taško statyba. Figūros su dviem simetrijos ašimis. Tautos. Trikampiai. Proporcingumas.
„Panašių trikampių apibrėžimas“ – daugiakampiai. Proporcingi segmentai. Ploto santykis panašūs trikampiai. Du trikampiai vadinami panašiais. Sąlygos. Sukurkite trikampį naudodami du nurodytus kampus ir pusiaukampę viršūnėje. Tarkime, kad turime nustatyti atstumą iki stulpo. Trečiasis trikampių panašumo ženklas. Pastatykime kažkokį trikampį. ABC. Trikampiai ABC ir ABC yra lygūs iš trijų kraštinių. Objekto aukščio nustatymas.
„Pitagoro teoremos sprendimas“ – langų dalys. Paprasčiausias įrodymas. Hamurabis. Įstrižainė. Visiškas įrodymas. Įrodymas atimties metodu. pitagoriečiai. Įrodymas skilimo metodu. Teoremos istorija. Skersmuo. Įrodymas pridėjimo būdu. Epsteino įrodymas. Kantoras. Trikampiai. Sekėjai. Pitagoro teoremos taikymai. Pitagoro teorema. Teoremos teiginys. Perigalo įrodymas. Teoremos taikymas.
Šiandien jūsų dėmesiui pristatome dar vieną pristatymą nuostabia ir paslaptinga tema – geometrija. Šiame pristatyme supažindinsime su nauju turtu geometrines figūras, ypač su proporcingų atkarpų stačiakampiuose trikampiuose koncepcija.
Pirmiausia turėtume prisiminti, kas yra trikampis? Tai paprasčiausias daugiakampis, susidedantis iš trijų viršūnių, sujungtų trimis atkarpomis. Trikampis, kurio vienas iš kampų lygus 90 laipsnių, vadinamas stačiu trikampiu. Jūs jau susipažinote su jais išsamiau mūsų ankstesniame mokomoji medžiaga pristatytas jūsų dėmesiui.
Taigi, grįždami prie šiandieninės temos, pažymėkime, kad stačiojo trikampio aukštis, nubrėžtas iš 90 laipsnių kampo, padalija jį į du trikampius, kurie yra panašūs vienas į kitą ir į pradinį. Visi jus dominantys brėžiniai ir grafikai yra pateikti siūlomoje pristatymo dalyje, kartu su aprašytu paaiškinimu.
Grafinį aukščiau pateikto darbo pavyzdį galima pamatyti antroje skaidrėje. Remiantis pirmuoju trikampių panašumo ženklu, trikampiai yra panašūs, nes turi du identiškus kampus. Jei patikslinsime išsamiau, tai aukštis, nuleistas iki hipotenuzės, sudaro su juo stačią kampą, tai yra, jau yra identiški kampai, o kiekvienas suformuotas kampas taip pat turi vieną bendrą kampą kaip pradinis. Rezultatas yra du kampai, lygūs vienas kitam. Tai yra, trikampiai yra panašūs.

Taip pat išsiaiškinkime, ką reiškia sąvoka „proporcinis vidurkis“ arba „geometrinis vidurkis“? Tai yra tam tikras XY segmentas segmentams AB ir CD, kai jis lygus kvadratinė šaknis jų ilgio gaminiai.
Iš to taip pat išplaukia, kad stačiojo trikampio kojelė yra geometrinis vidurkis tarp hipotenuzės ir šios kojos projekcijos į hipotenuzę, tai yra, kitą koją.

Kitas turtas taisyklingas trikampis yra tai, kad jo aukštis, nubrėžtas 90° kampu, yra vidurkis proporcingas tarp kojų projekcijų į hipotenuzą. Jei pažvelgsite į pristatymą ir kitą jūsų dėmesiui siūlomą medžiagą, pamatysite, kad šios disertacijos įrodymai yra labai paprasta ir prieinama forma. Anksčiau mes jau įrodėme, kad gauti trikampiai yra panašūs vienas į kitą ir į pradinį trikampį. Tada, naudodami šių geometrinių figūrų kojų santykį, darome išvadą, kad stačiojo trikampio aukštis yra tiesiogiai proporcingas segmentų sandaugai, susidariusiai sumažinus aukštį nuo pradinio trikampio stačiu kampu.

Paskutinis dalykas pristatyme yra tai, kad stačiojo trikampio kojelė yra hipotenuzės ir jos atkarpos, esančios tarp kojos ir aukščio, nubrėžtos 90 laipsnių kampu, geometrinis vidurkis. Šis atvejis turėtų būti vertinamas tuo požiūriu, kad nurodyti trikampiai yra panašūs vienas į kitą, o vieno iš jų kojelė pasirodo esanti kito hipotenuzė. Tačiau su tuo susipažinsite išstudijavę siūlomą medžiagą.
Stačiųjų trikampių panašumo testas
Pirmiausia pristatykime stačiųjų trikampių panašumo kriterijų.
1 teorema
Stačiųjų trikampių panašumo testas: du stačiakampiai trikampiai yra panašūs, kai kiekvienas turi po vieną smailųjį kampą (1 pav.).
1 pav. Panašūs stačiakampiai trikampiai
Įrodymas.
Tegu $\kampas B=\kampas B_1$. Kadangi trikampiai yra stačiakampiai, tai $\angle A=\angle A_1=(90)^0$. Todėl jie yra panašūs pagal pirmąjį trikampių panašumo kriterijų.
Teorema įrodyta.
Aukščio teorema stačiakampiame trikampyje
2 teorema
Stačiojo trikampio aukštinė, nubrėžta iš stačiojo kampo viršūnės, padalija trikampį į du panašius stačiuosius trikampius, kurių kiekvienas yra panašus į nurodytą trikampį.
Įrodymas.
Pateikiame stačią trikampį $ABC$ su stačiu kampu $C$. Nubraižykime aukštį $CD$ (2 pav.).

2 pav. 2 teoremos iliustracija
Įrodykime, kad trikampiai $ACD$ ir $BCD$ yra panašūs į trikampį $ABC$ ir kad trikampiai $ACD$ ir $BCD$ yra panašūs vienas į kitą.
Kadangi $\kampas ADC=(90)^0$, tai trikampis $ACD$ yra stačiakampis. Trikampiai $ACD$ ir $ABC$ turi bendrą kampą $A$, todėl pagal 1 teoremą trikampiai $ACD$ ir $ABC$ yra panašūs.
Kadangi $\kampas BDC=(90)^0$, tai trikampis $BCD$ yra stačiakampis. Trikampiai $BCD$ ir $ABC$ turi bendrą kampą $B$, todėl pagal 1 teoremą trikampiai $BCD$ ir $ABC$ yra panašūs.
Dabar panagrinėkime trikampius $ACD$ ir $BCD$
\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\kampas A\]
Todėl pagal 1 teoremą trikampiai $ACD$ ir $BCD$ yra panašūs.
Teorema įrodyta.
Vidutinis proporcingas
3 teorema
Stačiojo trikampio aukštis, nubrėžtas iš stačiojo kampo viršūnės, yra vidurkis, proporcingas atkarpoms, į kurias aukštis padalija duoto trikampio hipotenuzę.
Įrodymas.
Remiantis 2 teorema, mes turime, kad trikampiai $ACD$ ir $BCD$ yra panašūs
Teorema įrodyta.
4 teorema
Stačiakampio trikampio kojelė yra vidurkis, proporcingas tarp hipotenuzės ir hipotenuzės atkarpos, esančios tarp kojos, ir aukščio, nubrėžto iš kampo viršūnės.
Įrodymas.
Teoremos įrodyme naudosime 2 paveikslo žymėjimą.
Remiantis 2 teorema, mes turime, kad trikampiai $ACD$ ir $ABC$ yra panašūs
Teorema įrodyta.
Pamokos tikslai:
- pristatyti dviejų atkarpų proporcingojo vidurkio (geometrinio vidurkio) sąvoką;
- apsvarstykite stačiojo trikampio proporcingų atkarpų uždavinį: stačiojo trikampio, nubrėžto iš stačiojo kampo viršūnės, aukščio savybę;
- ugdyti mokinių gebėjimus panaudoti studijuojamą temą problemų sprendimo procese.
Pamokos tipas: naujos medžiagos mokymosi pamoka.
Planas:
- Org momentas.
- Žinių atnaujinimas.
- Stačiojo trikampio, nubrėžto iš stačiojo kampo viršūnės, aukščio savybės tyrimas:
– paruošiamasis etapas;
– įvadas;
– asimiliacija. - Vidurkio, proporcingo dviem segmentams, sąvokos įvedimas.
- Dviejų segmentų vidurkio proporcingumo sampratos įsisavinimas.
- Pasekmių įrodymas:
– stačiojo trikampio, nubrėžto iš stačiojo kampo viršūnės, aukštis yra vidurkis, proporcingas atkarpoms, į kurias iš šio aukščio padalijama hipotenuzė;
– stačiojo trikampio kojelė yra vidurkis, proporcingas tarp įvorės ir įdubos atkarpos, esančios tarp kojos ir aukščio. - Problemų sprendimas.
- Apibendrinant.
- Namų darbų nustatymas.
Per užsiėmimus
I. ORGANIZACIJOS AKMENTAS
- Sveiki, vaikinai, sėskite į vietą. Ar visi pasiruošę pamokoms?
Pradėkime darbą.
II. ŽINIOS ATNAUJINTOS
- Kaip svarbu matematinė sąvoka ar buvote susitikę ankstesnėse pamokose? ( su trikampių panašumo samprata)
– Prisiminkime, kurie du trikampiai vadinami panašiais? (du trikampiai vadinami panašiais, jei jų kampai atitinkamai lygūs ir vieno trikampio kraštinės yra proporcingos kito trikampio panašioms kraštinėms)
– Ką naudojame dviejų trikampių panašumui įrodyti? (
– Suformuluokite šiuos ženklus (suformuluokite tris trikampių panašumo ženklus)
III. STAČIAKAMPIO TRIKAMPIO AUKŠČIO SAVYBIŲ TYRIMAS IŠ STAČIAUS KAMPO VIRŠŪNĖS
a) parengiamasis etapas
– Vaikinai, pažiūrėkite į pirmąją skaidrę. ( Taikymas) Čia rodomi du stačiakampiai trikampiai – ir . ir yra aukščiai ir atitinkamai. ![]() .
.
1 užduotis. a) Nustatykite, ar ir yra panašūs.
– Kuo įrodinėjame trikampių panašumą? ( trikampių panašumo ženklai)
(pirmas ženklas, nes užduotyje nieko nežinoma apie trikampių kraštines)
. (Dvi poros: 1. ∟B= ∟B1 (tiesi), 2. ∟A= ∟A 1)
– Padarykite išvadą. pagal pirmąjį trikampių panašumo kriterijų ~)
1 užduotis. b) Nustatykite, ar ir yra panašūs.
– Kokį panašumo ženklą naudosime ir kodėl? (pirmasis ženklas, nes užduotyje nieko nežinoma apie trikampių kraštines)
– Kiek porų vienodų kampų turime rasti? Raskite šias poras (kadangi trikampiai stačiakampiai, tai užtenka vienos poros vienodų kampų: ∟A= ∟A 1)
- Padarykite išvadą. (remiantis pirmuoju trikampių panašumo kriterijumi, darome išvadą, kad šie trikampiai yra panašūs).
Dėl pokalbio 1 skaidrė atrodo taip:

b) teoremos atradimas
2 užduotis.
– Nustatykite, ar ir yra panašūs. Pokalbio metu sukuriami atsakymai, kurie atsispindi skaidrėje.

– Nuotraukoje buvo nurodyta, kad . Ar naudojome šį laipsnio matą atsakydami į užduoties klausimus? ( Ne, mes jo nenaudojome)
– Vaikinai, padarykite išvadą: į kokius trikampius dalijasi stačiakampis pagal aukštį, nubrėžtą iš stačiojo kampo viršūnės? (baigti)

– Kyla klausimas: ar šie du stačiakampiai trikampiai, į kuriuos aukštis dalija stačiąjį trikampį, bus panašūs vienas į kitą? Pabandykime surasti lygių kampų poras.
Pokalbio rezultatas yra įrašas:

– Dabar padarykime visas išvadas. IŠVADA: stačiojo trikampio aukštinė, nubrėžta iš stačiojo kampo viršūnės, padalija trikampį į dvi dalis panašus
- Tai. Suformulavome ir įrodėme teoremą apie stačiojo trikampio aukščio savybę.
Nustatykime teoremos struktūrą ir padarykime brėžinį. Kas pateikta teoremoje ir ką reikia įrodyti? Mokiniai į sąsiuvinį rašo:

– Įrodykime pirmąjį teoremos tašką naujam brėžiniui. Kokią panašumo savybę naudosime ir kodėl? (Pirmasis, nes teoremoje nieko nežinoma apie trikampių kraštines)
– Kiek porų vienodų kampų turime rasti? Raskite šias poras. (Šiuo atveju pakanka vienos poros: ∟A-bendras)
- Padarykite išvadą. Trikampiai yra panašūs. Dėl to parodomas teoremos pavyzdys

– Antrą ir trečią punktus išrašykite patys namuose.
c) teoremos įsisavinimas
- Taigi, dar kartą suformuluokite teoremą (Stačiojo trikampio aukštinė, nubrėžta iš stačiojo kampo viršūnės, padalija trikampį į dvi dalis panašus stačiakampiai trikampiai, kurių kiekvienas yra panašus į šį)
– Kiek porų panašių trikampių konstrukcijoje „stačiakampiame trikampyje aukštinė brėžiama iš stačiojo kampo viršūnės“ leidžia ši teorema rasti? ( Trys poros)
Mokiniams suteikiama tokia užduotis:

IV. DVIEJŲ SEGMENTŲ VIDUTINIO PROPORCINGO SĄVOKOS ĮVADAS
– O dabar su jumis išnagrinėsime naują koncepciją.
Dėmesio!
Apibrėžimas. Linijos segmentas XY paskambino vidutinis proporcingas (geometrinis vidurkis) tarp segmentų AB Ir CD, Jei
(užsirašykite į sąsiuvinį).
V. DVIEJŲ SEGMENTŲ VIDUTINIO PROPORCIO SĄVOKOS SUPRASTINIMAS
– Dabar pereikime prie kitos skaidrės.
1 pratimas. Raskite vidurkio ilgį proporcingus segmentus MN ir KP, jei MN = 9 cm, KP = 16 cm.
– Kas pateikta užduotyje? ( Du segmentai ir jų ilgiai: MN = 9 cm, KP = 16 cm)
– Ką tau reikia rasti? ( Vidurkio ilgis, proporcingas šiems segmentams)
– Kokia formulė išreiškia proporcingą vidurkį ir kaip jį randame?
(Pakeiskite duomenis į formulę ir suraskite vidutinio atramos ilgį.)
2 užduotis. Raskite atkarpos AB ilgį, jei atkarpų AB ir CD proporcingas vidurkis yra 90 cm, o CD = 100 cm
– Kas pateikta užduotyje? (atkarpos CD ilgis = 100 cm, o atkarpų AB ir CD proporcingas vidurkis yra 90 cm)
– Ką reikėtų rasti problemoje? ( Atkarpos AB ilgis)
– Kaip išspręsime problemą? (Užrašykime vidutinių proporcingų atkarpų AB ir CD formulę, išreikškime iš jos ilgį AB ir pakeiskime duomenis uždavinyje.)
VI. POVEIKIO IŠVADA
- Puiku vaikinai. Dabar grįžkime prie trikampių panašumo, kurį įrodėme teoremoje. Dar kartą išsakykite teoremą. ( Stačiojo trikampio aukštinė, nubrėžta iš stačiojo kampo viršūnės, padalija trikampį į dvi dalis panašus stačiųjų trikampių, kurių kiekvienas yra panašus į pateiktąjį)
– Pirmiausia panaudokime trikampių ir panašumą. Kas iš to seka? ( Pagal apibrėžimą panašumo pusės yra proporcingos panašioms pusėms)
– Kokia lygybė atsiras naudojant pagrindinę proporcijos savybę? ()
– Išreikškite kompaktinį diską ir padarykite išvadą (![]() ;
;![]() .
.
Išvada: stačiojo trikampio aukštis, nubrėžtas iš stačiojo kampo viršūnės, yra vidurkis, proporcingas atkarpoms, į kurias hipotenuzė yra padalinta iš šio aukščio)
– Dabar įrodykite patys, kad stačiojo trikampio kojelė yra vidurkis, proporcingas tarp kojelės ir įdubos atkarpos, esančios tarp kojos ir aukščio šiuo aukščiu )
Stačiojo trikampio kojelė yra vidurkis, proporcingas tarp...(-... hipotenuzė ir hipotenuzės segmentas, esantis tarp šios kojos ir aukščio )
– Kur pritaikysime išmoktus teiginius? ( Sprendžiant problemas)
IX. NAMŲ DARBŲ NUSTATYMAS
d/z: Nr. 571, Nr. 572 (a, d), savarankiškas darbas sąsiuvinyje, teorija.
Stačiųjų trikampių panašumo testas
Pirmiausia pristatykime stačiųjų trikampių panašumo kriterijų.
1 teorema
Stačiųjų trikampių panašumo testas: du stačiakampiai trikampiai yra panašūs, kai kiekvienas turi po vieną smailųjį kampą (1 pav.).
1 pav. Panašūs stačiakampiai trikampiai
Įrodymas.
Tegu $\kampas B=\kampas B_1$. Kadangi trikampiai yra stačiakampiai, tai $\angle A=\angle A_1=(90)^0$. Todėl jie yra panašūs pagal pirmąjį trikampių panašumo kriterijų.
Teorema įrodyta.
Aukščio teorema stačiakampiame trikampyje
2 teorema
Stačiojo trikampio aukštinė, nubrėžta iš stačiojo kampo viršūnės, padalija trikampį į du panašius stačiuosius trikampius, kurių kiekvienas yra panašus į nurodytą trikampį.
Įrodymas.
Pateikiame stačią trikampį $ABC$ su stačiu kampu $C$. Nubraižykime aukštį $CD$ (2 pav.).

2 pav. 2 teoremos iliustracija
Įrodykime, kad trikampiai $ACD$ ir $BCD$ yra panašūs į trikampį $ABC$ ir kad trikampiai $ACD$ ir $BCD$ yra panašūs vienas į kitą.
Kadangi $\kampas ADC=(90)^0$, tai trikampis $ACD$ yra stačiakampis. Trikampiai $ACD$ ir $ABC$ turi bendrą kampą $A$, todėl pagal 1 teoremą trikampiai $ACD$ ir $ABC$ yra panašūs.
Kadangi $\kampas BDC=(90)^0$, tai trikampis $BCD$ yra stačiakampis. Trikampiai $BCD$ ir $ABC$ turi bendrą kampą $B$, todėl pagal 1 teoremą trikampiai $BCD$ ir $ABC$ yra panašūs.
Dabar panagrinėkime trikampius $ACD$ ir $BCD$
\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\kampas A\]
Todėl pagal 1 teoremą trikampiai $ACD$ ir $BCD$ yra panašūs.
Teorema įrodyta.
Vidutinis proporcingas
3 teorema
Stačiojo trikampio aukštis, nubrėžtas iš stačiojo kampo viršūnės, yra vidurkis, proporcingas atkarpoms, į kurias aukštis padalija duoto trikampio hipotenuzę.
Įrodymas.
Remiantis 2 teorema, mes turime, kad trikampiai $ACD$ ir $BCD$ yra panašūs
Teorema įrodyta.
4 teorema
Stačiakampio trikampio kojelė yra vidurkis, proporcingas tarp hipotenuzės ir hipotenuzės atkarpos, esančios tarp kojos, ir aukščio, nubrėžto iš kampo viršūnės.
Įrodymas.
Teoremos įrodyme naudosime 2 paveikslo žymėjimą.
Remiantis 2 teorema, mes turime, kad trikampiai $ACD$ ir $ABC$ yra panašūs
Teorema įrodyta.