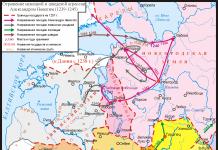
Та энд ирснээс хойш сурах бичигт энэ томъёог аль хэдийн харсан байх

мөн ийм царай гарга:

Найз минь, санаа зовох хэрэггүй! Үнэн хэрэгтээ бүх зүйл зүгээр л жигшүүртэй байдаг. Та бүх зүйлийг мэдээж ойлгох болно. Зөвхөн нэг хүсэлт - нийтлэлийг уншина уу аажмаар, алхам бүрийг ойлгохыг хичээ. Би аль болох энгийн бөгөөд ойлгомжтой бичсэн боловч та санааг ойлгох хэрэгтэй. Мөн нийтлэл дэх даалгавруудыг шийдвэрлэхээ мартуузай.

Нарийн төвөгтэй функц гэж юу вэ?

Та өөр орон сууц руу нүүж, том хайрцагт юм хийж байна гэж төсөөлөөд үз дээ. Сургуулийн бичгийн хэрэглүүр гэх мэт жижиг зүйлсийг цуглуулах хэрэгтэй гэж бодъё. Хэрэв та тэдгээрийг зүгээр л том хайрцагт хийвэл тэд бусад зүйлсийн дунд алга болно. Үүнээс зайлсхийхийн тулд та эхлээд уутанд хийж, дараа нь том хайрцагт хийж, дараа нь битүүмжилнэ. Энэхүү "цогцолбор" үйл явцыг доорх диаграммд үзүүлэв.

Математик үүнд ямар хамаатай юм шиг санагдаж байна? Тийм ээ, нарийн төвөгтэй функц нь яг ИТГЭЛ байдлаар үүсдэг ч гэсэн! Гагцхүү бид дэвтэр, үзэг биш \(x\) “баглаа” байхад “багц” болон “хайрцаг” нь өөр.

Жишээлбэл, x-г аваад үүнийг функц болгон "багц" болгоё:

Үүний үр дүнд бид мэдээж \(\cos⁡x\) авна. Энэ бол бидний "цүнх" юм. Одоо үүнийг "хайрцаг" дотор хийцгээе - жишээлбэл, куб функц болгон багцлаарай.

Эцсийн эцэст юу болох вэ? Тийм ээ, "хайрцагт юмны уут", өөрөөр хэлбэл "X кубын косинус" байх болно.

Үүссэн загвар нь нарийн төвөгтэй функц юм. Энэ нь энгийн зүйлээс ялгаатай Хэд хэдэн "нөлөөллийг" (багц) нэг X дээр дараалан хэрэглэнэЭнэ нь "функцоос функц" - "сав баглаа боодол доторх савлагаа" юм шиг харагдаж байна.

IN сургуулийн курсЭдгээр "багцуудын" маш цөөхөн төрөл байдаг бөгөөд ердөө дөрөв нь:

Одоо X-ийг эхлээд 7 суурьтай экспоненциал функц, дараа нь тригонометрийн функц болгон "багцгая". Бид авах:

\(x → 7^x → tg⁡(7^x)\)

Одоо x-г тригонометрийн функцууд руу хоёр удаа "багцгааж", эхлээд дотор, дараа нь:

\(x → sin⁡x → cotg⁡ (sin⁡x)\)

Энгийн, тийм үү?

Одоо функцүүдийг өөрөө бичээрэй, энд x:
- эхлээд косинус, дараа нь \(3\) суурьтай экспоненциал функцэд "багагддаг";
- эхлээд тав дахь зэрэглэлд, дараа нь шүргэгч рүү;
- эхлээд суурийн логарифм хүртэл \(4\) , дараа нь \(-2\) руу очно.

Энэ даалгаврын хариултыг өгүүллийн төгсгөлд олоорой.

Бид X-ийг хоёр биш, гурван удаа "баглаж" чадах уу? Асуудалгүй! Мөн дөрөв, тав, хорин таван удаа. Жишээлбэл, x нь \(4\) удаа "савласан" функц байна:

\(y=5^(\log_2⁡(\sin⁡(x^4)))\)

Гэхдээ ийм томъёолол сургуулийн дадлагауулзахгүй (оюутнууд илүү азтай байдаг - тэдэнд бүх зүйл илүү хэцүү байж магадгүй юм☺).

Нарийн төвөгтэй функцийг " задлах "

Өмнөх функцийг дахин харна уу. Та "савлах" дарааллыг олж чадах уу? Эхлээд юунд X чихэв, дараа нь юу гэх мэтээр эцсээ хүртэл. Өөрөөр хэлбэл, аль функц аль дотор нь үүрлэсэн бэ? Нэг хуудас цаас аваад юу гэж бодож байгаагаа бич. Та үүнийг дээр дурдсан сумтай гинжээр эсвэл өөр аргаар хийж болно.

Одоо зөв хариулт нь: эхлээд x-ийг \(4\)-р түвшинд "савласан", дараа нь үр дүнг синус болгон багцалж, улмаар \(2\) суурийн логарифмд байрлуулсан. , эцэст нь энэ бүхэл бүтэн бүтээн байгуулалтыг хүчирхэг тав болгон дүүргэв.

Өөрөөр хэлбэл та урвуу дарааллаар дарааллыг тайлах хэрэгтэй. Үүнийг хэрхэн хялбархан хийх талаар зөвлөгөө энд байна: нэн даруй X-г хараарай - та үүнээс бүжиглэх хэрэгтэй. Хэд хэдэн жишээг харцгаая.

Жишээлбэл, дараах функц байна: \(y=tg⁡(\log_2⁡x)\). Бид X-г хардаг - эхлээд юу болох вэ? Түүнээс авсан. Тэгээд? Үр дүнгийн тангенсыг авна. Дараалал нь ижил байх болно:

\(x → \log_2⁡x → tg⁡(\log_2⁡x)\)

Өөр нэг жишээ: \(y=\cos⁡((x^3))\). Шинжилгээ хийцгээе - эхлээд бид X-ийг куб болгож, дараа нь үр дүнгийн косинусыг авав. Энэ нь дараалал нь: \(x → x^3 → \cos⁡((x^3))\). Анхаарна уу, функц нь эхнийхтэй төстэй юм шиг байна (зурагтай газар). Гэхдээ энэ нь огт өөр функц юм: энд шоо дотор x (өөрөөр хэлбэл, \(\cos⁡((x·x·x)))\), харин шоо дотор косинус \(x\) байна ( өөрөөр хэлбэл, \(\cos⁡ x·\cos⁡x·\cos⁡x\)). Энэ ялгаа нь янз бүрийн "савлах" дарааллаас үүсдэг.

Сүүлийн жишээ (үндсэн чухал мэдээлэлтэй): \(y=\sin⁡((2x+5))\). Энд тэд эхлээд х-тэй арифметик үйлдлүүд хийж, дараа нь үр дүнгийн синусыг авсан нь тодорхой байна: \(x → 2x+5 → \sin⁡((2x+5))\). Энэ бол чухал зүйл юм: арифметик үйлдлүүд нь өөрөө функц биш боловч энд тэд бас "баглаа боох" арга болж ажилладаг. Энэ нарийн чанарыг бага зэрэг гүнзгийрүүлье.

Дээр хэлсэнчлэн энгийн функцүүдэд x нэг удаа "багагддаг", нарийн төвөгтэй функцүүдэд хоёр ба түүнээс дээш байдаг. Түүнээс гадна энгийн функцүүдийн аливаа хослол (өөрөөр хэлбэл тэдгээрийн нийлбэр, зөрүү, үржүүлэх, хуваах) нь бас энгийн функц юм. Жишээлбэл, \(x^7\) нь энгийн функц бөгөөд \(ctg x\) мөн адил. Энэ нь тэдгээрийн бүх хослолууд нь энгийн функцууд гэсэн үг юм:

\(x^7+ ctg x\) - энгийн,
\(x^7· ор х\) – энгийн,
\(\frac(x^7)(ctg x)\) – энгийн гэх мэт.

Гэсэн хэдий ч, хэрэв ийм хослолд өөр нэг функц ашиглавал энэ нь хоёр "багц" байх тул нарийн төвөгтэй функц болно. Диаграмыг үзнэ үү:

За, одоо яв. "Боох" функцүүдийн дарааллыг бичнэ үү:
\(y=cos(⁡(sin⁡x))\)
\(y=5^(x^7)\)
\(y=arctg⁡(11^x)\)
\(y=log_2⁡(1+x)\)
Хариултууд нь нийтлэлийн төгсгөлд дахин байна.

Дотоод болон гадаад функцууд

Бид яагаад үүрлэх функцийг ойлгох хэрэгтэй байна вэ? Энэ нь бидэнд юу өгөх вэ? Баримт нь ийм дүн шинжилгээ хийхгүйгээр бид дээр дурдсан функцүүдийн деривативуудыг найдвартай олох боломжгүй юм.

Мөн цааш явахын тулд бидэнд дотоод болон гадаад функц гэсэн хоёр ойлголт хэрэгтэй болно. Энэ бол маш энгийн зүйл, үүнээс гадна бид эдгээрийг аль хэдийн задлан шинжилсэн: хэрэв бид өөрсдийн аналогийг эхэндээ санаж байвал дотоод функц нь "багц", гадаад функц нь "хайрцаг" юм. Тэдгээр. Юуны өмнө X нь "боож" байгаа нь дотоод функц бөгөөд дотоод функц нь аль хэдийн гадаад байна. Яагаад гэдэг нь ойлгомжтой - тэр гадаа байгаа, энэ нь гаднах гэсэн үг юм.

Энэ жишээнд: \(y=tg⁡(log_2⁡x)\), \(\log_2⁡x\) функц нь дотоод бөгөөд
- гадна.

Үүнд: \(y=\cos⁡((x^3+2x+1))\), \(x^3+2x+1\) дотоод, мөн
- гадна.

Нарийн төвөгтэй функцүүдэд дүн шинжилгээ хийх сүүлчийн дадлагаа дуусгаад эцэст нь бидний эхлүүлсэн зүйл рүү шилжье - бид нарийн төвөгтэй функцүүдийн деривативуудыг олох болно.

Хүснэгтийн хоосон зайг бөглөнө үү:

Нарийн төвөгтэй функцийн дериватив

Сайн байцгаана уу, бид эцэст нь энэ сэдвийн "дарга" -д хүрлээ - үнэндээ дериватив нарийн төвөгтэй функц, ялангуяа өгүүллийн эхнээс тэр маш аймшигтай томьёо руу.☺

\((f(g(x))"=f"(g(x))\cdot g"(x)\)

Энэ томъёог дараах байдлаар уншина.

Нийлмэл функцийн уламжлал нь тогтмол дотоод функц болон дотоод функцийн деривативын гадаад функцийн деривативын үржвэртэй тэнцүү байна.

Юу болохыг ойлгохын тулд "үгээр үгээр" задлан шинжлэх диаграмыг нэн даруй хараарай.

"Үүсмэл" болон "бүтээгдэхүүн" гэсэн нэр томъёо нь ямар ч хүндрэл учруулахгүй гэж найдаж байна. "Цогцолбор функц" - бид үүнийг аль хэдийн ангилсан. Барилт нь "тогтмол дотоод функцтэй холбоотой гадаад функцийн дериватив"-д байна. Энэ юу вэ?

Хариулт: Энэ бол зөвхөн гадаад функц өөрчлөгддөг, дотоод функц нь өөрчлөгддөг гадаад функцийн ердийн уламжлал юм. Одоо хүртэл тодорхойгүй байна уу? За, жишээ татъя.

\(y=\sin⁡(x^3)\) функцтэй болгоё. Энд дотоод функц нь \(x^3\), гадаад функц болох нь тодорхой байна
. Одоо байнгын дотоод засалтай холбоотой гадна талын деривативыг олцгооё.

Математикийн физикийн асуудал эсвэл жишээг шийдвэрлэх нь дериватив, түүнийг тооцоолох аргуудын талаар мэдлэггүйгээр бүрэн боломжгүй юм. Дериватив нь математик шинжилгээний хамгийн чухал ойлголтуудын нэг юм. Энэ үндсэн сэдэвБид өнөөдрийн нийтлэлийг зориулахаар шийдсэн. Дериватив гэж юу вэ, түүний физик, геометрийн утга нь юу вэ, функцийн деривативыг хэрхэн тооцоолох вэ? Эдгээр бүх асуултыг нэг дор нэгтгэж болно: деривативыг хэрхэн ойлгох вэ?

Деривативын геометрийн болон физикийн утга

Функц байх болтугай f(x) , тодорхой интервалд заасан (а, б) . x ба x0 цэгүүд энэ интервалд хамаарна. X өөрчлөгдөхөд функц нь өөрөө өөрчлөгддөг. Аргументыг өөрчлөх - түүний утгуудын ялгаа x-x0 . Энэ ялгааг дараах байдлаар бичнэ дельта х ба аргументийн өсөлт гэж нэрлэдэг. Функцийн өөрчлөлт эсвэл өсөлт нь хоёр цэг дэх функцийн утгуудын зөрүү юм. Деривативын тодорхойлолт:

Тухайн цэг дэх функцийн үүсмэл утга нь өгөгдсөн цэг дэх функцийн өсөлтийг аргументийн өсөлттэй харьцуулсан харьцааны хязгаар нь тэг байх хандлагатай байдаг.

Үгүй бол дараах байдлаар бичиж болно.

Ийм хязгаар олох нь ямар учиртай юм бэ? Тэгээд энэ нь юу вэ:

цэг дээрх функцийн дериватив нь OX тэнхлэг хоорондын өнцгийн тангенс ба тухайн цэг дэх функцийн графиктай шүргэгчтэй тэнцүү байна.

Деривативын физик утга: цаг хугацааны хувьд замын дериватив нь шулуун хөдөлгөөний хурдтай тэнцүү байна.

Сургуулийн наснаас хойш хүн бүр хурд бол тодорхой зам гэдгийг мэддэг x=f(t) ба цаг хугацаа т . дундаж хурдтодорхой хугацаанд:

Цаг мөчид хөдөлгөөний хурдыг олж мэдэх t0 Та хязгаарыг тооцоолох хэрэгтэй:

Нэгдүгээр дүрэм: тогтмолыг тохируулах

Тогтмолыг дериватив тэмдгээс гаргаж авч болно. Түүнээс гадна үүнийг хийх ёстой. Математикийн жишээг шийдвэрлэхдээ үүнийг дүрмээр аваарай - Хэрэв та илэрхийлэлийг хялбарчилж чадвал түүнийг хялбарчлахаа мартуузай .

Жишээ. Деривативыг тооцоолъё:

Хоёрдугаар дүрэм: функцүүдийн нийлбэрийн дериватив

Хоёр функцийн нийлбэрийн дериватив нь эдгээр функцүүдийн деривативуудын нийлбэртэй тэнцүү байна. Функцийн зөрүүний деривативын хувьд ч мөн адил.

Бид энэ теоремын баталгааг өгөхгүй, харин практик жишээг авч үзэх болно.

Функцийн деривативыг ол:

Гуравдугаар дүрэм: функцүүдийн үржвэрийн дериватив

Хоёр дифференциалагдах функцийн үржвэрийн деривативыг дараах томъёогоор тооцоолно.

Жишээ нь: функцийн деривативыг ол:

Шийдэл:

Энд нарийн төвөгтэй функцүүдийн деривативыг тооцоолох талаар ярих нь чухал юм. Комплекс функцийн дериватив нь завсрын аргументтай харьцуулахад энэ функцийн деривативын үржвэртэй, бие даасан хувьсагчийн хувьд завсрын аргументийн деривативтай тэнцүү байна.

Дээрх жишээн дээр бид дараах илэрхийлэлтэй тулгардаг.

Энэ тохиолдолд завсрын аргумент нь тав дахь зэрэглэлд 8x байна. Ийм илэрхийллийн деривативыг тооцоолохын тулд эхлээд завсрын аргументтай холбоотойгоор гадаад функцийн деривативыг тооцож, дараа нь бие даасан хувьсагчийн хувьд завсрын аргументийн деривативаар үржүүлнэ.

Дөрөвдүгээр дүрэм: хоёр функцийн хуваалтын дериватив

Хоёр функцийн хуваалтын деривативыг тодорхойлох томъёо:

Бид даммигийн деривативын талаар эхнээс нь ярихыг хичээсэн. Энэ сэдэв нь тийм ч энгийн зүйл биш тул анхааруулах хэрэгтэй: жишээнүүдэд алдаанууд ихэвчлэн байдаг тул деривативыг тооцоолохдоо болгоомжтой байгаарай.

Энэ болон бусад сэдвээр асуух зүйл байвал оюутны үйлчилгээтэй холбогдож болно. Богино хугацаанд бид танд хамгийн хэцүү сорилтыг шийдэж, даалгавруудыг ойлгоход тань туслах болно, тэр ч байтугай та урьд өмнө хэзээ ч дериватив тооцоо хийж байгаагүй.

"Хуучин" сурах бичигт үүнийг "гинжин" дүрэм гэж бас нэрлэдэг. Тэгэхээр хэрэв y = f (u) ба u = φ (x), тэр бол

y = f (φ (x))

цогцолбор - нийлмэл функц (функцын бүрдэл) дараа нь

Хаана , тооцооны дараа авч үзнэ u = φ (x).

Энд бид ижил функцээс "өөр өөр" найрлагыг авсан бөгөөд ялгах үр дүн нь "холих" дарааллаас шууд хамааралтай болохыг анхаарна уу.

Гинжин дүрэм нь мэдээжийн хэрэг гурав ба түүнээс дээш функцтэй найрлагад хамаарна. Энэ тохиолдолд деривативыг бүрдүүлдэг "гинжин хэлхээнд" гурав ба түүнээс дээш "холбоос" байх болно. Үржүүлэхтэй ижил төстэй байдал энд байна: деривативын хүснэгт "бидэнд байна"; "тэнд" - үржүүлэх хүснэгт; "Бидэнтэй хамт" нь гинжин дүрэм, "байдаг" нь "багана" үржүүлэх дүрэм юм. Ийм "цогцолбор" деривативуудыг тооцоолохдоо мэдээжийн хэрэг туслах аргументуудыг (u¸v гэх мэт) оруулдаггүй, гэхдээ найрлагад хамаарах функцүүдийн тоо, дарааллыг тэмдэглээд харгалзах холбоосууд нь "тэгсэн" байна. заасан дарааллаар.

. Энд "y"-ийн утгыг олж авахын тулд "x"-ийн тусламжтайгаар таван үйлдлийг гүйцэтгэдэг, өөрөөр хэлбэл таван функцийн найрлагатай: "гадаад" (тэдгээрийн сүүлчийнх нь) - экспоненциал - e  ; дараа нь урвуу дарааллаар, хүч. (♦) 2 ; тригонометрийн нүгэл(); тайвшруулах. () 3 ба эцэст нь логарифм ln.(). Тийм ч учраас

Дараах жишээнүүдийн дагуу бид "хос шувууг нэг чулуугаар алах" болно: бид нарийн төвөгтэй функцуудыг ялгах дасгал хийж, деривативын хүснэгтэд нэмнэ. үндсэн функцууд. Тэгэхээр:

4. Хүчин чадлын функцийн хувьд - y = x α - үүнийг сайн мэддэг "үндсэн логарифмын ижилсэл" - b=e ln b - ашиглан x α = x α ln x хэлбэрээр дахин бичихэд бид олж авна.

5. Дурын экспоненциал функцийн хувьд ижил аргыг ашиглана

6. Дурын логарифм функцийн хувьд шинэ суурь руу шилжих сайн мэддэг томьёог ашиглан бид тогтмол олж авна.

.

7. Шүргэгч (котангенс)-ийг ялгахын тулд бид хуваалтыг ялгах дүрмийг ашигладаг.

Урвуу тригонометрийн функцүүдийн деривативыг олж авахын тулд бид хоёр харилцан урвуу функцийн деривативуудаар хангагдсан хамаарлыг ашигладаг, өөрөөр хэлбэл харилцаанд хамаарах φ (x) ба f (x) функцуудыг ашигладаг.

Энэ бол харьцаа юм

Энэ нь харилцан урвуу функцүүдийн хувьд энэ томъёоноос юм

Тэгээд
,

Эцэст нь дараах хүснэгтээс хялбархан олж авч болох эдгээр болон бусад деривативуудыг нэгтгэн дүгнэж үзье.

Үүний дээр бид хамгийн энгийн деривативуудыг судалж, мөн ялгах дүрэм, дериватив олох техникийн зарим техниктэй танилцсан. Тиймээс, хэрэв та функцийн деривативын талаар тийм ч сайн биш эсвэл энэ нийтлэлийн зарим зүйл бүрэн ойлгомжгүй байвал эхлээд дээрх хичээлийг уншина уу. Ноцтой сэтгэл хөдлөлөө аваарай - материал нь тийм ч энгийн биш, гэхдээ би үүнийг энгийн бөгөөд ойлгомжтой байдлаар танилцуулахыг хичээх болно.

Практик дээр та нарийн төвөгтэй функцийн деривативтай маш олон удаа харьцах хэрэгтэй болдог, тэр ч байтугай дериватив олох даалгавар өгөх үед бараг үргэлж гэж хэлэх болно.

Нарийн төвөгтэй функцийг ялгах дүрмийн (№ 5) хүснэгтийг бид харж байна.

Үүнийг олж мэдье. Юуны өмнө оруулгад анхаарлаа хандуулъя. Энд бид хоёр функцтэй - ба , функц нь дүрсээр хэлбэл функц дотор байрласан байна. Ийм төрлийн функцийг (нэг функц нөгөөд нь үүрлэсэн үед) нийлмэл функц гэж нэрлэдэг.

Би функцийг дуудах болно гадаад функц, болон функц – дотоод (эсвэл үүрлэсэн) функц.

! Эдгээр тодорхойлолтууд нь онолын хувьд биш бөгөөд даалгаврын эцсийн загварт тусгагдаагүй байх ёстой. Би зөвхөн материалыг ойлгоход хялбар болгох үүднээс "гадаад функц", "дотоод" функцийг албан бус хэллэгээр ашигладаг.

Нөхцөл байдлыг тодруулахын тулд дараахь зүйлийг анхаарч үзээрэй.

Жишээ 1

Функцийн деривативыг ол

Синусын доор бид зөвхөн "X" үсэг биш, харин бүхэл бүтэн илэрхийлэл байдаг тул үүсмэлийг хүснэгтээс шууд олох нь ажиллахгүй болно. Эхний дөрвөн дүрмийг энд хэрэглэх боломжгүй гэдгийг бид анзаарч байна, ялгаа байгаа юм шиг байгаа юм, гэхдээ синусыг "хэсэг болгон хувааж" болохгүй.

IN энэ жишээндФункц нь нийлмэл функц, олон гишүүнт нь дотоод функц (суулгах), гадаад функц гэдэг нь миний тайлбараас аль хэдийн ойлгомжтой болсон.

Эхний алхамнийлмэл функцийн деривативыг олоход юу хийх хэрэгтэй вэ? аль функц нь дотоод, аль нь гадаад болохыг ойлгох.

Хэзээ энгийн жишээнүүдСинусын дор олон гишүүнт багтсан нь тодорхой юм шиг байна. Гэхдээ бүх зүйл тодорхойгүй байвал яах вэ? Аль функц нь гадаад, аль нь дотоод гэдгийг хэрхэн зөв тодорхойлох вэ? Үүнийг хийхийн тулд оюун ухаанаар эсвэл ноорог хэлбэрээр хийж болох дараах техникийг ашиглахыг санал болгож байна.

Тооны машин дээр илэрхийллийн утгыг тооцоолох хэрэгтэй гэж төсөөлөөд үз дээ (нэгний оронд ямар ч тоо байж болно).

Бид эхлээд юуг тооцох вэ? Юуны өмнөхийх шаардлагатай болно дараагийн үйлдэл: , тиймээс олон гишүүнт дотоод функц болно:

Хоёрдугаартолох шаардлагатай тул синус нь гадаад функц болно:

Бидний дараа ХУДАЛДААдотоод болон гадаад функцтэй бол нарийн төвөгтэй функцуудыг ялгах дүрмийг хэрэглэх цаг болжээ .

Шийдвэрлэж эхэлцгээе. Хичээлээс Деривативыг хэрхэн олох вэ?Аливаа деривативын шийдлийн загвар үргэлж ингэж эхэлдэг гэдгийг бид санаж байна - бид илэрхийлэлийг хаалтанд хийж, баруун дээд буланд зураас тавьдаг:

Хамгийн эхэндбид гадаад функцийн деривативыг (синус) олоод, анхан шатны функцүүдийн деривативын хүснэгтийг хараад . Хэрэв "x"-г нийлмэл илэрхийллээр сольсон бол хүснэгтийн бүх томьёо мөн хамаарна, энэ тохиолдолд:

Дотоод функцийг анхаарна уу өөрчлөгдөөгүй, бид үүнд хүрдэггүй.

За энэ нь ойлгомжтой

Томьёог хэрэглэсний үр дүн эцсийн хэлбэрээр энэ нь дараах байдалтай байна.

Тогтмол хүчин зүйлийг ихэвчлэн илэрхийллийн эхэнд байрлуулдаг.

Хэрэв үл ойлголцол байвал шийдлийг цаасан дээр бичиж, тайлбарыг дахин уншина уу.

Жишээ 2

Функцийн деривативыг ол

Жишээ 3

Функцийн деривативыг ол

Бид үргэлж бичдэг:

Бидэнд гаднах функц, дотоод функц хаана байгааг олж мэдье. Үүнийг хийхийн тулд бид (сэтгэцийн хувьд эсвэл ноорог хэлбэрээр) илэрхийллийн утгыг тооцоолохыг оролддог. Та эхлээд юу хийх ёстой вэ? Юуны өмнө та суурь нь юутай тэнцүү болохыг тооцоолох хэрэгтэй: тиймээс олон гишүүнт нь дотоод функц юм.

Зөвхөн дараа нь экспонентацийг гүйцэтгэдэг тул чадлын функц нь гадаад функц болно.

Томъёоны дагуу , эхлээд та гадаад функцийн деривативыг олох хэрэгтэй, энэ тохиолдолд зэрэг. Хүснэгтээс шаардлагатай томъёог хайж байна: . Бид дахин давтана: Хүснэгтийн аливаа томьёо нь зөвхөн "X"-д төдийгүй нийлмэл илэрхийлэлд хүчинтэй байна. Тиймээс нарийн төвөгтэй функцийг ялгах дүрмийг хэрэглэсний үр дүн дараачийн:

Бид гадаад функцийн деривативыг авахад бидний дотоод функц өөрчлөгдөхгүй гэдгийг би дахин онцолж байна.

Одоо зөвхөн дотоод функцийн маш энгийн деривативыг олж, үр дүнг бага зэрэг өөрчлөхөд л үлдлээ.

Жишээ 4

Функцийн деривативыг ол

Энэ бол жишээ юм бие даасан шийдвэр(хичээлийн төгсгөлд хариулах).

Нарийн төвөгтэй функцийн деривативын талаархи ойлголтоо нэгтгэхийн тулд би тайлбаргүйгээр жишээ өгөх болно, үүнийг өөрөө олж мэдэхийг хичээ, гадаад, дотоод функц хаана байгааг, яагаад даалгавруудыг ингэж шийддэг вэ?

Жишээ 5

a) Функцийн деривативыг ол

б) Функцийн деривативыг ол

Жишээ 6

Функцийн деривативыг ол

Энд бид язгууртай бөгөөд уг үндсийг ялгахын тулд түүнийг хүч гэж төлөөлөх ёстой. Тиймээс бид эхлээд функцийг ялгахад тохиромжтой хэлбэрт оруулна.

Функцийг задлан шинжилж үзэхэд бид гурван гишүүний нийлбэр нь дотоод функц, хүчирхэг болгох нь гадаад функц гэсэн дүгнэлтэд хүрсэн. Бид нарийн төвөгтэй функцуудыг ялгах дүрмийг ашигладаг :

Бид дахин градусыг радикал (үндэс) болгон төлөөлдөг бөгөөд дотоод функцийн деривативын хувьд бид нийлбэрийг ялгах энгийн дүрмийг ашигладаг.

Бэлэн. Та мөн хаалт доторх илэрхийллийг өгч болно Ерөнхий хуваарьтэгээд бүгдийг нэг бутархай болгон бич. Энэ нь мэдээжийн хэрэг үзэсгэлэнтэй, гэхдээ урт урт деривативуудыг олж авбал үүнийг хийхгүй байх нь дээр (төөрөлдөх, шаардлагагүй алдаа гаргах, багш шалгахад эвгүй байх болно).

Жишээ 7

Функцийн деривативыг ол

Энэ бол та өөрөө шийдэх жишээ юм (хичээлийн төгсгөлд хариулах).

Заримдаа та нарийн төвөгтэй функцийг ялгах дүрмийн оронд хуваалтыг ялгах дүрмийг ашиглаж болно гэдгийг тэмдэглэх нь сонирхолтой юм. , гэхдээ ийм шийдэл нь ер бусын гажуудал мэт харагдах болно. Энд ердийн жишээ байна:

Жишээ 8

Функцийн деривативыг ол

Энд та хуваалтыг ялгах дүрмийг ашиглаж болно , гэхдээ цогц функцийг ялгах дүрмээр дамжуулан деривативыг олох нь илүү ашигтай байдаг.

Бид функцийг ялгахад бэлтгэдэг - бид хасах тэмдгийг дериватив тэмдгээс гаргаж, косинусыг тоологч руу өсгөнө.

Косинус нь дотоод функц, экспоненциал нь гадаад функц юм.
Өөрийн дүрмээ ашиглацгаая :

Бид дотоод функцийн деривативыг олж, косинусыг дахин тохируулна:

Бэлэн. Үзэж буй жишээн дээр шинж тэмдгүүдэд андуурахгүй байх нь чухал юм. Дашрамд хэлэхэд, дүрмийг ашиглан үүнийг шийдэхийг хичээ , хариултууд таарч байх ёстой.

Жишээ 9

Функцийн деривативыг ол

Энэ бол та өөрөө шийдэх жишээ юм (хичээлийн төгсгөлд хариулах).

Одоогоор бид нарийн төвөгтэй функцэд зөвхөн нэг үүртэй байсан тохиолдлуудыг авч үзсэн. Практик даалгаврын хувьд та үүрлэх хүүхэлдэй гэх мэт 3 эсвэл бүр 4-5 функцийг нэг дор байрлуулдаг деривативуудыг олж болно.

Жишээ 10

Функцийн деривативыг ол

Энэ функцийн хавсралтыг ойлгоцгооё. Туршилтын утгыг ашиглан илэрхийллийг тооцоолохыг оролдъё. Бид тооцоолуур дээр яаж тооцох вэ?

Эхлээд та олох хэрэгтэй бөгөөд энэ нь нуман синус нь хамгийн гүн шигтгээ гэсэн үг юм:

Дараа нь нэгийн энэ нуманыг квадрат болгох хэрэгтэй:

Эцэст нь бид долоог хүчирхэг болгож өсгөв:

Өөрөөр хэлбэл, энэ жишээн дээр бид гурван өөр функц, хоёр оруулгатай байгаа бол хамгийн дотоод функц нь арксинус, хамгийн гадна талын функц нь экспоненциал функц юм.

Шийдвэрлэж эхэлцгээе

Дүрмийн дагуу Эхлээд та гадаад функцийн деривативыг авах хэрэгтэй. Бид деривативын хүснэгтийг хараад экспоненциал функцийн деривативыг олно: Цорын ганц ялгаа нь "x"-ийн оронд нийлмэл илэрхийлэл байгаа нь энэ томъёоны хүчинтэй байдлыг үгүйсгэхгүй. Тиймээс нарийн төвөгтэй функцийг ялгах дүрмийг хэрэглэсний үр дүн дараачийн.

Функцүүд нарийн төвөгтэй төрөлнийлмэл функцийн тодорхойлолтод үргэлж тохирохгүй. Хэрэв y = sin x - (2 - 3) · a r c t g x x 5 7 x 10 - 17 x 3 + x - 11 хэлбэрийн функц байгаа бол y = sin 2 x-ээс ялгаатай нь нийлмэл гэж үзэж болохгүй.

Энэ нийтлэлд нарийн төвөгтэй функцийн тухай ойлголт, түүний тодорхойлолтыг харуулах болно. Дүгнэлт дэх шийдлийн жишээнүүдийн хамт деривативыг олох томьёотой ажиллацгаая. Деривативын хүснэгт ба ялгах дүрмийг ашиглах нь деривативыг олох хугацааг эрс багасгадаг.

Үндсэн тодорхойлолтууд

Тодорхойлолт 1

Аргумент нь мөн функц болох функцийг цогц функц гэнэ.

Үүнийг дараах байдлаар тэмдэглэв: f (g (x)). Бид g (x) функцийг f (g (x)) аргумент гэж үздэг.

Тодорхойлолт 2

Хэрэв f функц байгаа бөгөөд котангенс функц байвал g(x) = ln x функц болно байгалийн логарифм. f (g (x)) нийлмэл функц arctg(lnx) хэлбэрээр бичигдэхийг бид олж мэдсэн. Эсвэл g (x) = x 2 + 2 x - 3 нь бүхэл бүтэн рационал функц гэж тооцогддог 4-р зэрэглэлд өргөгдсөн функц болох f функцийг бид f (g (x)) = (x 2 +) гэж олж авна. 2 x - 3) 4 .

g(x) нь нарийн төвөгтэй байж болох нь ойлгомжтой. y = sin 2 x + 1 x 3 - 5 жишээнээс g-ийн утга нь бутархайн шоо язгууртай болох нь тодорхой байна. Энэ илэрхийллийг y = f (f 1 (f 2 (x))) гэж тэмдэглэж болно. Эндээс харахад f нь синусын функц, f 1 нь доор байрлах функц юм квадрат язгуур, f 2 (x) = 2 x + 1 x 3 - 5 - бутархай рационал функц.

Тодорхойлолт 3

Үүрлэх зэрэг нь аль нэгээр тодорхойлогддог натурал тооба y = f (f 1 (f 2 (f 3) (... (f n (x)))))) гэж бичнэ.

Тодорхойлолт 4

Функцийн бүрэлдэхүүн гэдэг ойлголт нь асуудлын нөхцөлийн дагуу үүрлэсэн функцүүдийн тоог илэрхийлдэг. Шийдвэрлэхийн тулд хэлбэрийн нийлмэл функцийн деривативыг олох томъёог ашиглана уу

(f (g (x))) " = f " (g (x)) g " (x)

Жишээ

Жишээ 1

y = (2 x + 1) 2 хэлбэрийн нийлмэл функцийн деривативыг ол.

Шийдэл

Нөхцөлөөс харахад f нь квадрат функц, g(x) = 2 x + 1 нь шугаман функц гэж тооцогддог.

Нарийн төвөгтэй функцийн дериватив томъёог хэрэглэж, бичье.

f " (g (x)) = ((g (x)) 2) " = 2 (g (x)) 2 - 1 = 2 g (x) = 2 (2 x + 1) ; g " (x) = (2 x + 1) " = (2 x) " + 1 " = 2 x " + 0 = 2 1 x 1 - 1 = 2 ⇒ (f (g (x))) " = f " (g (x)) g " (x) = 2 (2 x + 1) 2 = 8 x + 4

Функцийн хялбаршуулсан анхны хэлбэр бүхий деривативыг олох шаардлагатай. Бид авах:

y = (2 x + 1) 2 = 4 x 2 + 4 x + 1

Эндээс бидэнд ийм байна

y " = (4 x 2 + 4 x + 1) " = (4 x 2) " + (4 x) " + 1 " = 4 (x 2) " + 4 (x) " + 0 = = 4 · 2 · x 2 - 1 + 4 · 1 · x 1 - 1 = 8 x + 4

Үр дүн нь адилхан байсан.

Энэ төрлийн асуудлыг шийдвэрлэхдээ f ба g (x) хэлбэрийн функц хаана байрлаж байгааг ойлгох нь чухал юм.

Жишээ 2

Та y = sin 2 x ба y = sin x 2 хэлбэрийн нарийн төвөгтэй функцүүдийн деривативуудыг олох хэрэгтэй.

Шийдэл

Эхний функцийн тэмдэглэгээ нь f нь квадратын функц, g(x) нь синусын функц юм. Дараа нь бид үүнийг авдаг

y " = (нүгэл 2 х) " = 2 нүгэл 2 - 1 x (нүгэл x) " = 2 нүгэл x cos x

Хоёр дахь оруулга нь f нь синус функц бөгөөд g(x) = x 2 гэж тэмдэглэсэн болохыг харуулж байна эрчим хүчний функц. Эндээс бид нийлмэл функцийн үржвэрийг бичнэ

y " = (нүгэл x 2) " = cos (x 2) (x 2) " = cos (x 2) 2 x 2 - 1 = 2 x cos (x 2)

Дериватив y = f (f 1 (f 2 (f 3 (... (f n (x))))) томъёог y " = f " (f 1 (f 2 (f 3 (.)) гэж бичнэ. . . ( f n (x))))) · f 1 "(f 2 (f 3 (. . . (f n (x))))) · · f 2 " (f 3 (. . . (f n (x)) ))) )) · . . . fn "(x)

Жишээ 3

y = sin (ln 3 a r c t g (2 x)) функцийн уламжлалыг ол.

Шийдэл

Энэ жишээ нь функцүүдийн байршлыг бичих, тодорхойлоход хүндрэлтэй байгааг харуулж байна. Дараа нь y = f (f 1 (f 2 (f 3 (f 4 (x)))) f , f 1 , f 2 , f 3 , f 4 (x) нь синусын функц, өсгөх функц гэдгийг тэмдэглэнэ. 3 градус хүртэл, логарифм ба суурьтай функц e, арктангенс ба шугаман функц.

Нарийн төвөгтэй функцийг тодорхойлох томъёоноос бид үүнийг олж авна

y " = f " (f 1 (f 2 (f 3 (f 4 (x))))) f 1 " (f 2 (f 3 (f 4 (x))) f 2 " (f 3 (f 4) (x)) f 3 " (f 4 (x)) f 4 " (x)

Бид олох ёстой зүйлээ авдаг

1. f " (f 1 (f 2 (f 3 (f 4 (x)))) деривативын хүснэгтийн дагуу синусын дериватив, дараа нь f " (f 1 (f 2 (f 3 (f 4)) x)))) ) = cos (ln 3 a r c t g (2 x)) .
2. f 1 " (f 2 (f 3 (f 4 (x))) чадлын функцийн дериватив, дараа нь f 1 " (f 2 (f 3 (f 4 (x)))) = 3 ln 3 - 1 a r c t g (2 x) = 3 ln 2 a r c t g (2 x) .
3. f 2 "(f 3 (f 4 (x))) логарифмын дериватив байдлаар, дараа нь f 2 " (f 3 (f 4 (x))) = 1 a r c t g (2 x) .
4. f 3 " (f 4 (x)) арктангентын дериватив, дараа нь f 3 " (f 4 (x)) = 1 1 + (2 x) 2 = 1 1 + 4 x 2.
5. f 4 (x) = 2 x деривативыг олохдоо 1-тэй тэнцүү илтгэгчтэй чадлын функцийн деривативын томъёог ашиглан деривативын тэмдгээс 2-ыг хасаад f 4 "(x) = (2 x) болно. " = 2 x " = 2 · 1 · x 1 - 1 = 2.

Бид завсрын үр дүнг нэгтгэж, үүнийг авдаг

y " = f " (f 1 (f 2 (f 3 (f 4 (x))))) f 1 " (f 2 (f 3 (f 4 (x))) f 2 " (f 3 (f 4) (x)) f 3 " (f 4 (x)) f 4 " (x) = = cos (ln 3 a r c t g (2 x)) 3 ln 2 a r c t g (2 x) 1 a r c t g (2 x) 1 1 + 4 x 2 2 = = 6 cos (ln 3 a r c t g (2 x)) ln 2 a r c t g (2 x) a r c t g (2 x) (1 + 4 x 2)

Ийм функцүүдийн шинжилгээ нь үүрлэсэн хүүхэлдэйг санагдуулдаг. Дериватив хүснэгтийг ашиглан ялгах дүрмийг үргэлж тодорхой хэрэглэж болохгүй. Ихэнхдээ нарийн төвөгтэй функцүүдийн деривативыг олох томъёог ашиглах шаардлагатай байдаг.

Нарийн төвөгтэй харагдах байдал, нарийн төвөгтэй функцүүдийн хооронд зарим ялгаа байдаг. Үүнийг ялгах тодорхой чадвартай бол дериватив олох нь ялангуяа хялбар байх болно.

Жишээ 4

Кастинг хийхдээ анхаарч үзэх хэрэгтэй ижил төстэй жишээ. y = t g 2 x + 3 t g x + 1 хэлбэрийн функц байгаа бол g (x) = t g x, f (g) = g 2 + 3 g + 1 хэлбэрийн нийлмэл функц гэж үзэж болно. . Мэдээжийн хэрэг, нарийн төвөгтэй деривативын томъёог ашиглах шаардлагатай:

f " (г (х)) = (г 2 (х) + 3 г (х) + 1) " = (г 2 (х)) " + (3 г (х)) " + 1 " = = 2 · g 2 - 1 (x) + 3 g "(x) + 0 = 2 g (x) + 3 1 g 1 - 1 (x) = = 2 g (x) + 3 = 2 t g x + 3 ; g " (x) = (t g x) " = 1 cos 2 x ⇒ y " = (f (g (x))) " = f " (g (x)) g " (x) = (2 t g x + 3 ) · 1 cos 2 x = 2 t g x + 3 cos 2 x

y = t g x 2 + 3 t g x + 1 хэлбэрийн функц нь t g x 2, 3 t g x ба 1-ийн нийлбэртэй тул нарийн төвөгтэй гэж үзэхгүй. Гэсэн хэдий ч t g x 2 нь нарийн төвөгтэй функц гэж тооцогддог бол бид g (x) = x 2 ба f хэлбэрийн чадлын функцийг олж авдаг бөгөөд энэ нь шүргэгч функц юм. Үүнийг хийхийн тулд дүнгээр нь ялгана. Бид үүнийг ойлгодог

y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + (3 t g x) " + 1 " = = (t g x 2) " + 3 (t g x) " + 0 = (t g x 2) " + 3 учир 2 x

Нарийн төвөгтэй функцийн деривативыг (t g x 2) олох руу шилжье ":

f " (g (x)) = (t g (g (x))) " = 1 cos 2 g (x) = 1 cos 2 (x 2) g " (x) = (x 2) " = 2 x 2 - 1 = 2 x ⇒ (t g x 2) " = f " (g (x)) g " (x) = 2 x cos 2 (x 2)

Бид y " = (t g x 2 + 3 t g x + 1) " = (t g x 2) " + 3 cos 2 x = 2 x cos 2 (x 2) + 3 cos 2 x гэсэн утгыг олж авна.

Нарийн төвөгтэй төрлийн функцууд нь нарийн төвөгтэй функцүүдэд багтаж болох ба нарийн төвөгтэй функцууд нь өөрөө нарийн төвөгтэй төрлийн функцүүдийн бүрэлдэхүүн хэсэг байж болно.

Жишээ 5

Жишээлбэл, y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) хэлбэрийн цогц функцийг авч үзье.

Энэ функцийг y = f (g (x)) хэлбэрээр илэрхийлж болох бөгөөд f-ийн утга нь 3 суурь логарифмын функц, g (x) нь h (x) = хэлбэрийн хоёр функцийн нийлбэр гэж тооцогддог. x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 ба k (x) = ln 2 x · (x 2 + 1) . Мэдээжийн хэрэг, y = f (h (x) + k (x)).

h(x) функцийг авч үзье. Энэ нь l (x) = x 2 + 3 cos 3 (2 x + 1) + 7 ба m (x) = e x 2 + 3 3 харьцаа юм.

Бидэнд l (x) = x 2 + 3 cos 2 (2 x + 1) + 7 = n (x) + p (x) нь n (x) = x 2 + 7 ба p ( гэсэн хоёр функцийн нийлбэр юм. x) = 3 cos 3 (2 x + 1) , энд p (x) = 3 p 1 (p 2 (p 3 (x))) нь 3 тоон коэффициенттэй нийлмэл функц, p 1 нь куб функц, p 2 косинусын функцээр, p 3 (x) = 2 x + 1 шугаман функцээр.

m (x) = e x 2 + 3 3 = q (x) + r (x) нь q (x) = e x 2 ба r (x) = 3 3 гэсэн хоёр функцийн нийлбэр болохыг олж мэдсэн бөгөөд энд q (x) = q 1 (q 2 (x)) нь нийлмэл функц, q 1 нь экспоненциалтай функц, q 2 (x) = x 2 нь чадлын функц юм.

Энэ нь h (x) = l (x) m (x) = n (x) + p (x) q (x) + r (x) = n (x) + 3 p 1 (p 2 ( p 3) гэдгийг харуулж байна. (x))) q 1 (q 2 (x)) + r (x)

k (x) = ln 2 x · (x 2 + 1) = s (x) · t (x) хэлбэрийн илэрхийлэл рүү шилжих үед функц нь s ( комплекс) хэлбэрээр илэрхийлэгдэх нь тодорхой байна. x) = ln 2 x = s 1 ( s 2 (x)) рационал бүхэл тоо t (x) = x 2 + 1, энд s 1 нь квадрат функц, s 2 (x) = ln x нь логарифм байна. суурь e.

Эндээс илэрхийлэл нь k (x) = s (x) · t (x) = s 1 (s 2 (x)) · t (x) хэлбэртэй болно.

Дараа нь бид үүнийг авдаг

y = log 3 x 2 + 3 cos 3 (2 x + 1) + 7 e x 2 + 3 3 + ln 2 x (x 2 + 1) = = f n (x) + 3 p 1 (p 2 (p 3) x))) q 1 (q 2 (x)) = r (x) + s 1 (s 2 (x)) t (x)

Функцийн бүтцэд үндэслэн илэрхийллийг ялгахдаа хэрхэн, ямар томьёог ашиглах шаардлагатай байгаа нь тодорхой болсон. Ийм асуудал, тэдгээрийн шийдлийн талаархи ойлголттой танилцахын тулд функцийг ялгах, өөрөөр хэлбэл түүний деривативыг олох цэг рүү шилжих шаардлагатай.

Хэрэв та текстэнд алдаа байгааг анзаарсан бол үүнийг тодруулаад Ctrl+Enter дарна уу