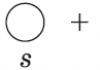Жишээ (алгебрийн тэгшитгэлийн язгуурын тоо)
1) x 2 – 4x+ 5 = 0 - хоёрдугаар зэргийн алгебрийн тэгшитгэл (квадрат тэгшитгэл) 
2 
= 2 би- хоёр үндэс;
2) x 3 + 1 = 0 - 3-р зэргийн алгебрийн тэгшитгэл (биномиаль тэгшитгэл) 
;
3) П 3 (x) = x 3 + x 2 – x– 1 = 0 – гуравдугаар зэргийн алгебрийн тэгшитгэл;
тоо x 1 = 1 нь түүний үндэс, учир нь П 3 (1) 
0, тиймээс Безутын теоремоор 
; олон гишүүнт хуваагдана П 3 (x) биномоор ( x– 1) "багананд":
|
|
анхны тэгшитгэл П 3 (x) = x 3 + x 2 – x – 1 = 0 (x – 1)(x 2 + 2x + 1) = 0 (x – 1)(x + 1) 2 = 0 x 1 = 1 - энгийн үндэс, x 2 = –1 - давхар үндэс. |
|
2-р шинж чанар (бодит коэффициент бүхий алгебр тэгшитгэлийн цогц язгууруудын тухай) |
|
Хэрэв бодит коэффициент бүхий алгебрийн тэгшитгэл нь нийлмэл язгууртай бол эдгээр үндэс нь үргэлж хос комплекс коньюгат, өөрөөр хэлбэл тоо |
тэгшитгэлийн үндэс юм
, дараа нь тоо 
нь мөн энэ тэгшитгэлийн үндэс юм. Үүнийг батлахын тулд та нийлмэл холболтын үйл ажиллагааны тодорхойлолт болон дараах хялбар шалгаж болох шинж чанаруудыг ашиглах хэрэгтэй.
Хэрэв 
, Тэр 
ба тэгш байдал хүчинтэй байна:
,
,
,
,
Хэрэв 
бол бодит тоо юм 
.
Учир нь 
тэгшитгэлийн үндэс юм 
, Тэр 
Хаана 
-- бодит тоо 
.
Сүүлчийн тэгшитгэлийн хоёр талаас коньюгацийг авч, залгах үйлдлийн жагсаасан шинж чанаруудыг ашиглая:
, өөрөөр хэлбэл тоо 
мөн тэгшитгэлийг хангана 
, тиймээс түүний үндэс
Жишээ (бодит коэффициент бүхий алгебрийн тэгшитгэлийн нийлмэл үндэс)
Алгебр тэгшитгэлийн нийлмэл язгуурыг бодит коэффициенттэй хослуулах нь батлагдсан шинж чанарын үр дүнд олон гишүүнтийн өөр шинж чанарыг олж авсан.
Бид олон гишүүнтийн тэлэлт (6)-аас эхэлнэ 
шугаман хүчин зүйлүүдэд:
Дугаарыг нь өгөөч x 0
= а
+ би- олон гишүүнтийн цогц үндэс П n (x), өөрөөр хэлбэл энэ нь тоонуудын нэг юм 
. Хэрэв энэ олон гишүүнтийн бүх коэффициентүүд нь бодит тоо бол тоо 
нь мөн түүний үндэс, өөрөөр хэлбэл тоонуудын дунд байдаг 
бас тоо байна 
.
Хоёр гишүүний үржвэрийг тооцоолъё 
:
Үр дүн нь квадрат гурвалжин юм бодит магадлалаар
Тиймээс (6) томъёонд заасан нийлмэл язгуур бүхий дурын хос биномууд нь бодит коэффициент бүхий квадрат гурвалжинд хүргэдэг.
Жишээ (бодит коэффициент бүхий олон гишүүнтийг үржүүлэх)
1)П 3 (x) = x 3 + 1 = (x + 1)(x 2 – x + 1);
2)П 4 (x) = x 4 – x 3 + 4x 2 – 4x = x(x –1)(x 2 + 4).
|
3-р шинж чанар (бодит бүхэл тооны коэффициент бүхий алгебрийн тэгшитгэлийн бүхэл ба рационал язгуур дээр) |
|
Бидэнд алгебрийн тэгшитгэл өгье
 |
, бүх коэффициентүүд 
бодит бүхэл тоонууд,1. Энэ нь бүхэл тоо байг 
тэгшитгэлийн үндэс юм
Бүхэл тооноос хойш 
бүхэл тооны үржвэрээр илэрхийлэгдэнэ 
болон бүхэл тоон утгатай илэрхийллүүд.
2. Алгебрийн тэгшитгэлийг бичье 
оновчтой үндэстэй
, үүнээс гадна тоонууд х
Тэгээд qхарьцангуй анхдагч байдаг 
.
Энэ таних тэмдгийг хоёр хувилбараар бичиж болно:
Тэмдэглэгээний эхний хувилбараас үүнийг дагаж мөрддөг 
, хоёр дахь нь - юу 
, тооноос хойш х
Тэгээд qхарьцангуй анхдагч байдаг.
Жишээ (бүхэл тоон коэффициент бүхий алгебрийн тэгшитгэлийн бүхэл тоо эсвэл рационал язгуурыг сонгох)
Квадрат тэгшитгэлийн язгуурын томъёо. Бодит, олон, төвөгтэй язгуурын тохиолдлыг авч үзнэ. Квадрат гурвалжны коэффициент. Геометрийн тайлбар. Үндэс ба факторинг тодорхойлох жишээ.
АгуулгаМөн үзнэ үү: Квадрат тэгшитгэлийг онлайнаар шийдвэрлэх
Үндсэн томъёо
Квадрат тэгшитгэлийг авч үзье.
(1)
.
Квадрат тэгшитгэлийн үндэс(1) томъёогоор тодорхойлно:
;
.
Эдгээр томъёог дараах байдлаар нэгтгэж болно.
.
Квадрат тэгшитгэлийн язгуурыг мэддэг бол хоёр дахь зэрэглэлийн олон гишүүнтийг хүчин зүйлийн үржвэр (фактор) хэлбэрээр илэрхийлж болно.
.
Дараа нь бид бодит тоо гэж таамаглаж байна.
Ингээд авч үзье квадрат тэгшитгэлийн дискриминант:
.
Хэрэв дискриминант эерэг бол квадрат тэгшитгэл (1) нь хоёр өөр бодит язгууртай болно.
;
.
Дараа нь квадрат гурвалсан тоог үржүүлэх нь дараах хэлбэртэй байна.
.
Хэрэв дискриминант нь тэгтэй тэнцүү бол квадрат тэгшитгэл (1) нь хоёр олон (тэнцүү) бодит язгууртай байна.
.
Факторчилол:
.
Хэрэв дискриминант нь сөрөг байвал квадрат тэгшитгэл (1) нь хоёр нийлмэл нийлмэл үндэстэй байна.
;
.
Энд төсөөллийн нэгж байна, ;
ба язгуурын бодит ба төсөөллийн хэсгүүд нь:
;
.
Дараа нь
.
График тайлбар
Хэрэв та функцийг зурвал
,
Энэ нь парабол бол графикийн тэнхлэгтэй огтлолцох цэгүүд нь тэгшитгэлийн үндэс болно.
.
Үед график нь х тэнхлэгийг (тэнхлэг) хоёр цэгээр () огтолно.
үед график нь нэг цэгт () х тэнхлэгт хүрнэ.
үед график нь х тэнхлэгтэй огтлолцдоггүй ().
Квадрат тэгшитгэлтэй холбоотой ашигтай томьёо
(f.1) ;
(f.2) ;
(f.3) .
Квадрат тэгшитгэлийн язгуурын томъёог гарган авах
Бид хувиргалтыг хийж (f.1) ба (f.3) томъёог ашигладаг:
,
Хаана
;
.
Тиймээс бид хоёрдугаар зэргийн олон гишүүнтийн томъёог дараах хэлбэрээр авсан.
.
Энэ нь тэгшитгэл байгааг харуулж байна
дээр гүйцэтгэсэн
Мөн .
Энэ нь квадрат тэгшитгэлийн үндэс юм
.
Квадрат тэгшитгэлийн үндсийг тодорхойлох жишээ
Жишээ 1
(1.1)
.
.
Бидний (1.1) тэгшитгэлтэй харьцуулбал коэффициентүүдийн утгыг олно.
.
Бид ялгагчийг олдог:
.
Дискриминант эерэг тул тэгшитгэл нь хоёр жинхэнэ үндэстэй байна.
;
;
.
Эндээс бид квадрат гурвалжны үржвэрийг олж авна.
.
y = функцийн график 2 x 2 + 7 x + 3х тэнхлэгийг хоёр цэгээр огтолж байна.
Функцийн графикийг зурцгаая
.
Энэ функцийн график нь парабол юм. Энэ нь абсцисса тэнхлэгийг (тэнхлэг) хоёр цэгээр дайран өнгөрдөг.
Мөн .
Эдгээр цэгүүд нь анхны тэгшитгэлийн үндэс юм (1.1).
;
;
.
Жишээ 2
Квадрат тэгшитгэлийн язгуурыг ол:
(2.1)
.
Квадрат тэгшитгэлийг ерөнхий хэлбэрээр бичье.
.
Анхны тэгшитгэл (2.1)-тэй харьцуулбал бид коэффициентүүдийн утгыг олно.
.
Бид ялгагчийг олдог:
.
Дискриминант нь тэг тул тэгшитгэл нь хоёр олон (тэнцүү) үндэстэй байна.
;
.
Дараа нь гурвалсан тоог үржүүлэх нь дараах хэлбэртэй байна.
.
y = x функцийн график 2 - 4 x + 4нэг цэгт х тэнхлэгт хүрнэ.
Функцийн графикийг зурцгаая
.
Энэ функцийн график нь парабол юм. Энэ нь x тэнхлэгт (тэнхлэг) нэг цэгт хүрдэг:
.
Энэ цэг нь анхны тэгшитгэлийн үндэс юм (2.1). Учир нь энэ үндсийг хоёр удаа хүчин зүйлээр ялгасан болно:
,
тэгвэл ийм язгуурыг ихэвчлэн олон тоо гэж нэрлэдэг. Өөрөөр хэлбэл, тэд хоёр ижил үндэстэй гэдэгт итгэдэг.
.
;
.
Жишээ 3
Квадрат тэгшитгэлийн язгуурыг ол:
(3.1)
.
Квадрат тэгшитгэлийг ерөнхий хэлбэрээр бичье.
(1)
.
Анхны тэгшитгэлийг (3.1) дахин бичье:
.
(1) -тэй харьцуулбал бид коэффициентүүдийн утгыг олно.
.
Бид ялгагчийг олдог:
.
Ялгаварлагч нь сөрөг, . Тиймээс жинхэнэ үндэс байхгүй.
Та нарийн төвөгтэй үндэс олж болно:
;
;
.
Дараа нь
.
Функцийн график нь х тэнхлэгийг огтолдоггүй. Жинхэнэ үндэс байхгүй.
Функцийн графикийг зурцгаая
.
Энэ функцийн график нь парабол юм. Энэ нь x тэнхлэгтэй огтлолцдоггүй. Тиймээс жинхэнэ үндэс байхгүй.
Жинхэнэ үндэс байхгүй. Нарийн төвөгтэй үндэс:
;
;
.
Төсөл нь алгебрийн тэгшитгэлийн үндсийг ойролцоогоор олох аргыг - Лобачевский-Греффийн аргыг авч үздэг. Аргын санаа, түүний тооцооллын схемийг уг ажилд тодорхойлж, уг аргыг хэрэглэх нөхцөлийг олно. Лобачевский-Греффийн аргын хэрэгжилтийг үзүүлэв.
1 ОНОЛЫН 6-Р ХЭСЭГ
1.1 Асуудлын мэдэгдэл 6
1.2 Алгебрийн тэгшитгэл 7
1.2.1 Алгебр тэгшитгэлийн тухай үндсэн ойлголт 7
1.2.2 Алгебрийн тэгшитгэлийн үндэс 7
1.2.3 Олон гишүүнтийн бодит язгуурын тоо 9
1.3 Алгебрийн тэгшитгэлийн ойролцоо шийдлийн Лобачевский-Греффийн арга 11
1.3.1 Аргын санаа 11
1.3.2 Квадрат үндэс 13
2.1 Даалгавар 1 16
2.2 Даалгавар 2 18
2.4 Гарсан үр дүнгийн шинжилгээ 20
Ашигласан материалын жагсаалт 23
ОРШИЛ
Өнөөгийн тооцоолох технологи нь тоолох ажлыг бодитоор гүйцэтгэх хүчирхэг хэрэгслүүдээр хангадаг. Үүний ачаар олон тохиолдолд хэрэглээний асуудлын ойролцоо тайлбараас татгалзаж, асуудлыг яг нарийн томъёогоор шийдвэрлэхэд шилжих боломжтой болсон. Ойролцоогоор болон тоон шинжилгээний аргуудыг чадварлаг ашиглахгүйгээр орчин үеийн компьютерийн технологийг зохистой ашиглах боломжгүй юм.
Тоон аргууд нь практикт гарч буй асуудлыг шийдвэрлэхэд чиглэгддэг. Тоон аргуудыг ашиглан асуудлыг шийдвэрлэх нь тоон дээрх арифметик болон логик үйлдлүүдтэй холбоотой бөгөөд энэ нь хувийн компьютерт зориулсан орчин үеийн оффисын програмуудын хүснэгтийн процессор зэрэг компьютерийн технологийг ашиглахыг шаарддаг.
"Тоон аргууд" хичээлийн зорилго нь тодорхой асуудлыг шийдвэрлэх хамгийн үр дүнтэй аргыг олох явдал юм.
Алгебрийн тэгшитгэлийг шийдвэрлэх нь хэрэглээний анализын чухал асуудлын нэг бөгөөд энэ хэрэгцээ нь үгийн өргөн утгаараа физик, механик, технологи, байгалийн шинжлэх ухааны олон, олон янзын хэсэгт үүсдэг.
Энэхүү сургалтын төсөл нь алгебрийн тэгшитгэлийг шийдвэрлэх аргуудын нэг болох Лобачевский-Греффийн аргад зориулагдсан болно.
Энэхүү ажлын зорилго нь алгебрийн асуудлыг шийдвэрлэх Лобачевский-Греффийн аргын санааг авч үзэх, MS Office Excel програмыг ашиглан бодит үндсийг олох тооцооллын схемийг өгөх явдал юм. Төсөл нь Лобачевский-Греффийн аргыг ашиглан алгебрийн тэгшитгэлийн язгуурыг олохтой холбоотой онолын үндсэн асуудлуудыг судалсан бөгөөд энэ ажлын практик хэсэгт Лобачевский-Греффийн аргыг ашиглан алгебрийн тэгшитгэлийн шийдлүүдийг танилцуулсан болно.
ОНОЛЫН 1 ХЭСЭГ
1.1 Асуудлын мэдэгдэл
x элементийн X олонлог ба y элементтэй Y олонлогийг өгье. Мөн X олонлог дээр оператор тодорхойлогдсон гэж үзье, энэ нь X элемент бүрт X-ээс Y-ээс зарим y-г оноодог. Зарим элементийг ав.
мөн ийм элементүүдийг олох зорилго тавьсан 
, Үүний төлөө 
зураг юм. Энэ бодлого нь тэгшитгэлийг шийдэхтэй тэнцүү юм
(1.1)
Үүний тулд дараах асуудлууд гарч ирж болно.
Тэгшитгэлийн шийдэл байх нөхцөл.
Тэгшитгэлийн шийдийн өвөрмөц байдлын нөхцөл.
Шийдлийн алгоритм бөгөөд үүний дараа зорилго, нөхцлөөс хамааран (1.1) тэгшитгэлийн яг эсвэл ойролцоогоор бүх шийдлүүд, эсвэл урьдчилан тодорхойлсон аль нэг шийдлүүд эсвэл одоо байгаа аль нэг шийдлийг олох боломжтой болно.
зарим функц байх болно. Энэ тохиолдолд (1.1) тэгшитгэлийг хэлбэрээр бичиж болно 
(1.2)
Тоон аргын онолд хүн (1.2) тэгшитгэлийн шийдлийг урьдчилан тодорхойлсон нарийвчлалтайгаар олох боломжтой тооцоолох үйл явцыг бий болгохыг эрмэлздэг. Конвергент процессууд нь онцгой ач холбогдолтой бөгөөд энэ нь тэгшитгэлийг жижиг гэлтгүй ямар ч алдаатай шийдвэрлэх боломжийг олгодог.
Бидний даалгавар бол ерөнхийдөө ойролцоогоор элементийг олох явдал юм 
. Энэ зорилгоор ойролцоогоор шийдлүүдийн дарааллыг гаргадаг алгоритмыг боловсруулж байна 
, мөн ийм байдлаар харилцаа тогтоогддог
1.2 Алгебрийн тэгшитгэл
1.2.1 Алгебрийн тэгшитгэлийн талаархи үндсэн ойлголтууд
n-р зэргийн алгебрийн тэгшитгэлийг авч үзье
коэффициентүүд хаана байна 
бодит тоонууд ба 
.
Теорем 1.1 (алгебрын үндсэн теорем). n-р зэрэглэлийн алгебрийн тэгшитгэл (1.3) нь язгуур бүрийг үржвэрийнхээ хэмжээгээр олон удаа тоолох нөхцөлд бодит ба нийлмэл яг n үндэстэй байна.
Энэ тохиолдолд (1.3) тэгшитгэлийн язгуур нь s бол үржвэртэй байна гэж тэд хэлдэг
, 
.
(1.3) тэгшитгэлийн нийлмэл язгуурууд нь хос хосолсон шинж чанартай байдаг.
Теорем 1.2. Хэрэв алгебрийн тэгшитгэлийн коэффициентүүд (1.3) бодит бол энэ тэгшитгэлийн цогцолбор үндэс нь хос хосолсон цогц коньюгат байна. Хэрэв 
(
бодит тоонууд) тэгшитгэлийн үндэс (1.3), үржвэрийн s, дараа нь тоо 
нь мөн энэ тэгшитгэлийн үндэс бөгөөд ижил үржвэртэй s байна.
Үр дагавар. Бодит коэффициент бүхий сондгой зэрэгтэй алгебрийн тэгшитгэл дор хаяж нэг бодит язгууртай.
1.2.2 Алгебрийн тэгшитгэлийн үндэс
Хэрэв
тэгшитгэлийн үндэс (1.3) бол зүүн тал нь дараах өргөтгөлтэй байна. . (1.6)
Томъёо (1.6) дахь хоёр гишүүнийг үржүүлж, тэгш байдлын (1.6) зүүн ба баруун талын х-ийн ижил түвшний коэффициентүүдийг тэнцүүлэх замаар бид (1.3) алгебрийн тэгшитгэлийн үндэс ба коэффициентүүдийн хоорондын хамаарлыг олж авна.
(1.7)
Хэрэв бид үндэсийн олон талт байдлыг харгалзан үзвэл өргөтгөл (1.6) хэлбэрийг авна
,
Хаана
– (1) тэгшитгэлийн өөр үндэс ба 
– тэдгээрийн олон талт байдал, ба 
.
Дериватив 
дараах байдлаар илэрхийлэгдэнэ.
Энд Q(x) нь олон гишүүнт юм
k=1,2,…,m үед Тиймээс олон гишүүнт
олон гишүүнтийн хамгийн том нийтлэг хуваагч юм
ба түүний дериватив 
, мөн Евклидийн алгоритмыг ашиглан олж болно. Нэг хэсэг болгоцгооё 
,
мөн бид олон гишүүнтийг авна
бодит магадлалаар
, A 1 , A 2 ,…, A m , тэдгээрийн үндэс 
ялгаатай. Тиймээс олон үндэстэй алгебрийн тэгшитгэлийг шийдэх нь өөр өөр үндэстэй доод эрэмбийн алгебрийн тэгшитгэлийг шийдвэрлэхэд хүргэдэг.
1.2.3 Олон гишүүнтийн бодит язгуурын тоо
(a,b) интервал дээрх тэгшитгэлийн (1.3) бодит язгуурын тооны ерөнхий санааг функцийн графикаар өгсөн болно.
, үндэс хаана байна 
Графикийн Ox тэнхлэгтэй огтлолцох цэгүүдийн абсциссууд юм. P(x) олон гишүүнтийн зарим шинж чанарыг тэмдэглэе:
Хэрэв P(a)P(b) бол
Хэрэв P(a)P(b)>0 бол (a, b) интервал дээр P(x) олон гишүүнт тэгш тоо байх юм уу язгуур байхгүй байна.
Тодорхойлолт. Тэг биш бодит тоонуудын эрэмбэлэгдсэн төгсгөлтэй системийг өгье.
,
,…,
(1.9)
Тэд зэргэлдээх элементүүдийн хувьд гэж хэлдэг
, 
систем (1.9) хэрэв эдгээр элементүүд нь эсрэг тэмдэгтэй бол тэмдгийн өөрчлөлт байдаг, өөрөөр хэлбэл. 
,
мөн тэдгээрийн тэмдгүүд ижил байвал тэмдгийн өөрчлөлт байхгүй, i.e.
.
Тодорхойлолт. Зэргэлдээх элементүүдийн бүх хосын тэмдгийн өөрчлөлтийн нийт тоо
, 
системийг (1.9) систем дэх тэмдгийн өөрчлөлтийн тоо (1.9) гэж нэрлэдэг. Тодорхойлолт. Өгөгдсөн P(x) олон гишүүнтийн хувьд Штурмын систем нь олон гишүүнтийн систем юм
,
, 
, 
,…, 
,
Хаана 
, – олон гишүүнтийг хуваахад эсрэг тэмдгээр авах үлдэгдэл, – олон гишүүнтийг хуваахад эсрэг тэмдэгтэй үлдэгдэл гэх мэт.
Тайлбар 1. Хэрэв олон гишүүнт олон үндэсгүй бол Штурмын системийн сүүлчийн элемент нь тэгээс өөр бодит тоо байна.
Тайлбар 2. Штурмын системийн элементүүдийг эерэг тоон коэффициент хүртэл тооцоолж болно.
Энэ системийн тэг элементүүдийг зурсан тохиолдолд Sturm систем дэх тэмдгийн өөрчлөлтийн тоог x=c үед N(c)-ээр тэмдэглэе.
Теорем 1.5. (Штурмын теорем). P(x) олон гишүүнт олон морь байхгүй бол ба 
, 
, дараа нь түүний жинхэнэ язгуурын тоо 
интервал дээр 
олон гишүүнтийн Штурмын системийн алдагдсан тэмдгийн өөрчлөлтийн тоотой яг тэнцүү байна 
-аас шилжих үед 
өмнө 
, өөрөөр хэлбэл
.
Дүгнэлт 1. Хэрэв
, дараа нь тоо 
эерэг ба тоо 
олон гишүүнтийн сөрөг язгуурууд нь тэнцүү байна 
,
.
Дүгнэлт 2. Олон үндэсгүй n зэрэгтэй P(x) олон гишүүнтийн бүх язгуур бодит байхын тулд нөхцөл хангагдсан байх шаардлагатай бөгөөд хангалттай.
.
Тиймээс (1.3) тэгшитгэлийн бүх үндэс нь зөвхөн дараах тохиолдолд хүчинтэй байх болно.
Sturm системийг ашиглан тэгшитгэлийн бүх бодит язгуурыг агуулсан интервалыг (a,b) хязгаарлагдмал тооны хэсэгчилсэн интервалд хуваах замаар та алгебрийн тэгшитгэлийн үндсийг салгаж болно.
тиймэрхүү 
.
1.3 Алгебрийн тэгшитгэлийн ойролцоо шийдлийн Лобачевский-Греффийн арга
1.3.1 Аргын талаархи санаа
(1.3) алгебрийн тэгшитгэлийг авч үзье.Ингэж жүжиглэе
, (1.15)
тэдгээр. үндэс нь модулийн хувьд өөр бөгөөд өмнөх үндэс бүрийн модуль нь дараагийнхаас хамаагүй их байна. Өөрөөр хэлбэл, тоонуудынх нь буурах дарааллаар тоолж байгаа хоёр зэргэлдээ язгуурын харьцаа нь үнэмлэхүй утгаараа бага хэмжигдэхүүн байна гэж үзье.
, (1.16)
Хаана 
Тэгээд 
- бага үнэ цэнэ. Ийм үндэсийг тусгаарлагдсан гэж нэрлэдэг.
(1.17)
Хаана 
, 
,…, 
– нэгдмэл байдалтай харьцуулахад үнэмлэхүй үнэ цэнэ багатай хэмжигдэхүүнүүд. (1.17) системд хэмжигдэхүүнийг үл тоомсорлодог 
, бид ойролцоогоор харилцаатай байх болно 
(1.18)
Бид үндсийг хаанаас олох вэ? 
(1.19)
Тэгш байдлын систем дэх язгууруудын нарийвчлал (1.20) нь хэмжигдэхүүнүүдийн үнэмлэхүй утгаараа хэр бага байхаас хамаарна. 
харилцаанд (1.16)
(1.3) тэгшитгэлд үндэслэн үндсийг тусгаарлахын тулд хувиргасан тэгшитгэлийг бүрдүүлнэ.
, (1.20)
хэний үндэс
, 
,…, 
язгуурын m-e хүч юм 
, 
,…, 
тэгшитгэл (1.3). Хэрэв (1.3) тэгшитгэлийн бүх язгуурууд өөр бөгөөд тэдгээрийн модулиуд нь (1.17) нөхцлийг хангаж байвал хангалттай том m-ийн хувьд (1.20) тэгшитгэлийн , ,..., үндэс тусгаарлагдах болно.
цагт 
.
Үндэс нь өгөгдсөн тэгшитгэлийн язгуурын квадратууд байх тэгшитгэлийг олох алгоритмыг бүтээхэд хангалттай байх нь ойлгомжтой. Дараа нь язгуур нь анхны тэгшитгэлийн язгууртай тэнцүү байх тэгшитгэлийг авах боломжтой болно.
.
1.3.2 Үндэсийг квадрат болгох
Бид олон гишүүнт (1.3)-ийг дараах хэлбэрээр бичнэМөн үүнийг хэлбэрийн олон гишүүнтээр үржүүлнэ
Дараа нь бид авна
Сэлгээ хийсэн
ба үржүүлэх 
, байх болно . (1.21)
Олон гишүүнтийн язгуур (1.21) нь олон гишүүнт (1.3)-ын үндэстэй дараах хамаарлаар холбогдоно.
.
Тиймээс бидний сонирхож буй тэгшитгэл нь юм
,
(1.22) томъёог ашиглан коэффициентийг тооцдог.
, (1.22)
хаана гэж таамаглаж байна
цагт 
.
Олон гишүүнт (1.3) үндэсийг квадрат болгох үйл явцыг k дахин дараалан хэрэглэснээр бид олон гишүүнтийг олж авна.
, (1.23)
аль нь
, 
, гэх мэт. Хангалттай том k хувьд (1.23) тэгшитгэлийн үндэс нь системийг хангаж байгаа эсэхийг баталгаажуулах боломжтой.
(1.24)
Өгөгдсөн нарийвчлалд аль систем (1.24) хангагдсаныг k тоог тодорхойлъё.
Шаардлагатай k-д аль хэдийн хүрсэн ба тэгшитгэлүүд (1.24) хүлээн зөвшөөрөгдсөн нарийвчлалд хангагдсан гэж үзье. Дахиад нэг хувиргалт хийж олон гишүүнтийг олъё
,
аль системд (1.24) мөн тохирно
.
(1.22) томъёоны дагуу
, (1.25)
Дараа нь (1.25) -ийг системд (1.24) орлуулснаар коэффициентүүдийн үнэмлэхүй утгыг олж авна.
коэффициентуудын квадратуудын хүлээн зөвшөөрөгдсөн нарийвчлалтай тэнцүү байх ёстой 
. Эдгээр тэгшитгэлийн биелэлт нь k-ийн шаардлагатай утгад аль хэдийн k-р алхамд хүрсэн болохыг харуулах болно. Тиймээс (1.3) томъёоны баруун талд зөвхөн квадрат коэффициентууд нь хүлээн зөвшөөрөгдсөн нарийвчлалтайгаар үлдсэн бөгөөд бүтээгдэхүүний хоёр дахин нэмэгдсэн нийлбэр нь нарийвчлалын хязгаараас доогуур байвал (1.3) тэгшитгэлийн язгуурыг квадрат болгохыг зогсоох хэрэгтэй.
Дараа нь тэгшитгэлийн бодит язгууруудыг салгаж, тэдгээрийн модулиудыг томъёогоор олно
(1.26)
Утгыг орлуулах замаар язгуурын тэмдгийг ойролцоогоор тооцоолж тодорхойлж болно 
Тэгээд 
(1.3) тэгшитгэлд оруулна.
2 ПРАКТИК ХЭСЭГ
2.1 Даалгавар 1
. (2.1)
Эхлээд (2.1) тэгшитгэлийн бодит ба комплекс язгуурын тоог тогтооё. Үүнийг хийхийн тулд Штурмын теоремыг ашиглана.
(2.1) тэгшитгэлийн Sturm систем нь дараах хэлбэртэй байна.
Бид хаанаас авах вэ?
Хүснэгт 2.1.
|
Олон гишүүнт |
Бодит тэнхлэг дээрх цэгүүд |
|
 |
 |
|
 |
+ |
+ |
 |
– |
+ |
 |
– |
– |
 |
– |
+ |
 |
– |
– |
|
Тэмдгийн өөрчлөлтийн тоо |
1 |
3 |
Тиймээс (2.1) тэгшитгэлийн бодит язгууруудын тоо тэнцүү болохыг олж мэдэв
,
тэдгээр. тэгшитгэл (2.1) нь 2 бодит ба хоёр нийлмэл язгуурыг агуулна.
Тэгшитгэлийн язгуурыг олохын тулд бид Лобачевский-Греффын аргыг хос нийлмэл язгуур үндэст ашигладаг.
Тэгшитгэлийн язгуурыг квадрат болгоё. Коэффициентийг дараах томъёогоор тооцоолсон 
, (2.2)
Хаана 
, (2.3)
А 
үед 0-тэй тэнцүү гэж үзнэ 
.
Найман чухал үзүүлэлт бүхий тооцооллын үр дүнг Хүснэгт 2.2-т үзүүлэв
Хүснэгт 2.2.
|
би |
0 |
1 |
2 |
3 |
4 |
 |
|||||
 |
0 |
-3.8000000E+01 |
3.5400000E+02 |
3.8760000E+03 |
0 |
 |
1 |
4.3000000E+01 |
7.1500000E+02 |
4.8370000E+03 |
1.0404000E+04 |
 |
|||||
 |
0 |
-1.4300000E+03 |
-3.9517400E+05 |
-1.4877720E+07 |
0 |
 |
1 |
4.1900000E+02 |
1.1605100E+05 |
8.5188490E+06 |
1.0824322E+08 |
 |
|||||
 |
0 |
-2.3210200E+05 |
-6.9223090E+09 |
-2.5123467E+13 |
0 |
 |
1 |
-5.6541000E+04 |
6.5455256E+09 |
4.7447321E+13 |
1.1716594E+16 |
 |
|||||
 |
0 |
-1.3091051E+10 |
5.3888712E+18 |
-1.5338253E+26 |
0 |
 |
1 |
-9.8941665E+09 |
4.8232776E+19 |
2.0978658E+27 |
1.3727857E+32 |
 |
|||||
 |
0 |
-9.6465552E+19 |
4.1513541E+37 |
-1.3242653E+52 |
0 |
 |
1 |
1.4289776E+18 |
2.3679142E+39 |
4.3877982E+54 |
1.8845406E+64 |
 |
|||||
 |
0 |
-4.7358285E+39 |
-1.2540130E+73 |
-8.9248610+103 |
0 |
 |
1 |
-4.7337865E+39 |
5.6070053E+78 |
1.9252683+109 |
3.5514932+128 |
 |
|||||
 |
0 |
-1.1214011E+79 |
1.8227619+149 |
-3.9826483+207 |
0 |
 |
1 |
1.1194724E+79 |
3.1438509+157 |
3.7066582+218 |
1.2613104+257 |
Хүснэгт 2.2-оос харахад 7-р шатанд үндэс 
, 
(модульүүдийн буурах дарааллаар тоолох) салангид гэж үзэж болно. Бид (1.27) томъёог ашиглан язгуурын модулиудыг олж, тэдгээрийн тэмдгийг ойролцоогоор тооцоогоор тодорхойлно.
Хувиргасан коэффициентээс хойш 
тэмдэг өөрчлөгдвөл энэ тэгшитгэл нь (1.29) ба (1.30) томъёог ашиглан (1.31) тэгшитгэлээс тодорхойлогддог нийлмэл язгууртай байна.
би.
2.2 Даалгавар 2
Лобачевский-Греффийн аргыг ашиглан тэгшитгэлийг шийд.. (2.4)
Эхлэхийн тулд Штурмын теоремыг ашиглан бид (2.2) тэгшитгэлийн бодит ба нийлмэл язгуурын тоог тодорхойлно.
Энэ тэгшитгэлийн хувьд Штурмын систем нь хэлбэртэй байна
Бид хаанаас авах вэ?
Хүснэгт 2.3.
|
Олон гишүүнт |
Бодит тэнхлэг дээрх цэгүүд |
|
|
|
|
|
|
|
+ |
+ |
|
|
– |
+ |
|
|
+ |
+ |
|
|
– |
+ |
|
|
– |
– |
|
Тэмдгийн өөрчлөлтийн тоо |
3 |
1 |
Тиймээс (2.2) тэгшитгэлийн бодит язгуурын тоо тэнцүү болохыг олж мэдэв
,
тэдгээр. тэгшитгэл (2.2) нь 2 бодит, хоёр цогц язгуурыг агуулна.
Тэгшитгэлийн үндсийг ойролцоогоор олохын тулд бид Лобачевский-Греффийн аргыг хос нийлмэл язгуур үндэст ашиглах болно.
Тэгшитгэлийн язгуурыг квадрат болгоё. Бид (2.2) ба (2.3) томъёог ашиглан коэффициентийг тооцоолох болно.
Найман чухал үзүүлэлт бүхий тооцооллын үр дүнг Хүснэгт 2.4-т үзүүлэв
Хүснэгт 2.4.
|
би |
0 |
1 |
2 |
3 |
4 |
|
|
|||||
|
|
0 |
-9.2000000E+00 |
-3.3300000E+01 |
1.3800000E+02 |
0 |
.
Тэгээд 
тэгшитгэл (2.4)-д байгаа бөгөөд энэ нь ижил тооны давталтын хувьд өөр өөр дарааллын алдаа (4.52958089E–11 ба 4.22229789E–06 тус тус) үүсгэдэг.гэх мэт. ерөнхий боловсролын шинж чанартай бөгөөд дээд математикийн БҮХЭЛДСЭН хичээлийг судлахад чухал ач холбогдолтой. Өнөөдөр бид "сургуулийн" тэгшитгэлийг давтах болно, гэхдээ зөвхөн "сургуулийн" тэгшитгэл биш, харин янз бүрийн вишматтай холбоотой асуудлуудад хаа сайгүй байдаг. Ердийнх шигээ түүхийг хэрэглээний аргаар ярих болно, өөрөөр хэлбэл. Би тодорхойлолт, ангилалд анхаарлаа хандуулахгүй, харин үүнийг шийдвэрлэх хувийн туршлагаа тантай хуваалцах болно. Мэдээлэл нь анхлан суралцагчдад зориулагдсан боловч ахисан түвшний уншигчид өөрсдөдөө сонирхолтой олон зүйлийг олох болно. Мэдээжийн хэрэг ахлах сургуулиас давсан шинэ материалууд байх болно.
Тэгэхээр тэгшитгэл .... Энэ үгийг олон хүн чичирсээр санаж байна. Үндэстэй "боловсронгуй" тэгшитгэл гэж юу вэ... ... тэдгээрийг март! Учир нь та энэ зүйлийн хамгийн хор хөнөөлгүй "төлөөлөгчид" -тэй уулзах болно. Эсвэл олон арван шийдлийн аргуудтай уйтгартай тригонометрийн тэгшитгэлүүд. Үнэнийг хэлэхэд би тэдэнд үнэхээр дургүй байсан ... Бүү сандар! - тэгвэл ихэвчлэн 1-2 алхамаар тодорхой шийдэл бүхий "данделионууд" таныг хүлээж байна. Хэдийгээр "burdock" наалддаг ч гэсэн та энд бодитой хандах хэрэгтэй.
Хачирхалтай нь, дээд математикийн хувьд маш энгийн тэгшитгэлтэй харьцах нь илүү түгээмэл байдаг шугамантэгшитгэл
Энэ тэгшитгэлийг шийдэх нь юу гэсэн үг вэ? Энэ нь "x" (үндэс)-ийн ИЙМ утгыг олох бөгөөд үүнийг жинхэнэ тэгшитгэл болгон хувиргана гэсэн үг юм. Тэмдгийг өөрчилснөөр "гурвыг" баруун тийш шидье.
"хоёр"-ыг баруун тал руу нь буулгана (эсвэл ижил зүйл - хоёр талыг үржүүлнэ)
:
Шалгахын тулд хожсон цомыг анхны тэгшитгэлд орлъё: 
Зөв тэгш байдлыг олж авсан бөгөөд энэ нь олсон утга нь үнэхээр энэ тэгшитгэлийн үндэс юм гэсэн үг юм. Эсвэл тэдний хэлснээр энэ тэгшитгэлийг хангадаг.
Үндэсийг аравтын бутархай хэлбэрээр бичиж болно гэдгийг анхаарна уу.
Мөн энэ муу хэв маягийг баримтлахгүй байхыг хичээгээрэй! Би шалтгааныг нэгээс олон удаа давтсан, ялангуяа эхний хичээл дээр дээд алгебр.
Дашрамд хэлэхэд тэгшитгэлийг "араб хэлээр" шийдэж болно.
Хамгийн сонирхолтой нь энэ бичлэг бүрэн хууль ёсных! Гэхдээ хэрэв та багш биш бол үүнийг хийхгүй байх нь дээр, учир нь оригинал нь энд шийтгэгддэг =)
Тэгээд одоо бага зэрэг
график шийдлийн арга
Тэгшитгэл нь хэлбэртэй, үндэс нь байна "X" координат уулзвар цэгүүд шугаман функцийн графикшугаман функцийн графиктай (x тэнхлэг):
Жишээ нь маш энгийн тул энд задлан шинжлэх зүйл байхгүй, гэхдээ үүнээс өөр нэг гэнэтийн нюансыг "шахаж" болно: ижил тэгшитгэлийг хэлбэрээр танилцуулж, функцүүдийн графикийг байгуулъя. 
Үүнд, Энэ хоёр ойлголтыг битгий хольж хутгаарай: тэгшитгэл нь тэгшитгэл бөгөөд функц- энэ бол функц! Функцүүд зөвхөн туслахтэгшитгэлийн язгуурыг ол. Үүнээс хоёр, гурав, дөрөв, бүр хязгааргүй олон байж болно. Энэ утгаараа хамгийн ойрын жишээ бол олны танил юм квадрат тэгшитгэл, тусдаа догол мөрийг хүлээн авсан шийдлийн алгоритм "халуун" сургуулийн томъёо. Мөн энэ нь санамсаргүй биш юм! Хэрэв та квадрат тэгшитгэлийг шийдэж чадвал мэдэж байгаа бол Пифагорын теорем, тэгвэл "дээд математикийн тал нь таны халаасанд байна" гэж хэлж болно =) Мэдээжийн хэрэг хэтрүүлсэн, гэхдээ үнэнээс тийм ч хол биш!
Тиймээс залхуу байж, квадрат тэгшитгэлийг ашиглан шийдье стандарт алгоритм:
, энэ нь тэгшитгэл нь хоёр өөр байна гэсэн үг юм хүчинтэйүндэс: 
Олдсон утгууд хоёулаа энэ тэгшитгэлийг хангаж байгаа эсэхийг шалгахад хялбар байдаг. 
Хэрэв та шийдлийн алгоритмаа гэнэт мартаж, туслах хэрэгсэл байхгүй бол яах вэ? Ийм нөхцөл байдал, жишээлбэл, шалгалт эсвэл шалгалтын үеэр үүсч болно. Бид график аргыг ашигладаг! Мөн хоёр арга бий: та чадна цэгээр барихпарабол 
, ингэснээр тэнхлэгтэй хаана огтлолцож байгааг олж мэднэ (хэрэв огт гаталж байвал). Гэхдээ илүү зальтай зүйл хийх нь дээр: тэгшитгэлийг хэлбэрээр төсөөлж, илүү энгийн функцуудын графикийг зур. "X" координатТэдний огтлолцох цэгүүд тод харагдаж байна! 
Хэрэв шулуун шугам параболд хүрч байгаа бол тэгшитгэл нь хоёр тохирох (олон) үндэстэй байна. Хэрэв шулуун шугам нь параболыг огтлолцоогүй бол жинхэнэ үндэс байхгүй болно.
Үүнийг хийхийн тулд мэдээж бүтээн байгуулалт хийх чадвартай байх хэрэгтэй энгийн функцүүдийн графикууд, гэхдээ нөгөө талаас сургуулийн хүүхэд хүртэл эдгээр чадварыг хийж чадна.
Мөн дахин - тэгшитгэл нь тэгшитгэл бөгөөд функцууд нь функцууд юм зөвхөн тусалсантэгшитгэлийг шийд!
Энд, дашрамд хэлэхэд, бас нэг зүйлийг санах нь зүйтэй болов уу. Хэрэв тэгшитгэлийн бүх коэффициентийг тэгээс өөр тоогоор үржүүлбэл түүний үндэс өөрчлөгдөхгүй..
Жишээлбэл, тэгшитгэл 
ижил үндэстэй. Энгийн "баталгаа" болгон би тогтмолыг хаалтнаас гаргана: 
мөн би үүнийг өвдөлтгүй арилгах болно (Би хоёр хэсгийг "хасах хоёр" гэж хуваана):
ГЭХДЭЭ!Хэрэв бид функцийг авч үзвэл 
, тэгвэл та энд тогтмол байдлаас салж чадахгүй! Зөвхөн үржүүлэгчийг хаалтнаас гаргахыг зөвшөөрнө. 
.
Олон хүмүүс график шийдлийн аргыг дутуу үнэлж, үүнийг "үнэгүй" гэж үздэг бөгөөд зарим нь энэ боломжийг бүрмөсөн мартдаг. График зурах нь заримдаа нөхцөл байдлыг авардаг тул энэ нь үндсэндээ буруу юм!
Өөр нэг жишээ: та хамгийн энгийн тригонометрийн тэгшитгэлийн үндсийг санахгүй байна гэж бодъё: . Ерөнхий томъёо нь сургуулийн сурах бичиг, бага ангийн математикийн бүх лавлах номонд байдаг, гэхдээ тэдгээр нь танд байхгүй. Гэсэн хэдий ч тэгшитгэлийг шийдвэрлэх нь маш чухал ("хоёр"). Гарах гарц байна! - функцүүдийн графикийг бүтээх: 
Үүний дараа бид тэдгээрийн огтлолцлын цэгүүдийн "X" координатыг тайвнаар бичнэ. 
Хязгааргүй олон үндэс байдаг бөгөөд алгебрт тэдгээрийн хураангуй тэмдэглэгээг хүлээн зөвшөөрдөг:
, Хаана ( – бүхэл тоонуудын багц)
.
"Явахгүйгээр" нэг хувьсагчтай тэгш бус байдлыг шийдвэрлэх график аргын талаар хэдэн үг хэлье. Энэ зарчим нь адилхан. Жишээлбэл, тэгш бус байдлын шийдэл нь дурын "x" юм, учир нь Синусоид нь шулуун шугамын доор бараг бүрэн байрладаг. Тэгш бус байдлын шийдэл нь синусоидын хэсгүүд шулуун шугамаас яг дээгүүр байрлах интервалуудын багц юм. (х тэнхлэг):
эсвэл товчхондоо:
Гэхдээ тэгш бус байдлын олон шийдэл энд байна: хоосон, учир нь синусоидын ямар ч цэг шулуун шугамаас дээгүүр оршдоггүй.
Ойлгохгүй байгаа зүйл байна уу? тухай хичээлүүдийг яаралтай судлаарай багцТэгээд функцын графикууд!
Дулааццгаая:
Дасгал 1
Дараах тригонометрийн тэгшитгэлийг графикаар шийд.
Хичээлийн төгсгөлд хариултууд
Таны харж байгаагаар нарийн шинжлэх ухааныг судлахын тулд томьёо, лавлах номыг хавчих шаардлагагүй! Түүнээс гадна энэ нь үндсэндээ алдаатай арга юм.
Хичээлийн эхэнд би таныг тайвшруулж хэлсэнчлэн дээд математикийн стандарт курст тригонометрийн нийлмэл тэгшитгэлийг шийдвэрлэх нь маш ховор байдаг. Бүх нарийн төвөгтэй байдал нь дүрмээр бол тэгшитгэлээр төгсдөг бөгөөд тэдгээрийн шийдэл нь хамгийн энгийн тэгшитгэлээс гаралтай хоёр бүлэг үндэс юм. 
. Сүүлчийн асуудлыг шийдэх гэж бүү санаа зов - номноос хайж эсвэл интернетээс олоорой =)
График шийдлийн арга нь өчүүхэн жижиг тохиолдлуудад тусалж чадна. Жишээлбэл, дараах "ragtag" тэгшитгэлийг авч үзье.
Үүний шийдлийн хэтийн төлөв нь ... огтхон ч харагдахгүй байна, гэхдээ та тэгшитгэлийг хэлбэрээр төсөөлж, бүтээх хэрэгтэй. функцын графикуудтэгээд бүх зүйл гайхалтай энгийн болж хувирах болно. Өгүүллийн дундуур зураг байна хязгааргүй жижиг функцууд (дараагийн таб дээр нээгдэнэ).
Ижил график аргыг ашигласнаар та тэгшитгэл нь аль хэдийн хоёр үндэстэй болохыг олж мэдэх боломжтой бөгөөд тэдгээрийн нэг нь тэгтэй тэнцүү, нөгөө нь, бололтой, үндэслэлгүйсегментэд хамаарах ба . Энэ үндсийг ойролцоогоор тооцоолж болно, жишээлбэл, шүргэгч арга. Дашрамд хэлэхэд, зарим асуудалд үндсийг нь олох шаардлагагүй, харин олж мэдээрэй тэд ерөөсөө байдаг уу?. Энд ч гэсэн зураг нь тусалж чадна - хэрвээ графикууд огтлолцохгүй бол үндэс байхгүй болно.
Бүхэл тооны коэффициент бүхий олон гишүүнтийн рационал үндэс.
Хорнерын схем
Одоо би та бүхнийг Дундад зууны үе рүү харцаа хандуулж, сонгодог алгебрийн өвөрмөц уур амьсгалыг мэдрэхийг урьж байна. Материалыг илүү сайн ойлгохын тулд бага ч гэсэн уншихыг зөвлөж байна нийлмэл тоо.
Тэд бол хамгийн шилдэг нь. Олон гишүүнт.
Бидний сонирхож буй объект нь хэлбэрийн хамгийн түгээмэл олон гишүүнтүүд байх болно бүхэлд нькоэффициентүүд Натурал тоо гэж нэрлэдэг олон гишүүнтийн зэрэг, тоо – хамгийн дээд зэргийн коэффициент (эсвэл хамгийн өндөр коэффициент), мөн коэффициент нь байна чөлөөт гишүүн.
Би энэ олон гишүүнтийг товчоор тэмдэглэнэ.
Олон гишүүнтийн үндэстэгшитгэлийн язгуурыг дууд
Би төмөр логикт дуртай =)
Жишээлбэл, нийтлэлийн эхэнд очно уу: 
1 ба 2-р зэрэглэлийн олон гишүүнтүүдийн үндсийг олоход ямар ч асуудал байхгүй, гэхдээ та үүнийг нэмэгдүүлэх тусам энэ даалгавар улам бүр хэцүү болно. Хэдийгээр нөгөө талаас бүх зүйл илүү сонирхолтой юм! Хичээлийн хоёр дахь хэсгийг яг ийм зүйлд зориулах болно.
Нэгдүгээрт, онолын дэлгэцийн хагас нь:
1) Үр дүнгийн дагуу алгебрийн үндсэн теорем, зэрэгтэй олон гишүүнт яг байна цогцолборүндэс. Зарим үндэс (эсвэл бүр бүгд) нь ялангуяа байж болно хүчинтэй. Түүнээс гадна жинхэнэ үндэс дунд ижил (олон) үндэс байж болно (хамгийн багадаа хоёр, дээд тал нь).
Хэрэв олон гишүүнт ямар нэг нийлмэл тоо нь үндэс бол коньюгаттүүний тоо нь мөн энэ олон гишүүнтийн үндэс байх ёстой (коньюгат нийлмэл үндэс нь хэлбэртэй байна).
Хамгийн энгийн жишээ бол 8-д анх тааралдсан квадрат тэгшитгэл юм (дуртай)анги, бид эцэст нь уг сэдвийг "дуусгасан" нийлмэл тоо. Би танд сануулъя: квадрат тэгшитгэл нь хоёр өөр бодит язгууртай, олон үндэстэй, эсвэл нийлмэл нийлмэл язгууртай.
2) -аас Безутын теоремХэрэв тоо нь тэгшитгэлийн язгуур бол харгалзах олон гишүүнтийг хүчин зүйлээр ангилж болно.
, энд зэрэгтэй олон гишүүнт байна .
Дахин хэлэхэд бидний хуучин жишээ: оноос хойш тэгшитгэлийн язгуур, тэгвэл . Үүний дараа алдартай "сургуулийн" өргөтгөлийг олж авах нь тийм ч хэцүү биш юм.
Безутын теоремын үр дагавар нь маш их практик ач холбогдолтой: хэрэв бид 3-р зэргийн тэгшитгэлийн язгуурыг мэддэг бол бид үүнийг хэлбэрээр илэрхийлж болно. 
ба квадрат тэгшитгэлээс үлдсэн үндсийг олоход хялбар байдаг. Хэрэв бид 4-р зэргийн тэгшитгэлийн язгуурыг мэддэг бол зүүн талыг бүтээгдэхүүн болгон өргөжүүлэх боломжтой.
Мөн энд хоёр асуулт байна:
Асуулт нэг. Энэ үндсийг хэрхэн олох вэ? Юуны өмнө түүний мөн чанарыг тодорхойлъё: дээд математикийн олон асуудалд үүнийг олох шаардлагатай байна оновчтой, Тухайлбал бүхэлд ньолон гишүүнтийн үндэс, үүнтэй холбогдуулан цаашид бид тэдгээрийг голчлон сонирхох болно.... ... тэд маш сайн, сэвсгэр тул та зүгээр л тэднийг олохыг хүсч байна! =)
Сонгох арга нь хамгийн түрүүнд санаанд орж ирдэг. Жишээлбэл, тэгшитгэлийг авч үзье. Энд байгаа зүйл бол чөлөөт нэр томъёо юм - хэрэв энэ нь тэгтэй тэнцүү байсан бол бүх зүйл сайхан болно - бид "x" тэмдгийг хаалтнаас гаргаж, үндэс нь өөрөө гадаргуу дээр "унадаг": 
Гэхдээ бидний чөлөөт нэр томъёо нь "гурван" -тай тэнцүү тул бид "язгуур" гэж үздэг тэгшитгэлд янз бүрийн тоог орлуулж эхэлдэг. Юуны өмнө, нэг утгыг орлуулах нь өөрийгөө санал болгож байна. Орлуулж үзье: 
Хүлээн авсан буруутэгш байдал, ингэснээр нэгж "тохирохгүй". За, орлуулъя: 
Хүлээн авсан үнэнтэгш байдал! Өөрөөр хэлбэл, утга нь энэ тэгшитгэлийн үндэс юм.
3-р зэргийн олон гишүүнтийн үндсийг олохын тулд аналитик арга байдаг (Кардано томъёо гэж нэрлэгддэг), гэхдээ одоо бид арай өөр даалгавар сонирхож байна.
- нь манай олон гишүүнтийн язгуур учир олон гишүүнт хэлбэрт дүрслэгдэж, үүсдэг Хоёр дахь асуулт: "дүү" яаж олох вэ?
Хамгийн энгийн алгебрийн санаанууд үүнийг хийхийн тулд бид -д хуваах хэрэгтэйг харуулж байна. Олон гишүүнтийг олон гишүүнт хэрхэн хуваах вэ? Энгийн тоог хуваах сургуулийн ижил арга - "багана"! Хичээлийн эхний жишээн дээр би энэ аргыг нарийвчлан авч үзсэн. Цогцолборын хязгаар, одоо бид өөр аргыг авч үзэх болно, үүнийг гэж нэрлэдэг Хорнерын схем.
Эхлээд бид "хамгийн өндөр" олон гишүүнт бичнэ хүн бүртэй
, үүнд тэг коэффициентүүд орно:
, үүний дараа бид эдгээр коэффициентүүдийг (хатуу дарааллаар) хүснэгтийн дээд эгнээнд оруулна.
Бид зүүн талд үндсийг бичнэ:
Хэрэв "улаан" тоо байвал Хорнерын схем ч бас ажилладаг гэдгийг би даруй анхааруулах болно Үгүйолон гишүүнтийн үндэс юм. Гэсэн хэдий ч яарах хэрэггүй.
Дээрхээс бид тэргүүлэх коэффициентийг хасдаг.
Доод нүдийг дүүргэх үйл явц нь хатгамалыг зарим талаар санагдуулдаг бөгөөд "хасах нэг" нь дараагийн алхмуудыг нэвт шингээдэг нэг төрлийн "зүү" юм. Бид "зөөгдсөн" тоог (–1)-ээр үржүүлж, дээд нүднээс гарсан тоог бүтээгдэхүүнд нэмнэ.
Бид олсон утгыг "улаан зүү" -ээр үржүүлж, бүтээгдэхүүнд дараахь тэгшитгэлийн коэффициентийг нэмнэ.
Эцэст нь, үүссэн утгыг "зүү" ба дээд коэффициентээр дахин "боловсруулна".
Сүүлчийн нүдэн дэх тэг нь олон гишүүнт хуваагдаж байгааг хэлдэг ул мөргүй (байх ёстой шиг), тэлэлтийн коэффициентүүд хүснэгтийн доод мөрөөс шууд "арилгасан" бол:
Тиймээс бид тэгшитгэлээс ижил тэгшитгэл рүү шилжсэн бөгөөд үлдсэн хоёр үндэстэй бүх зүйл тодорхой болсон. (энэ тохиолдолд бид нэгдмэл цогц үндэсийг авдаг).
Дашрамд хэлэхэд тэгшитгэлийг графикаар шийдэж болно: график "аянга" 
График нь х тэнхлэгийг огтолж байгааг харна уу ()
цэг дээр. Эсвэл ижил "зальтай" заль мэх - бид тэгшитгэлийг хэлбэрээр дахин бичиж, энгийн график зурж, тэдгээрийн огтлолцлын цэгийн "X" координатыг илрүүлдэг.
Дашрамд хэлэхэд, 3-р зэргийн олон гишүүнт функцийн график нь тэнхлэгийг дор хаяж нэг удаа огтолж байгаа бөгөөд энэ нь харгалзах тэгшитгэлтэй байна гэсэн үг юм. ядажнэг хүчинтэйүндэс. Энэ баримт нь сондгой зэрэгтэй олон гишүүнт функцийн хувьд үнэн юм.
Энд би бас энд анхаарлаа хандуулахыг хүсч байна чухал цэгнэр томьёотой холбоотой: олон гишүүнтТэгээд олон гишүүнт функц – энэ нь ижил зүйл биш юм! Гэхдээ практик дээр тэд ихэвчлэн "олон гишүүнтийн график" гэж ярьдаг бөгөөд энэ нь мэдээжийн хэрэг хайхрамжгүй байдал юм.
Гэсэн хэдий ч Хорнерын схем рүү буцъя. Би саяхан дурьдсанчлан, энэ схем нь бусад тоонуудад ажилладаг, гэхдээ хэрэв тоо ҮгүйЭнэ нь тэгшитгэлийн үндэс бол бидний томъёонд тэг биш нэмэлт (үлдэгдэл) гарч ирнэ.
Хорнерын схемийн дагуу "амжилтгүй" утгыг "ажиллуулъя". Энэ тохиолдолд ижил хүснэгтийг ашиглах нь тохиромжтой - зүүн талд шинэ "зүү" бичиж, тэргүүлэх коэффициентийг дээрээс нь хөдөлгө. (зүүн ногоон сум), тэгээд бид явлаа: 
Үүнийг шалгахын тулд хаалтуудыг нээж, ижил төстэй нэр томъёог танилцуулъя:
, БОЛЖ БАЙНА УУ.
Үлдэгдэл ("зургаан") нь олон гишүүнтийн яг ижил утгатай болохыг харахад хялбар байдаг. Үнэн хэрэгтээ энэ нь юу вэ: 
, бүр илүү сайхан - иймэрхүү:
Дээрх тооцооллуудаас харахад Хорнерын схем нь олон гишүүнтийг хүчин зүйлээр тооцох төдийгүй үндсийг "соёл иргэншсэн" сонгох боломжийг олгодог гэдгийг ойлгоход хялбар юм. Тооцооллын алгоритмыг жижиг даалгавраар нэгтгэхийг би танд санал болгож байна.
Даалгавар 2
Хорнерын схемийг ашиглан тэгшитгэлийн бүхэл язгуурыг олж, харгалзах олон гишүүнтийг үржүүл.
Өөрөөр хэлбэл, энд та 1, –1, 2, –2, ... – гэсэн тоог сүүлийн баганад тэг үлдэгдэл “зурах” хүртэл дараалан шалгах хэрэгтэй. Энэ нь энэ шугамын "зүү" нь олон гишүүнтийн үндэс болно гэсэн үг юм
Тооцооллыг нэг хүснэгтэд хийх нь тохиромжтой. Хичээлийн төгсгөлд дэлгэрэнгүй шийдэл, хариулт.
Үндэс сонгох арга нь харьцангуй энгийн тохиолдлуудад тохиромжтой боловч хэрэв олон гишүүнтийн коэффициент ба/эсвэл зэрэг нь их байвал процесс удаан үргэлжилж болно. Эсвэл ижил жагсаалтаас 1, –1, 2, –2 гэсэн утгууд байгаа бөгөөд авч үзэх нь утгагүй юм болов уу? Үүнээс гадна үндэс нь бутархай болж хувирах бөгөөд энэ нь шинжлэх ухааны үндэслэлгүй нудрахад хүргэдэг.
Аз болоход, оновчтой язгуурын "нэр дэвшигч" утгыг хайхыг эрс багасгах хоёр хүчирхэг теорем байдаг.
Теорем 1Ингээд авч үзье бууруулж боломгүйбутархай , хаана . Хэрэв тоо нь тэгшитгэлийн үндэс бол чөлөөт гишүүнийг хувааж, тэргүүлэх коэффициентийг хуваана.
Тухайлбал, хэрэв тэргүүлэх коэффициент нь бол энэ оновчтой үндэс нь бүхэл тоо болно:
Мөн бид теоремыг зөвхөн энэ амттай нарийн ширийн зүйлээр ашиглаж эхэлдэг.
Тэгшитгэл рүү буцъя. Түүний тэргүүлэх коэффициент нь , тэгвэл таамагласан рационал язгуур нь зөвхөн бүхэл тоо байж болох бөгөөд чөлөөт нэр томъёог эдгээр үндэст үлдэгдэлгүйгээр хуваах ёстой. Мөн "гурав" -ыг зөвхөн 1, -1, 3, -3 гэж хувааж болно. Өөрөөр хэлбэл, манайд ердөө 4 “үндсэн нэр дэвшигч” байна. Тэгээд дагуу Теорем 1, бусад рационал тоо нь ЗАРЧИМ ДЭЭР энэ тэгшитгэлийн үндэс байж болохгүй.
Тэгшитгэлд арай илүү "өрсөлдөгчид" байна: чөлөөт нэр томъёо нь 1, –1, 2, – 2, 4, –4-т хуваагдана.
1, –1 тоонууд нь боломжит язгууруудын жагсаалтын "ердийн" тоо гэдгийг анхаарна уу (теоремын тодорхой үр дагавар)мөн тэргүүлэх сорилтын хамгийн сайн сонголт.
Илүү утга учиртай жишээнүүд рүү шилжье:
Асуудал 3
Шийдэл: тэргүүлэх коэффициент нь , учир нь таамагласан рационал язгуур нь зөвхөн бүхэл тоо байж болох бөгөөд тэдгээр нь заавал чөлөөт гишүүний хуваагч байх ёстой. "Хасах дөч" нь дараах хос тоонд хуваагдана.
– нийт 16 “нэр дэвшигч”.
Энд тэр даруй сэтгэл татам бодол гарч ирнэ: бүх сөрөг эсвэл эерэг үндсийг арилгах боломжтой юу? Зарим тохиолдолд боломжтой! Би хоёр тэмдгийг томъёолох болно:
1) Хэрэв БүгдХэрэв олон гишүүнтийн коэффициентүүд нь сөрөг биш эсвэл бүгд эерэг биш бол эерэг үндэстэй байж болохгүй. Харамсалтай нь энэ нь бидний тохиолдол биш юм (Одоо, хэрэв бидэнд тэгшитгэл өгсөн бол - тийм ээ, олон гишүүнтийн аль нэг утгыг орлуулах үед олон гишүүнтийн утга нь хатуу эерэг байдаг бөгөөд энэ нь бүх эерэг тоонууд гэсэн үг юм. (мөн үндэслэлгүй)тэгшитгэлийн үндэс байж болохгүй.
2) Хэрэв сондгой зэрэглэлийн коэффициентүүд сөрөг биш, бүх тэгш байдлын хувьд (үнэгүй гишүүн орно)сөрөг байвал олон гишүүнт сөрөг үндэстэй байж болохгүй. Эсвэл "толин тусгал": сондгой зэрэглэлийн коэффициентүүд эерэг биш, бүх тэгш чадлын хувьд эерэг байна.
Энэ бол бидний хэрэг! Жаахан ойроос харвал тэгшитгэлд дурын сөрөг "X"-ийг орлуулахад зүүн тал нь хатуу сөрөг байх бөгөөд энэ нь сөрөг үндэс алга болно гэсэн үг юм.
Ингээд судалгаа явуулахад 8 тоо үлдлээ.
Бид тэднийг Хорнерын схемийн дагуу "цэнэглэдэг". Та сэтгэцийн тооцооллыг аль хэдийн эзэмшсэн гэж найдаж байна: 
"Хоёр" -ыг туршиж үзэхэд биднийг аз хүлээж байв. Тиймээс авч үзэж буй тэгшитгэлийн үндэс, ба
Тэгшитгэлийг судлах л үлдлээ 
. Үүнийг ялгаварлан гадуурхах замаар хийхэд хялбар байдаг, гэхдээ би ижил схемийг ашиглан заагч тест хийх болно. Нэгдүгээрт, чөлөөт нэр томъёо нь 20-той тэнцэх бөгөөд энэ нь гэсэн үг юм Теорем 1 8 ба 40 тоо нь боломжит язгууруудын жагсаалтаас хасагдаж, судалгааны утгыг үлдээдэг (Нэг нь Хорнерын схемийн дагуу хасагдсан).
Бид шинэ хүснэгтийн дээд эгнээнд гурвалсан тооны коэффициентийг бичнэ Бид ижил "хоёр" -оор шалгаж эхэлдэг.. Яагаад? Үндэс нь үржвэр байж болох тул: - энэ тэгшитгэл нь 10 ижил үндэстэй. Гэхдээ анхаарал сарниулахгүй байцгаая: 
Энд мэдээжийн хэрэг үндэс нь оновчтой гэдгийг мэдсээр байж жаахан худлаа хэлсэн. Эцсийн эцэст, хэрэв тэдгээр нь үндэслэлгүй эсвэл төвөгтэй байсан бол би үлдсэн бүх тоог амжилтгүй шалгахтай тулгарах болно. Тиймээс практик дээр ялгаварлагчаар удирдуулах хэрэгтэй.
Хариулт: оновчтой үндэс: 2, 4, 5
Бидний дүн шинжилгээ хийсэн асуудалд бид азтай байсан, учир нь: а) сөрөг утгууд нэн даруй унасан, б) бид үндсийг нь маш хурдан олсон (мөн онолын хувьд бид бүх жагсаалтыг шалгаж болно).
Гэвч бодит байдал дээр нөхцөл байдал хамаагүй муу байна. Би таныг "Сүүлчийн баатар" нэртэй сонирхолтой тоглоом үзэхийг урьж байна.
Асуудал 4
Тэгшитгэлийн рационал язгуурыг ол
Шийдэл: By Теорем 1таамагласан рационал язгууруудын тоологч нь нөхцөлийг хангасан байх ёстой (бид "арван хоёрыг элээр хуваадаг" гэж уншдаг), мөн хуваагч нь нөхцөлтэй тохирч байна. Үүний үндсэн дээр бид хоёр жагсаалтыг авна.
"list el":
болон "жагсаалт": (Аз болоход энд байгаа тоонууд нь байгалийн юм).
Одоо бүх боломжит язгууруудын жагсаалтыг гаргая. Эхлээд бид "el list" -ийг хуваана. Яг ийм тоо гарах нь туйлын тодорхой. Тохиромжтой болгохын тулд тэдгээрийг хүснэгтэд оруулъя:
Олон тооны фракцууд буурч, үр дүнд нь "баатрын жагсаалт" -д аль хэдийн орсон утгууд бий болсон. Бид зөвхөн "шинэхэн"-ийг нэмнэ: 
Үүний нэгэн адил бид ижил "жагсаалтыг" дараахь байдлаар хуваана. 
тэгээд эцэст нь
Ийнхүү манай тоглоомд оролцогчдын баг бүрдэв. 
Харамсалтай нь, энэ асуудлын олон гишүүнт нь "эерэг" эсвэл "сөрөг" шалгуурыг хангахгүй байгаа тул бид дээд эсвэл доод эгнээнээс татгалзаж чадахгүй. Та бүх тоонуудтай ажиллах хэрэгтэй болно.
Таны сэтгэл ямар байна вэ? Алив, толгойгоо өргө - "алуурчин теорем" гэж нэрлэж болох өөр нэг теорем бий. ..."нэр дэвшигчид", мэдээжийн хэрэг =)
Гэхдээ эхлээд та Хорнерын диаграммыг дор хаяж нэгийг нь гүйлгэх хэрэгтэй бүхэлтоо. Уламжлал ёсоор бол нэгийг нь авч үзье. Дээд мөрөнд бид олон гишүүнтийн коэффициентүүдийг бичдэг бөгөөд бүх зүйл ердийнх шиг байна.
Дөрөв нь тэг биш нь тодорхой тул утга нь тухайн олон гишүүнтийн үндэс биш юм. Гэхдээ тэр бидэнд маш их туслах болно.
Теорем 2Зарим хүмүүсийн хувьд бол ерөнхийдөөолон гишүүнтийн утга тэгээс ялгаатай: , дараа нь түүний рационал үндэс (хэрэв тэд байгаа бол)нөхцөлийг хангана
Манай тохиолдолд, тиймээс бүх боломжит үндэс нь нөхцөлийг хангах ёстой (Нөхцөл No1 гэж нэрлэе). Энэ дөрөв олон “нэр дэвшигч”-ийн “алуурчин” болно. Үзүүлэн болгон би хэд хэдэн шалгалтыг авч үзэх болно:
"Нэр дэвшигч"-ийг шалгая. Үүнийг хийхийн тулд үүнийг бутархай хэлбэрээр зохиомлоор илэрхийлье, үүнээс тодорхой харагдаж байна. Туршилтын зөрүүг тооцоолъё: . Дөрөвийг "хасах хоёр" гэж хуваана: , энэ нь боломжит үндэс нь шалгалтыг давсан гэсэн үг юм.
Утгыг шалгацгаая. Тестийн ялгаа энд байна: 
. Мэдээжийн хэрэг, хоёр дахь "субъект" нь жагсаалтад хэвээр байна.
Тоонуудыг хүчийг нэмэгдүүлэх дараах дарааллаар багц болгон хувааж болно.
1. Багц - анхны тоонуудын багц (өөрөөсөө өөр анхны хуваагчгүй).
2. Set - натурал тоонуудын багц.
3. Set - бүхэл тоонуудын багц (эдгээр нь натурал тоо, тэг, сөрөг бүхэл тоонууд).
4. Багц - рационал тоонуудын багц (эдгээр нь бүхэл тоо буюу бутархай хэлбэрээр илэрхийлэгдэх тоо, хүртэгч ба хуваагч нь бүхэл тоо юм. Рациональ тоон аравтын бутархайн тэмдэглэгээ нь төгсгөлтэй эсвэл бутархай хэлбэрээр илэрхийлэгдэх тоонууд бөгөөд үүнд байна. заавал үе үе давтах).
5. Багц - бодит тоонуудын талбарт радикал хэлбэрээр дүрслэгдэх бодит тоонуудын дэд олонлог. Үүнд бүх рациональ (Q), түүнчлэн зарим иррациональ, жишээ нь. 
. Илүү нарийвчлалтай хэлэхэд, энэ олонлогт хүчин чадал нь рационал тоо байх ба нэг зэрэглэлд хүрсэн аливаа тоо нь оновчтой эерэг тоо байх болно гэсэн тэмдэглэгээ хэлбэрээр дүрслэгдэх тоонууд байдаг.
6. Олонлог - цогц тоонуудын талбарт радикал хэлбэрээр дүрслэгдэх бодит тоонуудын дэд олонлог. Үүнд бүх оновчтой (Q), түүнчлэн зарим үндэслэлгүй, жишээлбэл эцэст нь хүчинтэй болох нь орно. Нарийвчлан хэлэхэд, энэ багцад хүчин чадал нь рационал тоо, зэрэглэлд нэмэгдэж байгаа тоо нь рационал бөгөөд сөрөг байж болох тоонууд байдаг. .
6-р олонлог ба 5-ын ялгаа. Жишээлбэл, тэгшитгэлийн үндэс,
, тэнцүү байна.
Үүний зэрэгцээ куб тэгшитгэлийг мэддэг радикалуудад уусдаг. Энэ нь эдгээр ижил язгууруудыг тоо, математикийн үйлдлүүд, эрх мэдэл бүхий тэмдэглэгээ хэлбэрээр илэрхийлж болно гэсэн үг юм.
Асуулт. Энэ оруулгын хэсгүүд нь нарийн төвөгтэй тоо байх болно гэж би таамаглаж байна, өөрөөр хэлбэл. чи түүнгүйгээр хийж чадахгүй. Сөрөг тоонуудаас үндэс гарах нь гарцаагүй. Таамаглал зөв үү?
Хэрэв таамаглал зөв бол куб тэгшитгэлийн жинхэнэ язгуур нь олонлогт хамаарах боловч олонлогт хамаарахгүй байж болно. Гэхдээ квадрат тэгшитгэлийн үндэс нь үргэлж бага чадлын олонлогт хамаардаг.
Асуулт. Рационал тоогоор илэрхийлсэн аргументийн синус (градус) нь олонлогт (эсвэл тэгш) хамаарах уу, i.e. үүнийг үргэлж радикалаар илэрхийлж болох уу?
Гэхдээ илүү хүчирхэг тоонуудын багц руу шилжье. 5-р зэргийн тэгшитгэлийн жинхэнэ үндсийг үргэлж радикалаар илэрхийлэх боломжгүй, өөрөөр хэлбэл. Тэд бүр багтахгүй байж магадгүй, гэхдээ тэдгээрийг багтаасан багц байдаг -
7. Багц - алгебрийн тооны багц, (бодит тооны дэд олонлог). Энэ олонлогт бүх боломжит алгебрийн тэгшитгэлийн аль ч зэрэгтэй, ямар ч оновчтой коэффициент бүхий бодит язгуурууд багтсан болно.
Математикт тооцогдохоос илүү хүчирхэг багц юу вэ (хамгийн өргөн багцуудыг тооцохгүй - бодит ба нарийн төвөгтэй)? Би илүү хүчирхэг хүмүүстэй таарч байгаагүй; ихэвчлэн хэрэв тоо нь ороогүй бол үүнийг трансцендентал гэж нэрлэдэг. Би бас нэг багцыг танилцуулъя -
8. Багц - ямар ч мэдэгдэж буй функцтэй (синус, зета функц, интеграл логарифм гэх мэт) ямар ч математик тэгшитгэлийн үндэс (заавал алгебрийн биш) байж болох тооны багцыг хэлбэрээр танилцуулж болно. цуврал эсвэл хэд хэдэн эгнээ. Ийм дугааруудыг АНАЛИТИК гэж нэрлэе. Энгийнээр хэлбэл, та эцсийн хэмжээсийн тайлбарыг зааж өгч болно, ингэснээр та энэ тайлбараас өгөгдсөн тооны аравтын бутархайн араас ямар ч цифрийг олох боломжтой - ad infinitum.
Өнөөг хүртэл авч үзсэн бүх багцууд нь дараах дэд олонлогууд байсан, i.e. дэд хэсэг гэх мэт. - дэд хэсэг. Дараагийн багц нь тусдаа (үүнд ороогүй), гэхдээ хамгийн хүчирхэг.
9. Set - эмх замбараагүй тоонуудын багц. (эмх замбараагүй байдал бол миний тодорхойлолт). Энэ нь -д ороогүй бүх бодит тоонуудын багц юм. Хэрэв тоо багтсан бол энэ тоог хязгаарлагдмал хэмжээтэй (цуваа, функц гэх мэт) ямар ч математик тайлбараар илэрхийлэх боломжгүй. Хэрэв бид хязгаарлагдмал хэмжигдэхүүнүүдийн тайлбарыг өгвөл өгөгдсөн тооны аравтын бутархайн араас хойшхи цифрийг олохын тулд энэ тайлбарыг ашиглах боломжгүй болно - ad infinitum.
10. Set - БҮХ бодит тоонуудын багц. Энэ нь салангид олонлогуудын нэгдэл ба . Түүнчлэн, олонлог доторх олонлог нь тэг хэмжигдэхүүнтэй байдаг. Тэдгээр. бодит тоонуудын олонлогт тоонуудын ихэнх нь эмх замбараагүй, цөөнх нь аналитик байдаг.
11. Set - бүх цогцолбор тоонуудын олонлог. Үүнийг ижил төстэй дэд бүлэгт (алгебрийн цогцолбор, аналитик, эмх замбараагүй гэх мэт) хуваах боломжтой байсан ч энэ нь шаардлагагүй гэж би бодож байна.
Миний ангилал зөв үү? Математикчдад трансцендент тоонуудын дэд олонлогууд байдаг ч алгебрийн тоо биш өөр ямар олонлогууд байдаг вэ?
