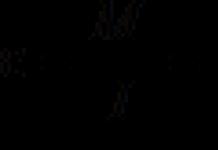Тодорхой интеграл нь интеграл нийлбэрийн хязгаар юм

нөхцөл хангагдсан тохиолдолд л оршин тогтнох боломжтой (өөрөөр хэлбэл тодорхой эцсийн утгатай).

Хэрэв эдгээр нөхцлүүдийн дор хаяж нэг нь зөрчигдсөн бол тодорхойлолт нь утгаа алддаг. Үнэн хэрэгтээ, хязгааргүй сегментийн хувьд, жишээлбэл [ а; ) гэж хувааж болохгүй Пхязгаарлагдмал урттай хэсгүүд
, үүнээс гадна сегментийн тоо нэмэгдэх тусам тэг болох хандлагатай байна. Хэзээ нэгэн цагт хязгааргүй тохиолдолд -тай[а; б] дур зоргоороо оноо сонгох шаардлагыг зөрчсөн хэсэгчилсэн сегмент дээр - сонгох боломжгүй =-тай, учир нь энэ цэг дэх функцийн утга тодорхойгүй байна. Гэсэн хэдий ч эдгээр тохиолдлуудад ч гэсэн хязгаарт өөр нэг хэсгийг оруулах замаар тодорхой интегралын тухай ойлголтыг нэгтгэх боломжтой. Хязгааргүй интервал ба тасалдалгүй (хязгааргүй) функцийг интеграл гэж нэрлэдэг чинийх биш.

Тодорхойлолт.

Функцийг зөвшөөр
интервал дээр тодорхойлогддог [ а; ) ба дурын төгсгөлтэй интервалд интегралдах боломжтой [ а; б], i.e. байдаг
хэний ч төлөө б > а. Төрөл хязгаар
дуудсан буруу интеграл анхны төрөл (эсвэл төгсгөлгүй интервал дээрх буруу интеграл) ба тэмдэглэнэ
.

Тиймээс, тодорхойлолтоор,
=
.

Хэрэв баруун талын хязгаар байгаа бөгөөд төгсгөлтэй бол буруу интеграл
дуудсан нэгдэх . Хэрэв энэ хязгаар хязгааргүй эсвэл огт байхгүй бол буруу интеграл гэж хэлдэг ялгаатай .

Үүний нэгэн адил бид функцийн буруу интеграл гэсэн ойлголтыг танилцуулж болно
интервалын дагуу (–; б]:

=
.

Мөн функцийн буруу интеграл
(–; +) интервалыг дээр дурдсан интегралуудын нийлбэрээр тодорхойлно.

=
+
,

Хаана А- дурын цэг. Энэ интеграл нь хоёр гишүүн нийлэх юм бол нийлдэг, ядаж нэг гишүүн нь зөрөөд байвал салдаг.

Геометрийн үүднээс авч үзвэл интеграл
,
, функцийн график дээр хязгаарлагдсан хязгааргүй муруйн трапецын талбайн тоон утгыг тодорхойлно.
, зүүн - шулуун
, доороос – OX тэнхлэгээр. Интегралын нэгдэл гэдэг нь ийм трапецын хязгаарлагдмал талбай байгаа бөгөөд хөдөлгөөнт баруун ханатай муруйн трапецын талбайн хязгаартай тэнцүү байна гэсэн үг юм.
.

Хязгааргүй хязгаартай интегралын хувьд бид ерөнхийд нь дүгнэж болно Ньютон-Лейбницийн томъёо:

=
= F( + ) – F( а),

хаана F( + ) =
. Хэрэв энэ хязгаар байгаа бол интеграл нийлнэ, эс бөгөөс сална.

Хязгааргүй интервалтай тохиолдолд тодорхой интеграл гэсэн ойлголтыг ерөнхийд нь авч үзсэн.

Одоо хязгааргүй функцийн тухай ерөнхий дүгнэлтийг авч үзье.

Тодорхойлолт

Функцийг зөвшөөр
интервал дээр тодорхойлогддог [ а; б), цэгийн зарим хөршид хязгааргүй байдаг б, ямар ч интервал дээр тасралтгүй байна
, энд >0 (тиймээс энэ интервал дээр интегралдах боломжтой, i.e.
байдаг). Төрөл хязгаар
дуудсан хоёр дахь төрлийн буруу интеграл (эсвэл хязгааргүй функцийн буруу интеграл) ба тэмдэглэсэн байна
.

Тиймээс цэг дээрх хязгааргүй буруу интеграл бфункцууд нь тодорхойлолтоор байдаг

=
.

Хэрэв баруун талын хязгаар байгаа бөгөөд хязгаарлагдмал бол интеграл гэж нэрлэдэг нэгдэх. Хэрэв төгсгөлийн хязгаар байхгүй бол буруу интеграл гэж нэрлэдэг ялгаатай.

Үүний нэгэн адил бид функцийн буруу интегралыг тодорхойлж болно
цэг дээр хязгааргүй тасалдалтай байх А:

=
.

Хэрэв функц
дотоод цэг дээр хязгааргүй завсар байна -тай
, тэгвэл зохисгүй интегралыг дараах байдлаар тодорхойлно

=
+
=
+
.

Энэ интеграл нь хоёр гишүүн нийлэх юм бол нийлж, ядаж нэг гишүүн зөрөөд байвал сална.

Геометрийн үүднээс авч үзвэл хязгааргүй функцийн буруу интеграл нь мөн хязгааргүй муруй трапецын талбайг тодорхойлдог.

Зохисгүй интеграл нь тодорхой интегралаас хязгаарт шилжих замаар үүсдэг тул тодорхой интегралын бүх шинж чанарыг эхний болон хоёрдугаар төрлийн буруу интегралд шилжүүлж болно (зохистой сайжруулалттай).

Зохисгүй интеграл үүсэхэд хүргэдэг олон асуудалд энэ интеграл нь юутай тэнцүү болохыг мэдэх шаардлагагүй бөгөөд зөвхөн түүний нийлмэл байдал, зөрүүг шалгахад л хангалттай. Үүний тулд тэд ашигладаг нэгдэх шинж тэмдэг. Буруу интегралуудын нийлэх шинж тэмдэг:

1) Харьцуулах тэмдэг.

Энэ нь хүн бүрт байх болтугай X

. Дараа нь бол
нийлж, дараа нь нийлдэг
, ба

. Хэрэв
diverges, дараа нь ялгарах ба
.

2) Хэрэв нийлж байвал
, дараа нь нийлдэг ба
(энэ тохиолдолд сүүлчийн интеграл гэж нэрлэдэг туйлын нэгдмэл).

Хязгааргүй функцүүдийн зохисгүй интегралуудын нэгдэх ба салгах шинж тэмдгүүд нь дээр дурдсантай төстэй юм.

Асуудлыг шийдвэрлэх жишээ.

Жишээ 1.

A)
; б)
; V)

G)
; г)
.

Шийдэл.

a) Тодорхойлолтоор бид:

.

б) Үүнтэй адил

Тиймээс энэ интеграл нийлж, тэнцүү байна .

в) Тодорхойлолтоор
=
+
, ба А- дурын тоо. Өөрийнхөө хэргийг оруулъя
, дараа нь бид дараахь зүйлийг авна.

Энэ интеграл нийлдэг.

Энэ нь интеграл нь ялгаатай гэсэн үг юм.

e) авч үзье
. Интегралын эсрэг деривативыг олохын тулд хэсгүүдээр интеграцийн аргыг хэрэглэх шаардлагатай. Дараа нь бид:

Аль нь ч биш
, аль нь ч биш
байхгүй, тэгвэл байхгүй ба

Тиймээс энэ интеграл нь ялгаатай байна.

Жишээ 2.

Интегралын нийлэлтийг судал -аас хамаарна П.

Шийдэл.

At
бидэнд байгаа:

Хэрэв
, Тэр
Мөн . Тиймээс интеграл нь ялгаатай байна.

Хэрэв
, Тэр
, А
, Дараа нь

= ,

Тиймээс интеграл нийлдэг.

Хэрэв
, Тэр

тиймээс интеграл нь ялгаатай байна.

Тиймээс,

Жишээ 3.

Зохисгүй интегралыг тооцоолох эсвэл түүний зөрүүг тогтоох:

A)
; б)
; V)
.

Шийдэл.

a) Интеграл
нь интегралаас хойш хоёр дахь төрлийн зохисгүй интеграл юм
нэг цэгт хязгаарлагдахгүй

. Дараа нь тодорхойлолтоор,

.

Интеграл нь нийлдэг ба тэнцүү байна .

б) авч үзэх
. Энд мөн интеграл нь цэг дээр хязгаарлагдахгүй
. Тиймээс, энэ интеграл нь хоёр дахь төрлийн зохисгүй бөгөөд тодорхойлолтоор:

Тиймээс интеграл нь ялгаатай байна.

в) авч үзэх
. Интеграл
хоёр цэг дээр хязгааргүй цоорхойд өртдөг:
Тэгээд
, эхнийх нь интеграцийн интервалд хамаарна
. Иймээс энэ интеграл нь хоёр дахь төрлийн зохисгүй интеграл юм. Дараа нь, тодорхойлолтоор

=

=

.

Тиймээс интеграл нь нийлж, тэнцүү байна
.

Эхний төрлийн буруу интегралууд.Үндсэндээ энэ нь ижил тодорхой интеграл боловч интегралууд нь интегралын дээд доод хязгаар хязгааргүй, эсвэл интегралын аль аль нь хязгааргүй байдаг тохиолдолд.

Хоёр дахь төрлийн буруу интегралууд.Үндсэндээ энэ нь ижил тодорхой интеграл боловч интегралыг хязгааргүй функцээс авсан тохиолдолд хязгааргүй тооны цэг дээрх интеграл нь төгсгөлгүй интегралын сегментгүй, төгсгөлгүй болж хувирдаг.

Харьцуулбал.Тодорхой интеграл гэсэн ойлголтыг оруулахдаа функц гэж үзсэн е(x) [ интервал дээр тасралтгүй байна а, б] ба интеграцийн сегмент нь хязгаарлагдмал, өөрөөр хэлбэл хязгааргүй тоогоор хязгаарлагддаг. Зарим ажил нь эдгээр хязгаарлалтыг орхих шаардлагатай болдог. Зохисгүй интегралууд ингэж гарч ирдэг.

Буруу интегралын геометрийн утгаЭнэ нь маш энгийн харагдаж байна. Функцийн график байх тохиолдолд y = е(x) тэнхлэгээс дээш байна Үхэр, тодорхой интеграл нь муруйгаар хязгаарлагдсан муруйн трапецын талбайг илэрхийлдэг. y = е(x) , х тэнхлэг ба ординатууд x = а , x = б. Хариуд нь буруу интеграл нь шугамын хооронд хязгааргүй (хязгааргүй) муруйн трапецын талбайг илэрхийлдэг. y = е(x) (доорх зурган дээр - улаан), x = аба абсцисса тэнхлэг.

Буруу интеграл нь бусад хязгааргүй интервалын хувьд ижил төстэй байдлаар тодорхойлогддог.

Хязгааргүй муруй трапецын талбай нь төгсгөлтэй тоо байж болох бөгөөд энэ тохиолдолд буруу интегралыг конвергент гэж нэрлэдэг. Талбай нь мөн хязгааргүй байж болох бөгөөд энэ тохиолдолд буруу интегралыг дивергент гэж нэрлэдэг.

Зохисгүй интегралын оронд интегралын хязгаарыг ашиглах.Буруу интегралыг үнэлэхийн тулд та тодорхой интегралын хязгаарыг ашиглах хэрэгтэй. Хэрэв энэ хязгаар байгаа бөгөөд хязгаарлагдмал (хязгааргүйтэй тэнцүү биш) байвал зохисгүй интегралыг конвергент, өөрөөр хэлбэл дивергент гэж нэрлэдэг. Хязгаарын тэмдгийн дор хувьсагч ямар хандлагатай байх нь бид эхний төрлийн эсвэл хоёр дахь төрлийн зохисгүй интегралтай харьцаж байгаа эсэхээс хамаарна. Одоо энэ талаар олж мэдье.

Эхний төрлийн буруу интегралууд - хязгааргүй хязгаартай ба тэдгээрийн нийлмэл байдал

Хязгааргүй дээд хязгаартай буруу интеграл

Тэгэхээр буруу интеграл бичих нь интегралын дээд хязгаар хязгааргүй байдгаараа ердийн тодорхой интегралаас ялгаатай.

Тодорхойлолт. Тасралтгүй функцийн интегралын хязгааргүй дээд хязгаартай буруу интеграл е(x) хүртэлх зайд а өмнө ∞ интегралын дээд хязгаартай энэ функцийн интегралын хязгаарыг гэнэ б ба интеграцийн доод хязгаар а интеграцийн дээд хязгаар хязгааргүй өсөх нөхцөлд, өөрөөр хэлбэл

.

Хэрэв энэ хязгаар байгаа бөгөөд хязгааргүй биш харин зарим тоотой тэнцүү бол буруу интегралыг конвергент гэнэ, мөн хязгаар нь тэнцүү байгаа тоог түүний утга гэж авна. Үгүй бол буруу интегралыг дивергент гэнэмөн үүнд ямар ч утга учир байхгүй.

Жишээ 1. Буруу интегралыг тооцоол(хэрэв энэ нь нэгдэж байвал).

Шийдэл. Зохисгүй интегралын тодорхойлолт дээр үндэслэн бид олдог

Хязгаар нь 1-тэй тэнцүү байгаа тул энэ нь буруу интеграл нийлдэгба 1-тэй тэнцүү байна.

Дараах жишээнд интеграл нь 1-р жишээтэй бараг ижил, зөвхөн x зэрэг нь хоёр биш, альфа үсэг бөгөөд нийлэгжилтийн буруу интегралыг судлах даалгавар юм. Өөрөөр хэлбэл, асуултад хариулах хэвээр байна: энэ буруу интеграл альфагийн ямар утгуудад нийлж, ямар утгуудад зөрөөд байна вэ?

Жишээ 2. Буруу интегралыг нэгтгэх эсэхийг шалга(интеграцийн доод хязгаар нь тэгээс их).

Шийдэл. Эхлээд тэгж төсөөлье, тэгвэл

Үүссэн илэрхийлэлд бид хязгаар руу шилжинэ:

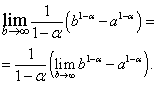
Баруун талын хязгаар нь байгаа бөгөөд тэгтэй тэнцүү байх үед , өөрөөр хэлбэл , хэзээ байхгүй гэдгийг харахад хялбар байдаг .

Эхний тохиолдолд, өөрөөр хэлбэл, хэзээ . Хэрэв бол мөн байхгүй.

Бидний судалгааны дүгнэлт дараах байдалтай байна: энэ буруу интеграл нийлдэгболон ялгаатайцагт.

Судалж буй буруу интегралын төрөлд Ньютон-Лейбницийн томъёог хэрэглэх , та үүнтэй маш төстэй дараах томъёог гаргаж болно.

.

Энэ бол Ньютон-Лейбницийн ерөнхий томъёо юм.

Жишээ 3. Буруу интегралыг тооцоол(хэрэв энэ нь нэгдэж байвал).

Энэ интегралын хязгаар нь:

Анхны интегралыг илэрхийлэх нийлбэрийг бүрдүүлдэг хоёр дахь интеграл:

Энэ интегралын хязгаар бас бий:

.

Бид хоёр интегралын нийлбэрийг олдог бөгөөд энэ нь хоёр хязгааргүй хязгаартай анхны буруу интегралын утга юм.

Хоёрдахь төрлийн зохисгүй интегралууд - хязгааргүй функцууд ба тэдгээрийн нийлэлтээс

Функцийг зөвшөөр е(x) -аас сегмент дээр өгөгдсөн а өмнө б мөн үүн дээр хязгааргүй. Функц цэг дээр хязгааргүйд хүрнэ гэж бодъё б , харин сегментийн бусад бүх цэгүүдэд энэ нь тасралтгүй байна.

Тодорхойлолт. Функцийн буруу интеграл е(x) -аас сегмент дээр а өмнө б интегралын дээд хязгаартай энэ функцийн интегралын хязгаарыг гэнэ в , хэрэв хичээх үед в руу б функц нь хязгааргүй, мөн цэг дээр нэмэгддэг x = б функц тодорхойлогдоогүй байна, өөрөөр хэлбэл

.

Хэрэв энэ хязгаар байгаа бол хоёр дахь төрлийн зохисгүй интегралыг конвергент гэж нэрлэдэг, үгүй ​​бол дивергент гэж нэрлэдэг.

Ньютон-Лейбницийн томъёог ашиглан бид гаргаж авдаг.

Хоёр төрлийн зохисгүй интервалыг авч үзье.

• 1. Интегралын төгсгөлгүй хязгаартай эхний төрлийн буруу интеграл;
• 2. Хязгааргүй тасалдалтай функцүүдийн хоёр дахь төрлийн буруу интеграл.

Хязгааргүй интегралын хязгаартай эхний төрлийн буруу интегралууд

Тодорхойлолт: Хэлбэрийн интегралуудыг: хязгаарыг ашиглан тодорхойлогддог хязгааргүй хязгаартай эхний төрлийн буруу интеграл гэж нэрлэдэг.

Тодорхойлолт Эдгээр интегралуудыг тодорхойлох хязгаарлагдмал хязгаартай бол буруу интегралыг нийлдэг гэж нэрлэдэг.

Хэрэв эдгээр хязгаар байхгүй эсвэл хязгааргүй бол буруу интегралыг дивергент гэж нэрлэдэг.

Үнэн хэрэгтээ, бидэнд байгаа функцүүдийн хагас төгсгөлгүй сегментээс x = in дурын утгын хувьд f(x) функц тодорхойлогдсон ба үргэлжилсэн байг:

Энэ нь 1-т нийлнэ.Тэгвэл теорем 1-ийн дагуу жижиг функцийн буруу интеграл: мөн нийлж, утга нь 1-ээс бага байна.

Теорем 2. 0?g(x)?f(x) тэгш бус байдал биелэх эерэг функцүүдийн хувьд дурын х? ба жижиг функцийн буруу интеграл ялгарах үед том функцийн буруу интеграл мөн хуваагдана.

Жишээ. Интегралын нийлэлтийг судал:

Шийдэл. Интегралыг функцтэй харьцуулж үзье. Интервал дээрх эерэг тэмдгүүдийн хувьд . Хоёрдахь төрлийн зохисгүй интегралууд нь [ интервал дахь тасалдлын цэгүүдийн байршлаас хамааран өөр өөрөөр тодорхойлогддог. а; б].

1) Функц гэж бодъё е(x) интеграцийн домайн зарим дотоод цэг дээр хязгааргүй тасалдалтай байна ( вÎ( а; б)) Сегментийн бусад цэгүүдэд [ а; б] функцийг тасралтгүй гэж үзнэ.

Дараа нь, хэрэв хязгаарууд байдаг ба төгсгөлтэй бол интеграл нь нийлж, тэнцүү байна гэж хэлдэг.

. (8.22)
2) Функцийн цорын ганц тасалдлын цэгийг үзье е(x) цэгтэй давхцаж байна А

. (8.23)
3) Функцийн цорын ганц тасалдлын цэгийг үзье е(x) цэгтэй давхцаж байна б. Дараа нь хэрэв хязгаар байгаа бөгөөд хязгаарлагдмал бол интеграл нь нийлдэг ба тэнцүү байна.

. (8.24)
Энэ нь бүхэлдээ e > 0 ба d > 0 гэж үздэг.

Асуудал 8.12.Буруу интегралыг тооцоол.

Шийдэл. x= 2. Тиймээс,

Асуудал 8.13.Буруу интегралыг тооцоол.

Шийдэл.Интеграл нь цэг дээр хоёр дахь төрлийн тасалдалтай байна x= 0 (интеграцийн бүс дотор). Тиймээс,

Эхний хязгаар нь байдаг бөгөөд төгсгөлтэй боловч хоёр дахь хязгаар нь хязгааргүй (at) -тай тэнцүү байна. Тиймээс энэ интеграл нь ялгаатай байна.

Бүлэг 9. Хэд хэдэн хувьсагчийн функцууд

§9.1. Тодорхойлолт n- хэмжээст Евклидийн орон зай Rn.

Олон хувьсагчийн функцуудыг судлахын өмнө уг ойлголтыг танилцуулах нь зүйтэй n- аливаад зориулсан хэмжээст орон зай n = 1, 2, 3,… .

2 Цэг x n-хэмжээт орон зай (вектор) нь эрэмбэлэгдсэн цуглуулга юм nбодит тоо.

дугаарыг дуудаж байна бивекторын координат.

2 Хоёр цэгийн хоорондох зай n-хэмжээт орон зай нь дараах томъёогоор тодорхойлогддог.

Нэг цэгээс цэг хүртэлх зай xвекторын модуль гэж нэрлэдэг xболон томилогдсон. Томъёо (9.1)-ээс дараах нь .

IN n-хэмжээт орон зай, скаляр бүтээгдэхүүний тухай ойлголт байгалийн гаралтай:

Векторуудын хоорондох өнцөг xТэгээд yтомъёогоор тодорхойлж болно:

Өмнөх шиг векторууд xТэгээд yЗөвхөн скаляр үржвэр нь тэг байвал перпендикуляр байна.

2 Бүх онооны багц n-(9.1) томъёоны дагуу зайг тодорхойлж, скаляр үржвэрийг дууддаг хэмжээст орон зай n-хэмжээт Евклидийн вектор орон зай ба -аар тэмдэглэнэ.

Хэзээ n= 1 тохиолдолд зай нь шугамтай давхцаж байна n= 2 – онгоцтой, мөн тохиолдолд n= 3 - зайтай.

2 ба . , гэсэн бүх цэгүүдийн олонлогийг дуудна n- цэг дээр төвтэй хэмжсэн бөмбөг xэсвэл д- цэгийн хөрш xорон зайд байх ба -ээр тэмдэглэгдсэн байна.

Координатын хэлбэрээр энэ тодорхойлолт дараах байдалтай байна.

Шууд шугамын хувьд, i.e. цагт n= 1, цэгийн хөрш нь радиус цэг дээр төвлөрсөн интервал юм д. Онгоцны хувьд, i.e. цагт n= 2, цэгийн хөрш нь радиус цэг дээр төвтэй нээлттэй тойрог юм д. Орон зайн хувьд, i.e. цагт n= 3 цэгийн хөрш нь радиус цэг дээр төвлөрсөн нээлттэй бөмбөг юм д.

§9.2. Хэд хэдэн хувьсагчийн функцийг тодорхойлох домэйн. Тасралтгүй байдал

2 Функц nхувьсагч нь багц бүрээс бүрдэх дүрэм (хууль) юм nзарим бүсээс авсан хувьсагч Дн-хэмжээт орон зайг нэг тоонд хуваарилдаг z. Хамгийн энгийн тохиолдолд.

2 2 хувьсагчийн функц нь цэг бүрийг дагаж мөрдөх дүрэм (хууль) юм М(x; y), зарим нутаг дэвсгэрт хамаарах Донгоц xOy, ганц тоотой таарч байна z.

Координаттай сансар огторгуйн олон цэг нь тухайн талбайгаас дээш өргөгдсөн тодорхой гадаргууг үүсгэдэг (Зураг 9.1). Д(хоёр хувьсагчийн функцийн геометрийн утга).

2 талбай Д, үүний төлөө дээрх захидал харилцааг бий болгосон функцийг тодорхойлох домэйн гэж нэрлэдэг.

Асуудал 9.1.Функцийн домайныг ол

Шийдэл.Тодорхойлолтын шаардлагатай домэйн нь хавтгай дээрх цэгүүдийн багц юм xOy, тэгш бус байдлын системийг хангах. Дараах шугамууд огтлолцох үед тэгш бус байдал ба тэдгээрийн тэмдгийг эсрэгээр нь (тус тус) өөрчил. x = yТэгээд x = 0, y= 0. Эдгээр шугамууд нь хавтгайг хуваана xOy 6 бүс нутагт. Домэйн бүрийн дурын цэгүүдийг системд орлуулснаар бид (1) ба (3) домэйнуудын нэгдэл нь анхны функцийг тодорхойлох домэйн гэдэгт итгэлтэй байна. Түүнээс гадна, энэ нь шулуун байна x = y, цэгийг эс тооцвол (0; 0) нь тодорхойлолтын мужид багтсан бөгөөд шулуун шугамууд x= 0, ба y= 0 – оруулаагүй (Зураг 9.2).

2 Бүсийн хаалт гэдэг нь орон зай дахь цэгүүдийн багц бөгөөд тус бүр нь тухайн бүс нутгийн цэгүүдийг агуулна. Д.

Жишээлбэл, Д– Онгоцны зарим нээлттэй (хил ороогүй) хэсэг xOy. Дараа нь бүс нутагт бол бүс нутгийг хаах авах болно Дхилээ хавсаргана Г .

2 Зарим газар оруул Донгоц xOyфункц өгөгдсөн бөгөөд тухайн бүс нутгийн хаалтын зарим цэг байг Д(). Тоо Ацэг дээрх функцийн хязгаар гэж нэрлэдэг МХэрэв ямар нэгэн тоо байвал 0 д> 0 ийм тоо байна δ > 0, энэ нь цэгээс бусад бүх цэгүүдийн хувьд М 0 ба түүнээс бага зайд δ , тэгш бус байдал хангагдана.

2 Функц нь энэ цэг дээр () тодорхойлогдсон бөгөөд тэгш байдал хангагдвал тухайн цэг дээр тасралтгүй гэж нэрлэгддэг.

§9.3. Хоёр хувьсагчийн функцийн түвшний шугамууд

Онгоц дээрх 2 шугам xOy, тэгшитгэлээр өгөгдсөн , хаана ХАМТ– функцын түвшний шугам гэж нэрлэгддэг дурын тогтмол.

Түвшингийн шугамууд нь гадаргуу, өгөгдсөн функц ба хавтгайн огтлолцох шугам юм z = C, хавтгайтай зэрэгцээ xOy. Түвшингийн шугамыг ашиглан та функцээр тодорхойлсон гадаргуугийн хэлбэрийг судалж болно.

Жишээ 9.2.Түвшингийн шугамуудыг олж, тэгшитгэлээр өгөгдсөн гадаргуугийн хэлбэрийг тодорхойлно.

Энэ тохиолдолд түвшний шугамын тэгшитгэл нь хэлбэртэй байна. C-д< 0 уравнение дает пустое множество решений (следовательно, вся поверхность расположена выше плоскости xOy). At C= 0 нь түвшний шугамын тэгшитгэлийг зөвхөн нэг цэг хангана x = 0, y= 0 (онгоцтой xOyгадаргуу нь зөвхөн координатын гарал үүслээр огтлолцдог). At C> 0 түвшний шугамууд нь хагас тэнхлэгтэй эллипс ба . Янз бүрийн утгуудад тохирох түвшний шугамууд ХАМТ, Зурагт үзүүлэв. 9.3. Тэгшитгэлээр тодорхойлсон гадаргууг эллипс параболоид гэж нэрлэдэг (Зураг 9.4).

§9.4. Нэгдүгээр эрэмбийн хэсэгчилсэн дериватив

Зарим газар оруул Донгоц xOyфункц өгөгдсөн бөгөөд бүс нутгийн тодорхой цэг юм Д.

x

, (9.2)

2 Хувьсагчтай холбоотой цэг дээрх функцийн хэсэгчилсэн дериватив y(эсвэл ) гэж нэрлэдэг

, (9.3)
хэрэв энэ хязгаар байгаа бөгөөд төгсгөлтэй бол.

2 Хэсэгчилсэн дериватив функц nхувьсагчийг хувьсагчаар нэг цэгт x iдуудсан

, (9.4)
хэрэв энэ хязгаар байгаа бөгөөд төгсгөлтэй бол.

(9.2) – (9.4) томъёоноос харахад хэсэгчилсэн деривативыг нэг хувьсагчийн функцийн деривативыг тодорхойлсонтой ижил аргаар тодорхойлно. Хязгаарыг тооцоолохдоо хувьсагчийн зөвхөн нэг нь нэмэгдэл авдаг, үлдсэн хувьсагчид нэмэгдэл авдаггүй бөгөөд тогтмол хэвээр байна. Иймээс хэсэгчилсэн деривативыг энгийн деривативтай ижил дүрмийн дагуу тооцоолж, бүх чөлөөт хувьсагчдыг (ялгаалахаас бусад) тогтмол гэж үзэж болно.

Асуудал 9.3.Функцийн хэсэгчилсэн деривативуудыг ол

Шийдэл. .

Асуудал 9.4.Функцийн хэсэгчилсэн деривативуудыг ол.

Шийдэл.Өгөгдсөн функцийг хувьсагчийн хувьд ялгах үед xБид чадлын функцийг ялгах, хувьсагчтай холбоотой хэсэгчилсэн деривативыг олохдоо дүрмийг ашигладаг. y– экспоненциал функцийг ялгах дүрэм:

Асуудал 9.5.Цэг дэх функцийн хэсэгчилсэн деривативуудыг тооцоол.

Шийдэл.Нарийн төвөгтэй функцийг ялгах дүрмийг ашигласнаар бид хэсэгчилсэн деривативуудыг олдог

Цэгийн координатыг хэсэгчилсэн дериватив болгон орлуулах М, бид авдаг

§9.5. Хэд хэдэн хувьсагчийн функцийн градиент.
Чиглэлийн дериватив

2 Нэг цэг дэх функцийн градиент нь тухайн цэг дээр тооцоолсон өгөгдсөн функцийн хэсэгчилсэн деривативуудаас бүрдэх вектор юм.

2 Векторын чиглэлийн цэг дээрх функцийн дериватив нь тухайн цэг дээр тооцсон энэ функцийн градиент векторын проекц юм. М 0, энэ чиглэлд

(2.6) томъёоны дагуу векторын векторын проекцийг тооцоолсноор бид олж авна

. (9.7)
Хаана байгааг анзаарсан а– векторын тэнхлэгтэй харьцах өнцөг ҮХЭР, бид векторын чиглэлтэй холбоотой деривативыг тооцоолох өөр томъёог олж авна

Асуудал 9.6.Нэг цэг дээрх функцийн градиентийг ол М 0 (4; 2) ба векторын чиглэлийн дериватив

Шийдэл.Хэсэгчилсэн деривативуудыг олцгооё

Цэг дэх хэсэгчилсэн деривативын утгыг тооцоолъё М 0:

Нэг цэг дэх функцийн градиент М 0-ийг (9.5) томъёог ашиглан олох болно:

Асуудал 9.7.Яг цэг дээр М 0 (0; 1) хоёр дахь координатын өнцгийн биссектрисын чиглэлд функцийн деривативыг тооцоол.

Шийдэл.Функцийн хэсэгчилсэн деривативуудыг олцгооё.

Хэсэгчилсэн деривативын утгууд ба цэг дээрх функцийн градиентийг тооцоолъё М 0:

Нэг цэг дэх функцийн дериватив МХоёр дахь координатын өнцгийн биссектрисын чиглэлд 0 (энэ чиглэл нь тэнхлэгтэй ҮХЭРбулан а= 135°) томъёог (9.8) ашиглан олж болно.

§9.6. Хэд хэдэн хувьсагчийн функцийн дифференциал
болон ойролцоо тооцоололд хэрэглэх

1 Хэрэв функц нь нэг цэг дээр тасралтгүй хэсэгчилсэн дериватив ба , цэгээс шилжих үед түүний нийт өсөлт М 0 хүртэлх цэгийг дараах байдлаар илэрхийлж болно.

, (9.9)
хаана нь , .

2 Илэрхийллийг цэг дээрх функцийн нийт дифференциал гэнэ.

(9.9) томъёоноос харахад функцийн дифференциал нь функцийн нийт өсөлтийн үндсэн шугаман хэсэг болно. Хангалттай жижиг D xболон Д yилэрхийлэл нь дифференциалаас хамаагүй бага бөгөөд үүнийг үл тоомсорлож болно. Тиймээс бид дараах ойролцоо томъёонд хүрнэ.

. (9.10)
Сэтгэгдэл.Формула (9.10) нь зөвхөн цэгт хангалттай ойрхон байгаа цэгүүдэд функцүүдийн утгыг ойролцоогоор тооцоолоход ашиглаж болно. Утга нь бага байх тусам (9.9) томъёог ашиглан олдсон утгыг илүү нарийвчлалтай гаргах болно.

Жишээ 9.8.Дифференциал ашиглан ойролцоогоор тооцоол.

Функцийг авч үзье. Үнэ цэнийг тооцоолох шаардлагатай zцэг дээр энэ функцийн 1 ( x 1 ; y 1) = (0.09; 6.95). Ойролцоо томъёог (9.9) ашиглан (0; 7) цэгийг цэг болгон сонгоцгооё. Тэгвэл Д x = x 1 – x 0 = 0.09 – 0 = 0.09, D y =y 1 – y 0 = 6,95 – 7 = – 0,05.

Тиймээс,

§9.7. Дээд эрэмбийн хэсэгчилсэн дериватив

Талбайд оруул ДЭнэ мужид тасралтгүй хэсэгчилсэн деривативтай функц өгөгдсөн. Тиймээс тухайн бүс нутагт ДБид хоёр хувьсагчийн хоёр шинэ тасралтгүй функцийг олж авсан ба . Хэзээ нэгэн цагт бүс нутагт байгаа бол Дфункцтэй ба хувьсагчийн хувьд аль алинд нь хэсэгчилсэн дериватив байна x, мөн өөрчлөлтөөр y, тэгвэл эдгээр деривативуудыг функцийн хоёрдугаар эрэмбийн дериватив гэж нэрлэдэг. Тэдгээрийг дараах байдлаар томилно.

1 Хэрэв тухайн бүс нутгийн аль нэг цэгт Дфункц нь тасралтгүй холимог деривативтай ба , тэгвэл эдгээр деривативууд тэнцүү байх цэгт: . D, дараах нөхцөлийг хангасан байх ёстой: D = 32 – 9 = 23.

Дискриминант нь тэгээс их байх тул цэг дээр Мфункц нь экстремумтай. Тухайлбал, орон нутгийн доод хэмжээ, оноос хойш АТэгээд ХАМТТэгээс дээш. Хаана

Дуудсан Буруу интеграл ФункцээсФ(X) хязгааргүй дээд хязгаартай.Хэрэв энэ хязгаар байгаа бөгөөд төгсгөлтэй байвал зохисгүй интеграл гэж нэрлэдэг Конвергент. Гэхдээ энэ нь байхгүй эсвэл тэнцүү бол
± ¥ бол энэ буруу интеграл гэж нэрлэгддэг Зөрчилтэй.

Хэрэв Ф(X) ≥ 0 бүгдэд нь X ≥ А, Тэр Узохисгүй интеграл (6.1) нь энгийн тодорхой интегралын геометрийн утгаас (4.3) үүсэлтэй илэрхий геометрийн утгатай байна. Үнэн хэрэгтээ, Зурагт заасны дагуу. 5.14

(6.2)

(6.3)

Энд С¥ - тэнхлэгийн чиглэлд хязгааргүй сунгасан талбай Өөмуруй шугаман трапец (Зураг 5.15). Хязгааргүй цар хүрээтэй хэдий ч энэ нь бас төгсгөлтэй болж хувирдаг. Гэхдээ энэ нь тохиолдож болно, Зураг дээр заасны дагуу. 5.15, зөвхөн тохиолдолд Ю = Ф(X) → 0 цагт X → ¥ . Тэгээд ч гэсэн, хэрэв функц Ю = Ф(X) → 0 цагт X → ¥ хангалттай хурдан.

Жишээ 1. Талбайг олох С¥ , Зурагт үзүүлэв. 5.16.

,
оноос хойш ln Б → ¥ цагт Б → ¥ .

Тэгэхээр, С¥ = ¥. Мөн энэ нь хэдий ч функц нь хэзээ X → ¥ . Зохисгүй интеграл, энэ нь зөрүүтэй гэсэн үг.

Жишээ 2. Талбайг олох С¥ , Зурагт үзүүлэв. 5.17.

Энд С¥ = 1. Өөрөөр хэлбэл, хязгааргүй өргөтгөсөн талбай нь төгсгөлтэй болсон. Энэ нь интеграл функцийн үед болсон X → ¥ хангалттай хурдан (наад зах нь өмнөх жишээн дэх интегралаас хамаагүй хурдан). Буруу интеграл (тоо), энэ нь нийлж байна гэсэн үг.

Жишээ 3 . Буруу интеграл нь нийлэх эсвэл салах эсэхийг олж мэд.

Шийдэл . Энэ интегралыг тооцоолъё:

Байдаггүй. Хэрэв бид функцийн графикийн үйлдлийг эргэн санах юм бол энэ нь тодорхой юм Ю= = Нүгэл X(синусоидууд) at X → ¥ . Тиймээс энэ нь байхгүй, энэ нь ялгаатай гэсэн үг юм. Гэсэн хэдий ч энэ нь өөрөөр байж болохгүй, учир нь интеграл функц cos Xүед тэглэх хандлагатай байдаггүй X →¥ .

Төрөл бүрийн зохисгүй интегралыг тооцоолох, түүнчлэн энгийн тодорхой интегралыг тооцоолохдоо та Ньютон-Лейбницийн томъёог шууд хэрэглэж болно гэдгийг анхаарна уу.

Энд

Үнэхээр:

Хэрэв үнэ цэнэ Ф(¥ ) байдаг ба төгсгөлтэй бол Ньютон-Лейбницийн (6.4) томъёоны дагуу буруу интеграл мөн нийлдэг.

Анхаарна уу.Хязгааргүй дээд хязгаартай интегралтай ижил төстэй интегралын төгсгөлгүй доод хязгаартай, тэр ч байтугай интегралын хязгааргүй хязгаартай зохисгүй интегралуудыг авч үзэж болно. Энэ нь хэлбэрийн интеграл юм

Тэдгээрийг тооцоолохын тулд та Ньютон-Лейбницийн томъёог ашиглаж болно.

Жишээ 4.

Тэгэхээр, (тоо), өөрөөр хэлбэл энэ интеграл нийлдэг. Түүний π утга нь талбайтай тэнцүү байна С¥ Хоёр чиглэлд хязгааргүй сунгасан дүрсийг Зураг дээр үзүүлэв. 5.18.

Интегралын хязгааргүй хязгаартай зохисгүй интегралуудын конвергенц-дивергенцийн баримтыг эдгээр интегралуудыг шууд тооцоолох замаар тогтоох шаардлагагүй гэдгийг анхаарна уу. Энэхүү зохисгүй интегралыг конвергенц-дивергенцийг аль хэдийн тогтоосон бусад интегралтай харьцуулах замаар энэ асуултыг илүү энгийнээр шийдэж болно.

Жишээлбэл, хүн бүрт тэгш бус байдал байдаг гэж бодъё Ф(X) £ Г(X), Хаана Ю = Ф(X) БА Ю = Г(X) - Хоёр тасралтгүй ба сөрөг бус функц (Зураг 5.19). Тэгвэл энэ нь ойлгомжтой

Тэгш бус байдлаас (6.6) болон Зураг. 5.19 гэдэг зүйлийг дагаж байгаа нь ойлгомжтой Буруу интегралыг харьцуулах тест:

1) Хэрэв (тоо) нийлж байвал (тоо) - нийлдэг, ба Б 2) Хэрэв - тэгвэл зөрүүтэй - зөрүүтэй. 3) Хэрэв - зөрүүтэй, тэгвэл - энэ интегралын талаар юу ч хэлж чадахгүй. 4) Хэрэв (тоо) - нэгддэг, дараа нь - энэ интегралын талаар юу ч хэлж чадахгүй.

Функц байдлаар Г(X) , энэ функцийг интервал дээр харьцуулна Ф(X), функцийг ихэвчлэн ашигладаг бөгөөд интегралыг харьцуулах интеграл болгон ашигладаг. А > 0 ба аливаа α функц нь эерэг ба тасралтгүй функц бөгөөд тэр

Жишээ 5.

Шийдэл. Энэ нь ойлгомжтой бүгдэд нь X Î }