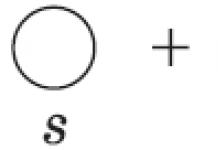бутархай гэж нэрлэдэг зөв, хэрэв тоологчийн хамгийн дээд зэрэг нь хуваагчийн хамгийн дээд зэргээс бага бол. Зөв рационал бутархайн интеграл нь дараах хэлбэртэй байна.

$$ \int \frac(mx+n)(ax^2+bx+c)dx $$

Рационал бутархайг нэгтгэх томъёо нь хуваагч дахь олон гишүүнтийн язгуураас хамаарна. Хэрэв $ ax^2+bx+c $ олон гишүүнт нь:

1. Зөвхөн нарийн төвөгтэй үндэс, дараа нь үүнээс бүрэн квадратыг гаргаж авах шаардлагатай: $$ \int \frac(mx+n)(ax^2+bx+c) dx = \int \frac(mx+n)(x^ 2 \pm a ^2) $$
2. Төрөл бүрийн жинхэнэ үндэс$ x_1 $ ба $ x_2 $, дараа нь та интегралыг өргөжүүлж, $ A $ ба $ B $ тодорхойгүй коэффициентүүдийг олох хэрэгтэй: $$ \int \frac(mx+n)(ax^2+bx+c) dx = \int \ frac(A)(x-x_1) dx + \int \frac(B)(x-x_2) dx $$
3. Нэг олон үндэс $ x_1 $, дараа нь бид интегралыг өргөжүүлж, дараах томъёоны хувьд тодорхойгүй $ A $ ба $ B $ коэффициентүүдийг олно: $$ \int \frac(mx+n)(ax^2+bx+c) dx = \int \frac(A)((x-x_1)^2)dx + \int \frac(B)(x-x_1) dx $$

Хэрэв бутархай бол буруу, өөрөөр хэлбэл, тоологчийн хамгийн дээд зэрэг нь хуваагчийн хамгийн дээд зэрэгтэй тэнцүү буюу их байвал эхлээд үүнийг багасгах хэрэгтэй. зөволон гишүүнтийг тоологчоос олон гишүүнт хуваах замаар үүсгэнэ. Энэ тохиолдолд рационал бутархайг нэгтгэх томъёо нь дараах хэлбэртэй байна.

$$ \int \frac(P(x))(ax^2+bx+c)dx = \int Q(x) dx + \int \frac(mx+n)(ax^2+bx+c)dx $$

Шийдлийн жишээ

Жишээ 1

Рационал бутархайн интегралыг ол: $$ \int \frac(dx)(x^2-10x+16) $$

Шийдэл

Бутархай нь зөв бөгөөд олон гишүүнт нь зөвхөн нийлмэл үндэстэй. Тиймээс бид бүрэн квадратыг сонгоно: $$ \int \frac(dx)(x^2-10x+16) = \int \frac(dx)(x^2-2\cdot 5 x+ 5^2 - 9) = $$ Бид бүтэн дөрвөлжин нугалж, $ x-5 $ дифференциал тэмдгийн доор байрлуулна. $$ = \int \frac(dx)((x-5)^2 - 9) = \int \frac(d(x-5))((x-5)^2-9) = $$ Интегралын хүснэгтийг ашиглан бид дараахь зүйлийг олж авна. $$ = \frac(1)(2 \cdot 3) \ln \bigg | \frac(x-5 - 3)(x-5 + 3) \bigg | + C = \frac(1)(6) \ln \bigg |\frac(x-8)(x-2) \bigg | +C$$ Хэрэв та асуудлаа шийдэж чадахгүй бол бидэнд илгээнэ үү. Бид хангах болно нарийвчилсан шийдэл. Та тооцооллын явцыг харж, мэдээлэл авах боломжтой болно. Энэ нь таныг багшаасаа цаг тухайд нь дүнгээ авахад тусална!

Хариулт

$$ \int \frac(dx)(x^2-10x+16) = \frac(1)(6) \ln \bigg |\frac(x-8)(x-2) \bigg | +C$$

Жишээ 2

Рационал бутархайн интеграцийг гүйцэтгэнэ: $$ \int \frac(x+2)(x^2+5x-6) dx $$

Шийдэл

Шийдье квадрат тэгшитгэл: $$ x^2+5x-6 = 0 $$ $$ x_(12) = \frac(-5\pm \sqrt(25-4\cdot 1 \cdot (-6)))(2) = \frac(-5 \pm 7)(2) $$ Бид үндсийг нь бичдэг: $$ x_1 = \frac(-5-7)(2) = -6; x_2 = \frac(-5+7)(2) = 1 $$ Олж авсан үндсийг харгалзан бид интегралыг хувиргана. $$ \int \frac(x+2)(x^2+5x-6) dx = \int \frac(x+2)((x-1)(x+6)) dx = $$ Бид оновчтой бутархайн өргөтгөлийг гүйцэтгэдэг. $$ \frac(x+2)((x-1)(x+6)) = \frac(A)(x-1) + \frac(B)(x+6) = \frac(A(x) -6)+B(x-1))((x-1)(x+6)) $$ Бид тоологчдыг тэнцүүлж, $ A $ ба $ B $ коэффициентүүдийг олно. $$ A(x+6)+B(x-1)=x+2 $$ $$ Ax + 6A + Bx - B = x + 2 $$ $$ \эхлэх(тохиолдол) A + B = 1 \\ 6A - B = 2 \төгсгөл(тохиолдол) $$ $$ \эхлэх(тохиолдол) A = \frac(3)(7) \\ B = \frac(4)(7) \төгсгөл(тохиолдол) $$ Бид олсон коэффициентүүдийг интегралд орлуулж, үүнийг шийднэ. $$ \int \frac(x+2)((x-1)(x+6))dx = \int \frac(\frac(3)(7))(x-1) dx + \int \frac (\frac(4)(7))(x+6) dx = $$ $$ = \frac(3)(7) \int \frac(dx)(x-1) + \frac(4)(7) \int \frac(dx)(x+6) = \frac(3) (7) \ln |x-1| + \frac(4)(7) \ln |x+6| +C$$

Хариулт

$$ \int \frac(x+2)(x^2+5x-6) dx = \frac(3)(7) \ln |x-1| + \frac(4)(7) \ln |x+6| +C$$

Би аль хэдийн тэмдэглэсэнчлэн интеграл тооцоололд бутархайг нэгтгэх тохиромжтой томъёо байдаггүй. Тиймээс гунигтай хандлага бий: бутархай нь илүү боловсронгуй байх тусам түүний интегралыг олоход хэцүү байдаг. Үүнтэй холбогдуулан та янз бүрийн заль мэхийг ашиглах хэрэгтэй бөгөөд би одоо танд хэлэх болно. Бэлтгэсэн уншигчид тэр даруй давуу талыг ашиглах боломжтой агуулгын хүснэгт:

• Энгийн бутархайн дифференциал тэмдгийг тооцох арга

Хиймэл тоологч хувиргах арга

Жишээ 1

Дашрамд хэлэхэд, авч үзсэн интегралыг хувьсагчийн аргыг өөрчлөх замаар шийдэж болно, гэхдээ шийдлийг бичих нь илүү урт байх болно.

Жишээ 2

Тодорхойгүй интегралыг ол. Шалгалт хийх.

Энэ бол жишээ юм бие даасан шийдвэр. Хувьсах солих арга энд цаашид ажиллахгүй гэдгийг тэмдэглэх нь зүйтэй.

Анхаар, чухал! Жишээ № 1, 2 нь ердийн бөгөөд байнга тохиолддог. Ялангуяа ийм интегралууд нь бусад интегралуудыг шийдвэрлэх явцад, ялангуяа иррационал функцуудыг (үндэс) нэгтгэх үед үүсдэг.

Энэ тохиолдолд авч үзсэн техник нь бас ажилладаг хэрэв тоологчийн хамгийн дээд зэрэг нь хуваагчийн хамгийн дээд зэргээс их бол.

Жишээ 3

Тодорхойгүй интегралыг ол. Шалгалт хийх.

Бид тоологчийг сонгож эхэлдэг.

Тоолуурыг сонгох алгоритм нь дараах байдалтай байна.

1) Тоолуур дээр би зохион байгуулах хэрэгтэй, гэхдээ тэнд . Юу хийх вэ? Би үүнийг хаалтанд хийж: -ээр үржүүлнэ.

2) Одоо би эдгээр хаалтуудыг нээхийг оролдсон, юу болох вэ? . Хмм... энэ нь дээр, гэхдээ анх тоологчийн хувьд хоёр байхгүй. Юу хийх вэ? Та үржүүлэх хэрэгтэй:

3) Би хаалтуудыг дахин нээв: . Мөн анхны амжилт энд байна! Энэ нь зөв болсон! Гэхдээ асуудал нь нэмэлт нэр томъёо гарч ирсэн явдал юм. Юу хийх вэ? Илэрхийлэл өөрчлөгдөхөөс сэргийлэхийн тулд би өөрийн бүтэцдээ ижил зүйлийг нэмэх ёстой:
. Амьдрал илүү хялбар болсон. Тоолуур дээр дахин зохион байгуулах боломжтой юу?

4) Энэ нь боломжтой. Оролдоод үзье: . Хоёрдахь гишүүний хаалтыг нээ:
. Уучлаарай, гэхдээ өмнөх алхам дээр надад байсан, гэхдээ . Юу хийх вэ? Та хоёр дахь гишүүнийг дараах байдлаар үржүүлэх хэрэгтэй.

5) Дахин хэлэхэд, шалгахын тулд би хоёр дахь улиралд хаалт нээнэ:
. Одоо энэ нь хэвийн: 3-р цэгийн эцсийн бүтээн байгуулалтаас гаралтай! Гэхдээ дахиад жижиг "гэхдээ" гэсэн нэмэлт нэр томъёо гарч ирсэн бөгөөд энэ нь би өөрийн илэрхийлэлд нэмэх ёстой гэсэн үг юм.

Хэрэв бүх зүйл зөв хийгдсэн бол бүх хаалтыг нээхэд бид интегралын анхны дугаарыг авах ёстой. Бид шалгаж байна:
Бүрээс.

Тиймээс:

Бэлэн. Сүүлийн үед би функцийг дифференциал дор оруулах аргыг ашигласан.

Хэрэв бид хариултын деривативыг олж, илэрхийллийг багасгавал Ерөнхий хуваарь, тэгвэл бид яг анхны интеграл функцийг авна. Нийлбэр болгон задлах арга нь илэрхийлэлийг нийтлэг хуваагч руу хүргэх урвуу үйлдлээс өөр зүйл биш юм.

Тоолуурыг сонгох алгоритм ижил төстэй жишээнүүдҮүнийг ноорог хэлбэрээр хийх нь дээр. Зарим ур чадварын хувьд энэ нь оюун санааны хувьд ажиллах болно. Би 11-р зэрэглэлийн сонгон шалгаруулалтыг хийж байхдаа рекорд эвдэрсэн тохиолдлыг санаж байна, тоологчийн өргөтгөл нь Вердын бараг хоёр мөрийг эзэлсэн.

Жишээ 4

Тодорхойгүй интегралыг ол. Шалгалт хийх.

Энэ бол та өөрөө шийдэх жишээ юм.

Энгийн бутархайн дифференциал тэмдгийг тооцох арга

Дараагийн төрлийн бутархайг авч үзье.
, , , (коэффициент ба тэгтэй тэнцүү биш).

Үнэн хэрэгтээ арксин ба арктангенс бүхий хэд хэдэн тохиолдлыг аль хэдийн хичээл дээр дурдсан Тодорхой бус интеграл дахь хувьсагчийг өөрчлөх арга. Ийм жишээг дифференциал тэмдгийн дор функцийг нэгтгэж, хүснэгтийг ашиглан дараа нь нэгтгэх замаар шийддэг. Энд урт ба өндөр логарифм бүхий ердийн жишээнүүд байна:

Жишээ 5

Жишээ 6

Эндээс интегралын хүснэгтийг авч, ямар томьёо болон байгааг харахыг зөвлөж байна Хэрхэнхувиргалт явагддаг. Анхаар, яаж, яагаадЭдгээр жишээн дэх квадратуудыг тодруулсан болно. Тухайлбал, 6-р жишээнд бид эхлээд хуваагчийг хэлбэрээр илэрхийлэх хэрэгтэй , дараа нь дифференциал тэмдгийн доор авчир. Стандарт хүснэгтийн томъёог ашиглахын тулд энэ бүгдийг хийх шаардлагатай .

7, 8-р жишээнүүдийг өөрөө шийдэж үзээрэй, ялангуяа тэдгээр нь нэлээд богино тул:

Жишээ 7

Жишээ 8

Тодорхой бус интегралыг ол:

Хэрэв та эдгээр жишээнүүдийг шалгаж чадвал маш их хүндэтгэлтэй байна - таны ялгах чадвар маш сайн байна.

Бүтэн квадрат сонгох арга

Маягтын интегралууд (коэффициент ба тэгтэй тэнцүү биш) шийдэгдсэн дөрвөлжин олборлох бүрэн арга, аль хэдийн хичээл дээр гарч ирсэн Графикийн геометрийн хувиргалт.

Үнэн хэрэгтээ ийм интегралууд нь бидний сая үзсэн дөрвөн хүснэгтэн интегралын аль нэгэнд нь буурдаг. Үүнийг мэддэг товчилсон үржүүлэх томъёог ашиглан хийдэг.

Томьёог яг энэ чиглэлд ашигладаг, өөрөөр хэлбэл аргын санаа нь илэрхийлэлийг хуваагч дахь зохиомлоор зохион байгуулж, дараа нь аль алинд нь хөрвүүлэх явдал юм.

Жишээ 9

Тодорхой бус интегралыг ол

Энэ хамгийн энгийн жишээ, аль нь нэр томъёотой - нэгжийн коэффициент(мөн зарим тоо эсвэл хасах биш).

Хуваагчийг харцгаая, энд бүх зүйл тохиолдлоос үүдэлтэй. Хуваагчийг хөрвүүлж эхэлцгээе:

Мэдээжийн хэрэг та 4-ийг нэмэх хэрэгтэй. Мөн илэрхийлэл өөрчлөгдөхгүйн тулд ижил дөрвийг хасна уу:

Одоо та томъёог хэрэглэж болно:

Хөрвүүлэлт дууссаны дараа ҮРГЭЛЖУрвуу хөдөлгөөн хийхийг зөвлөж байна: бүх зүйл зүгээр, алдаа байхгүй.

Тухайн жишээний эцсийн загвар нь иймэрхүү харагдах ёстой.

Бэлэн. Дифференциал тэмдгийн дор "чөлөөт" цогц функцийг тооцох нь зарчмын хувьд үл тоомсорлож болно

Жишээ 10

Тодорхой бус интегралыг ол:

Энэ бол та өөрөө шийдэх жишээ бөгөөд хариулт нь хичээлийн төгсгөлд байна

Жишээ 11

Тодорхой бус интегралыг ол:

Урд талд нь хасах байвал яах вэ? Энэ тохиолдолд бид хаалтнаас хасахыг авч, нэр томъёог шаардлагатай дарааллаар нь цэгцлэх хэрэгтэй: . Тогтмол(энэ тохиолдолд хоёр) бүү хүр!

Одоо бид хаалтанд нэгийг нэмнэ. Илэрхийлэлд дүн шинжилгээ хийснээр бид хаалтны гадна нэгийг нэмэх шаардлагатай гэсэн дүгнэлтэд хүрэв.

Энд бид томъёог авч, хэрэглэнэ:

ҮРГЭЛЖБид төслийг шалгана:
, үүнийг шалгах шаардлагатай байсан.

Цэвэр жишээ нь иймэрхүү харагдаж байна:

Даалгаврыг улам хүндрүүлж байна

Жишээ 12

Тодорхой бус интегралыг ол:

Энд нэр томъёо нь нэгжийн коэффициент байхаа больсон, харин "тав" гэсэн үг юм.

(1) Хэрэв тогтмол тоо байвал бид тэр даруй хаалтнаас гаргаж авдаг.

(2) Ерөнхийдөө энэ тогтмолыг интегралын гадна талд шилжүүлэх нь үргэлж дээр бөгөөд ингэснээр саад болохгүй.

(3) Мэдээжийн хэрэг, бүх зүйл томъёогоор буух болно. Бид "хоёр" гэсэн нэр томъёог ойлгох хэрэгтэй.

(4) Тийм ээ, . Энэ нь бид илэрхийлэл дээр нэмж, ижил бутархайг хасдаг гэсэн үг юм.

(5) Одоо бүтэн квадратыг сонго. Ерөнхий тохиолдолд бид бас тооцоолох хэрэгтэй, гэхдээ энд урт логарифмын томъёо байна , мөн үйлдлийг гүйцэтгэх нь ямар ч утгагүй бөгөөд яагаад гэдгийг доор тайлбарлах болно.

(6) Үнэндээ бид томъёог хэрэглэж болно , зөвхөн “X”-ийн оронд бидэнд байгаа нь хүснэгтийн интегралын хүчинтэй байдлыг үгүйсгэхгүй. Хатуухан хэлэхэд нэг алхам алдагдсан - интеграци хийхээс өмнө функцийг дифференциал тэмдгийн дор оруулах ёстой: , гэхдээ би олон удаа тэмдэглэж байсанчлан үүнийг ихэвчлэн үл тоомсорлодог.

(7) Үндэс дор хариулахдаа бүх хаалтыг буцааж томруулахыг зөвлөж байна:

Хэцүү үү? Энэ бол интеграл тооцооллын хамгийн хэцүү хэсэг биш юм. Хэдийгээр авч үзэж буй жишээнүүд нь сайн тооцоолох техник шаарддаг тул тийм ч төвөгтэй биш юм.

Жишээ 13

Тодорхой бус интегралыг ол:

Энэ бол та өөрөө шийдэх жишээ юм. Хариулт нь хичээлийн төгсгөлд байна.

Хуваарьт үндэстэй интегралууд байдаг бөгөөд тэдгээрийг орлуулалтыг ашиглан авч үзсэн төрлийн интеграл болгон бууруулсан байдаг; та тэдгээрийн талаар нийтлэлээс уншиж болно. Комплекс интеграл, гэхдээ маш их бэлтгэлтэй оюутнуудад зориулагдсан.

Тоолуурыг дифференциал тэмдгийн доор оруулах

Энэ бол хичээлийн эцсийн хэсэг боловч ийм төрлийн интегралууд нэлээд түгээмэл байдаг! Хэрэв та ядарсан бол маргааш уншсан нь дээр болов уу? ;)

Бидний авч үзэх интегралууд нь өмнөх догол мөрийн интегралтай төстэй бөгөөд тэдгээр нь дараах хэлбэртэй байна. (коэффициент , ба тэгтэй тэнцүү биш).

Өөрөөр хэлбэл, бид одоо тоологч дахь шугаман функцтэй болсон. Ийм интегралыг хэрхэн шийдэх вэ?

Асуудлыг хайж байна тодорхойгүй интегралбутархай рационал функцийг энгийн бутархай интеграл болгон бууруулсан. Тиймээс бид эхлээд бутархайн задралын онолын хамгийн энгийн хэсэгтэй танилцахыг зөвлөж байна.

Жишээ.

Тодорхойгүй интегралыг ол.

Шийдэл.

Интегралын хүртэгчийн зэрэг нь хуваарийн зэрэгтэй тэнцүү тул эхлээд олон гишүүнтийг олон гишүүнт баганагаар хувааж бүхэл хэсгийг сонгоно.

Тийм ч учраас, .

Үүссэн зөв рационал бутархайг энгийн бутархай болгон задлах нь хэлбэртэй байна . Тиймээс,

Үүссэн интеграл нь гурав дахь төрлийн хамгийн энгийн бутархайн интеграл юм. Цаашид бага зэрэг харвал дифференциал тэмдгийн доор оруулснаар та үүнийг авч болно гэдгийг бид тэмдэглэж байна.

Учир нь , Тэр . Тийм ч учраас

Тиймээс,

Одоо дөрвөн төрөл бүрийн энгийн бутархайг нэгтгэх аргуудыг тайлбарлах руу шилжье.

Эхний төрлийн энгийн бутархайг нэгтгэх

Шууд интеграцийн арга нь энэ асуудлыг шийдвэрлэхэд тохиромжтой.

Жишээ.

Функцийн эсрэг деривативуудын олонлогийг ол

Шийдэл.

Эсрэг деривативын шинж чанар, эсрэг деривативын хүснэгт, интегралчлалын дүрмийг ашиглан тодорхойгүй интегралыг олъё.

Хуудасны дээд талд

Хоёр дахь төрлийн энгийн бутархайг нэгтгэх

Шууд нэгтгэх арга нь энэ асуудлыг шийдвэрлэхэд тохиромжтой.

Жишээ.

Шийдэл.

Хуудасны дээд талд

Гурав дахь төрлийн энгийн бутархайг нэгтгэх

Эхлээд бид тодорхойгүй интегралыг танилцуулж байна нийлбэрээр:

Бид эхний интегралыг дифференциал тэмдгийн доор оруулан авдаг.

Тийм ч учраас,

Үүссэн интегралын хуваагчийг өөрчилье:

Тиймээс,

Гурав дахь төрлийн энгийн бутархайг нэгтгэх томъёо нь дараах хэлбэртэй байна.

Жишээ.

Тодорхойгүй интегралыг ол .

Шийдэл.

Бид үүссэн томъёог ашиглана:

Хэрэв бидэнд энэ томъёо байхгүй байсан бол бид юу хийх байсан бэ?

Хуудасны дээд талд

Дөрөв дэх төрлийн энгийн бутархайг нэгтгэх

Эхний алхам бол үүнийг дифференциал тэмдгийн доор тавих явдал юм.

Хоёрдахь алхам бол маягтын интегралыг олох явдал юм . Энэ төрлийн интегралуудыг давтагдах томьёо ашиглан олно. (Дахин давтагдах томъёог ашиглан нэгтгэх хэсгийг үзнэ үү.) Дараах давтагдах томъёо нь манай тохиолдолд тохиромжтой.

Жишээ.

Тодорхойгүй интегралыг ол

Шийдэл.

Энэ төрлийн интегралын хувьд бид орлуулах аргыг ашигладаг. Шинэ хувьсагчийг танилцуулъя (Интеграцийн хэсгийг үзнэ үү иррациональ функцууд):

Орлуулсны дараа бидэнд:

Бид дөрөв дэх төрлийн бутархайн интегралыг олохоор ирсэн. Манай тохиолдолд коэффициентүүд байдаг M = 0, p = 0, q = 1, N = 1Тэгээд n=3. Бид давтагдах томъёог ашигладаг:

Урвуу орлуулсны дараа бид дараах үр дүнг авна.

Интеграци тригонометрийн функцууд

1.Хэлбэрийн интеграл Тригонометрийн функцүүдийн үржвэрийг нийлбэр болгон хувиргах замаар тооцоолно: Жишээ нь: 2.Хэлбэрийн интеграл , Хаана мэсвэл n– сондгой эерэг тоо, үүнийг дифференциал тэмдгийн доор оруулан тооцно. Жишээлбэл, 3.Хэлбэрийн интеграл , Хаана мТэгээд n- тэр ч байтугай эерэг тоонууд, хүчийг бууруулах томъёог ашиглан тооцоолно: Жишээлбэл, 4. Интеграл хувьсагчийг өөрчилснөөр тооцоолно: эсвэл Жишээ нь, 5. Дараа нь бүх нийтийн тригонометрийн орлуулалтыг ашиглан хэлбэрийн интегралуудыг рационал бутархайн интеграл болгон бууруулна. =[тоолох ба хуваагчийг ]= хуваасны дараа ; Жишээлбэл, Бүх нийтийн орлуулалтыг ашиглах нь ихэвчлэн төвөгтэй тооцоололд хүргэдэг гэдгийг тэмдэглэх нь зүйтэй.

§5. Хамгийн энгийн зохисгүй байдлын интеграцчлал

Иррационалийн хамгийн энгийн төрлүүдийг нэгтгэх аргуудыг авч үзье. 1. Энэ төрлийн функцүүд нь 3-р төрлийн хамгийн энгийн рационал бутархайтай ижил аргаар нэгтгэгддэг: хуваарьт дөрвөлжин гурвалсан хэсгээс бүрэн квадратыг тусгаарлаж, шинэ хувьсагчийг оруулсан болно. Жишээ. 2. (интеграл тэмдгийн дор - аргументуудын оновчтой функц). Энэ төрлийн интегралыг орлуулах аргыг ашиглан тооцдог. Ялангуяа интеграл хэлбэрээр бид тэмдэглэдэг. Хэрэв интегралд өөр өөр зэрэгтэй үндэс байвал: , дараа нь хаана заана n– тоонуудын хамгийн бага нийтлэг үржвэр м,к. Жишээ 1. Жишээ 2. -буруу рационал бутархай, бүхэл хэсгийг сонгоно уу: – – – 3.Хэлбэрийн интеграл Тригонометрийн орлуулалтыг ашиглан тооцоолно:

44

45 Тодорхой интеграл

Тодорхой интеграл- хосуудын багц дээр тодорхойлогдсон нэмэлт монотон хэвийн функц, эхний бүрэлдэхүүн хэсэг нь интегралдах функц эсвэл функциональ, хоёр дахь нь энэ функцийг (функциональ) тодорхойлсон багц дахь домэйн юм.

Тодорхойлолт

-д тодорхойлогдох болно. Үүнийг хэд хэдэн дурын цэгүүдтэй хэсгүүдэд хуваацгаая. Дараа нь тэд сегментийг хуваасан гэж хэлдэг.Дараа нь дурын цэгийг сонго , ,

Интервал дээрх функцийн тодорхой интеграл нь хуваалт болон цэгийн сонголтоос хамааралгүй оршдог бол хуваалтын зэрэглэл тэг болох хандлагатай байдаг тул интеграл нийлбэрийн хязгаар юм.

Хэрэв заасан хязгаар байгаа бол функцийг Риманы интеграл гэж үзнэ.

Тэмдэглэл

· - доод хязгаар.

· - дээд хязгаар.

· - интеграл функц.

· - хэсэгчилсэн сегментийн урт.

· - харгалзах хуваалт дээрх функцийн интеграл нийлбэр.

· - хэсэгчилсэн сегментийн хамгийн их урт.

Үл хөдлөх хөрөнгө

Хэрэв функц нь Риман дээр интегралдах боломжтой бол түүн дээр хязгаарлагдана.

Геометрийн утга

Тодорхой интеграл нь дүрсийн талбай юм

Тоон хувьд тодорхой интеграл талбайтай тэнцүүх тэнхлэг, шулуун шугам, функцийн графикаар хязгаарлагдсан дүрс.

Ньютон-Лейбницийн теорем

[засварлах]

("Ньютон-Лейбницийн Формула" -аас өөрчилсөн)

Ньютон-Лейбницийн томъёоэсвэл шинжилгээний үндсэн теоремтодорхой интеграл авах ба эсрэг деривативыг тооцоолох гэсэн хоёр үйлдлийн хоорондын хамаарлыг өгдөг.

Баталгаа

Интегралдах функцийг интервал дээр өгье. Үүнийг тэмдэглэж эхэлцгээе

өөрөөр хэлбэл сегмент дээрх тодорхой интеграл дахь тэмдгийн доор аль үсэг (эсвэл) байх нь хамаагүй.

Дурын утгыг тогтоож, тодорхойлъё шинэ шинж тэмдэг . Энэ нь -ийн бүх утгын хувьд тодорхойлогддог, учир нь хэрэв on -ийн интеграл байгаа бол on -ын интеграл байдаг гэдгийг бид мэднэ. Тодорхойлолтоор авч үзсэнээ эргэн санацгаая

(1)

анзаараарай, тэр

Энэ нь интервал дээр тасралтгүй байгааг харуулъя. Үнэн хэрэгтээ, зөвшөөрөх; Дараа нь

мөн хэрэв , тэгвэл

Тиймээс энэ нь тасалдалтай эсэхээс үл хамааран тасралтгүй үргэлжилдэг; дээр нэгтгэх боломжтой байх нь чухал юм.

Зураг нь графикийг харуулж байна. Хувьсагчийн зургийн талбай нь . Түүний өсөлт нь зургийн талбайтай тэнцүү байна , энэ нь хязгаарлагдмал байдлаасаа шалтгаалан тасралтгүй эсвэл тасалдал, жишээ нь цэг байхаас үл хамааран тэг рүү чиглэх хандлагатай байдаг.

Одоо функц нь зөвхөн дээр интегралдах төдийгүй цэг дээр тасралтгүй байх болно. Энэ цэг дэх дериватив нь тэнцүү гэдгийг баталцгаая

(2)

Үнэн хэрэгтээ, заасан цэгийн хувьд

(1) , (3)

Бид , , TO -тай харьцангуй тогтмол байдаг тул тавьдаг . Цаашилбал, нэг цэг дэх тасралтгүй байдлын улмаас хэн ч үүнийг зааж өгч болно.

Энэ нь тэгш бус байдлын зүүн тал нь o(1) болохыг баталж байна.

(3)-д заасан хязгаарт шилжих нь тухайн цэг дэх дериватив байгаа ба тэгш байдлын (2) хүчин төгөлдөр болохыг харуулж байна. Бид энд тус тус баруун болон зүүн деривативуудын талаар ярьж байгаа бол.

Хэрэв функц нь дээр үргэлжилсэн бол дээр батлагдсан зүйл дээр үндэслэн харгалзах функц байна

(4)

-тэй тэнцүү дериватив байна. Тиймээс функц нь -ийн эсрэг дериватив юм.

Энэ дүгнэлтийг заримдаа хувьсагчийн дээд хязгаарын интеграл теорем эсвэл Барроугийн теорем гэж нэрлэдэг.

Интервал дээр үргэлжилсэн дурын функц нь (4) тэгшитгэлээр тодорхойлогддог энэ интервал дээр эсрэг деривативтай болохыг бид нотолсон. Энэ нь интервал дээр үргэлжилсэн аливаа функцийн эсрэг дериватив байдгийг нотолж байна.

-д функцийн дурын эсрэг дериватив байцгаая. Зарим тогтмол хаана байдгийг бид мэднэ. Энэ тэгш байдлыг харгалзан үзээд бид .

Ийнхүү, . Гэхдээ

Буруу интеграл

[засварлах]

Википедиагийн материал - үнэгүй нэвтэрхий толь

Тодорхой интегралдуудсан чинийх биш, дор хаяж нэг нөхцөл хангагдсан бол:

· a эсвэл b хязгаар (эсвэл хоёр хязгаар) хязгааргүй;

· f(x) функц нь сегмент дотор нэг буюу хэд хэдэн таслах цэгтэй байна.

[Засварлах]Эхний төрлийн буруу интегралууд

. Дараа нь:

1. Хэрэв ба интеграл гэж нэрлэдэг . Энэ тохиолдолд конвергент гэж нэрлэдэг.

, эсвэл зүгээр л ялгаатай.

ба-аас олонлог дээр тодорхойлогдсон ба үргэлжилсэн байг . Дараа нь:

1. Хэрэв , дараа нь тэмдэглэгээг ашиглана ба интеграл гэж нэрлэдэг Эхний төрлийн буруу Риманы интеграл. Энэ тохиолдолд конвергент гэж нэрлэдэг.

2. Төгсгөл гэж байхгүй бол (эсвэл ), тэгвэл интеграл нь хуваагдана гэж хэлнэ , эсвэл зүгээр л ялгаатай.

Хэрэв функц тодорхойлогдсон бөгөөд бүхэл тоон мөрөнд тасралтгүй байвал энэ функцийн интегралын хоёр хязгааргүй хязгаар бүхий буруу интеграл байж болох бөгөөд үүнийг томъёогоор тодорхойлно.

, энд c нь дурын тоо юм.

[засварлах] Эхний төрлийн буруу интегралын геометрийн утга

Буруу интеграл нь хязгааргүй урт муруй трапецын талбайг илэрхийлдэг.

[засварлах] Жишээ

[Засварлах]Хоёр дахь төрлийн буруу интегралууд

-д тодорхойлогдсон байг, x=a цэгт хязгааргүй тасалдлыг амсах ба . Дараа нь:

1. Хэрэв , дараа нь тэмдэглэгээг ашиглана ба интеграл гэж нэрлэдэг

дивергент гэж нэрлэдэг , эсвэл зүгээр л ялгаатай.

-д тодорхойлогдсон байг, x=b ба үед хязгааргүй тасалдлыг амсдаг . Дараа нь:

1. Хэрэв , дараа нь тэмдэглэгээг ашиглана ба интеграл гэж нэрлэдэг Хоёр дахь төрлийн зохисгүй Риманы интеграл. Энэ тохиолдолд интегралыг конвергент гэж нэрлэдэг.

2. Хэрэв эсвэл байвал тэмдэглэгээ хэвээр үлдэнэ, ба дивергент гэж нэрлэдэг , эсвэл зүгээр л ялгаатай.

Хэрэв функц сегментийн дотоод цэг дээр тасалдсан бол хоёр дахь төрлийн зохисгүй интегралыг дараах томъёогоор тодорхойлно.

[засварлах] Хоёр дахь төрлийн буруу интегралын геометрийн утга

Буруу интеграл нь хязгааргүй өндөр муруй трапецын талбайг илэрхийлдэг

[засварлах] Жишээ

[засварлах] Тусгаарлагдсан тохиолдол

Функцийг бүхэл тооны шулуун дээр тодорхойлж, цэгүүд дээр тасалдалтай байг.

Дараа нь бид зохисгүй интегралыг олж чадна

[засварлах] Коши шалгуур

1. ба-аас олонлог дээр тодорхойлогдоно .

Дараа нь нийлдэг

2. болон дээр тодорхойлогдоно .

Дараа нь нийлдэг

[засварлах]Үнэмлэхүй нэгдэл

Интеграл дуудсан туйлын нэгдмэл, Хэрэв нийлдэг.
Хэрэв интеграл үнэмлэхүй нийлж байвал нийлнэ.

[засварлах]Нөхцөлт нийлэлт

Интеграл гэж нэрлэдэг нөхцөлт нийлдэг, хэрвээ энэ нь нийлж байгаа боловч зөрөөд байвал.

48 12. Буруу интеграл.

Тодорхой интегралуудыг авч үзэхдээ бид интеграцийн бүсийг хязгаарлагдмал гэж үзсэн (илүү тодорхой хэлбэл энэ нь сегмент юм. а ,б ]); Тодорхой интеграл байхын тулд интеграл нь [ дээр хязгаарлагдах ёстой. а ,б ]. Бид залгах болно тодорхой интеграл, эдгээр хоёр нөхцөл хангагдсан (интеграцын домэйн болон интеграл функцийн аль алиных нь хязгаарлагдмал байдал) эзэмшдэг; Эдгээр шаардлагыг зөрчсөн интегралууд (жишээ нь интеграл эсвэл интеграцийн хүрээ хязгааргүй, эсвэл хоёулаа) чинийх биш. Энэ хэсэгт бид зохисгүй интегралуудыг судлах болно.

• 12.1. Хязгааргүй интервал дээрх буруу интеграл (эхний төрлийн буруу интеграл).
• 12.1.1. Хязгааргүй интервал дахь зохисгүй интегралын тодорхойлолт. Жишээ.
• 12.1.2. Буруу интегралын Ньютон-Лейбницийн томъёо.
• 12.1.3. Сөрөг бус функцүүдийн харьцуулах шалгуур.
• 12.1.3.1. Харьцуулалтын тэмдэг.
• 12.1.3.2. Хэт хэлбэрийн харьцуулалтын шинж тэмдэг.
• 12.1.4. Хязгааргүй интервал дахь зохисгүй интегралуудын үнэмлэхүй нэгдэл.
• 12.1.5. Абел ба Дирихлетийн нэгдмэл байдлын тестүүд.
• 12.2. -ийн буруу интегралууд хязгааргүй функцууд(хоёр дахь төрлийн буруу интеграл).
• 12.2.1. Хязгааргүй функцийн буруу интегралын тодорхойлолт.
• 12.2.1.1. Онцгой байдал нь интеграцийн интервалын зүүн төгсгөлд байна.
• 12.2.1.2. Ньютон-Лейбницийн томъёоны хэрэглээ.
• 12.2.1.3. Интеграцийн интервалын баруун төгсгөлд байгаа онцгой байдал.
• 12.2.1.4. Интеграцийн интервалын дотоод цэг дэх онцгой байдал.
• 12.2.1.5. Интеграцийн интервал дээрх хэд хэдэн онцлог.
• 12.2.2. Сөрөг бус функцүүдийн харьцуулах шалгуур.
• 12.2.2.1. Харьцуулалтын тэмдэг.
• 12.2.2.2. Хэт хэлбэрийн харьцуулалтын шинж тэмдэг.
• 12.2.3. Тасралтгүй функцүүдийн буруу интегралуудын абсолют ба нөхцөлт нийлэлт.
• 12.2.4. Абел ба Дирихлетийн нэгдмэл байдлын тестүүд.

12.1. Хязгааргүй интервал дээрх буруу интеграл

(эхний төрлийн буруу интеграл).

12.1.1. Хязгааргүй интервал дахь зохисгүй интегралын тодорхойлолт. Функцийг зөвшөөр е (x ) нь хагас тэнхлэг дээр тодорхойлогддог бөгөөд аль ч интервалд интегралдах боломжтой [ -аас, эдгээр тохиолдол бүрт харгалзах хязгааруудын оршихуй ба төгсгөлийг илэрхийлдэг. Одоо жишээнүүдийн шийдлүүд илүү энгийн харагдаж байна: .

12.1.3. Сөрөг бус функцүүдийн харьцуулах шалгуур. Энэ хэсэгт бид бүх интегралууд нь тодорхойлолтын бүх талбарт сөрөг биш байна гэж үзэх болно. Одоог хүртэл бид интегралын нийлэлтийг тооцоолох замаар тодорхойлж ирсэн: хэрвээ харгалзах хандлагатай ( эсвэл ) эсрэг деривативын хязгаарлагдмал хязгаар байгаа бол интеграл нийлдэг, үгүй ​​бол энэ нь хуваагддаг. Шийдвэр гаргахдаа практик асуудлуудГэсэн хэдий ч юуны өмнө нэгдлийн бодит үнэнийг тогтоох нь чухал бөгөөд зөвхөн дараа нь интегралыг тооцоолох нь чухал юм (үүнээс гадна эсрэг дериватив нь ихэвчлэн илэрхийлэгддэггүй. үндсэн функцууд). Сөрөг бус функцүүдийн буруу интегралуудын нийлбэр ба салангид байдлыг тооцоолохгүйгээр тогтоох боломжийг олгодог хэд хэдэн теоремуудыг томъёолж, баталцгаая.
12.1.3.1. Харьцуулах тэмдэг. Функцуудыг зөвшөөр е (x ) Мөн g (x ) интеграл

Бутархай-рационал функцийн интеграл.
Тодорхой бус коэффициент арга

Бид бутархайг нэгтгэх ажлыг үргэлжлүүлж байна. Хичээл дээр бид зарим төрлийн бутархайн интегралуудыг аль хэдийн авч үзсэн бөгөөд энэ хичээлийг нэг ёсондоо үргэлжлэл гэж үзэж болно. Материалыг амжилттай ойлгохын тулд интеграцийн үндсэн ур чадвар шаардагддаг тул хэрэв та интегралыг дөнгөж судалж эхэлсэн, өөрөөр хэлбэл та анхлан суралцагч бол нийтлэлээс эхлэх хэрэгтэй. Тодорхой бус интеграл. Шийдлийн жишээ.

Хачирхалтай нь, одоо бид интеграл олох биш, харин ... системийг шийдэх ажилд оролцох болно. шугаман тэгшитгэл. Энэ талаар яаралтайХичээлд хамрагдахыг зөвлөж байна. Тухайлбал, та орлуулах аргуудыг ("сургуулийн арга" ба системийн тэгшитгэлийг улирал бүрээр нэмэх (хасах) арга) сайн мэддэг байх хэрэгтэй.

Бутархай рационал функц гэж юу вэ? Энгийн үгээр хэлбэл, бутархай-рационал функц нь тоологч болон хуваагч нь олон гишүүнт эсвэл олон гишүүнтийн үржвэрийг агуулсан бутархай юм. Түүнээс гадна, фракцууд нь нийтлэлд хэлэлцсэнээс илүү боловсронгуй байдаг Зарим бутархайг нэгтгэх.

Зөв бутархай-рационал функцийг нэгтгэх

Шууд жишээ ба бутархай-рационал функцийн интегралыг шийдэх ердийн алгоритм.

Жишээ 1

1-р алхам.Бутархай рационал функцийн интегралыг шийдэхдээ бидний ҮРГЭЛЖ хийдэг хамгийн эхний зүйл бол дараах асуултыг тодруулах явдал юм. бутархай зөв үү?Энэ алхамыг амаар гүйцэтгэдэг бөгөөд одоо би хэрхэн яаж тайлбарлах болно:

Эхлээд бид тоологчийг хараад олж мэдье ахлах зэрэголон гишүүнт:

Тоолуурын тэргүүлэх хүч нь хоёр юм.

Одоо бид хуваагчийг хараад олж мэдье ахлах зэрэгхуваагч. Мэдээжийн хэрэг бол хаалтуудыг онгойлгож, авчрах явдал юм ижил төстэй нэр томъёо, гэхдээ та үүнийг илүү хялбар хийж чадна тус бүрхаалт доторх хамгийн дээд зэргийг ол

ба оюун ухаанаар үржүүлбэл: - ингээд хуваагчийн дээд зэрэг нь гуравтай тэнцүү байна. Үнэхээр хаалтаа нээвэл гурваас дээш зэрэг авахгүй нь ойлгомжтой.

Дүгнэлт: Тоолуурын үндсэн зэрэг ХАТУУнь хувагчийн хамгийн дээд хүчнээс бага бөгөөд энэ нь бутархай зөв байна гэсэн үг.

Хэрэв орвол энэ жишээндтоологч нь олон гишүүнт 3, 4, 5 гэх мэтийг агуулж байв. градус, дараа нь бутархай байх болно буруу.

Одоо бид зөвхөн зөв бутархай рационал функцуудыг авч үзэх болно. Хичээлийн төгсгөлд тоологчийн зэрэг нь хуваагчаас их буюу тэнцүү байх тохиолдлыг авч үзэх болно.

Алхам 2.Хусагчийг үржвэр болгоё. Бидний хуваагчийг харцгаая:

Ерөнхийдөө энэ нь аль хэдийн хүчин зүйлийн үр дүн юм, гэхдээ бид өөрөөсөө асууж байна: өөр зүйлийг өргөжүүлэх боломжтой юу? Эрүү шүүлтийн объект нь дөрвөлжин гурвалжин байх нь дамжиггүй. Квадрат тэгшитгэлийг шийдвэрлэх:

Ялгаварлан гадуурхах утга нь тэгээс их байгаа нь гурвалсан тоог үржвэрлэх боломжтой гэсэн үг юм.

Ерөнхий дүрэм: Хуваарьт хамааруулж болох БҮХ ЗҮЙЛ - бид үүнийг тооцдог

Шийдлийг боловсруулж эхэлцгээе:

Алхам 3.Тодорхой бус коэффициентийн аргыг ашиглан бид интегралыг энгийн (элементар) бутархайн нийлбэр болгон өргөжүүлдэг. Одоо илүү тодорхой болно.

Интеграл функцээ харцгаая:

Том фракцыг хэд хэдэн жижиг хэсэг болгон хувиргах нь сайхан байх болно гэсэн зөн совингийн бодол ямар нэгэн байдлаар гарч ирдэг. Жишээлбэл, иймэрхүү:

Асуулт гарч ирнэ, үүнийг хийх боломжтой юу? Математик анализын харгалзах теорем нь тайвширч амьсгаа авцгаая - БОЛОМЖТОЙ. Ийм задрал байдаг бөгөөд өвөрмөц юм.

Ганц л барьдаг, магадлал өндөр БаяртайБид мэдэхгүй тул нэр нь тодорхойгүй коэффициентийн арга юм.

Таны таамаглаж байсанчлан биеийн дараачийн хөдөлгөөнүүд ийм байна, битгий хашгир! Тэднийг зүгээр л таних - тэд юутай тэнцүү болохыг олж мэдэхэд чиглэгдэх болно.

Болгоомжтой байгаарай, би зөвхөн нэг удаа дэлгэрэнгүй тайлбарлах болно!

Ингээд бүжиглэж эхэлцгээе:

Зүүн талд бид илэрхийллийг нийтлэг хуваагч болгон бууруулна.

Одоо бид хуваагчаас найдвартай салж чадна (учир нь тэдгээр нь адилхан):

Зүүн талд бид хаалтуудыг нээдэг, гэхдээ одоогоор үл мэдэгдэх коэффициентүүдэд хүрч болохгүй.

Үүний зэрэгцээ бид олон гишүүнтийг үржүүлэх сургуулийн дүрмийг давтана. Би багш байхдаа энэ дүрмийг шулуун царайгаар хэлж сурсан: Олон гишүүнтийг олон гишүүнтээр үржүүлэхийн тулд нэг олон гишүүнт гишүүн бүрийг нөгөө олон гишүүнт гишүүн бүрээр үржүүлэх шаардлагатай..

Тодорхой тайлбарын үүднээс коэффициентүүдийг хаалтанд оруулах нь дээр (хэдийгээр би цаг хэмнэхийн тулд үүнийг хэзээ ч хийдэггүй).

Бид шугаман тэгшитгэлийн системийг бүрдүүлдэг.
Эхлээд бид ахлах зэрэг хайж байна:

Мөн бид системийн эхний тэгшитгэлд холбогдох коэффициентүүдийг бичнэ.

Дараахь зүйлийг сайн санаарай. Баруун талд нь огт s байхгүй бол юу болох байсан бэ? Ямар ч дөрвөлжингүйгээр зүгээр л шоудах байсан гэж бодъё? Энэ тохиолдолд системийн тэгшитгэлийн баруун талд тэг тавих шаардлагатай болно: . Яагаад тэг гэж? Гэхдээ баруун талд та энэ квадратыг үргэлж тэгтэй оноож болно: Хэрэв баруун талд хувьсагч ба/эсвэл чөлөөт гишүүн байхгүй бол системийн харгалзах тэгшитгэлийн баруун талд тэгийг тавина.

Системийн хоёр дахь тэгшитгэлд бид холбогдох коэффициентүүдийг бичнэ.

Эцэст нь, рашаан, бид чөлөөт гишүүдийг сонгодог.

Аа... би нэг ёсондоо тоглоом хийсэн юм. Хошигнолоос гадна математик бол ноцтой шинжлэх ухаан юм. Манай хүрээлэнгийн бүлэгт туслах профессор гишүүн нэр томьёог тоон шугамын дагуу тарааж, томыг нь сонгоно гэж хэлэхэд хэн ч инээгээгүй. Нухацтай ярилцъя. Хэдийгээр... энэ хичээлийн төгсгөлийг харах хүртэл амьдарсан хүн чимээгүйхэн инээмсэглэх болно.

Систем бэлэн байна:

Бид системийг шийддэг:

(1) Эхний тэгшитгэлээс бид үүнийг илэрхийлж, системийн 2, 3-р тэгшитгэлд орлуулна. Үнэн хэрэгтээ өөр тэгшитгэлээс (эсвэл өөр үсгийг) илэрхийлэх боломжтой байсан ч энэ тохиолдолд 1-р тэгшитгэлээс үүнийг илэрхийлэх нь ашигтай байдаг. хамгийн бага магадлал.

(2) Бид 2 ба 3-р тэгшитгэлд ижил төстэй нэр томъёог үзүүлэв.

(3) Бид 2, 3-р тэгшитгэлийг гишүүнээр нэмж, тэгшитгэлийг олж авах бөгөөд үүнээс дараахь зүйлийг гаргана.

(4) Бид үүнийг олж мэдсэн хоёр дахь (эсвэл гурав дахь) тэгшитгэлд орлуулдаг

(5) Орлуулж эхний тэгшитгэлд оруулаад .

Хэрэв танд системийг шийдвэрлэх арга барилд бэрхшээл тулгарвал ангид дадлага хий. Шугаман тэгшитгэлийн системийг хэрхэн шийдэх вэ?

Системийг шийдсэний дараа шалгах нь үргэлж хэрэгтэй байдаг - олсон утгыг орлуулах бүрсистемийн тэгшитгэлийн үр дүнд бүх зүйл "нийсэх" ёстой.

Бараг тэнд. Коэффициентүүд олдсон ба:

Дууссан ажил нь иймэрхүү харагдах ёстой.

Таны харж байгаагаар даалгаврын гол бэрхшээл нь шугаман тэгшитгэлийн системийг зохиох (зөв!) ба шийдвэрлэх (зөв!) байв. Эцсийн шатанд бүх зүйл тийм ч хэцүү биш: бид тодорхойгүй интегралын шугаман шинж чанарыг ашиглаж, нэгтгэдэг. Гурван интеграл бүрийн доор бид "үнэгүй" байгааг анхаарна уу. нарийн төвөгтэй функц, Би ангидаа түүнийг нэгтгэх онцлогуудын талаар ярьсан Тодорхой бус интеграл дахь хувьсагчийг өөрчлөх арга.

Шалгах: Хариултыг ялгана уу:

Анхны интеграл функцийг авсан нь интеграл зөв олдсон гэсэн үг.
Баталгаажуулах явцад бид илэрхийллийг нийтлэг хуваагч болгон багасгах шаардлагатай болсон бөгөөд энэ нь санамсаргүй хэрэг биш юм. Тодорхойгүй коэффициентийн арга ба илэрхийлэлийг нийтлэг хуваагч болгон багасгах арга нь харилцан урвуу үйлдэл юм.

Жишээ 2

Тодорхойгүй интегралыг ол.

Эхний жишээнээс бутархай руу буцъя: . Хуваарьт бүх хүчин зүйлүүд ӨӨР БАЙДГИЙГ анзаарахад амархан. Жишээлбэл, дараах фракцыг өгвөл юу хийх вэ гэсэн асуулт гарч ирнэ. ? Энд бид хуваагчийн зэрэгтэй, эсвэл математикийн хувьд, олон тоо. Нэмж дурдахад хүчин зүйлээр ангилагдах боломжгүй квадрат гурвалж байна (тэгшитгэлийн ялгаварлагч гэдгийг шалгахад хялбар байдаг. сөрөг байна, тиймээс гурвалсан гишүүнийг үржүүлэх боломжгүй). Юу хийх вэ? Энгийн бутархайн нийлбэр болгон өргөтгөх нь иймэрхүү харагдах болно дээд талд нь үл мэдэгдэх коэффициенттэй эсвэл өөр зүйлтэй юу?

Жишээ 3

Функцийг танилцуулна уу

1-р алхам.Бидэнд тохирох бутархай байгаа эсэхийг шалгаж байна
Гол тоологч: 2
Хуваагчийн дээд зэрэг: 8
, энэ нь бутархай зөв гэсэн үг.

Алхам 2.Хуваарьт ямар нэг зүйлийг оруулах боломжтой юу? Мэдээжийн хэрэг үгүй, бүх зүйл аль хэдийн тавигдсан. Дээр дурдсан шалтгааны улмаас дөрвөлжин гурвалжинг бүтээгдэхүүн болгон өргөжүүлэх боломжгүй. Бүрээс. Ажил багатай.

Алхам 3.Бутархай-рационал функцийг энгийн бутархайн нийлбэр гэж төсөөлье.
Энэ тохиолдолд өргөтгөл нь дараах хэлбэртэй байна.

Бидний хуваагчийг харцгаая:
Бутархай-рационал функцийг энгийн бутархайн нийлбэр болгон задлахдаа гурван үндсэн цэгийг ялгаж салгаж болно.

1) Хэрэв хуваагч нь эхний зэрэглэлд "ганцаардсан" хүчин зүйлийг агуулж байвал (бидний тохиолдолд) дээд талд нь тодорхойгүй коэффициент тавьдаг (манай тохиолдолд). 1, 2-р жишээнүүд зөвхөн ийм “ганцаардсан” хүчин зүйлсээс бүрдсэн.

2) Хэрэв хуваагч нь байвал олонүржүүлэгч бол та үүнийг дараах байдлаар задлах хэрэгтэй.
- өөрөөр хэлбэл, "X"-ийн бүх зэрэглэлийг нэгдүгээр зэрэглэлээс n-р зэрэгт дараалан дамжуулна. Бидний жишээн дээр хоёр олон хүчин зүйл байна: мөн , миний өгсөн өргөтгөлийг дахин харж, тэдгээрийг яг энэ дүрмийн дагуу өргөжүүлсэн эсэхийг шалгаарай.

3) Хэрэв хуваагч нь 2-р зэргийн задрах боломжгүй олон гишүүнтэй байвал (бидний тохиолдолд) тоологчийг задлахдаа тодорхойгүй коэффициент бүхий шугаман функцийг бичих хэрэгтэй (бидний тохиолдолд тодорхойгүй коэффициент ба ).

Үнэндээ өөр 4-р тохиолдол бий, гэхдээ практик дээр энэ нь маш ховор тохиолддог тул би энэ талаар чимээгүй байх болно.

Жишээ 4

Функцийг танилцуулна уу үл мэдэгдэх коэффициенттэй энгийн бутархайн нийлбэр.

Энэ бол та өөрөө шийдэх жишээ юм. Бүрэн шийдэлмөн хичээлийн төгсгөлд хариулт.
Алгоритмыг чанд дагаж мөрдөөрэй!

Хэрэв та бутархай-рационал функцийг нийлбэр болгон өргөжүүлэх зарчмуудыг ойлгож байгаа бол авч үзэж буй төрлийн бараг бүх интегралыг зажилж болно.

Жишээ 5

Тодорхойгүй интегралыг ол.

1-р алхам.Мэдээжийн хэрэг, бутархай зөв:

Алхам 2.Хуваарьт ямар нэг зүйлийг оруулах боломжтой юу? Чадах. Энд кубуудын нийлбэр байна . Товчилсон үржүүлэх томъёог ашиглан хуваагчийг хүчин зүйлээр тооц

Алхам 3.Тодорхой бус коэффициентийн аргыг ашиглан бид интегралыг энгийн бутархайн нийлбэр болгон өргөжүүлнэ.

Олон гишүүнтийг үржүүлэх боломжгүй гэдгийг анхаарна уу (дискриминант сөрөг эсэхийг шалгана уу), тиймээс дээд талд нь зөвхөн нэг үсэг биш харин үл мэдэгдэх коэффициент бүхий шугаман функцийг тавьдаг.

Бид бутархайг нийтлэг хуваагч руу авчирдаг:

Системийг зохиож, шийдье:

(1) Бид эхний тэгшитгэлээс илэрхийлж, системийн хоёр дахь тэгшитгэлд орлуулна (энэ бол хамгийн оновчтой арга юм).

(2) Бид хоёр дахь тэгшитгэлд ижил төстэй нэр томъёог үзүүлэв.

(3) Бид системийн гишүүний хоёр ба гурав дахь тэгшитгэлийг гишүүнээр нь нэмдэг.

Систем нь энгийн тул цаашдын бүх тооцоо нь зарчмын хувьд аман байна.

(1) Бид олсон коэффициентүүдийн дагуу бутархайн нийлбэрийг бичнэ.

(2) Бид тодорхойгүй интегралын шугаман шинж чанарыг ашигладаг. Хоёр дахь интегралд юу болсон бэ? Хичээлийн сүүлийн догол мөрөнд та энэ аргатай танилцаж болно. Зарим бутархайг нэгтгэх.

(3) Бид шугаман байдлын шинж чанарыг дахин ашигладаг. Гурав дахь интеграл дээр бид бүтэн квадратыг тусгаарлаж эхэлдэг (хичээлийн төгсгөлийн догол мөр Зарим бутархайг нэгтгэх).

(4) Бид хоёр дахь интегралыг авч, гуравдугаарт бид бүтэн квадратыг сонгоно.

(5) Гурав дахь интегралыг ав. Бэлэн.

Доор харж байгаачлан энгийн функц бүр үндсэн функцээр илэрхийлэгдсэн интегралтай байдаггүй. Иймд интеграл нь энгийн функцээр илэрхийлэгддэг функцүүдийн ангиллыг тодорхойлох нь маш чухал юм. Эдгээр ангиллын хамгийн энгийн нь рационал функцуудын анги юм.

Аливаа рационал функцийг рационал бутархай, өөрөөр хэлбэл хоёр олон гишүүнтийн харьцаагаар илэрхийлж болно.

Аргументийн ерөнхий байдлыг хязгаарлахгүйгээр бид олон гишүүнт нийтлэг үндэсгүй гэж үзэх болно.

Хэрэв тоологчийн зэрэг нь хуваагчаас бага байвал бутархайг зөв, эс бөгөөс бутархайг буруу гэж нэрлэдэг.

Хэрэв бутархай буруу байвал тоологчийг хуваагчаар хуваах замаар (олон гишүүнийг хуваах дүрмийн дагуу) та энэ бутархайг олон гишүүнт ба зарим зөв бутархайн нийлбэрээр илэрхийлж болно.

энд олон гишүүнт, а нь зөв бутархай юм.

Жишээ t. Буруу рационал бутархай өгье

Тоолуурыг хуваагчаар хуваах (олон гишүүнийг хуваах дүрмийг ашиглан) бид олж авна.

Олон гишүүнтийг нэгтгэх нь тийм ч хэцүү биш тул рационал бутархайг нэгтгэх гол бэрхшээл нь зөв рационал бутархайг нэгтгэх явдал юм.

Тодорхойлолт. Маягтын зөв оновчтой бутархай

I, II, III, IV төрлийн энгийн бутархай гэж нэрлэдэг.

I, II, III төрлийн хамгийн энгийн бутархайг нэгтгэх нь тийм ч хэцүү биш тул бид нэмэлт тайлбаргүйгээр тэдгээрийг нэгтгэх болно.

Илүү нарийн төвөгтэй тооцоолол нь IV төрлийн энгийн бутархайг нэгтгэхийг шаарддаг. Энэ төрлийн интегралыг бидэнд өгье:

Өөрчлөлтүүдийг хийцгээе:

Эхний интегралыг орлуулах замаар авна

Хоёрдахь интеграл - бид үүнийг хэлбэрээр бичиж тэмдэглэнэ

Таамаглалаар хуваагчийн үндэс нь нарийн төвөгтэй тул бид дараах байдлаар ажиллана.

Интегралыг хувиргацгаая:

Хэсэгээр нь нэгтгэж, бид байна

Энэ илэрхийллийг тэгш байдал (1) болгон орлуулснаар бид олж авна

Баруун гар тал нь ижил төрлийн интеграл агуулж байгаа боловч интегралын хуваагчийн илтгэгч нэг бага байна; Тиймээс бид үүнийг дамжуулан илэрхийлсэн. Үүнтэй ижил замаар үргэлжлүүлэн бид сайн мэддэг интегралд хүрдэг.