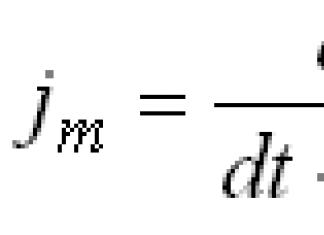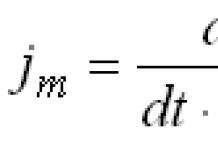Хэсгүүд: Математик

Хичээлийн төрөл: хосолсон.

Хичээлийн зорилго:интеграл ашиглан хувьсгалын биетүүдийн эзлэхүүнийг тооцоолж сурах.

Даалгаварууд:

• хэд хэдэн геометрийн дүрсээс муруйн трапецийг тодорхойлох чадварыг нэгтгэх, муруйн трапецын талбайг тооцоолох чадварыг хөгжүүлэх;
• гурван хэмжээст дүрсийн тухай ойлголттой танилцах;
• хувьсгалын биетүүдийн эзлэхүүнийг тооцоолж сурах;
• хөгжлийг дэмжих логик сэтгэлгээ, чадварлаг математикийн яриа, зураг зурахдаа нарийвчлал;
• сэдвийг сонирхох, мэс засал хийх математикийн ойлголтуудболон дүр төрх, эцсийн үр дүнд хүрэх хүсэл эрмэлзэл, бие даасан байдал, тууштай байдлыг төлөвшүүлэх.

Хичээлийн үеэр

I. Зохион байгуулалтын мөч.

Группээс мэндчилж байна. Хичээлийн зорилгыг оюутнуудад хүргэх.

Тусгал. Тайван аялгуу.

-Би өнөөдрийн хичээлээ сургаалт зүйрлэлээр эхэлмээр байна. “Эрт урьд цагт бүхнийг мэддэг нэгэн мэргэн хүн амьдарч байжээ. Нэгэн хүн мэргэн хүн бүхнийг мэддэггүй гэдгийг батлахыг хүссэн юм. Алгандаа эрвээхэй бариад: "Мэргэн минь, надад хэлээч, аль эрвээхэй миний гарт байна: үхсэн үү эсвэл амьд уу?" Тэгээд тэр өөрөө: "Хэрэв амьд хүн гэвэл би түүнийг ална, үхсэн нь түүнийг суллана гэж хэлэх болно" гэж боддог. Мэргэн бодсоны эцэст хариулав: "Бүх зүйл таны гарт". (Танилцуулга.Слайд)

- Тиймээс өнөөдөр үр бүтээлтэй ажиллаж, шинэ мэдлэг олж авч, олж авсан ур чадвар, чадвараа ирээдүйн амьдрал, практик үйл ажиллагаандаа хэрэгжүүлцгээе. "Бүх зүйл таны гарт".

II. Өмнө нь судалсан материалыг давтах.

- Өмнө нь судалсан материалын гол санааг санацгаая. Үүнийг хийхийн тулд даалгавраа гүйцээцгээе "Нэмэлт үгийг хас."(Слайд.)

(Оюутан ID-д очно. Илүү үгийг арилгахын тулд баллуур ашигладаг.)

- Зөв "Диференциал". Үлдсэн үгсийг нэг гэж нэрлэхийг хичээ ерөнхий утгаараа. (Интеграл тооцоо.)

– Интеграл тооцоололтой холбоотой үндсэн үе шат, ойлголтуудыг санацгаая.

"Математикийн багц".

Дасгал хийх. Цоорхойг нөхөх. (Оюутан гарч ирээд шаардлагатай үгсийг үзгээр бичнэ.)

– Бид дараа нь интегралын хэрэглээний талаарх хураангуйг сонсох болно.

Тэмдэглэлийн дэвтэр дээр ажиллах.

– Ньютон-Лейбницийн томьёог Английн физикч Исаак Ньютон (1643–1727), Германы гүн ухаантан Готфрид Лейбниц (1646–1716) нар гаргаж авсан. Математик бол байгалиасаа ярьдаг хэл учраас энэ нь гайхмаар зүйл биш юм.

- Энэ томъёог практик асуудлыг шийдвэрлэхэд хэрхэн ашигладаг талаар авч үзье.

Жишээ 1: Зургийн талбайг тооцоолох, шугамаар хязгаарлагддаг

Шийдэл: Үргэлжлүүлье координатын хавтгайфункцын графикууд . Зургийн олох шаардлагатай хэсгийг сонгоцгооё.

III. Шинэ материал сурах.

- Дэлгэцэнд анхаарлаа хандуулаарай. Эхний зураг дээр юу харагдаж байна вэ? (Слайд) (Зураг нь хавтгай дүрсийг харуулж байна.)

-Хоёр дахь зурагт юу харагдаж байна вэ? Энэ зураг тэгш үү? (Слайд) (Зураг нь гурван хэмжээст дүрсийг харуулж байна.)

– Сансарт, дэлхий дээр, дотор Өдөр тутмын амьдралБид зөвхөн хавтгай дүрстэй төдийгүй гурван хэмжээст дүрстэй тулгардаг, гэхдээ ийм биетүүдийн эзэлхүүнийг хэрхэн тооцоолох вэ? Жишээлбэл, гариг, сүүлт од, солир гэх мэт эзэлхүүн.

– Хүмүүс байшин барихдаа ч, нэг савнаас нөгөө сав руу ус асгахдаа ч эзлэхүүнийг боддог. Эзлэхүүнийг тооцоолох дүрэм, техник гарч ирэх ёстой байсан бөгөөд тэдгээр нь хэр үнэн зөв, үндэслэлтэй байсан нь өөр асуудал юм.

Оюутны мессеж. (Тюрина Вера.)

1612 он бол алдарт одон орон судлаач Иоганнес Кеплерийн амьдарч байсан Австрийн Линц хотын оршин суугчдын хувьд, ялангуяа усан үзмийн хувьд маш их үр өгөөжтэй жил байв. Хүмүүс дарсны торх бэлтгэж, түүний хэмжээг хэрхэн бодитоор тодорхойлохыг мэдэхийг хүсч байв. (Слайд 2)

- Тиймээс Кеплерийн авч үзсэн бүтээлүүд нь 17-р зууны сүүлийн улиралд оргилдоо хүрсэн бүхэл бүтэн судалгааны үндэс суурийг тавьсан юм. I. Newton, G.V нарын бүтээлүүд дэх дизайн. Лейбниц дифференциал ба интегралын тооцоо. Энэ үеэс эхлэн хувьсагчийн математик математикийн мэдлэгийн системд тэргүүлэх байр суурийг эзэлдэг.

- Өнөөдөр та бид хоёр ийм практик үйл ажиллагаа явуулах болно, тиймээс

Бидний хичээлийн сэдэв: "Тодорхой интеграл ашиглан эргэлтийн биеийн эзлэхүүнийг тооцоолох." (Слайд)

– Та дараах даалгаврыг гүйцэтгэснээр эргэлтийн биеийн тодорхойлолтыг сурах болно.

"Лабиринт".

Лабиринт (грек үг) нь газар доогуур орох гэсэн утгатай. Лабиринт бол зам, гарц, хоорондоо холбогдсон өрөөнүүдийн нарийн төвөгтэй сүлжээ юм.

Гэхдээ энэ тодорхойлолт нь "эвдэрсэн" байсан бөгөөд сум хэлбэрээр сэжүүр үлдээжээ.

Дасгал хийх. Төөрөгдөлтэй нөхцөл байдлаас гарах арга замыг хайж, тодорхойлолтыг бич.

Слайд. “Газрын зургийн заавар” Эзлэхүүнийг тооцоолох.

Тодорхой интеграл ашиглан та тодорхой биеийн эзэлхүүнийг, тухайлбал эргэлтийн биеийг тооцоолж болно.

Хувьсгалт бие нь муруй трапецийг суурийн эргэн тойронд эргүүлснээр олж авсан бие юм (Зураг 1, 2).

Эргэлтийн биеийн эзэлхүүнийг томъёоны аль нэгийг ашиглан тооцоолно.

1. OX тэнхлэгийн эргэн тойронд.

2. , хэрэв муруй трапецын эргэлт op-amp-ийн тэнхлэгийн эргэн тойронд.

Оюутан бүр зааврын карт авдаг. Багш гол санааг онцолдог.

– Багш самбар дээрх жишээнүүдийн шийдлийг тайлбарлана.

-ээс ишлэл авч үзье алдартай үлгэрА.С.Пушкин "Цар Салтан, түүний алдарт, хүчирхэг баатар хунтайж Гидон Салтанович ба үзэсгэлэнт хун гүнжийн тухай үлгэр" (Слайд 4):

…..
Тэгээд согтуу элч авчирсан
Тухайн өдөр захиалга дараах байдалтай байна.
"Хаан боярууддаа тушаажээ.
Цаг алдахгүйгээр,
Мөн хатан ба үр удам
Усны ангал руу нууцаар хая."
Хийх зүйл алга: бойяр,
Тусгаар тогтнолын төлөө санаа зовж байна
Мөн залуу хатанд,
Түүний унтлагын өрөөнд олон хүн ирэв.
Тэд хааны хүслийг тунхаглав -
Тэр болон түүний хүү муу хувьтай,
Бид тогтоолыг чангаар уншиж,
Мөн яг тэр цагт хатан хаан
Тэд намайг хүүтэйгээ хамт торхонд хийж,
Тэд шавар шавхаж, машинаа жолоодов
Тэгээд тэд намайг окиян руу оруулав -
Энэ бол Салтан хаан зарлиг болсон юм.

Торхны эзэлхүүн ямар байх ёстой вэ гэвэл хатан хүү хоёр түүнд багтах уу?

- Дараах ажлуудыг анхаарч үзээрэй

1. Шулуунаар хүрээлэгдсэн муруйн трапецын ординатын тэнхлэгийг тойрон эргэснээр олж авсан биеийн эзэлхүүнийг ол. x 2 + y 2 = 64, y = -5, y = 5, x = 0.

Хариулт: 1163 см 3 .

Парабол трапецийг абсцисса тэнхлэгийг тойруулан эргүүлснээр олж авсан биеийн эзэлхүүнийг ол y = , x = 4, y = 0.

IV. Шинэ материалыг нэгтгэх

Жишээ 2. Дэлбээ нь х тэнхлэгийг тойрон эргэхэд үүссэн биеийн эзэлхүүнийг тооцоол. y = x 2 , y 2 = x.

Функцийн графикуудыг байгуулъя. y = x 2 , y 2 = x. Хуваарь y2 = xхэлбэрт шилжүүлэх y= .

Бидэнд байгаа V = V 1 – V 2Функц бүрийн эзлэхүүнийг тооцоолъё

-Одоо Оросын алдарт инженер, гавьяат академич В.Г.Шуховын загвараар баригдсан Москвагийн Шаболовка дахь радио станцын цамхагийг харцгаая. Энэ нь эргэлтийн гиперболоид хэсгүүдээс бүрдэнэ. Түүнээс гадна тэдгээр нь тус бүр нь зэргэлдээ тойргийг холбосон шулуун металл саваагаар хийгдсэн байдаг (Зураг 8, 9).

- Асуудлыг авч үзье.

Гиперболын нумуудыг эргүүлснээр олж авсан биеийн эзэлхүүнийг ол Зурагт үзүүлсэн шиг түүний төсөөллийн тэнхлэгийн эргэн тойронд. 8, хаана

шоо нэгж

Бүлгийн даалгавар. Сурагчид даалгавраар сугалаа сугалж, ватман цаасан дээр зураг зурж, бүлгийн төлөөлөгчдийн нэг нь ажлыг хамгаална.

1-р бүлэг.

Цохих! Цохих! Өөр нэг цохилт!
Бөмбөг хаалга руу нисдэг - BALL!
Мөн энэ бол тарвасны бөмбөг юм
Ногоон, дугуй, амттай.
Илүү сайн хараарай - ямар бөмбөг вэ!
Энэ нь тойргоос өөр юу ч биш юм.
Тарвасыг дугуйлан хайчилж ав
Мөн тэдгээрийг амтлаарай.

Хязгаарлагдмал функцийн OX тэнхлэгийг тойрон эргүүлснээр олж авсан биеийн эзэлхүүнийг ол

Алдаа! Хавчуурга тодорхойлогдоогүй байна.

- Энэ хүн хаана таарч байгааг хэлж өгөөч?

Байшин. 1 бүлгийн даалгавар. ЦИЛИНДР (слайд) .

"Цилиндр - энэ юу вэ?" - Би ааваасаа асуув.
Аав инээгээд: Дээд талын малгай бол малгай.
Зөв санаатай байхын тулд
Цилиндр бол цагаан тугалга лааз гэж хэлье.
Уурын завины хоолой - цилиндр,
Манай дээвэр дээрх хоолой бас

Бүх хоолой нь цилиндртэй төстэй.
Би ийм жишээ өгсөн -
Калейдоскоп Миний хайр,
Чи түүнээс нүдээ салгаж чадахгүй
Мөн энэ нь цилиндр шиг харагдаж байна.

- Дасгал хийх. Гэрийн даалгаварфункцийн графикийг зурж, эзлэхүүнийг тооцоол.

2-р бүлэг. КОНУСАН (слайд).

Ээж: Тэгээд одоо
Миний түүх конусын тухай байх болно.
Өндөр малгайтай оддыг харагч
Жилийн турш оддыг тоолдог.
CONE - оддыг ажиглагчийн малгай.
Тэр ийм л хүн. Ойлгосон уу? Ингээд л болоо.
Ээж нь ширээний ард зогсож байсан,
Би лонхонд тос асгав.
-Юүлүүр хаана байдаг вэ? Юүлүүр байхгүй.
Үүнийг хай. Хажуу талд бүү зогс.
- Ээж ээ, би хөдлөхгүй.
Конусын талаар илүү ихийг хэлээрэй.
– Юүлүүр нь услах савны конус хэлбэртэй.
Алив, түүнийг надад хурдан олоорой.
Би юүлүүр олдсонгүй
Гэхдээ ээж цүнх хийсэн,
Би цаасан цаасыг хуруугаараа ороов
Тэгээд тэр үүнийг цаасан хавчаараар овжиноор бэхэлсэн.
Газрын тос урсаж байна, ээж баяртай байна,
Конус яг л гарч ирэв.

Дасгал хийх. Абсцисса тэнхлэгийг тойрон эргэснээр олж авсан биеийн эзэлхүүнийг тооцоол

Байшин. 2-р бүлгийн даалгавар. ПИРАМИД(слайд).

Би зургийг харсан. Энэ зурган дээр
Элсэн цөлд ПИРАМИД байдаг.
Пирамид дахь бүх зүйл ер бусын,
Үүнд ямар нэгэн нууцлаг, нууцлаг зүйл байдаг.
Улаан талбай дээрх Спасская цамхаг
Энэ нь хүүхэд, насанд хүрэгчдэд маш сайн танил юм.
Хэрэв та цамхаг руу харвал энэ нь энгийн харагдаж байна.
Дээрээс нь юу байгаа юм бэ? Пирамид!

Дасгал хийх.Гэрийн даалгавар: функцийн графикийг зурж, пирамидын эзэлхүүнийг тооцоолох

- Эзлэхүүн өөр өөр биебид интеграл ашиглан биеийн эзэлхүүний үндсэн томъёонд үндэслэн тооцоолсон.

Энэ нь тодорхой интеграл нь математикийн судалгаанд үндэс суурь болж байгаагийн бас нэг баталгаа юм.

-За одоо жаахан амарцгаая.

Хос олоорой.

Математикийн домино аялгуу тоглодог.

"Миний хайж байсан зам хэзээ ч мартагдахгүй ..."

Судалгааны ажил. Интегралыг эдийн засаг, технологид ашиглах.

Хүчтэй оюутнууд болон математикийн хөлбөмбөгт зориулсан тестүүд.

Математикийн симулятор.

2. Өгөгдсөн функцийн бүх эсрэг деривативуудын олонлогийг нэрлэнэ

A) тодорхойгүй интеграл;

B) функц,

B) ялгах.

7. Шулуунаар хязгаарлагдсан муруйн трапецын абсцисса тэнхлэгийг тойрон эргэснээр олж авсан биеийн эзэлхүүнийг ол.

Д/З. Эргэлтийн биеийн эзэлхүүнийг тооцоол.

Тусгал.

Маягт дахь тусгалыг хүлээн авах syncwine(таван мөр).

1-р мөр - сэдвийн нэр (нэг нэр үг).

2-р мөрөнд - сэдвийг хоёр үг, хоёр нэр томъёогоор тайлбарлана.

3-р мөрөнд - энэ сэдвийн хүрээнд хийсэн үйлдлийг гурван үгээр тайлбарлана.

4-р мөр нь сэдэвт хандах хандлагыг харуулсан дөрвөн үгийн хэллэг юм (бүхэл бүтэн өгүүлбэр).

5-р мөр нь сэдвийн мөн чанарыг давтдаг ижил утгатай үг юм.

1. Эзлэхүүн.
2. Тодорхой интеграл,интегралдах функц.
3. Бид бүтээдэг, эргэдэг, тооцоолдог.
4. Муруй трапецийг эргүүлэх замаар олж авсан бие (түүний суурийн эргэн тойронд).
5. Эргэлтийн бие (эзэлхүүний геометрийн бие).

Дүгнэлт (слайд).

• Тодорхой интеграл нь математикийн судалгааны тодорхой үндэс суурь бөгөөд практик асуудлыг шийдвэрлэхэд орлуулашгүй хувь нэмэр оруулдаг.
• "Интеграл" сэдэв нь математик ба физик, биологи, эдийн засаг, технологийн хоорондын уялдаа холбоог тодорхой харуулж байна.
• Хөгжил орчин үеийн шинжлэх ухаанинтегралыг ашиглахгүйгээр төсөөлөхийн аргагүй юм. Үүнтэй холбогдуулан дунд мэргэжлийн боловсролын хүрээнд үүнийг судалж эхлэх шаардлагатай байна!

Дүгнэлт. (Тайлбарын хамт.)

Агуу Омар Хайям - математикч, яруу найрагч, гүн ухаантан. Тэр биднийг хувь заяаныхаа эзэн байхыг уриалдаг. Ингээд түүний уран бүтээлээс түүвэрлэн сонсоё.

Та энэ амьдрал нэг хором гэж хэлэх болно.
Үүнийг үнэлж, түүнээс урам зориг аваарай.
Үүнийг зарцуулах тусам энэ нь өнгөрөх болно.
Бүү март: тэр бол таны бүтээл.

Бид тодорхой интегралын геометрийн утгыг олж мэдээд х тэнхлэг ба шулуун шугамаар хязгаарлагдсан муруйн трапецын талбайг олоход ашиглаж болох томьёог гаргасан. x = a, x = b, түүнчлэн тасралтгүй (сөрөг эсвэл эерэг биш) функц y = f(x).Заримдаа параметрийн хэлбэрээр дүрсийг хязгаарлах функцийг зааж өгөх нь илүү тохиромжтой байдаг, i.e. t параметрээр функциональ хамаарлыг илэрхийлнэ. Энэ материалд бид тухайн зургийн талбайг параметрийн дагуу тодорхойлсон муруйгаар хязгаарласан бол хэрхэн олохыг харуулах болно.

Онолыг тайлбарлаж, томъёог гаргасны дараа бид ийм тоонуудын талбайг олохын тулд хэд хэдэн ердийн жишээг авч үзэх болно.

Тооцооллын үндсэн томъёо

Хил нь x = a, x = b шулуун шугамууд, O x тэнхлэг ба параметрийн тодорхойлогдсон муруй x = φ (t) y = ψ (t), мөн муруй шугаман трапец байна гэж үзье. x = φ (t) ба y = ψ (t) функцууд α интервал дээр тасралтгүй байна; β, α< β , x = φ (t) будет непрерывно возрастать на нем и φ (α) = a , φ (β) = b .

Тодорхойлолт 1

Ийм нөхцөлд трапецын талбайг тооцоолохын тулд S (G) = ∫ α β ψ (t) · φ "(t) d t томъёог ашиглах хэрэгтэй.

Бид үүнийг муруйн трапецын талбайн томъёоноос S (G) = ∫ a b f (x) d x орлуулах аргаар х = φ (t) y = ψ (t) гаргаж авсан.

S (G) = ∫ a b f (x) d x = ∫ α β ψ (t) d (φ (t)) = ∫ α β ψ (t) φ " (t) d t

Тодорхойлолт 2

β интервал дээр x = φ (t) функцийн монотон бууралтыг харгалзан үзэх; α, β< α , нужная формула принимает вид S (G) = - ∫ β α ψ (t) · φ " (t) d t .

Хэрэв x = φ (t) функц нь үндсэн үндсэн функцүүдийн нэг биш бол функц нь нэмэгдэж, буурах эсэхийг тодорхойлохын тулд интервал дахь функцийг нэмэгдүүлэх, багасгах үндсэн дүрмийг санах хэрэгтэй.

Энэ догол мөрөнд бид дээр дурдсан томъёог ашиглан хэд хэдэн асуудлыг шинжлэх болно.

Жишээ 1

Нөхцөл байдал: x = 2 cos t y = 3 sin t хэлбэрийн тэгшитгэлээр өгөгдсөн шугамаар үүссэн зургийн талбайг ол.

Шийдэл

Бид параметрийн дагуу тодорхойлсон шугамтай. Графикаар үүнийг 2 ба 3-р хагас тэнхлэгтэй эллипс хэлбэрээр үзүүлж болно. Зураг харна уу:

Үүссэн зургийн эхний квадратыг эзэлдэг 1 4 талбайг олохыг хичээцгээе. Тухайн муж нь x ∈ a интервалд байна; b = 0; 2. Дараа нь үүссэн утгыг 4-ээр үржүүлж, бүх зургийн талбайг ол.

Бидний тооцооллын явц энд байна:

x = φ (t) = 2 cos t y = ψ (t) = 3 sin t φ α = a ⇔ 2 cos α = 0 ⇔ α = π 2 + πk , k ∈ Z , φ β = b ⇔ 2 cos β = 2 ⇔ β = 2 πk , k ∈ Z

k нь 0-тэй тэнцүү бол бид β интервалыг авна; α = 0; π 2. X = φ (t) = 2 cos t функц нь үүн дээр монотон буурах болно (дэлгэрэнгүй мэдээллийг үндсэн нийтлэлээс үзнэ үү. үндсэн функцуудба тэдгээрийн шинж чанарууд). Энэ нь та талбайг тооцоолох томъёог хэрэглэж, Ньютон-Лейбницийн томъёог ашиглан тодорхой интегралыг олох боломжтой гэсэн үг юм.

- ∫ 0 π 2 3 sin t · 2 cos t " d t = 6 ∫ 0 π 2 sin 2 t d t = 3 ∫ 0 π 2 (1 - cos (2 t) d t = = 3 · t - sin (2 t) 2 0 π 2 = 3 π 2 - нүгэл 2 π 2 2 - 0 - нүгэл 2 0 2 = 3 π 2

Энэ нь анхны муруйгаар өгөгдсөн зургийн талбай нь S (G) = 4 · 3 π 2 = 6 π-тэй тэнцүү байна гэсэн үг юм.

Хариулт: S(G) = 6π

Дээрх асуудлыг шийдэхдээ эллипсийн дөрөвний нэгийг төдийгүй түүний талыг буюу дээд эсвэл доод хэсгийг авах боломжтой гэдгийг тодруулцгаая. Нэг тал нь x ∈ a интервал дээр байрлана; b = - 2 ; 2. Энэ тохиолдолд бид дараах зүйлсийг хийх болно:

φ (α) = a ⇔ 2 cos α = - 2 ⇔ α = π + π k, k ∈ Z, φ (β) = b ⇔ 2 cos β = 2 ⇔ β = 2 π k, k ∈ Z

Тиймээс k нь 0-тэй тэнцүү бол бид β-ийг авна; α = 0; π. Энэ интервалд x = φ (t) = 2 cos t функц монотон буурна.

Үүний дараа бид хагас эллипсийн талбайг тооцоолно.

- ∫ 0 π 3 sin t · 2 cos t " d t = 6 ∫ 0 π sin 2 t d t = 3 ∫ 0 π (1 - cos (2 t) d t = = 3 · t - sin (2 t) 2 0 π = 3 π - нүгэл 2 π 2 - 0 - нүгэл 2 0 2 = 3 π

Та зөвхөн дээд эсвэл доод хэсгийг авч болно, гэхдээ баруун эсвэл зүүн талыг авч болохгүй гэдгийг анхаарах нь чухал юм.

Та өгөгдсөн эллипсийн хувьд параметрийн тэгшитгэлийг үүсгэж болох бөгөөд түүний төв нь эх цэг дээр байрлана. Энэ нь x = a · cos t y = b · sin t шиг харагдах болно. Дээрх жишээн дээрхтэй ижил аргаар бид S e l ба p эллипсийн талбайг a = πab-ээр тооцоолох томъёог олж авна.

Та x = R · cos t y = R · sin t тэгшитгэлийг ашиглан төв нь эх дээр байрлах тойргийг тодорхойлж болно, энд t нь параметр, R нь энэ тойргийн радиус юм. Хэрэв бид нэн даруй эллипсийн талбайн томъёог ашиглавал R радиустай тойргийн талбайг тооцоолох томъёог авах болно: S k r y r a = πR 2 .

Өөр нэг асуудлыг авч үзье.

Жишээ 2

Нөхцөл: x = 3 cos 3 t y = 2 sin 3 t гэсэн параметрээр тодорхойлогдсон муруйгаар хязгаарлагдсан зургийн талбай ямар хэмжээтэй тэнцүү болохыг ол.

Шийдэл

Энэ муруй нь сунасан астроид хэлбэртэй гэдгийг нэн даруй тодруулцгаая. Ихэвчлэн астроидыг x = a · cos 3 t y = a · sin 3 t хэлбэрийн тэгшитгэлийг ашиглан илэрхийлдэг.

Одоо ийм муруйг хэрхэн яаж барих талаар дэлгэрэнгүй авч үзье. Хувь хүний ​​оноон дээр тулгуурлан бүтээцгээе. Энэ бол хамгийн түгээмэл арга бөгөөд ихэнх ажилд тохиромжтой. Илүү нарийн төвөгтэй жишээнүүдпараметрийн тодорхойлогдсон функцийг тодорхойлохын тулд дифференциал тооцоолол шаарддаг.

Бидэнд x = φ (t) = 3 cos 3 t, y = ψ (t) = 2 sin 3 t байна.

Эдгээр функцууд нь t-ийн бүх бодит утгуудын хувьд тодорхойлогддог. Нүгэл ба cos-ийн хувьд тэдгээр нь үе үе бөгөөд тэдгээрийн хугацаа нь 2 пи байдаг гэдгийг мэддэг. Зарим t = t 0 ∈ 0-ийн хувьд x = φ (t) = 3 cos 3 t, y = ψ (t) = 2 sin 3 t функцуудын утгыг тооцоолсон; 2 π π 8 , π 4 , 3 π 8 , π 2 , . . . , 15 π 8, бид x 0 оноо авдаг; y 0 = (φ (t 0) ; ψ (t 0)) .

Нийт утгын хүснэгтийг хийцгээе:

t 0	0	π 8	π 4	3 π 8	π 2	5 π 8	3 π 4	7 π 8	π
x 0 = φ (t 0)	3	2 . 36	1 . 06	0 . 16	0	- 0 . 16	- 1 . 06	- 2 . 36	- 3
y 0 = ψ (t 0)	0	0 . 11	0 . 70	1 . 57	2	1 . 57	0 . 70	0 . 11	0

t 0	9 π 8	5 π 4	11 π 8	3 π 2	13 π 8	7 π 4	15 π 8	2π
x 0 = φ (t 0)	- 2 . 36	- 1 . 06	- 0 . 16	0	0 . 16	1 . 06	2 . 36	3
y 0 = ψ (t 0)	- 0 . 11	- 0 . 70	- 1 . 57	- 2	- 1 . 57	- 0 . 70	- 0 . 11	0

Үүний дараа онгоцонд шаардлагатай цэгүүдийг тэмдэглэж, тэдгээрийг нэг шугамаар холбоно.

Одоо бид координатын эхний хэсэгт байрлах зургийн хэсгийн талбайг олох хэрэгтэй. Үүний хувьд x ∈ a; b = 0; 3:

φ (α) = a ⇔ 3 cos 3 t = 0 ⇔ α = π 2 + πk , k ∈ Z , φ (β) = b ⇔ 3 cos 3 t = 3 ⇔ β = 2 πk , k ∈ Z

Хэрэв k нь 0-тэй тэнцүү бол β интервалыг авна; α = 0; π 2 , мөн үүн дээр x = φ (t) = 3 cos 3 t функц монотон буурах болно. Одоо бид талбайн томьёог аваад тооцоолно:

- ∫ 0 π 2 2 sin 3 t · 3 cos 3 t " d t = 18 ∫ 0 π 2 sin 4 t · cos 2 t d t = = 18 ∫ 0 π 2 sin 4 t · (1 - sin 2 t) d t = 18 ∫ 0 π 2 sin 4 t d t - ∫ 0 π 2 sin 6 t d t

Бид Ньютон-Лейбницийн томъёогоор тооцоолж болох тодорхой интегралуудыг олж авсан. Энэ томьёоны эсрэг деривативуудыг J n (x) = - cos x · sin n - 1 (x) n + n - 1 n J n - 2 (x) , J n (x) = ∫ гэсэн давтагдах томъёог ашиглан олж болно. нүгэл n x d x.

∫ sin 4 t d t = - cos t · sin 3 t 4 + 3 4 ∫ sin 2 t d t = = - cos t · sin 3 t 4 + 3 4 - cos t · sin t 2 + 1 2 ∫ sin 0 t d t = = - cos t sin 3 t 4 - 3 cos t sin t 8 + 3 8 t + C ⇒ ∫ 0 π 2 sin 4 t d t = - cos t sin 3 t 4 - 3 cos t sin t 8 + 3 8 t 0 π 2 = 3 π 16 ∫ sin 6 t d t = - cos t · sin 5 t 6 + 5 6 ∫ sin 4 t d t ⇒ ∫ 0 π 2 sin 6 t d t = - cos t · sin 5 t 6 0 π 2 + π2 sin 4 t d t = 5 6 3 π 16 = 15 π 96

Бид зургийн дөрөвний нэгийг тооцсон. Энэ нь 18 ∫ 0 π 2 sin 4 t d t - ∫ 0 π 2 sin 6 t d t = 18 3 π 16 - 15 π 96 = 9 π 16-тай тэнцүү байна.

Хэрэв бид энэ утгыг 4-ээр үржүүлбэл бүх зургийн талбайг авна - 9 π 4.

Яг үүнтэй адил бид астроид гаригийн талбайг баталж чадна. тэгшитгэлээр өгөгдсөн x = a · cos 3 t y = a · sin 3 t , S a str o id y = 3 πa 2 8 томьёогоор олдож болох ба зургийн талбай нь x = a шугамаар хязгаарлагдана. · cos 3 t y = b · sin 3 t, S = 3 πab 8 томъёогоор тооцоолно.

Хэрэв та текстэнд алдаа байгааг анзаарсан бол үүнийг тодруулаад Ctrl+Enter дарна уу

Циклоид нуман хаалганы суурийг тойруулан эргэснээр үүссэн биеийн эзэлхүүнийг олъё. Робервал үүнийг олж авсан өндөг хэлбэртэй биеийг (Зураг 5.1) хязгааргүй нимгэн давхаргад хувааж, эдгээр давхаргад цилиндрийг бичиж, эзлэхүүнийг нь нэмсэн. Нотолгоо нь урт, уйтгартай, тийм ч хатуу биш байсан. Тиймээс үүнийг тооцоолохын тулд бид дээд математикт ханддаг. Циклоид тэгшитгэлийг параметрийн аргаар тодорхойлъё.

Интеграл тооцоололд эзлэхүүнийг судлахдаа дараахь тэмдэглэгээг ашиглана.

Хэрэв муруйн трапецийг хязгаарлах муруй нь параметрийн тэгшитгэлээр өгөгдсөн бөгөөд эдгээр тэгшитгэлийн функцууд нь тодорхой интеграл дахь хувьсагчийн өөрчлөлтийн тухай теоремын нөхцлийг хангаж байвал Окс тэнхлэгийг тойрсон трапецын эргэлтийн биеийн эзэлхүүн . томъёогоор тооцоолно:

Энэ томьёог ашиглан өөрт хэрэгтэй эзлэхүүнээ олъё.

Үүнтэй адилаар бид энэ биеийн гадаргууг тооцоолно.

L=((x,y): x=a(t - sin t), y=a(1 - зардал), 0 ? t ? 2р)

Интеграл тооцоололд сегмент дээр параметрийн дагуу тодорхойлсон муруйн х тэнхлэгийг тойрсон эргэлтийн биеийн гадаргуугийн талбайг олох дараах томъёо байдаг (t 0 ?t ?t 1):

Энэ томьёог циклоидын тэгшитгэлд ашигласнаар бид дараах зүйлийг олж авна.

Циклоид нумын эргэлтээс үүссэн өөр гадаргууг авч үзье. Үүний тулд бид циклоидын нуман хаалганы суурьтай харьцуулахад толин тусгал дүрсийг бүтээх ба циклоид болон түүний тусгалаас үүссэн зууван дүрсийг KT тэнхлэгийн эргэн тойронд эргүүлнэ (Зураг 5.2).

Эхлээд КТ тэнхлэгийн эргэн тойронд циклоидын нуман эргэлтээс үүссэн биеийн эзэлхүүнийг олъё. Бид түүний эзлэхүүнийг (*) томъёогоор тооцоолно.

Тиймээс бид энэ манжин хэлбэртэй биеийн хагасын эзэлхүүнийг тооцоолсон. Дараа нь бүх эзлэхүүн тэнцүү байх болно

Хувьсгалын гадаргуугийн талбайн томьёо руу шилжихийн өмнө бид хувьсгалын гадаргуугийн талаар товч томъёолол өгөх болно. Хувьслын гадаргуу, эсвэл ижил зүйл бол хувьсгалт биеийн гадаргуу нь сегментийн эргэлтээс үүссэн орон зайн дүрс юм. ABтэнхлэгийг тойрон муруй Үхэр(доорх зураг).

Дээр дурдсан муруйн сегментээр хязгаарлагдсан муруй трапецийг төсөөлье. Энэ трапецийг ижил тэнхлэгт эргүүлснээр үүссэн бие Үхэр, ба эргэлтийн бие юм. Шулуун шугамын тэнхлэгийн эргэн тойронд эргэлдэж буй тойргийг тооцохгүйгээр хувьсгалын гадаргуу эсвэл хувьсгалт биеийн гадаргуугийн талбай нь түүний гаднах бүрхүүл юм. x = аТэгээд x = б .

Хувьсгалын бие, үүний дагуу түүний гадаргууг тэнхлэгийн эргэн тойронд биш дүрсийг эргүүлэх замаар үүсгэж болно гэдгийг анхаарна уу. Үхэр, мөн тэнхлэгийг тойруулан Өө.

Тэгш өнцөгт координатаар тодорхойлсон эргэлтийн гадаргуугийн талбайг тооцоолох

Тэгшитгэлийг хавтгай дээрх тэгш өнцөгт координатаар оруулъя y = е(x) координатын тэнхлэгийг тойрон эргэх нь эргэлтийн биеийг үүсгэдэг муруйг тодорхойлсон.

Хувьсгалын гадаргуугийн талбайг тооцоолох томъёо нь дараах байдалтай байна.

(1).

Жишээ 1.Түүний тэнхлэгийг тойрон эргэх үед үүссэн параболоидын гадаргуугийн талбайг ол Үхэрөөрчлөлтөд харгалзах параболын нум x-аас x= 0 хүртэл x = а .

Шийдэл. Параболагийн нумыг тодорхойлох функцийг тодорхой илэрхийлье.

Энэ функцийн деривативыг олъё:

Хувьсгалын гадаргуугийн талбайг олохын тулд томьёог ашиглахын өмнө түүний язгуурыг төлөөлдөг интегралын хэсгийг бичиж, тэнд дөнгөж олсон деривативыг орлъё.

Хариулт: Муруйн нумын урт нь байна

.

Жишээ 2.Тэнхлэгийг тойрон эргэхэд үүссэн гадаргуугийн талбайг ол Үхэрастроид.

Шийдэл. Эхний улиралд байрлах астроид гаригийн нэг салбарыг эргүүлснээс үүсэх гадаргуугийн талбайг тооцоолж, 2-оор үржүүлэхэд хангалттай. Асроид тэгшитгэлээс бид орлуулах шаардлагатай функцийг тодорхой илэрхийлэх болно. Эргэлтийн гадаргуугийн талбайг олох томъёо:

.

Бид 0-ээс нэгтгэдэг а:

Параметрээр тодорхойлсон эргэлтийн гадаргуугийн талбайн тооцоо

Хувьсгалын гадаргууг бүрдүүлж буй муруйг параметрийн тэгшитгэлээр өгөгдсөн тохиолдлыг авч үзье

Дараа нь эргэлтийн гадаргуугийн талбайг томъёогоор тооцоолно

(2).

Жишээ 3.Тэнхлэгийг тойрон эргэхэд үүссэн эргэлтийн гадаргуугийн талбайг ол ӨөЦиклоид ба шулуун шугамаар хүрээлэгдсэн дүрс y = а. Циклоидыг параметрийн тэгшитгэлээр тодорхойлно

Шийдэл. Циклоид ба шулуун шугамын огтлолцох цэгүүдийг олъё. Циклоид ба шулуун шугамын тэгшитгэлийг тэгшитгэх y = а, олъё

Үүнээс үзэхэд интеграцийн хил хязгаар нь нийцэж байна

Одоо бид (2) томъёог хэрэглэж болно. Деривативуудыг олцгооё:

Олдсон деривативуудыг орлуулж томъёонд радикал илэрхийллийг бичье.

Энэ илэрхийллийн үндсийг олъё:

.

Олсон зүйлээ томьёо (2)-д орлъё:

.

Сэлгээ хийцгээе:

Тэгээд эцэст нь бид олдог

Илэрхийллийг хувиргахад тригонометрийн томъёог ашигласан

Хариулт: Хувьсгалын гадаргуугийн талбай нь .

Туйлын координатаар тодорхойлсон эргэлтийн гадаргуугийн талбайг тооцоолох

Гадаргууг бүрдүүлдэг муруйг туйлын координатаар тодорхойл.

Талбайг олох асуудлын нэгэн адил танд өөртөө итгэлтэй зурах ур чадвар хэрэгтэй - энэ нь бараг хамгийн чухал зүйл юм (учир нь интеграл нь өөрөө амархан байх болно). Та чадварлаг, хурдан график зурах арга техникийг ашиглаж болно сургалтын материалГрафикийн геометрийн хувиргалт. Гэхдээ үнэндээ би зургийн ач холбогдлын талаар хэд хэдэн удаа хичээл дээр ярьж байсан.

Ерөнхийдөө интеграл тооцоололд маш олон сонирхолтой програмууд байдаг; тодорхой интеграл ашиглан та зургийн талбай, эргэлтийн биеийн эзэлхүүн, нумын урт, эргэлтийн гадаргуугийн талбай болон бусад зүйлийг тооцоолох боломжтой. илүү. Тиймээс хөгжилтэй байх болно, өөдрөг байгаарай!

Заримыг төсөөлөөд үз дээ хавтгай дүрскоординатын хавтгай дээр. Танилцуулсан уу? ... Хэн юу бэлэглэсэн юм бол... =))) Бид аль хэдийн талбайг нь олчихсон. Гэхдээ үүнээс гадна энэ зургийг хоёр аргаар эргүүлж, эргүүлж болно.

- абсцисса тэнхлэгийн эргэн тойронд;
– ордны тэнхлэгийн эргэн тойронд.

Энэ нийтлэлд хоёр тохиолдлыг авч үзэх болно. Эргэлтийн хоёрдахь арга нь ялангуяа сонирхолтой бөгөөд энэ нь хамгийн их хүндрэл учруулдаг боловч үнэн хэрэгтээ шийдэл нь x тэнхлэгийг тойрон илүү түгээмэл эргэлттэй бараг ижил байдаг. Бонус болгон би буцаж очно дүрсийн талбайг олох асуудал, мөн би тэнхлэгийн дагуу хоёр дахь аргаар талбайг хэрхэн олохыг танд хэлье. Материал нь сэдэвт сайн нийцэж байгаа тул энэ нь урамшуулал биш юм.

Хамгийн алдартай эргэлтийн төрлөөс эхэлье.

тэнхлэгийг тойрсон хавтгай дүрс

Жишээ 1

Нэг тэнхлэгийн эргэн тойронд шугамаар хязгаарлагдсан дүрсийг эргүүлснээр олж авсан биеийн эзэлхүүнийг тооцоол.

Шийдэл: Талбайг олох асуудлын нэгэн адил, шийдэл нь хавтгай дүрс зурахаас эхэлдэг. Өөрөөр хэлбэл, хавтгай дээр шугамаар хязгаарлагдсан дүрсийг бүтээх шаардлагатай бөгөөд тэгшитгэл нь тэнхлэгийг зааж өгдөг гэдгийг мартаж болохгүй. Зургийг хэрхэн илүү үр дүнтэй, хурдан дуусгах талаар хуудаснаас олж болно Анхан шатны функцүүдийн график ба шинж чанаруудТэгээд Тодорхой интеграл. Зургийн талбайг хэрхэн тооцоолох вэ. Энэ бол хятадын сануулга бөгөөд энэ мөчид би цаашид ярихгүй.

Энд байгаа зураг нь маш энгийн:

Хүссэн хавтгай дүрсийг цэнхэр өнгөөр ​​сүүдэрлэсэн бөгөөд энэ нь тэнхлэгийг тойрон эргэлддэг бөгөөд үр дүнд нь тэнхлэгт тэгш хэмтэй, бага зэрэг өндгөвч хэлбэртэй нисдэг таваг гарч ирнэ. Үнэн хэрэгтээ, бие нь математикийн нэртэй боловч лавлах номонд байгаа зүйлийг тодруулахаас залхуурсан тул бид цаашаа явлаа.

Хувьсгалын биеийн эзэлхүүнийг хэрхэн тооцоолох вэ?

Хувьсгалын биеийн эзэлхүүнийг томъёогоор тооцоолж болно:

Томъёонд интегралын өмнө тоо байх ёстой. Ийм зүйл тохиолдсон - амьдралд эргэдэг бүх зүйл энэ тогтмолтой холбоотой байдаг.

Дууссан зургаас "a" болон "be" гэсэн интеграцийн хязгаарыг хэрхэн тогтоохыг таахад хялбар гэж бодож байна.

Функц... энэ функц юу вэ? Зургийг харцгаая. Хавтгайн дүрс нь дээд талд байгаа параболын графикаар хязгаарлагддаг. Энэ бол томьёонд тусгагдсан функц юм.

IN практик даалгавархавтгай дүрс нь заримдаа тэнхлэгийн доор байрлаж болно. Энэ нь юу ч өөрчлөгдөхгүй - томьёо дахь интеграл нь квадрат: , тэгэхээр интеграл нь үргэлж сөрөг биш байдаг, энэ нь маш логик юм.

Энэ томъёог ашиглан эргэлтийн биеийн эзэлхүүнийг тооцоолъё.

Өмнө дурьдсанчлан интеграл нь бараг үргэлж энгийн байдаг, гол зүйл бол болгоомжтой байх явдал юм.

Хариулт:

Хариултдаа та хэмжээсийг - куб нэгжийг зааж өгөх ёстой. Өөрөөр хэлбэл, бидний эргэлтийн биед ойролцоогоор 3.35 "шоо" байдаг. Яагаад куб гэж нэгж? Учир нь хамгийн түгээмэл жор. Байж болно шоо см, байж болно Куб метр, магадгүй шоо километр гэх мэт, таны төсөөллөөр нисдэг таваганд хичнээн жижиг ногоон эрчүүд хийж чадах вэ.

Жишээ 2

, , шугамаар хүрээлэгдсэн дүрсийн тэнхлэгийг тойрон эргэхэд үүссэн биеийн эзэлхүүнийг ол.

Энэ бол жишээ юм бие даасан шийдвэр. Бүрэн шийдэлмөн хичээлийн төгсгөлд хариулт.

Практикт ихэвчлэн тулгардаг өөр хоёр төвөгтэй асуудлыг авч үзье.

Жишээ 3

, ба шугамаар хязгаарлагдсан зургийн абсцисса тэнхлэгийг тойрон эргэснээр олж авсан биеийн эзэлхүүнийг тооцоол.

Шийдэл: Зураг дээр тэгшитгэл нь тэнхлэгийг тодорхойлдог гэдгийг мартахгүйгээр , , , шугамаар хязгаарлагдсан хавтгай дүрсийг дүрсэлцгээе.

Хүссэн дүрс нь цэнхэр өнгөөр ​​будагдсан байна. Энэ нь тэнхлэгээ тойрон эргэвэл дөрвөн булантай сюрреал гурилан бүтээгдэхүүн болж хувирдаг.

Эргэлтийн биеийн эзэлхүүнийг тооцоолъё биеийн эзэлхүүний ялгаа.

Эхлээд улаанаар дугуйлсан дүрсийг харцгаая. Энэ нь тэнхлэгийг тойрон эргэх үед таслагдсан конусыг олж авна. Энэ таслагдсан конусын эзэлхүүнийг -ээр тэмдэглэе.

Ногооноор дугуйлсан дүрсийг анхаарч үзээрэй. Хэрэв та энэ дүрсийг тэнхлэгийн эргэн тойронд эргүүлбэл, та бас бага зэрэг жижиг зүсэгдсэн конус авах болно. Түүний эзлэхүүнийг -ээр тэмдэглэе.

Мэдээжийн хэрэг, эзлэхүүний ялгаа нь бидний "пончик" -ийн хэмжээ юм.

Хувьсгалын биеийн эзэлхүүнийг олохын тулд бид стандарт томъёог ашигладаг.

1) Улаанаар дугуйлсан дүрс нь шулуун шугамаар хүрээлэгдсэн тул:

2) Ногооноор дугуйлсан дүрс нь шулуун шугамаар хүрээлэгдсэн тул:

3) Хүссэн эргэлтийн хэмжээ:

Хариулт:

Сонирхолтой нь, энэ тохиолдолд шийдлийг ашиглан шалгаж болно сургуулийн томъёотаслагдсан конусын эзэлхүүнийг тооцоолох.

Шийдвэр нь өөрөө ихэвчлэн богино хэлбэрээр бичигдсэн байдаг.

Одоо жаахан амарч, геометрийн хуурмаг байдлын талаар танд хэлье.

Хүмүүс ихэвчлэн ботьтой холбоотой хуурмаг зүйлтэй байдаг бөгөөд үүнийг Перелман (өөр) номонд анзаарсан байдаг Хөгжилтэй геометр. Шийдвэрлэсэн асуудалд байгаа хавтгай дүрсийг хараарай - энэ нь талбайн хувьд жижиг юм шиг санагдаж, хувьсгалын биеийн эзэлхүүн нь 50 шоо нэгжээс илүү байгаа нь хэтэрхий том юм шиг санагддаг. Дашрамд хэлэхэд, дундаж хүн амьдралынхаа туршид 18 талбайтай өрөөтэй тэнцэх хэмжээний уудаг. метр квадрат, энэ нь эсрэгээрээ хэтэрхий жижиг хэмжээ юм шиг санагддаг.

Ер нь ЗХУ-ын боловсролын систем үнэхээр хамгийн шилдэг нь байсан. Перелманы 1950 онд хэвлэгдсэн ижил ном нь хошин шогийн хэлснээр маш сайн хөгжиж, асуудлын анхны, стандарт бус шийдлүүдийг эрэлхийлж, танд зааж өгдөг. Би саяхан зарим бүлгийг маш их сонирхож уншсан, би үүнийг санал болгож байна, энэ нь хүмүүнлэгийн хүмүүст ч хүртээмжтэй юм. Үгүй ээ, надад чөлөөт цаг, мэдлэг, харилцааны өргөн цар хүрээг санал болгож байна гэж инээмсэглэх шаардлагагүй.

Уянгын ухралт хийсний дараа шийдэх нь зүйтэй юм бүтээлч даалгавар:

Жишээ 4

, , , шугамаар хязгаарлагдсан хавтгай дүрсийн тэнхлэгийг тойрон эргэхэд үүссэн биеийн эзэлхүүнийг тооцоол.

Энэ бол та өөрөө шийдэх жишээ юм. Бүх тохиолдлууд нь хамтлагт тохиолддог гэдгийг анхаарна уу, өөрөөр хэлбэл, нэгтгэх бэлэн хязгаар нь үнэндээ өгсөн байна. Графикуудыг зөв зур тригонометрийн функцууд, тухай хичээлийн материалыг танд сануулъя графикийн геометрийн хувиргалт: хэрэв аргументыг хоёр хуваавал: , дараа нь графикуудыг тэнхлэгийн дагуу хоёр удаа сунгана. Хамгийн багадаа 3-4 оноо олохыг зөвлөж байна тригонометрийн хүснэгтийн дагуузургийг илүү нарийвчлалтай дуусгах. Хичээлийн төгсгөлд бүрэн шийдэл, хариулт. Дашрамд хэлэхэд, даалгаврыг оновчтой биш харин оновчтой шийдэж болно.

Эргэлтийн үед үүссэн биеийн эзэлхүүний тооцоо
тэнхлэгийг тойрсон хавтгай дүрс

Хоёр дахь догол мөр нь эхнийхээс ч илүү сонирхолтой байх болно. Ординат тэнхлэгийн эргэн тойрон дахь эргэлтийн биеийн эзэлхүүнийг тооцоолох ажил нь бас нэлээд байнгын зочин юм. туршилтууд. Замдаа үүнийг анхаарч үзэх болно дүрсийн талбайг олох асуудалХоёрдахь арга нь тэнхлэгийн дагуу нэгтгэх бөгөөд энэ нь ур чадвараа дээшлүүлэх төдийгүй хамгийн ашигтай шийдлийн замыг олоход тань туслах болно. Үүнд амьдралын бодит утга учир бас бий! Математикийн заах аргын багш маань инээмсэглэн дурсахад олон төгсөгчид "Таны хичээл бидэнд маш их тусалсан, одоо бид үр дүнтэй менежерүүд, боловсон хүчнийг оновчтой удирдаж байна" гэж түүнд талархал илэрхийлэв. Энэ завшааныг ашиглаад би түүнд маш их талархаж байгаагаа илэрхийлж байна, ялангуяа олж авсан мэдлэгээ зориулалтын дагуу ашигладаг =).

Би үүнийг хүн бүрт, бүр бүрэн дамми хүртэл зөвлөж байна. Түүнчлэн, хоёр дахь догол мөрөнд сурсан материал нь давхар интегралыг тооцоолоход үнэлж баршгүй тусламж үзүүлэх болно..

Жишээ 5

, , , шугамаар хязгаарлагдсан хавтгай дүрс өгөгдсөн.

1) Эдгээр шугамаар хүрээлэгдсэн хавтгай дүрсийн талбайг ол.
2) Эдгээр шугамаар хязгаарлагдсан хавтгай дүрсийг тэнхлэгийн эргэн тойронд эргүүлснээр олж авсан биеийн эзэлхүүнийг ол.

Анхаар!Хэдийгээр та зөвхөн хоёр дахь цэгийг уншихыг хүсч байсан ч эхлээд Заавалэхнийхийг нь унш!

Шийдэл: Даалгавар нь хоёр хэсгээс бүрдэнэ. Дөрвөлжин талбайгаас эхэлье.

1) Зураг зурцгаая:

Функц нь параболын дээд салбарыг, функц нь параболын доод салбарыг зааж байгааг харахад хялбар байдаг. Бидний өмнө "хажуу талдаа" байдаг өчүүхэн парабол байна.

Хүссэн дүрс, талбайг нь цэнхэр өнгөөр ​​будна.

Зургийн талбайг хэрхэн олох вэ? Үүнийг ангид хэлэлцсэн "ердийн" аргаар олж болно Тодорхой интеграл. Зургийн талбайг хэрхэн тооцоолох вэ. Түүнчлэн, зургийн талбайг талбайн нийлбэрээр олно.
- сегмент дээр ;
- сегмент дээр.

Тийм учраас:

Энэ тохиолдолд ердийн шийдэл яагаад муу байна вэ? Нэгдүгээрт, бид хоёр интеграл авсан. Хоёрдугаарт, интеграл нь үндэс бөгөөд интеграл дахь үндэс нь бэлэг биш бөгөөд үүнээс гадна та интегралын хязгаарыг орлуулахдаа андуурч болно. Үнэн хэрэгтээ интегралууд нь мэдээжийн хэрэг алуурчин биш, гэхдээ практик дээр бүх зүйл илүү гунигтай байж болох юм, би зүгээр л асуудалд "илүү сайн" функцуудыг сонгосон.

Илүү оновчтой шийдэл байдаг: энэ нь урвуу функц руу шилжих, тэнхлэгийн дагуу нэгтгэхээс бүрдэнэ.

Урвуу функцууд руу хэрхэн орох вэ? Товчхондоо та “x”-ийг “y”-ээр илэрхийлэх хэрэгтэй. Эхлээд параболыг харцгаая:

Энэ нь хангалттай, гэхдээ ижил функцийг доод салбараас гаргаж авах боломжтой эсэхийг шалгацгаая:

Шулуун шугамаар энэ нь илүү хялбар байдаг:

Одоо тэнхлэгээ хараарай: тайлбарлахдаа толгойгоо үе үе баруун 90 градусаар хазайлгана уу (энэ нь хошигнол биш!). Бидэнд хэрэгтэй зураг нь улаан тасархай шугамаар тэмдэглэгдсэн сегмент дээр байрладаг. Энэ тохиолдолд сегмент дээр шулуун шугам нь параболын дээгүүр байрладаг бөгөөд энэ нь зургийн талбайг танд аль хэдийн танил болсон томъёог ашиглан олох ёстой гэсэн үг юм. . Томъёонд юу өөрчлөгдсөн бэ? Зүгээр л захидал, өөр юу ч биш.

! Анхаарна уу: Тэнхлэгийн дагуух интеграцийн хязгаарыг тогтоох хэрэгтэй хатуу доороос дээш!

Талбайг олох нь:

Тиймээс сегмент дээр:

Би интеграцчлалыг хэрхэн гүйцэтгэсэн болохыг анхаарна уу, энэ бол хамгийн оновчтой арга бөгөөд даалгаврын дараагийн догол мөрөнд яагаад гэдгийг тодорхой харуулах болно.

Интеграцийн зөв эсэхэд эргэлзэж буй уншигчдын хувьд би деривативуудыг олох болно.

Анхны интеграл функцийг олж авсан бөгөөд энэ нь интеграцчлал зөв хийгдсэн гэсэн үг юм.

Хариулт:

2) Энэ дүрсийг тэнхлэгийн эргэн тойронд эргүүлснээр үүссэн биеийн эзэлхүүнийг тооцоолъё.

Би зургийг арай өөр загвараар дахин зурах болно:

Тиймээс цэнхэр өнгөөр ​​сүүдэрлэсэн дүрс нь тэнхлэгийг тойрон эргэлддэг. Үр дүн нь тэнхлэгээ тойрон эргэлддэг "хөлөөх эрвээхэй" юм.

Эргэлтийн биеийн эзэлхүүнийг олохын тулд бид тэнхлэгийн дагуу нэгтгэх болно. Эхлээд бид урвуу функцууд руу шилжих хэрэгтэй. Үүнийг аль хэдийн хийсэн бөгөөд өмнөх догол мөрөнд дэлгэрэнгүй тайлбарласан болно.

Одоо бид толгойгоо дахин баруун тийш хазайлгаж, дүр төрхөө судалж байна. Эргэлтийн биеийн эзэлхүүнийг эзлэхүүний зөрүүгээр олох нь ойлгомжтой.

Бид улаанаар дугуйлсан дүрсийг тэнхлэгийн эргэн тойронд эргүүлж, тайрсан конус үүсгэдэг. Энэ эзлэхүүнийг -ээр тэмдэглэе.

Бид ногооноор дугуйлсан дүрсийг тэнхлэгийн эргэн тойронд эргүүлж, үүссэн эргэлтийн биеийн эзэлхүүнээр тэмдэглэнэ.

Манай эрвээхэйн эзлэхүүн нь эзлэхүүний зөрүүтэй тэнцүү байна.

Хувьсгалын биеийн эзэлхүүнийг олохын тулд бид дараах томъёог ашигладаг.

Өмнөх догол мөр дэх томъёоноос юугаараа ялгаатай вэ? Зөвхөн захидалд.

Гэхдээ миний саяхан ярьсан интеграцийн давуу талыг олоход илүү хялбар байдаг , эхлээд интегралыг 4-р зэрэглэлд хүргэхээс илүү.

Хариулт:

Гэсэн хэдий ч өвчтэй эрвээхэй биш.

Хэрэв ижил хавтгай дүрсийг тэнхлэгийн эргэн тойронд эргүүлбэл та огт өөр эргэлттэй, өөр эзэлхүүнтэй биеийг олж авах болно гэдгийг анхаарна уу.

Жишээ 6

Шугаман болон тэнхлэгээр хязгаарлагдсан хавтгай дүрс өгөгдсөн.

1) Урвуу функцууд руу орж, хувьсагч дээр нэгтгэх замаар эдгээр шугамаар хязгаарлагдсан хавтгай дүрсийн талбайг ол.
2) Эдгээр шугамаар хязгаарлагдсан хавтгай дүрсийг тэнхлэгийн эргэн тойронд эргүүлснээр олж авсан биеийн эзэлхүүнийг тооцоол.

Энэ бол та өөрөө шийдэх жишээ юм. Сонирхсон хүмүүс зургийн талбайг "ердийн" аргаар олж, 1) цэгийг шалгаж болно. Гэхдээ давтан хэлэхэд, хэрэв та тэнхлэгийн эргэн тойронд хавтгай дүрсийг эргүүлбэл, та өөр эзэлхүүнтэй огт өөр эргэлтийн биеийг авах болно, дашрамд хэлэхэд, зөв ​​хариулт (мөн асуудлыг шийдэх дуртай хүмүүст).

Даалгаврын санал болгож буй хоёр цэгийн бүрэн шийдэл нь хичээлийн төгсгөлд байна.

Тийм ээ, эргэлтийн бие болон интеграцийн хязгаарыг ойлгохын тулд толгойгоо баруун тийш хазайхаа бүү мартаарай!