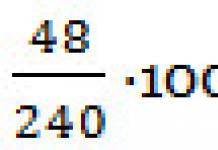Тодорхойлолт 1

$$ сегмент дээрх $y=f(x)$ функцийн эсрэг дериватив $F(x)$ нь энэ сегментийн цэг бүрт ялгах боломжтой функц бөгөөд түүний деривативын хувьд дараах тэгш байдал биелнэ.

Тодорхойлолт 2

Тодорхой сегмент дээр тодорхойлогдсон $y=f(x)$ функцийн бүх эсрэг деривативуудын олонлогийг $y=f(x)$ функцийн тодорхойгүй интеграл гэнэ. Тодорхой бус интегралыг $\int f(x)dx $ тэмдгээр тэмдэглэнэ.

Деривативын хүснэгт ба тодорхойлолт 2-оос бид үндсэн интегралын хүснэгтийг олж авна.

Жишээ 1

7-р томьёоны хүчинтэй эсэхийг интегралын хүснэгтээс шалгана уу.

\[\int tgxdx =-\ln |\cos x|+C,\, \, C=const.\]

Баруун талыг нь ялгаж үзье: $-\ln |\cos x|+C$.

\[\left(-\ln |\cos x|+C\right)"=-\frac(1)(\cos x) \cdot (-\sin x)=\frac(\sin x)(\cos x) =tgx\]

Жишээ 2

Интегралын хүснэгтээс 8-р томьёоны үнэн зөвийг шалгана уу.

\[\int ctgxdx =\ln |\sin x|+C,\, \, C=const.\]

Баруун талыг нь ялгаж үзье: $\ln |\sin x|+C$.

\[\left(\ln |\sin x|\right)"=\frac(1)(\sin x) \cdot \cos x=ctgx\]

Дериватив нь интегралтай тэнцүү болсон. Тиймээс томъёо нь зөв юм.

Жишээ 3

Интегралын хүснэгтээс 11" томъёоны хүчинтэй эсэхийг шалгана уу.

\[\int \frac(dx)(a^(2) +x^(2) ) =\frac(1)(a) arctg\frac(x)(a) +C,\, \, C=const .\]

Баруун талыг нь ялгаж үзье: $\frac(1)(a) arctg\frac(x)(a) +C$.

\[\left(\frac(1)(a) arctg\frac(x)(a) +C\right)"=\frac(1)(a) \cdot \frac(1)(1+\left( \frac(x)(a) \right)^(2) ) \cdot \frac(1)(a) =\frac(1)(a^(2) ) \cdot \frac(a^(2) ) (a^(2) +x^(2) ) \]

Дериватив нь интегралтай тэнцүү болсон. Тиймээс томъёо нь зөв юм.

Жишээ 4

12-р томьёоны хүчинтэй эсэхийг интегралын хүснэгтээс шалгана уу.

\[\int \frac(dx)(a^(2) -x^(2) ) =\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \баруун|+ C,\, \, C=const.\]

Баруун талыг нь ялгаж үзье: $\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \right|+C$.

$\left(\frac(1)(2a) \ln \left|\frac(a+x)(a-x) \right|+C\right)"=\frac(1)(2a) \cdot \frac( 1)(\frac(a+x)(a-x) ) \cdot \left(\frac(a+x)(a-x) \баруун)"=\frac(1)(2a) \cdot \frac(a-x)( a+x) \cdot \frac(a-x+a+x)((a-x)^(2) ) =\frac(1)(2a) \cdot \frac(a-x)(a+x) \cdot \ frac(2a)((a-x)^(2) ) =\frac(1)(a^(2) -x^(2) ) $ Дериватив нь интегралтай тэнцүү болсон. Тиймээс томъёо нь зөв юм.

Жишээ 5

Интегралын хүснэгтээс 13" томъёоны хүчинтэй эсэхийг шалгана уу.

\[\int \frac(dx)(\sqrt(a^(2) -x^(2) ) ) =\arcsin \frac(x)(a) +C,\, \, C=const.\]

Баруун талыг нь ялгаж үзье: $\arcsin \frac(x)(a) +C$.

\[\left(\arcsin \frac(x)(a) +C\right)"=\frac(1)(\sqrt(1-\left(\frac(x)(a) \баруун)^(2 ) ) ) \cdot \frac(1)(a) =\frac(a)(\sqrt(a^(2) -x^(2) ) ) \cdot \frac(1)(a) =\frac( 1)(\sqrt(a^(2) -x^(2) ) ) \]

Дериватив нь интегралтай тэнцүү болсон. Тиймээс томъёо нь зөв юм.

Жишээ 6

14-р томьёоны хүчинтэй эсэхийг интегралын хүснэгтээс шалгана уу.

\[\int \frac(dx)(\sqrt(x^(2) \pm a^(2) ) =\ln |x+\sqrt(x^(2) \pm a^(2) ) |+ C ,\, \, C=const.\]

Баруун талыг нь ялгаж үзье: $\ln |x+\sqrt(x^(2) \pm a^(2) ) |+C$.

\[\left(\ln |x+\sqrt(x^(2) \pm a^(2) ) |+C\right)"=\frac(1)(x+\sqrt(x^(2) \pm) a^(2) ) \cdot \left(x+\sqrt(x^(2) \pm a^(2) ) \right)"=\frac(1)(x+\sqrt(x^(2) \ pm a^(2) ) \cdot \left(1+\frac(1)(2\sqrt(x^(2) \pm a^(2) ) ) \cdot 2x\right)=\] \[ =\ frac(1)(x+\sqrt(x^(2) \pm a^(2) ) \cdot \frac(\sqrt(x^(2) \pm a^(2) ) +x)( \sqrt( x^(2) \pm a^(2) ) =\frac(1)(\sqrt(x^(2) \pm a^(2) ) ) \]

Дериватив нь интегралтай тэнцүү болсон. Тиймээс томъёо нь зөв юм.

Жишээ 7

Интегралыг ол:

\[\int \left(\cos (3x+2)+5x\right) dx.\]

Нийлбэрийн интеграл теоремыг ашиглая:

\[\int \left(\cos (3x+2)+5x\right) dx=\int \cos (3x+2)dx +\int 5xdx .\]

Тогтмол хүчин зүйлийг интеграл тэмдгийн гадна байрлуулах тухай теоремыг ашиглацгаая.

\[\int \cos (3x+2)dx +\int 5xdx =\int \cos (3x+2)dx +5\int xdx .\]

Интегралын хүснэгтийн дагуу:

\[\int \cos x dx=\sin x+C;\] \[\int xdx =\frac(x^(2) )(2) +C.\]

Эхний интегралыг тооцоолохдоо бид 3-р дүрмийг ашигладаг.

\[\int \cos (3x+2) dx=\frac(1)(3) \sin (3x+2)+C_(1) .\]

Тиймээс,

\[\int \left(\cos (3x+2)+5x\right) dx=\frac(1)(3) \sin (3x+2)+C_(1) +\frac(5x^(2) )(2) +C_(2) =\frac(1)(3) \sin (3x+2)+\frac(5x^(2) )(2) +C,\, \, C=C_(1) ) +C_(2) \]

Энэ хуудсан дээр та дараах зүйлсийг олох болно:

1. Үнэндээ антидеривативуудын хүснэгт - үүнийг PDF форматаар татаж аваад хэвлэх боломжтой;

2. Энэ хүснэгтийг хэрхэн ашиглах тухай видео;

3. Төрөл бүрийн сурах бичиг, тестийн эсрэг деривативыг тооцоолох олон жишээ.

Видео бичлэг дээр бид функцүүдийн эсрэг деривативуудыг тооцоолох шаардлагатай олон асуудлыг шинжлэх болно, ихэвчлэн нэлээд төвөгтэй боловч хамгийн чухал нь эдгээр нь хүч чадал биш юм. Дээр санал болгож буй хүснэгтэд нэгтгэсэн бүх функцууд нь дериватив шиг цээжээр мэддэг байх ёстой. Тэдгээргүйгээр интегралуудыг цаашид судлах, практик асуудлыг шийдвэрлэхэд ашиглах боломжгүй юм.

Өнөөдөр бид анхдагч зүйлийг үргэлжлүүлэн судалж, арай илүү төвөгтэй сэдэв рүү шилжиж байна. Хэрэв бид хамгийн сүүлд зөвхөн хүч чадлын функцүүдийн эсрэг деривативууд ба арай илүү төвөгтэй бүтэцтэй байсан бол өнөөдөр бид тригонометр болон бусад олон зүйлийг авч үзэх болно.

Сүүлийн хичээл дээр хэлсэнчлэн антидериватив нь деривативаас ялгаатай нь ямар ч стандарт дүрмийг ашиглан хэзээ ч "нэн даруй" шийдэгддэггүй. Түүнээс гадна муу мэдээ гэвэл деривативаас ялгаатай нь эсрэг деривативыг огт авч үзэхгүй байж магадгүй юм. Хэрэв бид бүрэн санамсаргүй функц бичиж, түүний деривативыг олох гэж оролдвол маш өндөр магадлалтайгаар амжилтанд хүрэх болно, гэхдээ энэ тохиолдолд эсрэг деривативыг бараг хэзээ ч тооцохгүй. Гэхдээ сайн мэдээ байна: үндсэн функц гэж нэрлэгддэг нэлээд том функцүүд байдаг бөгөөд тэдгээрийн эсрэг деривативуудыг тооцоолоход маш хялбар байдаг. Бүх төрлийн тест, бие даасан шалгалт, шалгалтууд дээр өгөгдсөн бусад бүх нарийн төвөгтэй бүтэц нь үнэндээ нэмэх, хасах болон бусад энгийн үйлдлүүдийн тусламжтайгаар эдгээр үндсэн функцуудаас бүрддэг. Ийм функцүүдийн прототипүүдийг удаан хугацаанд тооцоолж, тусгай хүснэгтэд нэгтгэсэн. Өнөөдөр бид эдгээр функцууд болон хүснэгтүүдтэй ажиллах болно.

Гэхдээ бид урьдын адил давталтаар эхлэх болно: эсрэг дериватив гэж юу болох, яагаад тэд хязгааргүй олон байдаг, тэдгээрийн ерөнхий дүр төрхийг хэрхэн тодорхойлох талаар санацгаая. Үүнийг хийхийн тулд би хоёр энгийн асуудлыг сонгов.

Хялбар жишээнүүдийг шийдвэрлэх

Жишээ №1

$\frac(\text( )\!\!\pi\!\!\text( ))(6)$ болон ерөнхийдөө $\text( )\!\!\pi\ байгааг нэн даруй тэмдэглэе. !\!\ text( )$ нь функцийн шаардлагатай эсрэг дериватив нь тригонометртэй холбоотой болохыг бидэнд шууд сануулж байна. Хэрэв бид хүснэгтийг харвал $\frac(1)(1+((x)^(2)))$ нь $\text(arctg)x$-аас өөр зүйл биш гэдгийг олж мэдэх болно. Тиймээс үүнийг бичье:

Үүнийг олохын тулд та дараахь зүйлийг бичих хэрэгтэй.

\[\frac(\pi )(6)=\text(arctg)\sqrt(3)+C\]

\[\frac(\text( )\!\!\pi\!\!\text( ))(6)=\frac(\text( )\!\!\pi\!\!\text( )) (3)+C\]

Жишээ №2

Энд бид бас тригонометрийн функцуудын тухай ярьж байна. Хэрэв бид хүснэгтийг харвал үнэхээр ийм зүйл тохиолддог.

Бид бүхэл бүтэн антидеривативуудын дунд заасан цэгээр дамждагийг олох хэрэгтэй.

\[\text( )\!\!\pi\!\!\text( )=\arcsin \frac(1)(2)+C\]

\[\text( )\!\!\pi\!\!\text( )=\frac(\text( )\!\!\pi\!\!\text( ))(6)+C\]

Эцэст нь бичье:

Ийм энгийн. Ганц асуудал бол энгийн функцүүдийн эсрэг деривативуудыг тооцоолохын тулд та эсрэг деривативуудын хүснэгтийг сурах хэрэгтэй. Гэсэн хэдий ч, танд зориулж дериватив хүснэгтийг судалсны дараа энэ нь асуудалгүй байх болно гэж би бодож байна.

Экспоненциал функц агуулсан асуудлыг шийдвэрлэх

Эхлэхийн тулд дараах томьёог бичье.

\[((e)^(x))\((e)^(x))\]

\[((a)^(x))\to \frac(((a)^(x)))(\ln a)\]

Энэ бүхэн практикт хэрхэн хэрэгжиж байгааг харцгаая.

Жишээ №1

Хэрэв бид хаалтны агуулгыг харвал эсрэг деривативуудын хүснэгтэд $((e)^(x))$ квадрат дотор байхын тулд ийм илэрхийлэл байхгүй тул энэ квадратыг томруулах шаардлагатай. Үүнийг хийхийн тулд бид үржүүлэх товчилсон томъёог ашигладаг.

Нэр томьёо бүрийн эсрэг деривативыг олцгооё.

\[((e)^(2x))=((\left(((e)^(2)) \баруун))^(x))\to \frac(((\left(((e))^ (2)) \баруун))^(x)))(\ln ((e)^(2)))=\frac(((e)^(2x)))(2)\]

\[((e)^(-2x))=((\left(((e)^(-2)) \баруун))^(x))\to \frac(((\left(((e)) )^(-2)) \баруун))^(x)))(\ln ((e)^(-2)))=\frac(1)(-2((e)^(2x))) \]

Одоо бүх нэр томъёог нэг илэрхийлэл болгон цуглуулж, ерөнхий эсрэг деривативыг авцгаая:

Жишээ №2

Энэ удаад зэрэг нь илүү том тул товчилсон үржүүлэх томъёо нь нэлээд төвөгтэй байх болно. Тиймээс хаалтуудыг нээцгээе:

Одоо энэ бүтцээс томъёоныхоо эсрэг деривативыг авахыг хичээцгээе.

Таны харж байгаагаар экспоненциал функцийн эсрэг деривативуудад төвөгтэй, ер бусын зүйл байдаггүй. Эдгээрийг бүгдийг нь хүснэгтээр тооцсон боловч анхааралтай суралцагчид $((e)^(2x))$ эсрэг дериватив нь $((a)-аас энгийн $((e)^(x))$-тэй ойрхон байгааг анзаарах байх. )^(x ))$. Тэгэхээр $((e)^(x))$ эсрэг деривативыг мэдэж байж $((e)^(2x))$ олох боломжийг олгодог өөр тусгай дүрэм байдаг болов уу? Тиймээ, ийм дүрэм байдаг. Түүнээс гадна энэ нь антидеривативуудын хүснэгттэй ажиллах салшгүй хэсэг юм. Одоо бид жишээ болгон ажиллаж байсан ижил илэрхийлэлүүдийг ашиглан дүн шинжилгээ хийх болно.

Антидеривативуудын хүснэгттэй ажиллах дүрэм

Функцээ дахин бичье:

Өмнөх тохиолдолд бид шийдвэрлэхийн тулд дараах томъёог ашигласан.

\[((a)^(x))\to \frac(((a)^(x)))(\operatorname(lna))\]

Харин одоо үүнийг арай өөрөөр хийцгээе: ямар үндэслэлээр $((e)^(x))\((e)^(x))$ гэдгийг санацгаая. Би аль хэдийн хэлсэнчлэн $((e)^(x))$ дериватив нь $((e)^(x))$-аас өөр зүйл биш тул түүний эсрэг дериватив нь ижил $((e) ^-тэй тэнцүү байх болно. (x))$. Гэхдээ асуудал нь бидэнд $((e)^(2x))$ болон $((e)^(-2x))$ байгаа явдал юм. Одоо $((e)^(2x))$-ийн деривативыг олохыг хичээцгээе:

\[((\left(((e)^(2x)) \баруун))^(\prime ))=((e)^(2x))\cdot ((\left(2x \баруун))^( \prime ))=2\cdot ((e)^(2x))\]

Бүтээн байгуулалтаа дахин бичье:

\[((\left(((e)^(2x)) \баруун))^(\prime ))=2\cdot ((e)^(2x))\]

\[((e)^(2x))=((\left(\frac(((e)^(2x)(2) \баруун))^(\prime ))\]

Энэ нь $((e)^(2x))$ эсрэг деривативыг олох үед бид дараах зүйлийг олж авна гэсэн үг юм.

\[((e)^(2x))\frac(((e)^(2x)))(2)\]

Таны харж байгаагаар бид өмнөхтэй ижил үр дүнд хүрсэн боловч $((a)^(x))$-г олохдоо томьёог ашиглаагүй. Одоо энэ нь тэнэг юм шиг санагдаж магадгүй: стандарт томьёо байхад яагаад тооцооллыг хүндрүүлдэг вэ? Гэсэн хэдий ч, арай илүү төвөгтэй хэллэгээр та энэ техник нь маш үр дүнтэй болохыг олж мэдэх болно, i.e. эсрэг деривативыг олохын тулд дериватив ашиглах.

Бэлтгэлийн хувьд $((e)^(2x))$-ын эсрэг деривативыг ижил төстэй аргаар олъё.

\[((\left(((e)^(-2x)) \баруун))^(\prime ))=((e)^(-2x))\cdot \left(-2 \баруун)\]

\[((e)^(-2x))=((\left(\frac(((e)^(-2x)))(-2) \баруун))^(\prime ))\]

Тооцоолохдоо бидний барилгын ажлыг дараах байдлаар бичнэ.

\[((e)^(-2x))\to -\frac(((e)^(-2x)))(2)\]

\[((e)^(-2x))\to -\frac(1)(2\cdot ((e)^(2x)))\]

Бид яг ижил үр дүнд хүрсэн ч өөр замаар явсан. Энэ зам нь одоо бидэнд арай илүү төвөгтэй мэт санагдаж байгаа бөгөөд ирээдүйд илүү төвөгтэй антидеривативуудыг тооцоолох, хүснэгтүүдийг ашиглахад илүү үр дүнтэй байх болно.

Анхаар! Энэ бол маш чухал цэг юм: дериватив гэх мэт антидеривативуудыг янз бүрийн аргаар тоолж болно. Гэсэн хэдий ч, хэрэв бүх тооцоо, тооцоолол тэнцүү байвал хариулт нь ижил байх болно. Үүнийг бид сая $((e)^(-2x))$ жишээн дээр харлаа - нэг талаас бид энэ эсрэг деривативыг "зөв дамжин" тооцоолж, тодорхойлолтыг ашиглан хувиргах замаар тооцоолсон, нөгөө талаас, Бид $ ((e)^(-2x))$-г $((\left(((e)^(-2)) \right))^(x))$ хэлбэрээр төлөөлж болохыг санаж, зөвхөн дараа нь ашигласан. $( (a)^(x))$ функцийн эсрэг дериватив. Гэсэн хэдий ч бүх өөрчлөлтүүдийн дараа үр дүн нь хүлээгдэж байсан шигээ байв.

Одоо бид энэ бүхнийг ойлгосон тул илүү чухал зүйл рүү шилжих цаг болжээ. Одоо бид хоёр энгийн бүтцийг шинжлэх болно, гэхдээ тэдгээрийг шийдвэрлэхэд ашиглах техник нь хүснэгтээс хөрш антидеривативуудын хооронд зүгээр л "гүйх"-ээс илүү хүчирхэг, ашигтай хэрэгсэл юм.

Асуудлыг шийдвэрлэх: функцийн эсрэг деривативыг олох

Жишээ №1

Тоолуурт байгаа дүнг гурван тусдаа бутархай болгон хувааж үзье.

Энэ бол нэлээд байгалийн бөгөөд ойлгомжтой шилжилт юм - ихэнх оюутнууд үүнтэй холбоотой асуудалгүй байдаг. Илэрхийлэлээ дараах байдлаар дахин бичье.

Одоо энэ томъёог санацгаая:

Манай тохиолдолд бид дараахь зүйлийг авах болно.

Эдгээр бүх гурван давхар бутархайг арилгахын тулд би дараахь зүйлийг хийхийг санал болгож байна.

Жишээ №2

Өмнөх бутархайгаас ялгаатай нь хуваагч нь үржвэр биш, харин нийлбэр юм. Энэ тохиолдолд бид бутархайгаа хэд хэдэн энгийн бутархайн нийлбэр болгон хувааж болохгүй, гэхдээ бид ямар нэгэн байдлаар тоологч нь хуваагчтай ойролцоогоор ижил илэрхийллийг агуулсан эсэхийг шалгах хэрэгтэй. Энэ тохиолдолд үүнийг хийх нь маш энгийн:

Математикийн хэлээр "тэг нэмэх" гэж нэрлэгддэг энэхүү тэмдэглэгээ нь бутархайг дахин хоёр хэсэгт хуваах боломжийг олгоно.

Одоо бид хайж байсан зүйлээ олцгооё:

Энэ бол бүх тооцоо юм. Өмнөх асуудлаас илүү төвөгтэй байсан ч тооцооллын хэмжээ бүр ч бага болсон.

Шийдлийн нюансууд

Хүснэгтийн эсрэг деривативуудтай ажиллахад тулгарч буй гол бэрхшээл нь энд байгаа бөгөөд энэ нь ялангуяа хоёрдугаар даалгаварт мэдэгдэхүйц юм. Баримт нь хүснэгтээр хялбархан тооцоолж болох зарим элементүүдийг сонгохын тулд бид яг юу хайж байгаагаа мэдэх хэрэгтэй бөгөөд эдгээр элементүүдийг хайхдаа антидеривативын бүх тооцоог хийдэг.

Өөрөөр хэлбэл, антидеривативуудын хүснэгтийг цээжлэх нь хангалтгүй юм - та хараахан байхгүй байгаа зүйлийг олж харах чадвартай байх ёстой, гэхдээ энэ асуудлыг зохиогч, эмхэтгэгч юу гэсэн үг болохыг олж мэдэх хэрэгтэй. Тийм ч учраас олон математикч, багш, профессорууд: "Антидериватив эсвэл интеграци гэж юу вэ - энэ нь зүгээр л нэг хэрэгсэл юм уу эсвэл жинхэнэ урлаг юм уу?" гэж байнга маргаж байдаг. Үнэн хэрэгтээ, миний хувийн бодлоор, интеграци бол урлаг биш юм - үүнд ямар ч агуу зүйл байхгүй, энэ бол зүгээр л дадлага, илүү дадлага юм. Дадлага хийхийн тулд өөр гурван ноцтой жишээг шийдье.

Бид практик дээр интеграцид сургадаг

Даалгавар №1

Дараах томьёог бичье.

\[((x)^(n))\frac(((x)^(n+1)))(n+1)\]

\[\frac(1)(x)\to \ln x\]

\[\frac(1)(1+((x)^(2)))\text(arctg)x\]

Дараахыг бичье.

Асуудал №2

Үүнийг дараах байдлаар дахин бичье.

Нийт эсрэг дериватив нь дараахтай тэнцүү байна.

Асуудал №3

Энэ даалгаврын хүндрэл нь өмнөх функцүүдээс ялгаатай нь $x$ хувьсагч огт байхгүй, i.e. дор хаяж ижил төстэй зүйлийг авахын тулд юу нэмэх, хасах нь бидэнд тодорхойгүй байна. Гэсэн хэдий ч үнэн хэрэгтээ энэ илэрхийлэл нь өмнөх ямар ч илэрхийллээс илүү энгийн гэж тооцогддог, учир нь энэ функцийг дараах байдлаар дахин бичиж болно.

Та одоо асууж магадгүй: яагаад эдгээр функцүүд тэнцүү байна вэ? Шалгацгаая:

Үүнийг дахин бичье:

Өөрийнхөө илэрхийлэлийг бага зэрэг өөрчилье:

Би энэ бүгдийг оюутнууддаа тайлбарлахад бараг үргэлж ижил асуудал гарч ирдэг: эхний функцээр бүх зүйл бага эсвэл тодорхой байдаг, хоёр дахь функцээр та үүнийг азаар эсвэл дадлага хийж болно, гэхдээ та ямар өөр ухамсартай вэ? Гурав дахь жишээг шийдэхийн тулд заавал байх шаардлагатай юу? Үнэндээ, бүү ай. Сүүлчийн эсрэг деривативыг тооцоолохдоо бидний ашигласан техникийг "функцийг хамгийн энгийн болгон задлах" гэж нэрлэдэг бөгөөд энэ нь маш ноцтой арга бөгөөд тусдаа видео хичээлийг үүнд зориулах болно.

Энэ хооронд би саяхан судалсан зүйлдээ, тухайлбал экспоненциал функцууд руу буцаж, тэдгээрийн агуулгын талаархи асуудлуудыг зарим талаар хүндрүүлэхийг санал болгож байна.

Эсрэг дериватив экспоненциал функцийг шийдвэрлэх илүү төвөгтэй асуудлууд

Даалгавар №1

Дараахь зүйлийг тэмдэглэе.

\[((2)^(x))\cdot ((5)^(x))=((\left(2\cdot 5 \баруун))^(x))=((10)^(x) )\]

Энэ илэрхийллийн эсрэг деривативыг олохын тулд энгийн томъёог ашиглана уу - $((a)^(x))\frac(((a)^(x)))(\ln a)$.

Манай тохиолдолд эсрэг дериватив нь дараах байдалтай байна.

Мэдээжийн хэрэг, бидний саяхан шийдсэн загвартай харьцуулахад энэ нь илүү энгийн харагдаж байна.

Асуудал №2

Дахин хэлэхэд, энэ функцийг хоёр тусдаа нэр томъёонд хялбархан хувааж болно - хоёр тусдаа бутархай. Дахин бичье:

Дээр тайлбарласан томъёог ашиглан эдгээр нэр томъёо тус бүрийн эсрэг деривативыг олох хэрэгтэй.

Хүчин чадлын функцтэй харьцуулахад экспоненциал функцууд илүү төвөгтэй байсан ч тооцоолол, тооцооллын нийт хэмжээ нь илүү хялбар болсон.

Мэдээжийн хэрэг, мэдлэгтэй оюутнуудын хувьд бидний дөнгөж сая хэлэлцсэн зүйл (ялангуяа өмнө нь ярилцсан зүйлийн арын дэвсгэр дээр) энгийн илэрхийлэл мэт санагдаж магадгүй юм. Гэсэн хэдий ч өнөөдрийн видео хичээлд зориулж эдгээр хоёр бодлогыг сонгохдоо би өөр нэг нарийн төвөгтэй, боловсронгуй техникийг танд хэлэх зорилго тавиагүй - миний танд үзүүлэхийг хүссэн зүйл бол та анхны функцийг өөрчлөхийн тулд стандарт алгебрийн техникийг ашиглахаас айх хэрэггүй юм. .

"Нууц" техникийг ашиглах

Эцэст нь хэлэхэд би өөр нэг сонирхолтой техникийг авч үзэхийг хүсч байна, энэ нь нэг талаараа өнөөдрийн бидний ярилцсан зүйлээс давж гардаг, гэхдээ нөгөө талаас, энэ нь нэгдүгээрт, огт төвөгтэй биш юм. Анхан шатны оюутнууд ч гэсэн үүнийг эзэмшиж чаддаг, хоёрдугаарт, энэ нь бүх төрлийн шалгалт, бие даасан ажилд ихэвчлэн олддог. Үүний талаархи мэдлэг нь эсрэг деривативуудын хүснэгтийн талаархи мэдлэгээс гадна маш их хэрэгтэй болно.

Даалгавар №1

Бидэнд чадлын функцтэй маш төстэй зүйл байгаа нь ойлгомжтой. Энэ тохиолдолд бид юу хийх ёстой вэ? Бодоод үз дээ: $x-5$ нь $x$-ээс тийм ч их ялгаатай биш - тэд зүгээр л $-5$ нэмсэн. Үүнийг ингэж бичье.

\[((x)^(4))\frac(((x)^(5)))(5)\]

\[((\left(\frac(((x)^(5)))(5) \баруун))^(\prime ))=\frac(5\cdot ((x)^(4))) (5)=((x)^(4))\]

$((\left(x-5 \right))^(5))$-ын деривативыг олохыг хичээцгээе:

\[((\left(((\left(x-5 \баруун))^(5)) \баруун))^(\prime ))=5\cdot ((\left(x-5 \баруун)) ^(4))\cdot ((\left(x-5 \баруун))^(\prime ))=5\cdot ((\left(x-5 \баруун))^(4))\]

Энэ нь:

\[((\зүүн(x-5 \баруун))^(4))=((\зүүн(\frac(((\зүүн(x-5 \баруун))^(5)))(5) \ баруун))^(\prime ))\]

Хүснэгтэнд ийм утга байхгүй тул бид чадлын функцийн стандарт эсрэг дериватив томъёог ашиглан бид өөрсдөө энэ томьёог гаргаж авсан. Хариултаа ингэж бичье.

Асуудал №2

Эхний шийдлийг харсан олон оюутнууд бүх зүйл маш энгийн гэж бодож магадгүй: хүчний функц дэх $x$-г шугаман илэрхийллээр солиход л бүх зүйл байрандаа орно. Харамсалтай нь бүх зүйл тийм ч энгийн биш, одоо бид үүнийг харах болно.

Эхний илэрхийлэлтэй зүйрлэснээр бид дараах зүйлийг бичнэ.

\[((x)^(9))\frac(((x)^(10)))(10)\]

\[((\left(((\left(4-3x \баруун))^(10)) \баруун))^(\prime ))=10\cdot ((\left(4-3x \баруун)) ^(9))\cdot ((\left(4-3x \баруун))^(\prime ))=\]

\[=10\cdot ((\left(4-3x \баруун))^(9))\cdot \left(-3 \right)=-30\cdot ((\left(4-3x \баруун)) ^(9))\]

Бидний дериватив руу буцаж очоод бид дараахь зүйлийг бичиж болно.

\[((\left((\left(4-3x \баруун))^(10)) \баруун))^(\prime ))=-30\cdot ((\left(4-3x \баруун)) )^(9))\]

\[((\left(4-3x \баруун))^(9))=((\left(\frac(((\left(4-3x \баруун)))^(10)))(-30) \баруун))^(\prime ))\]

Энэ нь нэн даруй дараах байдалтай байна:

Шийдлийн нюансууд

Анхаарна уу: хэрэв өнгөрсөн удаад юу ч өөрчлөгдөөгүй бол хоёр дахь тохиолдолд $-10$-ын оронд $-30$ гарч ирсэн. -10$ ба -30$ хооронд ямар ялгаа байдаг вэ? Мэдээжийн хэрэг, -3 доллараар. Асуулт: Энэ хаанаас ирсэн бэ? Хэрэв та анхааралтай ажиглавал нийлмэл функцийн деривативыг тооцоолсны үр дүнд авсан болохыг харж болно - $ x $ байсан коэффициент нь доорх эсрэг дериватив дээр гарч ирнэ. Энэ бол маш чухал дүрэм бөгөөд үүнийг би өнөөдрийн видео хичээл дээр огт хэлэлцэхээр төлөвлөөгүй байсан ч үүнгүйгээр хүснэгтийн эсрэг деривативуудын танилцуулга бүрэн бус байх болно.

Тиймээс дахин хийцгээе. Бидний гол чадлын функц байгаасай:

\[((x)^(n))\frac(((x)^(n+1)))(n+1)\]

Одоо $x$-ийн оронд $kx+b$ илэрхийллийг орлъё. Дараа нь юу болох вэ? Бид дараахь зүйлийг олох хэрэгтэй.

\[((\left(kx+b \баруун))^(n))\to \frac(((\left(kx+b \баруун))^(n+1)))(\left(n+ 1) \right)\cdot k)\]

Үүнийг бид ямар үндэслэлээр баталж байна вэ? Маш энгийн. Дээр бичсэн барилгын деривативыг олъё:

\[((\left(\frac((\left(kx+b \баруун)))^(n+1)))(\left(n+1 \баруун)\cdot k) \баруун))^( \prime ))=\frac(1)(\left(n+1 \баруун)\cdot k)\cdot \left(n+1 \баруун)\cdot ((\left(kx+b \баруун))^ (n))\cdot k=((\left(kx+b \баруун))^(n))\]

Энэ бол анх байсан илэрхийлэл юм. Тиймээс энэ томъёо нь бас зөв бөгөөд үүнийг антидеривативуудын хүснэгтийг нөхөхөд ашиглаж болно, эсвэл хүснэгтийг бүхэлд нь цээжлэх нь дээр.

"Нууц: техник:"-ийн дүгнэлт:

• Бидний сая үзсэн хоёр функц нь үнэндээ зэрэглэлийг өргөжүүлэх замаар хүснэгтэд заасан эсрэг дериватив болгон бууруулж болох боловч хэрвээ бид дөрөвдүгээр зэрэглэлийг ямар нэгэн байдлаар даван туулж чадвал би есдүгээр зэрэглэлийг ч авч үзэхгүй. илчилж зүрхэлсэн.
• Хэрэв бид зэрэглэлийг өргөжүүлэх юм бол бид маш их тооцоолол хийх бөгөөд энгийн ажил нь бидэнд зохисгүй их цаг хугацаа шаардах болно.
• Ийм учраас шугаман илэрхийлэл агуулсан ийм бодлогуудыг “толгойгоор” шийдэх шаардлагагүй. Хүснэгтээс зөвхөн $kx+b$ илэрхийлэл байгаагаараа ялгаатай эсрэг деривативтай тааралдмагц дээр бичсэн томъёог санаж, хүснэгтийнхээ эсрэг дериватив дээр орлуулаарай, тэгвэл бүх зүйл сайн болно. илүү хурдан бөгөөд хялбар.

Мэдээжийн хэрэг, энэ техникийн нарийн төвөгтэй байдал, ноцтой байдлаас шалтгаалан бид дараагийн видео хичээлүүдэд үүнийг олон удаа авч үзэх болно, гэхдээ энэ нь өнөөдрийн хувьд юм. Энэ хичээл нь антидериватив болон интеграцчлалыг ойлгохыг хүсдэг оюутнуудад үнэхээр тусална гэж найдаж байна.

Интегралыг шийдэх нь хялбар ажил боловч зөвхөн сонгогдсон цөөхөн хүмүүст зориулагдсан. Энэ нийтлэл нь интегралуудыг ойлгож сурахыг хүсдэг боловч тэдгээрийн талаар юу ч мэдэхгүй эсвэл бараг юу ч мэдэхгүй хүмүүст зориулагдсан болно. Интеграл... Яагаад хэрэгтэй байна вэ? Үүнийг хэрхэн тооцоолох вэ? Тодорхой ба тодорхойгүй интеграл гэж юу вэ?

Хэрэв интегралын хувьд таны мэддэг цорын ганц хэрэглээ бол хүрэхэд хэцүү газраас хэрэгтэй зүйл авахын тулд салшгүй дүрс хэлбэртэй зүүгээр дэгээ ашиглах явдал юм бол тавтай морилно уу! Математикийн хувьд хамгийн энгийн болон бусад интегралуудыг хэрхэн шийдвэрлэх, яагаад үүнгүйгээр хийж чадахгүй байгааг олж мэдээрэй.

Бид үзэл баримтлалыг судалж байна « интеграл »

Интеграци нь Эртний Египтэд мэдэгдэж байсан. Мэдээжийн хэрэг, орчин үеийн хэлбэрээр биш, гэхдээ одоо ч гэсэн. Түүнээс хойш математикчид энэ сэдвээр олон ном бичсэн. Ялангуяа өөрсдийгөө онцолсон Ньютон Тэгээд Лейбниц , гэхдээ юмсын мөн чанар өөрчлөгдөөгүй.

Интегралыг эхнээс нь хэрхэн ойлгох вэ? Арга ч үгүй! Энэ сэдвийг ойлгохын тулд танд математик анализын үндсэн суурь мэдлэг хэрэгтэй хэвээр байх болно. Манай блог дээр интегралыг ойлгоход шаардлагатай -ын тухай мэдээлэл аль хэдийн бий.

Тодорхой бус интеграл

Бидэнд ямар нэгэн функцтэй байцгаая f(x) .

Тодорхой бус интеграл функц f(x) энэ функцийг дууддаг F(x) , түүний дериватив нь функцтэй тэнцүү байна f(x) .

Өөрөөр хэлбэл интеграл нь урвуу дериватив эсвэл эсрэг дериватив юм. Дашрамд хэлэхэд, хэрхэн яаж хийх талаар манай нийтлэлээс уншина уу.

Бүх тасралтгүй функцүүдэд эсрэг дериватив байдаг. Мөн тогтмол тэмдэгтээр ялгаатай функцүүдийн деривативууд давхцдаг тул эсрэг дериватив дээр тогтмол тэмдэг нэмж өгдөг. Интегралыг олох үйл явцыг интеграл гэж нэрлэдэг.

Энгийн жишээ:

Энгийн функцүүдийн эсрэг деривативуудыг байнга тооцоолохгүйн тулд тэдгээрийг хүснэгтэд оруулж, бэлэн утгыг ашиглах нь тохиромжтой.

Оюутнуудад зориулсан интегралын бүрэн хүснэгт

Тодорхой интеграл

Интеграл гэдэг ойлголттой харьцахдаа бид хязгааргүй жижиг хэмжигдэхүүнтэй харьцаж байна. Интеграл нь зургийн талбай, жигд бус биеийн масс, жигд бус хөдөлгөөний үед туулсан зай болон бусад олон зүйлийг тооцоолоход тусална. Интеграл гэдэг нь хязгааргүй олон тооны хязгааргүй жижиг гишүүний нийлбэр гэдгийг санах нь зүйтэй.

Жишээ болгон зарим функцийн графикийг төсөөлөөд үз дээ.

Функцийн графикаар хязгаарлагдсан дүрсийн талбайг хэрхэн олох вэ? Интеграл ашиглах! Координатын тэнхлэгүүд болон функцийн графикаар хязгаарлагдсан муруй шугаман трапецийг хязгааргүй жижиг хэрчмүүдэд хуваацгаая. Ингэснээр зургийг нимгэн багана болгон хуваах болно. Баганын талбайн нийлбэр нь трапецын талбай болно. Гэхдээ ийм тооцоолол нь ойролцоогоор үр дүнг өгөх болно гэдгийг санаарай. Гэсэн хэдий ч сегментүүд нь жижиг, нарийхан байх тусам тооцоолол илүү нарийвчлалтай болно. Хэрэв бид тэдгээрийг урт нь тэг рүү чиглүүлэх хэмжээгээр багасгах юм бол сегментүүдийн талбайн нийлбэр нь зургийн талбай руу чиглэх болно. Энэ бол тодорхой интеграл бөгөөд үүнийг дараах байдлаар бичсэн болно.

a ба b цэгүүдийг интегралын хязгаар гэж нэрлэдэг.

« Интеграл »

Дашрамд хэлэхэд! Уншигчиддаа зориулж 10% хямдралтай байгаа

Даммигийн интегралыг тооцоолох дүрэм

Тодорхойгүй интегралын шинж чанарууд

Тодорхойгүй интегралыг хэрхэн шийдэх вэ? Энд бид тодорхойгүй интегралын шинж чанаруудыг авч үзэх бөгөөд энэ нь жишээг шийдвэрлэхэд хэрэг болно.

• Интегралын дериватив нь интегралтай тэнцүү байна:

• Тогтмолыг интеграл тэмдгийн доороос гаргаж болно.

• Нийлбэрийн интеграл нь интегралын нийлбэртэй тэнцүү байна. Энэ нь мөн ялгааны хувьд үнэн юм:

Тодорхой интегралын шинж чанарууд

• Шугаман чанар:

• Интегралын хязгаарыг сольсон тохиолдолд интегралын тэмдэг өөрчлөгдөнө.

• At ямар чоноо а, бТэгээд -тай:

Тодорхой интеграл нь нийлбэрийн хязгаар гэдгийг бид аль хэдийн олж мэдсэн. Гэхдээ жишээг шийдэхдээ тодорхой утгыг хэрхэн авах вэ? Үүний тулд Ньютон-Лейбницийн томъёо байдаг:

Интегралыг шийдвэрлэх жишээ

Доор бид тодорхойгүй интеграл болон шийдлийн жишээг авч үзэх болно. Бид танд шийдлийн нарийн ширийнийг өөрөө олж мэдэхийг санал болгож байна, хэрэв ямар нэг зүйл тодорхойгүй байвал сэтгэгдэл дээр асуулт асуугаарай.

Материалыг бататгахын тулд интегралыг практикт хэрхэн шийддэг тухай видеог үзээрэй. Хэрэв интегралыг шууд өгөхгүй бол цөхрөл бүү зов. Оюутнуудад зориулсан мэргэжлийн үйлчилгээтэй холбоо бариарай, битүү гадаргуу дээрх гурвалсан эсвэл муруй интеграл нь таны хүчин чадалд багтах болно.

Эсрэг деривативуудын хүснэгт ("интеграл"). Интегралын хүснэгт. Хүснэгтийн тодорхойгүй интеграл. (Хамгийн энгийн интеграл ба параметртэй интеграл). Хэсэгээр нь нэгтгэх томъёо. Ньютон-Лейбницийн томъёо.

Эсрэг деривативуудын хүснэгт ("интеграл"). Хүснэгтийн тодорхойгүй интеграл. (Хамгийн энгийн интеграл ба параметртэй интеграл).
Хүчин чадлын функцийн интеграл.	Хүчин чадлын функцийн интеграл.
Дифференциал тэмдгийн дор х-г жолоодвол чадлын функцийн интеграл болж буурдаг интеграл.
	Экспоненциалын интеграл, энд a нь тогтмол тоо.
Нарийн төвөгтэй экспоненциал функцийн интеграл.	Экспоненциал функцийн интеграл.
Натурал логарифмтай тэнцүү интеграл.	Интеграл: "Урт логарифм".
	Интеграл: "Урт логарифм".
Интеграл: "Өндөр логарифм".	Тоолуур дахь х-г дифференциал тэмдгийн доор байрлуулсан интеграл (тэмдэгтийн доорх тогтмолыг нэмж эсвэл хасаж болно) нь эцсийн дүндээ натурал логарифмтай тэнцүү интегралтай төстэй.
Интеграл: "Өндөр логарифм".
Косинусын интеграл.	Синусын интеграл.
Тангенстай тэнцүү интеграл.	Котангенстай тэнцүү интеграл.
Арксин ба арккосин хоёртой тэнцүү интеграл
Арксин ба арккосин хоёртой тэнцүү интеграл.	Арктангенс ба арккотангенстай тэнцүү интеграл.
Косеканттай тэнцүү интеграл.	Секанттай тэнцүү интеграл.
Арксеканттай тэнцүү интеграл.	Арккосеканттай тэнцүү интеграл.
Арксеканттай тэнцүү интеграл.	Арксеканттай тэнцүү интеграл.
Гиперболын синустай тэнцүү интеграл.	Гипербол косинустай тэнцүү интеграл.
Интеграл нь гипербол синустай тэнцүү бөгөөд энд sinhx нь англи хувилбарт гиперболын синус юм.	Гиперболын косинустай тэнцүү интеграл, энд sinhx нь англи хэл дээрх гиперболын синус юм.
Гипербол тангенстай тэнцүү интеграл.	Гипербол котангенстай тэнцүү интеграл.
Гиперболын секанттай тэнцүү интеграл.	Гипербол косеканттай тэнцүү интеграл.

Хэсэгээр нь нэгтгэх томъёо. Интеграцийн дүрэм.

Хэсэгээр нь нэгтгэх томъёо. Ньютон-Лейбницийн томьёо.Интеграцийн дүрэм.
Бүтээгдэхүүнийг (функцийг) тогтмол тоогоор нэгтгэх:
Функцийн нийлбэрийг нэгтгэх:
тодорхойгүй интегралууд:
Хэсэгээр нь нэгтгэх томъёо тодорхой интегралууд:
Ньютон-Лейбницийн томъёо тодорхой интегралууд:	Энд F(a),F(b) нь b ба a цэгүүдийн эсрэг деривативуудын утгууд юм.

Деривативын хүснэгт. Хүснэгтийн деривативууд. Бүтээгдэхүүний дериватив. Хэсгийн дериватив. Нарийн төвөгтэй функцийн дериватив.

Хэрэв x нь бие даасан хувьсагч бол:

Деривативын хүснэгт. Хүснэгтийн дериватив."хүснэгтийн дериватив" - тийм ээ, харамсалтай нь тэдгээрийг интернетээс яг ингэж хайдаг.
	Хүчин чадлын функцийн дериватив
	Экспонентийн дериватив
Нарийн төвөгтэй экспоненциал функцийн дериватив	Экспоненциал функцийн дериватив
Логарифм функцийн дериватив	Байгалийн логарифмын дериватив
	Функцийн натурал логарифмын дериватив
Синусын дериватив	Косинусын дериватив
Косекантын дериватив	Секантын дериватив
Арксины дериватив	Нумын косинусын дериватив
Арксины дериватив	Нумын косинусын дериватив
Тангенсийн дериватив	Котангенсийн дериватив
Артангенсийн дериватив	Нумын котангенсын дериватив
Артангенсийн дериватив	Нумын котангенсын дериватив
Арксекантын дериватив	Арккосекантын дериватив
Арксекантын дериватив	Арккосекантын дериватив
Гиперболын синусын дериватив Англи хэл дээрх гиперболын синусын дериватив	Гипербол косинусын дериватив Англи хэл дээрх гипербол косинусын дериватив
Гипербол тангенсийн дериватив	Гипербол котангентын дериватив
Гипербол секантын дериватив	Гипербол косекантын дериватив

Ялгах дүрэм. Бүтээгдэхүүний дериватив. Хэсгийн дериватив. Нарийн төвөгтэй функцийн дериватив.
Тогтмол тоогоор бүтээгдэхүүн (функц)-ийн дериватив:
Нийлбэрийн дериватив (функц):
Бүтээгдэхүүний дериватив (функц):
Хэсгийн (функцийн) дериватив:
Нарийн төвөгтэй функцийн дериватив:

Логарифмын шинж чанарууд. Логарифмын үндсэн томъёо. Аравтын тоо (lg) ба натурал логарифм (ln).

Үндсэн логарифмын таних тэмдэг
a b хэлбэрийн дурын функцийг хэрхэн экспоненциал болгож болохыг харуулъя. e x хэлбэрийн функцийг экспоненциал гэж нэрлэдэг тул
a b хэлбэрийн аливаа функцийг аравын зэрэглэлээр илэрхийлж болно

Натурал логарифм ln (е суурьтай логарифм = 2.718281828459045...) ln(e)=1; log(1)=0

Тейлорын цуврал. Функцийн Тейлорын цуврал өргөтгөл.

Энэ нь олонхи болсон нь харагдаж байна практикт тулгарсанМатематик функцийг тодорхой цэгийн ойролцоо хувьсагчийн хүчийг нэмэгдүүлэх дарааллаар агуулсан чадлын цуваа хэлбэрээр ямар ч нарийвчлалтайгаар дүрсэлж болно. Жишээлбэл, x=1 цэгийн ойролцоо:

гэж нэрлэдэг цуврал ашиглах үед Тейлорын эгнээ,Алгебр, тригонометр, экспоненциал функц агуулсан холимог функцийг цэвэр алгебрийн функцээр илэрхийлж болно. Цувралыг ашигласнаар та ялгах, нэгтгэх ажлыг хурдан гүйцэтгэх боломжтой.

a цэгийн ойролцоох Тейлорын цуврал дараах хэлбэртэй байна.

1) , энд f(x) нь x = a үед бүх дарааллын деривативтай функц юм. R n - Тейлорын цувралын үлдэгдэл гишүүнийг илэрхийллээр тодорхойлно

2)

Цувралын k-р коэффициент (х k дээр) томъёогоор тодорхойлогдоно

3) Тейлорын цувралын онцгой тохиолдол бол Маклаурин (=McLaren) цуврал юм (а=0 цэгийн эргэн тойронд тэлэлт явагдана)

a=0 үед

цувралын гишүүдийг томъёогоор тодорхойлно

Тейлорын цувралыг ашиглах нөхцөл.

1. f(x) функцийг (-R;R) интервал дээр Тейлорын цуваа болгон өргөжүүлэхийн тулд үүнд Тейлор (Маклаурин (=Мкларен)) томъёоны үлдэгдэл гишүүн байх шаардлагатай бөгөөд хангалттай. функц нь заасан интервал (-R;R) дээр k →∞ гэж тэг рүү чиглэдэг.

2. Бидний ойролцоох Тейлорын цувралыг байгуулах гэж буй цэг дээр өгөгдсөн функцийн деривативууд байх шаардлагатай.

Тейлорын цувралын шинж чанарууд.

Хэрэв f нь аналитик функц бол f-ийн тодорхойлолтын муж дахь аль ч цэг дэх Тейлорын цуваа нь a-ийн зарим хэсэгт f-д нийлдэг.

Тэйлорын цуваа нь нийлдэг, гэхдээ нэгэн зэрэг a-ийн аль ч хэсэгт байгаа функцээс ялгаатай хязгааргүй дифференциал функцүүд байдаг. Жишээлбэл:

Тейлорын цуваа нь функцийг олон гишүүнтээр ойртуулах (ойролцоогоор зарим объектыг бусад зүйлээр солихоос бүрдэх шинжлэх ухааны арга юм. Ялангуяа шугаманчлал ((linearis - шугаман)), шугаман бус системийг судлахдаа шугаман системийн шинжилгээгээр солигдсон, ямар нэгэн утгаараа анхныхтай дүйцэхүйц хаалттай шугаман бус системийг ойролцоогоор дүрслэх аргуудын нэг юм. .) тэгшитгэлийг Тейлорын цуврал болгон өргөжүүлж, эхний эрэмбээс дээш бүх гишүүнийг таслах замаар үүсдэг.

Тиймээс бараг бүх функцийг өгөгдсөн нарийвчлалтайгаар олон гишүүнт хэлбэрээр илэрхийлж болно.

Маклаурины цуврал (=МкЛарен, Тейлор 0-р цэгийн ойролцоо) ба 1-р цэгийн ойролцоох Тейлор дахь чадлын функцүүдийн зарим нийтлэг өргөтгөлийн жишээ. Тейлор ба МакЛарен цувралын үндсэн функцүүдийн өргөтгөлийн эхний нөхцөлүүд.

Маклаурины цуврал дахь чадлын функцүүдийн зарим нийтлэг өргөтгөлийн жишээ (= McLaren, Taylor 0 цэгийн ойролцоо)

1-р цэгийн ойролцоох зарим нийтлэг Тейлорын цуврал өргөтгөлүүдийн жишээ

>>Интеграцийн аргууд

Интеграцийн үндсэн аргууд

Интеграл, тодорхой ба тодорхойгүй интегралын тодорхойлолт, интегралын хүснэгт, Ньютон-Лейбницийн томьёо, хэсгээр интеграл, интеграл тооцох жишээ.

Тодорхой бус интеграл

Өгөгдсөн X интервалд дифференциалагдах F(x) функцийг дуудна функцийн эсрэг дериватив f(x) буюу f(x)-ийн интеграл, хэрэв x ∈X бүрт дараах тэгшитгэл биелнэ:

F "(x) = f(x). (8.1)

Өгөгдсөн функцийн бүх эсрэг деривативыг олохыг түүний гэнэ интеграци. Тодорхой бус интеграл функцӨгөгдсөн X интервал дээрх f(x) нь f(x) функцийн бүх эсрэг дериватив функцүүдийн олонлог юм; тэмдэглэгээ -

Хэрэв F(x) нь f(x) функцийн эсрэг дериватив бол ∫ f(x)dx = F(x) + C, (8.2)

Энд C нь дурын тогтмол юм.

Интегралын хүснэгт

Тодорхойлолтоос шууд бид тодорхойгүй интегралын үндсэн шинж чанарууд болон хүснэгтэн интегралуудын жагсаалтыг олж авдаг.

1) d∫f(x)dx=f(x)

2)∫df(x)=f(x)+C

3) ∫af(x)dx=a∫f(x)dx (a=const)

4) ∫(f(x)+g(x))dx = ∫f(x)dx+∫g(x)dx

Хүснэгтийн интегралуудын жагсаалт

1. ∫x m dx = x m+1 /(m + 1) +C; (м ≠ -1)

3.∫a x dx = a x /ln a + C (a>0, a ≠1)

4.∫e x dx = e x + C

5.∫sin x dx = cosx + C

6.∫cos x dx = - sin x + C

7. = арктан х + С

8. = arcsin x + C

10. = - ctg x + C

Хувьсах солих

Олон функцийг нэгтгэхийн тулд хувьсагчийг солих аргыг ашиглана уу орлуулалт,интегралыг хүснэгт хэлбэрт оруулах боломжийг танд олгоно.

Хэрэв f(z) функц нь [α,β] дээр тасралтгүй байвал z =g(x) функц нь тасралтгүй дериватив ба α ≤ g(x) ≤ β байна.

∫ f(g(x)) g " (x) dx = ∫f(z)dz, (8.3)

Мөн баруун талд интеграцчилсны дараа z=g(x) орлуулалтыг хийх ёстой.

Үүнийг батлахын тулд анхны интегралыг дараах хэлбэрээр бичихэд хангалттай.

∫ f(g(x)) g " (x) dx = ∫ f(g(x)) dg(x).

Жишээлбэл:

1)

2) .

Хэсэгээр нь нэгтгэх арга

u = f(x) ба v = g(x) функцуудыг тасралтгүй . Дараа нь ажлын дагуу

d(uv))= udv + vdu эсвэл udv = d(uv) - vdu.

d(uv) илэрхийллийн хувьд эсрэг дериватив нь uv байх нь ойлгомжтой тул томъёо нь дараах байдалтай байна.

∫ udv = uv - ∫ vdu (8.4.)

Энэ томъёо нь дүрмийг илэрхийлдэг хэсгүүдээр нэгтгэх. Энэ нь udv=uv"dx илэрхийллийг vdu=vu"dx илэрхийллийг нэгтгэхэд хүргэдэг.

Жишээлбэл, та ∫xcosx dx-г олохыг хүсч байна. u = x, dv = cosxdx гэж тавья, тэгэхээр du=dx, v=sinx. Дараа нь

∫xcosxdx = ∫x d(sin x) = x sin x - ∫sin x dx = x sin x + cosx + C.

Хэсэгчилсэн интеграцийн дүрэм нь хувьсагчдыг орлуулахаас илүү хязгаарлагдмал хүрээтэй байдаг. Гэхдээ интегралын бүхэл бүтэн анги байдаг, жишээлбэл,

∫x k ln m xdx, ∫x k sinbxdx, ∫ x k cosbxdx, ∫x k e ax болон бусад хэсгүүдийг интеграцчлах замаар нарийн тооцдог.

Тодорхой интеграл

Тодорхой интеграл гэдэг ойлголтыг дараах байдлаар оруулав. f(x) функцийг интервал дээр тодорхойлъё. [a,b] сегментийг хувааж үзье n a= x 0 цэгээр хэсгүүд< x 1 <...< x n = b. Из каждого интервала (x i-1 , x i) возьмем произвольную точку ξ i и составим сумму f(ξ i) Δx i где
Δ x i =x i - x i-1. f(ξ i)Δ x i хэлбэрийн нийлбэрийг нэрлэнэ интеграл нийлбэр, ба түүний хязгаарыг λ = maxΔx i → 0, хэрэв байгаа бөгөөд төгсгөлтэй бол гэж нэрлэдэг. тодорхой интеграл-ийн f(x) функцууд аөмнө ббөгөөд дараахыг тодорхойлсон:

F(ξ i)Δx i (8.5).

Энэ тохиолдолд f(x) функцийг дуудна интервал дээр интегралдах боломжтой, a ба b тоонуудыг дуудна интегралын доод ба дээд хязгаар.

Тодорхой интегралын хувьд дараах шинж чанарууд үнэн байна.

4), (k = const, k∈R);

5)

6)

7) f(ξ)(b-a) (ξ∈).

Сүүлийн үл хөдлөх хөрөнгө гэж нэрлэдэг дундаж утгын теорем.

f(x) дээр үргэлжилсэн байг. Дараа нь энэ сегмент дээр тодорхойгүй интеграл байна

∫f(x)dx = F(x) + C

ба явагддаг Ньютон-Лейбницийн томъёо, тодорхой интегралыг тодорхойгүй интегралтай холбох:

F(b) - F(a). (8.6)

Геометрийн тайлбар: тодорхой интеграл нь y=f(x) муруй, x = a ба x = b шулуун шугамууд ба тэнхлэгийн сегментээр дээрээс хязгаарлагдсан муруйн трапецын талбай юм. Үхэр.

Буруу интеграл

Хязгааргүй хязгаартай интеграл ба тасалдалгүй (хязгааргүй) функцүүдийн интегралуудыг гэнэ. чинийх биш. Эхний төрлийн буруу интегралууд -Эдгээр нь хязгааргүй интервалын интеграл бөгөөд дараах байдлаар тодорхойлогддог.

(8.7)

Хэрэв энэ хязгаар байгаа бөгөөд төгсгөлтэй бол түүнийг дуудна f(x)-ийн нийлсэн буруу интеграл[a,+ ∞) интервал дээр f(x) функц дуудагдана хязгааргүй интервалаар интегралдах боломжтой[a,+ ∞). Үгүй бол интеграл нь байх болно байхгүй эсвэл зөрөөд байна.

(-∞,b] ба (-∞, + ∞) интервал дээрх зохисгүй интегралууд ижил төстэй байдлаар тодорхойлогддог.

Хязгааргүй функцийн интеграл гэсэн ойлголтыг тодорхойлъё. Хэрэв f(x) бүх утгын хувьд тасралтгүй байвал x f(x) төгсгөлгүй тасалдалтай c цэгээс бусад сегмент хоёр дахь төрлийн буруу интеграл f(x) а-аас б хүртэлхэмжээ гэж нэрлэдэг:

хэрэв эдгээр хязгаарууд байгаа бөгөөд хязгаарлагдмал бол. Зориулалт:

Интеграл тооцооллын жишээ

Жишээ 3.30.∫dx/(x+2)-ийг тооцоол.

Шийдэл. t = x+2 гэж тэмдэглэе, тэгвэл dx = dt, ∫dx/(x+2) = ∫dt/t = ln|t| + C = ln|x+2| +C.

Жишээ 3.31. ∫ tgxdx-г ол.

Шийдэл.∫ tgxdx = ∫sinx/cosxdx = - ∫dcosx/cosx. t=cosx, тэгвэл ∫ tgxdx = -∫ dt/t = - ln|t| + C = -ln|cosx|+C.

Жишээ3.32 . ∫dx/sinx-г ол

Шийдэл.

Жишээ3.33. олох.

Шийдэл. =

.

Жишээ3.34 . ∫arctgxdx-г ол.

Шийдэл. Хэсэгээр нь нэгтгэе. u=arctgx, dv=dx гэж тэмдэглэе. Дараа нь du = dx/(x 2 +1), v=x, эндээс ∫arctgxdx = xarctgx - ∫ xdx/(x 2 +1) = xarctgx + 1/2 ln(x 2 +1) +C; учир нь
∫xdx/(x 2 +1) = 1/2 ∫d(x 2 +1)/(x 2 +1) = 1/2 ln(x 2 +1) +C.

Жишээ3.35 . ∫lnxdx-г тооцоол.

Шийдэл.Интеграцийг хэсэгчилсэн томъёогоор ашигласнаар бид дараахь зүйлийг олж авна.
u=lnx, dv=dx, du=1/x dx, v=x. Дараа нь ∫lnxdx = xlnx - ∫x 1/x dx =
= xlnx - ∫dx + C= xlnx - x + C.

Жишээ3.36 . ∫e x sinxdx-ийг тооцоол.

Шийдэл. u = e x, dv = sinxdx, дараа нь du = e x dx, v =∫ sinxdx= - cosx → ∫ e x sinxdx = - e x cosx + ∫ e x cosxdx гэж тэмдэглэе. Мөн бид ∫e x cosxdx интегралыг хэсгүүдээр нэгтгэдэг: u = e x , dv = cosxdx, du=e x dx, v=sinx. Бидэнд байгаа:
∫ e x cosxdx = e x sinx - ∫ e x sinxdx. Бид ∫e x sinxdx = - e x cosx + e x sinx - ∫ e x sinxdx хамаарлыг олж авсан бөгөөд үүнээс 2∫e x sinx dx = - e x cosx + e x sinx + C.

Жишээ 3.37. J = ∫cos(lnx)dx/x-ийг тооцоол.

Шийдэл. dx/x = dlnx тул J= ∫cos(lnx)d(lnx) болно. lnx-г t-ээр сольсноор бид J = ∫ costdt = sint + C = sin(lnx) + C интеграл хүснэгтэд хүрнэ.

Жишээ 3.38 . J =-г тооцоол.

Шийдэл.= d(lnx) гэж үзвэл lnx = t-г орлуулна. Дараа нь J = .