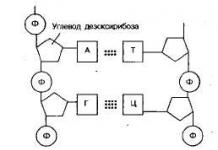
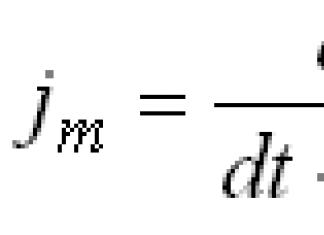Тодорхойлолт 1.Хязгааргүй шугамын х цэгийг (x n) дарааллын хязгааргүй цэг гэж нэрлэдэг бөгөөд энэ цэгийн аль ч цахим хөршид дарааллын (x n) хязгааргүй олон элемент байгаа бол.

Лемма 1.Хэрэв x нь дарааллын (x k ) хязгаарын цэг бол энэ дарааллаас бид х тоонд нийлэх дэд дарааллыг (x n k) сонгож болно.

Сэтгэгдэл.Эсрэг заалт нь бас үнэн юм. Хэрэв (x k) дарааллаас x тоонд нийлэх дэд дарааллыг сонгох боломжтой бол x тоо нь дарааллын (x k) хязгаарын цэг болно. Үнэн хэрэгтээ, x цэгийн аль ч цахим хөршид дэд дарааллын, тиймээс дарааллын өөрөө (x k) хязгааргүй олон элементүүд байдаг.

Лемма 1-ээс бид 1-р тодорхойлолттой дүйцэх дарааллын хязгаарын цэгийн өөр нэг тодорхойлолтыг өгч болно.

Тодорхойлолт 2.Хязгааргүй шугамын х цэгийг дарааллын хязгаарын цэг (x k ) гэнэ, хэрэв энэ дарааллаас х-д нийлэх дэд дарааллыг сонгох боломжтой бол.

Лемма 2.Конвергент дараалал бүр зөвхөн нэг хязгаарын цэгтэй бөгөөд энэ нь тухайн дарааллын хязгаартай давхцдаг.

Сэтгэгдэл.Хэрэв дараалал нийлж байвал Лемма 2-оор энэ нь зөвхөн нэг хязгаарын цэгтэй болно. Гэсэн хэдий ч хэрэв (xn) нийлэхгүй бол хэд хэдэн хязгаарын цэгүүдтэй байж болно (мөн ерөнхийдөө хязгааргүй олон хязгаарын цэгүүд). Жишээлбэл, (1+(-1) n ) нь хоёр хязгаарын цэгтэй болохыг харуулъя.

Үнэхээр (1+(-1) n )=0,2,0,2,0,2,... нь 0 ба 2 гэсэн хоёр хязгаарын цэгтэй учир Энэ дарааллын (0)=0,0,0,... ба (2)=2,2,2,... зэрэгт 0 ба 2 гэсэн тоонууд хязгаар болно.Энэ дараалалд өөр хязгаарын цэг байхгүй. Үнэхээр x нь тооны тэнхлэг дээрх 0 ба 2 цэгээс бусад дурын цэг байя.

жижиг тул e - 0, x ба 2 цэгүүдийн хөршүүд огтлолцохгүй. 0 ба 2-р цэгийн цахим хөрш нь дарааллын бүх элементүүдийг агуулдаг тул x цэгийн цахим хөрш нь хязгааргүй олон элемент (1+(-1) n ) агуулж болохгүй тул энэ дарааллын хязгаарын цэг биш юм.

Теорем.Хязгаарлагдмал дараалал бүр дор хаяж нэг хязгаарын цэгтэй байдаг.

Сэтгэгдэл.-аас хэтэрсэн x тоо нь (x n) дарааллын хязгаарлах цэг болно, i.e. - дарааллын хамгийн том хязгаарын цэг (x n).

x -ээс их тоо байг. Маш бага байхаар e>0 гэж сонгоцгооё

ба x 1 О(x), x 1-ийн баруун талд (x n) дарааллын хязгаарлагдмал тооны элементүүд байгаа эсвэл огт байхгүй, өөрөөр хэлбэл. x нь дарааллын (x n) хязгаарын цэг биш юм.

Тодорхойлолт.Дарааллын хамгийн том хязгаарын цэгийг (x n) дарааллын дээд хязгаар гэж нэрлэх ба тэмдэгтээр тэмдэглэнэ. Хязгаарлагдмал дараалал бүр дээд хязгаартай байдаг нь тайлбараас харагдаж байна.

Үүний нэгэн адил доод хязгаарын тухай ойлголтыг (х n ) дарааллын хамгийн бага хязгаарын цэг болгон) нэвтрүүлсэн.

Тиймээс бид дараах мэдэгдлийг нотолсон. Хязгаарлагдмал дараалал бүр дээд ба доод хязгаартай байдаг.

Дараах теоремыг нотолгоогүйгээр томъёолъё.

Теорем.(x n) дараалал нийлэхийн тулд хязгаарлагдмал байх, дээд доод хязгаар нь давхцах шаардлагатай бөгөөд хангалттай.

Энэ хэсгийн үр дүн нь Болзано-Вейерштрассын дараах үндсэн теоремд хүргэдэг.

Болзано-Вейерштрассын теорем.Аливаа хязгаарлагдмал дарааллаас нийлэх дэд дарааллыг гаргаж болно.

Баталгаа.(x n ) дараалал нь хязгаарлагдмал тул хамгийн багадаа нэг х хязгаарын цэгтэй байна. Дараа нь энэ дарааллаас бид x цэгт нийлэх дэд дарааллыг сонгож болно (хязгаарын цэгийн 2-р тодорхойлолтоос дагана).

Сэтгэгдэл.Аливаа хязгаарлагдмал дарааллаас монотон конвергент дарааллыг тусгаарлаж болно.

Болзано-Вейерштрассын теорем

Болзано-Вейерштрассын теорем, эсвэл Хязгаарын цэг дээрх Болзано-Вейерштрасс лемма- Шинжилгээний санал, түүний томъёоллын нэг нь: сансар огторгуйн хязгаарлагдмал цэгүүдийн дарааллаас нэг нийлэх дэд дарааллыг сонгож болно. Болзано-Вейерштрассын теорем, ялангуяа тооны дарааллын тохиолдол ( n= 1 ), дүн шинжилгээ хийх хичээл бүрт багтсан болно. Шинжилгээнд олон санааг нотлоход ашигладаг, тухайлбал, яг дээд ба доод хязгаарт хүрэх интервал дээр үргэлжилдэг функцийн тухай теорем. Теорем нь Чехийн математикч Болзано, Германы математикч Вейерштрасс нарын нэрийг бие даан томъёолж, нотолсон.

Найрлага

Болзано-Вейерштрассын теоремын хэд хэдэн томъёоллыг мэддэг.

Эхний жор

Сансар огторгуй дахь цэгүүдийн дарааллыг санал болгоё.

мөн энэ дараалал нь хязгаарлагдмал байг, өөрөөр хэлбэл

Хаана C> 0 - зарим тоо.

Дараа нь энэ дарааллаас бид дэд дарааллыг гаргаж болно

сансар огторгуйн аль нэг цэгт нийлдэг.

Энэ томъёолол дахь Болзано-Вейерштрассын теоремыг заримдаа нэрлэдэг хязгаарлагдмал дарааллын нягт байх зарчим.

Эхний найруулгын өргөтгөсөн хувилбар

Болзано-Вейерштрассын теорем нь ихэвчлэн дараах өгүүлбэрээр нэмэгддэг.

Хэрэв орон зай дахь цэгүүдийн дараалал нь хязгааргүй бол түүнээс хязгаартай дарааллыг сонгох боломжтой.

Энэ үйл явдалд зориулж n= 1, энэ томъёоллыг боловсронгуй болгож болно: дурын хязгааргүй тоон дарааллаас хязгаар нь тодорхой тэмдгийн (эсвэл) хязгааргүй дэд дарааллыг сонгож болно.

Тиймээс тооны дараалал бүр бодит тоонуудын өргөтгөсөн багцад хязгаартай дэд дарааллыг агуулдаг.

Хоёр дахь томъёолол

Дараахь санал бол Болзано-Вейерштрассын теоремын өөр хувилбар юм.

Аливаа хязгаарлагдмал хязгааргүй дэд олонлогууд Эзайд дор хаяж нэг хязгаарын цэг байна.

Нарийвчилсан байдлаар хэлбэл, энэ нь хороолол бүрт хязгааргүй тооны цэгүүдийг агуулсан цэг байдаг гэсэн үг юм. Э .

Болзано-Вейерштрассын теоремын хоёр томьёоны эквивалентийн баталгаа

Болъё Э- орон зайн хязгаарлагдмал хязгааргүй дэд олонлог. Орцгооё Эөөр өөр цэгүүдийн дараалал

Энэ дараалал нь хязгаарлагдмал тул Болзано-Вейерштрассын теоремын анхны томъёололын ачаар бид үүнээс дэд дарааллыг тусгаарлаж болно.

тодорхой цэгт ойртох. Дараа нь нэг цэгийн хөрш бүр x 0 нь олонлогийн хязгааргүй тооны цэгүүдийг агуулна Э .

Эсрэгээр, орон зай дахь цэгүүдийн дурын хязгаарлагдмал дарааллыг өгье.

Олон утгатай ЭӨгөгдсөн дарааллын хэмжээ хязгаарлагдмал боловч хязгааргүй эсвэл төгсгөлтэй байж болно. Хэрэв ЭМэдээжийн хэрэг, дараа нь утгуудын нэг нь дарааллаар хязгааргүй олон удаа давтагдана. Дараа нь эдгээр нэр томъёо нь цэг рүү нийлдэг суурин дэд дарааллыг үүсгэдэг а .

Хэрэв олон байвал Энь хязгааргүй, тэгвэл Болзано-Вейерштрассын теоремын хоёр дахь томьёоллоор дарааллын хязгааргүй олон өөр нөхцлүүдийн аль ч орчимд цэг байдаг.

Бид дарааллаар нь сонгоно оноо , тоо нэмэгдэх нөхцөлийг ажиглахад:

Дараа нь дараагийн дараалал нь цэг рүү нийлдэг x 0 .

Баталгаа

Болзано-Вейерштрассын теорем нь бодит тооны олонлогийн бүрэн байдлын шинж чанараас гаралтай. Баталгаажуулалтын хамгийн алдартай хувилбар нь бүрэн байдлын шинж чанарыг үүрлэсэн сегментийн зарчим хэлбэрээр ашигладаг.

Нэг хэмжээст хэрэг

Аль ч хязгаарлагдмал тооны дарааллаас нэг нийлэх дэд дарааллыг сонгож болохыг баталцгаая. Дараахь нотлох аргыг нэрлэдэг Болзано арга, эсвэл хагас хуваах арга.

Хязгаарлагдмал тооны дарааллыг өгье

Дарааллын хязгаарлагдмал байдлаас үзэхэд түүний бүх гишүүд нь тоон шулууны тодорхой сегмент дээр байрладаг бөгөөд үүнийг бидний тэмдэглэдэг [ а 0 ,б 0 ] .

Хэсэг хуваах [ а 0 ,б 0 ] хагасыг хоёр тэнцүү сегмент болгон хуваана. Үүссэн сегментүүдийн дор хаяж нэг нь дарааллын хязгааргүй тооны гишүүнчлэлийн тоог агуулна. Үүнийг тэмдэглэе [ а 1 ,б 1 ] .

Дараагийн алхамд бид [ сегменттэй процедурыг давтах болно. а 1 ,б 1 ]: тэнцүү хоёр сегментэд хувааж, тэдгээрээс дарааллын хязгааргүй тооны гишүүн байх хэсгийг сонгоно. Үүнийг тэмдэглэе [ а 2 ,б 2 ] .

Процессыг үргэлжлүүлснээр бид үүрлэсэн сегментүүдийн дарааллыг олж авна

Дараах бүр нь өмнөхийнх нь хагас бөгөөд дарааллын хязгааргүй тооны гишүүн ( x к } .

Сегментүүдийн урт тэг байх хандлагатай байна:

Коши-Канторын үүрлэсэн сегментийн зарчмын дагуу бүх сегментүүдэд хамаарах нэг цэг ξ байдаг:

Сегмент бүр дээр бүтээн байгуулалтаар [а м ,б м ] дарааллын хязгааргүй тооны гишүүн байдаг. Дараалсан сонголт хийцгээе

тоо нэмэгдэх нөхцөлийг ажиглахдаа:

Дараа нь дэд дараалал ξ цэгт нийлнэ. Энэ нь ξ хүртэлх зай нь тэдгээрийг агуулсан сегментийн уртаас хэтрэхгүй байна гэсэн үг юм [а м ,б м ] , хаана

Дурын хэмжээсийн орон зайн тохиолдолд өргөтгөл

Болзано-Вейерштрассын теоремыг дурын хэмжигдэхүүнтэй орон зайн хувьд хялбархан ерөнхийлж болно.

Орон зай дахь цэгүүдийн дарааллыг өгье.

(доод индекс нь дарааллын гишүүний дугаар, дээд индекс нь координатын дугаар юм). Хэрэв орон зай дахь цэгүүдийн дараалал хязгаарлагдмал бол координатын тоон дараалал бүр нь:

бас хязгаарлагдмал ( - координатын дугаар).

Дараалалаас Болзано-Вейрштрассын теоремын нэг хэмжээст хувилбарын ачаар ( x к) эхний координатууд нь нийлэх дараалал үүсгэдэг цэгүүдийн дэд дарааллыг сонгож болно. Үүссэн дэд дарааллаас бид хоёр дахь координатын дагуу нийлэх дэд дарааллыг дахин сонгоно. Энэ тохиолдолд нэгдэх дарааллын дараагийн дараалал бүр нийлдэг тул эхний координатын дагуу нийлэх байдал хадгалагдана. гэх мэт.

Дараа нь nБид тодорхой дарааллыг авдаг

-ийн дэд дараалал бөгөөд координат бүрийн дагуу нийлдэг. Үүнээс үзэхэд энэ дэд дараалал нийлдэг.

Өгүүллэг

Болзано-Вейерштрассын теорем (тохиолдлын хувьд n= 1) анх 1817 онд Чехийн математикч Болзано нотолсон. Болзаногийн ажилд энэ нь одоо Болзано-Коши теорем гэгддэг тасралтгүй функцын завсрын утгуудын теоремыг батлахад лемма үүрэг гүйцэтгэсэн. Гэсэн хэдий ч Коши, Вейерштрасс нарын өмнө Болзаногийн нотолсон эдгээр болон бусад үр дүн нь анзаарагдсангүй.

Зөвхөн хагас зуун жилийн дараа Вейерштрасс Болзанооос үл хамааран энэ теоремыг дахин нээж, баталжээ. Болзаногийн бүтээл мэдэгдэж, хүлээн зөвшөөрөгдөхөөс өмнө анх Вейерштрассын теорем гэж нэрлэгддэг байсан.

Өнөөдөр энэ теорем нь Болзано, Вейерштрасс нарын нэрийг агуулдаг. Энэ теоремыг ихэвчлэн нэрлэдэг Болзано-Вейерштрасс лемма, заримдаа хязгаарын цэгийн лемма.

Болзано-Вейерштрассын теорем ба авсаархан байдлын тухай ойлголт

Болзано-Вейерштрассын теорем нь хязгаарлагдмал олонлогийн дараах сонирхолтой шинж чанарыг тогтоодог: цэгүүдийн дараалал бүр. Мнийлсэн дэд дарааллыг агуулна.

Шинжилгээнд янз бүрийн саналыг нотлохдоо тэд ихэвчлэн дараахь арга техникийг ашигладаг: тэд хүссэн шинж чанартай цэгүүдийн дарааллыг тодорхойлж, дараа нь үүнээс өөр өөр дарааллыг сонгосон боловч аль хэдийн нийлдэг. Жишээлбэл, интервал дээр үргэлжилсэн функц нь хязгаарлагдмал бөгөөд хамгийн их ба хамгийн бага утгыг авдаг гэж Вейерштрассын теорем ингэж нотлогддог.

Ерөнхийдөө ийм аргын үр дүнтэй байдал, түүнчлэн Вейерштрассын теоремыг дурын метрийн орон зайд хүргэх хүсэл эрмэлзэл нь Францын математикч Морис Фречетийг 1906 онд уг үзэл баримтлалыг нэвтрүүлэхэд хүргэсэн. нягтрал. Болзано-Вейерштрассын теоремоор тогтоосон хязгаарлагдмал олонлогуудын шинж чанар нь дүрслэлээр хэлбэл, олонлогийн цэгүүд нэлээд "ойрхон" эсвэл "авсаархан" байрладаг: энэ олонлогийн дагуу хязгааргүй олон алхмуудыг хийснээр бид үүнийг хийх болно. Сансар огторгуйн зарим цэгт бидний хүссэнээр ойртох нь гарцаагүй.

Frechet дараах тодорхойлолтыг танилцуулж байна: багц Мдуудсан авсаархан, эсвэл авсаархан, хэрэв түүний цэгүүдийн дараалал бүр энэ олонлогийн аль нэг цэгт нийлэх дэд дарааллыг агуулж байвал. Зураг авалт дээр байгаа гэж таамаглаж байна Мхэмжигдэхүүн нь тодорхойлогддог, өөрөөр хэлбэл энэ нь

Тодорхойлолт v.7. Дурын U (x) болон дурын натурал N тооны хувьд энэ хүрээлэлд хамаарах xn элементийг түүнээс их тоотой олох боломжтой бол тооны шулуун дээрх x € R цэгийг дарааллын (xn) хязгаарын цэг гэнэ. LG, өөрөөр хэлбэл. x 6 R - хязгаарын цэг бол. Өөрөөр хэлбэл, x цэг нь (xn)-ийн хязгаарын цэг байх бөгөөд хэрвээ түүний хөршүүдийн аль нэг нь n > N тоотой бүх элемент биш ч гэсэн дур зоргоороо их тоотой энэ дарааллын элементүүдийг агуулж байвал дараах мэдэгдэл маш тодорхой байна. . Мэдэгдэл b.b. Хэрэв lim(xn) = 6 6 R бол b нь (xn) дарааллын цорын ганц хязгаар цэг болно. Үнэн хэрэгтээ, дарааллын хязгаарын 6.3-р тодорхойлолтын дагуу түүний бүх элементүүд нь тодорхой тооноос эхлэн 6-р цэгийн дурын жижиг хороололд ордог тул дур мэдэн их тоо бүхий элементүүд өөр ямар ч цэгийн ойролцоо орох боломжгүй. . Иймээс 6.7-р тодорхойлолтын нөхцөл нь зөвхөн нэг цэг 6-д хангагдана. Гэсэн хэдий ч дарааллын хязгаарын цэг бүр (заримдаа нимгэн хураангуй цэг гэж нэрлэдэг) түүний хязгаар биш юм. Иймд (b.b) дараалалд хязгаар байхгүй (жишээ 6.5-ыг үзнэ үү), гэхдээ x = 1 ба x = - 1 гэсэн хоёр хязгаарын цэгтэй байна. ((-1)pp) дараалал нь хоёр хязгааргүй цэг +oo ба хязгаарын цэгүүдтэй - байна. Өргөтгөсөн тооны шугамтай, тэдгээрийн нэгдлийг нэг тэмдгээр oo гэж тэмдэглэнэ. Ийм учраас бид хязгааргүй хязгаарын цэгүүд давхцаж, (6.29)-ын дагуу хязгааргүй oo цэг нь энэ дарааллын хязгаар гэж үзэж болно. Дарааллын дугаарын шугамын хязгаарын цэгүүд Вейерштрассын тест ба Коши шалгуурын баталгаа. (jn) дарааллыг өгөөд k тоонууд эерэг бүхэл тоонуудын өсөх дараалал үүсгэнэ. Дараа нь дарааллыг (Vnb энд yn = xkn> эх дарааллын дэд дараалал гэж нэрлэдэг. Мэдээжийн хэрэг, хэрэв (i„) 6-ын тоо хязгаартай байвал тодорхой тооноос эхлэн түүний аль нэг дэд дараалал нь ижил хязгаартай байна. Анхны дарааллын аль алиных нь бүх элементүүд болон түүний дэд дарааллын аль нэг нь 6-р цэгийн сонгосон аль ч хэсэгт багтана. Үүний зэрэгцээ дэд дарааллын дурын хязгаарын цэг нь мөн дарааллын хязгаарын цэг болно.Теорем 9. хязгаарын цэгийн хувьд энэ хязгаарын цэгийг өөрийн хязгаар болгон авах дэд дарааллыг сонгож болно.(xn) дарааллын хязгаарын цэгийг b гэж үзээд 6-р тодорхойлолтын дагуу. 7 хязгаарын цэг, n бүрийн хувьд 1/n радиустай b цэгийн U (6, 1/n) орчимд хамаарах элемент байна. ijtj, ...1 ... цэгүүдээс бүрдэх дэд дараалал нь zjfcn€U(6, 1/n) Vn 6 N нь 6-р цэгт хязгаартай. Үнэн хэрэгтээ дурын e > 0-ийн хувьд N-г сонгож болно. тиймэрхүү. Дараа нь км-ийн тооноос эхлэн дэд дарааллын бүх элементүүд 6-р цэгийн ^-хөрш U(6, e)-д орох бөгөөд энэ нь дарааллын хязгаарын тодорхойлолтын 6.3-р нөхцөлтэй тохирч байна. Эсрэг теорем нь бас үнэн юм. Дарааллын дугаарын шугамын хязгаарын цэгүүд Вейерштрассын тест ба Коши шалгуурын баталгаа. Теорем 8.10. Хэрэв зарим дараалал 6-р хязгаартай дэд дараалалтай бол b нь энэ дарааллын хязгаарын цэг болно. Дарааллын хязгаарын 6.3-р тодорхойлолтоос тодорхой тооноос эхлэн b хязгаартай дэд дарааллын бүх элементүүд нь дурын e радиусын U(b, ​​e) хүрээлэлд ордог. нь нэгэн зэрэг дарааллын элементүүд (xn)> xn элементүүд нь дур зоргоороо олон тоотой энэ хөршид багтах бөгөөд энэ нь 6.7-р тодорхойлолтын дагуу b нь (n) дарааллын хязгаарын цэг гэсэн үг юм. Тайлбар 0.2. 6.9 ба 6.10 теоремууд нь U(6, 1 /n)-ийн merto хөршийг нотлохдоо хөрш (эсвэл хөршүүд)-ийг авч үзвэл хязгаарын цэг хязгааргүй тохиолдолд мөн хүчинтэй байна.Нэгдэх дэд дараалал үүсэх нөхцөл дарааллаас тусгаарлаж болохыг дараах теоремоор тогтооно.Теорем 6.11 (Болзано - Вейерштрас) Хязгаарлагдмал дараалал бүр нь хязгаарлагдмал хязгаарт нийлэх дэд дарааллыг агуулна.(an) дарааллын бүх элементүүд a ба 6 тоонуудын хооронд байг. , өөрөөр хэлбэл xn € [a, b] Vn € N. [a , b] хэрчмийг хагасаар хуваа. Дараа нь түүний хагасын нэгээс доошгүй нь дарааллын хязгааргүй тооны элементүүдийг агуулна, өөрөөр хэлбэл бүх сегмент [a, b] нь хязгаарлагдмал тоог агуулсан байх бөгөөд энэ нь боломжгүй юм. ] нь дарааллын (zn) хязгааргүй олонлог элементүүдийг агуулсан [a , 6] сегментийн хагасыг (эсвэл хоёр тал нь ийм байвал) гэж үзье. , дараа нь тэдгээрийн аль нэг нь).Үүний нэгэн адил дарааллын хязгааргүй олонлог элементүүдийг агуулсан сегментээс гэх мэт. Энэ процессыг үргэлжлүүлснээр бид bn - an = (6- a)/2P бүхий үүрлэсэн сегментүүдийн системийг байгуулна. Үүрлэсэн сегментийн зарчмын дагуу эдгээр бүх сегментүүдэд хамаарах x цэг байдаг. Энэ цэг нь (xn) дарааллын хязгаарын цэг байх болно - Үнэн хэрэгтээ аливаа цахим хөршийн U(x, e) = (xx + e) ​​x цэгийн хувьд C U(x, e) сегмент байдаг (энэ нь) дарааллын хязгааргүй тооны элементүүдийг агуулсан (sn) тэгш бус байдлаас n-ийг сонгоход л хангалттай. 6.7-д зааснаар x нь энэ дарааллын хязгаарын цэг юм. Дараа нь теорем 6.9-ийн дагуу х цэгт нийлэх дэд дараалал байна. Энэ теоремыг батлахад ашигласан үндэслэлийн аргыг (заримдаа Болзано-Вейер-Страссын лемма гэж нэрлэдэг) авч үзэж буй сегментүүдийн дараалсан хуваагдалтай холбоотой үндэслэлийг Болзаногийн арга гэж нэрлэдэг. Энэ теорем нь олон нийлмэл теоремуудын нотолгоог ихээхэн хялбаршуулдаг. Энэ нь хэд хэдэн гол теоремуудыг өөр (заримдаа энгийн) аргаар батлах боломжийг олгодог. Хавсралт 6.2. Weierstrass test ба Cauchy шалгуурын баталгаа Эхлээд бид мэдэгдлийг 6.1 (Хязгаарлагдмал монотон дарааллын нийлэлтийг тодорхойлох Weierstrass тест) нотолж байна. Дараалал (jn) буурахгүй байна гэж үзье. Дараа нь түүний утгуудын олонлог нь дээр хязгаарлагдах ба теорем 2.1-ээр дээд цэгтэй байх бөгөөд үүнийг бид sup(xn) R гэж тэмдэглэнэ. Дээд талын шинж чанараас шалтгаалан (2.7-г үзнэ үү) Дарааллын хязгаарын цэгүүд нь тоо юм. шугам.Weierstrass тест ба Коши шалгуурын баталгаа. Тодорхойлолт 6.1-ийн дагуу бид буурахгүй дарааллын хувьд эсвэл Дараа нь > Ny ба (6.34)-ийг харгалзан бид дарааллын хязгаарын 6.3-р тодорхойлолттой тохирч байгааг олж авна, өөрөөр хэлбэл. 31im(sn) ба lim(xn) = 66R. Хэрэв дараалал (xn) өсөхгүй бол нотлох явц ижил байна. Шалгуурын нөхцөл зайлшгүй шаардлагатай нь теорем 6.7-аас үүдэлтэй тул дарааллын нийлэх Кочиа шалгуурын хангалттай эсэхийг нотлох ажлыг үргэлжлүүлье (Мэдэгдэл 6.3-ыг үзнэ үү). (jn) дарааллыг үндсэн гэж үзье. Тодорхойлолт 6.4-ийн дагуу дурын € > 0 байвал m^N ба n^N-ийг илэрхийлэх N(s) тоог олж болно. Дараа нь m - N-ийг авч Vn > N-ийн хувьд бид € £ авна. Харж буй дараалал нь N-ээс ихгүй тоотой хязгаарлагдмал тооны элементтэй тул (6.35)-аас үндсэн дараалал нь хязгаарлагдмал байна (харьцуулахын тулд 1-р зүйлийг үзнэ үү) нийлсэн дарааллын хязгаарлагдмал байдлын тухай теорем 6.2-ын баталгаа). Хязгаарлагдмал дарааллын утгуудын багцын хувьд доод ба дээд хязгаарууд байдаг (Теорем 2.1-ийг үзнэ үү). n > N элементийн утгуудын багцын хувьд бид эдгээр нүүрийг an = inf xn ба bjy = sup xn гэж тэмдэглэнэ. N нэмэгдэхэд яг инфимум буурахгүй, яг дээд хэмжээ нэмэгдэхгүй, i.e. . Би агааржуулалтын систем авах уу? сегментүүд Үүрлэсэн сегментийн зарчмын дагуу бүх сегментүүдэд хамаарах нийтлэг цэг байдаг. Үүнийг b гэж тэмдэглэе. Тиймээс харьцуулалтаас (6. 36) ба (6.37)-ын үр дүнд бид дарааллын хязгаарын 6.3-д нийцэхийг олж авна, өөрөөр хэлбэл. 31im(x„) ба lim(sn) = 6 6 Р.Бользано үндсэн дарааллыг судалж эхлэв. Гэвч түүнд бодит тоонуудын хатуу онол байгаагүй тул үндсэн дарааллын нийлэлтийг баталж чадаагүй юм. Коши үүнийг хийж, үүрлэсэн сегментийн зарчмыг энгийн зүйл болгон авч, Кантор үүнийг хожим нотолсон. Зөвхөн дарааллын нэгдэх шалгуурыг Коши гэж нэрлээд зогсохгүй үндсэн дарааллыг Коши дараалал гэж нэрлэдэг ба үүрлэсэн сегментийн зарчмыг Канторын нэрээр нэрлэсэн байдаг. Асуулт, даалгавар 8.1. Үүнийг батлах: 6.2. Q ба R\Q олонлогт хамаарах элементүүдтэй нийлэхгүй дарааллын жишээг өг. 0.3. Ямар нөхцөлд арифметик ба геометрийн прогрессийн гишүүд буурах ба өсөх дараалал үүсгэдэг вэ? 6.4. Хүснэгтээс үүссэн хамаарлыг батал. 6.1. 6.5. Хязгааргүй +oo, -oo, oo цэгүүд рүү чиглэсэн дарааллын жишээ, 6 € цэгт ойртож буй дарааллын жишээг бүтээ. R. c.v. Хязгааргүй дараалал b.b байж болохгүй гэж үү? Хэрэв тийм бол жишээ хэлнэ үү. 7 цагт. Эерэг элементүүдээс бүрдэх, төгсгөлгүй, хязгааргүй хязгааргүй салангид дарааллын жишээг байгуул. 6.8. sn+i = sin(xn/2) давтагдах томьёогоор өгөгдсөн (jn) дарааллын нийлэлтийг “1 = 1. 6.9. sn+i/xn-»g€) бол lim(xn)=09 гэдгийг батал.