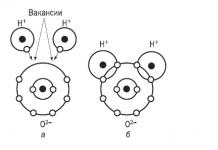
- (хоногийн тархалт) Аливаа зүйл тохиолдох магадлалыг тооцоолох боломжийг олгодог тархалт санамсаргүй үйл явдал, хэд хэдэн бие даасан үйл явдлын ажиглалтын үр дүнд олж авсан, хэрэв түүний бүрдүүлэгч элементар тохиолдох магадлал бол ... ... Эдийн засгийн толь бичиг

- (Бернуллигийн тархалт) давтан бие даасан туршилтын явцад тодорхой үйл явдал тохиолдох магадлалын тархалт, хэрэв туршилт бүрт энэ үйл явдал тохиолдох магадлал p(0 p 1) -тэй тэнцүү бол. Яг тоо нь? Энэ үйл явдлын тохиолдлууд нь ... ... Том нэвтэрхий толь бичиг

бином тархалт- - Харилцаа холбооны сэдэв, үндсэн ойлголтууд EN хоёр нэрийн тархалт ...

- (Бернуллигийн тархалт), хэрэв туршилт бүрт энэ үйл явдал тохиолдох магадлал p (0≤p≤1) -тэй тэнцүү бол давтан бие даасан туршилтын явцад тодорхой үйл явдлын тохиолдлын тооны магадлалын тархалт. Тухайлбал, энэ үйл явдлын тохиолдлын μ тоо ... ... нэвтэрхий толь бичиг

бином тархалт- 1.49. бином тархалт Дискретийн магадлалын тархалт санамсаргүй хувьсагч X, x = 0, 1, 2, ..., n болон n = 1, 2, ... ба 0 параметрүүдийн хувьд 0-ээс n хүртэлх бүхэл тоон утгыг авна.< p < 1, где Источник … Норматив, техникийн баримт бичгийн нэр томъёоны толь бичиг-лавлах ном

Бернуллигийн тархалт, санамсаргүй хэмжигдэхүүн X-ийн магадлалын тархалт, магадлал бүхий бүхэл тоон утгыг тус тус авна (бином коэффициент; B. r-ийн p параметрийг эерэг үр дүнгийн магадлал гэж нэрлэдэг, утгыг авч ... Математик нэвтэрхий толь бичиг

Давтан бие даасан туршилтын явцад тодорхой үйл явдал тохиолдох магадлалын хуваарилалт. Туршилт бүрийн явцад тохиолдох үйл явдлын магадлал 0 ≤ p ≤ 1-тэй тэнцүү бол p-тэй тэнцүү бол n бие даасан үйл явдлын μ тоо ... ... Том Зөвлөлтийн нэвтэрхий толь бичиг

- (Бернуллигийн тархалт), давтан бие даасан туршилтын явцад тодорхой үйл явдлын тохиолдлын тооны магадлалын тархалт, хэрэв туршилт бүрт энэ үйл явдал тохиолдох магадлал p (0) -тэй тэнцүү бол<или = p < или = 1). Именно, число м появлений … Байгалийн шинжлэх ухаан. нэвтэрхий толь бичиг

Бином магадлалын тархалт- (хоёр нэрийн тархалт) Бие даасан туршилт бүрийн үр дүн (статистикийн ажиглалт) ялалт эсвэл ялагдал, оруулах эсвэл хасах, нэмэх эсвэл ... гэсэн хоёр боломжит утгын аль нэгийг авсан тохиолдолд ажиглагддаг тархалт. Эдийн засаг-математикийн толь бичиг

бином магадлалын тархалт- Бие даасан туршилт (статистикийн ажиглалт) бүрийн үр дүн нь ялалт эсвэл ялагдал, оруулах эсвэл хасах, нэмэх эсвэл хасах, 0 эсвэл 1 гэсэн хоёр боломжит утгын аль нэгийг авсан тохиолдолд ажиглагддаг хуваарилалт. Энэ нь ... ... Техникийн орчуулагчийн гарын авлага

Номууд

• Бодлого дахь магадлалын онол, математик статистик. 360 гаруй асуудал, дасгал, Д.А.Борзых. Санал болгож буй гарын авлага нь янз бүрийн түвшний нарийн төвөгтэй ажлуудыг агуулдаг. Гэсэн хэдий ч гол анхаарал нь дунд зэргийн нарийн төвөгтэй ажлуудад чиглэгддэг. Энэ нь оюутнуудыг...
• Бодлого дахь магадлалын онол, математик статистик 360 гаруй бодлого, дасгал, Д.Борзых Санал болгож буй гарын авлагад янз бүрийн түвшний нарийн төвөгтэй асуудлууд багтсан болно. Гэсэн хэдий ч гол анхаарал нь дунд зэргийн нарийн төвөгтэй ажлуудад чиглэгддэг. Энэ нь оюутнуудыг...

Бүх юмс үзэгдлийг 1, 2, 3... 100500... гэх мэт тоон хэмжүүрээр хэмждэггүй. Аливаа үзэгдэл үргэлж хязгааргүй эсвэл олон тооны янз бүрийн төлөвийг авч чаддаггүй. Жишээлбэл, хүний ​​хүйс нь M эсвэл F байж болно. Буудагч нь бай онох эсвэл алдаж байна. Та "Тэмдэг" эсвэл "эсрэг" гэх мэт санал өгөх боломжтой. гэх мэт. Өөрөөр хэлбэл, ийм өгөгдөл нь өөр шинж чанарын төлөвийг илэрхийлдэг - "тийм" (үйл явдал болсон) эсвэл "үгүй" (үйл явдал болоогүй). Болж буй үйл явдлыг (эерэг үр дүн) мөн "амжилт" гэж нэрлэдэг.

Ийм өгөгдөлтэй туршилтыг дууддаг Бернулли схем, олон тооны туршилтаар эерэг үр дүнг нийт туршилтын тоонд харьцуулсан харьцаа нь энэ үйл явдал тохиолдох магадлалд нөлөөлдөг болохыг олж мэдсэн Швейцарийн алдарт математикчийг хүндэтгэн тэмдэглэв.

Альтернатив шинж чанарын хувьсагч

Математикийн аппаратыг шинжилгээнд ашиглахын тулд ийм ажиглалтын үр дүнг тоон хэлбэрээр тэмдэглэнэ. Үүнийг хийхийн тулд эерэг үр дүнг 1-р тоогоор, сөрөг үр дүнг - 0-ээр оноодог. Өөрөөр хэлбэл, бид зөвхөн хоёр утгыг авах боломжтой хувьсагчтай харьцаж байна: 0 эсвэл 1.

Үүнээс ямар ашиг тус авч болох вэ? Ер нь энгийн мэдээллээс дутахгүй. Тиймээс эерэг үр дүнгийн тоог тооцоолоход хялбар байдаг - бүх утгыг нэгтгэн дүгнэхэд хангалттай, жишээлбэл. бүгд 1 (амжилт). Та цааш явж болно, гэхдээ энэ нь танд хэд хэдэн тэмдэглэгээг оруулах шаардлагатай болно.

Анхаарах зүйл бол эерэг үр дүн (энэ нь 1-тэй тэнцүү) гарах магадлал багатай байдаг. Жишээлбэл, зоос шидэх үед толгой авах нь ½ эсвэл 0.5 байна. Энэ магадлалыг уламжлал ёсоор латин үсгээр тэмдэглэдэг х. Тиймээс альтернатив үйл явдлын магадлал нь тэнцүү байна 1 - х, үүнийг мөн тэмдэглэдэг q, тэр бол q = 1 – х. Эдгээр тэмдэглэгээг хувьсах хуваарилалтын хүснэгт хэлбэрээр тодорхой системчилж болно X.

Бид боломжит утгууд болон тэдгээрийн магадлалын жагсаалтыг хүлээн авсан. Тооцоолж болно хүлээгдэж буй үнэ цэнэТэгээд тархалт. Хүлээлт нь бүх боломжит утгуудын бүтээгдэхүүн ба тэдгээрийн харгалзах магадлалын нийлбэр юм.

Дээрх хүснэгтүүдийн тэмдэглэгээг ашиглан хүлээлтийг тооцоолъё.

Альтернатив тэмдгийн математикийн хүлээлт нь энэ үйл явдлын магадлалтай тэнцүү байна. х.

Одоо альтернатив шинж чанарын хэлбэлзэл гэж юу болохыг тодорхойлъё. Тархалт гэдэг нь математикийн хүлээлтээс хазайсан дундаж квадрат юм. Ерөнхий томъёо (дискрет өгөгдлийн хувьд) нь:

Тиймээс альтернатив шинж чанарын хэлбэлзэл:

Энэ тархалт хамгийн ихдээ 0.25 (хамт p=0.5).

Стандарт хазайлт нь дисперсийн үндэс юм:

Хамгийн их утга нь 0.5-аас хэтрэхгүй.

Таны харж байгаагаар математикийн хүлээлт ба альтернатив шинж чанарын хэлбэлзэл нь маш нягт хэлбэртэй байдаг.

Санамсаргүй хэмжигдэхүүний бином тархалт

Нөхцөл байдлыг өөр өнцгөөс харцгаая. Үнэхээр нэг шидэхэд толгойн дундаж алдагдал 0.5 байх нь хэнд хамаатай юм бэ? Төсөөлөх ч боломжгүй. Өгөгдсөн тооны шидэлтэнд тохиолддог толгойн тооны тухай асуулт асуух нь илүү сонирхолтой юм.

Өөрөөр хэлбэл, судлаач тодорхой тооны амжилттай үйл явдал тохиолдох магадлалыг ихэвчлэн сонирхдог. Энэ нь шалгасан багц дахь гэмтэлтэй бүтээгдэхүүний тоо (1 - гэмтэлтэй, 0 - сайн) эсвэл эдгэрэлтийн тоо (1 - эрүүл, 0 - өвчтэй) гэх мэт байж болно. Ийм "амжилтын" тоо нь хувьсагчийн бүх утгуудын нийлбэртэй тэнцүү байх болно X, өөрөөр хэлбэл ганц үр дүнгийн тоо.

Санамсаргүй утга Ббином гэж нэрлэгддэг ба 0-ээс утгыг авна n(цагт Б= 0 – бүх хэсгүүд тохиромжтой, хамт Б = n– бүх эд анги гэмтэлтэй). Энэ нь бүх үнэт зүйлс гэж үздэг xбие биенээсээ хараат бус. Хоёр тоот хувьсагчийн үндсэн шинж чанарыг авч үзье, өөрөөр хэлбэл бид түүний математик хүлээлт, тархалт, тархалтыг тогтоох болно.

Хоёр тоот хувьсагчийн хүлээлтийг олж авахад маш хялбар байдаг. Хэмжигдэхүүний нийлбэрийн математик хүлээлт нь нэмсэн хэмжигдэхүүн бүрийн математик хүлээлтийн нийлбэр бөгөөд энэ нь хүн бүрт ижил байдаг тул:

Жишээлбэл, 100 удаа шидэгдсэн толгойн тоог математикийн хүлээлт 100 × 0.5 = 50 байна.

Одоо бид хоёрт хувьсагчийн дисперсийн томъёог гаргаж авлаа. Бие даасан санамсаргүй хэмжигдэхүүний нийлбэрийн дисперс нь хэлбэлзлийн нийлбэр юм. Эндээс

Стандарт хазайлт тус тус

100 зоос шидэхэд толгойн тооны стандарт хазайлт нь байна

Эцэст нь, бином утгын тархалтыг авч үзье, i.e. санамсаргүй хэмжигдэхүүн байх магадлал Бөөр өөр үнэ цэнийг авах болно к, Хаана 0≤k≤n. Зоосны хувьд энэ асуудал дараах байдлаар харагдаж болно: 100 шидэхэд 40 толгой авах магадлал хэд вэ?

Тооцооллын аргыг ойлгохын тулд зоосыг ердөө 4 удаа шидсэн гэж төсөөлөөд үз дээ. Аль ч тал нь хэзээ ч унаж болно. Бид өөрөөсөө асуудаг: 4 шидэлтээс 2 толгой авах магадлал хэд вэ? Шидэлт бүр бие биенээсээ хамааралгүй. Энэ нь аливаа хослолыг авах магадлал нь шидэлт бүрийн өгөгдсөн үр дүнгийн магадлалын үржвэртэй тэнцүү байна гэсэн үг юм. O толгойнууд, P нь сүүлтэй байг. Жишээлбэл, бидэнд тохирсон хослолуудын нэг нь OOPP шиг харагдаж болно, өөрөөр хэлбэл:

Ийм хослолын магадлал нь толгой авах хоёр магадлал ба толгой авахгүй байх хоёр магадлалын үржвэртэй тэнцүү байна (урвуу үйл явдлыг дараах байдлаар тооцно. 1 - х), i.e. 0.5×0.5×(1-0.5)×(1-0.5)=0.0625. Энэ нь бидэнд тохирсон хослолуудын аль нэгний магадлал юм. Гэхдээ асуулт нь ямар нэг тодорхой дарааллын тухай биш нийт бүргэдийн тоо байсан юм. Дараа нь та яг 2 толгойтой бүх хослолын магадлалыг нэмэх хэрэгтэй. Тэд бүгд адилхан (хүчин зүйл өөрчлөгдөхөд бүтээгдэхүүн өөрчлөгдөхгүй) нь ойлгомжтой. Тиймээс та тэдгээрийн тоог тооцоолж, дараа нь ийм хослолын магадлалаар үржүүлэх хэрэгтэй. RROO, RORO, ROOR, ORRO, OROR, OORR гэсэн 2 толгойтой 4 шидэлтийн бүх хослолыг тоолж үзье. Нийтдээ 6 сонголт байна.

Тиймээс 4 шидэлтийн дараа 2 толгой авахыг хүссэн магадлал 6×0,0625=0,375 байна.

Гэсэн хэдий ч ингэж тоолох нь уйтгартай юм. Аль хэдийн 10 зоосны хувьд нийт сонголтыг харгис хүчээр олж авахад маш хэцүү байх болно. Тиймээс ухаалаг хүмүүс аль хэдийн өөр өөр хослолуудын тоог тооцоолох томъёог зохион бүтээжээ nэлементүүд к, Хаана n- нийт элементийн тоо; к– зохион байгуулалтын сонголтуудыг тооцсон элементүүдийн тоо. -ийн хослолын томъёо nэлементүүд кэнэ нь:

Комбинаторик хэсэгт үүнтэй төстэй зүйл тохиолддог. Тэнд мэдлэгээ дээшлүүлэхийг хүссэн хүн бүрийг би явуулдаг. Эндээс дурдвал, хоёр гишүүний тархалтын нэр (дээрх томьёо нь Ньютоны биномийн тэлэлтийн коэффициент юм).

Магадлалыг тодорхойлох томъёог ямар ч хэмжигдэхүүнд хялбархан ерөнхийлж болно nТэгээд к. Үүний үр дүнд бином тархалтын томъёо дараах хэлбэртэй байна.

Нөхцөлийг хангасан хослолын тоог тэдгээрийн аль нэгнийх нь магадлалаар үржүүлнэ.

Практикт ашиглахын тулд бином тархалтын томъёог мэдэхэд л хангалттай. Эсвэл та мэдэхгүй байж магадгүй - доор бид Excel ашиглан магадлалыг хэрхэн тодорхойлохыг харуулав. Гэхдээ мэдэх нь дээр.

Энэ томъёог ашиглан бид 100 шидэлтэнд 40 толгой авах магадлалыг тооцоолно.

Эсвэл ердөө 1.08%. Харьцуулбал, энэ туршилтын математикийн хүлээлт, өөрөөр хэлбэл 50 толгой байх магадлал 7.96% байна. Хоёр тоот утгын хамгийн их магадлал нь математикийн хүлээлтэд тохирох утгад хамаарна.

Excel дээр хоёр нэрийн тархалтын магадлалыг тооцоолох

Хэрэв та зөвхөн цаас, тооцоолуур ашигладаг бол интеграл байхгүй ч бином тархалтын томъёог ашиглан тооцоо хийх нь нэлээд хэцүү байдаг. Жишээлбэл, утга нь 100 байна! - 150 гаруй тэмдэгттэй. Өмнө нь, одоо ч гэсэн ийм хэмжигдэхүүнийг тооцоолохын тулд ойролцоогоор томъёог ашигладаг байсан. Одоогийн байдлаар MS Excel гэх мэт тусгай програм хангамжийг ашиглахыг зөвлөж байна. Тиймээс дурын хэрэглэгч (сургалттай хүмүүнлэг ч гэсэн) хоёр тоогоор тархсан санамсаргүй хэмжигдэхүүний утгын магадлалыг хялбархан тооцоолж чадна.

Материалыг нэгтгэхийн тулд бид Excel програмыг ердийн тооцоолуур болгон ашиглах болно, жишээлбэл. Хоёр тоот тархалтын томъёог ашиглан алхам алхмаар тооцооллыг хийцгээе. Жишээ нь 50 толгой авах магадлалыг тооцоод үзье. Тооцооллын үе шат, эцсийн үр дүн бүхий зургийг доор харуулав.

Таны харж байгаагаар завсрын үр дүн нь FACTOR (факторыг тооцоолох), POWER (тоог хүчин чадалд өсгөх), үржүүлэх, хуваах операторууд гэх мэт энгийн функцууд боловч нүдэнд багтахгүй хэмжээтэй байна. хаа сайгүй ашигладаг. Түүнээс гадна энэ тооцоо нь нэлээд төвөгтэй бөгөөд ямар ч тохиолдолд энэ нь нягт биш юм, учир нь олон эсүүд оролцдог. Тийм ээ, тэр даруй ойлгоход хэцүү байдаг.

Ерөнхийдөө Excel нь бином тархалтын магадлалыг тооцоолоход бэлэн функцээр хангадаг. Функцийг дууддаг BINOM.DIST.

Амжилтын тоо - амжилттай тестийн тоо. Бидэнд 50 ширхэг бий.

Туршилтын тоо - шидэлтийн тоо: 100 удаа.

Амжилтанд хүрэх магадлал – нэг шидэхэд толгой гарах магадлал 0.5 байна.

Интеграл – 1 эсвэл 0-ийн аль нэгийг заана.0 бол магадлалыг тооцно P(B=k); хэрэв 1 бол бином тархалтын функцийг тооцоолно, өөрөөр хэлбэл. -аас гарах бүх магадлалын нийлбэр B=0өмнө B=kбагтаасан.

OK дарж дээрхтэй ижил үр дүнг авна, зөвхөн бүх зүйлийг нэг функцээр тооцоолсон.

Маш тухтай. Туршилт хийхийн тулд сүүлийн параметр 0-ийн оронд бид 1-ийг тавьдаг. Бид 0.5398-ыг авдаг. Энэ нь 100 зоос шидэхэд 0-ээс 50 хүртэлх оноо авах магадлал бараг 54% гэсэн үг юм. Гэхдээ эхлээд 50 хувь байх ёстой юм шиг санагдсан. Ерөнхийдөө тооцооллыг хурдан бөгөөд хялбархан хийдэг.

Жинхэнэ шинжээч нь функц хэрхэн ажилладагийг (түүний тархалт гэж юу вэ) ойлгох ёстой, тиймээс бид 0-ээс 100 хүртэлх бүх утгын магадлалыг тооцоолох болно. Өөрөөр хэлбэл, бид нэг толгой байхгүй байх магадлал хэд вэ гэсэн асуултыг тавих болно. 2, 3, 50, 90 эсвэл 100 гэсэн 1 бүргэд гарч ирнэ. Тооцооллыг дараах зурагт үзүүлэв. Цэнхэр шугам нь өөрөө бином тархалт, улаан цэг нь тодорхой тооны амжилтын магадлал юм.

Хоёр гишүүний тархалт нь үүнтэй төстэй эсэхийг асууж магадгүй ... Тийм ээ, маш төстэй. Мойвр (1733 онд) хүртэл том дээж бүхий бином тархалт ойртож байна (тэр үед үүнийг юу гэж нэрлэж байсныг би мэдэхгүй) гэж хэлсэн боловч хэн ч түүнийг сонссонгүй. Гаусс, дараа нь 60-70 жилийн дараа Лаплас л хэвийн тархалтын хуулийг дахин нээж, сайтар судалжээ. Математикийн хүлээлтэд хамгийн их магадлал унадаг, түүнээс хазайх тусам огцом буурч байгааг дээрх график тодорхой харуулж байна. Ердийн хууль шиг.

Дуран тархалт нь маш их практик ач холбогдолтой бөгөөд ихэвчлэн тохиолддог. Excel ашиглан тооцооллыг хурдан бөгөөд хялбархан хийдэг.

Мэдээжийн хэрэг, хуримтлагдсан тархалтын функцийг тооцоолохдоо та дурьдсан хоёртын болон бета тархалтын хоорондох холболтыг ашиглах хэрэгтэй. Энэ арга нь n > 10 бол шууд нийлбэрээс илүү сайн байх нь ойлгомжтой.

Статистикийн сонгодог сурах бичгүүдэд бином тархалтын утгыг олж авахын тулд хязгаарын теорем дээр үндэслэсэн томъёог ашиглахыг зөвлөж байна (Мойвр-Лапласын томъёо гэх мэт). Үүнийг тэмдэглэх нь зүйтэй цэвэр тооцооллын үүднээсЭдгээр теоремуудын үнэ цэнэ тэгтэй ойролцоо байна, ялангуяа одоо бараг бүх ширээ хүчирхэг компьютертэй үед. Дээрх ойролцоо тооцооллын гол дутагдал нь ихэнх хэрэглээний n шинж чанарын утгын хувьд бүрэн хангалтгүй нарийвчлал юм. Үүний дутагдалтай тал бол энэ эсвэл өөр ойролцооллыг ашиглах талаар тодорхой зөвлөмж байхгүй (стандарт бичвэрүүд нь зөвхөн асимптотик томъёолол өгдөг; тэдгээр нь нарийвчлалын тооцоолол дагалддаггүй, тиймээс бага зэрэг ашиг тустай байдаг). Хоёр томьёо нь зөвхөн n-д тохиромжтой гэж би хэлье< 200 и для совсем грубых, ориентировочных расчетов, причем делаемых “вручную” с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.

Би энд квантил олох асуудлыг авч үзэхгүй байна: салангид тархалтын хувьд энэ нь өчүүхэн бөгөөд ийм хуваарилалт үүссэн асуудлуудад энэ нь дүрмийн хувьд хамааралгүй юм. Хэрэв тоо хэмжээ шаардлагатай хэвээр байгаа бол би асуудлыг p-утга (ажиглагдсан ач холбогдол) -тай ажиллах байдлаар дахин боловсруулахыг зөвлөж байна. Энд жишээ дурдъя: хайлтын зарим алгоритмыг хэрэгжүүлэхдээ алхам бүрт хоёр тоот санамсаргүй хэмжигдэхүүний талаарх статистик таамаглалыг шалгах шаардлагатай байдаг. Сонгодог аргын дагуу алхам бүрт шалгуур үзүүлэлтийн статистикийг тооцоолж, түүний утгыг чухал багцын хилтэй харьцуулах шаардлагатай байдаг. Гэсэн хэдий ч алгоритм нь бүрэн гүйцэд учраас чухал багцын хил хязгаарыг тухай бүрт нь шинээр тодорхойлох шаардлагатай байдаг (эцэст нь түүврийн хэмжээ алхам тутамд өөрчлөгддөг) бөгөөд энэ нь цаг хугацааны зардлыг үр ашиггүй нэмэгдүүлдэг. Орчин үеийн хандлагаажигласан ач холбогдлыг тооцоолж, итгэлийн магадлалтай харьцуулж, квантил хайхад хэмнэхийг зөвлөж байна.

Иймд доорх кодуудад урвуу функцийн тооцоо байхгүй бөгөөд үүний оронд өгөгдсөн туршилтын n тоо, тэдгээрийн амжилтын тоо, m тоогоор бие даасан туршилтын амжилтын магадлалын p-ийг тооцдог rev_binomialDF функцийг өгсөн болно. эдгээр m амжилтыг олж авах магадлалын y утга. Энэ нь бином ба бета тархалтын хооронд дээр дурдсан холболтыг ашигладаг.

Үнэн хэрэгтээ энэ функц нь итгэлцлийн интервалын хил хязгаарыг олж авах боломжийг олгодог. Үнэн хэрэгтээ, n хоёрын туршилтанд бид m амжилтанд хүрсэн гэж бодъё. Мэдэгдэж байгаагаар итгэлийн түвшинтэй p параметрийн хоёр талт итгэлийн интервалын зүүн хил нь m = 0 бол 0-тэй тэнцүү ба for нь тэгшитгэлийн шийдэл юм. . Үүний нэгэн адил баруун хязгаар нь m = n бол 1, for нь тэгшитгэлийн шийдэл юм . Үүнээс үзэхэд зүүн хилийг олохын тулд харьцангуй тэгшитгэлийг шийдэх ёстой , зөвийг нь олохын тулд - тэгшитгэл . Тэдгээрийг binom_leftCI болон binom_rightCI функцээр шийддэг бөгөөд энэ нь хоёр талын итгэлийн интервалын дээд ба доод хязгаарыг буцаадаг.

Хэрэв танд үнэхээр гайхалтай нарийвчлал шаардлагагүй бол хангалттай том n-ийн хувьд та дараах ойролцоо тооцоог ашиглаж болно гэдгийг тэмдэглэхийг хүсч байна [B.L. Ван дер Ваерден, Математик статистик. М: IL, 1960, бүлэг. 2, хэсэг 7]: , энд g нь хэвийн тархалтын квантил юм. Энэ ойролцоо тооцооллын үнэ цэнэ нь хэвийн тархалтын квантилуудыг тооцоолох боломжийг олгодог маш энгийн ойролцоо тооцоолол байдаг (хэвийн тархалтыг тооцоолох текст болон энэ лавлах номын харгалзах хэсгийг үзнэ үү). Миний практикт (ихэвчлэн n> 100) энэ ойролцоо тоо нь ойролцоогоор 3-4 цифрийг өгсөн бөгөөд энэ нь дүрмээр бол хангалттай юм.

Дараах кодуудыг ашиглан тооцоолохын тулд танд betaDF.h, betaDF.cpp (бета түгээлтийн хэсгийг үзнэ үү), мөн logGamma.h, logGamma.cpp (Хавсралт А-г үзнэ үү) файлууд хэрэгтэй болно. Та мөн функцүүдийг ашиглах жишээг харж болно.

binomialDF.h файл

#ifndef __BINOMIAL_H__ #include "betaDF.h" double binomialDF(давхар туршилт, давхар амжилт, давхар p); /* * Бие даасан ажиглалтын "туршилт" байх болтугай. * Амжилтын тоо 0 ба "амжилт" (хамааруулсан) хооронд байх B(амжилт|туршилт,p) магадлалыг тооцоол. */ давхар rev_binomialDF(давхар туршилт, давхар амжилт, давхар у); /* * Бернулли схемийг турших туршилтуудад хамгийн багадаа m амжилтанд хүрэх y магадлалыг * мэдэж байг. Энэ функц нь бие даасан туршилтын амжилтын магадлалын p*-ийг олдог. * * Тооцоололд дараах хамаарлыг ашигласан * * 1 - p = rev_Beta(туршилт-амжилт| амжилт+1, у). */ double binom_leftCI(давхар туршилт, давхар амжилт, давхар түвшин); /* Бие даасан ажиглалтын * "туршилт" тус бүрд амжилтын "p" магадлалтай * ба амжилтын тоо нь "амжилт"-тай тэнцэх болтугай. * Хоёр талт итгэлцлийн интервалын зүүн хязгаарыг * ач холбогдлын түвшний түвшинд тооцно. */ давхар binom_rightCI(давхар n, давхар амжилт, давхар түвшин); /* Бие даасан ажиглалтын * "туршилт" тус бүрд амжилтын "p" магадлалтай * ба амжилтын тоо нь "амжилт"-тай тэнцэх болтугай. * Хоёр талт итгэлцлийн интервалын баруун хязгаарыг * ач холбогдлын түвшингээр тооцно. */ #endif /* Төгсгөл #ifndef __BINOMIAL_H__ */

binomialDF.cpp файл

/************************************************ * *********/ /* бином тархалт */ /******************************** * *************************/ #хамаарна #оруулна #include "betaDF.h" ENTRY double binomialDF(double n, double m, double p) /* * "n" бие даасан ажиглалтууд байх болтугай * тус бүрд "p" амжилттай байх магадлалтай. * B(m|n,p) магадлалыг амжилтын тоо нь * 0-ээс "m" (хамааруулсан) хооронд, өөрөөр хэлбэл. * 0-ээс m хүртэлх хоёртын магадлалын нийлбэр: * * m * -- (n) j n-j * > () p (1-p) * -- (j) * j=0 * * Тооцоолол нь мохоо нийлбэрийг илэрхийлэхгүй - * нь төв бета тархалттай дараах хамаарлыг ашиглана: * * B(m|n,p) = Бета(1-p|n-m,m+1). * * Аргументууд эерэг байх ёстой бөгөөд 0 байх ёстой<= p <= 1. */ { assert((n >0) && (p >= 0) && (х<= 1)); if (m < 0) return 0; else if (m == 0) return pow(1-p, n); else if (m >= n) буцаах 1; өөрөөр буцах BetaDF(n-m, m+1).утга(1-p); )/* binomialDF */ ENTRY double rev_binomialDF(double n, double m, double y) /* * Бернулли схемийн n туршилтанд m-ээс багагүй амжилтын y магадлал * тохиолдоно. Энэ функц нь бие даасан туршилтын амжилтын магадлалын p*-ийг олдог. * * Тооцоололд дараах хамаарлыг ашигласан * * 1 - p = rev_Beta(y|n-m,m+1). */ ( assert((n > 0) && (m >= 0) && (m<= n) && (y >= 0) && (y<= 1)); return 1-BetaDF(n-m, m+1).inv(y); }/*rev_binomialDF*/ ENTRY double binom_leftCI(double n, double m, double y) /* Пусть имеется "n" независимых наблюдений * с вероятностью "p" успеха в каждом * и количество успехов равно "m". * Вычисляется левая граница двухстороннего доверительного интервала * с уровнем значимости y. */ { assert((n >0) && (m >= 0) && (м<= n) && (y >= 0.5) && (y< 1)); return BetaDF(m, n-m+1).inv((1-y)/2); }/*binom_leftCI*/ ENTRY double binom_rightCI(double n, double m, double y) /* Пусть имеется "n" независимых наблюдений * с вероятностью "p" успеха в каждом * и количество успехов равно "m". * Вычисляется правая граница доверительного интервала * с уровнем значимости y. */ { assert((n >0) && (m >= 0) && (м<= n) && (y >= 0.5) && (y< 1)); return BetaDF(m+1, n-m).inv((1+y)/2); }/*binom_rightCI*/

Магадлалын онол бидний амьдралд үл үзэгдэх байдлаар оршдог. Бид үүнийг анхаарч үздэггүй, гэхдээ бидний амьдралд тохиолдох үйл явдал бүр нэг магадлалтай байдаг. Олон тооны боломжит хувилбаруудыг харгалзан үзэхэд бид тэдгээрийн хамгийн боломжит, хамгийн бага магадлалтайг тодорхойлох шаардлагатай болж байна. Ийм магадлалын өгөгдлийг графикаар шинжлэх нь хамгийн тохиромжтой. Үүнийг түгээх нь бидэнд тусалж чадна. Binamial бол хамгийн хялбар бөгөөд үнэн зөвийн нэг юм.

Математик ба магадлалын онол руу шууд шилжихээсээ өмнө энэ төрлийн тархалтыг хэн анх гаргаж ирсэн, энэ үзэл баримтлалын математик аппаратын хөгжлийн түүх юу болохыг олж мэдье.

Өгүүллэг

Магадлалын тухай ойлголт эрт дээр үеэс мэдэгдэж байсан. Гэвч эртний математикчид үүнд нэг их ач холбогдол өгөөгүй бөгөөд хожим магадлалын онол болсон онолын үндэс суурийг л тавьж чадсан юм. Тэд дараа нь онолыг өөрөө бий болгож, хөгжүүлсэн хүмүүст ихээхэн тусалсан зарим нэгдмэл аргуудыг бий болгосон.

XVII зууны хоёрдугаар хагаст магадлалын онолын үндсэн ойлголт, арга зүй бүрэлдэж эхэлсэн. Санамсаргүй хэмжигдэхүүний тодорхойлолт, энгийн болон зарим нийлмэл бие даасан, хамааралтай үйл явдлын магадлалыг тооцоолох аргуудыг танилцуулав. Санамсаргүй хэмжигдэхүүн ба магадлалыг сонирхох нь мөрийтэй тоглоомоор тодорхойлогддог: хүн бүр тоглоомд ялах боломжоо мэдэхийг хүсдэг байв.

Дараагийн шат нь магадлалын онолд математик шинжилгээний аргуудыг ашиглах явдал байв. Лаплас, Гаусс, Пуассон, Бернулли зэрэг нэрт математикчид энэ ажлыг гүйцэтгэсэн. Математикийн энэ чиглэлийг шинэ түвшинд ахиулсан хүмүүс нь тэд юм. Хоёр тоот тархалтын хуулийг нээсэн хүн бол Жеймс Бернулли юм. Дашрамд хэлэхэд, бид дараа нь олж мэдэх болно, энэ нээлтийн үндсэн дээр өөр хэд хэдэн нээлт хийсэн нь хэвийн тархалтын хууль болон бусад олон зүйлийг бий болгох боломжийг олгосон юм.

Одоо бид бином тархалтыг тайлбарлахаасаа өмнө магадгүй сургуулиасаа мартсан магадлалын онолын тухай ойлголтыг бага зэрэг сэргээх болно.

Магадлалын онолын үндэс

Бид ийм системийг авч үзэх болно, үүний үр дүнд "амжилт" ба "бүтэлгүйтэл" гэсэн хоёр л үр дүн гарах боломжтой. Үүнийг жишээгээр ойлгоход амархан: бид зоос шидээд, энэ нь толгой дээр гарах болно гэж найдаж байна. Зоос төгс тэнцвэртэй, туршилтанд нөлөөлж болох бусад хүчин зүйл байхгүй тохиолдолд боломжит үйл явдал бүрийн магадлал (унасан толгой - "амжилт", унах толгой - "бүтэлгүйтэл") 50 хувьтай тэнцүү байна.

Энэ бол хамгийн энгийн үйл явдал байсан. Гэхдээ дараалсан үйлдлүүдийг гүйцэтгэдэг нарийн төвөгтэй системүүд байдаг бөгөөд эдгээр үйлдлүүдийн үр дүнгийн магадлал өөр өөр байх болно. Жишээлбэл, дараах системийг авч үзье: агуулгыг нь харж чадахгүй байгаа хайрцагт яг ижил зургаан бөмбөг, гурван хос хөх, улаан, цагаан өнгөтэй байна. Бид санамсаргүй байдлаар хэдэн бөмбөг авах ёстой. Үүний дагуу эхлээд цагаан бөмбөгний аль нэгийг нь сугалж авснаар бид дараа нь цагаан бөмбөг авах магадлалыг эрс багасгах болно. Энэ нь систем дэх объектуудын тоо өөрчлөгддөгтэй холбоотой юм.

IN дараагийн хэсэгилүү төвөгтэй зүйлсийг харцгаая математикийн ойлголтууд, энэ үгс нь ямар утгатай болохыг бидэнд ойртуулдаг " хэвийн тархалт"," биномын тархалт " гэх мэт.

Математик статистикийн элементүүд

Магадлалын онолын хэрэглээний нэг салбар болох статистикт дүн шинжилгээ хийх өгөгдлийг тодорхой өгөөгүй олон жишээ байдаг. Энэ нь тоогоор биш, харин шинж чанар, жишээлбэл, хүйсээр хуваах хэлбэрээр юм. Ийм өгөгдөлд математикийн хэрэгслийг ашиглах, олж авсан үр дүнгээс зарим дүгнэлт гаргахын тулд анхны өгөгдлийг тоон формат руу хөрвүүлэх шаардлагатай. Ихэвчлэн үүнийг хийхийн тулд эерэг үр дүнд 1, сөрөг үр дүнд 0 гэсэн утгыг өгдөг. Тиймээс бид математикийн аргуудыг ашиглан дүн шинжилгээ хийх боломжтой статистик мэдээллийг олж авдаг.

Санамсаргүй хэмжигдэхүүний хоёртын тархалт гэж юу болохыг ойлгох дараагийн алхам бол санамсаргүй хэмжигдэхүүний дисперс ба математикийн хүлээлтийг тодорхойлох явдал юм. Энэ талаар бид дараагийн хэсэгт ярих болно.

Хүлээгдэж буй үнэ цэнэ

Үнэн хэрэгтээ математикийн хүлээлт гэж юу болохыг ойлгоход хэцүү биш юм. Олон байдаг системийг авч үзье янз бүрийн арга хэмжээөөр өөр магадлалтай. Математикийн хүлээлтийг эдгээр үйл явдлын утгуудын бүтээгдэхүүний нийлбэр (сүүлийн хэсэгт бидний ярьсан математик хэлбэрээр) болон тэдгээрийн үүсэх магадлалын нийлбэртэй тэнцүү утга гэж нэрлэнэ.

Хоёр тоот тархалтын математик хүлээлтийг ижил схемийн дагуу тооцоолно: бид санамсаргүй хэмжигдэхүүний утгыг авч, эерэг үр дүнгийн магадлалаар үржүүлж, дараа нь бүх хувьсагчийн үр дүнгийн өгөгдлийг нэгтгэнэ. Энэ өгөгдлийг графикаар харуулах нь маш тохиромжтой - ингэснээр өөр өөр утгуудын математикийн хүлээлт хоорондын ялгаа илүү сайн мэдрэгддэг.

Дараагийн хэсэгт бид өөр нэг ойлголт болох санамсаргүй хэмжигдэхүүний дисперсийн талаар бага зэрэг ярих болно. Энэ нь мөн хоёрт магадлалын тархалтын ойлголттой нягт холбоотой бөгөөд түүний шинж чанар юм.

Бином тархалтын хэлбэлзэл

Энэ утга нь өмнөхтэй нягт холбоотой бөгөөд статистикийн мэдээллийн тархалтыг тодорхойлдог. Энэ нь математикийн хүлээлтээс утгын хазайлтын дундаж квадратыг илэрхийлнэ. Өөрөөр хэлбэл, санамсаргүй хэмжигдэхүүний дисперс нь санамсаргүй хэмжигдэхүүний утга ба түүний математик хүлээлт хоёрын квадрат зөрүүний нийлбэрийг энэ үйл явдлын магадлалаар үржүүлсэн байна.

Ерөнхийдөө энэ нь хоёр төрлийн магадлалын тархалт гэж юу болохыг ойлгохын тулд дисперсийн талаар мэдэх ёстой зүйл юм. Одоо үндсэн сэдэв рүүгээ шууд орцгооё. Тодруулбал, "хостой тархалтын хууль" гэсэн нэлээд төвөгтэй хэллэгийн ард юу нуугдаж байна.

Бином тархалт

Юуны өмнө энэ тархалт яагаад бином болохыг олж мэдье. Энэ нь "бином" гэсэн үгнээс гаралтай. Магадгүй та Ньютоны дурын хоёр тоон a ба b тооны нийлбэрийг сөрөг бус n хүртэл өсгөх томъёоны талаар сонссон байх.

Магадгүй та аль хэдийн таамаглаж байсанчлан Ньютоны бином томьёо болон хоёрын тархалтын томъёо нь бараг ижил томъёо юм. Цорын ганц үл хамаарах зүйл нь хоёр дахь нь тодорхой хэмжигдэхүүнүүдэд практик ач холбогдолтой бөгөөд эхнийх нь зөвхөн ерөнхий математикийн хэрэгсэл бөгөөд практикт хэрэглэх нь өөр байж болно.

Түгээлтийн томъёо

Хоёр нэр томъёоны тархалтын функцийг дараах нэр томъёоны нийлбэрээр бичиж болно.

(n!/(n-k)!k!)*p k *q n-k

Энд n нь бие даасан тоо юм санамсаргүй туршилтууд, p нь амжилттай үр дүнгийн тоо, q нь амжилтгүй үр дүнгийн тоо, k нь туршилтын тоо (0-ээс n хүртэлх утгыг авч болно)! - факториалын тэмдэглэгээ, утга нь өмнөх бүх тооны үржвэртэй тэнцүү тооны функц (жишээ нь: 4 тоо: 4!=1*2*3*4=24).

Үүнээс гадна, бином тархалтын функцийг бүрэн бус бета функц гэж бичиж болно. Гэсэн хэдий ч энэ нь зөвхөн нарийн төвөгтэй статистикийн асуудлыг шийдвэрлэхэд хэрэглэгддэг илүү төвөгтэй тодорхойлолт юм.

Дээрх жишээнүүдийг авч үзсэн бином тархалт нь магадлалын онолын хамгийн энгийн тархалтуудын нэг юм. Мөн нэг төрөл болох хэвийн тархалт байдаг. Энэ нь ихэвчлэн ашиглагддаг бөгөөд тооцоолоход хамгийн хялбар байдаг. Мөн Бернуллигийн тархалт, Пуассоны тархалт, нөхцөлт тархалтууд байдаг. Эдгээр нь бүгд өөр өөр нөхцөлд тодорхой үйл явцын магадлалын хүрээг графикаар тодорхойлдог.

Дараагийн хэсэгт бид энэ математикийн төхөөрөмжийг ашиглахтай холбоотой асуудлуудыг авч үзэх болно жинхэнэ амьдрал. Мэдээжийн хэрэг, өнгөцхөн харахад энэ нь ердийнх шиг бодит амьдрал дээр хэрэглэгдэхгүй, математикчдаас өөр хэнд ч хэрэггүй өөр нэг математикийн зүйл юм шиг санагддаг. Гэсэн хэдий ч энэ нь тийм биш юм. Эцсийн эцэст, бүх төрлийн тархалт, тэдгээрийн график дүрслэлийг зөвхөн эрдэмтдийн хүсэл тэмүүлэл биш харин практик зорилгоор бүтээсэн болно.

Өргөдөл

Мэдээжийн хэрэг, хамгийн их чухал хэрэглээхуваарилалт нь статистикт байдаг, учир нь тэдэнд хэрэгтэй цогц дүн шинжилгээмаш их өгөгдөл. Практикаас харахад олон өгөгдлийн багц нь ойролцоогоор ижил утгын тархалттай байдаг: маш бага ба маш өндөр утгатай чухал бүсүүд нь дүрмээр бол дундаж утгуудаас цөөн элемент агуулдаг.

Том өгөгдлийн багцад дүн шинжилгээ хийх нь зөвхөн статистикт шаардлагатай биш юм. Энэ нь зайлшгүй шаардлагатай, жишээлбэл, онд физик хими. Энэ шинжлэх ухаанд атом, молекулуудын санамсаргүй чичиргээ, хөдөлгөөнтэй холбоотой олон хэмжигдэхүүнийг тодорхойлоход ашигладаг.

Дараагийн хэсэгт бид бином гэх мэт статистик ойлголтуудыг ашиглах нь ямар чухал болохыг ойлгох болно -д санамсаргүй хэмжигдэхүүний тархалт Өдөр тутмын амьдралчи бид хоёрын төлөө.

Яагаад надад хэрэгтэй байна вэ?

Математикийн тухай ярихад олон хүмүүс өөрөөсөө энэ асуултыг асуудаг. Дашрамд хэлэхэд математикийг шинжлэх ухааны хатан хаан гэж хэлээгүй. Энэ нь физик, хими, биологи, эдийн засгийн үндэс суурь бөгөөд эдгээр шинжлэх ухаан бүрт зарим тархалтыг ашигладаг: энэ нь салангид бином тархалт эсвэл хэвийн аль нь ч хамаагүй. Хэрэв бид эргэн тойрныхоо ертөнцийг сайтар ажиглавал математикийг хаа сайгүй ашигладаг болохыг олж харах болно: өдөр тутмын амьдралд, ажил дээрээ, тэр ч байтугай хүмүүсийн харилцааг статистик мэдээлэл хэлбэрээр илэрхийлж, дүн шинжилгээ хийх боломжтой (дашрамд хэлэхэд, энэ нь). , ажилладаг хүмүүс юу вэ тусгай байгууллагуудмэдээлэл цуглуулахад оролцдог).

Одоо энэ нийтлэлд дурьдсанаас илүү энэ сэдвээр илүү ихийг мэдэх шаардлагатай бол юу хийх талаар бага зэрэг ярилцъя.

Энэ нийтлэлд бидний өгсөн мэдээлэл бүрэн гүйцэд биш юм. Түгээлт ямар хэлбэртэй байж болох талаар олон нюансууд байдаг. Бидний аль хэдийн олж мэдсэнээр хоёр нэрийн тархалт нь бүхэлдээ хамаарах үндсэн төрлүүдийн нэг юм математикийн статистикба магадлалын онол.

Хэрэв та сонирхож байгаа бол эсвэл ажилтай холбоотойгоор энэ сэдвээр илүү ихийг мэдэх шаардлагатай бол тусгай уран зохиол судлах шаардлагатай болно. Та математикийн анализын чиглэлээр их сургуулийн курсээс эхэлж, магадлалын онолын хэсэг рүү шилжих хэрэгтэй. Хоёрдахь магадлалын тархалт нь дараалсан нэр томъёоны цуваанаас өөр зүйл биш тул цувралын талаархи мэдлэг бас хэрэг болно.

Дүгнэлт

Нийтлэлээ дуусгахын өмнө бид танд бас нэг сонирхолтой зүйлийг хэлмээр байна. Энэ нь манай нийтлэлийн сэдэв болон ерөнхийдөө бүх математикийн сэдэвтэй шууд холбоотой юм.

Математик бол ашиггүй шинжлэх ухаан гэж олон хүмүүс ярьдаг бөгөөд сургуульд сурч байсан зүйл нь тэдэнд хэрэгтэй байсангүй. Гэхдээ мэдлэг хэзээ ч илүүддэггүй бөгөөд амьдралд ямар нэг зүйл танд ашиггүй байвал та үүнийг санахгүй байна гэсэн үг юм. Хэрэв танд мэдлэг байгаа бол тэд танд тусалж чадна, гэхдээ үгүй ​​бол тэднээс тусламж хүлээж болохгүй.

Тиймээс бид хоёр нэрийн тархалтын тухай ойлголт, түүнтэй холбоотой бүх тодорхойлолтыг авч үзээд бидний амьдралд хэрхэн хэрэглэгдэх талаар ярилцав.

7-р бүлэг.

Санамсаргүй хэмжигдэхүүний тархалтын тусгай хуулиуд

Дискрет санамсаргүй хэмжигдэхүүний тархалтын хуулийн төрлүүд

Дискрет санамсаргүй хэмжигдэхүүнийг утгыг авъя X 1 , X 2 , …, x n,…. Эдгээр утгын магадлалыг янз бүрийн томъёогоор, жишээлбэл магадлалын онолын үндсэн теоремууд, Бернуллигийн томъёо эсвэл бусад томъёог ашиглан тооцоолж болно. Эдгээр томъёоны заримын хувьд хуваарилалтын хууль нь өөрийн гэсэн нэртэй байдаг.

Дискрет санамсаргүй хэмжигдэхүүний тархалтын хамгийн түгээмэл хуулиуд нь бином, геометр, гипергеометр, Пуассоны тархалтын хууль юм.

Бином тархалтын хууль

Үүнийг үйлдвэрлэе nбие даасан туршилтууд, тэдгээрт үйл явдал тохиолдож болох эсвэл харагдахгүй байж болно А. Туршилт бүрт тохиолдох энэ үйл явдлын магадлал тогтмол бөгөөд туршилтын тооноос хамаарахгүй бөгөөд үүнтэй тэнцүү байна. Р=Р(А). Тиймээс үйл явдал тохиолдохгүй байх магадлал Атест бүрт мөн тогтмол бөгөөд тэнцүү байна q=1–Р. Санамсаргүй хэмжигдэхүүнийг авч үзье Xүйл явдлын тохиолдлын тоотой тэнцүү байна АВ nтуршилтууд. Мэдээжийн хэрэг, энэ хэмжигдэхүүний утга тэнцүү байна

X 1 =0 – үйл явдал АВ nтуршилтууд гарч ирээгүй;

X 2 =1 – үйл явдал АВ nтуршилтанд нэг удаа гарч ирсэн;

X 3 =2 – үйл явдал АВ nтуршилтууд хоёр удаа гарсан;

…………………………………………………………..

x n +1 = n- үйл явдал АВ nТуршилтын үеэр бүх зүйл гарч ирэв nнэг удаа.

Эдгээр утгын магадлалыг Бернулли томъёог (4.1) ашиглан тооцоолж болно.

Хаана руу=0, 1, 2, …,n .

Бином тархалтын хууль X, тоотой тэнцүү байнаамжилт nБернулли тестүүд амжилттай болох магадлалтай Р.

Тиймээс, салангид санамсаргүй хэмжигдэхүүн нь боломжит утга нь 0, 1, 2, ... байвал бином тархалттай (эсвэл хоёрномын хуулийн дагуу тархсан) байна. n, харгалзах магадлалыг (7.1) томъёог ашиглан тооцоолно.

Бином тархалт нь хоёроос хамаарна параметрүүд РТэгээд n.

Хоёр гишүүний хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүний тархалтын цуваа нь дараах хэлбэртэй байна.

X			…	к	…	n
Р			…		…

Жишээ 7.1 . Зорилтот руу гурван бие даасан буудлага хийдэг. Буудсан тус бүрийг онох магадлал 0.4 байна. Санамсаргүй утга X- зорилтот цохилтын тоо. Түүний түгээлтийн цувралыг байгуул.

Шийдэл. Санамсаргүй хэмжигдэхүүний боломжит утгууд Xбайна X 1 =0; X 2 =1; X 3 =2; X 4 =3. Бернуллигийн томьёог ашиглан харгалзах магадлалыг олъё. Энэ томъёог энд ашиглах нь бүрэн үндэслэлтэй гэдгийг харуулах нь тийм ч хэцүү биш юм. Нэг сумаар бай онохгүй байх магадлал 1-0.4=0.6 байх болно гэдгийг анхаарна уу. Бид авдаг

Түгээлтийн цуврал нь дараах хэлбэртэй байна.

X
Р	0,216	0,432	0,288	0,064

Бүх магадлалын нийлбэр нь 1-тэй тэнцүү гэдгийг шалгахад хялбар. Санамсаргүй хэмжигдэхүүн өөрөө Xбином хуулийн дагуу хуваарилагдана. ■

Хоёр гишүүний хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүний математик хүлээлт ба дисперсийг олъё.

Жишээ 6.5-ыг шийдвэрлэхэд тухайн үйл явдал тохиолдох тооны математик хүлээлтийг харуулсан. АВ nбие даасан туршилт, хэрэв үүсэх магадлал Атест бүрт тогтмол бөгөөд тэнцүү байна Р, тэнцүү байна n· Р

Энэ жишээнд дуран хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүнийг ашигласан. Иймд жишээ 6.5-ын шийдэл нь үндсэндээ дараах теоремын баталгаа болно.

Теорем 7.1.Хоёрномын хуулийн дагуу тархсан дискрет санамсаргүй хэмжигдэхүүний математикийн хүлээлт нь туршилтын тоо ба "амжилт"-ын магадлалын үржвэртэй тэнцүү байна, өөрөөр хэлбэл. М(X)=n· Р.

Теорем 7.2.Хоёр гишүүний хуулийн дагуу тархсан дискрет санамсаргүй хэмжигдэхүүний дисперс нь туршилтын тоог "амжилт" ба "бүтэлгүйтлийн" магадлалаар үржүүлсэнтэй тэнцүү байна. Д(X)=nрq.

Дурангийн хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүний тэгш бус байдал ба куртозыг томъёогоор тодорхойлно.

Эдгээр томъёог анхдагч ба төвийн моментуудын ойлголтыг ашиглан олж авч болно.

Хоёр гишүүний тархалтын хууль нь бодит амьдралын олон нөхцөл байдлын үндэс суурь болдог. Том утгын хувьд nБусад тархалт, тухайлбал Пуассоны тархалтыг ашиглан binomial тархалтыг ойртуулж болно.

Пуассоны тархалт

Байг nБернулли тестүүд, туршилтын тоогоор nхангалттай том. Энэ тохиолдолд (түүнээс гадна магадлал байгаа бол) гэдгийг өмнө нь харуулсан Рүйл явдал Амаш жижиг) үйл явдал болох магадлалыг олох Агарч ирэх ТТуршилтанд орсны дараа та Пуассоны томъёог (4.9) ашиглаж болно. Хэрэв санамсаргүй хэмжигдэхүүн Xүйл явдлын тохиолдлын тоог илэрхийлнэ АВ nБернулли тест, дараа нь магадлал Xүнэ цэнийг авах болно ктомъёог ашиглан тооцоолж болно

, (7.2)

Хаана λ = nр.

Пуассоны тархалтын хуульдискрет санамсаргүй хэмжигдэхүүний тархалтыг гэнэ X, тэдгээрийн боломжит утгууд нь сөрөг бус бүхэл тоо, магадлал р тЭдгээр утгыг (7.2) томъёог ашиглан олно.

Хэмжээ λ = nрдуудсан параметрПуассоны хуваарилалт.

Пуассоны хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүн нь хязгааргүй тооны утгыг авч болно. Учир нь энэ хуваарилалтын хувьд магадлал РТуршилт бүрт үйл явдал гарах нь бага байдаг тул энэ хуваарилалтыг заримдаа ховор тохиолдлын хууль гэж нэрлэдэг.

Пуассоны хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүний тархалтын цуваа нь хэлбэртэй байна

X					…	Т	…
Р					…		…

Хоёрдахь эгнээний магадлалын нийлбэр нь 1-тэй тэнцүү байгаа эсэхийг шалгахад хялбар. Үүнийг хийхийн тулд функцийг Маклаурин цуврал болгон өргөжүүлж болох бөгөөд энэ нь дурын мөрөнд нийлдэг гэдгийг санах хэрэгтэй. X. Энэ тохиолдолд бидэнд байна

. (7.3)

Дээр дурдсанчлан Пуассоны хууль нь тодорхой хязгаарлагдмал тохиолдлуудад бином хуулийг орлуулдаг. Жишээ нь санамсаргүй хэмжигдэхүүн юм X, утгууд нь техникийн төхөөрөмжийг давтан ашиглах үед тодорхой хугацааны туршид гарсан эвдрэлийн тоотой тэнцүү байна. Энэ нь өндөр найдвартай төхөөрөмж гэж таамаглаж байна, i.e. Нэг хэрэглээнд алдаа гарах магадлал маш бага байна.

Ийм хязгаарлагдмал тохиолдлуудаас гадна практикт Пуассоны хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүнүүд байдаг бөгөөд тэдгээр нь бином тархалттай холбоогүй байдаг. Жишээлбэл, Пуассоны тархалтыг тодорхой хугацааны туршид тохиолдсон үйл явдлын тоог (нэг цагийн дотор утасны станцад хүлээн авсан дуудлагын тоо, өдрийн турш машин угаалгын газарт ирсэн машины тоо, долоо хоногт машин зогсох тоо гэх мэт.). Эдгээр бүх үйл явдлууд нь дарааллын онолын үндсэн ойлголтуудын нэг болох үйл явдлын урсгал гэгдэх ёстой. Параметр λ үйл явдлын урсгалын дундаж эрчмийг тодорхойлдог.

Жишээ 7.2 . Тус факультетэд 500 оюутан суралцдаг. 9-р сарын 1-нд тус тэнхимийн гурван оюутны төрсөн өдөр байх магадлал хэд вэ?

Шийдэл . Оюутны тооноос хойш n=500 нь нэлээд том бөгөөд Р– 9-р сарын 1-нд төрсөн сурагчдын аль нэгнийх нь магадлал нь , өөрөөр хэлбэл. хангалттай бага бол бид санамсаргүй хэмжигдэхүүн гэж үзэж болно X- 9-р сарын 1-нд төрсөн сурагчдын тоог Пуассоны хуулийн дагуу параметрийн дагуу хуваарилдаг. λ = n.p.= =1.36986. Дараа нь (7.2) томъёоны дагуу бид авна

Теорем 7.3.Санамсаргүй хэмжигдэхүүнийг үзье XПуассоны хуулийн дагуу хуваарилагдсан. Дараа нь түүний математикийн хүлээлт ба дисперс нь хоорондоо тэнцүү бөгөөд параметрийн утгатай тэнцүү байна λ , өөрөөр хэлбэл М(X) = Д(X) = λ = n.p..

Баталгаа.Пуассоны хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүний тархалтын цуваа болон (7.3) томъёог ашиглан математикийн хүлээлтийн тодорхойлолтоор бид олж авна.

Дисперсийг олохын өмнө бид эхлээд авч үзэж буй санамсаргүй хэмжигдэхүүний квадратын математик хүлээлтийг олно. Бид авдаг

Эндээс дисперсийн тодорхойлолтоор бид олж авдаг

Теорем нь батлагдсан.

Анхдагч ба төв моментуудын ойлголтыг ашиглан Пуассоны хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүний хувьд хазайлт ба куртозын коэффициентийг томъёогоор тодорхойлдог болохыг харуулж болно.

Параметрийн семантик агуулгаас хойш үүнийг ойлгоход хэцүү биш юм λ = n.p.эерэг байвал Пуассоны хуулийн дагуу тархсан санамсаргүй хэмжигдэхүүн нь үргэлж эерэг хазайлт, хазайлттай байдаг.