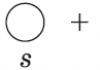Сайтын материалыг ашиглах гэрээ
Сайт дээр нийтлэгдсэн бүтээлүүдийг зөвхөн хувийн хэрэгцээнд ашиглахыг танаас хүсч байна. Бусад сайтад материал нийтлэхийг хориглоно.
Энэ ажлыг (болон бусад бүх зүйлийг) бүрэн үнэ төлбөргүй татаж авах боломжтой. Та түүний зохиогч болон сайтын хамт олонд талархаж болно.
Мэдлэгийн санд сайн ажлаа илгээх нь энгийн зүйл юм. Доорх маягтыг ашиглана уу
Мэдлэгийн баазыг суралцаж, ажилдаа ашигладаг оюутнууд, аспирантууд, залуу эрдэмтэд танд маш их талархах болно.
Үүнтэй төстэй баримт бичиг
Дарааллыг нэр томъёогоор нэмэх, үржүүлэх гэж тодорхойлогддог p-adic бүхэл тоог нэмэх, үржүүлэх. p-adic бүхэл тоонуудын цагираг, тэдгээрийн хуваагдлын шинж чанарыг судлах. Математикийн шинэ объектуудыг нэвтрүүлэх замаар өгөгдсөн тоог тайлбарлах.
курсын ажил, 2015-06-22 нэмэгдсэн
Хүмүүс хэрхэн тоолж сурсан, тоо, тоо, тооллын систем үүссэн. "Хуруу" дээрх үржүүлэх хүснэгт: 9 ба 8 тоог үржүүлэх арга. Хурдан тоолох жишээ. Хоёр оронтой тоог 11, 111, 1111 гэх мэтээр үржүүлэх арга замууд. мөн 999 гэсэн гурван оронтой тоо.
курсын ажил, 2011-10-22 нэмэгдсэн
Тоонуудыг үржүүлэх шинэ арга. Тооцооллын явцад үүссэн тоон матриц ба гурвалжны хоорондох ижил төстэй байдал харьцангуй боловч, ялангуяа гурван оронтой ба түүнээс дээш тоог үржүүлэхэд энэ нь хэвээр байна. Гурвалжин матриц.
нийтлэл, 2005 оны 02-р сарын 6-нд нэмэгдсэн
хураангуй, 2011 оны 01-р сарын 13-нд нэмэгдсэн
Математик дахь анхны тооны утгыг олох аргуудыг тайлбарлах замаар судлах түүхийн онцлог. Пьетро Катальдигийн анхны тооны онолыг хөгжүүлэхэд оруулсан хувь нэмэр. Эратосфенийн анхны тооны хүснэгтийг эмхэтгэх арга. Натурал тоонуудын найрсаг байдал.
тест, 2010 оны 12/24-нд нэмэгдсэн
R-ийн тайлбарлах боломжтой дэд олонлог болох сөрөг бус бодит тоонуудын олонлог. Үржүүлэх хагас бүлэгт хуваагдах чадвар. Хагас бүлгийн тоон gcd болон lcd-ийн бүтэц. 0 ба 1-тэй сөрөг бус бодит тоонуудын үржүүлэх хагас бүлгийг судлах.
дипломын ажил, 2008 оны 05-р сарын 27-нд нэмэгдсэн
Бодит тооны шинж чанарууд, тэдгээрийн математикийн хөгжилд гүйцэтгэх үүрэг. Түүхэн талаас нь бодит тоонуудын багцыг бүтээхэд дүн шинжилгээ хийх. Cantor, Weierstrass, Dedekind нарын дагуу бодит тооны онолыг бий болгох арга. Тэдний сургуулийн курст суралцдаг.
танилцуулга, 2011 оны 10-р сарын 09-нд нэмэгдсэн
Математикийн үндсэн элементүүд. Натурал тоонуудын шинж чанарууд. Тооны онолын тухай ойлголт. Харьцуулалт ба алгебрийн тэгшитгэлийн ерөнхий шинж чанарууд. Харьцуулалт бүхий арифметик үйлдлүүд. Арифметикийн үндсэн хуулиуд. Арифметик үйлдлийн үр дүнг шалгах.
курсын ажил, 2015/05/15 нэмэгдсэн
Үндсэн ойлголтын хувьд хэзээ
арифметикийн аксиоматик бүтэц
натурал тоо нь харьцааг авдаг
дээр өгөгдсөн "шууд дагах"
хоосон бус олонлог Н.
Дараах элемент
a элементийг a" гэж тэмдэглэнэ.
элемент нь шууд дагаж мөрддөггүй
Энэ олонлогийн аль элементийн ард. Бид ... болно
нэгж гэж нэрлэдэг.
Аксиом 2. N-ийн a элемент бүрийн хувьд
зөвхөн нэг элемент a",
нэн даруй дагаж a. Аксиом 3. N-ийн a элемент бүрийн хувьд
хамгийн ихдээ нэг элемент байна
Үүний дараа шууд а.
Аксиом 4. M-ийн дэд олонлог бүр
N багц нь дараах шинж чанартай:
1) нэгж нь M багцад хамаарна;
2) a нь М-д агуулагдаж байгаагаас дараахь зүйлийг гаргана
a" нь M-д агуулагддаг, тэгвэл M нь давхцдаг
тогтоосон Н.
Натурал тооны тодорхойлолт
Элементүүдэд нь хамаарал тогтоогдсон N олонлог"шууд дагах", 1-4 аксиомыг хангасан,
натурал тоонуудын олонлог гэж нэрлэгддэг ба түүний элементүүд нь натурал тоонууд юм.
Нэмэлт
Тодорхойлолт. Натурал тоонуудыг нэмэхийг нэрлэдэгДараах шинж чанаруудтай алгебрийн үйл ажиллагаа:
1) (Ɐa ∈ N) a + 1 = a",
2) (Ɐa, b ∈ N) a + b"=(a+b)".
a+b тоог a, b тоонуудын нийлбэр, a, b тоог өөрөө гэнэ
нөхцөл.
Дараах тэмдэглэгээг хүлээн зөвшөөрье.
1" = 2; 2" = 3; 3" = 4; 4" = 5 гэх мэт.
Нэмэх шинж чанарууд
Теорем 3. Натурал тооны нэмэгдэл байдаг ба энэзөвхөн
Теорем 4. (Ɐ a, b, c ∈ N)(a + b) + c = a + (b + c)
Теорем 5. (Ɐ a, b ∈ N) a+b = b+a
Үржүүлэх
Натурал тоог үржүүлэхийг алгебр гэж нэрлэдэгдараах шинж чанаруудтай үйл ажиллагаа:
1)(Ɐ a ∈ N) a·1 =a;
2)(Ɐ a, b ∈ N) a·b" = a·b + a.
a b тоог a ба b тоонуудын үржвэр гэж нэрлэдэг ба тоонууд нь өөрөө а ба
b - үржүүлэгч
Үржүүлэх шинж чанарууд
Теорем 7. Натурал тоог үржүүлэх үйл ажиллагаа байдаг ба тэрзөвхөн.
Теорем 8. (Ɐ a, b, c ∈ N)(a + b) c = ac + b c - тархалт
нэмэхтэй харьцуулахад баруун тийш.
Теорем 9. (Ɐ a, b, c ∈ N) a·(b + c) = + a·c - зүүн тархалт
нэмэх талаар.
Теорем 10. (Ɐ a, b, c ∈ N) (a b) c = a (b c) - ассоциатив байдал
үржүүлэх.
Теорем 11. (Ɐ a, b ∈ N) a·b = a·b - үржүүлэхийн хувирах чадвар
Өөрийгөө шалгах асуултууд
1. 3-р аксиомыг дараах байдлаар томъёолж болох уу: “Элемент бүрийн хувьдба N-ийн араас нэн даруй нэг элемент байна
ёстой"?
2. Натурал тооны тодорхойлолтыг үргэлжлүүлэх: “Натурал тоо
олонлогийн элемент гэж нэрлэдэг...”
3. Натурал тоо бүрийг өмнөх тооноос нь авсан гэдэг үнэн үү?
нэгийг нэмснээр үү?
4. Олгохдоо үржүүлэхийн ямар шинж чанарыг ашиглаж болох вэ
илэрхийллийн утга:
a) 5·(10 + 4); b) 125·15·6; в) (8·379)·125?
Уран зохиол
Стойлова Л.П.Математик: Оюутнуудад зориулсан сурах бичиг. илүү өндөр ped. сурах бичиг байгууллагууд.
М .: "Академи" хэвлэлийн төв. 2002. - 424 х.
Аксиомын системд тавигдах шаардлага, Пеано аксиомууд. Математикийн аливаа онолыг аксиомат аргаар бүтээхдээ тодорхой дүрмийг баримтална: 1) онолын зарим ойлголтыг үндсэн гэж сонгож, тодорхойлолтгүйгээр хүлээн зөвшөөрдөг; 2) үндсэн зүйлийн жагсаалтад ороогүй онолын үзэл баримтлал бүрд тодорхойлолт өгсөн болно. Энэ нь үндсэн болон өмнөх ойлголтуудын тусламжтайгаар түүний утгыг тайлбарладаг. 3) аксиомуудыг томъёолсон, өөрөөр хэлбэл тухайн онолд нотлох баримтгүйгээр хүлээн зөвшөөрөгдсөн саналууд юм. Аксиомууд нь үндсэн ойлголтуудын шинж чанарыг илтгэдэг. 4) аксиомын жагсаалтад ороогүй онолын санал бүрийг батлах ёстой. Ийм саналуудыг теорем гэж нэрлэдэг. Эдгээр нь өмнөх аксиом ба теоремуудын үндсэн дээр батлагдсан.
ЭНЭ. Математикийн онолыг бий болгох аксиоматик арга нь хэд хэдэн үе шатыг дамждаг: 1) тодорхойгүй үндсэн ойлголтуудыг (жишээ нь: олонлогийн онол дахь олонлогийн элемент) нэвтрүүлэх. 2) үндсэн харилцааны танилцуулга (жишээ нь: олонлогын онол дахь гишүүнчлэлийн хамаарал). 3) үндсэн ойлголт, үндсэн харилцааг зааж өгснөөр бусад ойлголт, харилцааны тодорхойлолтыг танилцуулна (жишээлбэл: олонлогын онолд нэгдэл, огтлолцол, ялгаа, нэмэлт гэсэн ойлголтууд).
Онолын аксиоматик бүтцэд бүх мэдэгдлийг аксиомоос нотлох замаар гаргаж авдаг. Ийм онолын үндэс нь аксиомын систем бөгөөд аксиомын системд тусгай шаардлага тавьдаг: 1) аксиомын систем тууштай байх ёстой. Аксиомын системээс бие биенээ үгүйсгэсэн хоёр саналыг логикоор гаргаж авах боломжгүй бол түүнийг тууштай гэж нэрлэдэг. Өөрөөр хэлбэл, нэгэн зэрэг үнэн байхын тулд өгөгдсөн мэдэгдлийн мэдэгдэл ба үгүйсгэлийг гаргаж авах боломжгүй юм. Аксиомын системийн нийцтэй байдлыг шалгахын тулд энэ системийн загварыг бий болгоход хангалттай. 2) аксиомын систем нь бие даасан байх ёстой. Хэрэв энэ системийн аксиомуудын аль нь ч бусад аксиомын үр дагавар биш бол аксиомын системийг бие даасан гэж нэрлэдэг. Өөрөөр хэлбэл, энэ системийн аксиом бүрийг бусад аксиомуудаас гаргаж авах боломжгүй. Аксиомын системийн бие даасан байдлыг батлахын тулд энэ системийн загварыг бүтээхэд хангалттай. 3) аксиомын систем бүрэн байх ёстой, өөрөөр хэлбэл. Тухайн онолд сонгосон аксиомын тоо нь шинэ ойлголт, харилцааг нэвтрүүлэх, теоремуудыг батлах, онолыг бүхэлд нь бүтээхэд хангалттай байх ёстой.
Нэг онолыг аксиомат аргаар бүтээхдээ аксиомын өөр өөр системийг ашиглаж болох боловч тэдгээр нь эквивалент байх ёстой. Натурал тооны системийг аксиоматик байгуулахад "шууд дагах" хамаарлыг үндсэн ойлголт болгон авдаг. "Их олонлог", "олонлогийн элемент", логикийн дүрэм гэсэн ойлголтуудыг мөн сайн мэддэг гэж үздэг. a элементийн нэн даруй дараах элементийг a - prime гэж тэмдэглэнэ.
"Шууд дагах" харилцааны мөн чанар нь дараахь аксиомуудад илчлэгдсэн: 1) натурал тооны олонлогт энэ олонлогийн аль ч элементийг шууд дагаж мөрддөггүй элемент байдаг, энэ элемент 1 (нэг). 2) натурал тоонуудын (N) олонлогийн a элемент бүрт өвөрмөц a элемент байна уу? , нэн даруй дараах a. 3) N-ийн a элемент бүрийн хувьд хамгийн ихдээ нэг элементийн дараа нь a байна. 4) N олонлогийн аль нэг М дэд олонлог нь: 1 M шинж чанартай, мөн M-д a агуулагдаж байгаа тул a гэж юу вэ? M-д агуулагдах нь N олонлогтой давхцаж байна.
Жагсаалтад орсон аксиомын системийг Пеано аксиом гэж нэрлэдэг. ЭНЭ. Пеано аксиомуудыг хангасан шууд дараах хамаарлыг тогтоосон тооны багцыг натурал тооны олонлог, түүний элементийг натурал тоо гэж нэрлэдэг. Дөрөв дэх аксиом нь тоонуудын натурал цувааны хязгааргүй байдлыг дүрсэлсэн ба индукцийн аксиом гэж нэрлэдэг. Үүний үндсэн дээр янз бүрийн мэдэгдлийн нотолгоог математик индукцийн аргыг ашиглан хийдэг бөгөөд энэ нь дараах байдалтай байна: аливаа натурал тооны хувьд өгөгдсөн мэдэгдэл үнэн болохыг батлахын тулд дараахь зүйлийг батлах шаардлагатай: 1) энэ мэдэгдэл нэгийн хувьд үнэн, 2) дурын k тооны хувьд энэ нь үнэн гэсэн саналаас дараагийн k тоонд үнэн болохыг нотлох уу?.
N олонлогийн тодорхойлолт нь энэ олонлогийн мөн чанарын талаар юу ч хэлээгүй бөгөөд энэ нь юу ч байж болно гэсэн үг юм. Пеано аксиомуудыг нэн даруй дагаж мөрдөх, хангах хамаарлыг өгөх аливаа олонлогийг N олонлог болгон сонгосноор бид энэхүү аксиомын системийн загварыг олж авна. Ийм бүх загваруудын хооронд ганцаарчилсан захидал харилцааг үүсгэж болно. Эдгээр загварууд нь зөвхөн элементүүдийн шинж чанар, нэр, тэмдэглэгээгээр ялгаатай байх болно. Үгүй.: 1, 2, 3, 4, 5… 0.00,000,0000,00000,… Ѕ, 1/3, ј, 1/5,
Онолыг аксиомат байдлаар бүтээхдээ тодорхой дүрмийг баримтална.
гэж онолын зарим ойлголтыг сонгосон үндсэн,мөн тодорхойлолтгүйгээр хүлээн зөвшөөрөгдөж, тодорхойгүй гэж нэрлэдэг.
аксиомуудыг томъёолсон - өгөгдсөн онолд нотлох баримтгүйгээр хүлээн зөвшөөрөгдсөн саналууд; тэд үндсэн ойлголтуудын шинж чанарыг илчилдэг;
Үндсэн зүйлийн жагсаалтад ороогүй онолын үзэл баримтлал бүрийг өгсөн болно тодорхойлолт, энэ нь үндсэн болон өмнөх ойлголтуудын тусламжтайгаар түүний утгыг тайлбарладаг;
аксиомуудын жагсаалтад ороогүй онолын санал бүрийг батлах ёстой; Ийм саналуудыг теорем гэж нэрлэдэг бөгөөд авч үзэж буйн өмнөх аксиом ба теоремын үндсэн дээр нотлогддог.
Онолын аксиоматик бүтцэд үндсэндээ бүх мэдэгдлийг аксиомоос нотлох замаар гаргаж авдаг. Тиймээс аксиомын системд тусгай шаардлага тавьдаг. Юуны өмнө энэ нь тууштай, бие даасан байх ёстой.
Аксиомын системийг нэрлэдэг тууштай,Хэрэв үүнээс бие биенээ үгүйсгэсэн хоёр өгүүлбэрийг логикоор гаргаж чадахгүй бол.
Тогтвортой аксиомын систем гэж нэрлэдэг бие даасан,хэрэв энэ системийн аксиомуудын аль нь ч энэ системийн бусад аксиомуудын үр дагавар биш бол.
Аксиомууд нь дүрмээр бол хүмүүсийн олон зуун жилийн практик үйл ажиллагааны тусгал бөгөөд энэ нь тэдний хүчинтэй байдлыг тодорхойлдог.
Натурал тооны арифметикийг аксиоматик бүтээх үндсэн ойлголт болохын хувьд хоосон бус олонлог дээр тодорхойлсон "шууд дагах" хамаарлыг авдаг. Н.Олонлогийн тухай ойлголт, олонлогийн элемент болон бусад олонлогийн онолын үзэл баримтлал, түүнчлэн логикийн дүрмийг сайн мэддэг гэж үздэг.
Элементийг шууд дагаж буй элемент А,тэмдэглэнэ А".Италийн математикч Г.Пеаногийн 1891 онд дэвшүүлсэн дараах аксиомуудад “шууд дагах” харилцааны мөн чанар илэрсэн байна.
Аксиом 1.элбэг дэлбэг НЭнэ олонлогийн аль ч элементийг шууд дагаж мөрддөггүй элемент байдаг. Үүнийг нэгж гэж нэрлэдэг бөгөөд 1 тэмдгээр тэмдэглэгдсэн байдаг.
Аксиом 2.Элемент бүрийн хувьд А-аас Нзөвхөн нэг элемент байдаг A",нэн даруй дагаж байна А.
Аксиом 3.Элемент бүрийн хувьд a-ийн Ндор хаяж нэг элемент байдаг бөгөөд үүнийг шууд дагаж мөрддөг А.
Аксиом 4. (Индукцийн аксиом).Аливаа дэд хэсэг Мбагц НДараах шинж чанартай бол N-тэй давхцана: 1) 1-д агуулагдана М; 2) аливаа элементээс А-д агуулагддаг М,үүнийг дагадаг А"-д агуулагддаг М.
Томъёолсон аксиомуудыг ихэвчлэн Пианогийн аксиом гэж нэрлэдэг бөгөөд дөрөв дэх аксиомыг индукцийн аксиом гэж нэрлэдэг.
Эдгээр аксиомуудыг бэлгэдлийн хэлбэрээр бичье.
А 1 )( 1 Н)( а N)А" 1;
А 2 )( а Н)( !b N)А"=б
А 3 ) ( А,б, Хамт Н)c = a" c = b" А= b;
A 4) М Н 1 М (а М А" М) М=Н
"Шууд дагах" хамаарал болон Пианогийн 1-4 аксиомуудыг ашиглан натурал тооны дараах тодорхойлолтыг өгч болно.
Тодорхойлолт 1. 1-4-р аксиомуудыг хангасан элементүүдийнх нь хувьд "шууд дагах" хамаарал тогтсон N олонлогийг натурал тооны олонлог ба түүний элементүүд гэнэ. натурал тоонууд.
___________________________________________________________________
Тодорхойлолт 2 . Хэрэв натурал тоо болбнэн даруй а тоог дагаж, дараа нь a тоог шууд өмнөх (өмнөх) тоо гэж нэрлэдэгб.
______________________________________________________________________________________________
Теорем 1. Нэгж нь өмнөх натурал тоогүй (теоремын үнэн нь аксиомоос шууд гардаг А 1 ).
Теорем 2.Натурал тоо бүр А,нэгээс ялгаатай нь өмнөх тоотой b , ийм b " = А.
Натурал тооны тодорхойлолт нь олонлогийн элементүүдийн мөн чанарын талаар юу ч хэлдэггүй Н.Тиймээс энэ нь юу ч байж болно. Пеано аксиом системийн стандарт загвар нь нийгмийн түүхэн хөгжлийн явцад бий болсон хэд хэдэн тоо юм.
1, 2, 3, 4, 5 ,..,
Энэ цувралын дугаар бүр өөрийн гэсэн тэмдэглэгээ, нэртэй байдаг бөгөөд бид үүнийг мэддэг гэж үзэх болно.
Натурал тооны тодорхойлолтод аль ч аксиомыг орхигдуулж болохгүй гэдгийг анхаарах нь чухал.
1 а б в г
…
б
Цагаан будаа. 16 Цагаан будаа. 17
Даалгавар 1.
Зураг дээр элемент бүрийг дагах элементтэй сумаар холбосон байна.
15 ба 16-р зурагт үзүүлсэн багцуудын аль нь Пеано аксиом системийн загвар болохыг тодорхойл.
1. Зураг дээр. Зураг 16-д 2 ба 3-р аксиомууд хангагдсан боловч 1-р аксиом хангагдаагүй олонлогийг үзүүлэв.
Аксиом 4 нь утгагүй болно, учир нь олонлогт бусдыг шууд дагаж мөрддөггүй элемент байхгүй.
2. Зураг дээр. Зураг 17-д 1, 2, 3-р аксиомууд хангагдсан боловч 4-р аксиом хангагдаагүй олонлогийг үзүүлэв - туяа дээр хэвтэж буй цэгүүдийн багц нь 1-ийг агуулж байгаа бөгөөд тоо бүртэй хамт түүний араас дагах тоог агуулна, гэхдээ энэ нь тийм байна. зурагт үзүүлсэн бүх тогтоосон цэгүүдтэй давхцахгүй. Дүгнэлт: Зураг дээр үзүүлсэн багцуудын аль нь ч байхгүй. 16 ба 17-г Peano аксиом системийн загвар гэж үзэх боломжгүй.
Даалгавар 2.
Натурал тоо бүр түүний араас гарч буй натурал тооноос ялгаатай гэдгийг баталцгаая, өөрөөр хэлбэл. ( X )X X"
Баталгаа
Бид индукцийн аксиомыг ашигладаг - А 4 .
Болъё М=(х/х , X X"}, учир нь . X М Н.
Нотлох баримт нь хоёр хэсгээс бүрдэнэ.
Үүнийг баталцгаая 1 М,тэдгээр. 1 1" . Энэ нь дараахаас гардаг А 1 .
Үүнийг баталцгаая X М=> X" М.Болъё X Мтэдгээр. X X".Үүнийг баталцгаая X" М, өөрөөр хэлбэл X" (X")". БАаксиомууд А 3 ёстой X" (X")". Нээрээ, дагуу А 3 , хэрэв x" = (x)" дараа нь x = x", ба түүнээс хойш танилцуулах саналаар x М,дараа нь x X",Үүний үр дүнд бид зөрчилдөөнд хүрч байна. гэсэн үг, X" (X")" , X" М.
Энд зөрчилдөөнөөр нотлоход өргөн хэрэглэгддэг зөрчилдөөний дүрмийг (PC) ашигладаг.
Тиймээс бид авсан:
М Н (1 М (x M => x" M)) М = N, i.e. мэдэгдэл x x" нь аливаа натурал тооны хувьд үнэн юм.
Хяналтын асуултууд
Аксиоматик онол байгуулахын мөн чанар юу вэ?
Сургуулийн планиметрийн хичээлийн үндсэн ойлголтуудыг нэрлэнэ үү. Энэ хичээлийн аксиом системийг санаарай. Тэдэнд ямар үзэл баримтлалын шинж чанарыг тодорхойлсон бэ?
Пианогийн аксиомуудыг бэлгэдлийн хэлбэрээр томьёолж бич. "
Натурал тооны аксиоматик тодорхойлолтыг томъёол.
Натурал тооны тодорхойлолтыг үргэлжлүүлнэ үү: “Натурал тоо нь олонлогийн элемент юм Н,... » .
Бага ангийн математикийн сурах бичгүүдээс дараах жишээг өг.
a) шинэ (оюутны хувьд) тоо нь байгалийн цувралын үр дүнд бий болсон сегментийн үргэлжлэл болж ажилладаг;
б) натурал тоо бүрийг зөвхөн нэг натурал тоо шууд дагаж байгаа нь тогтоогдсон.
Дасгал
285. Олонлогийн элементүүд нь зураасны бүлгүүд (I, II, III, IIII,...). Энэ багц Пеаногийн аксиомыг хангаж байна уу? Энд тодорхойлсончлон "шууд дагах" харилцааг энд тодорхойлсон. Багцын (0, 00, 000, 0000,...) ижил асуултуудыг авч үзье.



Цагаан будаа. 17
286. Зураг 17-д а) элемент бүрийг дагах элементтэй сумаар холбосон. Олонлогийг Пеано аксиом системийн загвар гэж үзэж болох уу? Зураг 17 b), c), d) дээрх багцуудын ижил асуултууд.
287. Тоонуудын багц (1, 2, 3) Пеано аксиомыг хангаж байна уу? P, ...),Хэрэв дарааллын хамаарлыг дараах байдлаар тодорхойлсон бол:
1 3 5 7….
2 4 6 8….
288. Бага ангийн математикийн сурах бичгүүдээс даалгавруудыг зөв гүйцэтгэхийг Пианогийн аксиомоор тайлбарласан даалгаврын жишээг өг.
Математик дахь аксиоматик арга.
Байгалийн цувааны аксиоматик онолын үндсэн ойлголт, хамаарал. Натурал тооны тодорхойлолт.
Натурал тооны нэмэх.
Натурал тоог үржүүлэх.
Натурал тооны олонлогийн шинж чанарууд
Натурал тоог хасах ба хуваах.
Математик дахь аксиоматик арга
Аливаа математикийн онолыг аксиоматик бүтээхдээ дараах дүрмийг баримтална. тодорхой дүрэм:
1. Онолын зарим ойлголтыг сонгосон голмөн тодорхойлолтгүйгээр хүлээн зөвшөөрдөг.
2. Томъёолсон аксиомуудЭнэ онолд нотлох баримтгүйгээр хүлээн зөвшөөрөгдсөн , тэдгээр нь үндсэн ойлголтуудын шинж чанарыг илчилдэг.
3. Үндсэн зүйлийн жагсаалтад ороогүй онолын үзэл баримтлал бүрийг өгсөн болно тодорхойлолт, энэ нь үндсэн болон өмнөх ойлголтуудын тусламжтайгаар түүний утгыг тайлбарладаг.
4. Аксиомын жагсаалтад ороогүй онолын санал бүрийг батлах ёстой. Ийм саналуудыг дууддаг теоремуудавч үзэж буйн өмнөх аксиом ба теоремын үндсэн дээр тэдгээрийг нотлох.
Аксиом систем нь дараах байдалтай байх ёстой.
а) тууштай:өгөгдсөн аксиомын системээс боломжтой бүх дүгнэлтийг гаргаснаар бид хэзээ ч зөрчилдөхгүй гэдэгт итгэлтэй байх ёстой;
б) бие даасан: ямар ч аксиом энэ системийн бусад аксиомуудын үр дагавар байх ёсгүй.
V) дүүрэн, хэрэв түүний хүрээнд өгөгдсөн мэдэгдэл эсвэл түүний үгүйсгэлийн аль нэгийг батлах боломжтой бол.
Аксиоматик онолыг бий болгох анхны туршлага бол Евклидийн "Элементүүд" (МЭӨ 3-р зуун) номон дахь геометрийн танилцуулга гэж үзэж болно. Геометр, алгебрийг бүтээх аксиоматик аргыг хөгжүүлэхэд ихээхэн хувь нэмэр оруулсан Н.И. Лобачевский, Э.Галуа нар. 19-р зууны төгсгөлд. Италийн математикч Пеано арифметикийн аксиомын системийг боловсруулсан.
Натурал тооны аксиоматик онолын үндсэн ойлголт, хамаарал. Натурал тооны тодорхойлолт.
Тодорхой багц дахь үндсэн (тодорхойгүй) ойлголт Н сонгосон байна хандлага , мөн олонлогийн онолын үзэл баримтлал, түүнчлэн логикийн дүрмийг ашигладаг.
Элементийг шууд дагаж буй элемент А,тэмдэглэнэ А".
"Шууд дагах" харилцаа нь дараах аксиомуудыг хангадаг.
Пеаногийн аксиомууд:
Аксиом 1. элбэг дэлбэг Н шууд элемент байдаг дараагийн бишэнэ багцын аль ч элементийн хувьд биш. Түүнийг дуудъя нэгжба тэмдгээр тэмдэглэнэ 1 .
Аксиом 2. Элемент бүрийн хувьд А -аас Н зөвхөн нэг элемент байдаг А" , нэн даруй дагаж байна А .
Аксиом 3. Элемент бүрийн хувьд А -аас Ндор хаяж нэг элемент байдаг бөгөөд үүнийг шууд дагаж мөрддөг А .
Аксиом 4.Аливаа дэд хэсэг М багц Н -тай давхцаж байна Н , хэрэв энэ нь дараах шинж чанартай бол: 1) 1 -д агуулагддаг М ; 2) үүнээс үүдэн А -д агуулагддаг М , үүнийг дагадаг А" -д агуулагддаг М.
Тодорхойлолт 1. Цөөн хэдэн Н , тэдгээрийн элементүүдийн хувьд харилцаа тогтоогдсон "шууд дагаж мөрдөөрэй", 1-4-р аксиомуудыг хангасан, гэж нэрлэдэг натурал тоонуудын багц, түүний элементүүд нь натурал тоонууд.
Энэхүү тодорхойлолт нь олонлогийн элементүүдийн мөн чанарын талаар юу ч хэлдэггүй Н . Тиймээс энэ нь юу ч байж болно. Багц болгон сонгох Н 1-4-р аксиомуудыг хангасан "шууд дагах" тодорхой хамаарлыг өгсөн зарим тодорхой багцыг бид олж авна. энэ системийн загвар аксиом.
Пеано аксиомын системийн стандарт загвар нь нийгмийн түүхэн хөгжлийн явцад бий болсон тоонуудын цуваа: 1,2,3,4,... Байгалийн цуваа 1-ээс эхэлдэг (аксиом 1); натурал тоо бүрийг нэн даруй нэг натурал тоо (аксиом 2); натурал тоо бүр хамгийн ихдээ нэг натурал тоог шууд дагаж мөрддөг (аксиом 3); 1-ээс эхлэн натурал тоонууд руу шилжих замаар бид эдгээр тооны бүхэл бүтэн багцыг олж авна (аксиом 4).
Тиймээс бид үндсэн тоог сонгох замаар натурал тоон системийн аксиоматик бүтцийг эхлүүлсэн "шууд дагах" харилцаамөн түүний шинж чанарыг тодорхойлсон аксиомууд. Онолын цаашдын бүтээн байгуулалт нь натурал тоонуудын мэдэгдэж буй шинж чанарууд, тэдгээрийн үйлдлүүдийг авч үзэх явдал юм. Тэдгээрийг тодорхойлолт, теоремуудад илчлэх ёстой, өөрөөр хэлбэл. "шууд дагах" хамаарал болон 1-4 аксиомуудаас цэвэр логикоор үүсэлтэй.
Натурал тоог тодорхойлсны дараа бидний танилцуулах эхний ойлголт бол хандлага "нэн даруй өмнө нь" , байгалийн цувралын шинж чанарыг харгалзан үзэхэд ихэвчлэн ашиглагддаг.
Тодорхойлолт 2.Хэрэв натурал тоо бол б шууд дагадагнатурал тоо А, тэр тоо А дуудсан шууд өмнөх(эсвэл өмнөх) тоо b .
"Урьдчилах" харилцаа нь байна хэд хэдэн өмч.
Теорем 1. Нэгжид өмнөх натурал тоо байхгүй.
Теорем 2. Натурал тоо бүр А, 1-ээс бусад нь өмнөх ганц дугаартай б,тиймэрхүү б"= А.
Натурал тооны онолын аксиоматик бүтцийг бага болон дунд сургуульд авч үздэггүй. Гэсэн хэдий ч Пеаногийн аксиомуудад тусгагдсан "шууд дагаж мөрддөг" харилцааны эдгээр шинж чанарууд нь математикийн анхан шатны сургалтын сэдэв юм. Нэгдүгээр ангид байхдаа эхний арвын тоог авч үзэхэд тоо бүрийг хэрхэн яаж авах нь тодорхой болно. "Дагадаг" ба "өмнө" гэсэн ойлголтуудыг ашигладаг. Шинэ тоо бүр нь байгалийн цуврал тоонуудын судлагдсан сегментийн үргэлжлэл болж ажилладаг. Оюутнууд тоо бүрийг дараагийнх нь дагаж мөрддөг бөгөөд үүнээс гадна зөвхөн нэг л зүйл байдаг бөгөөд тоонуудын натурал цуваа нь хязгааргүй байдаг гэдэгт оюутнууд итгэлтэй байдаг.
Натурал тооны нэмэх
Аксиоматик онолыг бий болгох дүрмийн дагуу натурал тоог нэмэх тодорхойлолтыг зөвхөн хамаарлыг ашиглан нэвтрүүлэх ёстой. "шууд дагах", ба үзэл баримтлал "натурал тоо"Тэгээд "өмнөх тоо".
Нэмэлтийн тодорхойлолтын өмнө дараахь зүйлийг анхаарч үзье. Хэрэв аль нэг натурал тоо А 1-ийг нэмбэл бид тоог авна A",нэн даруй дагаж байна А, өөрөөр хэлбэл А+ 1= a"Тиймээс бид дурын натурал тоонд 1-ийг нэмэх дүрмийг олж авдаг. Гэхдээ тоонд яаж нэмэх вэ Анатурал тоо б, 1-ээс ялгаатай юу? Дараах баримтыг ашиглая: хэрвээ бид 2 + 3 = 5 гэдгийг мэдэж байвал нийлбэр нь 5-ын тоог шууд дагаж 2 + 4 = 6 болно. Энэ нь 2 + 4 нийлбэрт хоёр дахь гишүүн нь шууд дараах тоо байх тул ийм зүйл тохиолддог. тоо 3. Тиймээс 2 + 4 =2+3 " =(2+3)". Ерөнхийдөө манайд байгаа , .
Эдгээр баримтууд нь аксиоматик онол дахь натурал тоог нэмэхийг тодорхойлох үндэс суурь болдог.
Тодорхойлолт 3. Натурал тоог нэмэхнь дараах шинж чанартай алгебрийн үйлдэл юм.
Тоо a + b дуудсан тоонуудын нийлбэр АТэгээд б , мөн тоонууд өөрсдөө АТэгээд б - нөхцөл.