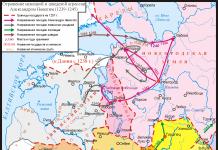
Тодорхойлолт 1.11Хоёр хувьсагчийн функцийг өгье z=z(x,y), (x,y)D . Цэг М 0 (х 0 ;y 0 ) - талбайн дотоод цэг Д .
Хэрэв орвол Д ийм хороолол байдаг У.М. 0 оноо М 0 , энэ нь бүх цэгүүдэд зориулагдсан
дараа нь зааж өгнө М 0 локал максимум цэг гэж нэрлэдэг. Мөн утга нь өөрөө z(М 0 ) - орон нутгийн дээд хэмжээ.
Мөн бүх онооны хувьд
дараа нь зааж өгнө М 0 функцийн орон нутгийн хамгийн бага цэг гэж нэрлэдэг z(x,y) . Мөн утга нь өөрөө z(М 0 ) - орон нутгийн доод хэмжээ.
Орон нутгийн максимум ба орон нутгийн минимумыг функцийн орон нутгийн экстремум гэж нэрлэдэг z(x,y) . Зураг дээр. 1.4 орон нутгийн максимумын геометрийн утгыг тайлбарлав. М 0 - гадаргуу дээр байгаа тул хамгийн дээд цэг z =z (x,y) түүний харгалзах цэг C 0 зэргэлдээх цэгээс өндөр байна C (энэ бол хамгийн их нутаг дэвсгэр).
Гадаргуу дээр ерөнхийдөө цэгүүд байдаг гэдгийг анхаарна уу (жишээлбэл, IN ) дээр байрладаг C 0 , гэхдээ эдгээр цэгүүд (жишээлбэл, IN ) цэг рүү "хөрш" биш байна C 0 .
Ялангуяа цэг IN нь дэлхийн дээд зэргийн үзэл баримтлалд нийцдэг:
Дэлхийн хамгийн бага хэмжээг ижил төстэй байдлаар тодорхойлсон:
Глобал максимум ба минимумыг олох талаар 1.10-р хэсэгт авч үзэх болно.
Теорем 1.3(экстремумын зайлшгүй нөхцөл).
Функцийг өгье z =z (x,y), (x,y)D . Цэг М 0 (х 0 ;y 0 Д - орон нутгийн экстремум цэг.
Хэрэв энэ үед байгаа бол z" x Тэгээд z" y , Тэр
Геометрийн баталгаа нь "илэрхий" юм. Хэрэв цэг дээр байвал C 0 дээр шүргэгч хавтгай зурах (Зураг 1.4), дараа нь энэ нь "байгалийн" хэвтээ, өөрөөр хэлбэл өнцгөөр өнгөрөх болно. 0° тэнхлэг рүү Өө ба тэнхлэг рүү OU .
Дараа нь хэсэгчилсэн деривативуудын геометрийн утгын дагуу (Зураг 1.3):
Энэ нь нотлох шаардлагатай байсан юм.
Тодорхойлолт 1.12.
Хэрэв цэг дээр байвал М 0 (1.41) нөхцөл хангагдсан бол функцийн суурин цэг гэнэ z(x,y) .
Теорем 1.4(экстремум үүсэх хангалттай нөхцөл).
Өгчихье z =z (x,y), (x,y)D , энэ нь тухайн цэгийн зарим хэсэгт хоёрдугаар эрэмбийн хэсэгчилсэн деривативтай М 0 (х 0 , у 0 )D . Түүнээс гадна М 0 - суурин цэг (жишээ нь, шаардлагатай нөхцөлүүд (1.41) хангагдсан). Тооцоолъё:
Теоремыг батлахдаа энэ зааварт тусгагдаагүй сэдвүүдийг (хэд хэдэн хувьсагчийн функцийн Тейлорын томъёо ба квадрат хэлбэрийн онол) ашигладаг.
Жишээ 1.13.
Хэт ихийг судлах:
Шийдэл
1. (1.41) системийг шийдэх замаар суурин цэгүүдийг ол:
өөрөөр хэлбэл дөрвөн суурин цэг олддог. 2.
1.4 теоремын дагуу цэг дээр хамгийн бага байна. Түүнээс гадна 
цэг дээр теорем 1.4-ээр
Хамгийн их. Түүнээс гадна
Олон хувьсагчтай функцийн тухай ойлголт
n-хувьсагч байх ба тодорхой x олонлогийн x 1, x 2 ... x n тус бүрд тодорхойлолт өгөгдсөн байг. тоо Z байвал олон хувьсагчийн Z = f (x 1, x 2 ... x n) функц х олонлог дээр өгөгдсөн болно.
X - функцийн тодорхойлолтын талбар
x 1, x 2 ... x n – бие даасан хувьсагч (аргументууд)
Z – функц Жишээ: Z=P x 2 1 *x 2 (Цилиндрийн эзэлхүүн)
Z=f(x;y) – 2 хувьсагчийн функцийг (x 1, x 2-г x,y-ээр сольсон) авч үзье. Үр дүнг олон хувьсагчийн бусад функцуудтай аналоги байдлаар шилжүүлдэг. 2 хувьсагчийн функцийг тодорхойлох талбар нь бүхэл утсыг (өө) эсвэл түүний хэсэг юм. 2 хувьсагчийн функцийн утгын тоо нь 3 хэмжээст орон зай дахь гадаргуу юм.
График байгуулах арга техник: - Гадаргуугийн хөндлөн огтлолыг квадратаар авч үзэх || координатын квадратууд.
Жишээ нь: x = x 0, zn. квадрат X || 0уz y = y 0 0хz Функцийн төрөл: Z=f(x 0 ,y); Z=f(x,y 0)
Жишээ нь: Z=x 2 +y 2 -2y
Z= x 2 +(y-1) 2 -1 x=0 Z=(y-1) 2 -1 y=1 Z= x 2 -1 Z=0 x 2 +(y-1) 2 -1
Парабола хүрээлэх(төв(0,1)
Хоёр хувьсагчийн функцүүдийн хязгаар ба тасралтгүй байдал
Z=f(x;y) гэж өгвөл t.(x 0 ,y 0) дахь функцийн хязгаар нь дурын жижиг олонлогийн хувьд А болно. E>0 тоо нь эерэг тоо b>0 бөгөөд энэ нь бүх x, y-ийн хувьд |x-x 0 |<б; |y-y 0 |<б выполняется нерав-во |f(x,y)-A| Z=f(x;y) нь t-д тасралтгүй (x 0 ,y 0) байвал: - энэ t.-д тодорхойлогдсон; - финалтай x-д хязгаарлах, x 0 болон y-ээс y 0 руу чиглэх; - энэ хязгаар = утга t дахь функцууд (x 0 ,y 0), өөрөөр хэлбэл. limf(x;y)=f(x 0 ,y 0) Хэрэв функц тус бүрд тасралтгүй байвал t.mn-va X, тэгвэл энэ хэсэгт тасралтгүй байна Дифференциал функц, түүний геом утга. Ойролцоо утгуудад дифференциал хэрэглэх. dy=f’(x)∆x – дифференциал функц dy = dx, өөрөөр хэлбэл. y=x бол dy=f ’(x)dx Геологийн үүднээс авч үзвэл функцийн дифференциал гэдэг нь абсцисса х 0 цэг дээрх функцийн график руу татсан шүргэгчийн ординатын өсөлт юм. Dif-l нь ойролцоогоор тооцоолоход хэрэглэгддэг. томъёоны дагуу функцийн утгууд: f(x 0 +∆x)~f(x 0)+f’(x 0)∆x ∆x нь x-тэй ойр байх тусам үр дүн нь илүү нарийвчлалтай болно Эхний болон хоёрдугаар эрэмбийн хэсэгчилсэн деривативууд Эхний эрэмбийн дериватив (үүнийг хэсэгчилсэн гэж нэрлэдэг) A. X мужаас аль нэг цэгт х, у бие даасан хувьсагчдын өсөлтийг x, y гэж үзье. Тэгвэл z = f(x+ x, y+ y) = f(x,y)-тэй тэнцүү утгыг нийт гэнэ. x 0, y 0 цэг дэх өсөлт. Хэрэв бид x хувьсагчийг засаад у хувьсагчд у-ийн өсөлтийг өгвөл zу = f(x,y,+ y) – f(x,y) болно. y хувьсагчийн хэсэгчилсэн дериватив нь ижил төстэй байдлаар тодорхойлогддог, i.e. 2 хувьсагчийн функцийн хэсэгчилсэн деривативыг нэг хувьсагчийн функцтэй ижил дүрмийг ашиглан олно. Ялгаа нь функцийг х хувьсагчаар ялгахдаа y-г const, y, x-ээр ялгахдаа const гэж үзнэ. Тусгаарлагдсан const нь нэмэх/хасах үйлдлийг ашиглан функцтэй холбогддог. Bound const нь үржүүлэх/хуваах үйлдлээр функцтэй холбогддог. Тусгаарлагдсан const-ийн дериватив = 0 1.4.2 хувьсагчийн бүрэн дифференциал функц ба түүний хэрэглээ
z = f(x,y) гэж үзье tz = 2-р эрэмбийн хэсэгчилсэн дериватив 2 хувьсагчийн тасралтгүй функцүүдийн хувьд 2-р эрэмбийн холимог хэсэгчилсэн деривативууд давхцдаг. Макс ба мин функцүүдийн хэсэгчилсэн деривативыг тодорхойлохдоо хэсэгчилсэн деривативыг экстремум гэж нэрлэдэг. A. Энэ хөршөөс бүх x ба y-ийн хувьд f(x,y) хэрчмүүд байвал тэдгээрийг max эсвэл min z = f(x,y) гэж нэрлэнэ. T. Хэрэв 2 хувьсагчтай функцийн экстремум цэг өгөгдсөн бол энэ цэг дэх хэсэгчилсэн деривативуудын утга 0-тэй тэнцүү байна, өөрөөр хэлбэл. , Нэгдүгээр эрэмбийн хэсэгчилсэн деривативын цэгүүдийг суурин эсвэл критик гэж нэрлэдэг. Иймд 2 хувьсагчийн функцийн экстремум цэгийг олохын тулд хангалттай экстремум нөхцөлийг ашигладаг. z = f(x,y) функц нь хоёр дахин дифференциалагдах ба хөдөлгөөнгүй цэг, 1) , ба maxA<0, minA>0. 1.4.(*)Бүрэн дифференциал. Дифференциалын геометрийн утга. Ойролцоогоор тооцоололд дифференциал хэрэглэх
A. y = f(x) функцийг цэгүүдэд тодорхой хороололд тодорхойл. f(x) функц нь тухайн цэг дэх өсөлт нь байвал тухайн цэг дээр дифференциалагдах функцтэй гэнэ Энд A нь тогтмол x цэг дээрх -ээс хамааралгүй тогтмол утга бөгөөд -д хязгааргүй бага байна. Харьцангуй шугаман А функцийг цэг дээрх f(x) функцийн дифференциал гэж нэрлэдэг ба df() эсвэл dy гэж тэмдэглэнэ. Тиймээс (1) илэрхийллийг дараах байдлаар бичиж болно (1) илэрхийлэл дэх функцийн дифференциал нь dy = A хэлбэртэй байна. Аливаа шугаман функцийн нэгэн адил энэ нь ямар ч утгын хувьд тодорхойлогддог Дифференциал бичихэд хялбар болгох үүднээс өсөлтийг dx гэж тэмдэглэж, бие даасан x хувьсагчийн дифференциал гэж нэрлэдэг. Тиймээс дифференциалыг dy = Adx гэж бичнэ. Хэрэв f(x) функц нь тодорхой интервалын цэг бүрт дифференциал болдог бол түүний дифференциал нь x цэг ба dx хувьсагч гэсэн хоёр хувьсагчийн функц болно. T. y = g(x) функц хэзээ нэгэн цагт дифференциалагдахын тулд энэ цэгт дериватив байх шаардлагатай бөгөөд хангалттай бөгөөд (*) Нотлох баримт. Хэрэгцээ. f(x) функц нь цэг дээр дифференциалагдах боломжтой байг, өөрөөр хэлбэл. Иймээс f’() дериватив байгаа бөгөөд A-тай тэнцүү байна. Иймээс dy = f’()dx Хангалттай байдал. f’(), i.e. дериватив байх болтугай. = f'(). Тэгвэл y = f(x) муруй нь шүргэгч сегмент болно. Х цэг дээрх функцийн утгыг тооцоолохын тулд f() ба f’()/-ийг олоход хэцүү биш байхаар түүний ойролцоох цэгийг ав. Хэд хэдэн хувьсагчийн функцийг хамарсан бодлогод хэсэгчилсэн деривативыг ашигладаг. Олдох дүрэм нь нэг хувьсагчийн функцтэй яг адилхан бөгөөд ялгаа нь ялгах үед хувьсагчийн аль нэгийг тогтмол (тогтмол тоо) гэж үзэх ёстой гэсэн цорын ганц ялгаа юм. $ z(x,y) $ гэсэн хоёр хувьсагчийн функцийн хэсэгчилсэн деривативуудыг $ z"_x, z"_y $ хэлбэрээр дараах томъёогоор бичдэг бөгөөд томъёог ашиглан олно. Нэгдүгээр эрэмбийн хэсэгчилсэн дериватив $$ z"_x = \frac(\хэсэг z)(\хэсэг х) $$ $$ z"_y = \frac(\хэсэг z)(\хэсэг y) $$ Хоёр дахь эрэмбийн хэсэгчилсэн дериватив $$ z""_(xx) = \frac(\хэсэг^2 z)(\хэсэг х \хэсэг x) $$ $$ z""_(yy) = \frac(\хэсэг^2 z)(\хэсэг y \хэсэг y) $$ Холимог дериватив $$ z""_(xy) = \frac(\хэсэг^2 z)(\хэсэг х \хэсэг y) $$ $$ z""_(yx) = \frac(\хэсэг^2 z)(\хэсэг y \хэсэг x) $$ Нарийн төвөгтэй функцийн хэсэгчилсэн дериватив a) $ z (t) = f(x(t), y(t)) $ гэж бодвол нийлмэл функцийн деривативыг дараах томъёогоор тодорхойлно. $$ \frac(dz)(dt) = \frac(\partial z)(\partial x) \cdot \frac(dx)(dt) + \frac(\partial z)(\partial y) \cdot \frac (dy)(dt)$$ б) $ z (u,v) = z(x(u,v),y(u,v)) $ байвал функцийн хэсэгчилсэн деривативуудыг дараах томъёогоор олно. $$ \frac(\partial z)(\partial u) = \frac(\partial z)(\partial x) \cdot \frac(\partial x)(\partial u) + \frac(\partial z)( \partial y) \cdot \frac(\partial y)(\partial u) $$ $$ \frac(\partial z)(\partial v) = \frac(\partial z)(\partial x) \cdot \frac(\partial x)(\partial v) + \frac(\partial z)( \partial y) \cdot \frac(\partial y)(\partial v) $$ Далд функцийн хэсэгчилсэн деривативууд a) $ F(x,y(x)) = 0 $, дараа нь $$ \frac(dy)(dx) = -\frac(f"_x)(f"_y) $$ байг. б) $ F(x,y,z)=0 $, тэгвэл $$ z"_x = - \frac(F"_x)(F"_z); z"_y = - \frac(F"_y)( F"_z) $$ $ x $-ийн хэсэгчилсэн деривативыг олохын тулд $ y $ -ийг тогтмол утга (тоо) гэж үзнэ. $$ z"_x = (x^2-y^2+4xy+10)"_x = 2x - 0 + 4y + 0 = 2x+4y $$ $y$-д хамаарах функцийн хэсэгчилсэн деривативыг олохын тулд $y$-ийг тогтмолоор тодорхойлно. $$ z"_y = (x^2-y^2+4xy+10)"_y = -2y+4x $$ Хэрэв та асуудлаа шийдэж чадахгүй бол бидэнд илгээнэ үү. Бид нарийвчилсан шийдлийг өгөх болно. Та тооцооллын явцыг харж, мэдээлэл авах боломжтой болно. Энэ нь таныг багшаасаа цаг тухайд нь дүнгээ авахад тусална! Эхлээд та эхний деривативуудыг олох хэрэгтэй, дараа нь тэдгээрийг мэдсэнээр хоёр дахь эрэмбийн деривативуудыг олох боломжтой. $y$ тогтмол байг: $$ z"_x = (e^(xy))"_x = e^(xy) \cdot (xy)"_x = ye^(xy) $$ Одоо $ x $-г тогтмол утга болгон тохируулцгаая. $$ z"_y = (e^(xy))"_y = e^(xy) \cdot (xy)"_y = xe^(xy) $$ Эхний деривативуудыг мэдсэнээр бид хоёр дахь нь адилхан олдог. $y$-г тогтмол болгох: $$ z""_(xx) = (z"_x)"_x = (ye^(xy))"_x = (y)"_x e^(xy) + y(e^(xy))"_x = 0 + ye^(xy)\cdot (xy)"_x = y^2e^(xy) $$ Бид $ x $-г тогтмол болгож тохируулсан: $$ z""_(yy) = (z"_y)"_y = (xe^(xy))"_y = (x)"_y e^(xy) + x(e^(xy))"_y = 0 + x^2e^(xy) = x^2e^(xy) $$ Одоо зөвхөн холимог деривативыг олох л үлдлээ. Та $ z"_x $-г $ y $-оор ялгаж болно, мөн $ z"_y $-г $ x $-оор ялгаж болно, учир нь теоремоор $ z""_(xy) = z""_(yx) $ байна. $$ z""_(xy) = (z"_x)"_y = (ye^(xy))"_y = (y)"_y e^(xy) + y (e^(xy))"_y = та^(xy)\cdot (xy)"_y = yxe^(xy) $$ Бид функцийг дараах форматаар бичнэ: $ F(x,y,z) = 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ ба деривативуудыг олно. $$ z"_x (y,z - const) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_x = 3 x^2 z - 4 $$ $$ z"_y (x,y - const) = (x^3 z - 2z^2 + 3yz^2-4x+z-5)"_y = 3z^2 $$ Бид хүн бүрийн дуртай математикийн шинжилгээний сэдэв болох деривативыг үргэлжлүүлж байна. Энэ нийтлэлд бид хэрхэн олох талаар сурах болно гурван хувьсагчийн функцийн хэсэгчилсэн деривативууд: эхний дериватив ба хоёр дахь дериватив. Материалыг эзэмшихийн тулд юу мэдэж, юу хийх чадвартай байх ёстой вэ? Та үүнд итгэх үү, үгүй юу, нэгдүгээрт, та нэг хувьсагчийн функцийн "ердийн" деривативуудыг олох чадвартай байх хэрэгтэй - өндөр эсвэл дор хаяж дундаж түвшинд. Хэрэв тэдэнтэй харьцах нь үнэхээр хэцүү байвал хичээлээс эхэл Деривативыг хэрхэн олох вэ?Хоёрдугаарт, нийтлэлийг уншиж, бүгдийг нь биш юм гэхэд ихэнх жишээг ойлгож, шийдвэрлэх нь маш чухал юм. Хэрэв энэ нь аль хэдийн хийгдсэн бол надтай итгэлтэй алхаарай, энэ нь сонирхолтой байх болно, тэр ч байтугай танд таалагдах болно! Олж олох арга, зарчим гурван хувьсагчийн функцийн хэсэгчилсэн деривативууднь үнэндээ хоёр хувьсагчийн функцийн хэсэгчилсэн деривативтай маш төстэй юм. Хоёр хувьсагчийн функц нь "x" ба "y" нь бие даасан хувьсагч гэсэн хэлбэртэй байдаг гэдгийг сануулъя. Геометрийн хувьд хоёр хувьсагчийн функц нь бидний гурван хэмжээст орон зайн тодорхой гадаргууг илэрхийлдэг. Гурван хувьсагчийн функц нь хэлбэртэй байх ба хувьсагчдыг дуудна бие даасанхувьсагчэсвэл аргументууд, хувьсагчийг дуудна хамааралтай хувьсагчэсвэл функц. Жишээ нь: – гурван хувьсагчийн функц Одоо шинжлэх ухааны зөгнөлт кино, харь гарагийнхны тухай бага зэрэг. Дөрвөн хэмжээст, таван хэмжээст, арван хэмжээст гэх мэтийн талаар та ихэвчлэн сонсож болно. зай. Дэмий юм уу, үгүй юу? – Дэлхий дээр дөрөв, тав гэх мэт байдаг уу? орон зайн тухай филистист ойлголтын утгаар хэмжилтүүд (урт/өргөн/өндөр)? – Дөрвөн хэмжээст, таван хэмжээст гэх мэтийг бүтээх боломжтой юу? өргөн утгаараа орон зай? Энэ нь бидний амьдралд ийм орон зайн жишээг өг. -Өнгөрсөн үе рүү аялах боломжтой юу? – Ирээдүй рүү аялах боломжтой юу? -Харь гарагийнхан байдаг уу? Аливаа асуултын хувьд та дөрвөн хариултаас аль нэгийг нь сонгож болно. Бүх асуултанд зөв хариулсан хүн ямар нэгэн зүйлтэй байх магадлалтай ;-) Хичээл ахих тусам би асуултуудад аажмаар хариулт өгөх болно, жишээнүүдийг бүү алдаарай! Үнэндээ тэд ниссэн. Тэгээд тэр даруй сайн мэдээ: Гурван хувьсагчийн функцийн хувьд ялгах дүрэм ба деривативын хүснэгт хүчинтэй байна. Тийм учраас та "энгийн"-тэй харьцахдаа сайн байх хэрэгтэй. функцүүдийн деривативууднэг хувьсагч. Маш цөөхөн ялгаа байна! Жишээ 1 Шийдэл:Таахад хэцүү биш - гурван хувьсагчийн функцийн хувьд байдаг гуравЭхний эрэмбийн хэсэгчилсэн деривативуудыг дараах байдлаар тэмдэглэв. Эсвэл – "x"-ын хувьд хэсэгчилсэн дериватив; Ерөнхий тэмдэгтэй тэмдэг нь илүү түгээмэл боловч цуглуулга, сургалтын гарын авлагыг эмхэтгэгчид асуудалд төвөгтэй тэмдэгтүүдийг ашиглах дуртай байдаг тул бүү алдаарай! Эдгээр "аймшигт фракцуудыг" хэрхэн чангаар зөв уншихаа хүн бүр мэддэггүй байх. Жишээ нь: "de u po de x" гэж дараах байдлаар унших ёстой. "x"-тэй холбоотой деривативаас эхэлье: . -д хамаарах хэсэгчилсэн деривативыг олох үед , дараа нь хувьсагчид Тэгээд тогтмол тоо (тогтмол тоо) гэж үздэг.Ямар ч тогтмолын дериватив, өө, нигүүлсэл, тэгтэй тэнцүү байна: Доорх тэмдэгтийг нэн даруй анхаарч үзээрэй - тэдгээрийг тогтмол гэж тэмдэглэхийг хэн ч хориглодоггүй. Энэ нь бүр илүү тохиромжтой, би эхлэгчдэд ийм бичлэг ашиглахыг зөвлөж байна, төөрөлдөх эрсдэл бага. (1) Бид деривативын шугаман шинж чанарыг ашигладаг, ялангуяа бид бүх тогтмолыг деривативын тэмдгээс цааш шилжүүлдэг. Хоёр дахь гишүүнд тогтмолыг хасах шаардлагагүй гэдгийг анхаарна уу: "Y" нь тогтмол тул энэ нь бас тогтмол байна. Нэр томьёогоор "ердийн" тогтмол 8 ба тогтмол "зэт" -ийг дериватив тэмдгээс хасав. (2) Бид хамгийн энгийн деривативуудыг олдог бөгөөд тэдгээр нь тогтмол гэдгийг мартаж болохгүй. Дараа нь бид хариултаа самна. Хэсэгчилсэн дериватив. "y"-тэй холбоотой хэсэгчилсэн деривативыг олох үед хувьсагч болно Тэгээд тогтмол гэж үздэг:
(1) Бид шугаман байдлын шинж чанарыг ашигладаг. Дахин хэлэхэд, , нэр томъёо нь тогтмол бөгөөд энэ нь дериватив тэмдгээс юу ч хасах шаардлагагүй гэсэн үг юм. (2) Деривативуудыг тогтмол гэдгийг мартаж болохгүй. Дараа нь бид хариултыг хялбарчлах болно. Эцэст нь, хэсэгчилсэн дериватив. Бид "zet" -тэй холбоотой хэсэгчилсэн деривативыг олоход хувьсагч болно Тэгээд тогтмол гэж үздэг:
Ерөнхий дүрэмилэрхий, мадаггүй зөв: Хэсэгчилсэн деривативыг олох үедямар ч шалтгаанаар
бие даасан хувьсагч, тэгвэлөөр хоёр
бие даасан хувьсагчдыг тогтмол гэж үзнэ. Эдгээр ажлыг гүйцэтгэхдээ та маш болгоомжтой байх хэрэгтэй, ялангуяа, Та жагсаалтаа алдаж болохгүй(ямар хувьсагчийг ялгахад ашиглаж байгааг заадаг). Индексийг алдах нь БҮХЭН ТӨРӨӨ БАЙДАЛ болно. Хмм…. Ийм айлган сүрдүүлсний дараа би тэднийг хаа нэг газар өнгөрөхийг зөвшөөрвөл инээдтэй байна) Жишээ 2 Гурван хувьсагчтай функцийн эхний эрэмбийн хэсэгчилсэн деривативуудыг ол Энэ бол та өөрөө шийдэх жишээ юм. Хичээлийн төгсгөлд бүрэн шийдэл, хариулт. Харгалзан үзсэн хоёр жишээ нь маш энгийн бөгөөд ижил төстэй хэд хэдэн асуудлыг шийдсэний дараа цайны аяга хүртэл тэдгээрийг амаар шийдвэрлэхэд дасдаг. Стрессээ тайлахын тулд асуулт хариултын эхний асуулт руу эргэн оръё: Дэлхий дээр дөрөв, тав гэх мэт байдаг уу? орон зайн тухай филистист ойлголтын утгаар хэмжилтүүд (урт/өргөн/өндөр)? Зөв хариулт: Шинжлэх ухаан үүнийг хориглодоггүй. Математикийн бүх суурь аксиоматик, теорем, математикийн аппаратууд нь үзэсгэлэнтэй бөгөөд тууштайямар ч хэмжээсийн орон зайд ажиллах. Орчлон ертөнцийн хаа нэгтээ бидний оюун санаанаас үл хамаарах хэт гадаргуу, тухайлбал, гурван хувьсагчийн функцээр тодорхойлогддог дөрвөн хэмжээст гипер гадаргуу байж болох юм. Эсвэл хэт гадаргуу нь бидний хажууд байгаа юм уу, эсвэл бид тэдний дотор байгаа ч байж болох юм, зүгээр л бидний алсын хараа, бусад мэдрэхүй, ухамсар нь зөвхөн гурван хэмжээсийг мэдэрч, ойлгох чадвартай байдаг. Жишээнүүд рүү буцъя. Тийм ээ, хэрэв хэн нэгэн асуулт хариултанд ачаалал ихтэй байгаа бол гурван хувьсагчийн функцийн хэсэгчилсэн деривативыг хэрхэн олох талаар сурсны дараа дараах асуултын хариултыг уншсан нь дээр. =) Хамгийн энгийн жишээ 1, 2-оос гадна практикт жижиг оньсого гэж нэрлэж болох даалгаварууд байдаг. Хичээлийг бүтээхэд ийм жишээнүүд миний харамссан Хоёр хувьсагчийн функцийн хэсэгчилсэн деривативууд. Хойшоод үзье: Жишээ 3 Шийдэл:Энд "бүх зүйл энгийн" мэт санагдаж байгаа ч анхны сэтгэгдэл нь хуурамч юм. Хэсэгчилсэн деривативыг олохдоо олон хүн цайны навчийг таамаглаж, алдаа гаргах болно. Жишээг тууштай, ойлгомжтой, ойлгомжтой авч үзье. "x"-тэй холбоотой хэсэгчилсэн деривативаас эхэлье. "x"-ийн хэсэгчилсэн деривативыг олоход хувьсагчдыг тогтмол гэж үзнэ. Тиймээс бидний функцийн илтгэгч нь мөн тогтмол байна. Даммиуудын хувьд би дараах шийдлийг санал болгож байна: ноорог дээр тогтмолыг тодорхой эерэг бүхэл тоо болгон өөрчлөх, жишээлбэл, "тав". Үр дүн нь нэг хувьсагчийн функц юм: Энэ хүчнийлмэл суурьтай функц (синус). Зохиогч: Одоо бид үүнийг санаж байна, тэгвэл: Эцсийн шатанд мэдээжийн хэрэг шийдлийг дараах байдлаар бичих ёстой. Бид "y"-тэй холбоотой хэсэгчилсэн деривативыг олдог бөгөөд тэдгээрийг тогтмол гэж үздэг. Хэрэв “x” тогтмол бол энэ нь мөн тогтмол байна. Ноорог дээр бид ижил заль мэхийг хийдэг: жишээлбэл, 3-аар солих "Z" - ижил "тав" -аар солино. Үр дүн нь дахин нэг хувьсагчийн функц юм: Энэ заалтнийлмэл илтгэгчтэй функц. By нарийн төвөгтэй функцуудыг ялгах дүрэм: Одоо солигдсоноо санацгаая: Тиймээс: Эцсийн хуудсан дээр мэдээжийн хэрэг дизайн сайхан харагдах ёстой: Мөн "zet" ( – тогтмол) -ын хэсэгчилсэн дериватив бүхий толин тусгал: Зарим туршлагатай бол шинжилгээг оюун ухаанаар хийж болно. Даалгаврын хоёр дахь хэсгийг гүйцээцгээе - нэгдүгээр эрэмбийн дифференциал зохио. Энэ нь маш энгийн бөгөөд хоёр хувьсагчийн функцтэй зүйрлэвэл эхний эрэмбийн дифференциалыг томъёогоор бичнэ. Энэ тохиолдолд: Мөн энэ бол бизнес. Практик асуудлуудад гурван хувьсагчийн функцийн хувьд 1-р эрэмбийн бүрэн дифференциалыг хоёр хувьсагчийн функцээс хамаагүй бага давтамжтайгаар байгуулах шаардлагатайг би тэмдэглэж байна. Үүнийг өөрөө шийдэх хөгжилтэй жишээ: Жишээ 4 Гурван хувьсагчийн функцийн нэгдүгээр эрэмбийн хэсэгчилсэн деривативуудыг олж, нэгдүгээр эрэмбийн бүрэн дифференциал байгуул. Хичээлийн төгсгөлд бүрэн шийдэл, хариулт. Хэрэв танд ямар нэгэн бэрхшээл тулгарвал "Чайниковский" алгоритмыг ашиглана уу, энэ нь танд туслах болно. Мөн өөр нэг ашигтай зөвлөгөө - битгий яар. Би ч гэсэн ийм жишээг хурдан шийдэж чадахгүй. Хоёрдахь асуултыг ухаж үзэцгээе: Дөрвөн хэмжээст, таван хэмжээст гэх мэтийг бүтээх боломжтой юу? өргөн утгаараа орон зай? Энэ нь бидний амьдралд ийм орон зайн жишээг өг. Зөв хариулт: Тиймээ. Үүнээс гадна, энэ нь маш хялбар юм. Жишээлбэл, бид урт/өргөн/өндөр - цаг дээр дөрөв дэх хэмжигдэхүүнийг нэмдэг. Эйнштейн Лобачевский, Пуанкаре, Лоренц, Минковски нараас хулгайлсан алдартай дөрвөн хэмжээст орон зай цаг ба харьцангуйн онолыг сайн мэддэг. Хүн бүр мэддэггүй. Эйнштейн яагаад Нобелийн шагнал хүртсэн бэ? Шинжлэх ухааны ертөнцөд аймшигт дуулиан дэгдээж, Нобелийн хороо хулгайчийн гавьяаг "Физикийн хөгжилд оруулсан хувь нэмрийг нь үнэлснийх нь төлөө" гэж ойролцоогоор томъёолжээ. Ингээд л болоо. Си оюутан Эйнштейний брэнд бол цэвэр сурталчилгаа, PR юм. Дөрвөн хэмжээст орон зайд тав дахь хэмжээсийг нэмэхэд хялбар байдаг, жишээлбэл: атмосферийн даралт. Гэх мэтчилэн, таны загварт зааж өгсөн хэмжээсүүд нь хэд байх болно. Энэ үгийн өргөн утгаараа бид олон хэмжээст орон зайд амьдарч байна. Өөр хэд хэдэн ердийн ажлыг авч үзье: Жишээ 5 Нэг цэгт эхний эрэмбийн хэсэгчилсэн деривативуудыг ол Шийдэл:Энэхүү томъёолол дахь даалгавар нь ихэвчлэн практикт олддог бөгөөд дараахь хоёр үйлдлийг агуулдаг. Бид шийднэ: (1) Бидний өмнө нарийн төвөгтэй функц байгаа бөгөөд эхний алхамд бид арктангенсын деривативыг авах ёстой. Энэ тохиолдолд бид арктангентын деривативын хүснэгтийн томъёог тайвнаар ашигладаг. By нарийн төвөгтэй функцуудыг ялгах дүрэмүр дүнг дотоод функцийн деривативаар үржүүлэх ёстой (суулгах): . (2) Бид шугаман байдлын шинж чанарыг ашигладаг. (3) Бид үлдсэн деривативуудыг авч, тэдгээр нь тогтмол гэдгийг мартаж болохгүй. Даалгаврын нөхцлийн дагуу тухайн цэг дээр олсон хэсэгчилсэн деривативын утгыг олох шаардлагатай. Олдсон деривативт цэгийн координатыг орлъё: Энэ даалгаврын давуу тал нь бусад хэсэгчилсэн деривативуудыг ижил төстэй схемийн дагуу олдог явдал юм. Таны харж байгаагаар шийдлийн загвар нь бараг ижил байна. Олдсон хэсэгчилсэн деривативын утгыг цэг дээр тооцоод үзье. Эцэст нь, "zet" -тэй холбоотой дериватив: Бэлэн. Шийдлийг өөр аргаар боловсруулж болно: эхлээд бүх гурван хэсэгчилсэн деривативыг олж, дараа нь тэдгээрийн утгыг цэг дээр тооцоол. Гэхдээ миний бодлоор дээрх арга нь илүү тохиромжтой юм шиг санагдаж байна - хэсэгчилсэн деривативыг олж, тэр даруй кассын бүртгэлээс гаралгүйгээр түүний утгыг тухайн цэг дээр тооцоол. Геометрийн хувьд цэг нь бидний гурван хэмжээст орон зайд маш бодит цэг гэдгийг тэмдэглэх нь сонирхолтой юм. Функц ба деривативын утга нь аль хэдийн дөрөв дэх хэмжээс бөгөөд геометрийн хувьд хаана байрлаж байгааг хэн ч мэдэхгүй. Тэдний хэлснээр хэн ч Орчлон ертөнцийг соронзон хальсны хэмжүүрээр мөлхөж, шалгаагүй. Нэгэнт гүн ухааны сэдэв дахин сөхөгдөж байгаа тул гурав дахь асуултыг авч үзье: Өнгөрсөн рүү аялах боломжтой юу? Зөв хариулт: Үгүй. Өнгөрсөн үе рүү аялах нь физик үйл явцын эргэлт буцалтгүй байдлын (энтропи) тухай термодинамикийн хоёрдугаар хуультай зөрчилддөг. Тиймээс усгүй усан сан руу бүү шумбаарай, энэ үйл явдлыг зөвхөн видеогоор л харуулах боломжтой =) "Хоёр удаа хэмжиж, нэг удаа огтол" гэсэн өдөр тутмын эсрэг хууль ардын мэргэн ухаан санаанаас гардаггүй юм. Хэдийгээр үнэндээ харамсалтай нь цаг хугацаа нэг чиглэлтэй, эргэлт буцалтгүй байдаг ч маргааш бидний хэн нь ч залуу биш байх болно. "Терминатор" гэх мэт янз бүрийн шинжлэх ухааны уран зөгнөлт кинонууд нь шинжлэх ухааны үүднээс бүрэн утгагүй зүйл юм. Өнгөрсөн үе рүүгээ буцаж ирсэн нөлөө нь өөрийн Шалтгааныг устгаж чадна гэдэг нь философийн үүднээс бас утгагүй юм. . Энэ нь "zet" деривативын хувьд илүү сонирхолтой боловч бараг ижил хэвээр байна: (1) Бид деривативын тэмдгээс тогтмолуудыг авдаг. (2) Энд дахин хоёр функцийн үржвэр байна. тус бүр нь хамаарна"амьд" хувьсагч "zet"-ээс. Зарчмын хувьд та категорийн деривативын томъёог ашиглаж болно, гэхдээ өөр замаар явах нь илүү хялбар байдаг - бүтээгдэхүүний деривативыг олох. (3) Дериватив нь хүснэгтийн дериватив юм. Хоёр дахь гишүүн нь нийлмэл функцийн аль хэдийн танил болсон деривативыг агуулдаг. Жишээ 9 Гурван хувьсагчтай функцийн эхний эрэмбийн хэсэгчилсэн деривативуудыг ол Энэ бол та өөрөө шийдэх жишээ юм. Энэ эсвэл хэсэгчилсэн деривативыг хэрхэн илүү оновчтой олох талаар бодож үзээрэй. Хичээлийн төгсгөлд бүрэн шийдэл, хариулт. Хичээлийн эцсийн жишээнүүд рүү шилжиж, үзэхийн өмнө хоёрдугаар эрэмбийн хэсэгчилсэн деривативГурван хувьсагчийн функцууд, би дөрөв дэх асуултаар хүн бүрийг дахин баярлуулах болно: Ирээдүй рүү аялах боломжтой юу? Зөв хариулт: Шинжлэх ухаан үүнийг хориглодоггүй. Хачирхалтай нь, ирээдүйд аялахыг хориглосон математик, физик, хими болон бусад байгалийн шинжлэх ухааны хууль байдаггүй! Дэмий юм шиг санагдаж байна уу? Гэхдээ амьдралын бараг бүх хүмүүс энэ эсвэл тэр үйл явдал тохиолдох болно гэсэн урьдчилсан таамаглалтай байсан (мөн ямар ч логик аргументаар дэмжигдээгүй). Тэгээд болсон! Мэдээлэл хаанаас ирсэн бэ? Ирээдүйгээс үү? Тиймээс ирээдүй рүү аялах тухай шинжлэх ухааны уран зөгнөлт кинонууд, дашрамд хэлэхэд бүх төрлийн мэргэ төлөгчид, зөн билэгчдийн таамаглалыг ийм утгагүй зүйл гэж нэрлэж болохгүй. Наад зах нь шинжлэх ухаан үүнийг үгүйсгээгүй. Бүх зүйл боломжтой байдаг! Тиймээс намайг сургуульд байхад киноны CD, хавтгай дэлгэц надад үнэхээр гайхалтай санагддаг байсан. Алдарт "Иван Васильевич мэргэжлээ өөрчилсөн нь" инээдмийн кино нь хагас уран зохиол юм (дээд тал нь). Шинжлэх ухааны ямар ч хууль Иван Грозныйг ирээдүйд байхыг хориглоогүй боловч хоёр чинжүү өнгөрсөнд дуусч, хааны үүргийг гүйцэтгэх боломжгүй юм. Гурван хувьсагчийн функцийн хоёрдугаар эрэмбийн хэсэгчилсэн деривативыг олох ерөнхий зарчим нь хоёр хувьсагчийн функцийн хоёрдугаар эрэмбийн хэсэгчилсэн деривативыг олох зарчимтай төстэй. Хоёрдахь эрэмбийн хэсэгчилсэн деривативуудыг олохын тулд эхлээд нэгдүгээр эрэмбийн хэсэгчилсэн деривативуудыг олох хэрэгтэй, эсвэл өөр тэмдэглэгээгээр: Хоёр дахь эрэмбийн есөн хэсэгчилсэн дериватив байдаг. Эхний бүлэг нь ижил хувьсагчтай холбоотой хоёр дахь деривативууд юм. Эсвэл - "x"-ийн хоёр дахь дериватив; Эсвэл – "Y"-ийн хоёр дахь дериватив; Эсвэл - "zet" -тэй холбоотой хоёр дахь дериватив. Хоёр дахь бүлэг нь холимог 2-р эрэмбийн хэсэгчилсэн дериватив, тэдгээрийн зургаа нь: Эсвэл - холимогдериватив "х igrek"; Эсвэл - холимог"х тоглоомоор" дериватив; Эсвэл - холимог"x z-ийн хувьд" дериватив; Эсвэл - холимогдериватив "zt x"; Эсвэл - холимогдериватив "igrek z-ийн хувьд"; Эсвэл - холимогдериватив "zt igrek". Хоёр хувьсагчийн функцийн нэгэн адил асуудлыг шийдвэрлэхдээ хоёр дахь эрэмбийн холимог деривативуудын дараах тэгшитгэлд анхаарлаа хандуулж болно. Анхаар: хатуухан хэлэхэд энэ нь үргэлж тийм байдаггүй. Холимог деривативууд тэнцүү байхын тулд тэдгээрийн тасралтгүй байдлын шаардлагыг хангасан байх ёстой. Энэ гутамшигт явдлыг чангаар хэрхэн зөв унших тухай цөөн хэдэн жишээ энд байна. - "хоёр цус харвалт нь нэг тоглолтонд хоёр удаа"; – “de two y by de z square”; – “X ба Z дээр хоёр цус харвалт байна”; - “де хоёр ы по де зэт по де игрек.” Жишээ 10 Гурван хувьсагчийн функцийн эхний болон хоёрдугаар эрэмбийн бүх хэсэгчилсэн деривативуудыг ол. Шийдэл:Эхлээд нэгдүгээр эрэмбийн хэсэгчилсэн деривативуудыг олъё: Бид олсон деривативыг авдаг мөн "Y"-ээр ялгана: Бид олсон деривативыг авдаг "x"-ээр ялгах: Тэгш байдал хангагдсан. Сайн байна. Холимог деривативын хоёр дахь хосыг авч үзье. Бид олсон деривативыг авдаг мөн үүнийг "z"-ээр ялгана: Бид олсон деривативыг авдаг "x"-ээр ялгах: Тэгш байдал хангагдсан. Сайн байна. Гурав дахь хос холимог деривативыг бид ижил төстэй байдлаар авч үздэг. Тэгш байдал хангагдсан. Сайн байна. Хийсэн ажлын дараа бид нэгдүгээрт, бүх 1-р эрэмбийн хэсэгчилсэн деривативуудыг зөв олсон, хоёрдугаарт, холимог 2-р эрэмбийн хэсэгчилсэн деривативуудыг зөв олсон гэдгийг баталж чадна. Хоёрдахь эрэмбийн гурван хэсэгчилсэн деривативыг олоход л үлдлээ; энд алдаа гаргахгүйн тулд та анхаарлаа аль болох төвлөрүүлэх хэрэгтэй. Бэлэн. Би давтан хэлье, даалгавар нь том хэмжээтэй тул тийм ч хэцүү биш юм. Уусмалыг богиносгож, холимог хэсэгчилсэн деривативуудын тэнцүү гэж нэрлэж болох боловч энэ тохиолдолд баталгаажуулалт байхгүй болно. Тиймээс цаг гаргаж, хайж олох нь дээр Бүгддериватив (үүнээс гадна багш үүнийг шаардаж болно), эсвэл эцсийн арга хэмжээ болгон төслийг шалгана уу. Жишээ 11 Гурван хувьсагчийн функцийн нэг ба хоёрдугаар эрэмбийн бүх хэсэгчилсэн деривативуудыг ол Энэ бол та өөрөө шийдэх жишээ юм. Шийдэл ба хариултууд:
Жишээ 2:Шийдэл:
Жишээ 4:Шийдэл:
Эхний эрэмбийн хэсэгчилсэн деривативуудыг олцгооё. Эхний эрэмбийн бүрэн дифференциал үүсгэцгээе: Жишээ 6:Шийдэл:
М(1, -1, 0):
Жишээ 7:Шийдэл:
Нэгдүгээр эрэмбийн хэсэгчилсэн деривативуудыг цэг дээр тооцоолъёМ(1, 1, 1):
Жишээ 9:Шийдэл:
Жишээ 11:Шийдэл:
Эхний эрэмбийн хэсэгчилсэн деривативуудыг олцгооё. Хоёрдахь эрэмбийн хэсэгчилсэн деривативуудыг олцгооё. Интеграл 8.1. Тодорхой бус интеграл. Нарийвчилсан жишээ шийдэл Сэдвээ судалж эхэлцгээе " Тодорхойгүй интеграл", мөн бид хамгийн энгийн (мөн тийм ч энгийн биш) интегралуудын шийдлийн жишээг нарийвчлан шинжлэх болно. Ердийнх шигээ бид олон тооны сурах бичигт байдаг хамгийн бага онолоор хязгаарлагдах болно; бидний даалгавар бол интегралыг хэрхэн шийдэж сурах явдал юм. Материалыг амжилттай эзэмшихийн тулд юу мэдэх хэрэгтэй вэ? Интеграл тооцооллыг даван туулахын тулд та дор хаяж дунд түвшинд дериватив олох чадвартай байх хэрэгтэй. Хэрэв танд хэдэн арван, эсвэл илүү сайн, хэдэн зуун бие даан олсон дериватив байгаа бол энэ нь туршлага дэмий зүйл биш байх болно. Наад зах нь та хамгийн энгийн бөгөөд хамгийн түгээмэл функцуудыг ялгах даалгавруудад андуурч болохгүй. Хэрэв нийтлэл интегралын тухай байвал дериватив нь үүнд ямар хамаатай юм шиг санагдаж байна?! Энэ нь энд байна. Баримт нь дериватив олох, тодорхойгүй интеграл олох (ялгарах ба интеграл) нь нэмэх/хасах, үржүүлэх/хуваах гэх мэт харилцан урвуу хоёр үйлдэл юм. Тиймээс дериватив олох ур чадвар, туршлагагүй бол харамсалтай нь та урагшлах боломжгүй юм. Үүнтэй холбогдуулан бидэнд дараахь сургалтын материал хэрэгтэй болно. Деривативын хүснэгтТэгээд Интегралын хүснэгт. Тодорхой бус интеграл сурахад ямар хүндрэл гардаг вэ? Хэрэв деривативуудад ялгах хатуу 5 дүрэм, деривативын хүснэгт, үйлдлийн нэлээд тодорхой алгоритм байдаг бол интегралд бүх зүйл өөр байна. Интеграцийн олон арван арга, техник байдаг. Хэрэв интеграцийн аргыг эхэндээ буруу сонгосон бол (жишээ нь, та яаж шийдэхээ мэдэхгүй байгаа бол) та жинхэнэ оньсого шиг интегралыг хэдэн өдрийн турш "хатгаж" янз бүрийн арга техник, заль мэхийг олж харах боломжтой. Зарим хүмүүс бүр дуртай байдаг. Дашрамд хэлэхэд, бид оюутнуудаас (хүмүүнлэгийн чиглэлээр мэргэшээгүй) "Би хэзээ ч хязгаар эсвэл деривативыг шийдэх сонирхолтой байгаагүй, гэхдээ интеграл бол огт өөр асуудал, энэ нь гайхалтай, үргэлж байдаг" гэсэн бодлыг ихэвчлэн сонсдог. нийлмэл интегралыг "хакердах" хүсэл." . Зогс. Хар хошигнол хангалттай, эдгээр маш тодорхойгүй интеграл руу шилжье. Нэгэнт шийдэх олон арга байгаа бол цайны сав хаанаас тодорхойгүй интеграл судалж эхлэх ёстой вэ? Интеграл тооцоонд бидний бодлоор гурван багана буюу бусад бүх зүйл эргэн тойронд нь эргэлддэг "тэнхлэг" байдаг. Юуны өмнө та хамгийн энгийн интегралуудын талаар сайн ойлголттой байх ёстой (энэ нийтлэл). Дараа нь та хичээлээ нарийвчлан судлах хэрэгтэй. ЭНЭ ХАМГИЙН ЧУХАЛ ТЕХНИК! Магадгүй интегралын талаархи бүх өгүүллүүдийн хамгийн чухал нийтлэл ч байж магадгүй. Гуравдугаарт, та заавал унших хэрэгтэй хэсгүүдийн аргаар нэгтгэх, учир нь энэ нь олон төрлийн функцуудыг нэгтгэдэг. Хэрэв та дор хаяж эдгээр гурван хичээлийг эзэмшсэн бол танд хоёр хичээл байхгүй болно. Мэдээгүйг чинь өршөөж магадгүй тригонометрийн функцүүдийн интеграл, бутархайн интеграл, бутархай-рационал функцүүдийн интеграл, иррационал функцүүдийн интеграл (үндэс), гэхдээ хэрэв та солих арга эсвэл эд ангиудыг нэгтгэх аргад "хүндрэлд орвол" энэ нь маш муу байх болно. Тиймээс, энгийнээр эхэлцгээе. Интегралын хүснэгтийг харцгаая. Деривативын нэгэн адил бид интеграцийн хэд хэдэн дүрэм, зарим энгийн функцүүдийн интегралуудын хүснэгтийг анзаардаг. Аливаа хүснэгтийн интеграл (мөн тодорхойгүй интеграл) дараах хэлбэртэй байна: Тэмдэглэгээ болон нэр томъёог нэн даруй ойлгоцгооё: - салшгүй дүрс. - интеграл функц ("s" үсгээр бичсэн). - дифференциал дүрс. Энэ юу болохыг бид тун удахгүй харах болно. Хамгийн гол нь интеграл бичих болон шийдлийн явцад энэ дүрсийг алдахгүй байх нь чухал юм. Мэдэгдэхүйц алдаа гарах болно. – интегралын илэрхийлэл буюу “бөглөх”. – эсрэг деривативфункц. – . Нэр томьёогоор их ачаалал өгөх шаардлагагүй, энд хамгийн чухал зүйл бол ямар ч тодорхойгүй интегралд хариулт дээр тогтмол нэмэгддэг. Тодорхойгүй интегралыг шийднэ гэдэг нь олно гэсэн үголон анхдагч функцуудөгөгдсөн интегралаас Бичлэгийг дахин харцгаая: Интегралын хүснэгтийг харцгаая. Юу болоод байна? Бидэнд зүүн хэсгүүд байна өөрчлөгдөхбусад функцууд руу: . Тодорхойлолтоо хялбаршуулъя: Тодорхой бус интегралыг шийд - энэ нь үүнийг тодорхойгүй (тогтмол хүртэл) функц болгон ХӨВЧЛҮҮЛнэ гэсэн үг , зарим дүрэм, техник, хүснэгтийг ашиглан.
Жишээлбэл, хүснэгтийн интегралыг ав Деривативын нэгэн адил интегралыг олж сурахын тулд онолын үүднээс интеграл эсвэл эсрэг дериватив функц гэж юу болохыг мэддэг байх шаардлагагүй. Зарим албан ёсны дүрмийн дагуу өөрчлөлтийг хийхэд л хангалттай. Тиймээс, тохиолдолд Ялгаварлах ба интеграцчилал нь эсрэг үйлдлүүд тул зөв олдсон аливаа эсрэг деривативын хувьд дараах зүйл үнэн болно. Өөрөөр хэлбэл, хэрэв та зөв хариултыг ялгах юм бол анхны интеграл функцийг авах ёстой. Нэг хүснэгтийн интеграл руу буцъя Энэ томъёоны үнэн зөвийг шалгацгаая. Бид баруун талын деривативыг авдаг: нь анхны интеграл функц юм. Дашрамд хэлэхэд, функцэд яагаад тогтмол тогтмол оноогдсон нь илүү тодорхой болсон. Ялгах үед тогтмол нь үргэлж тэг болж хувирдаг. Тодорхой бус интегралыг шийд- олох гэсэн үг бөөн хүн бүрэсрэг деривативууд бөгөөд зөвхөн нэг функц биш юм. Харж байгаа хүснэгтийн жишээнд, , , , гэх мэт – эдгээр бүх функц нь интегралын шийдэл юм. Хязгааргүй олон шийдэл байгаа тул бид үүнийг товч бичнэ: Тиймээс аливаа тодорхойгүй интегралыг шалгахад хялбар байдаг. Энэ нь янз бүрийн төрлийн олон тооны интегралуудын зарим нөхөн олговор юм. Тодорхой жишээнүүдийг авч үзье. Деривативыг судлахтай адил интеграцийн хоёр дүрмээр эхэлцгээе. Таны харж байгаагаар дүрэм нь үндсэндээ деривативтай адил байна. Заримдаа тэднийг дууддаг шугаман шинж чанаруудинтеграл. Жишээ 1 Тодорхойгүй интегралыг ол. Шалгалт хийх. Шийдэл:Үүнийг шиг хөрвүүлэх нь илүү тохиромжтой. (1) Дүрмийг хэрэгжүүл (2) Дүрмийн дагуу Нэмж дурдахад, энэ үе шатанд бид нэгтгэх үндэс, хүчийг бэлтгэдэг. Ялгарахтай адил үндэс нь хэлбэрээр илэрхийлэгдэх ёстой . Хуваарьт байгаа үндэс ба хүчийг дээш нь хөдөлгөнө.
Жич:Деривативаас ялгаатай нь интеграл дахь үндсийг үргэлж хэлбэрт оруулж болохгүй , мөн градусыг дээшлүүлнэ.
Жишээлбэл, - энэ бол таны өмнө тооцоолсон бэлэн хүснэгтийн интеграл бөгөөд Хятадын бүх төрлийн заль мэх юм. бүрэн шаардлагагүй. Үүний нэгэн адил: - энэ нь мөн хүснэгтийн интеграл бөгөөд бутархайг хэлбэрээр илэрхийлэх нь утгагүй юм . Хүснэгтийг анхааралтай судлаарай!
(3) Бидний бүх интегралууд хүснэгт хэлбэртэй байна. Бид дараах томъёог ашиглан хүснэгтийг ашиглан хувиргалтыг гүйцэтгэдэг. эрчим хүчний функцийн хувьд - Хүснэгтийн интеграл нь чадлын функцийн томъёоны онцгой тохиолдол гэдгийг тэмдэглэх нь зүйтэй. Тогтмол C илэрхийллийн төгсгөлд нэг удаа нэмэхэд хангалттай
(интеграл бүрийн ард тавихаас илүү).
(4) Бид олж авсан үр дүнг бүх хүч нь хэлбэртэй байх үед илүү нягт хэлбэрээр бичдэг дахин бид тэдгээрийг язгуур хэлбэрээр төлөөлж, сөрөг илтгэгчтэй хүчийг дахин хуваагч руу буцаана. Шалгалт. Шалгалт хийхийн тулд та хүлээн авсан хариултыг ялгах хэрэгтэй. Эх хувийг нь авсан интеграл, өөрөөр хэлбэл интеграл зөв олдсон. Тэдний бүжиглэсэн зүйл бол буцаж ирсэн зүйл юм. Интегралтай түүх ингэж дуусвал сайн. Үе үе, тодорхойгүй интегралыг шалгахдаа үүсмэл биш харин дифференциалыг хариултаас авдаг бол арай өөр арга байдаг. Үүний үр дүнд бид интеграл функц биш харин интеграл илэрхийлэлийг авдаг. Дифференциал гэдэг ойлголтоос бүү ай. Дифференциал нь деривативыг үржүүлсэн байна dx.
Гэсэн хэдий ч бидний хувьд чухал зүйл бол онолын нарийн ширийн зүйл биш, харин энэ дифференциалыг дараа нь яах вэ. Дифференциал нь дараах байдлаар илэрдэг: icon г
Бид үүнийг хасаад, хаалтны баруун талд праймерыг тавьж, илэрхийллийн төгсгөлд хүчин зүйл нэмнэ dx
: Оригинал хүлээн авсан интеграл, өөрөөр хэлбэл интеграл зөв олдсон. Таны харж байгаагаар дифференциал нь деривативыг олоход хүргэдэг. Би нэмэлт том хаалт зурж, дифференциал дүрсийг чирэх шаардлагатай болсон тул шалгах хоёр дахь арга нь надад бага таалагддаг. dx
чек дуусах хүртэл. Хэдийгээр энэ нь илүү зөв, эсвэл "илүү нэр хүндтэй" эсвэл өөр зүйл юм. Үнэн хэрэгтээ баталгаажуулалтын хоёр дахь аргын талаар чимээгүй байх боломжтой байсан. Гол нь аргадаа биш бид дифференциал нээж сурсандаа л байгаа юм. Дахин. Дифференциал дараахь байдлаар илэрдэг. 1) дүрс гарилгах; 2) хаалт дээрх баруун талд бид цус харвалт (деривативын тэмдэглэгээ) тавьдаг; 3) илэрхийллийн төгсгөлд бид хүчин зүйл оноодог dx
. Жишээлбэл: Үүнийг санаарай. Бидэнд энэ техник тун удахгүй хэрэг болно. Жишээ 2 Бид тодорхойгүй интеграл олохдоо ҮРГЭЛЖ шалгахыг хичээдэгТүүгээр ч зогсохгүй үүнд маш том боломж бий. Дээд математикийн бүх төрлийн бодлого нь энэ үүднээс авч үзвэл бэлэг биш юм. Хяналтын даалгаварт шалгалт хийх шаардлагагүй байх нь хамаагүй; хэн ч, юу ч танд ноорог дээр үүнийг хийхэд саад болохгүй. Зөвхөн хангалттай цаг байхгүй үед (жишээлбэл, шалгалт эсвэл шалгалтын үеэр) үл хамаарах зүйлийг хийж болно. Би хувьдаа интегралуудыг байнга шалгадаг бөгөөд шалгахгүй байгаа нь хакердсан ажил, муу гүйцэтгэсэн ажил гэж үздэг. Жишээ 3 Тодорхой бус интегралыг ол: Шийдэл: Интегралд дүн шинжилгээ хийхдээ бид интеграл дор хоёр функцын үржвэр, тэр ч байтугай бүхэл илэрхийллийн экспонентацийг олж харлаа. Харамсалтай нь салшгүй тулааны талбарт Үгүйсайн, тав тухтай бүтээгдэхүүн болон коэффициентийг нэгтгэх томъёозэрэг: Тиймээс, үржвэр эсвэл коэффициентийг өгөхдөө интегралыг нийлбэр болгон хувиргах боломжтой эсэхийг үргэлж харах нь утга учиртай юу? Энэ нь боломжтой тохиолдолд авч үзэх жишээ юм. Эхлээд бид бүрэн шийдлийг танилцуулах болно, тайлбарууд доор байх болно. (1) Бид аливаа бодит тоонуудад нийлбэрийн квадратын хуучин сайн томьёог ашиглаж, нийтлэг хаалт дээрх зэрэглэлийг арилгадаг. хаалтны гадна талд, товчилсон үржүүлэх томъёог эсрэг чиглэлд хэрэглэх: . Жишээ 4 Тодорхой бус интегралыг ол Шалгалт хийх. Энэ бол та өөрөө шийдэх жишээ юм. Хариулт, бүрэн шийдэл нь хичээлийн төгсгөлд байна. Жишээ 5 Тодорхой бус интегралыг ол Энэ жишээнд интеграл нь бутархай юм. Интеграл дахь бутархайг харахад хамгийн түрүүнд "Энэ бутархайг ямар нэгэн байдлаар арилгах эсвэл ядаж хялбарчлах боломжтой юу?" Гэсэн асуулт байх ёстой. Бид хуваагч нь "X"-ийн нэг язгуурыг агуулж байгааг анзаарсан. Талбайн нэг нь дайчин биш бөгөөд энэ нь бид тоологчийг хуваагч нэр томъёогоор хувааж болно гэсэн үг юм: Функцийн деривативын тухай нийтлэлд олон удаа хэлэлцсэн тул бид бутархайн эрх бүхий үйлдлийн талаар тайлбар хийдэггүй. Хэрэв та ийм жишээнд эргэлзсээр байвал ямар ч тохиолдолд зөв хариулт гарахгүй, Шийдэлд нэг алхам дутуу байгааг анхаарна уу, тухайлбал дүрмийг хэрэгжүүлэх Жишээ 6 Тодорхойгүй интегралыг ол. Шалгалт хийх. Энэ бол та өөрөө шийдэх жишээ юм. Хариулт, бүрэн шийдэл нь хичээлийн төгсгөлд байна. Ерөнхийдөө интеграл дахь бутархайн хувьд бүх зүйл тийм ч хялбар биш бөгөөд зарим төрлийн бутархай интегралын талаархи нэмэлт материалыг нийтлэлээс олж болно. Зарим бутархайг нэгтгэх. Гэхдээ дээрх нийтлэл рүү шилжихээсээ өмнө та хичээлтэй танилцах хэрэгтэй. Тодорхой бус интегралд орлуулах арга. Гол нь функцийг дифференциал эсвэл хувьсагчийг орлуулах аргын дор оруулах нь чухал юм гол цэгЭнэ сэдвийг судлахдаа энэ нь зөвхөн "орлуулах аргын талаархи цэвэр даалгавар" төдийгүй бусад олон төрлийн интегралуудаас олддог. Шийдэл ба хариултууд:
Жишээ 2: Шийдэл: Жишээ 4: Шийдэл: Энэ жишээнд бид үржүүлэх товчилсон томъёог ашигласан
Жишээ 6: Шийдэл: Тодорхой бус интеграл дахь хувьсагчийг өөрчлөх арга. Шийдлийн жишээ Энэ хичээлээр бид тодорхойгүй интегралыг шийдвэрлэхэд ашигладаг хамгийн чухал бөгөөд хамгийн түгээмэл аргуудын нэг болох хувьсагчийг өөрчлөх аргатай танилцах болно. Материалыг амжилттай эзэмшихийн тулд анхны мэдлэг, нэгтгэх чадварыг шаарддаг. Хэрэв та интеграл тооцоонд хоосон, дүүрэн данх мэт санагдаж байвал эхлээд материалтай танилцах хэрэгтэй. Тодорхой бус интеграл. Шийдлийн жишээ, интеграл гэж юу болохыг хүртээмжтэй хэлбэрээр тайлбарлаж, эхлэгчдэд зориулсан үндсэн жишээг нарийвчлан шинжлэх болно. Техникийн хувьд тодорхойгүй интеграл дахь хувьсагчийг өөрчлөх аргыг хоёр аргаар хэрэгжүүлдэг. – Функцийг дифференциал тэмдгийн доор оруулах. – Үнэн хэрэгтээ хувьсагчийг өөрчилж байна. Үндсэндээ эдгээр нь ижил зүйл боловч шийдлийн загвар нь өөр өөр харагдаж байна. Илүү энгийн тохиолдлоор эхэлцгээе.
- бүрэн өсөлт гэж нэрлэдэг
, (1) хэлбэрээр танилцуулсан
().
Функцийн өсөлтийг зөвхөн f(x) функцийн тодорхойлолтын мужид + хамаарагдах тохиолдолд авч үзэх ёстой.. Дараа нь
Томъёо
Шийдлийн жишээ
Жишээ 1
$ z (x,y) = x^2 - y^2 + 4xy + 10 $ эхний эрэмбийн хэсэгчилсэн деривативуудыг ол.
Шийдэл
Хариулт
$$ z"_x = 2x+4y; z"_y = -2y+4x $$
Жишээ 2
$ z = e^(xy) $ 2-р эрэмбийн функцийн хэсэгчилсэн деривативуудыг ол
Шийдэл
Хариулт
$$ z"_x = ye^(xy); z"_y = xe^(xy); z""_(xy) = yxe^(xy) $$
Жишээ 4
$ 3x^3z - 2z^2 + 3yz^2-4x+z-5 = 0 $ $ F(x,y,z) = 0 $ далд функцийг тодорхойл. Эхний эрэмбийн хэсэгчилсэн деривативуудыг ол.
Шийдэл
Хариулт
$$ z"_x = 3x^2 z - 4; z"_y = 3z^2; $$
Эцсийн эцэст, гурван хувьсагчийн функц нь бүх зүйл дөрвөн хэмжээст орон зайд (үнэхээр дөрвөн хувьсагч байдаг) явагддаг гэдгийг харуулж байна. Гурван хувьсагчийн функцийн графикийг гэж нэрлэдэг хэт гадаргуу. Бид гурван хэмжээст орон зайд (урт/өргөн/өндөр) амьдардаг тул үүнийг төсөөлөхийн аргагүй юм. Та надаас уйдахгүйн тулд би асуулт хариултыг санал болгож байна. Би хэд хэдэн асуулт асуух бөгөөд сонирхсон хүн бүр эдгээр асуултад хариулахыг оролдож болно:
Тийм / Үгүй (шинжлэх ухаан үүнийг хориглодог) / Шинжлэх ухаан үүнийг хориглодоггүй / Би мэдэхгүй
эсвэл – “y”-д хамаарах хэсэгчилсэн дериватив;
эсвэл – “zet”-ийн хэсэгчилсэн дериватив.
эсвэл та дараах байдлаар бичиж болно.
– та нэгдүгээр эрэмбийн хэсэгчилсэн деривативуудыг олох хэрэгтэй;
- та цэг дээр 1-р эрэмбийн хэсэгчилсэн деривативын утгыг тооцоолох хэрэгтэй.
.
.
.
. Юу болсон бэ? Бэлгэдлийн тэмдэглэгээ нь олон анхдагч функц болон хувирсан.Интеграл яагаад болж хувирдагийг ойлгох шаардлагагүй. Та энэ болон бусад томъёог энгийн зүйл гэж үзэж болно. Хүн бүр цахилгаан хэрэглэдэг боловч электронууд утсаар хэрхэн дамждаг талаар цөөхөн хүн боддог. .
- тогтмол Cинтеграл тэмдгээс гаргаж авч болно (мөн байх ёстой).
– хоёр функцийн нийлбэрийн (ялгаа) интеграл нь хоёр интегралын нийлбэр (ялгаа)тай тэнцүү байна. Энэ дүрэм нь хэд хэдэн нэр томъёонд хүчинтэй байна.
. Бид дифференциал дүрсийг бичихээ мартдаг dxинтеграл бүрийн доор. Яагаад тус бүрийн доор? dx– энэ бол бүрэн үржүүлэгч юм.Хэрэв бид үүнийг нарийвчлан тайлбарлавал эхний алхамыг дараах байдлаар бичих хэрэгтэй.
.бид бүх тогтмолуудыг интегралын тэмдгүүдийн цаана шилжүүлдэг. Сүүлийн үед гэдгийг анхаарна уу тг 5 нь тогтмол, бид үүнийг бас гаргадаг.
, Мөн
.
.
.
.
. Шалгалт хийх.
эсвэл 
.
. Шалгалт хийх.
, . Ихэвчлэн интегралыг шийдвэрлэх зарим туршлагатай бол эдгээр дүрмийг тодорхой баримт гэж үздэг бөгөөд үүнийг нарийвчлан тайлбарладаггүй.
