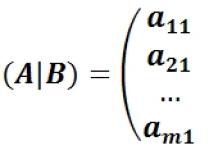Шугаман тэгшитгэлийн системийн жишээ. Шугаман тэгшитгэлийн системүүд

Системүүд мшугаман тэгшитгэлүүд nүл мэдэгдэх.
Шугаман тэгшитгэлийн системийг шийдвэрлэх- энэ бол ийм тооны багц юм ( x 1 , x 2 , …, x n), системийн тэгшитгэл тус бүрийг орлуулах үед зөв тэгшитгэлийг олж авна.
Хаана a ij , i = 1, …, m; j = 1, …, n- системийн коэффициент;
b i , i = 1, …, m- чөлөөт гишүүд;
x j , j = 1, …, n- үл мэдэгдэх.
Дээрх системийг матриц хэлбэрээр бичиж болно: A X = B,

Хаана ( А|Б) нь системийн үндсэн матриц;
А- өргөтгөсөн системийн матриц;
X- үл мэдэгдэх багана;
Б- чөлөөт гишүүдийн багана.
Хэрэв матриц Бтэг матриц ∅ биш бол энэ шугаман тэгшитгэлийн системийг нэгэн төрлийн бус гэж нэрлэдэг.
Хэрэв матриц Б= ∅ бол энэ шугаман тэгшитгэлийн системийг нэгэн төрлийн гэж нэрлэдэг. Нэг төрлийн системд үргэлж тэг (жижиг) шийдэл байдаг: x 1 = x 2 = …, x n = 0.
Шугаман тэгшитгэлийн хамтарсан системшийдэлтэй шугаман тэгшитгэлийн систем юм.
Шугаман тэгшитгэлийн үл нийцэх системнь шийдэгдээгүй шугаман тэгшитгэлийн систем юм.
Шугаман тэгшитгэлийн тодорхой системөвөрмөц шийдэлтэй шугаман тэгшитгэлийн систем юм.
Шугаман тэгшитгэлийн тодорхой бус системнь хязгааргүй тооны шийдтэй шугаман тэгшитгэлийн систем юм.
n үл мэдэгдэх n шугаман тэгшитгэлийн системүүд
Хэрэв үл мэдэгдэх тоо нь тэгшитгэлийн тоотой тэнцүү бол матриц нь квадрат болно. Матрицын тодорхойлогчийг шугаман тэгшитгэлийн системийн үндсэн тодорхойлогч гэж нэрлэдэг бөгөөд Δ тэмдгээр тэмдэглэнэ.
Крамер аргасистемийг шийдвэрлэхэд зориулагдсан nшугаман тэгшитгэлүүд nүл мэдэгдэх.
Крамерын дүрэм.
Хэрэв шугаман тэгшитгэлийн системийн гол тодорхойлогч нь тэгтэй тэнцүү биш бол систем нь тууштай, тодорхойлогддог бөгөөд цорын ганц шийдлийг Крамерын томъёогоор тооцоолно.
Энд Δ i нь системийн үндсэн тодорхойлогчоос Δ солих замаар олж авсан тодорхойлогч юм. би th баганаас чөлөөт гишүүдийн баганад. .
n үл мэдэгдэх m шугаман тэгшитгэлийн системүүд
Кронекер-Капелли теорем.

Өгөгдсөн шугаман тэгшитгэлийн систем тууштай байхын тулд системийн матрицын зэрэг нь системийн өргөтгөсөн матрицын зэрэгтэй тэнцүү байх шаардлагатай бөгөөд хангалттай. дуугарав(Α) = дуугарлаа(Α|B).
Хэрэв дуугарав(Α) ≠ дуугарав(Α|B), тэгвэл системд шийдэл байхгүй нь ойлгомжтой.
Хэрэв дуугарав(Α) = дуугарлаа(Α|B), дараа нь хоёр тохиолдол боломжтой:
1) зэрэглэл(Α) = n(үл мэдэгдэх тоо) - шийдэл нь өвөрмөц бөгөөд Крамерын томъёог ашиглан олж авах боломжтой;
2) зэрэглэл(Α)< n - Хязгааргүй олон шийдэл байдаг.
Гауссын аргашугаман тэгшитгэлийн системийг шийдвэрлэхэд зориулагдсан

Өргөтгөсөн матриц үүсгэцгээе ( А|Б) тодорхойгүй ба баруун талын коэффициентуудаас өгөгдсөн системийн.
Гауссын арга буюу үл мэдэгдэх зүйлийг арилгах арга нь өргөтгөсөн матрицыг багасгахаас бүрдэнэ. А|Б) эгнээнээсээ диагональ хэлбэрт (дээд гурвалжин хэлбэрт) энгийн хувиргалтыг ашиглана. Тэгшитгэлийн систем рүү буцаж ирэхэд бүх үл мэдэгдэх зүйл тодорхойлогддог.
Мөр дээрх үндсэн хувиргалтуудад дараахь зүйлс орно.
1) хоёр мөрийг солих;
2) мөрийг 0-ээс өөр тоогоор үржүүлэх;
3) өөр тэмдэгт мөрийг дурын тоогоор үржүүлсэн мөрөнд нэмэх;
4) тэг шугамыг хаях.
Диагональ хэлбэрт шилжүүлсэн өргөтгөсөн матриц нь өгөгдсөнтэй тэнцэх шугаман системтэй тохирч, шийдэл нь хүндрэл учруулдаггүй. .
Нэг төрлийн шугаман тэгшитгэлийн систем.
Нэг төрлийн систем нь дараахь хэлбэртэй байна.

энэ нь матрицын тэгшитгэлтэй тохирч байна A X = 0.
1) Нэг төрлийн систем үргэлж тууштай байдаг, учир нь r(A) = r(A|B), үргэлж тэг шийдэл байдаг (0, 0, …, 0).
2) Нэг төрлийн систем тэгээс өөр шийдэлтэй байхын тулд шаардлагатай бөгөөд хангалттай. r = r(A)< n Δ = 0-тэй тэнцүү байна.
3) Хэрэв r< n , тэгвэл мэдээж Δ = 0, тэгвэл чөлөөт үл мэдэгдэх зүйлс үүснэ c 1 , c 2 , …, c n-r, систем нь өчүүхэн бус шийдлүүдтэй бөгөөд тэдгээр нь хязгааргүй олон байдаг.
4) Ерөнхий шийдэл Xцагт r< n матриц хэлбэрээр дараах байдлаар бичиж болно.
X = c 1 X 1 + c 2 X 2 + … + c n-r X n-r,
шийдэл хаана байна X 1, X 2, …, X n-rшийдлийн үндсэн системийг бүрдүүлнэ.
5) Уусмалын үндсэн системийг нэгэн төрлийн системийн ерөнхий шийдлээс гаргаж авч болно.

,
хэрэв бид параметрийн утгуудыг (1, 0, …, 0), (0, 1, …, 0), …, (0, 0, …, 1)-тэй тэнцүүлэх юм бол.
Шийдлийн үндсэн системийн хувьд ерөнхий шийдлийг өргөжүүлэхүндсэн системд хамаарах шийдлүүдийн шугаман хослол хэлбэрийн ерөнхий шийдлийн бичлэг юм.
Теорем. Шугаман нэгэн төрлийн тэгшитгэлийн систем тэгээс өөр шийдэлтэй байхын тулд Δ ≠ 0 байх шаардлагатай бөгөөд хангалттай.
Тэгэхээр тодорхойлогч Δ ≠ 0 бол систем нь өвөрмөц шийдэлтэй байна.
Хэрэв Δ ≠ 0 бол шугаман нэгэн төрлийн тэгшитгэлийн систем хязгааргүй тооны шийдтэй байна.
Теорем. Нэг төрлийн систем тэгээс өөр шийдэлтэй байхын тулд энэ нь зайлшгүй бөгөөд хангалттай юм r(A)< n .
Баталгаа:
1) rилүү байж болохгүй n(матрицын зэрэглэл нь багана, мөрийн тооноос хэтрэхгүй);
2) r< n , учир нь Хэрэв r = n, дараа нь системийн гол тодорхойлогч Δ ≠ 0 бөгөөд Крамерын томъёоны дагуу өвөрмөц өчүүхэн шийдэл байдаг. x 1 = x 2 = … = x n = 0, энэ нь нөхцөлтэй зөрчилдөж байна. гэсэн үг, r(A)< n .
Үр дагавар. Нэг төрлийн системийг бий болгохын тулд nшугаман тэгшитгэлүүд nүл мэдэгдэх нь тэгээс өөр шийдэлтэй байсан тул Δ = 0 байх шаардлагатай бөгөөд хангалттай.

Шийдэл. A= . r(A)-г олъё. Учир нь матрицМөн 3х4 дараалалтай, дараа нь насанд хүрээгүй хүүхдүүдийн хамгийн дээд эрэмб нь 3 байна. Түүнээс гадна, бүх гуравдугаар зэрэглэлийн насанд хүрээгүй хүүхдүүд тэгтэй тэнцүү байна (өөрийгөө шалгаарай). гэсэн үг, r(A)< 3. Возьмем главный үндсэн бага = -5-4 = -9 ≠ 0. Иймд r(A) =2.

Ингээд авч үзье матриц ХАМТ = .

Бага гурав дахь захиалга ≠ 0. Тэгэхээр r(C) = 3 байна.

r(A)-аас хойш ≠ r(C) , тэгвэл систем нь нийцэхгүй байна.

Жишээ 2.Тэгшитгэлийн системийн нийцтэй байдлыг тодорхойлох

Хэрэв энэ систем тогтвортой байвал шийднэ үү.

Шийдэл.

A =, C = . r(A) ≤ 3, r(C) ≤ 4 гэдэг нь ойлгомжтой. detC = 0 тул r(C) болно.< 4. Ингээд авч үзье бага гурав дахь захиалга, А ба С матрицын зүүн дээд буланд байрладаг: = -23 ≠ 0. Тэгэхээр r(A) = r(C) = 3 байна.

Тоо үл мэдэгдэх системд n=3. Энэ нь систем нь өвөрмөц шийдэлтэй гэсэн үг юм. Энэ тохиолдолд дөрөв дэх тэгшитгэл нь эхний гурвын нийлбэрийг илэрхийлэх бөгөөд үүнийг үл тоомсорлож болно.

Крамерын томъёоны дагуубид x 1 = -98/23, x 2 = -47/23, x 3 = -123/23 болно.

2.4. Матрицын арга. Гауссын арга

систем nшугаман тэгшитгэл-тай nүл мэдэгдэх асуудлыг шийдэж болно матрицын аргатомъёоны дагуу X = A -1 B (Δ үед ≠ 0), энэ нь (2)-аас хоёр хэсгийг A -1-ээр үржүүлснээр гарна.

Жишээ 1. Тэгшитгэлийн системийг шийд

матрицын арга (2.2-р хэсэгт энэ системийг Крамерын томъёогоор шийдсэн)

Шийдэл. Δ = 10 ≠ 0 A = - доройтдоггүй матриц.

= (шаардлагатай тооцоог хийх замаар үүнийг өөрөө шалгана уу).

A -1 = (1/Δ)х= .

X = A -1 V = x= .

Хариулах: .

Практик талаас нь авч үзвэлматрицын арга ба томъёо Крамерих хэмжээний тооцоололтой холбоотой тул давуу эрх олгодог Гауссын арга, энэ нь үл мэдэгдэх зүйлсийг дараалан арилгахаас бүрддэг. Үүнийг хийхийн тулд тэгшитгэлийн системийг гурвалжин өргөтгөсөн матриц бүхий эквивалент систем болгон бууруулсан (үндсэн диагональаас доош байгаа бүх элементүүд тэгтэй тэнцүү). Эдгээр үйлдлийг урагшлах хөдөлгөөн гэж нэрлэдэг. Үүссэн гурвалжин системээс хувьсагчдыг дараалсан орлуулалтыг (урвуу) ашиглан олно.

Жишээ 2. Гауссын аргыг ашиглан системийг шийд

(Дээрх нь энэ системийг Крамерын томъёо болон матрицын аргыг ашиглан шийдсэн).

Шийдэл.

Шууд шилжих. Өргөтгөсөн матрицыг бичиж, энгийн хувиргалтуудыг ашиглан гурвалжин хэлбэрт оруулцгаая.

~ ~ ~ ~ .

Бид авдаг систем

Урвуу хөдөлгөөн.Сүүлийн тэгшитгэлээс бид олдог X 3 = -6 ба энэ утгыг хоёр дахь тэгшитгэлд орлуулна уу:

X 2 = - 11/2 - 1/4X 3 = - 11/2 - 1/4(-6) = - 11/2 + 3/2 = -8/2 = -4.

X 1 = 2 -X 2 + X 3 = 2+4-6 = 0.

Хариулах: .

2.5. Шугаман тэгшитгэлийн системийн ерөнхий шийдэл

Шугаман тэгшитгэлийн системийг өгье = б би(би=). r(A) = r(C) = r, i.e. систем нь хамтын ажиллагаа юм. r-ийн тэгээс бусад бага зэрэг нь үндсэн бага.Ерөнхий байдлыг алдалгүйгээр бид суурь минор нь А матрицын эхний r (1 ≤ r ≤ min(m,n)) мөр, баганад байрлана гэж үзнэ. Системийн сүүлчийн m-r тэгшитгэлийг хасаад бид a бичнэ. богиносгосон систем:

Энэ нь анхныхтай тэнцүү юм. Үл мэдэгдэх хүмүүсийг нэрлэе x 1 ,….x rүндсэн, ба x r +1 ,…, x rчөлөөтэй ба чөлөөт үл мэдэгдэх нэр томъёог таслагдсан системийн тэгшитгэлийн баруун талд шилжүүлнэ. Бид үндсэн үл мэдэгдэх системийг олж авдаг.

чөлөөт үл мэдэгдэх утгын багц бүрийн хувьд x r +1 = С 1 ,…, x n = С n-rганцхан шийдэлтэй x 1 (C 1 ,…, C n-r),…, x r (C 1 ,…, C n-r),Крамерын дүрмээр олдсон.

Холбогдох шийдэлбогиносгосон тул анхны систем нь дараах хэлбэртэй байна.

X(C 1 ,…, C n-r) = - системийн ерөнхий шийдэл.

Хэрэв бид ерөнхий шийдэлд чөлөөт үл мэдэгдэх тоон утгыг оноож өгвөл хэсэгчилсэн шийдэл гэж нэрлэгддэг шугаман системийн шийдлийг олж авна.

Жишээ. Тохиромжтой байдлыг бий болгож, системийн ерөнхий шийдлийг олох

Шийдэл. A = , C = .

Тэгэхээр Хэрхэн r(A)= r(C) = 2 (үүнийг өөрөө харна уу), тэгвэл анхны систем нь тууштай бөгөөд хязгааргүй тооны шийдэлтэй (r-ээс хойш)< 4).

Тэгшитгэлийн системийн хоёр төрлийн шийдлийг шинжлэхийг үзье.

1. Орлуулах аргыг ашиглан системийг шийдвэрлэх.
2. Системийн тэгшитгэлийг гишүүнээр нь нэмэх (хасах) аргаар системийг шийдвэрлэх.

Тэгшитгэлийн системийг шийдэхийн тулд орлуулах аргаарТа энгийн алгоритмыг дагах хэрэгтэй:
1. Экспресс. Аливаа тэгшитгэлээс бид нэг хувьсагчийг илэрхийлдэг.
2. Орлуулах. Бид гарсан утгыг илэрхийлсэн хувьсагчийн оронд өөр тэгшитгэлд орлуулна.
3. Үүссэн тэгшитгэлийг нэг хувьсагчтай шийд. Бид системийн шийдлийг олдог.

Шийдэхийн тулд системхэрэгтэй:
1. Бид ижил коэффициент гаргах хувьсагчийг сонго.
2. Бид тэгшитгэлийг нэмэх буюу хасахын үр дүнд нэг хувьсагчтай тэгшитгэл үүсдэг.
3. Үүссэн шугаман тэгшитгэлийг шийд. Бид системийн шийдлийг олдог.

Системийн шийдэл нь функцийн графикуудын огтлолцох цэгүүд юм.

Жишээнүүдийг ашиглан системийн шийдлийг нарийвчлан авч үзье.

Жишээ №1:

Орлуулах аргаар шийдье

Орлуулах аргыг ашиглан тэгшитгэлийн системийг шийдвэрлэх

2x+5y=1 (1 тэгшитгэл)
x-10y=3 (2-р тэгшитгэл)

1. Экспресс
Хоёр дахь тэгшитгэлд 1 коэффициенттэй х хувьсагч байгааг харж болно, энэ нь хоёр дахь тэгшитгэлээс х хувьсагчийг илэрхийлэхэд хамгийн хялбар гэсэн үг юм.
x=3+10y

2.Бид үүнийг илэрхийлсний дараа эхний тэгшитгэлд х хувьсагчийн оронд 3+10y-г орлуулна.
2(3+10y)+5y=1

3. Үүссэн тэгшитгэлийг нэг хувьсагчтай шийд.
2(3+10y)+5y=1 (хаалт нээх)
6+20ж+5у=1
25 нас=1-6
25y=-5 |: (25)
у=-5:25
y=-0.2

Тэгшитгэлийн системийн шийдэл нь графикуудын огтлолцлын цэгүүд тул огтлолцох цэг нь х ба у-аас бүрдэх тул х ба у-г олох хэрэгтэй.Х-ийг олъё, үүнийг илэрхийлсэн эхний цэг дээр y-г орлуулна.
x=3+10y
x=3+10*(-0.2)=1

Нэгдүгээрт бид x хувьсагч, хоёрдугаарт у хувьсагчийг бичдэг цэгүүдийг бичдэг заншилтай.
Хариулт: (1; -0.2)

Жишээ №2:

Нэр томьёогоор нэмэх (хасах) аргыг ашиглан шийдье.

Нэмэх аргыг ашиглан тэгшитгэлийн системийг шийдвэрлэх

3x-2y=1 (1 тэгшитгэл)
2x-3y=-10 (2-р тэгшитгэл)

1. Бид хувьсагчийг сонгосон, x-г сонгосон гэж бодъё. Эхний тэгшитгэлд х хувьсагч нь 3 коэффициенттэй, хоёр дахь нь - 2. Бид коэффициентүүдийг ижил болгох хэрэгтэй, үүний тулд бид тэгшитгэлийг үржүүлэх эсвэл дурын тоогоор хуваах эрхтэй. Бид эхний тэгшитгэлийг 2-оор, хоёр дахь нь 3-аар үржүүлж, нийт 6 коэффициентийг авна.

3x-2y=1 |*2
6х-4у=2

2х-3у=-10 |*3
6х-9у=-30

2. Эхний тэгшитгэлээс хоёр дахьыг хасаад х хувьсагчаас сална Шугаман тэгшитгэлийг шийд.
__6x-4y=2

5у=32 | :5
y=6.4

3. х-г ол. Бид олсон y-г аль нэг тэгшитгэлд орлуулж, эхний тэгшитгэлд оруулъя.
3х-2у=1
3х-2*6.4=1
3х-12.8=1
3х=1+12.8
3x=13.8 |:3
x=4.6

Уулзвар цэг нь x=4.6; y=6.4
Хариулт: (4.6; 6.4)

Та шалгалтандаа үнэ төлбөргүй бэлдмээр байна уу? Онлайн багш үнэгүй. Тоглоомгүй.

Шугаман алгебрийн тэгшитгэлийн системийг (SLAEs) шийдвэрлэх нь шугаман алгебрийн хичээлийн хамгийн чухал сэдэв болох нь дамжиггүй. Математикийн бүх салбараас асар олон тооны асуудлууд шугаман тэгшитгэлийн системийг шийдвэрлэхэд ирдэг. Эдгээр хүчин зүйлүүд нь энэ нийтлэлийн шалтгааныг тайлбарладаг. Өгүүллийн материалыг сонгож, зохион бүтээсэн бөгөөд ингэснээр түүний тусламжтайгаар та боломжтой болно

шугаман алгебрийн тэгшитгэлийн системийг шийдэх оновчтой аргыг сонгох;
сонгосон аргын онолыг судлах,
ердийн жишээ, асуудлын нарийвчилсан шийдлүүдийг авч үзэх замаар шугаман тэгшитгэлийн системийг шийдээрэй.

Өгүүллийн материалын товч тайлбар.

Нэгдүгээрт, бид шаардлагатай бүх тодорхойлолт, ойлголтыг өгч, тэмдэглэгээг нэвтрүүлдэг.

Дараа нь тэгшитгэлийн тоо нь үл мэдэгдэх хувьсагчийн тоотой тэнцүү, өвөрмөц шийдэлтэй шугаман алгебрийн тэгшитгэлийн системийг шийдэх аргуудыг авч үзэх болно. Нэгдүгээрт, бид Крамерын аргад анхаарлаа хандуулах болно, хоёрдугаарт, ийм тэгшитгэлийн системийг шийдвэрлэх матрицын аргыг харуулах болно, гуравдугаарт, Гауссын аргыг (үл мэдэгдэх хувьсагчдыг дараалан арилгах арга) шинжлэх болно. Онолыг нэгтгэхийн тулд бид хэд хэдэн SLAE-ийг янз бүрийн аргаар шийдвэрлэх нь гарцаагүй.

Үүний дараа бид тэгшитгэлийн тоо нь үл мэдэгдэх хувьсагчдын тоотой давхцдаггүй эсвэл системийн үндсэн матриц нь дан хэлбэртэй байдаг ерөнхий хэлбэрийн шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэхэд шилжих болно. SLAE-ийн нийцтэй байдлыг тогтоох боломжийг олгодог Кронекер-Капелли теоремыг томъёолъё. Матрицын минор суурь гэсэн ойлголтыг ашиглан системийн шийдлийг (хэрэв тэдгээр нь нийцтэй бол) дүн шинжилгээ хийцгээе. Бид мөн Гауссын аргыг авч үзэж, жишээнүүдийн шийдлүүдийг нарийвчлан тайлбарлах болно.

Шугаман алгебрийн тэгшитгэлийн нэгэн төрлийн ба нэгэн төрлийн бус системийн ерөнхий шийдлийн бүтцэд бид заавал анхаарлаа хандуулах болно. Шийдлийн үндсэн системийн тухай ойлголтыг өгч, шийдлийн үндсэн системийн векторуудыг ашиглан SLAE-ийн ерөнхий шийдийг хэрхэн бичихийг харуулъя. Илүү сайн ойлгохын тулд хэд хэдэн жишээг харцгаая.

Дүгнэж хэлэхэд бид шугаман болгон бууруулж болох тэгшитгэлийн системүүд, түүнчлэн шийдвэрлэхэд нь SLAE үүсдэг янз бүрийн асуудлуудыг авч үзэх болно.

Хуудасны навигаци.

Тодорхойлолт, ойлголт, тэмдэглэгээ.

Бид хэлбэрийн үл мэдэгдэх n хувьсагчтай (p нь n-тэй тэнцүү байж болно) p шугаман алгебрийн тэгшитгэлийн системийг авч үзэх болно.

Үл мэдэгдэх хувьсагч, - коэффициент (зарим бодит эсвэл нийлмэл тоо), - чөлөөт нэр томъёо (мөн бодит эсвэл нийлмэл тоо).

SLAE бичлэгийн энэ хэлбэрийг нэрлэдэг зохицуулах.

IN матриц хэлбэрЭнэ тэгшитгэлийн системийг бичих нь дараах хэлбэртэй байна.
Хаана - системийн үндсэн матриц, - үл мэдэгдэх хувьсагчийн баганын матриц, - чөлөөт нэр томъёоны баганын матриц.

Хэрэв бид чөлөөт нөхцлүүдийн матриц баганыг А матрицад (n+1)-р багана болгон нэмбэл бид ийм зүйлийг авна. өргөтгөсөн матрицшугаман тэгшитгэлийн системүүд. Ихэвчлэн өргөтгөсөн матрицыг T үсгээр тэмдэглэдэг бөгөөд чөлөөт нэр томъёоны баганыг үлдсэн баганаас босоо шугамаар тусгаарладаг, өөрөөр хэлбэл,

Шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэхсистемийн бүх тэгшитгэлийг таних тэмдэг болгон хувиргадаг үл мэдэгдэх хувьсагчдын утгуудын багц гэж нэрлэдэг. Үл мэдэгдэх хувьсагчдын өгөгдсөн утгуудын матрицын тэгшитгэл нь мөн адил болно.

Хэрэв тэгшитгэлийн систем дор хаяж нэг шийдэлтэй бол түүнийг дуудна хамтарсан.

Хэрэв тэгшитгэлийн систем шийдэлгүй бол түүнийг дуудна хамтарсан бус.

Хэрэв SLAE нь өвөрмөц шийдэлтэй бол түүнийг дуудна тодорхой; Хэрэв нэгээс олон шийдэл байгаа бол - тодорхойгүй.

Хэрэв системийн бүх тэгшитгэлийн чөлөөт гишүүд тэгтэй тэнцүү бол , дараа нь системийг дуудна нэгэн төрлийн, эс бөгөөс - гетероген.

Шугаман алгебрийн тэгшитгэлийн анхан шатны системийг шийдвэрлэх.

Хэрэв системийн тэгшитгэлийн тоо нь үл мэдэгдэх хувьсагчдын тоотой тэнцүү бөгөөд түүний үндсэн матрицын тодорхойлогч нь тэгтэй тэнцүү биш бол ийм SLAE-г нэрлэнэ. анхан шатны. Ийм тэгшитгэлийн системүүд нь өвөрмөц шийдэлтэй байдаг ба нэгэн төрлийн системийн хувьд үл мэдэгдэх бүх хувьсагч нь тэгтэй тэнцүү байна.

Бид ахлах сургуульд байхдаа ийм SLAE-г судалж эхэлсэн. Тэдгээрийг шийдвэрлэхдээ бид нэг тэгшитгэл авч, нэг үл мэдэгдэх хувьсагчийг бусдаар нь илэрхийлж, үлдсэн тэгшитгэлд орлуулж, дараа нь дараагийн тэгшитгэлийг авч, дараагийн үл мэдэгдэх хувьсагчийг илэрхийлж, өөр тэгшитгэлд орлуулах гэх мэт. Эсвэл тэд нэмэх аргыг ашигласан, өөрөөр хэлбэл зарим үл мэдэгдэх хувьсагчдыг арилгахын тулд хоёр ба түүнээс дээш тэгшитгэл нэмсэн. Эдгээр аргууд нь үндсэндээ Гауссын аргын өөрчлөлтүүд учраас бид тэдгээрийн талаар дэлгэрэнгүй ярихгүй.

Шугаман тэгшитгэлийн энгийн системийг шийдвэрлэх үндсэн аргууд нь Крамерын арга, матрицын арга, Гауссын арга юм. Тэднийг цэгцэлье.

Крамерын аргыг ашиглан шугаман тэгшитгэлийн системийг шийдвэрлэх.

Шугаман алгебрийн тэгшитгэлийн системийг шийдэх хэрэгтэй гэж бодъё

тэгшитгэлийн тоо нь үл мэдэгдэх хувьсагчдын тоотой тэнцүү байх ба системийн үндсэн матрицын тодорхойлогч нь тэгээс ялгаатай, өөрөөр хэлбэл, .

Системийн үндсэн матрицын тодорхойлогч байг, ба - орлуулах замаар А-аас олж авсан матрицын тодорхойлогч 1, 2, …, nthбагана нь чөлөөт гишүүдийн баганад:

Энэхүү тэмдэглэгээний тусламжтайгаар үл мэдэгдэх хувьсагчдыг Крамерын аргын томъёог ашиглан тооцдог . Крамерын аргыг ашиглан шугаман алгебрийн тэгшитгэлийн системийн шийдийг ингэж олдог.

Жишээ.

Крамерын арга .

Шийдэл.

Системийн үндсэн матриц нь хэлбэртэй байна . Тодорхойлогчийг тооцоолъё (шаардлагатай бол нийтлэлийг үзнэ үү):

Системийн үндсэн матрицын тодорхойлогч нь тэгээс ялгаатай тул систем нь Крамерын аргаар олох боломжтой өвөрмөц шийдэлтэй байдаг.

Шаардлагатай тодорхойлогчдыг бүрдүүлж, тооцоолъё (бид А матрицын эхний баганыг чөлөөт нөхцлийн баганаар, тодорхойлогчийг хоёр дахь баганыг чөлөөт нөхцлийн баганаар, А матрицын гурав дахь баганыг чөлөөт нөхцлийн баганаар солих замаар тодорхойлогчийг авна) :

Томъёо ашиглан үл мэдэгдэх хувьсагчдыг олох :

Хариулт:

Крамерын аргын гол сул тал (хэрэв үүнийг сул тал гэж нэрлэж болох юм бол) систем дэх тэгшитгэлийн тоо гурваас дээш байх үед тодорхойлогчийг тооцоолоход төвөгтэй байдаг.

Шугаман алгебрийн тэгшитгэлийн системийг матрицын аргаар шийдвэрлэх (урвуу матриц ашиглан).

Шугаман алгебрийн тэгшитгэлийн системийг матриц хэлбэрээр өгье, үүнд А матриц нь n-ээс n хэмжээтэй, тодорхойлогч нь тэгээс өөр байна.

А матриц нь урвуу байдаг тул урвуу матриц байдаг. Хэрэв тэгш байдлын хоёр талыг зүүн тийш үржүүлбэл үл мэдэгдэх хувьсагчийн матриц-баганыг олох томьёо гарна. Матрицын аргыг ашиглан шугаман алгебрийн тэгшитгэлийн системийн шийдлийг ингэж олж авсан юм.

Жишээ.

Шугаман тэгшитгэлийн системийг шийд матрицын арга.

Шийдэл.

Тэгшитгэлийн системийг матриц хэлбэрээр дахин бичье.

Учир нь

дараа нь SLAE-ийг матрицын аргыг ашиглан шийдэж болно. Урвуу матрицыг ашиглан энэ системийн шийдлийг дараах байдлаар олж болно .

А матрицын элементүүдийн алгебрийн нэмэлтүүдээс матрицыг ашиглан урвуу матрицыг байгуулъя (шаардлагатай бол өгүүллийг үзнэ үү):

Урвуу матрицыг үржүүлэх замаар үл мэдэгдэх хувьсагчдын матрицыг тооцоолоход л үлддэг чөлөөт гишүүдийн матриц баганад (шаардлагатай бол нийтлэлийг үзнэ үү):

Хариулт:

эсвэл өөр тэмдэглэгээнд x 1 = 4, x 2 = 0, x 3 = -1.

Матрицын аргыг ашиглан шугаман алгебрийн тэгшитгэлийн системийн шийдлийг олоход тулгардаг гол асуудал бол урвуу матрицыг олоход төвөгтэй байдаг, ялангуяа 3-аас дээш дарааллын квадрат матрицын хувьд.

Гауссын аргыг ашиглан шугаман тэгшитгэлийн системийг шийдвэрлэх.

Үл мэдэгдэх n хувьсагчтай n шугаман тэгшитгэлийн системийн шийдийг олох хэрэгтэй гэж бодъё.
үндсэн матрицын тодорхойлогч нь тэгээс ялгаатай.

Гауссын аргын мөн чанарүл мэдэгдэх хувьсагчдыг дараалан хасахаас бүрдэнэ: нэгдүгээрт, x 1-ийг системийн бүх тэгшитгэлээс хоёрдугаарт, дараа нь x 2-ыг гурав дахь хэсгээс эхлэн бүх тэгшитгэлээс хасна, зөвхөн үл мэдэгдэх хувьсагч x n хүртэл. сүүлчийн тэгшитгэлд хэвээр байна. Үл мэдэгдэх хувьсагчдыг дараалан арилгахын тулд системийн тэгшитгэлийг хувиргах энэ үйл явц гэж нэрлэгддэг шууд Гауссын арга. Гауссын аргын урагш харвалт хийж дууссаны дараа сүүлчийн тэгшитгэлээс x n-ийг олж, эцсийн өмнөх тэгшитгэлийн энэ утгыг ашиглан x n-1-ийг тооцоолж, эхний тэгшитгэлээс x 1-ийг олно. Системийн сүүлчийн тэгшитгэлээс эхний тэгшитгэл рүү шилжих үед үл мэдэгдэх хувьсагчдыг тооцоолох үйл явцыг гэнэ. Гауссын аргын урвуу.

Үл мэдэгдэх хувьсагчдыг арилгах алгоритмыг товч тайлбарлая.

Системийн тэгшитгэлийг дахин цэгцлэх замаар бид үүнийг үргэлж хийж чаддаг тул бид үүнийг таамаглах болно. Хоёр дахьээс эхлэн системийн бүх тэгшитгэлээс үл мэдэгдэх хувьсагч x 1-ийг хасъя. Үүнийг хийхийн тулд системийн хоёр дахь тэгшитгэлд бид эхний тэгшитгэлийг -ээр үржүүлж, гурав дахь тэгшитгэл дээр бид эхнийхийг нэмж, үржүүлж, n-р тэгшитгэлд бид эхнийхийг нэмээд үржүүлнэ. Ийм хувиргалт хийсний дараа тэгшитгэлийн систем хэлбэр болно

хаана ба .

Хэрэв бид системийн эхний тэгшитгэлд x 1-ийг бусад үл мэдэгдэх хувьсагчдаар илэрхийлж, гарсан илэрхийллийг бусад бүх тэгшитгэлд орлуулсан бол ижил үр дүнд хүрэх байсан. Тиймээс x 1 хувьсагчийг хоёр дахь хэсгээс эхлэн бүх тэгшитгэлээс хассан болно.

Дараа нь бид ижил төстэй арга замаар явна, гэхдээ зөвхөн зураг дээр тэмдэглэгдсэн үр дүнд бий болсон системийн нэг хэсгийг л хийнэ

Үүнийг хийхийн тулд системийн гурав дахь тэгшитгэлд бид хоёр дахь тэгшитгэлээр үржүүлж, дөрөв дэх тэгшитгэл дээр бид хоёр дахь, үржүүлсэн, гэх мэт, n-р тэгшитгэлд бид хоёр дахь тэгшитгэлийг нэмж, үржүүлсэн үржвэрийг нэмнэ. Ийм хувиргалт хийсний дараа тэгшитгэлийн систем хэлбэр болно

хаана ба . Тиймээс x 2 хувьсагчийг гурав дахь хэсгээс эхлэн бүх тэгшитгэлээс хассан болно.

Дараа нь бид үл мэдэгдэх x 3-ийг арилгахын зэрэгцээ зурагт тэмдэглэсэн системийн хэсэгтэй ижил төстэй үйлдэл хийнэ.

Тиймээс бид систем хэлбэрийг авах хүртэл Гауссын аргын шууд явцыг үргэлжлүүлнэ

Энэ мөчөөс эхлэн бид Гауссын аргын урвуу аргыг эхлүүлнэ: бид хамгийн сүүлийн тэгшитгэлээс x n-ийг тооцоолж, х n-ийн олж авсан утгыг ашиглан эцсийн өмнөх тэгшитгэлээс x n-1-ийг олно, мөн эхний тэгшитгэлээс x 1-ийг олно. .

Жишээ.

Шугаман тэгшитгэлийн системийг шийд Гауссын арга.

Шийдэл.

Системийн хоёр ба гурав дахь тэгшитгэлээс үл мэдэгдэх х 1 хувьсагчийг хасъя. Үүнийг хийхийн тулд хоёр ба гурав дахь тэгшитгэлийн хоёр талд бид эхний тэгшитгэлийн харгалзах хэсгүүдийг тус тусад нь үржүүлж нэмнэ.

Одоо бид гурав дахь тэгшитгэлээс x 2-ыг хасч, түүний зүүн ба баруун талд хоёр дахь тэгшитгэлийн зүүн ба баруун талыг нэмж, дараах байдлаар үржүүлэв.

Энэ нь Гауссын аргын урагшлах цохилтыг дуусгаж, бид урвуу цохилтыг эхлүүлнэ.

Үүссэн тэгшитгэлийн системийн сүүлчийн тэгшитгэлээс бид x 3-ийг олно.

Хоёр дахь тэгшитгэлээс бид олж авна.

Эхний тэгшитгэлээс бид үл мэдэгдэх хувьсагчийг олж, улмаар Гауссын аргын урвуу үйлдлийг гүйцээнэ.

Хариулт:

X 1 = 4, x 2 = 0, x 3 = -1.

Ерөнхий хэлбэрийн шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэх.

Ерөнхийдөө p системийн тэгшитгэлийн тоо нь үл мэдэгдэх n хувьсагчийн тоотой давхцдаггүй.

Ийм SLAE нь шийдэлгүй, нэг шийдэлтэй эсвэл хязгааргүй олон шийдэлтэй байж болно. Энэхүү мэдэгдэл нь үндсэн матриц нь дөрвөлжин ба дан хэлбэртэй тэгшитгэлийн системд мөн хамаарна.

Кронекер-Капелли теорем.

Шугаман тэгшитгэлийн системийн шийдлийг олохын өмнө түүний нийцтэй байдлыг тогтоох шаардлагатай. SLAE нь хэзээ нийцдэг, хэзээ нийцэхгүй вэ гэсэн асуултын хариултыг өгсөн Кронекер-Капелли теорем:
n үл мэдэгдэх (p нь n-тэй тэнцүү байж болно) p тэгшитгэлийн систем тууштай байхын тулд системийн үндсэн матрицын зэрэглэл нь өргөтгөсөн матрицын зэрэгтэй тэнцүү байх шаардлагатай бөгөөд хангалттай юм. , Зэрэг(A)=Зэрэглэл(T).

Шугаман тэгшитгэлийн системийн нийцтэй байдлыг тодорхойлохын тулд Кронекер-Капелли теоремыг жишээ болгон авч үзье.

Жишээ.

Шугаман тэгшитгэлийн систем байгаа эсэхийг олж мэд шийдлүүд.

Шийдэл.

. Насанд хүрээгүй хүүхдүүдийг хиллэх аргыг хэрэглэцгээе. Хоёр дахь зэрэглэлийн бага тэгээс ялгаатай. Түүнтэй хиллэдэг гурав дахь зэрэглэлийн насанд хүрээгүй хүүхдүүдийг харцгаая.

Гурав дахь зэрэглэлийн бүх хил залгаа насанд хүрээгүй хүүхдүүд тэгтэй тэнцүү тул үндсэн матрицын зэрэглэл хоёртой тэнцүү байна.

Эргээд өргөтгөсөн матрицын зэрэглэл насанд хүрээгүй нь гурав дахь зэрэгтэй тул гуравтай тэнцүү байна

тэгээс ялгаатай.

Тиймээс, Rang(A), тиймээс Кронекер-Капелли теоремыг ашиглан шугаман тэгшитгэлийн анхны систем нийцэхгүй байна гэж дүгнэж болно.

Хариулт:

Системд шийдэл байхгүй.

Тиймээс бид Кронекер-Капелли теоремыг ашиглан системийн үл нийцэлийг тогтоож сурсан.

Гэхдээ SLAE-ийн нийцтэй байдал тогтоогдвол хэрхэн шийдлийг олох вэ?

Үүний тулд бидэнд матрицын минор суурь гэсэн ойлголт, матрицын зэрэглэлийн тухай теорем хэрэгтэй.

Тэгээс ялгаатай А матрицын хамгийн дээд эрэмбийн минорыг гэнэ үндсэн.

Минор суурь гэсэн тодорхойлолтоос үзэхэд түүний дараалал нь матрицын зэрэгтэй тэнцүү байна. Тэг биш А матрицын хувьд хэд хэдэн суурь минор байж болно; үргэлж нэг суурь минор байдаг.

Жишээлбэл, матрицыг авч үзье .

Энэ матрицын гурав дахь эгнээний элементүүд нь эхний болон хоёр дахь эгнээний харгалзах элементүүдийн нийлбэр учраас энэ матрицын бүх гурав дахь эрэмбийн багачууд тэгтэй тэнцүү байна.

Дараах 2-р зэрэглэлийн насанд хүрээгүй хүүхдүүд нь тэг биш тул үндсэн юм

Насанд хүрээгүй хүмүүс тэгтэй тэнцүү тул үндсэн биш.

Матрицын зэрэглэлийн теорем.

Хэрэв p-ээс n дарааллын матрицын зэрэглэл нь r-тэй тэнцүү бол матрицын сонгосон минор суурь үүсгэдэггүй бүх мөр (ба багана) элементүүдийг шугаман байдлаар харгалзах мөр (ба багана) элементүүдээр илэрхийлнэ. суурь бага.

Матрицын зэрэглэлийн теорем бидэнд юу хэлэх вэ?

Хэрэв Кронекер-Капелли теоремын дагуу бид системийн нийцтэй байдлыг тогтоосон бол системийн үндсэн матрицын аль ч бага баазыг (түүний дараалал нь r-тэй тэнцүү) сонгож, бүх тэгшитгэлийг системээс хасна. сонгосон үндэслэлийг бүрдүүлэхгүй. Ийм аргаар олж авсан SLAE нь анхныхтай тэнцүү байх болно, учир нь хасагдсан тэгшитгэлүүд илүүдэл хэвээр байна (матрицын эрэмбийн теоремын дагуу тэдгээр нь үлдсэн тэгшитгэлүүдийн шугаман хослол юм).

Үүний үр дүнд системийн шаардлагагүй тэгшитгэлийг устгасны дараа хоёр тохиолдол гарч болно.

Хэрэв үүссэн систем дэх тэгшитгэлийн тоо r нь үл мэдэгдэх хувьсагчдын тоотой тэнцүү бол энэ нь тодорхой байх бөгөөд цорын ганц шийдлийг Крамерын арга, матрицын арга эсвэл Гауссын аргаар олох боломжтой.

Жишээ.

Шийдэл.

Системийн үндсэн матрицын зэрэглэл насанд хүрээгүй нь хоёрдугаар зэрэглэлийнх тул хоёртой тэнцүү байна тэгээс ялгаатай. Өргөтгөсөн матрицын зэрэглэл Гурав дахь зэрэглэлийн цорын ганц минор нь тэг учраас мөн хоёртой тэнцүү байна

мөн дээр авч үзсэн хоёр дахь эрэмбийн минор нь тэгээс ялгаатай. Rank(A)=Rank(T)=2 тул Кронекер-Капелли теорем дээр үндэслэн бид шугаман тэгшитгэлийн анхны системийн нийцтэй байдлыг баталж чадна.

Бага зэрэг үндэслэл болгон бид авдаг . Энэ нь эхний ба хоёр дахь тэгшитгэлийн коэффициентээр үүсгэгддэг.

Системийн гурав дахь тэгшитгэл нь суурь минор үүсэхэд оролцдоггүй тул матрицын зэрэглэлийн теорем дээр үндэслэн бид үүнийг системээс хасдаг.

Ингэж бид шугаман алгебрийн тэгшитгэлийн анхан шатны системийг олж авсан. Үүнийг Крамерын аргыг ашиглан шийдье.

Хариулт:

x 1 = 1, x 2 = 2.

Хэрэв үүссэн SLAE дахь r тэгшитгэлийн тоо нь үл мэдэгдэх хувьсагчдын тоо n-ээс бага байвал тэгшитгэлийн зүүн талд бид үндсэн суурь бүрдүүлэгч нөхцлүүдийг үлдээж, үлдсэн гишүүдийг баруун тал руу шилжүүлнэ. эсрэг тэмдэгтэй системийн тэгшитгэл.

Тэгшитгэлийн зүүн талд үлдсэн үл мэдэгдэх хувьсагчдыг (тэдгээрийн r) гэж нэрлэдэг гол.

Баруун талд байгаа үл мэдэгдэх хувьсагчдыг (n - r хэсэг) гэж нэрлэдэг үнэгүй.

Үнэгүй үл мэдэгдэх хувьсагч нь дур зоргоороо утгыг авч чаддаг бол үл мэдэгдэх үндсэн r хувьсагч нь үнэгүй үл мэдэгдэх хувьсагчаар өвөрмөц байдлаар илэрхийлэгдэх болно гэж бид үзэж байна. Тэдний илэрхийлэлийг Крамерын арга, матрицын арга эсвэл Гауссын аргыг ашиглан үүссэн SLAE-ийг шийдэх замаар олж болно.

Үүнийг жишээгээр харцгаая.

Жишээ.

Шугаман алгебрийн тэгшитгэлийн системийг шийд .

Шийдэл.

Системийн үндсэн матрицын зэрэглэлийг олъё насанд хүрээгүй хүүхдүүдийг хиллэх аргаар. 1 1 = 1-ийг эхний эрэмбийн 0 биш минор гэж үзье. Энэ насанд хүрээгүй хоёр дахь зэрэглэлийн 0-ээс бага насны хүүхдийг хайж эхэлцгээе.

Ингэж бид хоёр дахь зэрэглэлийн 0 биш минорыг олсон. Гурав дахь эрэмбийн 0-ээс өөр хил хязгаарыг хайж эхэлцгээе.

Тиймээс үндсэн матрицын зэрэглэл гурван байна. Өргөтгөсөн матрицын зэрэглэл нь гуравтай тэнцүү, өөрөөр хэлбэл систем нь тогтвортой байна.

Гурав дахь эрэмбийн олдсон тэг биш минорыг бид суурь болгон авдаг.

Тодорхой болгохын тулд бид минорын үндэс суурийг бүрдүүлдэг элементүүдийг харуулав.

Бид системийн тэгшитгэлийн зүүн талд үндсэн суурьт хамаарах нэр томъёог орхиж, үлдсэнийг нь эсрэг тэмдгээр баруун тал руу шилжүүлнэ.

Үнэгүй үл мэдэгдэх хувьсагчид x 2 ба x 5 дурын утгыг өгье, өөрөөр хэлбэл бид хүлээн зөвшөөрнө. , дурын тоо хаана байна. Энэ тохиолдолд SLAE нь маягтыг авна

Шугаман алгебрийн тэгшитгэлийн үндсэн системийг Крамерын аргыг ашиглан шийдье.

Тиймээс, .

Хариултдаа үл мэдэгдэх үнэгүй хувьсагчдыг зааж өгөхөө бүү мартаарай.

Хариулт:

Дурын тоонууд хаана байна.

Дүгнэж хэлье.

Ерөнхий шугаман алгебрийн тэгшитгэлийн системийг шийдэхийн тулд эхлээд Кронекер-Капелли теоремыг ашиглан түүний нийцтэй байдлыг тодорхойлно. Хэрэв үндсэн матрицын зэрэглэл нь өргөтгөсөн матрицын зэрэгтэй тэнцүү биш бол систем нь нийцэхгүй байна гэж бид дүгнэж байна.

Хэрэв үндсэн матрицын зэрэглэл нь өргөтгөсөн матрицын зэрэгтэй тэнцүү бол бид минор суурь сонгож, сонгосон минорыг бүрдүүлэхэд оролцдоггүй системийн тэгшитгэлийг устгана.

Хэрэв суурь минорын дараалал нь үл мэдэгдэх хувьсагчдын тоотой тэнцүү бол SLAE нь өвөрмөц шийдэлтэй бөгөөд үүнийг бидэнд мэдэгдэж буй ямар ч аргаар олж болно.

Хэрэв суурь минорын дараалал нь үл мэдэгдэх хувьсагчдын тооноос бага байвал системийн тэгшитгэлийн зүүн талд үндсэн үл мэдэгдэх хувьсагчтай нөхцлүүдийг үлдээж, үлдсэн нөхцөлүүдийг баруун тал руу шилжүүлж, дурын утгыг өгнө. үнэгүй үл мэдэгдэх хувьсагч. Үүссэн шугаман тэгшитгэлийн системээс бид Крамерын арга, матрицын арга эсвэл Гауссын аргыг ашиглан үндсэн үл мэдэгдэх хувьсагчдыг олдог.

Ерөнхий хэлбэрийн шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэх Гауссын арга.

Гауссын аргыг ямар ч төрлийн шугаман алгебрийн тэгшитгэлийн системийг эхлээд тууштай эсэхийг шалгахгүйгээр шийдвэрлэхэд ашиглаж болно. Үл мэдэгдэх хувьсагчдыг дараалан арилгах үйл явц нь SLAE-ийн нийцтэй байдал, үл нийцэх байдлын талаар дүгнэлт гаргах боломжтой бөгөөд хэрэв шийдэл байгаа бол түүнийг олох боломжтой болгодог.

Тооцооллын үүднээс Гауссын аргыг илүүд үздэг.

Ерөнхий шугаман алгебрийн тэгшитгэлийн системийг шийдвэрлэх Гауссын арга гэсэн өгүүлэлд түүний дэлгэрэнгүй тайлбар, дүн шинжилгээ хийсэн жишээг үзнэ үү.

Уусмалын үндсэн системийн векторуудыг ашиглан нэгэн төрлийн ба нэгэн төрлийн бус шугаман алгебрийн системийн ерөнхий шийдийг бичих.

Энэ хэсэгт бид хязгааргүй тооны шийдтэй шугаман алгебрийн тэгшитгэлийн нэгэн зэрэг нэгэн төрлийн ба нэгэн төрлийн бус системүүдийн талаар ярих болно.

Эхлээд нэгэн төрлийн системийг авч үзье.

Шийдлийн үндсэн систем n үл мэдэгдэх хувьсагчтай p шугаман алгебрийн тэгшитгэлийн нэгэн төрлийн систем нь энэ системийн (n – r) шугаман бие даасан шийдлүүдийн цуглуулга бөгөөд r нь системийн үндсэн матрицын суурь минорын дараалал юм.

Хэрэв бид нэгэн төрлийн SLAE-ийн шугаман бие даасан шийдлүүдийг X (1) , X (2) , …, X (n-r) (X (1) , X (2) , …, X (n-r) гэж тэмдэглэвэл n хэмжээсийн багана матрицууд болно. 1-ээр) , дараа нь энэхүү нэгэн төрлийн системийн ерөнхий шийдийг дурын тогтмол C 1, C 2, ..., C (n-r) коэффициент бүхий шийдлүүдийн үндсэн системийн векторуудын шугаман хослолоор илэрхийлнэ, өөрөөр хэлбэл, .

Шугаман алгебрийн тэгшитгэлийн нэгэн төрлийн системийн ерөнхий шийдэл (орослау) гэдэг нэр томъёо нь юу гэсэн үг вэ?

Утга нь энгийн: томьёо нь анхны SLAE-ийн бүх боломжит шийдлүүдийг зааж өгсөн бөгөөд өөрөөр хэлбэл C 1, C 2, ..., C (n-r) дурын тогтмолуудын утгуудын багцыг авч, томъёог ашиглан бид үүнийг хийх болно. анхны нэгэн төрлийн SLAE-ийн шийдлүүдийн аль нэгийг олж авна.

Тиймээс, хэрэв бид шийдлүүдийн үндсэн системийг олвол энэ нэгэн төрлийн SLAE-ийн бүх шийдлүүдийг гэж тодорхойлж болно.

Нэг төрлийн SLAE-ийн шийдлийн үндсэн системийг бий болгох үйл явцыг харуулъя.

Бид шугаман тэгшитгэлийн анхны системийн минорыг сонгож, бусад бүх тэгшитгэлийг системээс хасч, үл мэдэгдэх хувьсагч агуулсан бүх нэр томъёог эсрэг тэмдэгтэй системийн тэгшитгэлийн баруун гар талд шилжүүлдэг. Чөлөөт үл мэдэгдэх хувьсагчдад 1,0,0,...,0 утгыг өгч, үндсэн үл мэдэгдэх утгыг тооцоолж, шугаман тэгшитгэлийн үндсэн системийг ямар ч аргаар, жишээлбэл, Крамерын аргыг ашиглан шийдье. Үүний үр дүнд үндсэн системийн эхний шийдэл болох X (1) гарч ирнэ. Хэрэв бид чөлөөт үл мэдэгдэх утгуудад 0,1,0,0,…,0 утгыг өгөөд үндсэн үл мэдэгдэхийг тооцвол X (2) болно. гэх мэт. Хэрэв бид чөлөөт үл мэдэгдэх хувьсагчдад 0.0,…,0.1 утгыг оноож, үндсэн үл мэдэгдэхийг тооцвол X (n-r) -ийг авна. Ийм байдлаар нэгэн төрлийн SLAE-ийн шийдлийн үндсэн системийг байгуулж, түүний ерөнхий шийдлийг хэлбэрээр бичиж болно.

Шугаман алгебрийн тэгшитгэлийн нэгэн төрлийн бус системүүдийн хувьд ерөнхий шийд нь харгалзах нэгэн төрлийн системийн ерөнхий шийдэл бөгөөд чөлөөт үл мэдэгдэх утгуудыг өгөх замаар олж авсан анхны нэгэн төрлийн бус SLAE-ийн тодорхой шийдэл юм. 0,0,...,0 ба үндсэн үл мэдэгдэх утгуудыг тооцоолох.

Жишээнүүдийг харцгаая.

Жишээ.

Шугаман алгебрийн тэгшитгэлийн нэгэн төрлийн системийн шийдлийн үндсэн систем ба ерөнхий шийдийг олох .

Шийдэл.

Шугаман тэгшитгэлийн нэгэн төрлийн системийн үндсэн матрицын зэрэг нь өргөтгөсөн матрицын зэрэгтэй үргэлж тэнцүү байна. Насанд хүрээгүй хүүхдүүдийг хиллэх аргыг ашиглан үндсэн матрицын зэрэглэлийг олъё. Нэгдүгээр эрэмбийн тэг биш минорын хувьд бид системийн үндсэн матрицын 1 1 = 9 элементийг авна. Хоёрдахь эрэмбийн хилийн тэг биш минорыг олъё:

Хоёр дахь эрэмбийн минор, тэгээс ялгаатай нь олдсон. Тэг биш нэгийг хайж олохын тулд түүнтэй хиллэдэг гуравдугаар зэрэглэлийн насанд хүрээгүй хүүхдүүдийг авч үзье.

Гурав дахь зэрэглэлийн бүх насанд хүрээгүй хүүхдүүд тэгтэй тэнцүү тул үндсэн ба өргөтгөсөн матрицын зэрэглэл хоёртой тэнцүү байна. Авцгаая . Тодорхой болгохын тулд үүнийг бүрдүүлдэг системийн элементүүдийг тэмдэглэе.

Анхны SLAE-ийн гурав дахь тэгшитгэл нь үндсэн суурь үүсэхэд оролцдоггүй тул дараахь зүйлийг хасч болно.

Бид тэгшитгэлийн баруун талд үндсэн үл мэдэгдэх нэр томъёог үлдээж, чөлөөт үл мэдэгдэх нэр томъёог баруун тал руу шилжүүлнэ.

Шугаман тэгшитгэлийн анхны нэгэн төрлийн системийн шийдлийн үндсэн системийг байгуулъя. Энэхүү SLAE-ийн шийдлүүдийн үндсэн систем нь хоёр шийдлээс бүрдэнэ, учир нь анхны SLAE нь үл мэдэгдэх дөрвөн хувьсагчийг агуулдаг бөгөөд түүний суурь минорын дараалал нь хоёртой тэнцүү байна. X (1) -ийг олохын тулд бид үнэгүй үл мэдэгдэх хувьсагчдад x 2 = 1, x 4 = 0 утгуудыг өгч, дараа нь тэгшитгэлийн системээс үндсэн үл мэдэгдэх зүйлийг олно.
.

Үл мэдэгдэх зүйлийг дараалан арилгах арга гэж нэрлэгддэг Гауссын арга нь дараах байдалтай байна. Энгийн хувиргалтыг ашиглан шугаман тэгшитгэлийн системийг түүний коэффициентийн матриц болох хэлбэрт оруулдаг. трапец хэлбэрийн (гурвалжин эсвэл шаталсантай ижил) эсвэл трапецын ойролцоо (Гауссын аргын шууд харвалт, цаашид - зүгээр л шулуун цус харвалт). Ийм систем ба түүний шийдлийн жишээг дээрх зурагт үзүүлэв.

Ийм системд сүүлчийн тэгшитгэл нь зөвхөн нэг хувьсагчийг агуулдаг бөгөөд түүний утгыг хоёрдмол утгагүй олох боломжтой. Дараа нь энэ хувьсагчийн утгыг өмнөх тэгшитгэлд орлуулна ( Гауссын аргын урвуу , дараа нь зүгээр л урвуу), өмнөх хувьсагчийг олох гэх мэт.

Трапец хэлбэрийн (гурвалжин) системд бидний харж байгаагаар гурав дахь тэгшитгэл нь хувьсагчийг агуулаагүй болно. yТэгээд x, хоёр дахь тэгшитгэл нь хувьсагч юм x .

Системийн матриц нь трапец хэлбэртэй болсны дараа системийн нийцтэй байдлын асуудлыг ойлгох, шийдлүүдийн тоог тодорхойлох, шийдлийг өөрсдөө олоход хэцүү байхаа больсон.

Аргын давуу талууд:

гурваас дээш тэгшитгэл ба үл мэдэгдэх шугаман тэгшитгэлийн системийг шийдвэрлэхдээ Гауссын арга нь Крамерын арга шиг төвөгтэй биш, учир нь Гауссын аргаар шийдвэрлэх нь бага тооцоо шаарддаг;
Гауссын арга нь шугаман тэгшитгэлийн тодорхой бус системийг, өөрөөр хэлбэл ерөнхий шийдэлтэй (мөн бид энэ хичээлд дүн шинжилгээ хийх болно) шийдэж чаддаг бөгөөд Крамерын аргыг ашиглан бид зөвхөн систем нь тодорхойгүй гэж хэлж болно;
үл мэдэгдэх тоо нь тэгшитгэлийн тоотой тэнцүү биш шугаман тэгшитгэлийн системийг шийдэж чадна (бид энэ хичээлд мөн дүн шинжилгээ хийх болно);
Энэ арга нь анхан шатны (сургуулийн) аргууд дээр суурилдаг - үл мэдэгдэх зүйлийг орлуулах арга, тэгшитгэл нэмэх арга, бидний холбогдох нийтлэлд дурдсан.

Шугаман тэгшитгэлийн трапец хэлбэрийн (гурвалжин, шат) системийг шийдвэрлэх энгийн байдлыг ойлгохын тулд бид урвуу хөдөлгөөнийг ашиглан ийм системийн шийдлийг танилцуулж байна. Энэ системийн хурдан шийдлийг хичээлийн эхэнд зурагт үзүүлэв.

Жишээ 1.Урвууг ашиглан шугаман тэгшитгэлийн системийг шийд:

Шийдэл. Энэ трапецын системд хувьсагч zГурав дахь тэгшитгэлээс өвөрмөц байдлаар олж болно. Бид түүний утгыг хоёр дахь тэгшитгэлд орлуулж, хувьсагчийн утгыг авна y:

Одоо бид хоёр хувьсагчийн утгыг мэдэж байна - zТэгээд y. Бид тэдгээрийг эхний тэгшитгэлд орлуулж, хувьсагчийн утгыг авна x:

Өмнөх алхмуудаас бид тэгшитгэлийн системийн шийдлийг бичдэг.

Бидний маш энгийнээр шийдсэн ийм трапец хэлбэрийн шугаман тэгшитгэлийн системийг олж авахын тулд шугаман тэгшитгэлийн системийн элементар хувиргалттай холбоотой урагшлах цохилтыг ашиглах шаардлагатай. Энэ нь бас тийм ч хэцүү биш юм.

Шугаман тэгшитгэлийн системийн элементийн хувиргалт

Системийн тэгшитгэлүүдийг алгебрийн аргаар нэмэх сургуулийн аргыг давтаж, бид системийн нэг тэгшитгэл дээр системийн өөр нэг тэгшитгэлийг нэмж, тэгшитгэл бүрийг зарим тоогоор үржүүлж болохыг олж мэдсэн. Үүний үр дүнд бид үүнтэй тэнцэх шугаман тэгшитгэлийн системийг олж авдаг. Үүний дотор нэг тэгшитгэл нь зөвхөн нэг хувьсагчийг агуулж байсан бөгөөд түүний утгыг бусад тэгшитгэлд орлуулж, бид шийдэлд хүрдэг. Ийм нэмэлт нь системийн үндсэн өөрчлөлтийн нэг хэлбэр юм. Гауссын аргыг ашиглахдаа бид хэд хэдэн төрлийн хувиргалтыг ашиглаж болно.

Дээрх хөдөлгөөнт дүрс нь тэгшитгэлийн систем хэрхэн аажмаар трапец хэлбэртэй болж байгааг харуулж байна. Энэ нь таны анхны анимэйшн дээр харсан бөгөөд үүнээс үл мэдэгдэх бүх утгыг олоход хялбар гэж өөртөө итгүүлсэн зүйл юм. Ийм өөрчлөлтийг хэрхэн хийх, мэдээжийн хэрэг жишээнүүдийг цаашид авч үзэх болно.

Тэгшитгэлийн систем болон системийн өргөтгөсөн матрицад хэдэн ч тооны тэгшитгэлтэй ба үл мэдэгдэх шугаман тэгшитгэлийн системийг шийдвэрлэхдээ Чадах:

мөрүүдийг дахин цэгцлэх (энэ тухай өгүүллийн эхэнд дурдсан);
хэрэв бусад хувиргалтуудын үр дүнд тэнцүү эсвэл пропорциональ мөрүүд байвал нэгээс бусад тохиолдолд тэдгээрийг устгаж болно;
бүх коэффициентүүд тэгтэй тэнцүү байх "тэг" мөрүүдийг арилгах;
дурын мөрийг тодорхой тоогоор үржүүлэх буюу хуваах;
дурын мөрөнд тодорхой тоогоор үржүүлсэн өөр мөр нэмнэ.

Өөрчлөлтийн үр дүнд бид үүнтэй тэнцэх шугаман тэгшитгэлийн системийг олж авдаг.

Гауссын аргыг ашиглан системийн квадрат матрицтай шугаман тэгшитгэлийн системийг шийдвэрлэх алгоритм ба жишээнүүд

Үл мэдэгдэх тоо нь тэгшитгэлийн тоотой тэнцүү байх шугаман тэгшитгэлийн системийг эхлээд авч үзье. Ийм системийн матриц нь дөрвөлжин, өөрөөр хэлбэл доторх мөрүүдийн тоо нь баганын тоотой тэнцүү байна.

Жишээ 2.Шугаман тэгшитгэлийн системийг Гауссын аргыг ашиглан шийд

Сургуулийн аргуудыг ашиглан шугаман тэгшитгэлийн системийг шийдвэрлэхдээ бид нэг тэгшитгэлийн гишүүнийг гишүүнээр үржүүлснээр хоёр тэгшитгэлийн эхний хувьсагчийн коэффициентүүд эсрэг тоо байсан. Тэгшитгэл нэмэх үед энэ хувьсагчийг хасна. Гауссын арга нь мөн адил ажилладаг.

Уусмалын харагдах байдлыг хялбаршуулах системийн өргөтгөсөн матрицыг үүсгэцгээе:

Энэ матрицад үл мэдэгдэх коэффициентүүд нь босоо шугамын өмнө зүүн талд, чөлөөт гишүүн нь босоо шугамын дараа баруун талд байрлана.

Хувьсагчдын коэффициентийг хуваахад тохиромжтой байхын тулд (нэгдмэл байдлаар хуваахыг олж авах) Системийн матрицын эхний болон хоёр дахь мөрийг сольж үзье. Шугаман тэгшитгэлийн системд тэгшитгэлүүдийг сольж болох тул бид үүнтэй ижил төстэй системийг олж авдаг.

Эхний шинэ тэгшитгэлийг ашиглах хувьсагчийг арилгах xхоёр дахь болон дараагийн бүх тэгшитгэлээс. Үүнийг хийхийн тулд матрицын хоёр дахь эгнээнд бид үржүүлсэн эхний эгнээ (бидний тохиолдолд, -ээр), гурав дахь эгнээнд - эхний эгнээ, үржүүлсэн (бидний тохиолдолд, -ээр) нэмнэ.

Учир нь энэ нь боломжтой юм

Хэрэв манай системд гурваас илүү тэгшитгэл байсан бол бид дараагийн бүх тэгшитгэлд хасах тэмдгээр авсан харгалзах коэффициентүүдийн харьцаагаар үржүүлсэн эхний мөрийг нэмэх шаардлагатай болно.

Үүний үр дүнд бид шинэ тэгшитгэлийн системийн энэ системтэй тэнцэх матрицыг олж авдаг бөгөөд үүнд хоёр дахь хэсгээс эхлэн бүх тэгшитгэлүүд орно. хувьсагч агуулаагүй x :

Үүссэн системийн хоёр дахь мөрийг хялбарчлахын тулд үүнийг дахин дахин үржүүлж, энэ системтэй тэнцэх тэгшитгэлийн системийн матрицыг олоорой.

Одоо үүссэн системийн эхний тэгшитгэлийг хэвээр үлдээвэл, Хоёр дахь тэгшитгэлийг ашиглан бид хувьсагчийг арилгана y дараагийн бүх тэгшитгэлээс. Үүнийг хийхийн тулд системийн матрицын гурав дахь эгнээнд бид хоёр дахь эгнээ нэмж, үржүүлсэн (бидний тохиолдолд ).

Хэрэв манай системд гурваас илүү тэгшитгэл байсан бол бид дараагийн бүх тэгшитгэлд хасах тэмдгээр авсан харгалзах коэффициентүүдийн харьцаагаар үржүүлсэн хоёр дахь мөрийг нэмэх шаардлагатай болно.

Үүний үр дүнд бид шугаман тэгшитгэлийн системтэй тэнцэх системийн матрицыг дахин олж авна.

Бид шугаман тэгшитгэлийн эквивалент трапецын системийг олж авлаа.

Хэрэв тэгшитгэл ба хувьсагчийн тоо бидний жишээнээс их байвал хувьсагчдыг дэс дараалан арилгах үйл явц нь бидний үзүүлэх жишээн дээрх шиг системийн матриц трапец хэлбэртэй болох хүртэл үргэлжилнэ.

Бид "эцсээс нь" шийдлийг олох болно - урвуу хөдөлгөөн. Үүний төлөө Сүүлийн тэгшитгэлээс бид тодорхойлно z:
.
Энэ утгыг өмнөх тэгшитгэлд орлуулж, бид олох болно y:

Эхний тэгшитгэлээс бид олох болно x:

Хариулт: Энэ тэгшитгэлийн системийн шийдэл .

: энэ тохиолдолд систем өвөрмөц шийдэлтэй бол ижил хариулт өгнө. Хэрэв системд хязгааргүй тооны шийдэл байгаа бол энэ нь хариулт байх болно, энэ нь энэ хичээлийн тав дахь хэсгийн сэдэв юм.

Шугаман тэгшитгэлийн системийг Гауссын аргыг ашиглан өөрөө шийдэж, дараа нь шийдлийг хар

Энд дахин тэгшитгэлийн тоо нь үл мэдэгдэх тоотой тэнцүү байх шугаман тэгшитгэлийн тууштай бөгөөд тодорхой системийн жишээг авч үзье. Манай демо жишээнээс алгоритмаас ялгаатай нь аль хэдийн дөрвөн тэгшитгэл, дөрвөн үл мэдэгдэх зүйл байна.

Жишээ 4.Гауссын аргыг ашиглан шугаман тэгшитгэлийн системийг шийд.

Одоо та дараагийн тэгшитгэлээс хувьсагчийг хасахын тулд хоёр дахь тэгшитгэлийг ашиглах хэрэгтэй. Бэлтгэл ажлаа хийцгээе. Коэффициентийн харьцаагаар илүү тохиромжтой болгохын тулд та хоёр дахь эгнээний хоёр дахь баганад нэгийг авах хэрэгтэй. Үүнийг хийхийн тулд хоёр дахь мөрөөс гурав дахь хэсгийг хасаад, үүссэн хоёр дахь мөрийг -1-ээр үржүүлнэ.

Одоо гурав, дөрөв дэх тэгшитгэлээс хувьсагчийн бодит хасалтыг хийцгээе. Үүнийг хийхийн тулд гурав дахь мөрөнд -ээр үржүүлсэн хоёр дахь мөрийг, дөрөв дэх мөрөнд -ээр үржүүлсэн хоёр дахь мөрийг нэмнэ.

Одоо гурав дахь тэгшитгэлийг ашиглан дөрөв дэх тэгшитгэлээс хувьсагчийг хасна. Үүнийг хийхийн тулд дөрөв дэх мөрөнд гурав дахь мөрийг нэмээд үржүүлнэ. Бид өргөтгөсөн трапец хэлбэрийн матрицыг олж авдаг.

Бид өгөгдсөн системтэй тэнцэх тэгшитгэлийн системийг олж авлаа.

Иймээс үүссэн болон өгөгдсөн системүүд нь нийцтэй бөгөөд тодорхой юм. Бид эцсийн шийдлийг "эцсээс нь" олдог. Дөрөв дэх тэгшитгэлээс бид "x-four" хувьсагчийн утгыг шууд илэрхийлж болно.

Бид энэ утгыг системийн гурав дахь тэгшитгэлд орлуулж, авна

Эцэст нь үнэ цэнийг орлуулах

Эхний тэгшитгэл өгдөг

Бид "х"-ийг хаанаас олох вэ:

Хариулт: Энэ тэгшитгэлийн систем нь өвөрмөц шийдэлтэй .

Та мөн системийн шийдлийг Крамерын аргыг ашиглан тооцоолуур дээр шалгаж болно: энэ тохиолдолд системд өвөрмөц шийдэл байгаа бол ижил хариулт өгнө.

Хайлш дээрх бодлогын жишээг ашиглан Гауссын аргыг ашиглан хэрэглээний асуудлыг шийдвэрлэх

Шугаман тэгшитгэлийн системийг физик ертөнц дэх бодит объектуудыг загварчлахад ашигладаг. Эдгээр асуудлын нэг болох хайлшийг шийдье. Үүнтэй төстэй асуудал бол хольцтой холбоотой асуудал, нэг бүлэг барааны үнэ, хувь хэмжээ гэх мэт асуудал юм.

Жишээ 5.Гурван ширхэг хайлш нь нийт 150 кг жинтэй. Эхний хайлш нь 60% зэс, хоёр дахь нь 30%, гурав дахь нь 10% -ийг агуулдаг. Түүгээр ч зогсохгүй хоёр, гурав дахь хайлшийг нийлүүлэхэд эхний хайлшаас 28.4 кг, гурав дахь хайлш нь хоёр дахь хайлшаас 6.2 кг бага зэс байна. Хайлш бүрийн массыг ол.

Шийдэл. Бид шугаман тэгшитгэлийн системийг бүрдүүлдэг.

Бид хоёр ба гурав дахь тэгшитгэлийг 10-аар үржүүлснээр шугаман тэгшитгэлийн эквивалент системийг олж авна.

Бид системийн өргөтгөсөн матрицыг үүсгэдэг:

Анхаар, урагшаа. Нэг мөрийг тоогоор үржүүлсэн (бидний хувьд хасах) нэмснээр (бид үүнийг хоёр удаа ашигладаг) системийн өргөтгөсөн матрицад дараахь өөрчлөлтүүд хийгдэнэ.

Шууд нүүдэл дууслаа. Бид өргөтгөсөн трапец хэлбэрийн матрицыг олж авсан.

Бид урвуу хөдөлгөөнийг хийдэг. Бид төгсгөлөөс нь шийдлийг олдог. Бид үүнийг харж байна.

Хоёр дахь тэгшитгэлээс бид олдог

Гурав дахь тэгшитгэлээс -

Гауссын аргын энгийн гэдгийг Германы математикч Карл Фридрих Гаусс зохион бүтээхэд ердөө 15 минут зарцуулсан нь нотолж байна. Түүний нэрээр нэрлэгдсэн аргаас гадна "Бидэнд гайхалтай, байгалийн бус мэт санагдаж буй зүйлийг туйлын боломжгүй зүйлтэй андуурч болохгүй" гэсэн хэллэгийг Гауссын бүтээлүүдээс мэддэг - нээлт хийх тухай товч заавар.

Хэрэглэсэн олон асуудалд гуравдахь хязгаарлалт, өөрөөр хэлбэл гурав дахь тэгшитгэл байхгүй байж болно, тэгвэл та Гауссын аргыг ашиглан гурван үл мэдэгдэх хоёр тэгшитгэлийн системийг шийдэх хэрэгтэй, эсвэл эсрэгээрээ тэгшитгэлээс цөөн үл мэдэгдэх нь байдаг. Одоо бид ийм тэгшитгэлийн системийг шийдэж эхэлнэ.

Гауссын аргыг ашиглан аливаа систем нийцтэй эсвэл нийцэхгүй байгаа эсэхийг тодорхойлох боломжтой nшугаман тэгшитгэлүүд nхувьсагч.

Гауссын арга ба хязгааргүй олон шийд бүхий шугаман тэгшитгэлийн систем

Дараагийн жишээ бол шугаман тэгшитгэлийн тууштай боловч тодорхой бус систем, өөрөөр хэлбэл хязгааргүй тооны шийдлүүд юм.

Системийн өргөтгөсөн матрицад өөрчлөлт хийсний дараа (мөрүүдийг дахин зохион байгуулах, мөрийг тодорхой тоогоор үржүүлэх, хуваах, нэг мөрөнд өөр нэг мөр нэмэх) маягтын мөрүүд гарч ирж болно.

Хэрэв бүх тэгшитгэлд хэлбэртэй байвал

Чөлөөт нэр томъёо нь тэгтэй тэнцүү, энэ нь систем нь тодорхойгүй, өөрөөр хэлбэл хязгааргүй тооны шийдлүүдтэй, ийм төрлийн тэгшитгэлүүд "илүүдэл" бөгөөд бид тэдгээрийг системээс хасдаг гэсэн үг юм.

Жишээ 6.

Шийдэл. Системийн өргөтгөсөн матрицыг үүсгэцгээе. Дараа нь эхний тэгшитгэлийг ашиглан бид дараагийн тэгшитгэлээс хувьсагчийг хасна. Үүнийг хийхийн тулд хоёр, гурав, дөрөв дэх мөрөнд эхнийхийг нэмж, дараах байдлаар үржүүлнэ.

Одоо гурав, дөрөвт хоёр дахь мөрийг нэмье.

Үүний үр дүнд бид системд хүрдэг

Сүүлийн хоёр тэгшитгэл нь хэлбэрийн тэгшитгэл болж хувирав. Эдгээр тэгшитгэлүүд нь үл мэдэгдэх бүх утгын хувьд хангагдсан бөгөөд үүнийг хаяж болно.

Хоёрдахь тэгшитгэлийг хангахын тулд бид дурын утгуудыг сонгож болно, дараа нь утгыг өвөрмөц байдлаар тодорхойлно. . Эхний тэгшитгэлээс утгыг мөн өвөрмөц байдлаар олно: .

Өгөгдсөн болон сүүлийн систем хоёулаа нийцтэй, гэхдээ тодорхойгүй, томъёонууд

дур зоргоороо, өгөгдсөн системийн бүх шийдлийг бидэнд өгнө.

Гауссын арга ба шийдэлгүй шугаман тэгшитгэлийн систем

Дараагийн жишээ бол шугаман тэгшитгэлийн үл нийцэх систем, өөрөөр хэлбэл шийдэлгүй систем юм. Иймэрхүү асуудлын хариултыг ингэж томъёолдог: системд ямар ч шийдэл байхгүй.

Эхний жишээн дээр дурьдсанчлан хувиргалт хийсний дараа системийн өргөтгөсөн матрицад маягтын мөрүүд гарч ирж болно.

хэлбэрийн тэгшитгэлд харгалзах

Хэрэв тэдгээрийн дунд дор хаяж нэг тэгшитгэл байгаа бол тэгээс өөр чөлөөт гишүүнтэй (өөрөөр хэлбэл ) тэгшитгэлийн систем нь нийцэхгүй, өөрөөр хэлбэл шийдэлгүй бөгөөд шийдэл нь бүрэн дүүрэн байна.

Жишээ 7.Гауссын аргыг ашиглан шугаман тэгшитгэлийн системийг шийд.

Шийдэл. Бид системийн өргөтгөсөн матрицыг бүрдүүлдэг. Эхний тэгшитгэлийг ашиглан бид хувьсагчийг дараагийн тэгшитгэлээс хасдаг. Үүнийг хийхийн тулд эхний мөрийг хоёр дахь мөрөнд, эхний мөрийг гурав дахь мөрөнд, эхний мөрийг дөрөв дэх мөрөнд нэмнэ.

Одоо та дараагийн тэгшитгэлээс хувьсагчийг хасахын тулд хоёр дахь тэгшитгэлийг ашиглах хэрэгтэй. Коэффициентийн бүхэл тооны харьцааг олж авахын тулд бид системийн өргөтгөсөн матрицын хоёр ба гурав дахь мөрийг сольдог.

Гурав, дөрөв дэх тэгшитгэлийг хасахын тулд гурав дахь мөрөнд хоёр дахь нь -ээр үржүүлсэнийг, дөрөв дэх мөрөнд хоёр дахь нь -ээр үржүүлсэнийг нэмнэ.

Одоо гурав дахь тэгшитгэлийг ашиглан дөрөв дэх тэгшитгэлээс хувьсагчийг хасна. Үүнийг хийхийн тулд дөрөв дэх мөрөнд гурав дахь мөрийг нэмээд үржүүлнэ.

Тиймээс өгөгдсөн систем нь дараахтай тэнцүү байна.

Үүссэн систем нь үл нийцэх, учир нь түүний сүүлчийн тэгшитгэл нь үл мэдэгдэх утгуудаар хангагдах боломжгүй юм. Тиймээс энэ системд ямар ч шийдэл байхгүй.