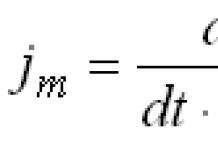Фибоначчийн дараалал, "Да Винчи код" киноноос хүн бүрийн мэддэг - 13-р зуунд Фибоначчи хочоор алдаршсан Италийн математикч Пизагийн Леонардогийн оньсого хэлбэрээр дүрсэлсэн цуврал тоо. Товчхондоо тааварын мөн чанар:

Хэрвээ туулайн шинж чанар нь сар бүр нэг хос туулай төрүүлж, чадвартай болдог бол жилд хэдэн хос туулай төрөхийг мэдэхийн тулд хэн нэгэн хос туулайг тодорхой битүү орон зайд байрлуулжээ. хоёр сартайд нь үр төл гаргах.

Үр дүн нь дараах тоонуудын цуваа юм. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 , энд арван хоёр сар бүрийн хос туулайн тоог таслалаар заана. Үүнийг тодорхойгүй хугацаагаар үргэлжлүүлж болно. Үүний мөн чанар нь дараагийн тоо бүр нь өмнөх хоёрын нийлбэр юм.

Энэ цуврал хэд хэдэн байна математикийн шинж чанарууд, үүнд хүрэх нь гарцаагүй. Энэ нь асимптотик байдлаар (илүү удаан ойртож) зарим тогтмол харьцаатай байдаг. Гэсэн хэдий ч энэ харьцаа нь иррациональ, өөрөөр хэлбэл бутархай хэсэгт аравтын оронтой тоонуудын хязгааргүй, урьдчилан тааварлашгүй дараалал бүхий тоо юм. Үүнийг нарийн илэрхийлэх боломжгүй юм.

Тиймээс цувралын аль нэг гишүүний өмнөх гишүүнтэй харьцуулсан харьцаа нь тооны орчим хэлбэлздэг 1,618 , заримдаа хэтрүүлэх, заримдаа хүрэхгүй байх. Дараахтай харьцуулсан харьцаа нь тоонд адилхан ойртдог 0,618 , энэ нь урвуу пропорциональ байна 1,618 . Хэрэв бид элементүүдийг нэгээр нь хуваах юм бол бид тоо гарна 2,618 Тэгээд 0,382 , тэдгээр нь мөн урвуу пропорциональ байна. Эдгээр нь Фибоначчийн харьцаа гэж нэрлэгддэг.

Энэ бүхэн юуны төлөө вэ? Байгалийн хамгийн нууцлаг үзэгдлүүдийн нэгэнд бид ингэж ханддаг. Ухаантай Леонардо үндсэндээ шинэ зүйл нээсэнгүй, тэр зүгээр л ийм үзэгдлийг дэлхийд сануулсан. Алтан харьцаа, энэ нь ач холбогдлын хувьд Пифагорын теоремоос дутахгүй.

Бид эргэн тойрон дахь бүх объектыг хэлбэр дүрсээр нь ялгадаг. Бид заримд нь илүү дуртай, зарим нь бага, зарим нь бүрмөсөн дургүй байдаг. Заримдаа сонирхлыг зааж өгч болно амьдралын нөхцөл байдал, заримдаа ажиглагдсан объектын гоо үзэсгэлэн. Тэгш хэмтэй, пропорциональ хэлбэр нь харааны хамгийн сайн ойлголтыг бий болгож, гоо үзэсгэлэн, эв найрамдлын мэдрэмжийг төрүүлдэг. Бүрэн дүрс нь үргэлж өөр хоорондоо болон бүхэлдээ тодорхой харилцаатай байдаг өөр өөр хэмжээтэй хэсгүүдээс бүрддэг. Алтан харьцаа - шинжлэх ухаан, урлаг, байгаль дахь бүхэл бүтэн болон түүний хэсгүүдийн төгс төгөлдөр байдлын хамгийн дээд илрэл.

Хэрэв асаалттай бол энгийн жишээ, тэгвэл Алтан харьцаа нь сегментийг хоёр хэсэгт хуваах бөгөөд тэдгээрийн нийлбэр (бүх сегмент) том хэсэгтэй том хэсэг нь жижиг хэсэгтэй холбоотой байдаг.

Хэрэв бид сегментийг бүхэлд нь авбал в ард 1 , дараа нь сегмент а тэнцүү байх болно 0,618 , шугамын хэсэг б - 0,382 , зөвхөн ийм байдлаар Алтан харьцааны нөхцөл хангана (0,618/0,382=1,618 ; 1/0,618=1,618 ) . Хандлага в руу а тэнцүү байна 1,618 , А -тай руу б 2,618 . Эдгээр нь бидэнд аль хэдийн танил болсон Фибоначчийн харьцаа юм.

Мэдээжийн хэрэг алтан тэгш өнцөгт, алтан гурвалжин, бүр алтан шоо хэлбэртэй байдаг. Хүний биеийн харьцаа олон талаараа Алтан хэсэгтэй ойролцоо байдаг.

Зураг: marcus-frings.de

Гэхдээ бид олж авсан мэдлэгээ нэгтгэснээр хөгжилтэй эхэлдэг. Зураг нь Фибоначчийн дараалал ба Алтан харьцаа хоорондын хамаарлыг тодорхой харуулж байна. Бид эхний хэмжээтэй хоёр квадратаас эхэлдэг. Дээрээс нь хоёр дахь хэмжээтэй квадрат нэмнэ. Хажууд нь өмнөх хоёр, гурав дахь хэмжээтэй талуудын нийлбэртэй тэнцүү талтай дөрвөлжин зур. Үүнтэй адилтгаж үзвэл таван хэмжээтэй квадрат гарч ирнэ. Ингээд ядрах хүртлээ гол зүйл бол дараагийн дөрвөлжин бүрийн хажуугийн урт нь өмнөх хоёр талын уртын нийлбэртэй тэнцүү байх явдал юм. Хажуугийн урт нь Фибоначчийн тоо бөгөөд хачирхалтай нь тэднийг Фибоначчийн тэгш өнцөгт гэж нэрлэдэг хэд хэдэн тэгш өнцөгтүүдийг бид харж байна.

Хэрэв бид квадратынхаа булангуудыг гөлгөр шугамаар зурах юм бол өсөлт нь үргэлж жигд байдаг Архимед спиральаас өөр зүйл олж авахгүй.

Танд юу ч сануулахгүй байна уу?

Зураг: этанхайн Flickr дээр

Зөвхөн нялцгай биетний бүрхүүлээс та Архимедийн спираль олж болно, гэхдээ олон цэцэг, ургамалд тэдгээр нь тийм ч тод харагддаггүй.

Aloe multifolia:

Зураг: шар айрагны дэвтэр Flickr дээр

Зураг: beart.org.uk
Зураг: эсдраскальдеран Flickr дээр
Зураг: manj98 Flickr дээр

Одоо Алтан хэсгийг санах цаг болжээ! Эдгээр гэрэл зургуудад байгалийн хамгийн үзэсгэлэнтэй, эв найртай бүтээлүүдийг дүрсэлсэн байна уу? Энэ нь бүгд биш юм. Хэрэв та анхааралтай ажиглавал ижил төстэй хэв маягийг олон хэлбэрээр олж болно.

Мэдээжийн хэрэг, эдгээр бүх үзэгдлүүд нь Фибоначчийн дараалалд үндэслэсэн гэсэн мэдэгдэл хэтэрхий чанга сонсогдож байгаа ч чиг хандлага нь тодорхой байна. Түүнээс гадна тэр өөрөө энэ дэлхийн бүх зүйл шиг төгс төгөлдөр байдлаас хол байна.

Фибоначчийн цуврал нь байгалиасаа илүү суурь, төгс алтан харьцааны логарифмын дараалалд дасан зохицох оролдлого гэсэн таамаглал байдаг бөгөөд энэ нь бараг ижил, зөвхөн хаанаас ч эхэлж, хаашаа ч хүрэхгүй юм. Байгальд эхэлж болох бүхэл бүтэн эхлэл зайлшгүй хэрэгтэй; тэр оргүйгээс ямар нэг зүйлийг бүтээж чадахгүй. Фибоначчийн дарааллын эхний нөхцлүүдийн харьцаа нь Алтан харьцаанаас хол байна. Гэхдээ бид цаашаа явах тусам эдгээр хазайлтууд улам бүр жигдрэх болно. Аливаа цувралыг тодорхойлохын тулд түүний дараалсан гурван нэр томъёог мэдэхэд хангалттай. Гэхдээ алтан дарааллын хувьд биш, хоёр нь хангалттай, энэ нь геометрийн ба арифметик прогресснэгэн зэрэг. Үүнийг бусад бүх дарааллын үндэс гэж бодож магадгүй юм.

Алтан логарифмын дарааллын гишүүн бүр нь Алтан харьцааны хүч юм ( z). Цувралын нэг хэсэг нь иймэрхүү харагдаж байна: ... z -5 ; z -4; z -3; z -2; z -1; z 0 ; z 1 ; z 2 ; z 3 ; z 4 ; z 5...Хэрэв бид Алтан харьцааны утгыг аравтын бутархайн гурван орон болгон бөөрөнхийлвөл бид авна z=1.618, дараа нь цуврал дараах байдалтай харагдана. ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Дараагийн нэр томъёо бүрийг зөвхөн өмнөхийг үржүүлээд зогсохгүй авах боломжтой 1,618 , гэхдээ өмнөх хоёрыг нэмснээр. Тиймээс, хоёр зэргэлдээ элементийг нэмснээр экспоненциал өсөлтийг олж авдаг. Энэ бол эхлэл төгсгөлгүй цуврал бөгөөд Фибоначчийн дараалал ийм байхыг хичээдэг. Маш тодорхой эхлэлтэй тэрээр идеал руу тэмүүлдэг, хэзээ ч түүндээ хүрдэггүй. Тэр бол амьдрал.

Гэсэн хэдий ч бидний харж, уншсан бүх зүйлтэй холбоотойгоор нэлээд логик асуултууд гарч ирдэг.
Эдгээр тоонууд хаанаас ирсэн бэ? Орчлон ертөнцийг төгс болгохыг хичээсэн энэ архитектор хэн бэ? Бүх зүйл түүний хүссэнээр байсан уу? Хэрэв тийм бол яагаад буруу болсон бэ? Мутаци? Чөлөөт сонголт? Дараа нь юу болох вэ? Спираль буржгар эсвэл тайлж байна уу?

Нэг асуултын хариултыг олсны дараа та дараагийн асуултыг авах болно. Хэрэв та үүнийг шийдвэл хоёр шинэ зүйл авах болно. Тэдэнтэй харьцсаны дараа дахиад гурав гарч ирнэ. Тэдгээрийг бас шийдсэний дараа та шийдэгдээгүй таван зүйлтэй болно. Дараа нь найм, дараа нь арван гурав, 21, 34, 55...

Эх сурвалж: ; ; ;

Байгальд тохиолддог тоо, томъёоны тухай. За, эдгээр ижил тоо, томъёоны талаар хэдэн үг хэлье.

Байгаль дээрх тоо, томьёо нь орчлон ертөнцийг хэн нэгэн бүтээсэн гэдэгт итгэдэг хүмүүс болон ертөнц өөрөө бий болсон гэдэгт итгэдэг хүмүүсийн хооронд саад тотгор болдог. Учир нь асуулт нь: "Хэрэв орчлон ертөнц өөрөө үүссэн бол бараг бүх амьд, амьгүй биетүүд ижил схемийн дагуу, ижил томъёоны дагуу баригдахгүй гэж үү?"

За, энэ дээр философийн асуултБид энд хариулахгүй (сайтын формат ижил биш 🙂), гэхдээ бид томъёоллыг дуудах болно. Тэгээд Фибоначчийн болон Алтан спираль тоонуудаас эхэлцгээе.

Тиймээс Фибоначчийн тоонууд нь элементүүд юм тооны дараалал, дараагийн тоо бүр нь өмнөх хоёр тооны нийлбэртэй тэнцүү байна. Энэ нь 0 +1=1, 1+1=2, 2+1=3, 3+2=5 гэх мэт.

Нийтдээ бид цувралыг авна: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6764,

Фибоначчийн цувралын өөр нэг жишээ: 0, 2, 2, 4, 6, 10, 16, 26, 42, 68, 110, 178 гэх мэт. Та өөрөө туршилт хийж болно :)

Фибоначчийн тоо байгальд хэрхэн харагддаг вэ? Маш энгийн:

1. Ургамлын навчны зохион байгуулалтыг Фибоначчийн дарааллаар дүрсэлсэн байдаг. Наранцэцгийн үр, нарсны боргоцой, цэцгийн дэлбээ, хан боргоцойны эсүүд нь Фибоначчийн дарааллын дагуу байрладаг.
2. Хүний хурууны фалангуудын урт нь Фибоначчийн тоотой ойролцоо байна.
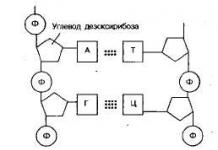
3. ДНХ-ийн молекул нь 34 ангстром урт, 21 ангстром өргөнтэй, босоо байдлаар холбогдсон хоёр мушгианаас тогтдог. 21 ба 34 тоонууд Фибоначчийн дарааллаар бие биенээ дагадаг.

Фибоначчийн тоог ашиглан та Алтан спираль бүтээх боломжтой. Тиймээс, 1-ийн талтай жижиг дөрвөлжин зуръя. Дараа нь сургуулиа санацгаая. 12 гэж юу вэ? Энэ нь 1 байх болно. Тэгэхээр эхнийхийнхээ хажууд өөр нэг дөрвөлжин зуръя. Дараа нь дараагийн Фибоначчийн тоо 2 (1+1) байна. 2 2 гэж юу вэ? Энэ нь 4 байх болно. Эхний хоёр квадратын ойролцоо өөр нэг квадрат зуръя, гэхдээ одоо тал нь 2, талбай нь 4. Дараагийн тоо нь 3 (1+2) тоо юм. 3-ын тооны квадрат нь 9. Аль хэдийн зурсан хэсгүүдийн хажууд 3 талтай, 9-р талбайтай дөрвөлжин зур. Дараа нь бид 5 талтай, 25 талбайтай дөрвөлжин, 8 талтай дөрвөлжин ба 64 талбайтай - мөн хязгааргүй.

Алтан спираль болох цаг болжээ. Квадратуудын хоорондох хилийн цэгүүдийг гөлгөр муруй шугамаар холбоно. Мөн бид байгаль дээрх олон амьд, амьгүй биетүүдийг бүтээсэн ижил алтан спираль авах болно.

Алтан харьцаа руу шилжихээсээ өмнө бодож үзье. Энд бид Фибоначчийн дарааллын квадратууд дээр үндэслэн спираль барьсан (дараалал 1, 1, 2, 3, 5, 8 ба 1, 1, 4, 9, 25, 64-р квадратууд). Гэхдээ бид тоонуудын квадратыг биш, харин тэдгээрийн кубыг ашиглавал юу болох вэ? Төвөөс шоо нь иймэрхүү харагдах болно.

Мөн хажуу талд нь:

За, спираль барихад энэ нь гарч ирнэ эзэлхүүнтэй алтан спираль:

Энэхүү том алтан спираль нь хажуу талаасаа иймэрхүү харагдаж байна.

Гэхдээ бид Фибоначчийн тоонуудын шоо авахгүй, дөрөв дэх хэмжээс рүү шилжих юм бол яах вэ?.. Энэ бол оньсого, тийм ээ?

Гэсэн хэдий ч Фибоначчийн тоонуудын шоо дөрвөлжингөөс хамаагүй бага тоон дээр үндэслэн эзэлхүүний алтан харьцаа байгальд хэрхэн илэрдэгийг би мэдэхгүй. Тиймээс бид онгоцон дээрх алтан харьцаа руу буцдаг. Тиймээс, талбайнуудаа дахин харцгаая. Математикийн хувьд энэ бол бидний олж авсан зураг юм.

Өөрөөр хэлбэл, бид алтан харьцааг олж авдаг - нэг тал нь хоёр хэсэгт хуваагдсан харьцаагаар жижиг хэсэг нь том хэсэгтэй, том хэсэг нь бүхэл бүтэн утгатай холбоотой байдаг.

Энэ нь a: b = b: c эсвэл c: b = b: a.

Энэ хэмжээсийн харьцаанд үндэслэн ердийн таван өнцөгт ба пентаграммыг бүтээдэг.

Лавлагааны хувьд: пентаграм барихын тулд та ердийн таван өнцөгт барих хэрэгтэй. Түүнийг барих аргыг Германы зураач, график зураач Альбрехт Дюрер (1471...1528) боловсруулсан. О-г тойргийн төв, А-г тойргийн цэг, Е-г ОА сегментийн дунд цэг гэж үзье. О цэг дээр сэргээгдсэн OA радиустай перпендикуляр нь D цэг дээр тойргийг огтолж байна. Луужин ашиглан диаметр дээр CE = ED хэрчмийг зур. Тойрог дотор бичсэн талын урт ердийн таван өнцөгт DC-тэй тэнцүү. Бид тойрог дээр DC сегментүүдийг зурж, ердийн таван өнцөгт зурах таван оноо авдаг. Бид таван өнцөгтийн булангуудыг диагональуудаар хооронд нь холбож, пентаграммыг авдаг. Пентагоны бүх диагональууд нь бие биенээ алтан харьцаагаар холбосон сегментүүдэд хуваадаг.

Ерөнхийдөө эдгээр нь хэв маяг юм. Түүгээр ч зогсохгүй тайлбарласнаас илүү олон янзын загварууд байдаг. Одоо эдгээр уйтгартай тоонуудын дараа бүх зүйл энгийн бөгөөд ойлгомжтой байх амласан видеог энд оруулав.

Таны харж байгаагаар математик үнэхээр байгальд байдаг. Зөвхөн видеонд жагсаасан объектуудад төдийгүй бусад олон газарт. Жишээлбэл, далайн эрэг дээр давалгаа эргэлдэх үед Алтан мушгиа дагуу эргэдэг. гэх мэт :)

Эртний Египетийн пирамидууд, Леонардо да Винчигийн Мона Лиза, наранцэцэг, эмгэн хумс, нарсны боргоцой, хүний ​​хуруунууд ямар нийтлэг зүйл байдгийг олж мэдье?

Энэ асуултын хариулт нь олдсон гайхалтай тоонуудад нуугдаж байна Фибоначчи нэрээрээ алдаршсан дундад зууны үеийн Италийн математикч Леонардо Пиза (1170 онд төрсөн - 1228 оноос хойш нас барсан), Италийн математикч . Дорнодоор аялж байхдаа Арабын математикийн ололттой танилцсан; Баруун руу шилжихэд хувь нэмэр оруулсан.

Түүний нээлтийн дараа эдгээр тоонуудыг алдарт математикчийн нэрээр нэрлэж эхэлсэн. Фибоначчийн тооны дарааллын гайхалтай мөн чанар нь үүнд оршино Энэ дарааллын тоо бүр өмнөх хоёр тооны нийлбэрээс гарна.

Тиймээс дарааллыг бүрдүүлж буй тоонууд:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, …

"Фибоначчийн тоо" гэж нэрлэдэг бөгөөд дарааллыг өөрөө Фибоначчийн дараалал гэж нэрлэдэг.

Фибоначчийн тоонд маш нэг тоо байдаг сонирхолтой онцлог. Дараалсан дурын тоог цувралын урд байгаа тоонд хуваахад үр дүн нь үргэлж эргэн тойронд хэлбэлздэг утгатай байх болно. үндэслэлгүй утга 1.61803398875... тэгээд бусад болгонд нэг бол хэтэрдэг, эсвэл хүрэхгүй. (Ойролцоогоор иррационал тоо, өөрөөр хэлбэл аравтын бутархай дүрслэл нь хязгааргүй бөгөөд үе үе бус тоо)

Түүнчлэн дарааллын 13 дахь тооны дараа энэ хуваалтын үр дүн цуваа хязгааргүй болтол тогтмол болно... Дундад зууны үед ийм тогтмол тооны хуваагдлыг тэнгэрлэг хувь хэмжээ гэж нэрлэдэг байсан бөгөөд одоо үүнийг алтан хэсэг, алтан дундж буюу алтан дундаж гэж нэрлэдэг. алтан харьцаа . Алгебрийн хувьд энэ тоог Грекийн phi (Ф) үсгээр тэмдэглэдэг.

Тэгэхээр алтан харьцаа = 1:1.618

233 / 144 = 1,618

377 / 233 = 1,618

610 / 377 = 1,618

987 / 610 = 1,618

1597 / 987 = 1,618

2584 / 1597 = 1,618

Хүний бие ба алтан харьцаа

Зураач, эрдэмтэд, загвар зохион бүтээгчид, дизайнерууд алтан харьцааны харьцаагаар тооцоолол, зураг эсвэл ноорог зурдаг. Тэд алтан харьцааны зарчмын дагуу бүтээгдсэн хүний ​​биеийн хэмжилтийг ашигладаг. Леонардо Да Винчи, Ле Корбюзье нар өөрсдийн бүтээлээ бүтээхээсээ өмнө Алтан пропорцын хуулийн дагуу бүтээгдсэн хүний ​​биеийн параметрүүдийг авчээ.

Хамгийн үндсэн номОрчин үеийн бүх архитекторуудын хувьд E. Neufert-ийн "Барилгын зураг төсөл" лавлах ном нь алтан харьцааг агуулсан хүний ​​их биений параметрүүдийн үндсэн тооцоог агуулдаг.

Пропорц янз бүрийн хэсгүүдбидний бие бол алтан харьцаатай маш ойрхон тоо юм. Хэрэв эдгээр харьцаа нь алтан харьцааны томъёотой давхцаж байвал тухайн хүний ​​гадаад төрх, бие нь хамгийн тохиромжтой пропорциональ гэж тооцогддог. Хүний биед алтны хэмжүүрийг тооцоолох зарчмыг диаграмм хэлбэрээр дүрсэлж болно.

М/м=1.618

Хүний биеийн бүтэц дэх алтан харьцааны анхны жишээ:
Хүйсний цэгийг хүний ​​биеийн төв, хүний ​​хөл ба хүйсний хоорондох зайг хэмжүүрээр авч үзвэл хүний ​​өндөр 1.618 гэсэн тоотой тэнцэнэ.

Үүнээс гадна бидний биеийн хэд хэдэн үндсэн алтан хувь хэмжээ байдаг:

* хурууны үзүүрээс бугуй хүртэл тохой хүртэлх зай 1:1.618;

* мөрний түвшнээс толгойн орой хүртэлх зай ба толгойн хэмжээ 1:1.618;

* хүйсний цэгээс толгойн титэм, мөрний түвшингээс толгойн титэм хүртэлх зай 1:1.618;

* хүйсний цэгээс өвдөг хүртэл, өвдөгнөөс хөл хүртэлх зай 1:1.618;

* эрүүний үзүүрээс дээд уруулын үзүүр хүртэл, дээд уруулын үзүүрээс хамрын нүх хүртэлх зай 1:1.618;

* эрүүний үзүүрээс хөмсөгний дээд шугам хүртэл, хөмсөгний дээд шугамаас титэм хүртэлх зай 1:1.618;

* эрүүний үзүүрээс хөмсөгний дээд шугам, хөмсөгний дээд шугамаас титэм хүртэлх зай 1:1.618:

Хүний нүүр царай дахь алтан харьцаа нь төгс гоо сайхны шалгуур юм.

Хүний нүүр царайны бүтцэд алтан харьцааны томьёотой ойролцоо олон жишээ байдаг. Гэсэн хэдий ч, бүх хүмүүсийн нүүрийг хэмжих захирагчийг нэн даруй бүү яар. Эрдэмтэн, зураач, уран барималч, уран барималчдын үзэж байгаагаар алтан харьцаатай яг таарч тохирох нь зөвхөн төгс гоо үзэсгэлэнтэй хүмүүст л байдаг. Үнэн хэрэгтээ хүний ​​нүүрэнд алтан хувь яг байх нь хүний ​​харцанд гоо сайхны хамгийн тохиромжтой зүйл юм.

Жишээлбэл, хэрэв бид хоёр урд дээд шүдний өргөнийг нэгтгэж, энэ нийлбэрийг шүдний өндрөөр хуваавал алтан харьцааны тоог олж авснаар эдгээр шүдний бүтэц хамгийн тохиромжтой гэж хэлж болно.

Хүний нүүрэн дээр алтан харьцааны дүрмийн бусад биелэлүүд байдаг. Эдгээр харилцааны зарим нь энд байна:

*Нүүрний өндөр/нүүрний өргөн;

* Уруулыг хамрын ёроолтой холбох төв цэг / хамрын урт;

* Нүүрний өндөр / эрүүний үзүүрээс уруул нийлэх төв цэг хүртэлх зай;

*Амны өргөн/хамрын өргөн;

* Хамрын өргөн / хамрын нүх хоорондын зай;

* Сурагчдын хоорондох зай / хөмсөг хоорондын зай.

Хүний гар

Зөвхөн алгаа өөртөө ойртуулж, долоовор хуруугаа анхааралтай ажиглахад л хангалттай бөгөөд та алтан харьцааны томъёог тэр даруй олох болно. Бидний гарын хуруу бүр гурван фалангаас бүрдэнэ.

* Хурууны эхний хоёр фалангуудын нийлбэр нь хурууны бүх урттай харьцуулахад алтан харьцааны тоог өгдөг (эрхий хуруунаас бусад);

* Үүнээс гадна дунд хуруу ба жижиг хурууны хоорондох харьцаа нь алтан харьцаатай тэнцүү байна;

* Хүн 2 гартай, гар тус бүрийн хуруу нь 3 фалангаас (эрхий хуруунаас бусад) бүрдэнэ. Гар тус бүр дээр 5 хуруу, өөрөөр хэлбэл нийт 10 хуруу байдаг, гэхдээ хоёр фаланксын хоёр эрхий хурууг эс тооцвол алтан харьцааны зарчмын дагуу ердөө 8 хуруу бий. Эдгээр бүх тоо 2, 3, 5, 8 нь Фибоначчийн дарааллын тоонууд юм:

Хүний уушигны бүтэц дэх алтан харьцаа

Америкийн физикч Б.Д.Уэст, доктор А.Л. Голдбергер физик, анатомийн судалгааны явцад алтан харьцаа нь хүний ​​уушигны бүтцэд бас байдаг болохыг тогтоожээ.

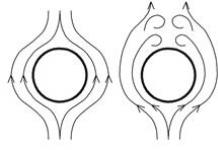
Хүний уушгийг бүрдүүлдэг гуурсан хоолойн өвөрмөц байдал нь тэдний тэгш бус байдалд оршдог. Гуурсан хоолой нь хоёр үндсэн амьсгалын замаас бүрддэг бөгөөд тэдгээрийн нэг нь (зүүн) урт, нөгөө нь (баруун) богино байдаг.

* Энэхүү тэгш бус байдал нь гуурсан хоолойн мөчрүүд, амьсгалын замын бүх жижиг хэсгүүдэд үргэлжилдэг болохыг тогтоожээ. Түүнчлэн богино ба урт гуурсан хоолойн уртын харьцаа нь алтан харьцаа бөгөөд 1: 1.618 байна.

Алтан ортогональ дөрвөлжин ба спираль хэлбэрийн бүтэц

Алтан харьцаа нь сегментийг тэгш бус хэсгүүдэд хуваах ийм пропорциональ хуваагдал бөгөөд үүнд сегмент бүхэлдээ том хэсэг нь өөрөө жижиг хэсэгтэй холбоотой байдаг; эсвэл өөрөөр хэлбэл, том хэсэг нь бүхэлдээ байхын хэрээр жижиг хэсэг нь том байх болно.

Геометрийн хувьд ийм харьцаатай тэгш өнцөгтийг алтан тэгш өнцөгт гэж нэрлэх болсон. Түүний урт талууд нь таарч байна богино талууд 1.168:1 харьцаатай.

Алтан тэгш өнцөгт нь бас олон гайхалтай шинж чанартай байдаг. Алтан тэгш өнцөгт нь олон ер бусын шинж чанартай байдаг. Тал нь тэгш өнцөгтийн жижиг талтай тэнцүү алтан тэгш өнцөгтөөс дөрвөлжин хайчилж авснаар бид дахин жижиг хэмжээтэй алтан тэгш өнцөгтийг олж авна. Энэ үйл явцыг тодорхойгүй хугацаагаар үргэлжлүүлж болно. Үргэлжлүүлэн дөрвөлжин зүсэх тусам бид жижиг, жижиг алтан тэгш өнцөгтүүдтэй болно. Түүнээс гадна тэдгээрийг логарифмын спираль хэлбэрээр байрлуулах бөгөөд энэ нь байгалийн объектуудын математик загварт чухал ач холбогдолтой (жишээлбэл, эмгэн хумсны бүрхүүл).

Спираль туйл нь анхны тэгш өнцөгт ба эхний зүсэгдсэн босоо тэнхлэгийн диагональуудын огтлолцол дээр байрладаг. Түүгээр ч барахгүй, дараачийн бүх буурдаг алтан тэгш өнцөгтүүдийн диагональууд нь эдгээр диагональууд дээр байрладаг. Мэдээж алтан гурвалжин бас бий.

Английн загвар зохион бүтээгч, гоо зүйч Уильям Чарлтон хүмүүс спираль хэлбэрийг нүдэнд тааламжтай гэж үзэж, олон мянган жилийн турш хэрэглэж ирсэн гэж мэдэгдээд үүнийг дараах байдлаар тайлбарлав.

"Бид спираль хэлбэртэй байх дуртай, учир нь бид үүнийг нүдээр харж чаддаг."

Байгальд

* Спираль бүтцийн үндэс суурь болох алтан харьцааны дүрэм нь байгальд хосгүй гоо үзэсгэлэнг бүтээхэд маш олон удаа байдаг. Хамгийн тайлбарлах жишээнүүд- спираль хэлбэрийг наранцэцгийн үр, боргоцой, хан боргоцой, какти, сарнайн дэлбээний бүтэц гэх мэт зохион байгуулалтаас харж болно;

* Ургамал судлаачид мөчир, наранцэцгийн үр эсвэл нарсны боргоцой дээрх навчийг байрлуулахад Фибоначчийн цуврал тод илэрдэг тул алтан харьцааны хууль илэрдэг болохыг тогтоожээ;

Төгс Хүчит Их Эзэн Өөрийн бүтээл бүрт тусгай хэмжүүр тогтоож, түүнд пропорциональ байдлыг өгсөн нь байгальд байдаг жишээнүүдээр нотлогддог. Амьд организмын өсөлтийн үйл явц нь логарифмын спираль хэлбэртэй яг таарч явагддаг олон жишээг дурдаж болно.

Спираль дахь бүх булаг нь байдаг ижил хэлбэр. Рашаануудын хэмжээ ихэссэн ч спираль хэлбэр өөрчлөгдөөгүй хэвээр байдгийг математикчид тогтоожээ. Спираль шиг өвөрмөц шинж чанартай өөр хэлбэр математикт байдаггүй.

Далайн хясааны бүтэц

Дотоод болон гадаад бүтэцДалайн ёроолд амьдардаг зөөлөн биетэй нялцгай биетүүдийн хясаа гэж дараахь зүйлийг тэмдэглэжээ.

"Бүрцгийн дотоод гадаргуу нь төгс гөлгөр бол гаднах гадаргуу нь барзгар, жигд бус байдлаар бүрхэгдсэн байдаг. Зөөлөн бие нь бүрхүүлд байсан бөгөөд үүний тулд бүрхүүлийн дотоод гадаргуу нь төгс гөлгөр байх ёстой. Гаднах булангууд - бүрхүүлийн гулзайлт нь түүний хүч чадал, хатуулгийг нэмэгдүүлж, улмаар түүний хүчийг нэмэгдүүлдэг. Бүрхүүлийн (эмгэн хумс) бүтцийн төгс байдал, гайхалтай оюун ухаан нь гайхалтай юм. Бүрхүүлийн спираль санаа нь төгс геометрийн хэлбэр бөгөөд гоёмсог гоо үзэсгэлэнгээрээ гайхалтай юм."

Бүрхүүлтэй ихэнх эмгэн хумсны бүрхүүл нь логарифмын спираль хэлбэрээр ургадаг. Гэсэн хэдий ч эдгээр үндэслэлгүй амьтад логарифмын спираль талаар ямар ч ойлголтгүй төдийгүй өөрсдөдөө спираль хэлбэртэй бүрхүүл бүтээх хамгийн энгийн математикийн мэдлэггүй гэдэгт эргэлзэх зүйл алга.

Гэвч эдгээр үндэслэлгүй амьтад хэрхэн өсч хөгжих, оршин тогтнох хамгийн тохиромжтой хэлбэрийг спираль бүрхүүл хэлбэрээр тодорхойлж, сонгож чадсан бэ? Эдгээр амьд биетүүд чадах болов уу, хэн эрдэмтдийн ертөнцАмьдралын анхдагч хэлбэрийг дуудаж, бүрхүүлийн логарифм хэлбэр нь тэдний оршин тогтноход тохиромжтой болохыг тооцоолох уу?

Мэдээжийн хэрэг үгүй, учир нь ийм төлөвлөгөө оюун ухаан, мэдлэггүйгээр биелэх боломжгүй юм. Гэхдээ эртний нялцгай биетүүд ч, ухамсаргүй байгальд ч ийм оюун ухаан байдаггүй боловч зарим эрдэмтэд дэлхий дээрх амьдралыг бүтээгч гэж нэрлэдэг (?!)

Амьдралын ийм хамгийн анхдагч хэлбэр ч бий болсон шалтгааныг байгалийн тодорхой нөхцөл байдлын санамсаргүй нийлбэрээр тайлбарлах гэж оролдох нь утгагүй юм. Энэ төсөл бол ухамсартай бүтээл гэдэг нь ойлгомжтой.

Биологич сэр Д'арки Томпсон далайн хясааны энэ төрлийн өсөлтийг гэж нэрлэдэг "Одойн өсөлтийн хэлбэр."

Сэр Томпсон дараах тайлбарыг хийж байна.

“Далайн хясаа ургах шиг энгийн систем байхгүй бөгөөд тэдгээр нь хувь хэмжээгээр ургаж, нэг хэлбэрээ хадгалж байдаг. Хамгийн гайхалтай нь бүрхүүл нь ургадаг ч хэлбэрээ хэзээ ч өөрчлөгддөггүй."

Хэдэн см диаметртэй "Наутилус" бол гном ургах зуршлын хамгийн тод жишээ юм. С.Моррисон хүний ​​оюун ухаанаар ч төлөвлөхөд нэлээд хэцүү мэт санагдах энэхүү наутилус ургах үйл явцыг дараах байдлаар дүрсэлжээ.

"Наутилус бүрхүүлийн дотор сувдан хана бүхий олон тасалгаанууд байдаг бөгөөд доторх бүрхүүл нь өөрөө төвөөсөө сунадаг спираль хэлбэртэй байдаг. Наутилус өсөхийн хэрээр хясааны урд хэсэгт өөр нэг өрөө ургасан боловч энэ удаад өмнөхөөсөө том болсон бөгөөд үлдсэн өрөөний хуваалтууд нь сувдан давхаргаар хучигдсан байдаг. Тиймээс спираль үргэлж пропорциональ хэмжээгээр тэлж байдаг."

Шинжлэх ухааны нэрсийн дагуу логарифмын өсөлтийн загвар бүхий спираль бүрхүүлийн зарим төрлийг энд дурдъя.
Haliotis Parvus, Dolium Perdix, Murex, Fusus Antiquus, Scalari Pretiosa, Solarium Trochleare.

Олдсон бүх хясааны үлдэгдэл нь спираль хэлбэртэй байв.

Гэсэн хэдий ч логарифмын өсөлтийн хэлбэр нь зөвхөн нялцгай биетүүдэд төдийгүй амьтны ертөнцөд байдаг. Цагаан зээр, ямаа, хуц болон бусад ижил төстэй амьтдын эвэр нь алтан харьцааны хуулийн дагуу спираль хэлбэрээр хөгждөг.

Хүний чихэнд байдаг алтан харьцаа

Хүний дотоод чихэнд дууны чичиргээг дамжуулах үүргийг гүйцэтгэдэг Чихний дун ("Эмгэн хумс") хэмээх эрхтэн байдаг.. Энэхүү ясны бүтэц нь шингэнээр дүүрсэн бөгөөд эмгэн хумс шиг хэлбэртэй бөгөөд тогтвортой логарифмын спираль хэлбэртэй = 73º 43'.

Амьтны эвэр, соёо нь спираль хэлбэртэй хөгжиж байна

Заан болон устаж үгүй ​​болсон хөхтөн амьтдын соёо, арслангийн хумс, тотьны хошуу нь логарифм хэлбэртэй бөгөөд спираль хэлбэртэй тэнхлэгийн хэлбэртэй төстэй. Аалзнууд сүлжээгээ үргэлж логарифмын спираль хэлбэрээр сүлждэг. Планктон (зүйл globigerinae, planorbis, vortex, terebra, turitellae, trochida) зэрэг бичил биетний бүтэц нь спираль хэлбэртэй байдаг.

Бичил ертөнцийн бүтэц дэх алтан харьцаа

Геометрийн дүрс нь зөвхөн гурвалжин, дөрвөлжин, таван өнцөгт эсвэл зургаан өнцөгтөөр хязгаарлагдахгүй. Хэрэв бид эдгээр дүрсийг өөр хоорондоо өөр өөр аргаар холбовол бид шинэ гурван хэмжээстийг олж авна геометрийн дүрсүүд. Үүний жишээ бол шоо эсвэл пирамид гэх мэт дүрсүүд юм. Гэсэн хэдий ч тэднээс гадна өөр гурван хэмжээст дүрсүүд байдаг бөгөөд тэдгээр нь бидний олж хараагүй байдаг Өдөр тутмын амьдрал, мөн хэний нэрийг бид анх удаа сонсож байна. Ийм гурван хэмжээст дүрсүүдийн дунд тетраэдр (ердийн дөрвөн талт дүрс), октаэдр, додекаэдр, икосаэдр гэх мэт орно. Додекаэдр нь 13 таван өнцөгт, икосаэдр нь 20 гурвалжингаас бүрдэнэ. Математикчид эдгээр тоонууд нь математикийн хувьд маш амархан хувирдаг бөгөөд тэдгээрийн хувирал нь алтан харьцааны логарифм спираль томъёоны дагуу явагддаг гэдгийг тэмдэглэжээ.

Бичил ертөнцөд алтан харьцаагаар бүтээгдсэн гурван хэмжээст логарифмын хэлбэрүүд хаа сайгүй байдаг. . Жишээлбэл, олон тооны вирусууд икозаэдр гурван хэмжээст геометрийн хэлбэртэй байдаг. Магадгүй эдгээр вирусуудаас хамгийн алдартай нь Адено вирус юм. Адено вирусын уургийн бүрхүүл нь тодорхой дарааллаар байрлуулсан 252 нэгж уургийн эсээс үүсдэг. Икосаэдрийн өнцөг булан бүрт таван өнцөгт призм хэлбэртэй 12 нэгж уургийн эсүүд байдаг бөгөөд эдгээр булангуудаас баяжуулалт хэлбэртэй бүтэцүүд үргэлжилдэг.

Вирусын бүтэц дэх алтан харьцааг 1950-иад онд анх илрүүлсэн. Лондонгийн Биркбек коллежийн эрдэмтэд А.Клуг, Д.Каспар нар. 13 Полио вирус нь логарифмын хэлбэрийг харуулсан анхны хүн юм. Энэ вирусын хэлбэр нь Rhino 14 вирусын хэлбэртэй төстэй болсон.

Хүний оюун ухаанд ч бүтээхэд хэцүү, бүтэц нь алтан харьцааг агуулсан гурван хэмжээст цогц хэлбэрийг вирус яаж үүсгэдэг вэ гэсэн асуулт гарч ирнэ. Вирусын эдгээр хэлбэрийг нээсэн вирус судлаач А.Клуг дараах тайлбарыг өгч байна.

“Доктор Каспар бид хоёр вирусын бөмбөрцөг бүрхүүлийн хувьд хамгийн оновчтой хэлбэр нь икосаэдрон хэлбэр гэх мэт тэгш хэм гэдгийг харуулсан. Энэ дараалал нь холбох элементүүдийн тоог багасгадаг ... Бакминстер Фуллерийн геодезийн хагас бөмбөрцөг кубуудын ихэнх нь ижил төстэй геометрийн зарчим дээр баригдсан. 14 Ийм шоо суурилуулах нь маш нарийвчлалтай, нарийвчилсан тайлбар диаграммыг шаарддаг. Харин ухамсаргүй вирусууд өөрсдөө уян хатан, уян хатан уургийн эсийн нэгжүүдээс ийм нарийн төвөгтэй бүрхүүлийг бүтээдэг."

GOU №1505 биеийн тамирын заал

"Москва хотын сурган хүмүүжүүлэх гимназийн лаборатори"

Эссэ

Фибоначчийн тоо ба Алтан харьцаа

Азов Никита

Удирдагч:Шалимова М.Н.

Оршил ………………………………………………….……………2

1-р бүлэг

Фибоначчийн тоонуудын түүх………………………………………..5

2-р бүлэг

Fibonacci numbers as a reciprocal progression………...…...………………………………………………………..….....12

3-р бүлэг

Фибоначчийн тоо ба алтан харьцаа ………………………

Дүгнэлт …………………………………………………...…...16

Ном зүй ………………………………………………………………….……..20

Оршил.

Судалгааны хамаарал. Миний бодлоор өнөө үед шинжлэх ухааны хөгжлийн түүхээс мэдэгдэж буй математик теорем, баримтуудад бага анхаарал хандуулдаг. Фибоначчийн тоонуудын жишээн дээр би тэдгээр нь ямар даяарчлалтай, зөвхөн математикт төдийгүй өдөр тутмын амьдралд хэр өргөн хэрэглэгдэх боломжтой болохыг харуулахыг хүсч байна.

Миний ажлын зорилго бол Фибоначчийн тоонуудын түүх, шинж чанар, хэрэглээ, алтан харьцаатай холболтыг судлах явдал юм.

Бүлэг 1. Фибоначчийн тоо ба тэдгээрийн түүх.

Леонардо (1170-1250) Пиза хотод төрсөн. Дараа нь тэрээр "сайн төрсөн хүү" гэсэн утгатай Фибоначчи хоч авсан. Түүний аав Хойд Африкийн Арабын орнуудад худалдаа эрхэлдэг байжээ. Тэнд Леонардо араб багш нартай математикийн чиглэлээр суралцаж, Энэтхэг, эртний Грекийн эрдэмтдийн ололт амжилттай танилцсан. Араб орчуулга. Судалсан бүх материалаа эзэмшсэнийхээ дараа тэрээр өөрийн "Абакийн ном" хэмээх номоо бүтээжээ (анхны хэвлэл нь 1202 онд бичигдсэн боловч зөвхөн 1228 оны дахин хэвлэлт бидэнд үлдсэн). Ийнхүү тэрээр дундад зууны анхны математикч болж, Европыг араб тоо, тоотой танилцуулсан. аравтын систембидний өдөр тутам хэрэглэдэг тооцоолол эхний жилүүдмөн хөгшрөх хүртэл.

Абакусын номыг агуулгын дагуу таван хэсэгт хувааж болно. Номын эхний таван бүлгийг аравтын бутархай тоололд суурилсан бүхэл тоон арифметикт зориулав. 6-7-р бүлэгт энгийн бутархайн үйлдлүүдийг тайлбарласан болно. 8-10-р бүлэгт пропорц ашиглан асуудлыг шийдвэрлэх арга техникийг тайлбарласан болно. 11-р бүлэгт холих асуудлуудыг авч үздэг бол 12-р бүлэгт Фибоначчийн тоо гэж нэрлэгддэг тоонуудыг авч үздэг. Доор бид тоонуудтай өөр хэд хэдэн арга техникийг тайлбарлаж, янз бүрийн сэдвээр асуудал өгдөг.

Фибоначчийн тооны цувралын гарал үүслийг тайлбарлах гол асуудал бол туулайн асуудал юм. Асуудлын асуулт бол: "Нэг хосоос нэг жилд хэдэн хос туулай төрдөг вэ?" Хос туулай сарын дараа дахин нэг хос төрдөг ба угаасаа туулай төрснөөс хойш хоёр дахь сараас эхлэн төллөж эхэлдэг асуудлын талаар тайлбар өгсөн. Зохиогч бидэнд асуудлын шийдлийг өгдөг. Эхний сард анхны хос өөр нэгийг төрүүлэх болно. Хоёрдугаарт, эхний хос өөр нэгийг төрүүлэх болно - гурван хос байх болно. Гурав дахь сард хоёр хос хүүхэд төрүүлэх болно - анх төрсөн болон эхний сард төрсөн хосууд. 5 хос хийдэг. Гэх мэтээр тайлбарлахдаа ижил логикийг ашиглан бид дөрөв дэх сард 8 хос, тавдугаар сард 13, зургаа дахь нь 21, долоо дахь нь 34, найм дахь нь 55, ес дэх нь 89, аравдугаарт 144, арван нэгдүгээрт 233, арван хоёрдугаарт 377.

Бид аль ч арван хоёр сарын туулайн тоог u n гэж тодорхойлж болно. Бид хэд хэдэн тоо авдаг:

Эдгээр тоонуудын цувралд гишүүн бүр нь өмнөх хоёрын нийлбэртэй тэнцүү байна. Тэгшитгэлийн аль ч гишүүнийг тэгшитгэлээр тодорхойлж болно.

u 1 ба u 2 =1 байх үед энэ тэгшитгэлийн чухал онцгой тохиолдлыг авч үзье. Бид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 гэсэн тооны дарааллыг авах болно... Бид туулайн тухай бодлогод ижил тооны дарааллыг хүлээн авсан. Эдгээр тоонуудыг зохиогчийнхоо хүндэтгэлд Фибоначчийн тоо гэж нэрлэдэг.

Эдгээр тоонууд болон тэгшитгэл (2) нь миний ажилд авч үзэх олон шинж чанартай байдаг.

Бүлэг 2. Фибоначчийн тооны цуврал ба прогрессийн хоорондын хамаарал. Цувралын үндсэн шинж чанарууд.

Цувралын үндсэн шинж чанарыг олж авахын тулд эхний таван тоог жишээ болгон авч үзье: 1, 1, 2, 3, 5, 8. Шинэ тоо бүр өмнөх хоёрын нийлбэртэй тэнцүү байгааг бид харж байна. Эндээс бид цувралын дурын тоог олж авах томьёо, мөн цувааны дурын тооны тооны нийлбэрийн томъёог гаргаж болно.

Томъёо нь арифметик ба геометрийн прогрессийн шинж чанараас эрс ялгаатай болохыг бид харж байна. Цувралын эхний хоёр тоо л ямар ч дэвшилттэй холбоотой байж болно гэж бид бас хэлж чадна.

Арифметик ба геометрийн прогресс нь өмнө дурдсан хоёр л томьёотой бөгөөд жишээлбэл, тэгш, сондгой, тоонуудын квадратуудын нийлбэрийг тооцоолохын тулд та тусдаа цувралын асуудлыг шийдэх бүрдээ хэрэгтэй болно. Гэхдээ Фибоначчийн тоонуудын тоо нь өөрчлөгддөггүй (алхам, хуваагч, прогрессийн янз бүрийн эхний нөхцөл байхгүй) тул энэ нь цувралын бие даасан элементүүдийн нийлбэрийг олж авах томъёог гаргаж авах боломжтой гэсэн үг юм. Тэгш тоо бүхий цувралын тоонуудын нийлбэрийг олж авах жишээ томъёо энд байна.

Сондгой тоонуудын хувьд ижил төстэй томъёо байдаг:

Цуврал квадратаас тоонуудын нийлбэрийг олж авах томъёо бас байдаг.

Фибоначчийн тоонууд нь арифметик болон геометрийн прогрессод байдаггүй өөр нэг өвөрмөц шинж чанартай байдаг. Цуврал тоонуудын харьцаа (өмнөх ба дараагийнх) нь 0.618 утга руу байнга чиглэдэг бөгөөд F n-ийг F n +2-д (харьцаа нь 0.382-д хүрэх хандлагатай), F n-ийг F n +3-д хуваах үед ижил төстэй нөхцөл байдал үүсдэг. харьцаа 0.236 хандлагатай байна) гэх мэт Цаашид. Үүний үр дүнд бид тодорхой харилцаатай болсон. Тэдний утгуудын багц ба урвуу утгыг Фибоначчийн харьцаа гэж нэрлэдэг. 0.618 – 1.618 урвуу утга нь тоо юм

(“fi”) Энэ нь мөн цувааны шинж чанарын x 2 -x-1 олон гишүүнтийн хос язгууруудын нэг юм.

Бүлэг 3. Алтан харьцаа ба Фибоначчийн тоо.

Алтан харьцаа (алтан харьцаа, туйлын болон дундаж харьцаагаар хуваагдах) - хуваагдал тасралтгүй утгажижиг хэсэг нь том хэсэгтэй, том хэсэг нь бүхэл хэмжээтэй холбоотой байхаар хоёр хэсэгт хуваагдана.

Үүнийг хязгааргүй шулуун шугамын жишээн дээр тайлбарлахыг хичээцгээе. c шулуун шугамыг бүхэлд нь нэг гэж авцгаая. Шугамыг 0.618 ба 0.382 гэх мэт 1-тэй тэнцүү хэсгүүдэд хуваадаг a ба b гэсэн хоёр хэсэгт хуваая. Мөн эдгээр тоо нь Фибоначчийн тооны цувралын коэффициентүүдийн нэг юм. Энэ шугамын том хэсгүүдийн жижиг хэсгүүдийн харьцаа нь тоонд асимптотоор ойртож байгааг бид олж мэдэв

.

Алтан харьцааны зарчмыг тусгасан хоёр үндсэн тоо байдаг.

Алтан харьцааг эртний Грекчүүд мэддэг байсан. Архимедийг Архимедийн спираль нээсэн гэж үздэг. Үүний утга нь шинэ буржгар бүр тодорхой тоогоор нэмэгдэж, эдгээр буржгар үсний харьцаа нь тоотой тэнцүү байна.

.

Хоёр дахь дүрс нь алтан гурвалжин юм. Энэ бол талуудын суурийн харьцаа тэнцүү байх тэгш өнцөгт гурвалжин юм

Математик болон байгаль дахь Фибоначчийн дараалал

Фибоначчийн дараалал, "Да Винчи код" киноноос хүн бүрийн мэддэг - 13-р зуунд Фибоначчи хочоор алдаршсан Италийн математикч Пизагийн Леонардогийн оньсого хэлбэрээр дүрсэлсэн цуврал тоо. Товчхондоо тааварын мөн чанар:

Хэрвээ туулайн шинж чанар нь сар бүр нэг хос туулай төрүүлж, чадвартай болдог бол жилд хэдэн хос туулай төрөхийг мэдэхийн тулд хэн нэгэн хос туулайг тодорхой битүү орон зайд байрлуулжээ. хоёр сартайд нь үр төл гаргах.

Үр дүн нь дараах дараалал юм. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 , энд арван хоёр сар бүрийн хос туулайн тоог таслалаар заана.

Энэ дарааллыг тодорхойгүй хугацаагаар үргэлжлүүлж болно. Үүний мөн чанар нь дараагийн тоо бүр нь өмнөх хоёрын нийлбэр юм.

Энэ дараалал нь зайлшгүй хөндөх шаардлагатай хэд хэдэн математик шинж чанартай байдаг. Энэ дараалал нь асимптотик байдлаар (удаан, удаан ойртож) зарим тогтмол руу чиглэдэг харьцаа. Гэсэн хэдий ч энэ харьцаа нь иррациональ, өөрөөр хэлбэл бутархай хэсэгт аравтын оронтой тоонуудын хязгааргүй, урьдчилан тааварлашгүй дараалал бүхий тоо юм. Үүнийг нарийн илэрхийлэх боломжгүй юм.

Ийнхүү дарааллын аль нэг гишүүний өмнөх гишүүнтэй харьцуулсан харьцаа нь тооны орчим хэлбэлздэг 1,618 , заримдаа хэтрүүлэх, заримдаа хүрэхгүй байх. Дараахтай харьцуулсан харьцаа нь тоонд адилхан ойртдог 0,618 , энэ нь урвуу пропорциональ байна 1,618 . Хэрэв бид дарааллын элементүүдийг нэгээр нь хуваавал тоонууд гарч ирнэ 2,618 Тэгээд 0,382 , тэдгээр нь мөн урвуу пропорциональ байна. Эдгээр нь Фибоначчийн харьцаа гэж нэрлэгддэг.

Энэ бүхэн юуны төлөө вэ? Байгалийн хамгийн нууцлаг үзэгдлүүдийн нэгэнд бид ингэж ханддаг. Фибоначчи үндсэндээ шинэ зүйл нээсэнгүй, тэр зүгээр л ийм үзэгдлийг дэлхийд сануулсан Алтан харьцаа, энэ нь ач холбогдлын хувьд Пифагорын теоремоос дутахгүй

Бид эргэн тойрон дахь бүх объектыг хэлбэр дүрсээр нь ялгадаг. Бид заримд нь илүү дуртай, зарим нь бага, зарим нь бүрмөсөн дургүй байдаг. Заримдаа сонирхол нь амьдралын нөхцөл байдлаас, заримдаа ажиглагдсан объектын гоо үзэсгэлэнгээс хамаардаг. Тэгш хэмтэй, пропорциональ хэлбэр нь харааны хамгийн сайн ойлголтыг бий болгож, гоо үзэсгэлэн, эв найрамдлын мэдрэмжийг төрүүлдэг. Бүрэн дүрс нь үргэлж өөр хоорондоо болон бүхэлдээ тодорхой харилцаатай байдаг өөр өөр хэмжээтэй хэсгүүдээс бүрддэг.

Алтан харьцаа- шинжлэх ухаан, урлаг, байгаль дахь бүхэл бүтэн болон түүний хэсгүүдийн төгс төгөлдөр байдлын хамгийн дээд илрэл.

Энгийн жишээ татахад, Алтан харьцаа гэдэг нь сегментийг хоёр хэсэгт хуваах бөгөөд тэдгээрийн нийлбэр (бүх сегмент) нь том хэсэгтэй харьцуулахад том хэсэг нь жижиг хэсэгтэй холбоотой байх болно.

Хэрэв бид сегментийг бүхэлд нь авбал вард 1 , дараа нь сегмент атэнцүү байх болно 0,618 , шугамын хэсэг б - 0,382 , зөвхөн ийм байдлаар Алтан хэсгийн нөхцөл хангагдана (0.618/0.382= 1,618 ; 1/0,618=1,618 ). Хандлага вруу атэнцүү байна 1,618 , А -тайруу b2.618. Эдгээр нь бидэнд аль хэдийн танил болсон Фибоначчийн харьцаа юм.

Мэдээжийн хэрэг алтан тэгш өнцөгт, алтан гурвалжин, бүр алтан шоо хэлбэртэй байдаг. Хүний биеийн харьцаа олон талаараа Алтан хэсэгтэй ойролцоо байдаг.

Зураг: marcus-frings.de

Гэхдээ бид олж авсан мэдлэгээ нэгтгэснээр хөгжилтэй эхэлдэг. Зураг нь Фибоначчийн дараалал ба Алтан харьцаа хоорондын хамаарлыг тодорхой харуулж байна. Бид эхний хэмжээтэй хоёр квадратаас эхэлдэг. Дээрээс нь хоёр дахь хэмжээтэй квадрат нэмнэ. Хажууд нь өмнөх хоёр, гурав дахь хэмжээтэй талуудын нийлбэртэй тэнцүү талтай дөрвөлжин зур. Үүнтэй адилтгаж үзвэл таван хэмжээтэй квадрат гарч ирнэ. Ингээд ядрах хүртлээ гол зүйл бол дараагийн дөрвөлжин бүрийн хажуугийн урт нь өмнөх хоёр талын уртын нийлбэртэй тэнцүү байх явдал юм. Хажуугийн урт нь Фибоначчийн тоо бөгөөд хачирхалтай нь тэднийг Фибоначчийн тэгш өнцөгт гэж нэрлэдэг хэд хэдэн тэгш өнцөгтүүдийг бид харж байна.

Хэрэв бид квадратынхаа булангуудыг гөлгөр шугамаар зурах юм бол өсөлт нь үргэлж жигд байдаг Архимед спиральаас өөр зүйл олж авахгүй.

Танд юу ч сануулахгүй байна уу?

Зураг: этанхайн Flickr дээр

Зөвхөн нялцгай биетний бүрхүүлээс та Архимедийн спираль олж болно, гэхдээ олон цэцэг, ургамалд тэдгээр нь тийм ч тод харагддаггүй.

Aloe multifolia:

Зураг: шар айрагны дэвтэр Flickr дээр

Зураг: beart.org.uk

Зураг: эсдраскальдеран Flickr дээр

Зураг: manj98 Flickr дээр

Одоо Алтан хэсгийг санах цаг болжээ! Эдгээр гэрэл зургуудад байгалийн хамгийн үзэсгэлэнтэй, эв найртай бүтээлүүдийг дүрсэлсэн байна уу? Энэ нь бүгд биш юм. Хэрэв та анхааралтай ажиглавал ижил төстэй хэв маягийг олон хэлбэрээр олж болно.

Мэдээжийн хэрэг, эдгээр бүх үзэгдлүүд нь Фибоначчийн дараалалд үндэслэсэн гэсэн мэдэгдэл хэтэрхий чанга сонсогдож байгаа ч чиг хандлага нь тодорхой байна. Түүнээс гадна, дараалал нь энэ ертөнцийн бүх зүйл шиг төгс төгөлдөр биш юм.

Фибоначчийн дараалал нь байгалиасаа илүү суурь, төгс алтан харьцаатай логарифм дараалалд дасан зохицох оролдлого гэсэн таамаг байдаг бөгөөд энэ нь бараг ижил, зөвхөн хаанаас ч эхэлж, хаашаа ч хүрэхгүй юм. Байгальд эхэлж болох бүхэл бүтэн эхлэл зайлшгүй хэрэгтэй; тэр оргүйгээс ямар нэг зүйлийг бүтээж чадахгүй. Фибоначчийн дарааллын эхний нөхцлүүдийн харьцаа нь Алтан харьцаанаас хол байна. Гэхдээ бид цаашаа явах тусам эдгээр хазайлтууд улам бүр жигдрэх болно. Аливаа дарааллыг тодорхойлохын тулд бие биенээ дагаж гурван нэр томъёог мэдэхэд хангалттай. Гэхдээ алтан дарааллын хувьд биш, хоёр нь хангалттай, энэ нь нэгэн зэрэг геометрийн болон арифметик прогресс юм. Үүнийг бусад бүх дарааллын үндэс гэж бодож магадгүй юм.

Алтан логарифмын дарааллын гишүүн бүр нь Алтан харьцааны хүч юм ( z). Цувралын нэг хэсэг нь иймэрхүү харагдаж байна: ... z -5 ; z -4; z -3; z -2; z -1; z 0 ; z 1 ; z 2 ; z 3 ; z 4 ; z 5...Хэрэв бид Алтан харьцааны утгыг аравтын бутархайн гурван орон болгон бөөрөнхийлвөл бид авна z=1.618, дараа нь цуврал дараах байдалтай харагдана. ... 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 ... Дараагийн нэр томъёо бүрийг зөвхөн өмнөхийг үржүүлээд зогсохгүй авах боломжтой 1,618 , гэхдээ өмнөх хоёрыг нэмснээр. Тиймээс дараалал дахь экспоненциал өсөлт нь хоёр зэргэлдээ элементийг нэмэхэд л хүрдэг. Энэ бол эхлэл төгсгөлгүй цуврал бөгөөд Фибоначчийн дараалал ийм байхыг хичээдэг. Маш тодорхой эхлэлтэй тэрээр идеал руу тэмүүлдэг, хэзээ ч түүндээ хүрдэггүй. Тэр бол амьдрал.

Гэсэн хэдий ч бидний харж, уншсан бүх зүйлтэй холбоотойгоор нэлээд логик асуултууд гарч ирдэг.
Эдгээр тоонууд хаанаас ирсэн бэ? Орчлон ертөнцийг төгс болгохыг хичээсэн энэ архитектор хэн бэ? Бүх зүйл түүний хүссэнээр байсан уу? Хэрэв тийм бол яагаад буруу болсон бэ? Мутаци? Чөлөөт сонголт уу? Дараа нь юу болох вэ? Спираль буржгар эсвэл тайлж байна уу?

Нэг асуултын хариултыг олсны дараа та дараагийн асуултыг авах болно. Хэрэв та үүнийг шийдвэл хоёр шинэ зүйл авах болно. Тэдэнтэй харьцсаны дараа дахиад гурав гарч ирнэ. Тэдгээрийг бас шийдсэний дараа та шийдэгдээгүй таван зүйлтэй болно. Дараа нь найм, дараа нь арван гурав, 21, 34, 55...