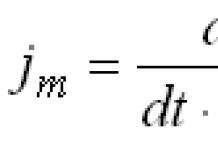Ердийн хуультархалт (ихэвчлэн Гауссын хууль гэж нэрлэдэг) нь магадлалын онолд маш чухал үүрэг гүйцэтгэдэг бөгөөд бусад тархалтын хуулиудын дунд онцгой байр суурь эзэлдэг. Энэ бол практикт хамгийн их тохиолддог түгээлтийн хууль юм. Ердийн хуулийг бусад хуулиас ялгаж буй гол онцлог нь энэ нь хязгаарлах хууль бөгөөд бусад хуваарилалтын хуулиуд маш нийтлэг ердийн нөхцөлд ханддагт оршино.

Аливаа тархалтын хуулинд (зарим маш сул хязгаарлалттай) хамаарах хангалттай олон тооны бие даасан (эсвэл сул хамааралтай) санамсаргүй хэмжигдэхүүний нийлбэр нь ердийн хуулинд ойролцоогоор захирагддаг нь нотлогдож болох бөгөөд энэ нь үнэн зөв байх тусам үнэн юм. их хэмжээнийсанамсаргүй хэмжигдэхүүнүүдийг нэгтгэн гаргадаг. Практикт тохиолдож буй санамсаргүй хэмжигдэхүүнүүдийн ихэнхийг жишээ нь хэмжилтийн алдаа, буудлагын алдаа гэх мэтийг маш олон тооны харьцангуй бага нэр томъёоны нийлбэрээр илэрхийлж болно - энгийн алдаа, тэдгээр нь тус бүр нь бусдаас үл хамааран тусдаа шалтгаан. Хувь хүний ​​энгийн алдаа нь тархалтын ямар хуулиудад захирагдахаас үл хамааран олон тооны нэр томъёоны нийлбэр дэх эдгээр хуваарилалтын онцлог шинж чанаруудыг тэгшитгэж, нийлбэр нь хэвийн хэмжээнд ойрхон хуульд захирагддаг. Дүгнэх алдаануудад тавигдсан гол хязгаарлалт нь тэдгээр нь бүгд нийтдээ харьцангуй бага үүрэг гүйцэтгэдэг явдал юм. Хэрэв энэ нөхцөл хангагдаагүй бөгөөд жишээлбэл, санамсаргүй алдаануудын аль нэг нь бусад бүхнээс илүү дүнгийн нөлөөгөөр огцом давамгайлж байвал энэхүү давамгайлсан алдааны тархалтын хууль нь хэмжээн дээр нөлөөлж, түүнийг тодорхойлох болно. хуваарилалтын хуулийн үндсэн шинж чанарууд.

Бие даасан жигд жижиг санамсаргүй гишүүдийн нийлбэрийн хязгаар болох хэвийн хуулийг тогтоосон теоремуудыг 13-р бүлэгт илүү дэлгэрэнгүй авч үзэх болно.

Хэвийн тархалтын хууль нь дараах хэлбэрийн магадлалын нягтралаар тодорхойлогддог.

Хэвийн тархалтын муруй нь тэгш хэмтэй толгод хэлбэртэй байдаг (Зураг 6.1.1). -тэй тэнцүү муруйн хамгийн их ординат нь цэгтэй тохирч байна; Цэгээс холдох тусам тархалтын нягт буурч, -д муруй асимптотоор абсцисс руу ойртоно.

Ердийн хуулийн илэрхийлэлд орсон тоон үзүүлэлтүүдийн утгыг олж мэдье (6.1.1); Утга нь математикийн хүлээлтээс өөр зүйл биш бөгөөд утга нь утгын стандарт хазайлт гэдгийг баталцгаая. Үүнийг хийхийн тулд бид хэмжигдэхүүний үндсэн тоон шинж чанарыг тооцоолдог - математикийн хүлээлт ба тархалт.

Хувьсагчийн өөрчлөлтийг ашиглах

Томъёоны (6.1.2) хоёр интервалын эхнийх нь байгаа эсэхийг шалгахад хялбар байдаг. тэгтэй тэнцүү; хоёр дахь нь алдарт Эйлер-Пуассоны интеграл юм.

Тиймээс,

тэдгээр. параметр нь утгын математик хүлээлтийг илэрхийлнэ. Энэ параметрийг, ялангуяа буудлагын асуудалд ихэвчлэн тархалтын төв (c.r. гэж товчилсон) гэж нэрлэдэг.

Хэмжигдэхүүний хэлбэлзлийг тооцоолъё:

.

Хувьсагчийн өөрчлөлтийг дахин хэрэглэж байна

Хэсэг хэсгүүдээр нэгтгэснээр бид дараахь зүйлийг авна.

Буржгар хаалтанд байгаа эхний гишүүн нь 0-тэй тэнцүү (утгад нь ямар ч хүч нэмэгдэхээс хурдан буурах), (6.1.3) томъёоны дагуу хоёр дахь гишүүн нь , эндээс.

Иймээс (6.1.1) томъёоны параметр нь утгын стандарт хазайлтаас өөр зүйл биш юм.

Параметр ба хэвийн тархалтын утгыг олж мэдье. Тархалтын тэгш хэмийн төв нь тархалтын төв болох нь (6.1.1) томъёоноос шууд тодорхой харагдаж байна. Энэ нь зөрүүний тэмдгийг урвуулахад илэрхийлэл (6.1.1) өөрчлөгдөхгүй гэдгээс тодорхой харагдаж байна. Хэрэв та тархалтын төвийг өөрчилбөл тархалтын муруй хэлбэрээ өөрчлөхгүйгээр абсцисса тэнхлэгийн дагуу шилжинэ (Зураг 6.1.2). Тархалтын төв нь абсцисса тэнхлэг дээрх тархалтын байрлалыг тодорхойлдог.

Тархалтын төвийн хэмжээ нь санамсаргүй хэмжигдэхүүний хэмжээстэй ижил байна.

Параметр нь байрлалыг бус харин тархалтын муруйн хэлбэрийг тодорхойлдог. Энэ бол тархалтын шинж чанар юм. Тархалтын муруйн хамгийн том ординат нь урвуу пропорциональ байна; нэмэгдэх тусам хамгийн их ординат буурна. Тархалтын муруйн талбай нь үргэлж нэгдмэл байдалтай байх ёстой тул ихсэх үед тархалтын муруй илүү хавтгай болж, x тэнхлэгийн дагуу сунадаг; эсрэгээр, буурах тусам тархалтын муруй нь дээшээ сунаж, хажуу талаас нь нэгэн зэрэг шахаж, илүү зүү хэлбэртэй болдог. Зураг дээр. 6.1.3-д гурван хэвийн муруйг (I, II, III) харуулав. Эдгээрээс I муруй нь хамгийн том, III муруй нь хамгийн бага утгатай тохирч байна. Параметрийг өөрчлөх нь тархалтын муруйн масштабыг өөрчлөхтэй адил юм - нэг тэнхлэгийн дагуу масштабыг нэмэгдүүлэх, нөгөө тэнхлэгийн дагуу ижил хэмжээгээр буурах.

Магадлалын онол нь нэлээд олон тооны өөр өөр тархалтын хуулиудыг авч үздэг. Хяналтын бүдүүвчийг барихтай холбоотой асуудлыг шийдэхийн тулд тэдгээрийн цөөн хэдэн нь л сонирхолтой байдаг. Тэдний хамгийн чухал нь хэвийн тархалтын хуульашигласан хяналтын диаграммыг бүтээхэд ашигладаг тоон хяналт, өөрөөр хэлбэл Бид тасралтгүй санамсаргүй хэмжигдэхүүнтэй харьцах үед. Хэвийн хуваарилалтын хууль нь бусад хуваарилалтын хуулиудын дунд онцгой байр суурь эзэлдэг. Энэ нь нэгдүгээрт, энэ нь практикт ихэвчлэн тохиолддог, хоёрдугаарт, энэ нь хязгаарлагдмал хууль бөгөөд бусад хуваарилалтын хуулиуд маш нийтлэг ердийн нөхцөлд ханддагтай холбон тайлбарлаж байна. Хоёрдахь нөхцөл байдлын хувьд аливаа тархалтын хуулинд (зарим маш сул хязгаарлалттай) хамаарах хангалттай олон тооны бие даасан (эсвэл сул хамааралтай) санамсаргүй хэмжигдэхүүний нийлбэр нь ердийн хуульд ойролцоогоор захирагддаг болохыг магадлалын онолоор нотолсон. , мөн илүү санамсаргүй хэмжигдэхүүнүүдийг нэмбэл энэ нь үнэн зөв байх болно. Практикт тохиолдох санамсаргүй хэмжигдэхүүнүүдийн ихэнхийг, тухайлбал хэмжилтийн алдааг маш олон тооны харьцангуй бага нэр томъёоны нийлбэрээр төлөөлж болно - энгийн алдаа, тэдгээр нь тус бүр нь бие даасан шалтгаанаас үүдэлтэй. бусад. Санамсаргүй хэмжигдэхүүн тохиолдсон тохиолдолд хэвийн хууль гарч ирдэг Xолон тооны янз бүрийн хүчин зүйлийн үр дүн юм. Хүчин зүйл бүр тус тусад нь үнэ цэнэтэй юм Xбага зэрэг нөлөөлдөг бөгөөд аль нь бусдаас илүү нөлөөлж байгааг тодорхойлох боломжгүй юм.

Хэвийн тархалт(Лаплас-Гаусын тархалт) – үргэлжлэх магадлалын тархалт санамсаргүй хувьсагч Xмагадлалын тархалтын нягт нь - ¥<х< + ¥ принимает действительное значение:

Exp (3)

Өөрөөр хэлбэл, хэвийн тархалт нь m ба s гэсэн хоёр параметрээр тодорхойлогддог бөгөөд энд m нь математикийн хүлээлт юм; s нь хэвийн тархалтын стандарт хазайлт юм.

Утга s 2 хэвийн тархалтын дисперс юм.

Математикийн хүлээлт m нь түгээлтийн төвийн байрлалыг тодорхойлдог ба стандарт хазайлт s (SD) нь тархалтын шинж чанар юм (Зураг 3).

f(x) f(x)

Зураг 3 – Хэвийн тархалтын нягтын функцууд:

a) өөр өөр математикийн хүлээлт m; b) өөр өөр стандарт хазайлт s.

Тиймээс үнэ цэнэ μ абсцисса тэнхлэг дээрх тархалтын муруйн байрлалаар тодорхойлогдоно. Хэмжээ μ - санамсаргүй хэмжигдэхүүний хэмжигдэхүүнтэй ижил X. Математикийн хүлээлт m нэмэгдэхийн хэрээр функц хоёулаа баруун тийш зэрэгцэн шилжинэ. Багассан хэлбэлзэлтэй s 2 нягтрал нь м орчимд улам бүр төвлөрч, харин тархалтын функц улам эгц болж байна.

σ-ийн утга нь тархалтын муруйн хэлбэрийг тодорхойлно. Тархалтын муруй доорх талбай үргэлж нэгдмэл байх ёстой тул σ ихсэх тусам тархалтын муруй хавтгай болно. Зураг дээр. Зураг 3.1-д өөр өөр σ-ийн гурван муруйг үзүүлэв: σ1 = 0.5; σ2 = 1.0; σ3 = 2.0.

Зураг 3.1 – Хэвийн тархалтын нягтын функцуудөөр өөр стандарт хазайлтууд s.

Тархалтын функц (интеграл функц) нь дараах хэлбэртэй байна (Зураг 4):

(4)

Зураг 4 – Интеграл (a) ба дифференциал (б) хэвийн тархалтын функцууд

Ялангуяа чухал зүйл бол ердийн тархалттай санамсаргүй хэмжигдэхүүнийг шугаман хувиргах явдал юм X, үүний дараа санамсаргүй хэмжигдэхүүнийг олж авна ЗМатематикийн хүлээлт 0 ба дисперс 1-тэй. Энэ хувиргалтыг хэвийн болгох гэж нэрлэдэг.

Үүнийг санамсаргүй хувьсагч бүрт хийж болно. Нормчилал нь хэвийн тархалтын бүх боломжит хувилбаруудыг нэг тохиолдол болгон бууруулах боломжийг олгодог: m = 0, s = 1.

m = 0, s = 1 байх хэвийн тархалтыг гэнэ хэвийн тархалт (стандарт).

Стандарт хэвийн тархалт(стандарт Лаплас-Гауссын тархалт эсвэл нормчлогдсон хэвийн тархалт) нь стандартчилагдсан хэвийн санамсаргүй хэмжигдэхүүний магадлалын тархалт юм. З, тархалтын нягт нь дараахтай тэнцүү байна.

цагт - ¥<z< + ¥

Функцийн утгууд Ф(z)томъёогоор тодорхойлно:

(7)

Функцийн утгууд Ф(z)ба нягтрал f(z)нормчлогдсон хэвийн тархалтыг тооцоолж, хүснэгтэд үзүүлэв. Хүснэгтийг зөвхөн эерэг утгуудын хувьд эмхэтгэсэн zТийм учраас:

F (–z) = 1–Ф(z) (8)

Эдгээр хүснэгтүүдийг ашиглан та зөвхөн функцийн утгууд болон өгөгдсөн хэвийн тархалтын нягтыг тодорхойлох боломжтой. z, гэхдээ бас ерөнхий хэвийн тархалтын функцийн утгууд, учир нь:

; (9)

. 10)

Ердийн тархалттай санамсаргүй хэмжигдэхүүнтэй холбоотой олон асуудалд санамсаргүй хэмжигдэхүүн үүсэх магадлалыг тодорхойлох шаардлагатай байдаг. X, тодорхой талбайн хувьд m ба s параметртэй ердийн хуульд захирагдана. Ийм хэсэг нь жишээлбэл, дээд утгаас параметрийн хүлцлийн талбар байж болно Удоод тал руу Л.

-аас интервалд орох магадлал X 1-ээс X 2-ыг дараах томъёогоор тодорхойлж болно.

Тиймээс санамсаргүй хэмжигдэхүүнийг цохих магадлал (параметрийн утга) Xхүлцлийн талбар дахь томъёогоор тодорхойлогдоно

Та санамсаргүй хэмжигдэхүүн байх магадлалыг олж болно Xμ дотор байх болно кс . -д зориулж авсан утгууд к=1,2 ба 3 нь дараах байдалтай байна (мөн 5-р зургийг үз):

Иймээс хэрэв бүх боломжит утгуудын 99.73%-ийг агуулсан гурван сигма мужаас гадуур утга гарч ирвэл ийм үйл явдал тохиолдох магадлал маш бага (1:270) байвал тухайн утга нь хэтэрхий их байсан гэж үзэх хэрэгтэй. жижиг эсвэл хэт том байх нь санамсаргүй өөрчлөлтөөс биш, харин тархалтын шинж чанарыг өөрчлөхөд хүргэдэг процессын өөрөө ихээхэн эвдрэлээс үүдэлтэй.

Гурван сигмагийн хил дотор байрлах газрыг мөн нэрлэдэг статистикийн хүлцлийн бүсхолбогдох машин эсвэл процесс.

(бодит, хатуу эерэг)

Хэвийн тархалт, бас нэрлэдэг Гауссын тархалтэсвэл Гаусс - Лаплас- нэг хэмжээст тохиолдолд Гауссын функцтэй давхцах магадлалын нягтын функцээр тодорхойлогддог магадлалын тархалт:

Энд μ параметр нь хүлээлт (дундаж утга), тархалтын медиан ба горим, σ параметр нь тархалтын стандарт хазайлт (σ² нь тархалт) юм.

Тиймээс нэг хэмжээст хэвийн тархалт нь тархалтын хоёр параметрийн гэр бүл юм. Олон хувьсагчийн тохиолдлыг “Олон хувьсагч-хэвийн-тархалт” нийтлэлд тайлбарласан болно.

Стандарт хэвийн тархалтматематикийн хүлээлт μ = 0, стандарт хазайлт σ = 1 байх хэвийн тархалт гэнэ.

Нэвтэрхий толь бичиг YouTube

• 1 / 5

  Шинжлэх ухааны олон салбарт (жишээлбэл, математик статистик, статистикийн физик) хэвийн тархалтын ач холбогдол нь магадлалын онолын төв хязгаарын теоремоос үүдэлтэй. Хэрэв ажиглалтын үр дүн нь санамсаргүй сул харилцан хамааралтай олон хэмжигдэхүүнүүдийн нийлбэр бөгөөд тэдгээр нь тус бүр нь нийт нийлбэртэй харьцуулахад багахан хэмжээний хувь нэмэр оруулдаг бол гишүүний тоо нэмэгдэх тусам төвлөрсөн болон хэвийн болсон үр дүнгийн тархалт хэвийн байх хандлагатай байдаг. Магадлалын онолын энэхүү хууль нь хэвийн тархалтыг өргөнөөр тараахад хүргэдэг бөгөөд энэ нь түүнийг нэрлэх нэг шалтгаан болсон юм.

  Үл хөдлөх хөрөнгө

  Хормууд

  Хэрэв санамсаргүй хэмжигдэхүүн X 1 (\displaystyle X_(1))Тэгээд X 2 (\displaystyle X_(2))бие даасан бөгөөд математикийн хүлээлттэй хэвийн тархалттай байна μ 1 (\displaystyle \mu _(1))Тэгээд μ 2 (\displaystyle \mu _(2))болон зөрүү σ 1 2 (\displaystyle \sigma _(1)^(2))Тэгээд σ 2 2 (\displaystyle \sigma _(2)^(2))үүний дагуу, тэгвэл X 1 + X 2 (\displaystyle X_(1)+X_(2))мөн математикийн хүлээлттэй хэвийн тархалттай байна μ 1 + μ 2 (\displaystyle \mu _(1)+\mu _(2))болон хэлбэлзэл σ 1 2 + σ 2 2 . (\displaystyle \sigma _(1)^(2)+\сигма _(2)^(2).)Эндээс харахад хэвийн санамсаргүй хэмжигдэхүүнийг дурын тооны бие даасан хэвийн санамсаргүй хэмжигдэхүүнүүдийн нийлбэрээр илэрхийлж болно.

  Хамгийн их энтропи

  Ердийн тархалт нь дисперс нь өгөгдсөн утгаас хэтрэхгүй бүх тасралтгүй тархалтуудын дунд хамгийн их дифференциал энтропитэй байдаг.

  Ердийн псевдор санамсаргүй хувьсагчдыг загварчлах

  Ойролцоо загварчлалын хамгийн энгийн аргууд нь төвийн хязгаарын теорем дээр суурилдаг. Тухайлбал, хэрэв та хязгаарлагдмал дисперстэй хэд хэдэн бие даасан ижил тархсан хэмжигдэхүүнийг нэмбэл нийлбэр нь хуваарилагдах болно. ойролцоогоорСайн байна. Жишээлбэл, хэрэв та 100 бие даасан стандартыг нэмбэл жигдтархсан санамсаргүй хэмжигдэхүүнүүд, дараа нь нийлбэрийн тархалт ойролцоогоор болно хэвийн.

  Хэвийн тархалттай псевдор санамсаргүй хувьсагчдыг программчлан үүсгэхийн тулд Box-Muller хувиргалтыг ашиглах нь зүйтэй. Энэ нь нэг жигд тархсан утга дээр үндэслэн нэг хэвийн тархсан утгыг үүсгэх боломжийг танд олгоно.

  Байгаль, хэрэглээнд хэвийн тархалт

  Ердийн тархалт ихэвчлэн байгальд байдаг. Жишээлбэл, дараах санамсаргүй хэмжигдэхүүнүүдийг хэвийн тархалтаар сайн загварчилсан болно.

  • буудах үед хазайлт.
  • хэмжилтийн алдаа (гэхдээ зарим хэмжих хэрэгслийн алдаа нь хэвийн тархалттай байдаггүй).
  • популяцийн амьд организмын зарим шинж чанарууд.

  Энэ тархалт нь хязгааргүй хуваагдах, хязгаарлагдмал дисперстэй тасралтгүй тархалт учраас маш өргөн тархсан. Тиймээс зарим нь үүнийг хязгаарт ойртдог, жишээлбэл, бином ба Пуассон. Энэхүү тархалт нь детерминистик бус олон физик процессуудыг загварчилдаг.

  Бусад хуваарилалттай харилцах харилцаа

  • Ердийн тархалт нь Pearson төрлийн XI тархалт юм.
  • Бие даасан стандарт хэвийн тархалттай санамсаргүй хэмжигдэхүүний хосын харьцаа нь Коши тархалттай байна. Энэ нь санамсаргүй хэмжигдэхүүн бол X (\displaystyle X)харилцааг илэрхийлдэг X = Y / Z (\displaystyle X=Y/Z)(Хаана Y (\displaystyle Y)Тэгээд Z (\displaystyle Z)- бие даасан стандарт хэвийн санамсаргүй хэмжигдэхүүнүүд), тэгвэл Коши тархалттай болно.
  • Хэрэв z 1 , … , z k (\displaystyle z_(1),\ldots ,z_(k))- хамтран бие даасан стандарт хэвийн санамсаргүй хэмжигдэхүүнүүд, өөрөөр хэлбэл z i ∼ N (0 , 1) (\displaystyle z_(i)\sim N\left(0,1\баруун)), дараа нь санамсаргүй хэмжигдэхүүн x = z 1 2 + … + z k 2 (\displaystyle x=z_(1)^(2)+\ldots +z_(k)^(2)) k эрх чөлөөний зэрэгтэй хи-квадрат тархалттай.
  • Хэрэв санамсаргүй хэмжигдэхүүн X (\displaystyle X)логнормаль тархалтад хамаарах бол түүний натурал логарифм нь хэвийн тархалттай байна. Өөрөөр хэлбэл, хэрэв X ∼ L o g N (μ , σ 2) (\displaystyle X\sim \mathrm (LogN) \left(\mu ,\sigma ^(2)\баруун)), Тэр Y = ln ⁡ (X) ∼ N (μ , σ 2) (\displaystyle Y=\ln \left(X\баруун)\sim \mathrm (N) \left(\mu ,\sigma ^(2)\баруун) )). Мөн эсрэгээр, хэрэв Y ∼ N (μ , σ 2) (\displaystyle Y\sim \mathrm (N) \left(\mu ,\sigma ^(2)\баруун)), Тэр X = exp ⁡ (Y) ∼ L o g N (μ , σ 2) (\displaystyle X=\exp \left(Y\баруун)\sim \mathrm (LogN) \left(\mu ,\sigma ^(2)) \баруун)).
  • Хоёр стандарт хэвийн санамсаргүй хэмжигдэхүүний квадратуудын харьцаа нь байна

  Санамсаргүй хувьсагч нь санамсаргүй үйл явдлуудтай холбоотой байдаг. Тодорхой нөхцөлд олж авах боломжтой үр дүнг хоёрдмол утгагүйгээр урьдчилан таамаглах боломжгүй болсон тохиолдолд бид санамсаргүй үйл явдлын талаар ярьдаг.

  Бид энгийн зоос шидэж байна гэж бодъё. Ихэвчлэн энэ процедурын үр дүн тодорхой тодорхойлогддоггүй. "Толгой" эсвэл "сүүл" гэсэн хоёр зүйлийн нэг нь тохиолдох болно гэдгийг бид баттай хэлж чадна. Эдгээр үйл явдлын аль нэг нь санамсаргүй байх болно. Та энэ санамсаргүй үйл явдлын үр дүнг тайлбарлах хувьсагчийг танилцуулж болно. Мэдээжийн хэрэг, энэ хувьсагч нь "толгой" ба "сүүл" гэсэн хоёр салангид утгыг авах болно. Энэ хувьсагч хоёр боломжит утгын алийг нь авахыг бид урьдчилан таамаглах боломжгүй тул бид энэ тохиолдолд санамсаргүй хэмжигдэхүүнтэй харьцаж байна гэж маргаж болно.

  Туршилтанд бид ямар нэгэн өдөөлтийг үзүүлэх үед тухайн субьектийн хариу үйлдэл үзүүлэх хугацааг үнэлж байна гэж бодъё. Дүрмээр бол туршилт хийгч нь туршилтын нөхцлийг стандартчилах, өдөөгчийг үзүүлэх боломжит өөрчлөлтийг багасгах, бүр арилгахын тулд бүх арга хэмжээг авсан ч гэсэн субъектын хэмжсэн урвалын хугацаа өөр байх болно. Энэ тохиолдолд субьектийн урвалын хугацааг санамсаргүй хэмжигдэхүүнээр тодорхойлдог гэж тэд хэлдэг. Зарчмын хувьд туршилтаар бид урвалын хугацааны ямар ч утгыг олж авах боломжтой байдаг - хэмжилтийн үр дүнд олж авах боломжтой урвалын хугацааны боломжит утгуудын багц нь хязгааргүй болж хувирдаг - бид энэ тухай ярьж байна. тасралтгүй байдал энэ санамсаргүй хэмжигдэхүүн.

  Асуулт гарч ирнэ: санамсаргүй хэмжигдэхүүнүүдийн зан төлөвт ямар нэгэн хэв маяг байдаг уу? Энэ асуултын хариулт эерэг болж хувирав.

  Иймд, хэрэв та нэг зоосыг хязгааргүй олон шидэх юм бол зоосны хоёр тал тус бүр дээр харагдах тоо нь ойролцоогоор ижил байгааг олж мэдэх болно, хэрэв мэдээж зоос хуурамч эсвэл нугалж байгаа бол. Энэ хэв маягийг онцлон тэмдэглэхийн тулд санамсаргүй үйл явдлын магадлалын тухай ойлголтыг нэвтрүүлсэн. Зоос шидсэн тохиолдолд боломжит хоёр үйл явдлын аль нэг нь гарцаагүй тохиолдох нь тодорхой. Учир нь энэ хоёр үйл явдлын нийлбэр магадлал буюу өөрөөр хэлбэл нийт магадлал 100% байна. Хэрэв бид зоосыг туршихтай холбоотой хоёр үйл явдал хоёулаа ижил магадлалтайгаар тохиолддог гэж үзвэл үр дүн тус бүрийн магадлал 50% -тай тэнцэх нь ойлгомжтой. Тиймээс онолын эргэцүүлэл нь өгөгдсөн санамсаргүй хэмжигдэхүүний зан төлөвийг дүрслэх боломжийг олгодог. Математик статистикт ийм тайлбарыг нэр томъёогоор тэмдэглэдэг "санамсаргүй хэмжигдэхүүний тархалт".

  Нөхцөл байдал нь тодорхой тодорхойлогдсон утгын багцгүй санамсаргүй хэмжигдэхүүнээр илүү төвөгтэй байдаг, i.e. тасралтгүй болж хувирдаг. Гэхдээ энэ тохиолдолд ч гэсэн түүний зан байдлын зарим чухал хэв маягийг тэмдэглэж болно. Тиймээс субьектийн урвалын хугацааг хэмжих туршилт хийхдээ тухайн субьектийн урвалын үргэлжлэх хугацааны янз бүрийн интервалыг янз бүрийн магадлалаар тооцдог болохыг тэмдэглэж болно. Субъект хэтэрхий хурдан хариу өгөх нь ховор байх магадлалтай. Жишээлбэл, семантик шийдвэрийн даалгавруудад субъектууд 500 мс (1/2 сек) -ээс бага хурдтайгаар илүү бага нарийвчлалтай хариу өгөх нь бараг боломжгүй юм. Үүний нэгэн адил туршилт хийгчийн зааврыг үнэнчээр дагадаг хүн хариугаа хэт хойшлуулах нь юу л бол. Жишээлбэл, семантик шийдвэр гаргах даалгавруудад үнэлгээ хийхэд 5 секундээс илүү хугацаа шаардагддаг хариултыг ихэвчлэн найдваргүй гэж үздэг. Гэсэн хэдий ч бид 100% итгэлтэйгээр субьектийн хариу үйлдэл хийх хугацаа O-оос +co хүртэлх мужид байна гэж үзэж болно. Гэхдээ энэ магадлал нь санамсаргүй хэмжигдэхүүний утга бүрийн магадлалын нийлбэр юм. Иймд тасралтгүй санамсаргүй хэмжигдэхүүний тархалтыг тасралтгүй функц гэж тодорхойлж болно y = f (X ).

  Хэрэв бид салангид санамсаргүй хэмжигдэхүүнтэй харьцаж байгаа бол түүний бүх боломжит утгыг урьдчилан мэдэж байх үед зоосны жишээн дээр түүний тархалтын загварыг бий болгох нь тийм ч хэцүү биш юм. Бид авч үзэж буй жишээн дээр дурдсанчлан зөвхөн зарим үндэслэлтэй таамаглалуудыг оруулахад хангалттай. Өмнө нь үл мэдэгдэх тооны утгыг авдаг тасралтгүй утгуудын хуваарилалт нь нөхцөл байдал илүү төвөгтэй байдаг. Мэдээжийн хэрэг, хэрэв бид жишээ нь семантик шийдвэрийн даалгаврыг шийдвэрлэхдээ хариу үйлдэл үзүүлэх хугацааг хэмжих туршилтын явцад субьектийн зан төлөвийг тодорхойлсон онолын загварыг боловсруулсан бол энэ загвар дээр үндэслэн онолын тархалтыг тодорхойлохыг оролдож болно. нэг сэдээлтийг үзүүлэх үед ижил сэдвийн хувьд тодорхой урвалын цаг хугацааны утгууд. Гэсэн хэдий ч энэ нь үргэлж боломжтой байдаггүй. Тиймээс туршилт хийгч нь түүний сонирхсон санамсаргүй хэмжигдэхүүний тархалтыг аль хэдийн судалсан зарим хуулиар тодорхойлсон гэж үзэхээс өөр аргагүй болдог. Ихэнх тохиолдолд энэ нь үргэлж зөв байж чаддаггүй ч эдгээр зорилгоор ердийн тархалтыг ашигладаг бөгөөд энэ нь мөн чанараас үл хамааран аливаа санамсаргүй хэмжигдэхүүнийг хуваарилах стандарт үүрэг гүйцэтгэдэг. Энэ тархалтыг 18-р зууны эхний хагаст математикийн хувьд анх тодорхойлсон. де Мойвр.

  Хэвийн тархалт Бидний сонирхсон үзэгдэлд бие биенээ тэнцвэржүүлдэг хязгааргүй олон тооны санамсаргүй хүчин зүйлс нөлөөлсөн үед үүсдэг. Албан ёсоор, де Мойврын үзүүлсэн хэвийн тархалтыг дараах хамаарлаар тодорхойлж болно.

  Хаана X бидний судалж буй зан төлөвийг сонирхож буй санамсаргүй хэмжигдэхүүнийг илэрхийлдэг; Р – энэ санамсаргүй хэмжигдэхүүнтэй холбоотой магадлалын утга; π ба e - тойргийн диаметр ба байгалийн логарифмын суурьтай харьцуулсан харьцааг тус тус тодорхойлдог математикийн алдартай тогтмолууд; μ ба σ2 – санамсаргүй хэмжигдэхүүний хэвийн тархалтын параметрүүд – санамсаргүй хэмжигдэхүүний математик хүлээлт ба дисперс тус тус X.

  Хэвийн тархалтыг тайлбарлахын тулд зөвхөн μ ба σ2 параметрүүдийг тодорхойлоход шаардлагатай бөгөөд хангалттай юм.

  Тиймээс, хэрэв бид санамсаргүй хэмжигдэхүүнтэй бол түүний зан төлөвийг μ ба σ2-ийн дурын утгуудаар (1.1) тэгшитгэлээр тодорхойлсон бол бид үүнийг дараах байдлаар тэмдэглэж болно. Ν (μ, σ2), энэ тэгшитгэлийн бүх нарийн ширийн зүйлийг санахгүйгээр.

  

  Цагаан будаа. 1.1.

  Аливаа тархалтыг график хэлбэрээр дүрсэлж болно. Графикийн хувьд хэвийн тархалт нь хонх хэлбэртэй муруй шиг харагддаг бөгөөд яг хэлбэр нь тархалтын параметрүүдээр тодорхойлогддог, i.e. математикийн хүлээлт ба дисперс. Хэвийн тархалтын параметрүүд нь бараг бүх утгыг авч болох бөгөөд энэ нь зөвхөн туршилтын хэмжүүрээр хязгаарлагддаг. Онолын хувьд математикийн хүлээлтийн утга нь -∞-аас +∞ хүртэлх тооны мужаас дурын тоотой тэнцүү байх ба дисперс нь сөрөг бус дурын тоотой тэнцүү байж болно. Тиймээс хязгааргүй тооны янз бүрийн хэвийн тархалтын хэлбэрүүд байдаг бөгөөд үүний дагуу түүнийг төлөөлдөг хязгааргүй тооны муруйнууд байдаг (гэхдээ тэдгээр нь ижил төстэй хонх хэлбэртэй байдаг). Тэднийг бүгдийг нь дүрслэх боломжгүй гэдэг нь ойлгомжтой. Гэсэн хэдий ч хэрэв тодорхой хэвийн тархалтын параметрүүд мэдэгдэж байгаа бол түүнийг гэж нэрлэгддэг зүйл рүү хөрвүүлж болно нэгж хэвийн тархалт, математикийн хүлээлт тэгтэй тэнцүү, дисперс нь нэгтэй тэнцүү байна. Үүнийг хэвийн тархалт гэж бас нэрлэдэг Стандарт эсвэл z-тархалт. Нэгж хэвийн тархалтын графикийг Зураг дээр үзүүлэв. 1.1-ээс харахад хэвийн тархалтын хонх хэлбэртэй муруйны дээд хэсэг нь математикийн хүлээлтийн утгыг тодорхойлдог нь тодорхой байна. Хэвийн тархалтын өөр нэг үзүүлэлт болох тархалт нь хэвтээ (х тэнхлэг) -тэй харьцуулахад хонх хэлбэртэй муруйны "хавтгай" түвшинг тодорхойлдог.

  Туршилтын үр дүнд тодорхой магадлал бүхий бодит утгыг авч чадвал санамсаргүй. Санамсаргүй хэмжигдэхүүний хамгийн бүрэн гүйцэд, цогц шинж чанар бол тархалтын хууль юм. Тархалтын хууль нь X санамсаргүй хэмжигдэхүүн нь тодорхой xi утгыг авах эсвэл тодорхой интервалд орох магадлалыг тодорхойлох боломжийг олгодог функц (хүснэгт, график, томъёо) юм. Хэрэв санамсаргүй хэмжигдэхүүн нь өгөгдсөн тархалтын хуультай бол энэ хуулийн дагуу тархсан эсвэл энэ тархалтын хуульд захирагддаг гэж хэлдэг.

  Бүр хуваарилалтын хуульмагадлалын үүднээс санамсаргүй хэмжигдэхүүнийг бүрэн дүрсэлсэн функц юм. Практикт X санамсаргүй хэмжигдэхүүний магадлалын тархалтыг зөвхөн туршилтын үр дүнгээс л дүгнэх шаардлагатай болдог.

  Хэвийн тархалт

  Хэвийн тархалт, мөн Гауссын тархалт гэж нэрлэдэг бөгөөд энэ нь мэдлэгийн олон салбарт, ялангуяа физикт чухал үүрэг гүйцэтгэдэг магадлалын тархалт юм. Физик хэмжигдэхүүн нь маш олон тооны санамсаргүй дуу чимээний нөлөөлөлд өртөх үед хэвийн тархалтыг дагаж мөрддөг. Энэ нөхцөл байдал туйлын түгээмэл байгаа нь тодорхой тул бид бүх тархалтаас ердийн тархалт нь байгальд хамгийн түгээмэл байдаг - иймээс түүний нэрсийн нэг гэж хэлж болно.

  Хэвийн тархалт нь нүүлгэн шилжүүлэлт ба масштаб гэсэн хоёр параметрээс хамаардаг, өөрөөр хэлбэл математикийн үүднээс авч үзвэл энэ нь нэг тархалт биш, харин бүхэл бүтэн гэр бүл юм. Параметрийн утга нь дундаж (математикийн хүлээлт) ба тархалтын (стандарт хазайлт) утгатай тохирч байна.

  

  

  Стандарт хэвийн тархалт нь математикийн хүлээлт 0, стандарт хазайлт нь 1 байх хэвийн тархалт юм.

  

  

  Асимметрийн коэффициент

  

  Хэрэв тархалтын баруун сүүл зүүнээс урт байвал хазайлтын коэффициент эерэг, бусад тохиолдолд сөрөг байна.

  Хэрэв тархалт нь математикийн хүлээлттэй харьцуулахад тэгш хэмтэй байвал түүний тэгш бус байдлын коэффициент нь тэг болно.

  

  Түүврийн хазайлтын коэффициент нь тэгш хэмийн тархалтыг шалгахын зэрэгцээ хэвийн байдлын урьдчилсан шалгалтанд ашиглагддаг. Энэ нь танд хэвийн байдлын таамаглалыг үгүйсгэх боломжийг олгодог боловч хүлээн зөвшөөрөхийг зөвшөөрдөггүй.

  Куртозын коэффициент

  

  Куртозын коэффициент (оргилын коэффициент) нь санамсаргүй хэмжигдэхүүний тархалтын оргилын хурц байдлын хэмжүүр юм.

  Томъёоны төгсгөлд "хасах гурвыг" оруулснаар хэвийн тархалтын куртозын коэффициент тэгтэй тэнцүү байна. Математикийн хүлээлтийн эргэн тойронд тархалтын оргил нь огцом байвал эерэг, жигд байвал сөрөг байна.

  

  Санамсаргүй хэмжигдэхүүний моментууд

  Санамсаргүй хэмжигдэхүүний момент нь өгөгдсөн санамсаргүй хэмжигдэхүүний тархалтын тоон шинж чанар юм.