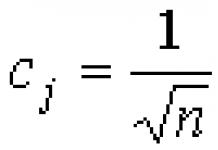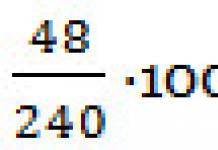Mathcad ашиглан тригонометрийн Фурье цуврал.

Ажлын зорилго

Mathcad ашиглан үечилсэн функцийг тригонометрийн Фурьегийн цуврал болгон өргөжүүлж, Фурье цувралын хэсэгчилсэн нийлбэрүүдийн графикийг байгуулж сур.

Тоног төхөөрөмж

MathCAD програм хангамжийн багц.

Ахиц дэвшил

Сонголт

1) Функцийг тригонометрийн Фурье цуврал болгон өргөжүүл

2) Функцийг косинус дахь тригонометрийн Фурье цуврал болгон өргөжүүл

3) Функцийг синусын хувьд тригонометрийн Фурье цуврал болгон өргөжүүл

Ажиллах зөвшөөрөл

3.2.1 Функцийн тригонометрийн Фурье цуврал нь хэлбэрийн функциональ цуваа юм

3.2.4 f(x) функцэд Фурье коэффициентийг тооцоолсон (косинусаар томруулсан үед)

a 1 = 5, a 2 = 6, a 3 = 7

Тригонометрийн Фурье цувралыг бич

3.2.5 f(x) функцийг синус (сондгой)-ын хувьд Фурьегийн цуваа болгон өргөтгөж, дараа нь

Хуудас

Баримт бичгийн дугаар.

Гарын үсэг

Хуудас

Баримт бичгийн дугаар.

Гарын үсэг

огноо

Хуудас

3.1.2. Санамсаргүй хэмжигдэхүүн x-ийн тоон шинж чанарыг ол (x нь нэг сугалааны тасалбар эзэмшигчийн ялалт).

____ тасалбарыг сугалаагаар сугалаа.

Эдгээрээс тэд тус бүр ____ рубль хождог

Эдгээрээс тэд тус бүр ____ рубль хождог.

3.1.3. “x” санамсаргүй хэмжигдэхүүний тоон шинж чанарыг ол.

A). 0.15 b) -0.35 c) 0.35 d) 0.25 e) тодорхойлох боломжгүй.

3.2.3 Сугалаанд 200 ширхэг тасалбар байгаа. 30 тасалбар хожсон байна.Тийм нь хожсон тасалбар биш байх магадлал хэд вэ?

A). 1.7 b) 0.7 c) 0.17 d) 0.85 d) 0.15

3.2.4 Дискрет санамсаргүй хэмжигдэхүүний дисперсийг тооцоолох томьёог бичнэ үү.

3.2.5 Дискрет санамсаргүй хэмжигдэхүүний стандарт хазайлтыг тооцоолох томьёог бичнэ үү.

________________________________________________________________________________

3.2.6. D (y) = 25. Стандарт хазайлт хэд вэ?

A). ± 5 b) 5 c) -5 d) тодорхойлох боломжгүй.

3.2.7 MathCAD дээр тэгшитгэлийг хэрхэн шийдвэрлэх вэ

______________________________________________________________________________

______________ ажиллахыг зөвшөөрнө

Ажлын үр дүн

4.1. M(x) = ____________ D(x) = ____________ σ (x) = ___________

Хуудас

Баримт бичгийн дугаар.

Гарын үсэг

огноо

Хуудас

PR.140448.00.00

ПРАКТИК АЖИЛ 12

Цэг ба интервалын тооцоог олох

Excel дэх үл мэдэгдэх түгээлтийн параметрүүд

1. Ажлын зорилго

Өгөгдсөн түүврийг ашиглан түүврийн тоон шинж чанарыг тодорхойлж, ерөнхий популяцийн үл мэдэгдэх параметрүүдийг тооцоолох, өгөгдсөн итгэлийн магадлалаар ерөнхий хүн амын математик хүлээлтийг тооцоолж сурах.

2. Тоног төхөөрөмж:

IBM PC, Microsoft Excel бүрхүүл.

Ахиц дэвшил

3. 1 Сонголт

Өгөгдсөн итгэлийн магадлал бүхий тооцоо γ = өгөгдсөн түүврийн ерөнхий популяцийн математик хүлээлт

_____________________________________________________________________________________

3. 2 Ажил хийх зөвшөөрөл

1. Түүврийн дундажийг хэрхэн тооцдог вэ?

2. Түүврийн зөрүүг хэрхэн тооцдог вэ?

____________________________________________________________________________________________________________________________________________________________

3. Стандарт хазайлтыг хэрхэн тооцдог вэ?

____________________________________________________________________________________________________________________________________________________________

4. Зассан түүврийн зөрүүг хэрхэн тооцдог вэ?

____________________________________________________________________________________________________________________________________________________________

5. Үл мэдэгдэх тархалтын параметрийн цэгийн үнэлгээ интервалын тооцооноос юугаараа ялгаатай вэ?

____________________________________________________________________________________________________________________________________________________________

6. Хүн амын математик хүлээлтийг тооцоолох интервалыг хэрхэн тооцдог вэ?

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

7. Оюутны коэффициентийг юу гэж тэмдэглэсэн бэ?

Өөрчлөх

Хуудас

Баримт бичгийн дугаар.

Гарын үсэг

огноо

Хуудас

PR.140448.00.00

____________________________________________________________________________________________________________________________________________________________

8. Оюутны коэффициентийн утга юунаас хамаарах вэ?

____________________________________________________________________________________________________________________________________________________________

Дараахь хүмүүсийг ажиллуулахыг зөвшөөрнө: ________________________________________________

Ажлын үр дүн

σ in = S in = t γ =

Дүгнэлт

Энэ ажлын явцад би цэг ба интервалын тооцооны томъёог ашигласан ______________________________________________________________________

_________________________________________________________________

Өөрчлөх Хуудас Баримт бичгийн дугаар. Гарын үсэг огноо Хуудас PR.140448.00.00

Mathcad нь хурдан салангид Фурье хувиргалт (FFT) болон түүний урвуу байдлыг гүйцэтгэх функцуудыг агуулдаг. Mathcad PLUS нь мөн нэг хэмжээст дискрет долгионы хувиргалт ба түүний урвуу байдлыг хангадаг. Эдгээр бүх функцууд нь вектор аргументуудтай. Векторыг тодорхойлохдоо vдолгионы хувиргалт эсвэл Фурье хувиргалтыг олохын тулд векторын эхний элемент нь тэг индекстэй байгаа эсэхийг шалгаарай: v 0 . Хэрэв v 0 тодорхойлогдоогүй бол Mathcad үүнийг автоматаар 0 болгож тохируулна. Энэ нь үр дүнг гажуудуулж болзошгүй.

Дискрет Фурье хувиргалтын танилцуулга

Mathcad нь хоёр төрлийн дискрет Фурье хувиргах функцийг агуулдаг: fft/ifftТэгээд cfft /icfft . Эдгээр функцууд нь салангид байдаг: тэд вектор ба матрицыг аргумент болгон авч буцаадаг. Тэдгээрийг бусад функцтэй хамт ашиглах боломжгүй. Функцуудыг ашиглана уу fftТэгээд ifft , дараах хоёр нөхцөл хангагдсан бол:

• аргументууд бодитой бөгөөд
• өгөгдлийн вектор нь 2 м элементтэй.

Онцлогуудыг ашигла cfftТэгээд icfftбусад бүх тохиолдолд.
Эхний нөхцөл шаардлагатай, учир нь функцууд fft/ifftБодит өгөгдлийн хувьд Фурье хувирлын хоёр дахь хагас нь эхнийх нь цогц коньюгат байдаг гэдгийг ашиглана уу. Mathcad үр дүнгийн векторын хоёр дахь хагасыг устгадаг. Энэ нь тооцооллын явцад цаг хугацаа, санах ойг хэмнэдэг.

Хос функцууд cfft/icfftхувиргалтанд тэгш хэмийг ашигладаггүй. Энэ шалтгааны улмаас тэдгээрийг нарийн төвөгтэй өгөгдөлд ашиглах шаардлагатай байна. Бодит тоо нь нийлмэл тоонуудын дэд олонлог тул та хосыг бас ашиглаж болно cfft/icfftбодит тоонуудын хувьд.

Хоёрдахь нөхцөл шаардлагатай, учир нь хос функцууд fft/ifftөндөр үр ашигтай хурдан Фурье хувиргах алгоритмыг ашигладаг. Үүнийг хийхийн тулд аргументийн векторыг ашиглана fft, 2 м-ийн элементтэй байх ёстой. Функцүүдэд сfft/icfftдурын хэмжээтэй матриц болон векторыг хоёуланг нь аргумент болгон хүлээн авах алгоритмыг ашигладаг. Энэ хос функцийг матрицыг аргумент болгон ашиглах үед хоёр хэмжээст Фурье хувиргалтыг тооцоолно.

Хэрэв функцийг ашиглаж байгаа бол гэдгийг анхаарна уу fftшууд хөрвүүлэхийн тулд та функцийг ашиглах хэрэгтэй ifftэсрэгээр. Үүний нэгэн адил, хэрэв та шууд хөрвүүлэхэд ашигладаг бол cfft, дараа нь эсрэгээр нь ашиглах шаардлагатай icfft.

Фурье хувиргалтыг тодорхойлох янз бүрийн томъёолол нь урагш ба урвуу хувиргалтын экспонент дахь төсөөллийн нэгжийн тэмдгийн талаархи өөр өөр нормчлолын коэффициент, конвенцуудыг ашигладаг. Функцүүд fft, ifft, cfftТэгээд icfftШууд хөрвүүлэхдээ 1/-ийг хэвийн болгох коэффициент ба эерэг илтгэгч болгон ашиглана. Функцүүд FFT , IFFT , CFFT Тэгээд ICFFTШууд хөрвүүлэхдээ 1/N-ийг хэвийн болгох коэффициент болон сөрөг экспонент болгон ашигла. Эдгээр функцийг хосоор нь ашиглах ёстой. Жишээлбэл, хэрэв та ашигладаг бол CFFTшууд хөрвүүлэхэд, шаардлагатайашиглах ICFFTэсрэгээрээ.

Бодит домайн дахь Фурье хувиргалт

2 м элемент бүхий бодит үнэ цэнэтэй векторуудын хувьд та хэд хэдэн функцийг ашиглаж болно fft/ifft. Эдгээр функцийг тооцоолох алгоритм нь зөвхөн бодит өгөгдөлд байдаг тэгш хэмийн давуу талыг ашигладаг. Энэ нь тооцоолол хийхэд шаардагдах цаг хугацаа, санах ойг хоёуланг нь хэмнэдэг. Вектор v 2 м-ийн элементтэй байх ёстой. Үр дүн нь 1+2 м-1 хэмжээтэй комплекс утгатай вектор юм. Хэрэв v 2 м-ээс өөр хэмжээстэй бол Mathcad алдааны мессежийг харуулдаг " буруу вектор хэмжээ”.

Векторын элементүүд буцаж ирэв fft,томъёогоор тооцоолно

Энэ томъёонд n- доторх элементүүдийн тоо v, би- төсөөллийн нэгж.

Функцийн буцаасан вектор дахь элементүүд fft, өөр өөр давтамжтай тохирч байна. Бодит давтамжийг сэргээхийн тулд анхны дохионы хэмжилтийн давтамжийг мэдэх шаардлагатай. Хэрэв vБайна n-хэмжээт векторыг функцэд шилжүүлсэн fft, мөн анхны дохиог хэмжих давтамж - fs, тэгвэл харгалзах давтамж нь тэнцүү байна

Энэ нь анхны дохионы хэмжилтийн давтамжаас өндөр давтамжийг илрүүлэх боломжгүй болгодог гэдгийг анхаарна уу. Энэ бол Mathcad-аас бус асуудлын мөн чанараас үүдэлтэй хязгаарлалт юм. Фурье хувиргалтаас дохиог зөв сэргээхийн тулд хамгийн багадаа зурвасын өргөнөөс хоёр дахин давтамжтайгаар анхны дохиог хэмжих шаардлагатай. Энэ үзэгдлийн талаархи бүрэн хэлэлцүүлэг нь энэхүү гарын авлагын хамрах хүрээнээс гадуур боловч дижитал дохио боловсруулах аливаа сурах бичгээс олж болно.

Вектор v 1+ 2 м элементтэй байх ёстой, хаана м-бүхэлд нь. Үр дүн нь 2 м+1 хэмжээтэй комплекс утгатай вектор юм. Хэрэв v 1+ 2 м-ээс өөр хэмжээстэй, Mathcad алдааны мессежийг харуулдаг " буруу вектор хэмжээ".Аргумент v- функцээр үүсгэсэнтэй төстэй вектор fft.Үр дүнг тооцоолохын тулд Mathcad эхлээд шинэ вектор үүсгэдэг w, цогц коньюгат v, мөн үүнийг векторт нэмнэ v. Дараа нь Mathcad векторыг тооцоолно г, тэдгээрийн элементүүдийг томъёогоор тооцоолно:

Энэ нь ижил томъёо юм fft, функц дэх хасах тэмдгийг эс тооцвол exp. Функцүүд fftТэгээд ifft- нарийн давж заалдах. Бүх бодит үнэлэмжийн хувьд vүнэн ifft(fft(v))=v.

Нарийн төвөгтэй муж дахь Фурье хувиргалт

Хувиргах хосыг ашиглах боломжгүй хоёр шалтгаан бий fft/ifft,өмнөх хэсэгт авч үзсэн:

• Өгөгдөл нь нарийн төвөгтэй үнэ цэнэтэй байж болно. Энэ нь Mathcad нь бодит тохиолдолд тохиолддог тэгш хэмийг ашиглах боломжгүй гэсэн үг юм.
• Өгөгдлийн вектор нь 2 м-ээс өөр хэмжээтэй байж болно. Энэ нь Mathcad нь хосын ашигладаг өндөр үр ашигтай FFT алгоритмын давуу талыг ашиглах боломжгүй гэсэн үг юм fft/ifft.

Фурьегийн цогц хувиргалт нь дараах функцуудыг шаарддаг.
Зураг 3: Mathcad дээр Фурьегийн хурдан хувиргалтыг ашиглах.

Хэд хэдэн өөрчлөлт cfft/icfftямар ч хэмжээтэй массивтай ажиллах боломжтой. Гэсэн хэдий ч мөр, баганын тоог олон тооны жижиг хүчин зүйлийн үржвэр болгон төлөөлөх боломжтой үед тэд илүү хурдан ажилладаг. Жишээлбэл, 2 м урттай векторууд, 100 эсвэл 120 гэх мэт урттай векторууд энэ ангилалд багтдаг. Нөгөө талаас, урт нь том анхны тоо болох вектор нь Фурье хувиргалтын тооцоог удаашруулна.

Функцүүд cfftТэгээд icfft- бие биенээсээ урвуу. Энэ нь icfft(cfft(v))=v гэсэн үг. Mathcad дээр Фурье хувиргалтыг ашиглах жишээг Зураг 3-т үзүүлэв.

Хэзээ маргаан мэт cfftматрицыг ашиглавал үр дүн нь анхны матрицын хоёр хэмжээст Фурье хувиргалт юм.

Фурье хувиргалтын өөр хэлбэрүүд

Дээр дурдсан Фурье хувиргалтын тодорхойлолтууд нь цорын ганц боломжтой зүйл биш юм. Жишээлбэл, дискрет Фурье хувиргалт ба түүний урвуу байдлын талаархи дараах тодорхойлолтыг Рональд Брэйвеллсийн номноос олж болно. Фурье хувиргалт ба түүний хэрэглээ(McGraw-Hill, 1986): Эдгээр тодорхойлолтууд нь техникийн ном зохиолд нэлээд түгээмэл байдаг. Өмнөх хэсэгт дурдсан тодорхойлолтуудын оронд эдгээр тодорхойлолтыг ашиглахын тулд функцуудыг ашиглана уу FFT, IFFT, CFFTТэгээд ICFFT. Тэд дараах байдлаар ялгаатай.

Функцүүд FFT, IFFT, CFFTТэгээд ICFFTӨмнөх хэсэгт авч үзсэн функцуудтай ижил төстэй байдлаар ашиглагддаг.

Долгион хувиргалт

Mathcad PLUS нь долгион хувиргах хоёр функцийг агуулдаг: шууд нэг хэмжээст дискрет долгионы хувиргалт ба түүний урвуу өөрчлөлтийг гүйцэтгэх. Хөрвүүлэлтийг дөрвөн коэффициентийн Даубечи долгионы суурь ашиглан гүйцэтгэнэ.

Mod(x, y) – х-ийг у-д хуваасны үлдэгдэл. Үр дүн нь x-тэй ижил тэмдэгтэй байна; өнцөг(х, у) – XY хавтгай дахь эерэг х тэнхлэг ба вектор (х, у) хоорондын өнцөг (радианаар). Аргументууд бодит байх ёстой. 0-2π хоорондох утгыг буцаана. тааз(3.25) = 4 давхар(3.25) = 3 мантис (x) := x − давхар(x) мантиса (3.45) = 0.45 Уламжлалт дугуйралт: дугуйрсан (x) := if(мантисса (х)< 0.5, floor(x) , ceil(x)) roundoff (3.46) = 3 roundoff (3.56) = 4 Рис. 14. Создание функций округления На рис. 14 показано, как из этих функций могут быть сформированы функции округления. 4.4. Дискретное преобразование Фурье В Mathcad входят два типа функций для дискретного прямого и об- ратного преобразования Фурье: fft/ifft и cfft/icfft. Эти функции дискрет- ны: они берут в качестве аргументов и возвращают векторы и матрицы. Они не могут быть использованы с другими функциями. Используйте функции fft и ifft, если выполнены два следующих ус- ловия: аргументы вещественны, и вектор данных имеет 2m элементов. Первое условие необходимо, потому что функции fft/ifft используют тот факт, что для вещественных данных вторая половина преобразова- ния Фурье является комплексно сопряженной с первой. Mathcad отбра- сывает вторую половину вектора-результата. Это сохраняет время и память при вычислениях. Пара функций cfft/icfft не использует симметрию в преобразова- нии. По этой причине необходимо использовать их для комплексных данных. 41 Второе условие требуется, потому что пара функций fft/ifft исполь- зует высоко эффективный алгоритм быстрого преобразования Фурье. Для этого вектор аргумента, используемого с fft, должен иметь 2m эле- ментов. В функциях cfft/icfft использован алгоритм, который допускает в качестве аргументов как матрицы, так и векторы произвольного раз- мера. Когда эта пара функций используется с матрицей в качестве аргу- мента, вычисляется двумерное преобразование Фурье. Следует иметь в виду, что если для прямого преобразования исполь- зована функция fft, то для обратного преобразования необходимо ис- пользовать функцию ifft. Аналогично используются функции cfft/icfft. 4.5. Преобразование Фурье в вещественной области Для вещественных векторов с 2m элементами предпочтительно ис- пользовать функции fft/ifft. Функция fft(v) возвращает дискретное пре- образование Фурье, векторный аргумент которой можно интерпретиро- вать как результат измерений через равные промежутки времени некоторого сигнала. Вектор v должен содержать 2m элементов. Резуль- тат – комплекснозначный вектор размерности 1 + 2m–1. Если v имеет размерность, отличную от 2m, Mathcad выдает сообщение об ошибке "неверный размер вектора". Элементы вектора, возвращаемого fft, вычисляются по формуле n −1 ∑ vk e 2 πi (j n) k . 1 Cj = n k =0 В этой формуле n – число элементов в v, i – мнимая единица. Эле- менты в векторе, возвращенном функцией fft, соответствуют различ- ным частотам. Чтобы восстановить фактическую частоту, необходимо знать частоту измерения исходного сигнала. Если v есть n-мерный век- тор, переданный функции fft, и частота измерения исходного сигнала – fs, то частота, соответствующая Ck k fk = fs. n Обратите внимание, что это делает невозможным обнаружить часто- ты выше частоты измерения исходного сигнала. Это ограничение, нала- гаемое не Mathcad, а самой сутью проблемы. Чтобы правильно восста- новить сигнал по его преобразованию Фурье, необходимо произвести 42 i:= 0 .. 63 xi:= sin  π⋅  + rnd (1) − 0.5 i Формирование сигнала:    10  Применяется комплексное преобразование Фурье: c:= fft(x) N:= last (c) N = 32 Обращение преобразования Фурье: z:= ifft(c) N2:= last (z) N2 = 63 j:= 0 .. N k:= 0 .. N2 Графическое представление сигнала zk = xj = 2 –0.499 –0.499 2.34·10 –3 2.34·10–3 0.673 0.673 xi 0 0.659 0.659 1.274 1.274 0.674 0.674 –2 0 20 40 60 80 1.162 1.162 i 0.613 0.613 Фурье-образ 0.179 0.179 4 –0.044 –0.044 0.489 0.489 –0.69 –0.69 cj 2 –1.079 –1.079 –0.777 –0.777 –0.849 –0.849 –1.334 –1.334 0 0 10 20 30 40 j Рис. 15. Быстрые пр6еобразования Фурье в Mathcad 43 измерения исходного сигнала с частотой, по крайней мере, вдвое боль- шей, чем ширина полосы частот. Подробное обсуждение этой пробле- мы содержится в специальных курсах. Функция ifft(v) возвращает обратное дискретное преобразование Фурье. Вектор v должен иметь 1 + 2m элементов, где m – целое. Резуль- тат есть вектор размерности 2m+1. Аргумент v – вектор, подобный созданному функцией fft. Чтобы вы- числить результат, Mathcad сначала создает новый вектор w, комплекс- но сопряженный v, и присоединяет его к вектору v. Затем Mathcad вы- числяет вектор d, элементы которого вычисляются по формуле n −1 ∑ wk e−2πi(j n)k . 1 dj = n k =0 Это та же самая формула, что и для fft, кроме знака минус в функции экспоненты. Функции fft и ifft – точные обращения. Для всех веще- ственных v справедливо ifft(fft(v)) = v. Пример использования прямого и обратного преобразований Фурье приведен на рис. 15. 4.6. Альтернативные формы преобразования Фурье Определения преобразования Фурье, рассмотренные выше, не явля- ются единственно возможными. Например, часто используются следу- ющие определения прямого и обратного преобразований Фурье: n n ∑ f (τ)e−2πi(ν n)τ ; f (τ) = ∑ F (ν) e () . 1 2 πi τ / n ν F (ν) = n τ=1 v =1 Эти определения реализованы во встроенных функциях FFT/IFFT и ICFFT. Они отличаются от быстрого преобразования Фурье следующим: вместо коэффициента 1 n перед обеими формулами стоит коэф- фициент 1/n и коэффициент 1 в обратном преобразовании; знак минус появляется в показателе экспоненты прямого преобразо- вания и исчезает в формуле обратного. 4.7. Кусочно-непрерывные функции Кусочно-непрерывные функции полезны для управления ветвлени- ями и остановками вычислительных процессов. Имеются пять функций 44 Использование условных операторов 2 x:= −2 , − 1.8 .. 2 f (x) := x − 1 g (x) := if(f (x) >0 , f (x) , 0) g(x) нь f(x) > 0 үед f(x)-тэй тэнцүү, өөрөөр хэлбэл 0 4 4 2 f (x) g(x) 2 0 2 0 2 0 2 2 0 2 x x h (x) := if(x ≥ 1 , f (x) , − f (x)) otherwise –f(x) 5 h(x) 0 Нөхцөл биелэх хүртэл тооцооллыг үргэлжлүүлнэ 5 2 0 2 2 асуулт − а< err x −2 N:= 100 i:= 0 .. N a:= 1000 quess 0:= 10 err:= 10  quess i + a   quess i  quess i+ 1:= until (quess i) − a − err ,  2  2  N2:= last (quess) − 1 j:= 0 .. N2 j= quess j = (quess j)2 = 0 10 100 Число итераций N2 = 5 1 55 3.025·10 3 answer:= quess N2 2 36.591 1.339·10 3 3 31.96 1.021·10 3 answer = 31.623 4 31.625 1·10 3 5 31.623 1·10 3 Рис. 16. Условные выражения в Mathcad 45 Mathcad, относящихся к этому классу. Функция if полезна для выбора одного из двух значений, определяемого условием. Ступенчатая функ- ция Хевисайда Ф(х) и символ Кронекера δ(m, n) во многом аналогичны функции if. Функция until используется, чтобы управлять процессом итераций. Функция if(cond, tval, fval) возвращает значение tval, если cond отли- чен от 0 (истина) и возвращает fval, если cond равен 0 (ложь). Обычно в качестве аргумента cond выбирается булево выражение вида w = z, x >у, х< y, x ≥ y, x ≤ y, w ≠ z. Можно объединять булевы операторы, чтобы записать более сложные условия. Например, условие (x < 1) ⋅ (x >0) логик "ба" шиг ажилладаг бөгөөд зөвхөн x нь 0-ээс 1-ийн хооронд байвал 1-ийг буцаана. Үүний нэгэн адил илэрхийлэл (x > 1) + (x)< 0) действует подобно логическому "или", возвращающему 1, если x >1 эсвэл x< 0, и 0, если x заключено между 0 и 1. Функция until (x, z) возвращает z, пока выражение x не становится отрицательным; должно содержать дискретный аргумент. Функция until позволяет останавливать вычисления для последовательных значений дискретного аргумента. Функция until полезна в итеративных процес- сах с определенным условием сходимости. На рис. 16 приведены примеры использования функций if и until. Функция Хевисайда эквивалентна следующей функции: Ф (x) := if (x < 0,0,1) Символ Кронекера δ(m, n) возвращает 1, если m = n; иначе 0. Оба аргумента должны быть целочисленными. Символ Кронекера эквива- лентен функции δ (m, n) := if (m = n,1,0) Ступенчатая функция Хевисайда может быть использована для со- здания импульса шириной w: pulse (x, w) := Ф (x) − Ф (x − w) Можно определить также две полезные функции lowpass и highpass. Они обе являются фильтрами – умножение на них какого-либо сигнала 46 вырезает из этого сигнала кусок вокруг точки x, имеющий ширину 2w. Разница состоит в том, что lowpass оставляет только вырезанный ку- сок, highpass – все, кроме вырезанного куска. lowpass (x, w) := pulse (x+w, 2 ⋅ w) highpass (x, w) := 1 − pulse (x+w, 2 ⋅ w) 4.8. Статистические функции Для вычисления статистических оценок случайных совокупностей чисел в Mathcad могут использоваться следующие функции: mean(A) – возвращает среднее значение элементов массива А раз- мерности m × n по формуле m −1 n −1 ∑ ∑ Aij ; 1 mean(A) = mn i =0 j =0 var(A) – возвращает дисперсию элементов массива А размерности m × n согласно формуле m −1 n −1 ∑ ∑ Aij − mean(A) 1 2 var(A) = ; mn i =0 j =0 stdev(A) - возвращает среднеквадратичное отклонение (квадратный корень из дисперсии) элементов m × n массива А stdev(A) = var(A). 4.9. Плотности распределения вероятности Эти функции показывают отношение вероятности того, что случай- ная величина попадает в малый диапазон значений с центром в задан- ной точке, к величине этого диапазона. В Mathcad имеются функции семнадцати плотностей вероятностей. Отметим только некоторые из них: dnorm(x, µ, σ) – возвращает плотность вероятности нормального рас- пределения 1  (x − µ) 2  dnorm(x, µ, σ) = exp  − , 2πσ  2σ 2  47 в котором µ и σ есть среднее значение и среднеквадратичное отклоне- ние, σ >0; dunif(x, a, b) – a ба b нь зааг байх  1, x ∈ ,  dunif(x, a, b) =  b − a  0,  x ∉ жигд тархалтын магадлалын нягтыг тооцоолно. цэгийн интервал, a< b. 4.10. Функции распределения Эти функции возвращают вероятность того, что случайная величи- на меньше или равна определенному значению. Функция распределе- ния вероятности – это функция плотности вероятности, проинтегриро- ванная от минус бесконечности до определенного значения. Приведем две из них: pnorm(x, µ, σ) – возвращает функцию нормального распределения со средним µ и среднеквадратическим отклонением σ (σ >0); punif(x, a, b) – жигд тархалтын функцийг буцаана. a ба b нь интервалын хилийн утгууд (a< b). Mathcad имеет ряд функций для генерирования случайных чисел, имеющих разнообразные распределения вероятностей. Приведем две из них: rnorm(m, µ, σ) – возвращает вектор m случайных чисел, имеющих нормальное распределение (σ >0); runif(m, a, b) – а ба b нь интервалын (a) хилийн цэгүүд болох жигд тархалттай санамсаргүй m тооны векторыг буцаана.< b). Остальные встроенные статистические функции и их описания мож- но посмотреть, выбрав команду Функция из меню Вставка. 4.11. Интерполяция и функции предсказания Интерполяция заключается в использовании значений некоторой функции, заданных в ряде точек, чтобы предсказать значения между ними. В Mathcad можно или соединять точки данных прямыми линия- ми (линейная интерполяция) или соединять их отрезками кубического полинома (кубическая сплайн-интерполяция). 48 В отличие от функций регрессии, обсуждаемых в следующем разде- ле, функции интерполяции определяют кривую, точно проходящую че- рез заданные точки. Из-за этого результат очень чувствителен к ошиб- кам данных. Если данные зашумлены, следует рассмотреть возможность использования регрессии вместо интерполяции. Для линейной интерполяции используется функция linterp(vx, vy, x), которая по векторным данным vx и vy возвращает линейно интерполи- руемое значение y, соответствующее третьему аргументу x. Аргументы vx и vy должны быть векторами одинаковой длины. Вектор vx должен содержать вещественные значения, расположенные в порядке возраста- ния. Эта функция соединяет точки данных отрезками прямых, созда- вая, таким образом, ломаную линию. Интерполируемое значение для конкретного x есть ордината y соответствующей точки ломаной. Пример линейной интерполяции показан на рис. 17. Кубическая сплайн-интерполяция позволяет провести кривую через набор точек таким образом, что первые и вторые производные кривой непрерывны в каждой точке. Эта кривая образуется путем создания ряда кубических полиномов, проходящих через наборы из трех смежных то- чек. Кубические полиномы состыковываются друг с другом, чтобы об- разовать одну кривую. Чтобы провести кубический сплайн через набор точек: создайте векторы vx и vy, содержащие координаты x и y, через кото- рые нужно провести кубичный сплайн. Элементы vx должны быть рас- положены в порядке возрастания; вычислите вектор vs:=cspline(vx, vy). Вектор vs содержит вторые про- изводные интерполяционной кривой в рассматриваемых точках. Чтобы найти интерполируемое значение в произвольной точке, ска- жем х0, вычислите interp(vs, vx, vy, x0), где vs, vx и vy – векторы, опи- санные ранее. Обратите внимание, что можно сделать то же самое, вычисляя interp(cspline(vx, vy),vx,vy, x0). Пример использования кубической сплайн-интерполяции приведен на рис. 17 внизу. 49 Линейная интерполяция i:= 0 .. 5 VXi:=i VYi:=vd(1) VXi = VYi = –3 linterp(VX, VY, 1.5) = 0.389 0 1.268·10 1 0.193 linterp(VX, VY, 3.75) = 0.705 2 0.585 linterp(VX, VY, 4.1) = 0.758 3 0.35 4 0.823 x:= 0 , 0.1.. 5 5 0.174 1 linterp(VX , VY , x) 0.5 VYi 0 0 2 4 6 x , VX i Кубическая сплайн-интерполяция i:= 0 .. 5 VXi:= i VYi:= rnd (1) VS:= lspline (VX, VY) interp (VS, VX, VY, 1.5) = 0.188 interp (VS, VX, VY, 3.75) = 0.868 interp (VS, VX, VY, 4.1) = 0.989 1 VYi = 0.71 interp(VS , VX , VY , x) 0.304 0.5 VYi 0.091 0.147 0.989 0 0 2 4 6 0.119 x , VX i Рис. 17. Примеры интерполяции 50

Өмнөх хэсэгт томьёогоор өгөгдсөн функцийн аналитик Фурье хувиргалтыг хийх боломжийг олгодог Mathcad симбол процессорын чадварыг тодорхойлсон. Үүний зэрэгцээ тооцооллын математикийн асар том асуудал нь хүснэгтэд өгөгдсөн функцүүдийн (жишээлбэл, зарим туршилтын үр дүнг илэрхийлэх) эсвэл аналитик байдлаар нэгтгэх боломжгүй функцүүдийн Фурье интегралыг тооцоолохтой холбоотой юм. Энэ тохиолдолд бэлгэдлийн хувиргалтуудын оронд интегралыг ялгахтай холбоотой тоон интеграцийн аргуудыг ашиглах шаардлагатай тул дискрет Фурье хувиргалт гэж нэрлэдэг.

Mathcad тоон процессорт дискрет Фурье хувиргалтыг хамгийн алдартай хурдан Фурье хувиргах алгоритм (товчилсон FFT) ашиглан хэрэгжүүлдэг. Энэхүү алгоритм нь зөвхөн хэвийн болгоход ялгаатай хэд хэдэн Mathcad функцэд хэрэгждэг.

• fft(y) - шууд Фурье хувиргах вектор;
• FFT (y) - өөр нормчлолд шууд Фурье хувиргалтын вектор;
• ifft (w) - урвуу Фурье хувирлын вектор;
• IFFT (w) нь урвуу Фурье хувиргалтын өөр нормчиллын вектор юм.
  • y нь аргументын утгуудын тэнцүү интервалаар авсан бодит өгөгдлийн вектор;
  • w нь давтамжийн утгын тэнцүү интервалаар авсан Фурье спектрийн бодит өгөгдлийн вектор юм.

Анхаар!
Фурьегийн шууд хувиргалтын аргумент, өөрөөр хэлбэл y вектор нь яг 2 n элементтэй байх ёстой (n нь бүхэл тоо). Үр дүн нь 1+2 n-1 элементтэй вектор юм. Эсрэгээр Фурьегийн урвуу хувиргалтын аргумент нь 1+2 n-1 элементтэй байх ёстой бөгөөд түүний үр дүн нь 2 n элементийн вектор болно. Хэрэв өгөгдлийн тоо 2-ын чадалтай давхцахгүй бол алга болсон элементүүдийг тэгээр нэмэх шаардлагатай..

Жагсаалт 4.14 нь өөр өөр далайцтай хоёр синусоидын нийлбэр болох f (x) загварын функцийн Фурье спектрийг тооцоолох жишээг харуулж байна (Зураг 4.10-ын дээд график). Тооцооллыг N=128 цэгийг ашиглан хийсэн ба i-ийн өгөгдлийн түүвэрлэлтийн интервал h-тэй тэнцүү гэж үзсэн. Жагсаалтын төгсгөлийн мөрөнд W давтамжийн харгалзах утгыг зөв тодорхойлж, сүүлчийн мөрөнд суурилуулсан FFT функцийг ашигладаг. Үүссэн Фурье спектрийн графикийг Зураг дээр үзүүлэв. 4.10 (доод). Тооцооллын үр дүнг түүний модулийн хэлбэрээр танилцуулж байгааг анхаарна уу, учир нь спектр нь өөрөө нарийн төвөгтэй байдаг. Жагсаалтын эхэнд олж авсан далайц ба спектрийн оргилуудын байршлыг синусоидуудын тодорхойлолттой харьцуулах нь маш ашигтай байдаг.

Анхаарна уу
Фурье хувиргалтын шинж чанар, практик хэрэглээний талаарх дэлгэрэнгүй мэдээллийг 14-р бүлгээс олж болно.

Жагсаалт 4.14. Загварын дохионы дискрет Фурье хувиргалт (FFT алгоритм):

Цагаан будаа. 4.10. Загварын функц ба түүний Фурье хувиргалт (Жагсаалт 4.14-с үргэлжлэл)

3-р хэсэг. Mathcad дээр энгийн дифференциал тэгшитгэлийг шийдвэрлэх

Дурын сегмент дээрх Фурье цуврал

2-р хэсэг. Фурье цуврал дахь функцүүдийн өргөтгөл

Комплекс тоо бүхий үйлдлүүд

1-р хэсэг. Mathcad дээр нийлмэл тоо бүхий тооцоолол

Лекц №5

Сэдэв: « Нарийн төвөгтэй хувьсагч. Фурье цуврал дахь функцүүдийн өргөтгөл. Дифференциал тэгшитгэлийг шийдвэрлэх»

Mathcad-д төсөөллийн нэгж i-г тодорхойлсон: тиймээс нийлмэл тоонууд болон тэдгээртэй хийх үйлдлүүд тодорхойлогддог.

Z=a+bi– комплекс тоог бичих алгебрийн хэлбэр.

a – бодит хэсэг, б – төсөөллийн хэсэг

Комплекс тоог бичих экспоненциал (экпоненциал) хэлбэр,

A – модуль, φ – аргумент (үе шат)

Комплекс тоог бичих тригонометрийн хэлбэр.

Хэмжигдэхүүний хоорондын хамаарал: a=A cos φ b=A sin φ

Z1=a1+j b1, Z2=a2+j b2

a) Нэмэх (хасах) Z3=Z1±Z2=(a1±a2)+j·(b1±b2)

b) Үржүүлэх c·Z1=a·c+j·b·c

Z3=Z1·Z2=(a1·a2-b1·b2)+j·(a1·b2+a2·b1)=A1A2ej(φ1+φ2)

в) хэлтэс

d) Хүч чадал n хүртэл өсгөх (байгалийн)

e) Үндэс олборлолт: , энд k =0,1,2...n-1

Машин нь зөвхөн радианыг хүлээн авдаг!!! радиан=градус=радиан

Жишээ нь:

Хэрэв интеграл байгаа бол f(x) функц нь [-p;p] интервал дээр үнэмлэхүй интеграл болно. [-p;p] интервал дээрх туйлын интегралдах f(x) функц бүрийг түүний тригонометрийн Фурье цувралтай холбож болно.

Тригонометрийн Фурье цувралын коэффициентүүдийг Фурьегийн коэффициент гэж нэрлэдэг бөгөөд Эйлер-Фурье томъёог ашиглан тооцоолно: ,

Хэсэгчилсэн гөлгөр функц f(x)-ын Фурье цувралын n-р хэсэгчилсэн нийлбэрийг [-p;p] интервал дээр тэмдэглэе. Стандарт хазайлтыг дараах томъёогоор тодорхойлно.

[-p;p] дээр интегралчлагдах аливаа хязгаарлагдмал f(x) функцийн хувьд Фурье цувралын хэсэгчилсэн нийлбэр нь n-р зэрэглэлийн хамгийн сайн ойролцоо утгатай тригонометрийн олон гишүүнт юм.

Жишээ:

Графикууд нь Фурье цувралын хэсэгчилсэн нийлбэрүүд хэрхэн нийлдэг болохыг харуулж байна. f(x) функцийн тасралтгүй байдлын цэгүүдийн ойролцоо х цэг дэх функцийн утга ба энэ цэг дэх цувааны хэсэгчилсэн нийлбэрийн утгын зөрүү n®¥ байдлаар тэг болох хандлагатай байна. онолтой бүрэн нийцэж байгаа тул энэ тохиолдолд. Функцийн тасалдлын цэгүүдээс x цэг холдох тусам ялгаа нь тэг болох хандлагатай байгааг харж болно.

Жишээ:

f(x) функцийн [-L;L] интервал дээрх хэсэгчилсэн гөлгөр функцийн хувьд шугаман орлуулалтаар [-L;L] интервал дээрх Фурьегийн цувааг өргөтгөх асуудлыг функцийг өргөтгөх асуудал болгон бууруулна. [-p;p] интервал дээр:

Төрөл бүрийн тэгш хэмийн нөхцөлд Фурье цувралын хялбаршлыг авч үзье.

томъёо (1) томъёо (2)

Тэгшитгэлийн шийдийг олох шаардлагатай байг

анхны нөхцөлтэй. Энэ даалгавар гэж нэрлэдэг Кошигийн асуудал . Хүссэн функцийг цэгийн ойролцоох цуврал болгон өргөжүүлж, өргөтгөлийн эхний хоёр нөхцөлөөр хязгаарлая. (1) тэгшитгэлийг харгалзан үзээд үүнийг тэмдэглэснээр бид энэ томьёог олон удаа хэрэглэж, функцийн утгыг улам олон шинэ цэгээс олох боломжтой болно.

Энгийн дифференциал тэгшитгэлийг шийдэх энэ аргыг нэрлэдэг Эйлерийн арга . Геометрийн хувьд Эйлерийн арга нь алхам бүрт бид уусмалыг (интеграл муруй) интервалын эхэнд уусмалын график руу татсан шүргэгч сегментээр ойртуулдаг гэсэн үг юм. Аргын нарийвчлал бага бөгөөд дараалалд байна h. Тэд Эйлерийн аргыг нэгдүгээр эрэмбийн арга, өөрөөр хэлбэл түүний нарийвчлал нь алхам буурах тусам шугаман нэмэгддэг гэж тэд хэлдэг. h.

Эйлерийн аргын нарийвчлалыг нэмэгдүүлэхийн тулд янз бүрийн өөрчлөлтүүд байдаг. Эдгээр нь бүгд интервалын эхэнд тооцоолсон деривативыг энэ интервал дахь деривативын дундаж утгаараа орлуулсанд үндэслэсэн болно.