Хүлээгдэж буй үнэ цэнэ. Математикийн хүлээлтдискрет санамсаргүй хэмжигдэхүүн X, хязгаарлагдмал тооны утгыг авч байна Xбимагадлал бүхий Рби, хэмжээг дараах байдлаар нэрлэнэ.

Математикийн хүлээлттасралтгүй санамсаргүй хэмжигдэхүүн Xутгуудын үржвэрийн интеграл гэж нэрлэдэг Xмагадлалын тархалтын нягт дээр е(x):

(6б)

Буруу интеграл (6 б) нь туйлын нийлдэг гэж үздэг (өөрөөр хэлбэл тэд математикийн хүлээлт гэж хэлдэг. М(X) байдаггүй). Математикийн хүлээлтийг тодорхойлдог дундаж утгасанамсаргүй хувьсагч X. Түүний хэмжээс нь санамсаргүй хэмжигдэхүүний хэмжигдэхүүнтэй давхцдаг.

Математикийн хүлээлтийн шинж чанарууд:

Тархалт. Зөрчилсанамсаргүй хувьсагч Xдугаар гэж нэрлэдэг:

Зөрчил нь тараах шинж чанарсанамсаргүй хувьсагчийн утгууд Xтүүний дундаж утгатай харьцуулахад М(X). Вариацын хэмжээс нь санамсаргүй хэмжигдэхүүний квадрат хэмжээтэй тэнцүү байна. Дискрет санамсаргүй хэмжигдэхүүний хувьд дисперс (8) ба математикийн хүлээлт (5) ба тасралтгүй санамсаргүй хэмжигдэхүүний хувьд (6) гэсэн тодорхойлолтод үндэслэн бид дисперсийн ижил төстэй илэрхийлэлүүдийг олж авна.

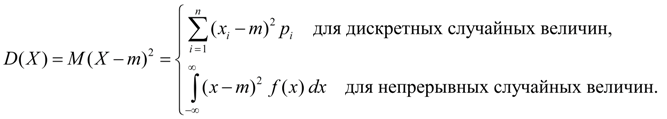(9)

Энд м = М(X).

Тархалтын шинж чанарууд:

Стандарт хэлбэлзэл:

(11)

Стандарт хазайлт нь санамсаргүй хэмжигдэхүүнтэй ижил хэмжээтэй байдаг тул үүнийг дисперсээс илүү тархалтын хэмжүүр болгон ашигладаг.

Түгээлтийн мөчүүд. Математикийн хүлээлт ба тархалтын тухай ойлголтууд нь илүү олон зүйлийн онцгой тохиолдол юм ерөнхий ойлголттоон шинж чанарын хувьд санамсаргүй хэмжигдэхүүн – түгээлтийн мөчүүд. Санамсаргүй хэмжигдэхүүний тархалтын моментуудыг санамсаргүй хэмжигдэхүүний зарим энгийн функцүүдийн математик хүлээлт болгон танилцуулсан. Тиймээс, захиалгын мөч кцэгтэй харьцуулахад X 0-ийг математикийн хүлээлт гэж нэрлэдэг М(X–X 0 )к. Гарал үүслийн талаархи мөчүүд X= 0 гэж нэрлэдэг анхны мөчүүдболон дараахыг тодорхойлсон:

(12)

Эхний эрэмбийн эхний момент нь авч үзэж буй санамсаргүй хэмжигдэхүүний тархалтын төв юм.

(13)

Түгээлтийн төвийн тухай мөчүүд X= мгэж нэрлэдэг төв цэгүүдболон дараахыг тодорхойлсон:

(14)

(7)-аас эхний эрэмбийн төв момент үргэлж байдаг тэгтэй тэнцүү:

Тогтмол утгаар шилжсэнээс хойш төв моментууд нь санамсаргүй хэмжигдэхүүний утгын гарал үүслээс хамаардаггүй. ХАМТтүүний түгээлтийн төв ижил утгаар шилждэг ХАМТ, мөн төвөөс хазайлт өөрчлөгдөхгүй: X – м = (X – ХАМТ) – (м – ХАМТ).
Одоо энэ нь тодорхой боллоо тархалт- Энэ хоёр дахь захиалгын төв мөч:

Тэгш бус байдал. Гурав дахь захиалгын төв мөч:

(17)

үнэлгээ хийх үүрэгтэй хуваарилалтын тэгш бус байдал. Хэрэв тархалт нь цэгийн хувьд тэгш хэмтэй байвал X= м, дараа нь гуравдахь эрэмбийн төв мөч нь тэгтэй тэнцүү байх болно (сондгой эрэмбийн бүх төв мөчүүд шиг). Тиймээс, хэрэв гурав дахь эрэмбийн төв момент тэгээс ялгаатай бол тархалт нь тэгш хэмтэй байж чадахгүй. Тэгш бус байдлын хэмжээг хэмжээсгүй хэмжигдэхүүн ашиглан үнэлдэг тэгш бус байдлын коэффициент:

(18)

Тэгш бус байдлын коэффициент (18) тэмдэг нь баруун эсвэл зүүн талын тэгш бус байдлыг илэрхийлдэг (Зураг 2).

Цагаан будаа. 2. Түгээлтийн тэгш бус байдлын төрлүүд.

Илүүдэл. Дөрөв дэх дарааллын төв мөч:

(19)

гэж нэрлэгддэгийг үнэлэхэд үйлчилдэг илүүдэл, энэ нь муруйтай харьцуулахад тархалтын төвийн ойролцоо тархалтын муруйн эгц (цовой) зэргийг тодорхойлдог. хэвийн тархалт. Хэвийн тархалтын хувьд куртоз гэж авсан утга нь:

(20)

Зураг дээр. Зураг 3-т өөр өөр куртозын утгатай тархалтын муруйнуудын жишээг үзүүлэв. Хэвийн хуваарилалтын хувьд Э= 0. Ердийнхөөс илүү шовх муруй нь эерэг, хавтгай оройтой нь сөрөг муруйтай байна.

Цагаан будаа. 3. Янз бүрийн түвшний эгц (куртоз) бүхий тархалтын муруй.

Инженерийн хэрэглээний өндөр эрэмбийн моментууд математик статистикихэвчлэн ашигладаггүй.

Загвар салангидсанамсаргүй хэмжигдэхүүн нь түүний хамгийн их магадлалтай утга юм. Загвар Үргэлжилсэнсанамсаргүй хэмжигдэхүүн нь магадлалын нягт хамгийн их байх үед түүний утга юм (Зураг 2). Хэрэв тархалтын муруй хамгийн ихдээ нэг байвал тархалтыг дуудна нэг загвартай. Хэрэв тархалтын муруй нь нэгээс олон максимумтай бол тархалтыг дуудна multimodal. Заримдаа муруй нь хамгийн их биш харин хамгийн багатай тархалт байдаг. Ийм хуваарилалтыг гэж нэрлэдэг эсрэг горим. Ерөнхий тохиолдолд санамсаргүй хэмжигдэхүүний горим ба математикийн хүлээлт давхцдаггүй. Онцгой тохиолдолд, төлөө модаль, өөрөөр хэлбэл горимтой, тэгш хэмтэй тархалттай бөгөөд математикийн хүлээлт байгаа тохиолдолд сүүлийнх нь тархалтын тэгш хэмийн горим ба төвтэй давхцдаг.

Медиан санамсаргүй хувьсагч X- энэ бол түүний утга юм Meh, тэгш байдал хангагдсан: i.e. санамсаргүй хэмжигдэхүүн байх магадлалтай Xбага эсвэл илүү байх болно Meh. Геометрийн хувьд дундажнь тархалтын муруйн доорх талбайг хагасаар хуваах цэгийн абсцисса юм (Зураг 2). Модаль тэгш хэмтэй тархалтын хувьд медиан, горим, математикийн хүлээлт ижил байна.

Олон асуудлыг шийдэхэд практик асуудлуудСанамсаргүй хэмжигдэхүүнийг бүрэн тодорхойлох, өөрөөр хэлбэл тархалтын хуулиудыг тодорхойлох нь үргэлж шаардлагатай байдаггүй. Нэмж дурдахад, салангид санамсаргүй хэмжигдэхүүн, нягтралын хувьд функц эсвэл цуврал тархалтыг бий болгох нь төвөгтэй бөгөөд шаардлагагүй юм.

Заримдаа тархалтын онцлогийг хэсэгчлэн тодорхойлдог бие даасан тоон параметрүүдийг зааж өгөхөд хангалттай. Санамсаргүй хэмжигдэхүүн тус бүрийн дундаж утгыг, түүний боломжит утгыг бүлэглэсэн эсвэл дундажтай харьцуулахад эдгээр утгын тархалтын зэрэг зэргийг мэдэх шаардлагатай.

Тархалтын хамгийн чухал шинж чанаруудын шинж чанарыг тоон шинж чанарууд гэж нэрлэдэг санамсаргүй хувьсагч.Тэдгээрийн тусламжтайгаар тархалтын хуулиудыг тодорхойлохгүйгээр магадлалын олон асуудлыг шийдвэрлэхэд хялбар байдаг.

Тооны тэнхлэг дээрх санамсаргүй хэмжигдэхүүний байрлалын хамгийн чухал шинж чанар хүлээгдэж буй үнэ цэнэ М[X]= a,заримдаа санамсаргүй хэмжигдэхүүний дундаж гэж нэрлэдэг. Учир нь дискрет санамсаргүй хэмжигдэхүүн Xболомжит утгууд x 1 , x 2 , … , x nболон магадлал х 1 , х 2 ,… , p nтомъёогоор тодорхойлогддог

=1 гэж үзвэл бид бичиж болно

Тиймээс, математикийн хүлээлт Дискрет санамсаргүй хэмжигдэхүүн нь түүний боломжит утгууд ба тэдгээрийн магадлалын бүтээгдэхүүний нийлбэр юм.Олон тооны туршилт хийснээр санамсаргүй хэмжигдэхүүний ажиглагдсан утгуудын арифметик дундаж нь түүний математик хүлээлтэд ойртдог.

Учир нь тасралтгүй санамсаргүй хэмжигдэхүүн Xматематикийн хүлээлт нь нийлбэрээр биш харин тодорхойлогддог интеграл

Хаана е(x) - тоо хэмжээний хуваарилалтын нягт X.

Математикийн хүлээлт бүх санамсаргүй хэмжигдэхүүнд байдаггүй. Тэдний заримын хувьд нийлбэр буюу интеграл нь зөрүүтэй байдаг тул математикийн хүлээлт байдаггүй. Эдгээр тохиолдолд нарийвчлалын үүднээс санамсаргүй хэмжигдэхүүн дэх боломжит өөрчлөлтийн хүрээг хязгаарлах хэрэгтэй X,нийлбэр буюу интеграл нь нийлэх болно.

Практикт горим ба медиан зэрэг санамсаргүй хэмжигдэхүүний байрлалын шинж чанаруудыг ашигладаг.

Санамсаргүй хувьсах горимтүүний хамгийн их магадлалтай утгыг нэрлэнэ.Ерөнхийдөө горим ба математикийн хүлээлт нь давхцдаггүй.

Санамсаргүй хэмжигдэхүүний медианX нь санамсаргүй хэмжигдэхүүний том юмуу бага утгыг олж авах магадлал тэнцүү байх түүний утга юм., өөрөөр хэлбэл энэ нь тархалтын муруйгаар хязгаарлагдсан талбайг хагасаар хуваах цэгийн абсцисса юм. Тэгш хэмтэй тархалтын хувьд бүх гурван шинж чанар ижил байна.

Математикийн хүлээлт, горим ба медианаас гадна бусад шинж чанаруудыг магадлалын онолд ашигладаг бөгөөд тэдгээр нь тус бүр нь тархалтын тодорхой шинж чанарыг тодорхойлдог. Жишээлбэл, санамсаргүй хэмжигдэхүүний тархалтыг тодорхойлдог тоон шинж чанарууд, өөрөөр хэлбэл түүний боломжит утгууд нь математикийн хүлээлтийн эргэн тойронд хэр ойрхон бүлэглэгдэж байгааг харуулсан тоон шинж чанарууд нь тархалт ба стандарт хазайлт юм. Эдгээр нь санамсаргүй хэмжигдэхүүнийг ихээхэн нөхдөг, учир нь практикт ижил математик хүлээлттэй санамсаргүй хэмжигдэхүүнүүд ихэвчлэн байдаг боловч тархалт нь өөр өөр байдаг. Тархалтын шинж чанарыг тодорхойлохдоо санамсаргүй хэмжигдэхүүний зөрүүг ашиглана Xболон түүний математик хүлээлт, i.e.

Хаана А = М[X] - хүлээгдэж буй үнэ цэнэ.

Энэ ялгааг нэрлэдэг төвлөрсөн санамсаргүй хэмжигдэхүүн,харгалзах утга X,болон томилогдсон :

Санамсаргүй хэмжигдэхүүний хэлбэлзэлнь математик хүлээлтээс утгын квадрат хазайлтын математик хүлээлт, өөрөөр хэлбэл:

D[ X]=М[( X–a) 2 ], эсвэл

D[ X]=М[ 2 ].

Санамсаргүй хэмжигдэхүүний тархалт нь түүний математик хүлээлтийн эргэн тойронд санамсаргүй хэмжигдэхүүний утгуудын тархалт, тархалтын тохиромжтой шинж чанар юм. Гэсэн хэдий ч энэ нь санамсаргүй хэмжигдэхүүний квадратын хэмжээтэй тул харагдахуйц биш юм.

Тархалтыг нүдээр харуулахын тулд хэмжээс нь санамсаргүй хэмжигдэхүүний хэмжигдэхүүнтэй давхцах утгыг ашиглах нь илүү тохиромжтой. Энэ тоо хэмжээ стандарт хэлбэлзэл санамсаргүй хэмжигдэхүүн нь эерэг үзүүлэлт юм Квадрат язгууртүүний хэлбэлзлээс.

Хүлээлт, горим, медиан, дисперс, стандарт хазайлт - санамсаргүй хэмжигдэхүүний хамгийн түгээмэл хэрэглэгддэг тоон шинж чанарууд. Практик асуудлыг шийдвэрлэхдээ тархалтын хуулийг тодорхойлох боломжгүй тохиолдолд санамсаргүй хэмжигдэхүүний ойролцоо тайлбар нь тархалтын зарим шинж чанарыг илэрхийлдэг тоон шинж чанар юм.

Төвийн тархалт (математикийн хүлээлт) ба дисперсийн (тархалт) үндсэн шинж чанаруудаас гадна бусдыг дүрслэх шаардлагатай байдаг. чухал шинж чанаруудхуваарилалт - тэгш хэмТэгээд хурц тод байдал,тархалтын моментуудыг ашиглан дүрсэлж болно.

Санамсаргүй хэмжигдэхүүний бүх момент нь мэдэгдэж байвал түүний тархалт бүрэн тодорхойлогдоно.Гэсэн хэдий ч олон тархалтыг эхний дөрвөн мөчийг ашиглан бүрэн дүрсэлж болох бөгөөд эдгээр нь зөвхөн тархалтыг тодорхойлдог параметрүүд төдийгүй эмпирик тархалтыг сонгоход чухал ач холбогдолтой, тухайлбал тухайн статистикийн моментуудын тоон утгыг тооцоолоход чухал ач холбогдолтой юм. цуврал болон тусгай график ашиглан та тархалтын хуулийг тодорхойлж болно.

Магадлалын онолын хувьд эхний ба төв гэсэн хоёр төрлийн моментийг ялгадаг.

k-р эрэмбийн эхний мөчсанамсаргүй хувьсагч Тхэмжигдэхүүний математик хүлээлт гэж нэрлэдэг Xk,өөрөөр хэлбэл

Иймээс салангид санамсаргүй хэмжигдэхүүний хувьд энэ нь нийлбэрээр илэрхийлэгдэнэ

ба тасралтгүй хувьд – интегралаар

Санамсаргүй хэмжигдэхүүний анхны моментуудын дотроос математикийн хүлээлт болох эхний эрэмбийн момент онцгой ач холбогдолтой. Дээд эрэмбийн эхний моментуудыг голчлон төв моментуудыг тооцоолоход ашигладаг.

k-р эрэмбийн төв мөчсанамсаргүй хэмжигдэхүүн нь утгын математик хүлээлт ( X - М [X])к

Хаана А = M[X].

Дискрет санамсаргүй хэмжигдэхүүний хувьд энэ нь нийлбэрээр илэрхийлэгдэнэ

Атасралтгүй хувьд - интегралаар

Санамсаргүй хэмжигдэхүүний төв мөчүүдийн дунд онцгой ач холбогдолтой байдаг хоёр дахь захиалгын төв мөч,Энэ нь санамсаргүй хэмжигдэхүүний дисперсийг илэрхийлдэг.

Эхний эрэмбийн төв мөч үргэлж тэг байна.

Гурав дахь эхлэх мөчтархалтын тэгш бус байдлыг (халуу) тодорхойлж, салангид ба тасралтгүй санамсаргүй хэмжигдэхүүнүүдийн ажиглалтын үр дүнд үндэслэн холбогдох илэрхийллээр тодорхойлно.

Энэ нь санамсаргүй хэмжигдэхүүний шоо хэмжээтэй тул хэмжээсгүй шинж чанарыг олж авахын тулд м 3гурав дахь зэрэгт стандарт хазайлтаар хуваагдана

Үүссэн утгыг тэгш бус байдлын коэффициент гэж нэрлэдэг бөгөөд тэмдэгээс хамааран эерэг ( гэх мэт> 0) эсвэл сөрөг ( гэх мэт< 0) тархалтын хазайлт (Зураг 2.3).

САНАМСАР ХУВЬСАГЧ БА ТҮҮНИЙ ТАРХАЛТЫН ХУУЛЬ.

Санамсаргүй Тэд санамсаргүй нөхцөл байдлын хослолоос хамааран утгыг авдаг хэмжигдэхүүнийг нэрлэдэг. Ялгах салангид болон санамсаргүй Үргэлжилсэн тоо хэмжээ.

Дискрет Хэмжигдэхүүн нь тоолж болох олонлог утгыг авсан бол түүнийг дуудна. ( Жишээ:эмчийн томилолт дээр байгаа өвчтөнүүдийн тоо, хуудасны үсгийн тоо, өгөгдсөн эзлэхүүн дэх молекулын тоо).

Үргэлжилсэн тодорхой интервал дотор утгыг авч чадах хэмжигдэхүүн юм. ( Жишээ:агаарын температур, биеийн жин, хүний ​​өндөр гэх мэт)

Хуваарилалтын хууль Санамсаргүй хэмжигдэхүүн нь энэ хувьсагчийн боломжит утгуудын багц бөгөөд эдгээр утгуудад харгалзах магадлал (эсвэл үүсэх давтамж) юм.

ЖИШЭЭ:

Санамсаргүй хэмжигдэхүүний тоон шинж чанар.

Ихэнх тохиолдолд санамсаргүй хэмжигдэхүүний тархалтын зэрэгцээ эсвэл түүний оронд эдгээр хэмжигдэхүүнүүдийн талаарх мэдээллийг тоон үзүүлэлтээр хангаж болно. санамсаргүй хэмжигдэхүүний тоон шинж чанар . Тэдгээрийн хамгийн түгээмэл нь:

1 .Хүлээгдэж буй үнэ цэнэ - Санамсаргүй хэмжигдэхүүний (дундаж утга) нь түүний бүх боломжит утгуудын бүтээгдэхүүн ба эдгээр утгуудын магадлалын нийлбэр юм.

2 .Тархалт санамсаргүй хувьсагч:

3 .Стандарт хэлбэлзэл :

"ГУРВАН СИГМА" дүрэм - Хэрэв санамсаргүй хэмжигдэхүүн нь ердийн хуулийн дагуу тархсан бол энэ утгын үнэмлэхүй утгын дундаж утгаас хазайх нь стандарт хазайлтаас гурав дахин ихгүй байна.

Гауссын хууль - хэвийн тархалтын хууль

Ихэнхдээ хуваарилагдсан тоо хэмжээ байдаг ердийн хууль (Гаусын хууль). гол онцлог : энэ нь хуваарилалтын бусад хуулиудад хандах хязгаарлалтын хууль юм.

Санамсаргүй хэмжигдэхүүн нь хэвийн хуулийн дагуу тархдаг магадлалын нягт хэлбэртэй байна:

М(X) - санамсаргүй хэмжигдэхүүний математик хүлээлт;

 - стандарт хазайлт.

Магадлалын нягт (тархалтын функц) нь интервалд хуваарилагдсан магадлал хэрхэн өөрчлөгдөж байгааг харуулдаг dx хувьсагчийн өөрийн утгаас хамааран санамсаргүй хэмжигдэхүүн:

Математик статистикийн үндсэн ойлголтууд

Математикийн статистик - магадлалын онолтой шууд залгаа хэрэглээний математикийн салбар. Математик статистик ба магадлалын онолын гол ялгаа нь математик статистик нь санамсаргүй хэмжигдэхүүний тархалтын хууль, тоон шинж чанарт хамаарах үйлдлүүдийг авч үздэггүй, харин туршилтын үр дүнд үндэслэн эдгээр хууль, тоон шинж чанарыг олох ойролцоо аргуудыг авч үздэгт оршино.

Үндсэн ойлголтууд Математик статистик нь:

Нийт хүн ам;

дээж;

вариацын цуврал;

загвар;

дундаж;

хувь,

давтамжийн олон өнцөгт,

баганат график.

Хүн ам - судалгааны объектын зарим хэсгийг сонгосон статистикийн томоохон хүн ам

(Жишээ:бүс нутгийн нийт хүн ам, тухайн хотын их сургуулийн оюутнууд гэх мэт)

Түүвэр (түүврийн популяци) - нийт хүн амын дундаас сонгосон объектуудын багц.

Вариацын цуврал - хувилбарууд (санамсаргүй хэмжигдэхүүний утга) ба тэдгээрийн холбогдох давтамжуудаас бүрдэх статистикийн тархалт.

Жишээ:

X , кг

м

x - санамсаргүй хэмжигдэхүүний утга (10 настай охидын масс);

м - тохиолдох давтамж.

Загвар – тохиолдох хамгийн өндөр давтамжтай тохирч буй санамсаргүй хэмжигдэхүүний утга. (Дээрх жишээнд загвар нь 24 кг-ийн утгатай тохирч байгаа бөгөөд энэ нь бусдаас илүү түгээмэл байдаг: m = 20).

Медиан - тархалтыг хагасаар хуваадаг санамсаргүй хэмжигдэхүүний утга: утгуудын тал хувь нь медианы баруун талд, хагас (илүү их биш) - зүүн талд байрлана.

Жишээ:

1, 1, 1, 1, 1. 1, 2, 2, 2, 3 , 3, 4, 4, 5, 5, 5, 5, 6, 6, 7 , 7, 7, 7, 7, 7, 8, 8, 8, 8, 8 , 8, 9, 9, 9, 10, 10, 10, 10, 10, 10

Жишээн дээр бид санамсаргүй хэмжигдэхүүний 40 утгыг ажиглаж байна. Бүх утгыг тэдгээрийн үүсэх давтамжийг харгалзан өсөх дарааллаар байрлуулна. Тодруулсан утгын баруун талд 7 нь 40 утгын 20 (хагас) байгааг харж болно. Тиймээс 7 нь медиан юм.

Тархалтыг тодорхойлохын тулд хэмжилтийн үр дүнгийн 25 ба 75% -иас ихгүй утгыг олох болно. Эдгээр утгыг 25, 75 гэж нэрлэдэг хувь хэмжээ . Хэрэв медиан нь тархалтыг хагасаар хуваавал 25 ба 75 дахь хувь нь дөрөвний нэгээр тасарна. (Дашрамд хэлэхэд медианыг өөрөө 50-р хувь гэж үзэж болно.) Жишээнээс харахад 25 ба 75-р хувь нь 3 ба 8-тай тэнцүү байна.

Ашиглах салангид (цэг) статистикийн тархалт ба Үргэлжилсэн (интервал) статистикийн тархалт.

Тодорхой болгохын тулд статистикийн тархалтыг график хэлбэрээр дүрсэлсэн болно давтамжийн хүрээ эсвэл - гистограмууд .

Давтамжийн олон өнцөгт - сегментүүд нь цэгүүдийг координаттай холбосон тасархай шугам ( x 1 , м 1 ), (x 2 , м 2 ), ..., эсвэл төлөө харьцангуй давтамжийн олон өнцөгт - координаттай ( x 1 ,Р * 1 ), (x 2 ,Р * 2 ), ...(Зураг 1).

мм би / nf(x)

x x

Зураг 1 Зураг 2

Давтамжийн гистограм - нэг шулуун дээр баригдсан зэргэлдээх тэгш өнцөгтүүдийн багц (Зураг 2), тэгш өнцөгтүүдийн суурь нь ижил бөгөөд тэнцүү байна. dx , мөн өндөр нь давтамжийн харьцаатай тэнцүү байна dx , эсвэл Р * руу dx (магадлалын нягт).

Жишээ:

х, кг

"Физик хэмжигдэхүүнийг хэмжих нэгж" - Үнэмлэхүй алдаа нь хэмжих хэрэгслийн хуваах утгын талтай тэнцүү байна. Микрометр. Үр дүнг хэмжих төхөөрөмжийг ашиглан шууд авдаг. Хайрцагны урт: дутагдалтай 4 см, илүүдэлтэй 5 см. Тус бүр физик хэмжигдэхүүнхолбогдох хэмжилтийн нэгжүүд байдаг. үзэх. Харьцангуй алдаа.

“Уртны утгууд” - 2. Ямар хэмжигдэхүүнүүдийг хооронд нь харьцуулж болох вэ: 2. Дараах асуудлыг яагаад нэмэх аргыг ашиглан шийдэж байгааг тайлбарла: 2. Бодлого шийдвэрлэхдээ үйлдлийн сонголтыг зөвтгөөрэй. Та хэдэн багц авсан бэ? Эдгээр гурван хайрцагт хэдэн үзэг байгаа вэ? Даашинзыг 12м даавуугаар хийсэн ба тус бүрдээ 4м ашигласан.Хэдэн даашинз урласан бэ?

"Физик хэмжигдэхүүн" - Физик болон бусад байгалийн шинжлэх ухааныг тусгаарлах хил хязгаар нь түүхэн нөхцөлтэй байдаг. Аливаа хэмжилтийн үр дүнд үргэлж зарим алдаа байдаг. Шинэ сэдэв. Хурд. Биеийн харилцан үйлчлэл. Физик хуулиудыг математикийн хэлээр илэрхийлсэн тоон харьцаа хэлбэрээр илэрхийлдэг. Хэмжилтийн алдаа.

“Хэмжигдэхүүнийг хэмжсэний үр дүнд гарсан тоо” - 1-р ангийн математикийн хичээл. Хэмжих саваа ашиглан сегментийн уртыг хэмжих.

"Тоо ба хэмжигдэхүүн" - Массын тухай ойлголтын танилцуулга. Хэмжилтгүйгээр массыг харьцуулах. Ромын бичгийн дугаарлалт. Хүчин чадал. Сурагч суралцана: Тоо ба хэмжигдэхүүн (30 цаг) Координатын туяа Координатын цацрагийн тухай ойлголт. 2-р ангийн “Тоо ба хэмжигдэхүүн” хэсгийн төлөвлөсөн хичээлийн үр дүн. Ерөнхий зарчимсудлагдсан тоонуудын хүрээнд үндсэн тоо үүсэх.

"Эрэлтийн хэмжээ" - Эрэлтийн өөрчлөлтийн шалтгаан. График дээр олж авсан DD муруйг (Англи эрэлтээс - "эрэлт") эрэлтийн муруй гэж нэрлэдэг. Уян хатан эрэлт (Epd>1). Эрэлтийн тоо хэмжээ. Эрэлтэд нөлөөлөх хүчин зүйлүүд. Эрэлтийн хэмжээ үнийн түвшнээс хамаарахыг эрэлтийн цар хүрээ гэж нэрлэдэг. Үнэмлэхүй мэдрэмжгүй эрэлт (Epd=0).