Ердийн хэлбэр Логик томьёо нь элемент бус томьёоны утга санаа, эквивалент, үгүйсгэлийн шинж тэмдгийг агуулдаггүй.

Ердийн хэлбэр нь хоёр хэлбэрээр ирдэг:

коньюнктив хэвийн хэлбэр (CNF)-- хэд хэдэн салгах холбоо, жишээ нь, $\left(A\vee \overline(B)\vee C\right)\wedge \left(A\vee C\right)$;

салгах хэвийн хэлбэр (DNF)-- хэд хэдэн холболтыг салгах, жишээ нь $\left(A\шаантаг \overline(B)\шаантаг C\right)\vee \left(B\шаантаг C\right)$.

SKNF

Төгс коньюнктив хэвийн хэлбэр (PCNF) нь гурван нөхцлийг хангасан CNF юм:

ижил элементийн дизьюнкц агуулаагүй;

салангид хэсгүүдийн аль нь ч ижил хувьсагчийг агуулаагүй;

анхан шатны дизьюнкц бүр нь өгөгдсөн CNF-д багтсан хувьсагч бүрийг агуулна.

SKNF-д ижил үнэн биш логикийн томъёог илэрхийлж болно.

Үнэний хүснэгтийг ашиглан SKNF-ийг байгуулах дүрэм

Функц нь 0-тэй тэнцүү хувьсах хэмжигдэхүүн бүрийн нийлбэрийг бичиж, 1-ийн утгатай хувьсагчдыг үгүйсгэх замаар авна.

SDNF

Төгс салгах хэвийн хэлбэр (PDNF) Энэ нь гурван нөхцлийг хангасан DNF юм:

ижил энгийн холбоо үг агуулаагүй;

холболтуудын аль нь ч ижил хувьсагч агуулаагүй;

Энгийн холбоос бүр нь өгөгдсөн DNF-д орсон хувьсагч бүрийг ижил дарааллаар агуулна.

Ижил худал биш логикийн томьёог SDNF-д өвөрмөц байдлаар илэрхийлж болно.

Үнэний хүснэгтийг ашиглан SDNF байгуулах дүрэм

Функц нь 1-тэй тэнцүү хувьсах хэмжигдэхүүн бүрийн хувьд үржвэр бичиж, 0 утгатай хувьсагчдыг үгүйсгэх замаар авна.

SCNF болон SDNF-ийг олох жишээ

Жишээ 1

Үнэний хүснэгтийг ашиглан логик функц бичнэ үү.

Зураг 1.

Шийдэл:

SDNF үүсгэх дүрмийг ашиглацгаая.

Зураг 2.

Бид SDNF авдаг:

SCNF байгуулах дүрмийг ашиглацгаая.

Энгийн салгах(eng. inclusive disjunction) эсвэл салгах(Англи хэлээр дизьюнкт) нь нэг буюу хэд хэдэн хувьсагч эсвэл тэдгээрийн үгүйсгэлийн дизьюнкц бөгөөд хувьсагч бүр нэгээс илүүгүй тохиолдох болно.

Энгийн салгах

• дүүрэн, хэрэв хувьсагч бүр (эсвэл түүний үгүйсгэл) яг нэг удаа гарч ирвэл;
• нэг хэвийн, хэрэв энэ нь хувьсагчийн үгүйсгэлийг агуулаагүй бол.

Холболтын хэвийн хэлбэр, CNF(eng. conjunctive normal form, CNF) Boolean функц нь хэд хэдэн энгийн өгүүлбэрийн холболтын хэлбэртэй байдаг хэвийн хэлбэр.

KNF жишээ:$f(x,y) = (x \lor y) \land (y \lor \neg ( z ))$

SKNF

Төгс коньюнктив хэвийн хэлбэр, SCNF(Англи хэлний төгс холболтын хэвийн хэлбэр, PCNF) нь дараах нөхцлийг хангасан CNF юм.

• Энэ нь ижил энгийн салалтуудыг агуулдаггүй
• энгийн салалт бүр бүрэн дүүрэн байдаг

SKNF жишээ:$f(x,y,z) = (x \lor \neg ( y ) \lor z) \land (x\lor y \lor \neg ( z ))$

Теорем:Тодорхойлолттой тэнцүү биш $f(\vec ( x ))$ ямар ч Булийн функцийн хувьд түүнийг тодорхойлох SCNF байна.

Нотолгоо:$\neg ( f ) (\vec x)$ функцийн урвуу нь $f(\vec x)$ тэгтэй тэнцүү байх олонлог дээрх нэгтэй тэнцүү тул $\neg ( f )-ийн SDNF (\vec x)$ дараах байдлаар бичиж болно.

$\neg ( f ) (\vec x) = \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) , x^ ( \sigma_ ( 2 ) ) , ... ,x^ ( \sigma_ ( n) ) )) = 0 ) (x_ ( 1 ) ^ ( \sigma_ ( 1 ) ) \шаантаг x_ ( 2 ) ^ ( \sigma_ ( 2 ) ) \шаантаг ... \шаантаг x_ ( n ) ^ ( \sigma_ ( n) ) )) $, энд $ \sigma_ ( i ) $ нь $ x_ ( i ) $ -д үгүйсгэл байгаа эсвэл байхгүй байгааг илэрхийлдэг.

Илэрхийллийн зүүн ба баруун талын урвуу байдлыг олцгооё.

$ f(\vec x) = \neg (( \bigvee\limits_ ( f(x^ ( \sigma_ ( 1 ) ) , x^ ( \sigma_ ( 2 ) ) , ... ,x^ ( \sigma_ ( n) ) )) = 0 ) (x_ ( 1 ) ^ ( \sigma_ ( 1 ) ) \шаантаг x_ ( 2 ) ^ ( \sigma_ ( 2 ) ) \шаантаг ... \шаантаг x_ ( n ) ^ ( \sigma_ ( n) ))) ))) $

Баруун талд олж авсан илэрхийлэлд де Морганы дүрмийг хоёр удаа хэрэглэснээр бид дараахийг олж авна: $ f(\vec x) = \bigwedge \limits_ ( f(x^ ( \sigma_1) , x^ ( \sigma_2 ) , \dots ,x) ^ ( \ sigma_n )) = 0 ) $ $(\нег ( x_1^ ( \sigma_1) ) \vee \neg ( x_2^ ( \sigma_2 ) ) \vee \dots \vee \neg ( x_n^ ( \sigma_n )) ) $

Сүүлийн илэрхийлэл нь SKNF юм. SCNF-ийг SDNF-ээс авсан тул ижил тэг биш ямар ч функцийг байгуулж болох тул теорем нь батлагдсан.

Үнэний хүснэгт ашиглан SCNF байгуулах алгоритм

• Үнэний хүснэгтэд функцийн утга нь $0$-тэй тэнцүү хувьсагчдын багцыг тэмдэглэнэ.
• Тэмдэглэгдсэн олонлог бүрийн хувьд бид бүх хувьсагчийн дизъюнкцийг дараах дүрмийн дагуу бичнэ: хэрэв зарим нэг хувьсагчийн утга $0$ бол бид хувьсагчийг өөрөө дизьюнкцэд оруулна, үгүй ​​бол үгүйсгэнэ.
• Бид үүссэн бүх салгах үйлдлүүдийг холболтын үйлдлүүдтэй холбодог.

Медианд зориулсан SCNF-ийг бүтээх жишээ

1). Үнэний хүснэгтэд функцийн утга нь $0$-тэй тэнцүү хувьсагчдын багцыг тэмдэглэнэ.

x	y	z	$ \langle x,y,z \rangle $
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

2). Тэмдэглэгдсэн олонлог бүрийн хувьд бид бүх хувьсагчийн холболтыг дараах дүрмийн дагуу бичнэ: хэрэв зарим нэг хувьсагчийн утга $0$ бол бид хувьсагчийг өөрөө дизьюнкцэд оруулна, үгүй ​​бол үгүйсгэнэ.

x	y	z	$ \langle x,y,z \rangle $
0	0	0	0	$(x \lor y \lor z)$
0	0	1	0	$(x \lor y \lor \neg ( z ))$
0	1	0	0	$(x \lor \neg ( y ) \lor z)$
0	1	1	1
1	0	0	0	$(\neg ( x ) \lor y \lor z)$
1	0	1	1
1	1	0	1
1	1	1	1

3). Бид үүссэн бүх салгах үйлдлүүдийг холболтын үйлдлүүдтэй холбодог.

$ \langle x,y,z \rangle = (x \lor y \lor z) \land (\neg ( x ) \lor y \lor z) \land (x \lor \neg ( y ) \lor z) \land (x \lor y \lor \neg ( z ))$

Зарим функцэд зориулсан SKNF-ийн жишээ

Пейрсийн сум: $ x \downarrow y = (\neg ( x ) \lor ( y )) \land (( x ) \lor \neg ( y )) \land (\neg ( x ) \lor \neg ( y ) )$

Онцгой эсвэл: $ x \oplus y \oplus z = (\neg ( x ) \lor \neg ( y ) \lor z) \land (\neg ( x ) \lor y \lor \neg ( z )) \land (x \lor \neg ( y ) \lor \neg ( z )) \land (x \lor y \lor z)$

Стандарт үндэслэл. Анхан шатны томьёо нь шууд утга юм. Анхан шатны холбоо (дизюнкц). Дизьюнктив (холбогч) хэвийн хэлбэр ба төгс хэлбэр. Теорем: 0-ээс (1-ээс) өөр ямар ч Булийн функцийг SDNF (SCNF) хэлбэрээр илэрхийлж болно. Стандарт үндэслэлийн бүрэн байдал. Бүрэн суурийн жишээ: Жегалкины суурь, Шефферийн харвалт, Пирс сум.

Стандарт үндэслэл нь Булийн алгебрын нэмэх (нэгдэл), үржүүлэх (огтлолцол) ба үгүйсгэх гэсэн гурван үндсэн үйлдлийн багц юм.

Энд бид залгах болно шууд утгаар хувьсагч х буюу түүний үгүйсгэх x ба xˆ-г тэмдэглэнэ. Өөр өөр хувьсагчаар тодорхойлогдсон хэд хэдэн литералуудын логикийн огтлолцол, i.e. X = xˆ 1 xˆ 2 хэлбэрийн илэрхийлэл. . . xˆ l, гэж нэрлэдэг үндсэн холбоос . Бүх хувьсагч өөр байх шаардлагыг дараах байдлаар тодорхойлно. Хэрэв холбогч нь хэд хэдэн ижил үсэг агуулж байвал холбоосын хувирах чанар, ассоциаци, идемпотент байдлаас шалтгаалан ижил утгатай томъёонд шилжиж, зөвхөн нэг литерал үлдээх боломжтой (жишээлбэл, x 1 x 1 = x 1). Хэрэв холбоос нь хувьсагч ба түүний үгүйсгэлийг агуулж байвал томьёо нь тогтмол 0-тэй тэнцүү байна, учир нь x x = 0, ямар ч Y томьёоны хувьд бид Y x x = 0 байна.

Хэд хэдэн энгийн холбоосуудын дизьюнкцийг гэнэ салангид хэвийн хэлбэр , эсвэл DNF . Жишээлбэл,

x 1 x 3 + x 2 x 3 x 4 + x 1 x 2 x 3 x 5.

Хэрэв өгөгдсөн DNF-ийн анхан шатны холболт бүрийн хувьсагчдын найрлага ижил байвал DNF гэж нэрлэдэг. төгс . Өгөгдсөн жишээ бол төгс биш DNF юм. Эсрэгээр нь томъёо

x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4 +x 1 x 2 x 3 x 4

төгс хэлбэр бий.

Булийн алгебр дээр нэмэх, үржүүлэх нь тэгш хэмтэй үйлдлүүд тул нэмэхийг үржүүлэх, үржүүлэхийг нэмэх гэж үргэлж тайлбарлаж болох тул давхар ойлголт байдаг - коньюнктив хэвийн хэлбэр (KNF ), энэ нь анхан шатны дизюнкцуудын холболт бөгөөд төгс холболтын хэлбэр (SKNF ). Тэгш хэмтэй хагас цагирагийн хоёрдмол байдлын зарчмаас үзэхэд DNF-ийн талаархи аливаа мэдэгдэлд CNF-ийн талаархи давхар мэдэгдлээр хариулдаг бөгөөд энэ нь нэмэх (дизьюнкц) -ийг үржүүлэх, үржүүлэх (холбоо) -ийг нэмэх, тогтмол 0-ийг тогтмол 1, тогтмолоор сольж олж авдаг. Тогтмол 0-тэй 1, давхар (урвуу) дарааллын харьцаа. Тиймээс бид зөвхөн DNF-ийг судлахад анхаарлаа хандуулах болно.

Теорем 1.4.Тогтмол 0-ээс бусад аливаа логик функцийг SDNF хэлбэрээр илэрхийлж болно.

◀Х σ гэж σ = 1 бол x томьёог, σ = 0 бол x томьёог ойлгоно гэдэгтэй санал нийлэе. f(y 1 , . . . . , y n) функц нь (t) вектор дээр 1 утгыг авъя. 1 , . . , t n ) (ийм векторыг нэрлэдэг бүрдүүлэгч нэгж ). Дараа нь энгийн холболт нь энэ олонлог дээрх 1-ийн утгыг авах боловч бусад бүх n хэмжээст Булийн векторууд дээр алга болно. Томьёог анхаарч үзээрэй

өгөгдсөн функц 1 утгыг авдаг аргументын утгуудын нийлбэр (нэгдэл) бүх олонлогт (t 1, . . . ., t n) хүрдэг. Ийм олонлогуудын олонлог хоосон биш гэдгийг анхаарна уу. нийлбэр нь дор хаяж нэг нэр томъёог агуулна.

Φ томьёо нь тухайн функц нь 1 болсон хувьсагчдын утгуудын хувьд 1 болж байгааг харахад хялбар байдаг. Энэ нь Ψ томьёо нь f функцийг илэрхийлнэ гэсэн үг.

Дүгнэлт 1.1.Стандарт суурь нь дууссан.

◀ Үнэн хэрэгтээ, хэрэв функц нь тогтмол 0 биш бол түүнийг стандарт үндсэн дээр томъёо болох SDNF хэлбэрээр илэрхийлж болно. Тогтмол 0-ийг жишээ нь f(x 1, x 2, . . . , x n) = x 1 x 1 томъёогоор илэрхийлж болно.

Жишээ 1.2.гэж нэрлэгддэг m(x 1, x 2, x 3) (Хүснэгт 1.4) гэсэн гурван хувьсагчийн функцийг авч үзье. олонхийн чиг үүрэг ̆. Хэрэв аргументуудынх нь талаас илүү хувь нь 1 утгатай байвал энэ функцийг 1 гэж үнэлдэг. Тиймээс үүнийг санал өгөх функц гэж нэрлэдэг. Үүний тулд SDNF бүтээцгээе.

Стандарт үндэслэлийн бүрэн бүтэн байдал нь бусад бүрэн функцүүдийн системийг сонгох боломжийг олгодог. F багцын бүрэн бүтэн байдлыг дараах үндэслэлээр тодорхойлж болно. Гурван стандарт автобусны функц бүрийг F дээр томъёогоор илэрхийлнэ гэж бодъё. Дараа нь теорем 1.3-аар F таних тэмдэг бүрэн болно.

Жишээ 1.3.Модуль 2 нэмэх, үржүүлэх, тогтмол 1 үйлдлийн багцыг дуудна Жегалкины үндэс . Нэмэлт модуль 2 ба үржүүлэх нь Z2 цагирагийн үндсэн үйлдлүүд бөгөөд тэдгээрийн тусламжтайгаар бүрдсэн илэрхийллүүд нь Z2 цагираг дээрх олон гишүүнтүүд юм. Энэ тохиолдолд тогтмол 1 нь чөлөөт нэр томъёог бичихэд шаардлагатай. хх=х тул олон гишүүнтийн бүх хүчин зүйлүүд 1 зэрэгтэй байна.Тиймээс олон гишүүнт бичихдээ зэрэглэлийн ойлголтгүйгээр хийж болно. Жегалкины үндсэн дээр томъёоны жишээ:

xy⊕x⊕y, x⊕1, xyz⊕xz⊕x⊕y⊕1.

Аливаа ийм томьёог Жегалкины олон гишүүнт гэж нэрлэдэг. Үнэн хэрэгтээ Жегалкины олон гишүүнт нь Z2 цагираг дээрх олон гишүүнт юм.

Стандарт баазыг нэмэх, үгүйсгэх үйлдлүүдийг илэрхийлдэг Жегалкины суурь дээр томъёог бүтээх нь тийм ч хэцүү биш юм (хоёр суурийн үржүүлэх нь түгээмэл):

x+y=x⊕y⊕xy, x =x⊕1.

Тиймээс Жегалкины суурь нь бүрэн цогц юм.
Аливаа Булийн функцийн хувьд Жегалкины олон гишүүнт өвөрмөц тодорхойлогддог болохыг харуулж байна

(илүү нарийвчлалтай, нэр томъёоны дараалал хүртэл). Цөөн тооны хувьсагчтай Жегалкины олон гишүүнтийн коэффициентийг тодорхой бус коэффициентийн аргыг ашиглан олж болно.

Жишээ 1.4.Нэг функцийн багцыг авч үзье - Шефферийн харвалт*. Дараах амархан баталгаажуулах таних тэмдгүүдийн дагуу энэ багц бүрэн байна:

x =x|x, xy=x|y =(x|y)|(x|y), x+y=x |y =(x|x)|(y|y).

Жишээ 1.5.Нэг функц болох Peirce сумаас бүрдэх суурь нь бас дууссан. Үүний тест нь Шефферийн цус харвалтын тохиолдолтой төстэй юм. Гэсэн хэдий ч энэ дүгнэлтийг тэгш хэмтэй хагас цагирагуудын хоёрдмол байдлын зарчмын үндсэн дээр хийж болно.

*Шефферийн харвалт нь хоёртын үйлдэл боловч ассоциатив биш. Тиймээс, infix маягтыг ашиглахдаа болгоомжтой байх хэрэгтэй: үр дүн нь үйлдлийн дарааллаас хамаарна. Энэ тохиолдолд хаалт ашиглан үйлдлийн дарааллыг тодорхой зааж өгөхийг зөвлөж байна, жишээлбэл (x | y) | z, x | биш у | z, хэдийгээр хоёр хэлбэр нь тэнцүү боловч.

Жишээ. CNF томъёог олох

~ ~

SDNF-ийн төгс салгах хэвийн хэлбэрийг дараах алгоритмыг ашиглан бүтээж болно.

1. = 1. DNF алгоритм

2. = 2. DNF алгоритм

3. = 3. DNF алгоритм

4. = 4. DNF алгоритм

5. Хуурамч нэр томъёог, өөрөөр хэлбэл маягтын нэр томъёог орхи

6. Үлдсэн нөхцлүүдийг дутуу хувьсагчаар гүйцээнэ үү

7. 4-р цэгийг давт.

Жишээ. SDNF томъёог олох.

~

SCNF-ийг бүтээхийн тулд та дараах схемийг ашиглаж болно.

Жишээ. SDNF томъёог олох.

~

SDNF ба SCNF нь томьёогоор өвөрмөц тодорхойлогддог тул томъёоны үнэний хүснэгтийг ашиглан тэдгээрийг байгуулж болно гэдгийг мэддэг (Теорем 2.11, 2.12).

Үнэний хүснэгтийн дагуу SDNF ба SCNF-ийг барих схемийг томъёоны хувьд доор өгөв. ~ :

			~
			1 0 1 0 1 1 0 1	SDNF; SKNF.

2.2. Дасгал хийх.

2.2.1 Доорх нь Булийн илэрхийлэл юм. Boole-ийн логикийн хуулиудыг ашиглан хувилбарынхаа илэрхийллийг аль болох хялбарчлаарай. Дараа нь өөрийн хялбаршуулсан илэрхийлэлийг анхныхтай харьцуулахын тулд үнэний хүснэгтийг ашиглана уу.

2.2.2. f 1 ба f 2-ийн эквивалентийн тухай асуултыг SDNF болгон бууруулж тодруулна уу (Хүснэгт 1).

2.2.3. Ерөнхий болон Булийн зарчмыг ашиглан f 3-ын хос функцийг ол (Хүснэгт 1). Үр дүнг харьцуул.

№	f 1	f 2	f 3

2.3. Хяналтын асуултууд.

2.3.1. Мэдэгдэлийг тодорхойл.

2.3.2. Мэдэгдэл дээрх үндсэн үйлдлүүдийг жагсаа.

2.3.3. Үнэний хүснэгт гэж юу вэ?

2.3.4. Дараах томъёоны үнэний хүснэгтийг үүсгэ.

~ ~ ~ ;

2.3.5. Үйлдлийн дарааллын талаархи конвенцуудыг харгалзан томъёонд "нэмэлт" хаалт, "" тэмдгийг орхино.

;

2.3.6. Эквивалент хувиргалтыг ашиглан томъёоны ижил үнэнийг нотлох:

2.3.7. Хос томьёог ол:

)

2.3.8. DNF (SDNF) хэлбэрийг төгс болгохын тулд дараах томьёог багасгана уу:

~

2.3.9. Төгс CNF (SCNF) хэлбэрт оруулахын тулд дараах томъёог багасга.

~

Лабораторийн ажил No3

Сэдэв:“Булийн функцийг багасгах. Логик"

Зорилтот:Булийн функцийг багасгах аргуудтай ажиллах практик ур чадвар эзэмших.

3.1. Онолын мэдээлэл.

Хамгийн бага хэлбэрүүд

Дээр дурдсанчлан, ямар ч Булийн функцийг төгс хэвийн хэлбэрээр (дисьюнктив эсвэл коньюнктив) төлөөлж болно. Түүнчлэн, ийм дүрслэл нь функцийн хүснэгтийн тодорхойлолтоос аналитик илэрхийлэл рүү шилжих эхний алхам юм. Дараахь зүйлд бид салгах хэлбэрээс гарах бөгөөд хоёрдмол байдлын зарчимд үндэслэн холболтын хэлбэрийн харгалзах үр дүнг гаргана.

Логик хэлхээг Булийн үндсэн дээр нэгтгэх каноник асуудал нь Булийн функцийг багасгахад хүргэдэг, i.e. Тэдгээрийг хамгийн бага тооны үсэг (хувьсагч ба тэдгээрийн үгүйсгэлт) агуулсан салангид хэвийн хэлбэрээр илэрхийлэх. Ийм хэлбэрийг хамгийн бага гэж нэрлэдэг. Каноник синтезийн хувьд дохио ба тэдгээрийн урвуу байдал хоёулаа хэлхээний оролтод нийлүүлдэг гэж үздэг.

Дизьюнкктив хэвийн хэлбэрээр үзүүлсэн томьёог наах, шингээх үйлдлийг давтан ашиглах замаар хялбаршуулсан болно (холболтын хэвийн хэлбэрийн хос таних тэмдэг нь: ба хэлбэртэй байна). Энд, ямар ч Булийн алгебрийн томъёо гэж ойлгож болно. Үүний үр дүнд бид цаашдын өөрчлөлт хийх боломжгүй болсон аналитик илэрхийлэлд хүрдэг, жишээлбэл. Бид мухардмал хэлбэрийг авдаг.

Үхсэн хэлбэрүүдийн дунд хамгийн бага салангид хэлбэр байдаг бөгөөд энэ нь өвөрмөц биш байж болно. Өгөгдсөн төгсгөлийн маягт хамгийн бага байгаа эсэхийг шалгахын тулд та бүх үхсэн маягтуудыг олж, тэдгээрийг агуулсан үсгийн тоогоор нь харьцуулах хэрэгтэй.

Жишээлбэл, функцийг төгс хэвийн салгах хэлбэрээр өгье.

Нэр томьёог бүлэглэн наах үйлдлийг хийснээр бид .

Өөр бүлэглэх аргын тусламжтайгаар бид дараахь зүйлийг авна.

Үхсэн хэлбэр нь хоёулаа хамгийн бага биш юм. Хамгийн бага хэлбэрийг авахын тулд та анхны томъёонд нэг нэр томъёог давтахыг таах хэрэгтэй (үүнийг үргэлж хийж болно, учир нь ). Эхний тохиолдолд ийм гишүүн байж болно . Дараа нь . Нэр томьёог нэмснээр бид: . Бүх боломжит хувилбаруудыг үзсэний дараа та сүүлийн хоёр хэлбэр хамгийн бага байгаа эсэхийг шалгаж болно.

Энэ түвшний томьёотой ажиллах нь харанхуйд тэнүүчлэхтэй адил юм. Хэрэв та энэ зорилгоор тусгайлан боловсруулсан график, аналитик дүрслэл, тэмдэглэгээг ашиглавал хамгийн бага хэлбэрийг хайх үйл явц илүү ойлгомжтой, зорилготой болно.

Олон хэмжээст шоо

Хэмжээст кубын орой бүрийг нэгжийн бүрэлдэхүүн хэсэгтэй холбож болно. Үүний үр дүнд тэмдэглэгдсэн оройн дэд олонлог нь хувьсагчдын логикийн функцийн хэмжээст куб дээр төгс салгах хэвийн хэлбэрийн зураглал юм. Зураг дээр. 3.1-д 3.7-д заасан функцийн зураглалыг харуулав.

Зураг 3.1 Гурван хэмжээст шоо дээр SDNF-д үзүүлсэн функцийг харуулах

Хувьсагчийн функцийг ямар нэгэн салангид хэвийн хэлбэрээр харуулахын тулд түүний минитерминууд болон хэмжээст кубын элементүүдийн хоорондын хамаарлыг тогтоох шаардлагатай.

(-1) зэрэглэлийн минитертийг хоёр зэрэглэлийн (эв нэгдлийг бүрдүүлэгч) наалдсаны үр дүн гэж үзэж болно. , Хэмжээст шоо дээр энэ нь зөвхөн эдгээр оройг ирмэгээр холбосон координатын утгаараа ялгаатай хоёр оройг солихтой тохирч байна (ирмэг нь түүнд тохиолдсон оройг хамардаг гэж хэлдэг). Тиймээс (-1)-р эрэмбийн минитерминууд нь хэмжээст кубын ирмэгтэй тохирч байна. Үүний нэгэн адил (-2)-р эрэмбийн мини гишүүнчлэлийн тохирлыг хэмжээст шоо тус бүр дөрвөн оройг (ба дөрвөн ирмэг) хамардаг нүүрнүүдээр тогтооно.

Хэмжээгээр тодорхойлогддог -хэмжээт кубын элементүүдийг -куб гэж нэрлэдэг. Тиймээс орой нь 0-шоо, ирмэг нь 1-шоо, нүүр нь 2-шоо гэх мэт. Дээрх үндэслэлийг ерөнхийд нь авч үзвэл, хувьсагчдын функцийн дизьюнктив хэвийн хэлбэрээр ()-р зэрэглэлийн мини гишүүнчийг -шоогоор илэрхийлдэг бөгөөд -куб бүр нь оройтой нь холбоотой доод хэмжээст бүх -кубуудыг хамардаг гэж бид үзэж болно. . Зураг дээр жишээ болгон. 3.2-т гурван хувьсагчийн функцийг харуулав. Энд минитерминууд нь 1-куб ()-тай тохирч, минитермин нь 2-шоо ()-ээр илэрхийлэгдэнэ.

Зураг.3.2 Функцийн хамрах хүрээ

Тиймээс аливаа салангид хэвийн хэлбэрийг нэгдмэл байдлын бүрэлдэхүүн хэсгүүдэд (0-шоо) харгалзах бүх оройг хамарсан -кубуудын багцаар -хэмжээтэй шоо дээр дүрслэгддэг. Эсрэг заалт нь бас үнэн юм: хэрэв -кубуудын тодорхой багц нь функцийн нэгж утгуудад харгалзах бүх оройн багцыг хамардаг бол эдгээр -кубуудад харгалзах минитерминуудын дизъюнкц нь энэ функцийг салгах нормал дахь илэрхийлэл болно. хэлбэр. Ийм -кубуудын цуглуулга (эсвэл тэдгээрийн харгалзах минитермин) нь функцийн бүрээсийг бүрдүүлдэг гэж хэлдэг.

Хамгийн бага хэлбэрийн хүсэл эрмэлзэл нь ийм бүрхүүлийг хайх гэж зөн совингоор ойлгогддог бөгөөд тэдгээрийн шоо дөрвөлжин тоо нь бага, хэмжээ нь илүү том байх болно. Хамгийн бага хэлбэрт тохирсон хамрах хүрээг хамгийн бага хамрах хүрээ гэнэ. Жишээлбэл, Зураг дээрх бүрэх функцийн хувьд. 3.3 хамгийн бага маягтыг хангасан Тэгээд .

Цагаан будаа. 3.3 Функцийн хамрах хүрээ.

зүүн – ; баруун талд –

Хэмжээст шоо дээрх функцийг харуулах нь тодорхой бөгөөд энгийн байх үед. Дөрвөн хэмжээст кубыг Зураг дээр үзүүлсэн шиг дүрсэлж болно. 3.4, энэ нь дөрвөн хувьсагчийн функц болон илэрхийлэлтэй харгалзах хамгийн бага хамрах хүрээг харуулсан . Энэ аргыг ашиглах нь ийм нарийн төвөгтэй барилга байгууламжийг шаарддаг тул түүний бүх давуу талууд алдагддаг.

Цагаан будаа. 3.4 Функцийн дэлгэц дөрвөн хэмжээст шоо дээр

Карногийн газрын зураг

Boolean функцийг графикаар харуулах өөр нэг аргыг ашигладаг Карногийн газрын зураг, эдгээр нь тусгайлан зохион байгуулсан захидал харилцааны хүснэгтүүд юм. Хүснэгтийн багана, мөрүүд нь хоёроос илүүгүй хувьсагчийн бүх боломжит багц утгуудтай тохирч байгаа бөгөөд эдгээр багцууд нь дараагийнх бүр нь өмнөхөөсөө зөвхөн нэг хувьсагчийн утгаараа ялгаатай байхаар байрлуулсан байна. . Үүний ачаар хүснэгтийн хөрш зэргэлдээх нүднүүд нь зөвхөн нэг хувьсагчийн утгаараа хэвтээ ба босоо байдлаар ялгаатай байдаг. Хүснэгтийн ирмэг дээр байрлах нүднүүд нь мөн зэргэлдээ гэж тооцогддог бөгөөд энэ шинж чанартай байдаг. Зураг дээр. Зураг 3.5-д хоёр, гурав, дөрвөн хувьсагчийн Карнаугийн газрын зургийг харуулав.

Цагаан будаа. 3.5 Хоёр, гурав, дөрвөн хувьсагчийн Carnaugh газрын зураг

Энгийн үнэний хүснэгтүүдийн нэгэн адил функц 1-ийн утгыг авдаг олонлогийн нүднүүд нэгээр дүүрсэн байдаг (тэг нь ихэвчлэн тохирохгүй, хоосон нүдтэй тохирдог). Жишээлбэл, Зураг дээр. 3.6, Афункцийн Карнаугийн газрын зургийг харуулсан бөгөөд дөрвөн хэмжээст шоо дээрх дэлгэцийг Зураг дээр үзүүлэв. 3.4. Аливаа зүйлийг хялбарчлахын тулд хувьсагчийн 1-ийн утгатай харгалзах мөр, багануудыг тухайн хувьсагчийг харуулсан буржгар хаалтаар тодруулна.

Цагаан будаа. 3.6 Дөрвөн хувьсагчийн функцийг Carnaugh газрын зураг дээр харуулах

(а) ба түүний хамгийн бага хамрах хүрээ (б)

Функцийн зураглалуудын хооронд n-хэмжээт шоо болон Карногийн газрын зураг дээр нэг нэгээр нь харилцаж байна. Карно газрын зураг дээр с-шоо нь эгнээ, багана, дөрвөлжин эсвэл тэгш өнцөгт (газрын зургийн эсрэг талын ирмэгүүдийн ойролцоо байдлыг харгалзан) байрлуулсан хөрш зэргэлдээх 2 нүдний багцад тохирно. Тиймээс дээр дурдсан бүх заалтыг (зүйл. олон хэмжээст шоо), Карнаугийн газрын зурагт хүчинтэй. Тиймээс, Зураг дээр. 3.6, бхамгийн бага салгах хэлбэрт тохирсон газрын зургийн нэгжийн хамрах хүрээг харуулав тухайн функц.

Карнаугийн газрын зургаас минитермийг унших нь энгийн дүрмийг дагаж мөрддөг. Эсүүд үүсэх с-шоо, сайд өгөөч (n–s)-тэдгээр зэрэг орно (n–s)үүн дээр ижил утгыг хадгалдаг хувьсагчид с-шоо, энд 1 утга нь хувьсагчид өөрсдөө, 0 утга нь тэдний үгүйсгэлттэй тохирч байна. Утгаа хадгалдаггүй хувьсагчид с-шоо, miniterm-д байхгүй байна. Унших янз бүрийн аргууд нь функцийг салгах хэвийн хэлбэрээр (баруун талд байгаа нь хамгийн бага) янз бүрийн дүрслэлд хүргэдэг (Зураг 3.7).

Карнаугийн газрын зургийг ашиглах нь зураглалтай харьцуулахад илүү хялбар бүтэц шаарддаг n-хэмжээт куб, ялангуяа дөрвөн хувьсагчийн хувьд. Таван хувьсагчийн функцийг харуулахын тулд дөрвөн хувьсагчийн хоёр Karnaugh газрын зургийг, зургаан хувьсагчийн функцийн хувьд дөрвөн ийм газрын зургийг ашигладаг. Хувьсагчийн тоо нэмэгдэхийн хэрээр Карнаугийн газрын зураг бараг ашиглах боломжгүй болж байна.

Уран зохиолд алдартай Veitch картуудТэд зөвхөн хувьсах утгуудын багцын өөр өөр дарааллаар ялгаатай бөгөөд Карнаугийн газрын зурагтай ижил шинж чанартай байдаг.

Кубуудын цогцолбор

График аргуудын олон тооны хувьсагчтай нийцэхгүй байдлыг Булийн функцийг илэрхийлэх янз бүрийн аналитик аргуудаар нөхдөг. Ийм нэг төлөөлөл юм кубын цогцолбор, олон хэмжээст логик орон зайн нэр томъёог тусгайлан боловсруулсан бэлгэдэлтэй хослуулан ашиглах.

). Нэгдлийн бүрэлдэхүүн хэсгүүдэд тохирох 0-кубуудыг функц нь нэгдмэл утгатай тэнцүү хувьсах утгуудын багцаар төлөөлдөг. Бичлэг дээр байгаа нь ойлгомжтой

Цагаан будаа. 3.8 Гурван хувьсагчтай функцийн шоо нийлбэр ( А) ба түүний бэлгэдлийн дүрслэл ( б)

Кубуудын цогцолбор үүсдэг хамгийн их функцийн хамрах хүрээ. Тэр бүхнээс бусад нь с-өндөр хэмжээст шоогаар хучигдсан шоо дөрвөлжин, бид үхсэн хэлбэрт тохирсон бүрээсийг авдаг. Тиймээс, авч үзэж буй жишээний хувьд (Зураг 3.8) бид үхсэн бүрхүүлтэй байна

,

функцтэй тохирч байна . Энэ тохиолдолд энэ хамрах хүрээ хамгийн бага байна.

Булийн хоёр функцийн хувьд салгах үйлдэл нь тэдгээрийн шоо цогцолборуудын нэгдэлд, холболтын үйлдэл нь тэдгээрийн шоо цогцолборуудын огтлолцолтой тохирч байна. Функцийн үгүйсгэл нь шоо дөрвөлжин цогцолборын нөхөж байгаатай тохирч, өөрөөр хэлбэл функц нь 0 утгыг авах бүх оройгоор тодорхойлогддог. Иймээс алгебрын хооронд нэгийг харьцах (изоморфизм) байна. Булийн функцууд ба шоо нийлбэрүүдийг төлөөлдөг Булийн олонлогууд.

Функцийг шоо дөрвөлжин нийлмэл хэлбэрээр дүрслэх нь харааны хувьд бага боловч түүний хамгийн чухал давуу тал нь хувьсагчийн тооны хязгаарлалтыг арилгаж, компьютер ашиглах үед мэдээллийн кодчилолыг хөнгөвчлөх явдал юм.

Булийн функцийг багасгах

Асуудлын томъёолол.Булийн үндсэн дээр хэлхээг багасгах нь хамгийн бага хамрах хүрээтэй тохирох хамгийн бага салгах хэлбэрийг олоход хүргэдэг. Ердийн хэлбэрт орсон үсгийн нийт тоог хамрах хүрээний зардлаар илэрхийлнэ , энд нь n хувьсагчийн өгөгдсөн функцийг бүрхэх шоо дөрвөлжингийн тоо. Хамгийн бага хамрах хүрээ нь түүний үнийн хамгийн бага үнэ цэнээр тодорхойлогддог.

Ерөнхийдөө багасгах асуудлыг хоёр үе шаттайгаар шийддэг. Нэгдүгээрт, бид хамгийн их хэмжээтэй бүх кубыг багтаасан багасгасан бүрхүүлийг хайж байгаа боловч энэ бүрхүүлийн аль ч шоогаар бүрхэгдсэн нэг шоо агуулаагүй болно. Харгалзах салангид хэвийн хэлбэрийг багасгасан гэж нэрлэдэг ба түүний минитерминуудыг энгийн импликантууд гэж нэрлэдэг. Өгөгдсөн функцийн хувьд багасгасан хамрах хүрээ нь өвөрмөц боловч зарим шоо нь бусад кубуудын цуглуулгаар бүрхэгдсэн тул энэ нь илүүц байж болно.

Хоёрдахь алхамд хамгийн бага хэлбэрийг сонгон авч, багасгасан салангид хэлбэрийн хэвийн хэлбэр рүү шилжинэ. Бүх илүүдэл шоо дөрвөлжин хэсгийг хассанаар мухардмал хэлбэрүүд үүсдэг бөгөөд үүнгүйгээр үлдсэн шоо дөрвөлжин хэсэг нь өгөгдсөн функцийн бүрээсийг бүрдүүлсэн хэвээр байгаа боловч цаашид аль нэг шоо хасагдсан тохиолдолд энэ нь шоо дөрвөлжингийн багцыг хамрахаа болино. функцын нэг утгуудад тохирох бүх оройнууд, өөрөөр хэлбэл энэ нь бүрхэвч байхаа болино.

Өгөгдсөн функцийн бусад шоогаар ороогүй оройг хамарсан багасгасан хамрах шоо нь илүүдэхгүй бөгөөд үргэлж хамгийн бага хамрах хүрээд багтах болно. Ийм кубыг харгалзах импликант шиг экстремаль (зайлшгүй импликант) гэж нэрлэдэг ба түүний хамарсан оройг цуцлагдсан орой гэж нэрлэдэг. Экстремалуудын багц нь бүрээсийн цөмийг бүрдүүлдэг бөгөөд багасгасан бүрхүүлээс хамгийн бага руу шилжихдээ юуны түрүүнд бүх экстремалуудыг тусгаарлах нь тодорхой байна. Хэрэв экстремалуудын багц нь бүрээс үүсгэдэггүй бол багасгасан бүрхүүлээс шоо дөрвөлжин хучилт хийхээр нэмэгддэг.

Өгөгдсөн тодорхойлолтуудыг Зураг дээр үзүүлэв. 3.9, хамрах хүрээ багассан тохиолдолд (Зураг 3.9а-г үзнэ үү, ) ба хамгийн бага хамрах хүрээ (Зураг 3.9б) ба (Зураг 3.9, b-ийг үз) дараах байдлаар илэрхийлнэ.

Аливаа логик томьёоны хувьд таних хувиргалтыг ашиглан түүнтэй дүйцэхүйц хязгааргүй олон томьёог байгуулж болно. Логикийн алгебрийн хувьд гол ажлуудын нэг бол каноник хэлбэрийг хайх явдал юм (жишээлбэл, нэг дүрмийн дагуу хийгдсэн томъёо, канон).

Хэрэв логик функц нь хувьсагчдыг дизьюнкц, коньюнкц, үгүйсгэх замаар илэрхийлдэг бол энэ дүрслэлийн хэлбэрийг хэвийн гэж нэрлэдэг.

Ердийн хэлбэрүүдийн дотроос төгс хэвийн хэлбэрүүд (функцийг өвөрмөц байдлаар бичсэн хэлбэрүүд) ялгагдана.

Төгс салгах хэвийн хэлбэр (PDNF)

Тодорхойлолт. Томъёо нь тодорхой тооны хувьсагч эсвэл тэдгээрийн үгүйсгэлүүдийн холболтоор үүссэн бол түүнийг элементар холбоо гэнэ.

Жишээ нь: y, ¬ y, x 1 ∧ ¬ x 2 ∧ x 3 ∧ x 4

Тодорхойлолт. Хэрэв томьёо нь давтагдахгүй энгийн холбоосуудын дизъюнкц бол түүнийг салгах хэвийн хэлбэр (DNF) гэж нэрлэдэг.

DNF-ийг дараах хэлбэрээр бичнэ: F 1 ∨ F 2 ∨ ... ∨ F n , энд F i нь анхан шатны холболт юм.

Жишээ нь: ¬ x 1 ∧ x 2 ∨ x 1 ∧ ¬ x 2 ∨ x 1 ∧ ¬ x 2 ∧ x 3 , ¬ y 1 ∨ y 1 ∧ y 2 ∨ ¬ y 2

Тодорхойлолт. k хувьсагчийн логик томьёог төгс салгах хэвийн хэлбэр (PDNF) гэж нэрлэдэг, хэрэв:
1) томъёо нь DNF бөгөөд үндсэн холболт бүр нь x 1, x 2, ..., x k хувьсагчийн холболт бөгөөд энэ холболтын i-р байранд x i хувьсагч эсвэл түүний үгүйсгэлт байна. ;
2) ийм DNF-ийн бүх энгийн холбоосууд хосоороо ялгаатай байдаг.

Жишээ нь: (¬ x 1 ∧ x 2 ∧ x 3) ∨ (x 1 ∧ ¬ x 2 ∧ x 3) ∨ (x 1 ∧ x 2 ∧ ¬ x 3)

Төгс коньюнктив хэвийн хэлбэр (PCNF)

Тодорхойлолт. Томьёог тодорхой тооны хувьсагчийн дизъюнкц эсвэл тэдгээрийн үгүйсгэлээс үүссэн бол түүнийг элементар дизъюнкц гэнэ.

Жишээ нь: ¬ x 3, x 1 ∨ x 2, x 1 ∨ x 2 ∨ ¬ x 3

Тодорхойлолт. Хэрэв томьёо нь давтагдахгүй энгийн дизюнкцуудын нэгдэл бол түүнийг коньюнктив хэвийн хэлбэр (CNF) гэж нэрлэдэг.

CNF-ийг дараах хэлбэрээр бичнэ: F 1 ∧ F 2 ∧ ... ∧ F n , энд F i нь элементар дизъюнкц юм.

Жишээ нь: (x 1 ∨ ¬ x 2) ∧ x 3, (x 1 ∨ x 2) ∧ (¬ x 1 ∨ x 2 ∨ x 3) ∧ (x 1 ∨ ¬ x 2 ∨ ¬ x 3)

Тодорхойлолт. k хувьсагчтай логик томъёог төгс коньюнктив хэвийн хэлбэр (CPNF) гэж нэрлэдэг, хэрэв:
1) томьёо нь CNF бөгөөд энгийн дизюнкц бүр нь x 1, x 2, ..., x k хэмжигдэхүүний дизъюнкц бөгөөд энэхүү дизъюнкцийн i-р байранд x i хувьсагч эсвэл түүний үгүйсгэл байгаа;
2) ийм CNF-ийн бүх элементар дизъюнкцууд нь хосоороо ялгаатай байдаг.

Жишээ: (x 1 ∨ x 2 ∨ x 3) ∧ (¬ x 1 ∨ ¬ x 2 ∨ x 3)

анзаараарай, тэр 0 эсвэл 1-тэй ижил биш аливаа логик функцийг SDNF эсвэл SKNF хэлбэрээр илэрхийлж болно..

Үнэний хүснэгт ашиглан SDNF байгуулах алгоритм

1. Функцийн утга нэгтэй тэнцүү байгаа хүснэгтийн бүх мөрийг сонгоно уу.
2. Ийм мөр бүрийн хувьд бүх хувьсагчийн холболтыг дараах байдлаар бичнэ үү: хэрэв энэ олонлогийн зарим хувьсагчийн утга 1-тэй тэнцүү бол бид хувьсагчийг өөрөө холболтод оруулна, үгүй ​​бол түүнийг үгүйсгэнэ.
3. Бид үүссэн бүх холболтыг салгах үйлдлүүдтэй холбодог.

Үнэний хүснэгт ашиглан SCNF байгуулах алгоритм

1. Функцийн утга тэг байх хүснэгтийн бүх мөрийг сонгоно уу.
2. Ийм мөр бүрийн хувьд бүх хувьсагчийн дизъюнкцийг дараах байдлаар бичнэ үү: хэрэв энэ олонлогийн зарим хувьсагчийн утга 0-тэй тэнцүү бол бид хувьсагчийг өөрөө коньюнкцид оруулна, үгүй ​​бол түүнийг үгүйсгэнэ.
3. Бид үүссэн бүх салгах үйлдлүүдийг холболтын үйлдлүүдтэй холбодог.

Алгоритмуудын дүн шинжилгээ нь хэрэв үнэний хүснэгтийн ихэнх мөрөнд функцийн утга 0 байвал түүний логик томьёог олж авахын тулд SDNF, эс тэгвээс SCNF байгуулах нь дээр гэдгийг харуулж байна.

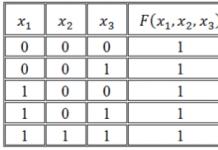
Жишээ: Гурван хувьсагчийн логик функцийн үнэний хүснэгтийг өгөв. Энэ функцийг хэрэгжүүлэх логик томъёог байгуул.

x	y	z	F(x, y, z)
0	0	0	1
0	0	1	1
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Учир нь үнэний хүснэгтийн ихэнх мөрөнд функцийн утга 1 байвал бид SCNF-ийг байгуулна. Үүний үр дүнд бид дараах логик томъёог олж авна.
F = (¬ x ∨ y ∨ z) ∧ (¬ x ∨ y ∨ ¬ z)

Үр дүнгийн томъёог шалгацгаая. Үүний тулд бид функцийн үнэний хүснэгтийг байгуулна.

x	y	z	¬ x	¬ x ∨ y ∨ z	¬z	¬ x ∨ y ∨ ¬ z	F(x, y, z)
0	0	0	1	1	1	1	1
0	0	1	1	1	0	1	1
0	1	0	1	1	1	1	1
0	1	1	1	1	0	1	1
1	0	0	0	0	1	1	0
1	0	1	0	1	0	0	0
1	1	0	0	1	1	1	1
1	1	1	0	1	0	1	1

Анхны үнэний хүснэгт болон логик томъёонд зориулж бүтээсэн хүснэгтийг харьцуулж үзвэл функцын утгуудын баганууд давхцаж байгааг бид тэмдэглэж байна. Энэ нь логик функц зөв хийгдсэн гэсэн үг юм.