Problema numarul 1

Logica este simplă: vom proceda așa cum am procedat înainte, în ciuda faptului că acum funcțiile trigonometrice au un argument mai complex!

Dacă ar fi să rezolvăm o ecuație de forma:

Apoi vom scrie următorul răspuns:

Sau (din moment ce)

Dar acum avem următoarea expresie în rolul nostru:

Apoi poți scrie:

Scopul nostru cu tine este să facem stânga să stea simplu, fără „impurități”!

Să scăpăm de ele treptat!

În primul rând, eliminăm numitorul la: pentru aceasta ne înmulțim egalitatea cu:

Acum să scăpăm de el împărțind ambele părți în el:

Acum să scăpăm de cele opt:

Expresia rezultată poate fi scrisă ca 2 serii de soluții (prin analogie cu o ecuație pătratică, în care fie adunăm, fie scădem discriminantul)

Trebuie să găsim cea mai mare rădăcină negativă! Este clar că este necesar să se rezolve.

Luați în considerare prima serie mai întâi:

Este clar că dacă luăm, atunci, ca rezultat, vom obține numere pozitive și nu ne interesează.

Deci trebuie să o luați negativ. Lăsa.

Când rădăcina este deja:

Și trebuie să găsim cel mai mare negativ !! Înseamnă că nu mai are sens să mergi în direcția negativă. Și cea mai mare rădăcină negativă pentru această serie va fi.

Acum să ne uităm la a doua serie:

Și din nou înlocuim:, apoi:

Nu sunt interesat!

Atunci nu mai are sens să crești! Vom reduce! Să fie, atunci:

Se potrivește!

Lăsa. Atunci

Apoi - cea mai mare rădăcină negativă!

Răspuns:

Problema numarul 2

Din nou rezolvăm, indiferent de argumentul cosinus complex:

Acum exprimăm din nou la stânga:

Înmulțim ambele părți cu

Împărțim ambele părți în

Tot ce rămâne este să-l mutați la dreapta, schimbându-i semnul din minus în plus.

Avem din nou 2 serii de rădăcini, una cu și alta cu.

Trebuie să găsim cea mai mare rădăcină negativă. Luați în considerare prima serie:

Este clar că vom primi prima rădăcină negativă la, va fi egală cu și va fi cea mai mare rădăcină negativă din 1 serie.

Pentru a doua serie

Prima rădăcină negativă se va obține și la și va fi egală cu. Deoarece, atunci este cea mai mare rădăcină negativă a ecuației.

Răspuns: .

Problema numarul 3

Rezolvați indiferent de argumentul tangentei complexe.

Pare să nu fie nimic complicat, nu?

Ca și înainte, exprimăm în partea stângă:

Ei bine, asta e grozav, există o singură serie de rădăcini aici! Găsiți din nou cel mai mare negativ.

Este clar că se dovedește dacă punem. Și această rădăcină este egală.

Răspuns:

Acum încercați să rezolvați singur următoarele probleme.

Teme sau 3 sarcini pentru o soluție independentă.

1. Ecuația decizii-shi-te.
   
2. Ecuația decizii-shi-te.
   În ot-ve-cele na-pi-shi-te, cea mai mică rădăcină po-li-tel.
3. Ecuația decizii-shi-te.
   În ot-ve-cele na-pi-shi-te, cea mai mică rădăcină po-li-tel.

Gata? Control. Nu voi descrie în detaliu întreg algoritmul de soluție, mi se pare că i s-a acordat deja suficientă atenție mai sus.

Ei bine, totul este corect? Oh, sinusurile alea urâte, mereu sunt unele necazuri cu ele!

Ei bine, acum poți rezolva cele mai simple ecuații trigonometrice!

Verificați soluțiile și răspunsurile:

Problema numarul 1

Să ne exprimăm

Cea mai mică rădăcină pozitivă se obține dacă punem, din moment ce, atunci

Răspuns:

Problema numarul 2

Cea mai mică rădăcină pozitivă se obține atunci când.

Va fi egal.

Răspuns: .

Problema numarul 3

Când ajungem, când ajungem.

Răspuns: .

Aceste cunoștințe te vor ajuta să rezolvi multe dintre problemele cu care te vei confrunta la examen.

Dacă aplicați pentru nota „5”, atunci trebuie doar să mergeți la citirea articolului pentru nivel mijlociu, care va fi dedicat rezolvării ecuaţiilor trigonometrice mai complexe (sarcina C1).

NIVEL MEDIU

În acest articol voi descrie rezolvarea de ecuaţii trigonometrice de tip mai complexși cum să-și aleagă rădăcinile. Aici voi construi pe următoarele subiecte:

1. Ecuații trigonometrice pentru nivelul de intrare (vezi mai sus).

Ecuațiile trigonometrice mai complexe stau la baza unor probleme mai complexe. În ele, se cere atât rezolvarea ecuației în sine în formă generală, cât și găsirea rădăcinilor acestei ecuații aparținând unui anumit interval specificat.

Rezolvarea ecuațiilor trigonometrice se reduce la două subsarcini:

1. Soluția ecuației
2. Selectarea rădăcinilor

Trebuie remarcat faptul că acesta din urmă nu este întotdeauna necesar, dar selecția este totuși necesară în majoritatea exemplelor. Și dacă nu este necesar, atunci puteți mai degrabă să simpatizați - aceasta înseamnă că ecuația este destul de complicată în sine.

Experiența mea în analizarea sarcinilor C1 arată că acestea sunt de obicei împărțite în aceste categorii.

Patru categorii de sarcini de complexitate crescută (fostul C1)

1. Ecuații care se reduc la factorizare.
2. Ecuații reducând la formă.
3. Ecuații rezolvate prin modificarea variabilei.
4. Ecuații care necesită o selecție suplimentară de rădăcini din cauza iraționalității sau numitorului.

Pentru a spune simplu: dacă dai peste unul dintre primele trei tipuri de ecuații atunci consideră-te norocos. Pentru ei, de regulă, trebuie în plus să ridicați rădăcini care aparțin unui anumit interval.

Dacă dați peste o ecuație de tip 4, atunci sunteți mai puțin norocoși: trebuie să o reparați puțin mai mult și mai îndeaproape, dar destul de des nu necesită o selecție suplimentară de rădăcini în ea. Cu toate acestea, voi analiza acest tip de ecuații în articolul următor, iar acesta va fi dedicat rezolvării ecuațiilor din primele trei tipuri.

Ecuații de factorizare

Cel mai important lucru de reținut pentru a rezolva ecuații de acest tip este

După cum arată practica, de regulă, aceste cunoștințe sunt suficiente. Să ne uităm la câteva exemple:

Exemplul 1. Reducerea ecuației la factorizare folosind formule de reducere și unghi dublu sinus

• Ecuația res-shi-te
• Nay-di-te toate rădăcinile acestei ecuații

Iată, așa cum am promis, formulele de casting funcționează:

Atunci ecuația mea va arăta astfel:

Atunci ecuația mea va lua următoarea formă:

Un student miop ar putea spune: iar acum voi scurta ambele părți, voi obține cea mai simplă ecuație și mă voi bucura de viață! Și va fi amarnic greșit!

REȚINEȚI: NU REDUCEȚI NICIODATĂ AMBELE PĂRȚI ALE ECUAȚIEI TRIGONOMETRICE CU O FUNCȚIE CARE CONȚINE UN NECUNOSCUT! Așa că îți pierzi rădăcinile!

Deci ce faci? Da, totul este simplu, mutați totul într-o singură direcție și eliminați factorul comun:

Ei bine, o includem în factori, hai! Acum decidem:

Prima ecuație are rădăcini:

Si al doilea:

Aceasta completează prima parte a problemei. Acum trebuie să selectăm rădăcinile:

Decalajul este astfel:

Sau poate fi scris și așa:

Ei bine, să luăm rădăcinile:

În primul rând, să lucrăm cu prima serie (și este mai ușor, ce putem spune!)

Deoarece intervalul nostru este în întregime negativ, nu este nevoie să luăm cele nenegative, totuși acestea vor da rădăcini nenegative.

Să luăm, atunci - un pic prea mult, nu se potrivește.

Să, atunci - nu a lovit din nou.

Încă o încercare - atunci - există, lovește! Prima rădăcină găsită!

Trag din nou: apoi - L-am lovit iar!

Ei bine, încă o dată:: - acesta este deja un zbor.

Deci din prima serie 2 rădăcini aparțin intervalului:.

Lucrăm cu a doua serie (construim într-o măsură conform regulii):

Undershoot!

Undershoot din nou!

Din nou undershoot!

Am înțeles!

Zbor!

Astfel, următoarele rădăcini aparțin intervalului meu:

Prin acest algoritm vom rezolva toate celelalte exemple. Să exersăm împreună cu încă un exemplu.

Exemplul 2. O ecuație care se reduce la factorizare folosind formule de reducere

• Rezolvați ecuația

Soluţie:

Din nou notoriile formule de turnare:

Din nou, nu încercați să reduceți!

Prima ecuație are rădăcini:

Si al doilea:

Acum caută din nou rădăcini.

O sa incep cu a doua serie, stiu deja totul despre ea din exemplul anterior! Priviți și asigurați-vă că rădăcinile aparținând golului sunt după cum urmează:

Acum primul episod și e mai simplu:

Dacă - se potrivește

Dacă - este de asemenea bun

Dacă - deja un zbor.

Apoi rădăcinile vor fi după cum urmează:

Muncă independentă. 3 ecuații.

Ei bine, tehnica este clară pentru tine? Rezolvarea ecuațiilor trigonometrice nu mai pare atât de dificilă? Apoi rezolvați rapid următoarele probleme și apoi voi și cu mine vom rezolva alte exemple:

1. Rezolvați ecuația
   Nu-di-acea sunt toate rădăcinile acestei ecuații, atașate intervalului.
2. Ecuația res-shi-te
   Indicați rădăcinile ecuației
3. Ecuația res-shi-te
   Nay-di-acea sunt toate rădăcinile acestei ecuații-non-niy, atașate-pe-le-zha-shi-pro-me-zhut-ku.

Ecuația 1.

Și din nou formula de turnare:

Prima serie de rădăcini:

A doua serie de rădăcini:

Se începe selecția pentru decalaj

Răspuns: , .

Ecuația 2. Verificarea muncii independente.

O grupare destul de complicată în factori (voi folosi formula sinusului cu unghi dublu):

apoi sau

Aceasta este o soluție generală. Acum trebuie să selectăm rădăcinile. Problema este că nu putem spune valoarea exactă a unghiului, al cărui cosinus este egal cu un sfert. Prin urmare, nu pot să scap pur și simplu de arccosină - este atât de păcat!

Ce pot face este să-mi dau seama ce și cum, atunci.

Să facem un tabel: interval:

Ei bine, prin căutări dureroase, am ajuns la concluzia dezamăgitoare că ecuația noastră are o rădăcină la intervalul indicat: \ displaystyle arccos \ frac (1) (4) -5 \ pi

Ecuația 3. Verificarea muncii independente.

O ecuație înspăimântătoare. Cu toate acestea, poate fi rezolvată destul de simplu prin aplicarea formulei sinusului cu unghi dublu:

Reduce cu 2:

Să grupăm primul termen cu al doilea și al treilea cu al patrulea și să scoatem factorii comuni:

Este clar că prima ecuație nu are rădăcini, iar acum luați în considerare a doua:

În general, aveam să mă opresc asupra soluției unor astfel de ecuații puțin mai târziu, dar, din moment ce a apărut, atunci nu este nimic de făcut, este necesar să rezolvăm ...

Ecuații de forma:

Această ecuație se rezolvă prin împărțirea ambelor părți la:

Astfel, ecuația noastră are o singură serie de rădăcini:

Este necesar să le găsiți pe acelea dintre ele care aparțin intervalului:.

Să construim din nou un tabel, așa cum am făcut mai devreme:

Răspuns: .

Ecuații care se reduc la forma:

Ei bine, acum este momentul să trec la al doilea lot de ecuații, mai ales că am spus deja în ce constă soluția ecuațiilor trigonometrice de un nou tip. Dar nu va fi de prisos să repetăm ​​că o ecuație a formei

Se rezolvă împărțind ambele părți la cosinus:

1. Ecuația res-shi-te
   Indicați rădăcinile ecuației-nu-nia, când-supra-întins-de-tăiere.
2. Ecuația res-shi-te
   Indicați rădăcinile ecuației-nu-nia, când-peste-le-zha-shi-pro-me-zhut-ku.

Exemplul 1.

Primul este foarte simplu. Deplasați-vă la dreapta și aplicați formula cosinusului cu unghi dublu:

Aha! Ecuația formei:. Împărțim ambele părți în

Facem cernerea rădăcinilor:

Decalaj:

Răspuns:

Exemplul 2.

Totul este, de asemenea, destul de banal: să extindem parantezele din dreapta:

Identitatea trigonometrică de bază:

Sinus dublu unghi:

În sfârșit obținem:

Pierderea rădăcinii: gol.

Răspuns: .

Ei bine, cum vă place tehnica, nu este prea complicată? Sper ca nu. Putem face imediat o rezervă: în forma lor pură, ecuațiile, care se reduc imediat la o ecuație pentru tangentă, sunt destul de rare. De obicei, această tranziție (diviziunea prin cosinus) este doar o parte a unei probleme mai complexe. Iată un exemplu pe care să îl exersați:

• Ecuația res-shi-te
• Nay-di-acea sunt toate rădăcinile acestei ecuații-nu-nia, atașată-peste-le-zha-shi-ku.

Sa verificam:

Ecuația se rezolvă imediat, este suficient să împărțiți ambele părți în:

Renunțarea la rădăcină:

Răspuns: .

Într-un fel sau altul, încă nu ne întâlnim cu ecuații de tipul pe care tocmai le-am analizat. Cu toate acestea, este prea devreme pentru a ne rotunji: mai există un „strat” de ecuații pe care nu l-am analizat. Asa de:

Rezolvarea ecuațiilor trigonometrice prin schimbarea unei variabile

Totul este transparent aici: ne uităm atent la ecuație, o simplificăm pe cât posibil, facem o înlocuire, rezolvăm, facem o înlocuire inversă! În cuvinte, totul este foarte ușor. Să vedem în acțiune:

Exemplu.

• Rezolvați ecuația:.
• Nay-di-acea sunt toate rădăcinile acestei ecuații-nu-nia, atașată-peste-le-zha-shi-ku.

Ei bine, aici înlocuitorul în sine cere să fie în mâinile noastre!

Atunci ecuația noastră se va transforma în asta:

Prima ecuație are rădăcini:

Și a doua este acestea:

Acum vom găsi rădăcinile aparținând intervalului

Răspuns: .

Să trecem împreună peste un exemplu puțin mai complex:

• Ecuația res-shi-te
• Indicați rădăcinile ecuației date-non-niy, when-over-le-za-shi-n-e-zhut-ku.

Aici înlocuirea nu este imediat vizibilă, în plus, nu este foarte evidentă. Să ne gândim mai întâi: ce putem face?

De exemplu, ne putem imagina

Și în același timp

Atunci ecuația mea va lua forma:

Acum atenție, concentrează-te:

Să împărțim ambele părți ale ecuației la:

Dintr-o dată, tu și cu mine avem o ecuație pătratică pentru! Să facem o înlocuire, apoi obținem:

Ecuația are următoarele rădăcini:

A doua serie urâtă de rădăcini, dar nu poate fi evitată! Selectăm rădăcinile în interval.

Trebuie să luăm în considerare și asta

De când și, atunci

Răspuns:

Pentru a consolida, înainte de a rezolva singur problemele, iată un alt exercițiu pentru tine:

• Ecuația res-shi-te
• Nay-di-acea sunt toate rădăcinile acestei ecuații-non-niy, atașate-pe-le-zha-shi-pro-me-zhut-ku.

Aici trebuie să ții ochii deschiși: acum avem numitori care pot fi zero! Prin urmare, trebuie să fii deosebit de atent la rădăcini!

În primul rând, trebuie să transform ecuația, astfel încât să pot face o substituție adecvată. Nu mă pot gândi la nimic mai bun acum decât să rescriu tangenta în termeni de sinus și cosinus:

Acum voi trece de la cosinus la sinus prin identitatea trigonometrică de bază:

Și, în sfârșit, voi aduce totul la un numitor comun:

Acum pot trece la ecuația:

Dar la (adică la).

Totul este acum gata pentru înlocuire:

Atunci fie

Cu toate acestea, vă rugăm să rețineți că dacă, atunci în același timp!

Cine suferă de asta? Problema cu tangentei, este nedefinită când cosinusul este zero (diviziunea cu zero).

Astfel, rădăcinile ecuației sunt următoarele:

Acum cernem rădăcinile în interval:

	- se potrivește
	- forta bruta

Astfel, ecuația noastră are o singură rădăcină în interval și este egală cu.

Vezi tu: apariția numitorului (precum și tangentei, duce la anumite dificultăți cu rădăcinile! Aici trebuie să fii mai atent!).

Ei bine, tu și cu mine aproape am terminat analiza ecuațiilor trigonometrice, a mai rămas foarte puțin - pentru a rezolva independent două probleme. Aici sunt ei.

1. Rezolvați ecuația
   Nay-di-acea sunt toate rădăcinile acestei ecuații-nu-nia, atașată-peste-le-zha-shi-ku.
2. Ecuația res-shi-te
   Indicați rădăcinile acestei ecuații, atașate la tăietură.

Hotărât? Nu foarte greu? Sa verificam:

1. Lucrăm după formulele de reducere:

   Înlocuiți în ecuație:

   Să rescriem totul în termeni de cosinus, astfel încât să fie mai convenabil să facem înlocuirea:

   Acum este ușor să faci înlocuirea:

   Este clar că aceasta este o rădăcină străină, deoarece ecuația nu are soluții. Atunci:

   Căutăm rădăcinile de care avem nevoie în interval

   Răspuns: .

2. 
   Aici înlocuitorul este imediat vizibil:

   Atunci fie

   	- se potrivește!	- se potrivește!
   	- se potrivește!	- se potrivește!
   	- mult!	- prea multe!

   Răspuns:

Ei bine, acum asta e! Dar rezolvarea ecuațiilor trigonometrice nu se termină aici, rămânem cu cele mai dificile cazuri: când există iraționalitate în ecuații sau tot felul de „numitori complecși”. Vom lua în considerare cum să rezolvăm astfel de sarcini în articol pentru nivelul avansat.

NIVEL AVANSAT

Pe lângă ecuațiile trigonometrice discutate în cele două articole precedente, vom lua în considerare o altă clasă de ecuații care necesită o analiză și mai atentă. Aceste exemple trigonometrice conțin fie iraționalitate, fie un numitor, ceea ce le face mai dificil de analizat.... Cu toate acestea, este posibil să întâlniți aceste ecuații în partea C a lucrării de examen. Cu toate acestea, există o căptușeală de argint: pentru astfel de ecuații, de regulă, întrebarea care dintre rădăcinile sale aparține unui interval dat nu este ridicată. Să nu dăm peste tufiș, ci doar exemple trigonometrice.

Exemplul 1.

Rezolvați ecuația și găsiți rădăcinile care aparțin segmentului.

Soluţie:

Avem un numitor care nu ar trebui să fie zero! Atunci rezolvarea acestei ecuații este la fel cu rezolvarea sistemului

Să rezolvăm fiecare dintre ecuațiile:

Și acum al doilea:

Acum să aruncăm o privire asupra seriei:

Este clar că opțiunea nu ne convine, deoarece în acest caz numitorul este zero (vezi formula pentru rădăcinile celei de-a doua ecuații)

Dacă, totuși, atunci totul este în ordine, iar numitorul nu este zero! Atunci rădăcinile ecuației sunt după cum urmează:,.

Acum selectăm rădăcinile aparținând intervalului.

	- nu se potriveste	- se potrivește
	- se potrivește	- se potrivește
	forta bruta	forta bruta

Apoi rădăcinile sunt după cum urmează:

Vedeți, chiar și apariția unui mic zgomot sub formă de numitor a afectat semnificativ soluția ecuației: am scăpat o serie de rădăcini care zero numitorul. Situația poate fi și mai dificilă dacă dai peste exemple trigonometrice care au iraționalitate.

Exemplul 2.

Rezolvați ecuația:

Soluţie:

Ei bine, cel puțin nu este nevoie să selectați rădăcinile și asta e bine! Să rezolvăm mai întâi ecuația, indiferent de iraționalitate:

Asta-i tot? Nu, vai, ar fi prea ușor! Trebuie amintit că numai numerele nenegative pot fi sub rădăcină. Atunci:

Soluția acestei inegalități:

Acum rămâne de aflat dacă unele dintre rădăcinile primei ecuații au ajuns accidental acolo unde inegalitatea nu este satisfăcută.

Pentru a face acest lucru, puteți utiliza din nou tabelul:

	: , dar	Nu!
		Da!
		Da!

Astfel, una dintre rădăcini a „căzut” de la mine! Se dovedește că dacă îl pui. Apoi răspunsul poate fi scris după cum urmează:

Răspuns:

Vedeți, rădăcina necesită o atenție și mai mare! Pentru a complica lucrurile: acum permiteți-mi să am o funcție trigonometrică sub rădăcină.

Exemplul 3.

Ca și înainte: mai întâi vom rezolva fiecare separat, apoi ne vom gândi la ce am făcut.

Acum a doua ecuație:

Acum, cel mai dificil lucru este să aflăm dacă se obțin valori negative sub rădăcina aritmetică dacă înlocuim acolo rădăcinile din prima ecuație:

Numărul trebuie înțeles ca radiani. Deoarece radianii sunt aproximativ grade, radianii sunt aproximativ grade. Acesta este colțul celui de-al doilea trimestru. Care este semnul cosinusului celui de-al doilea sfert? Minus. Și sinusul? Un plus. Deci, ce se poate spune despre expresia:

Este mai puțin de zero!

Aceasta înseamnă că nu este rădăcina ecuației.

Acum este rândul.

Să comparăm acest număr cu zero.

Cotangenta este o funcție care descrește într-un sfert (cu cât argumentul este mai mic, cu atât cotangenta este mai mare). radianii sunt aproximativ grade. În același timp

de atunci și de aici
,

Răspuns: .

Ar putea fi și mai dificil? Cu plăcere! Va fi mai dificil dacă funcția trigonometrică este încă sub rădăcină, iar a doua parte a ecuației este din nou funcția trigonometrică.

Cu cât mai multe exemple trigonometrice, cu atât mai bine, vezi mai departe:

Exemplul 4.

Rădăcina nu este potrivită din cauza cosinusului limitat

Acum al doilea:

În același timp, prin definiția rădăcinii:

Trebuie să ne amintim de cercul unitar: și anume acele sferturi în care sinusul este mai mic decât zero. Ce sferturi sunt? Al treilea și al patrulea. Atunci ne vor interesa acele soluții ale primei ecuații care se află în al treilea sau al patrulea trimestru.

Prima serie produce rădăcini la intersecția celui de-al treilea și al patrulea trimestru. A doua serie, care este diametral opusă acesteia, dă naștere rădăcinilor situate la granița primului și al doilea sferturi. Prin urmare, această serie nu ne convine.

Răspuns: ,

Și din nou exemple trigonometrice cu „iraționalitate dificilă”... Nu numai că avem din nou funcția trigonometrică sub rădăcină, dar acum este și la numitor!

Exemplul 5.

Ei bine, nu se poate face nimic - procedăm ca înainte.

Acum lucrăm cu numitorul:

Nu vreau să rezolv inegalitatea trigonometrică și, prin urmare, voi acționa cu viclenie: voi lua și voi înlocui seria mea de rădăcini în inegalitate:

Dacă - par, atunci avem:

deoarece, atunci toate unghiurile de vedere se află în al patrulea trimestru. Și din nou întrebarea sacră: care este semnul sinusurilor în al patrulea trimestru? Negativ. Apoi inegalitatea

Dacă este ciudat, atunci:

În ce cartier se află colțul? Acesta este colțul celui de-al doilea trimestru. Apoi, toate colțurile sunt din nou colțurile celui de-al doilea sfert. Sinusul este pozitiv acolo. Exact ce ai nevoie! Prin urmare, seria:

Se potrivește!

Tratați a doua serie de rădăcini în același mod:

Înlocuim în inegalitatea noastră:

Dacă - chiar, atunci

Colțuri din primul sfert. Sinusul este pozitiv acolo, deci seria este potrivită. Acum, dacă - impar, atunci:

se potriveste si!

Ei bine, acum scriem răspunsul!

Răspuns:

Ei bine, acesta a fost poate cel mai consumator de timp. Acum iti ofer probleme pentru propria ta rezolvare.

A face exerciții fizice

1. Rezolvați și găsiți toate rădăcinile ecuației care aparțin segmentului.

Solutii:

1. 
   Prima ecuație:
   sau
   rădăcină ODZ:

   A doua ecuație:

   Selectarea rădăcinilor care aparțin decalajului

   Răspuns:

Sau
sau
Dar

Considera:. Dacă - chiar, atunci
- nu se potriveste!
Dacă - impar,: - se potrivește!
Aceasta înseamnă că ecuația noastră are următoarea serie de rădăcini:
sau
Selectarea rădăcinilor în interval:

	- nu se potriveste	- se potrivește
	- se potrivește	- lot
	- se potrivește	lot

Răspuns: , .

Sau
Din moment ce, când tangenta nu este definită. Aruncăm imediat această serie de rădăcini!

A doua parte:

Totodată, potrivit ODZ, se cere ca

Verificăm rădăcinile găsite în prima ecuație:

Dacă semnul este:

Colțuri din primul sfert în care tangenta este pozitivă. Nu se potrivește!
Dacă semnul este:

Unghiul al patrulea sfert. Acolo tangenta este negativă. Se potrivește. Scriem răspunsul:

Răspuns: , .

Am acoperit împreună exemple trigonometrice complexe în acest articol, dar ar trebui să rezolvați singur ecuațiile.

REZUMAT ȘI FORMULE DE BAZĂ

O ecuație trigonometrică este o ecuație în care necunoscutul se află strict sub semnul funcției trigonometrice.

Există două moduri de a rezolva ecuații trigonometrice:

Prima modalitate este utilizarea formulelor.

A doua cale este prin cercul trigonometric.

Vă permite să măsurați unghiurile, să găsiți sinusurile, cosinusurile și multe altele.

Pregătirea pentru nivelul de profil al examenului unificat de stat la matematică. Materiale utile despre trigonometrie, prelegeri video teoretice mari, analize video ale problemelor și o selecție de sarcini din anii trecuți.

Materiale utile

Selecții video și cursuri online

Formule trigonometrice

Ilustrarea geometrică a formulelor trigonometrice

Funcții arc. Cele mai simple ecuații trigonometrice

Ecuații trigonometrice

1. Teoria necesară pentru rezolvarea problemelor.
2. a) Rezolvați ecuația $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [- \ dfrac (7 \ pi) (2); - \ dfrac (3 \ pi) (2) \ dreapta] $.
3. a) Rezolvați ecuația $ \ dfrac (6) (\ cos ^ 2 x) - \ dfrac (7) (\ cos x) + 1 = 0 $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [-3 \ pi; - \ pi \ dreapta] $.
4. Rezolvați ecuația $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $.
5. a) Rezolvați ecuația $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [- \ pi; \ dfrac (5 \ pi) (2) \ dreapta] $.
6. a) Rezolvați ecuația $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $.
   
7. Rezolvați ecuația $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $.
8. Rezolvați ecuația $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $.
9. 
   b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ dreapta) $.
10. a) Rezolvați ecuația $ \ cos 2x = \ sin \ left (\ dfrac (3 \ pi) (2) - x \ right) $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [\ dfrac (3 \ pi) (2); \ dfrac (5 \ pi) (2) \ dreapta] $.
11. a) Rezolvați ecuația $ 2 \ sin ^ 2 \ left (\ dfrac (3 \ pi) (2) + x \ right) = \ sqrt3 \ cos x $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ dreapta] $.

Analiza video a sarcinilor

b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ sqrt (3); \ sqrt (20) \ dreapta] $.

b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ dreapta] $.

b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ sqrt (3); \ sqrt (30) \ dreapta] $.

a) Rezolvați ecuația $ \ cos 2x = 1 - \ cos \ left (\ dfrac (\ pi) (2) - x \ right) $.
b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ dreapta) $.

a) Rezolvați ecuația $ \ cos ^ 2 (\ pi - x) - \ sin \ left (x + \ dfrac (3 \ pi) (2) \ right) = 0 $.
b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ dreapta] $.

b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [\ log_5 2; \ log_5 20 \ dreapta] $.

a) Rezolvați ecuația $ 8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) = 9 $.
b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ dreapta] $.

a) Rezolvați ecuația $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $.
b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ dreapta] $.

a) Rezolvați ecuația $ \ left (\ dfrac (1) (49) \ right) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $.
b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [\ dfrac (3 \ pi) (2); 3 \ pi \ dreapta] $.

a) Rezolvați ecuația $ \ sin x + \ left (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ right) \ left (\ cos \ dfrac (x) (2) + \ sin \ dfrac (x) (2) \ dreapta) = 0 $.
b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ dreapta] $.

a) Rezolvați ecuația $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $.
b) Aflați toate rădăcinile acestei ecuații care aparțin intervalului $ \ left [-4 \ pi; - \ dfrac (5 \ pi) (2) \ dreapta] $.

O selecție de sarcini din anii trecuți

1. a) Rezolvați ecuația $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ dreapta] $. (USE-2018. Val timpuriu)
2. a) Rezolvați ecuația $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ sqrt (3); \ sqrt (30) \ dreapta] $. (USE-2018. Val timpuriu, zi de rezervă)
3. a) Rezolvați ecuația $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) = \ cos x $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [-2 \ pi; - \ dfrac (\ pi) (2) \ dreapta] $. (USE-2018. Valul principal)
4. a) Rezolvați ecuația $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ left (x + \ dfrac (\ pi) (6) \ right) $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [3 \ pi; \ dfrac (9 \ pi) (2) \ dreapta] $. (USE-2018. Valul principal)
5. a) Rezolvați ecuația $ \ sin x + 2 \ sin \ left (2x + \ dfrac (\ pi) (6) \ right) = \ sqrt3 \ sin 2x + 1 $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ dreapta] $. (USE-2018. Valul principal)
6. a) Rezolvați ecuația $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [-4 \ pi; - \ dfrac (5 \ pi) (2) \ dreapta] $. (USE-2018. Valul principal)
7. a) Rezolvați ecuația $ 2 \ sin \ left (2x + \ dfrac (\ pi) (3) \ right) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $.
   
8. a) Rezolvați ecuația $ 2 \ sqrt3 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) - \ cos 2x = 3 \ cos x - 1 $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [2 \ pi; \ dfrac (7 \ pi) (2) \ dreapta] $. (USE-2018. Valul principal)
9. a) Rezolvați ecuația $ 2 \ sin \ left (2x + \ dfrac (\ pi) (6) \ right) - \ cos x = \ sqrt3 \ sin 2x - 1 $.
   b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ dreapta] $. (USE-2018. Valul principal)
10. a) Rezolvați ecuația $ \ sqrt2 \ sin \ left (\ dfrac (\ pi) (4) + x \ right) + \ cos 2x = \ sin x - 1 $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ dfrac (7 \ pi) (2); 5 \ pi \ dreapta] $. (USE-2018. Valul principal)
11. a) Rezolvați ecuația $ \ sqrt2 \ sin \ left (2x + \ dfrac (\ pi) (4) \ right) + \ sqrt2 \ cos x = \ sin 2x - 1 $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ dfrac (5 \ pi) (2); - \ pi \ dreapta] $. (USE-2018. Valul principal)
12. a) Rezolvați ecuația $ 2 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) + \ cos 2x = \ sqrt3 \ cos x + 1 $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [-3 \ pi; - \ dfrac (3 \ pi) (2) \ dreapta] $. (USE-2018. Valul principal)
13. 
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ dreapta] $. (USE-2018. Valul principal)
14. 
    
15. a) Rezolvați ecuația $ 2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) + \ cos 2x = \ sqrt2 \ cos x + 1 $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ pi; \ dfrac (5 \ pi) (2) \ dreapta] $. (USE-2018. Val principal, zi de rezervă)
16. a) Rezolvați ecuația $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ dfrac (7 \ pi) (2); -2 \ pi \ dreapta] $. (USE-2018. Val principal, zi de rezervă)
17. a) Rezolvați ecuația $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ dfrac (9 \ pi) (2); -3 \ pi \ dreapta] $. (USE-2018. Val principal, zi de rezervă)
18. a) Rezolvați ecuația $ 2 \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [-3 \ pi; - \ dfrac (3 \ pi) (2) \ dreapta] $. (USE-2018. Val principal, zi de rezervă)
19. a) Rezolvați ecuația $ x - 3 \ sqrt (x - 1) + 1 = 0 $.
    b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ sqrt (3); \ sqrt (20) \ dreapta] $. (USE-2018. Val principal, zi de rezervă)
20. a) Rezolvați ecuația $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ stânga [- \ dfrac (\ pi) (2); \ \ pi \ dreapta] $. (USE-2017, val principal, zi de rezervă)
21. a) Rezolvați ecuația $ \ log_3 (x ^ 2 - 2x) = 1 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ log_2 0 (,) 2; \ \ log_2 5 \ right] $. (USE-2017, val principal, zi de rezervă)
22. a) Rezolvați ecuația $ \ log_3 (x ^ 2 - 24x) = 4 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ log_2 0 (,) 1; \ 12 \ sqrt (5) \ right] $. (USE-2017, val principal, zi de rezervă)
23. a) Rezolvați ecuația $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [2 \ pi; \ \ dfrac (7 \ pi) (2) \ right] $. (USE-2017, val principal)
24. a) Rezolvați ecuația $ \ log_8 \ left (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ right) = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ stânga [\ dfrac (3 \ pi) (2); \ 3 \ pi \ dreapta] $. (USE-2017, val principal)
25. a) Rezolvați ecuația $ \ log_4 \ left (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ right) = x $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ stânga [\ dfrac (5 \ pi) (2); \ 4 \ pi \ dreapta] $. (USE-2017, val principal)
26. a) Rezolvați ecuația $ 2 \ log_2 ^ 2 \ left (\ sin x \ right) - 5 \ log_2 \ left (\ sin x \ right) - 3 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [- 3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2017, val principal)
27. a) Rezolvați ecuația $ 81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [- 4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2017, val principal)
28. a) Rezolvați ecuația $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ log_5 2; \ \ log_5 20 \ right] $. (USE-2017, val timpuriu)
29. a) Rezolvați ecuația $ 2 \ log ^ 2_9 x - 3 \ log_9 x + 1 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ stânga [\ sqrt (10); \ \ sqrt (99) \ dreapta] $. (USE-2016, val principal, zi de rezervă)
30. a) Rezolvați ecuația $ 6 \ log ^ 2_8 x - 5 \ log_8 x + 1 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ stânga [2; \ 2 (,) 5 \ dreapta] $. (USE-2016, val principal, zi de rezervă)
31. a) Rezolvați ecuația $ \ sin 2x = 2 \ sin x + \ sin \ left (x + \ dfrac (3 \ pi) (2) \ right) + 1 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2016, val principal, zi de rezervă)
32. a) Rezolvați ecuația $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ stânga [\ dfrac (3 \ pi) (2); \ 3 \ pi \ dreapta] $. (USE-2016, val principal)
33. a) Rezolvați ecuația $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [-2 \ pi; \ - \ dfrac (\ pi) (2) \ right] $. (USE-2016, val principal)
34. a) Rezolvați ecuația $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ log_2 5; \ \ log_2 11 \ right] $. (USE-2016, val timpuriu)
35. a) Rezolvați ecuația $ \ cos 2x + \ cos ^ 2 \ left (\ dfrac (3 \ pi) (2) - x \ right) = 0,25 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2016, val timpuriu)
36. a) Rezolvați ecuația $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2016, val timpuriu)
37. a) Rezolvați ecuația $ \ dfrac (\ sin2x) (\ sin \ left (\ dfrac (7 \ pi) (2) - x \ right)) = \ sqrt (2) $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ stânga $. (USE-2015, val principal)
38. a) Rezolvați ecuația $ 4 \ sin ^ 2 x = \ mathrm (tg) x $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ stânga [- \ pi; \ 0 \ dreapta] $. (USE-2015, val principal)
39. a) Rezolvați ecuația $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $. (USE-2015, val principal)
40. a) Rezolvați ecuația $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2015, val principal)
41. a) Rezolvați ecuația $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ pi; \ \ dfrac (5 \ pi) (2) \ right] $. (USE-2015, val timpuriu)
42. a) Rezolvați ecuația $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [2 \ pi; \ \ dfrac (7 \ pi) (2) \ right] $. (USE-2015, val timpuriu)
43. a) Rezolvați ecuația $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ dfrac (5 \ pi) (2); \ 4 \ pi \ dreapta] $. (USE-2014, val principal)
44. a) Rezolvați ecuația $ 2 \ sqrt (3) \ cos ^ 2 \ left (\ dfrac (3 \ pi) (2) + x \ right) - \ sin 2x = 0 $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ dfrac (3 \ pi) (2); \ 3 \ pi \ dreapta] $. (USE-2014, val principal)
45. a) Rezolvați ecuația $ \ cos 2x + \ sqrt (2) \ sin \ left (\ dfrac (\ pi) (2) + x \ right) + 1 = 0 $.
    b) Indicaţi rădăcinile acestei ecuaţii care aparţin segmentului $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ dreapta] $. (USE-2014, val principal)
46. a) Rezolvați ecuația $ - \ sqrt (2) \ sin \ left (- \ dfrac (5 \ pi) (2) + x \ right) \ cdot \ sin x = \ cos x $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [\ dfrac (9 \ pi) (2); \ 6 \ pi \ dreapta] $. (USE-2014, val timpuriu)
47. a) Rezolvați ecuația $ \ sin 2x = \ sin \ left (\ dfrac (\ pi) (2) + x \ right) $.
    b) Indicați rădăcinile acestei ecuații care aparțin segmentului $ \ left [- \ dfrac (7 \ pi) (2); \ - \ dfrac (5 \ pi) (2) \ dreapta] $. (USE-2013, val principal)
48. a) Rezolvați ecuația $ 6 \ sin ^ 2 x + 5 \ sin \ left (\ dfrac (\ pi) (2) - x \ right) - 2 = 0 $.
    b) Indicaţi rădăcinile acestei ecuaţii care aparţin segmentului $ \ left [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ dreapta] $. (USE-2012, al doilea val)

Scopul lecției:

A) pentru a consolida capacitatea de a rezolva cele mai simple ecuaţii trigonometrice;

b) învață să aleagă rădăcinile ecuațiilor trigonometrice dintr-un interval dat

În timpul orelor.

1. Actualizarea cunoștințelor.

a) Verificarea temei: clasa a primit o temă anticipativă - pentru a rezolva ecuația și a găsi o modalitate de a selecta rădăcini dintr-un interval dat.

1) cos X= -0,5, unde xI [-]. Răspuns:.

2) păcatul X=, unde xI. Răspuns: ; ...

3) cos 2 X= -, unde хI. Răspuns:

Elevii notează soluția pe tablă, cineva folosind un grafic, cineva folosind o metodă de selecție.

În acest moment clasa lucrează pe cale orală.

Găsiți sensul expresiei:

a) tg - sin + cos + sin. Raspunsul 1.

b) 2arccos 0 + 3 arccos 1. Răspuns: ?

c) arcsin + arcsin. Răspuns:.

d) 5 arctan (-) - arccos (-). Răspuns:-.

- Să vă verificăm temele, să vă deschidem caietele de teme.

Unii dintre voi ați găsit o soluție printr-o metodă de potrivire, iar alții printr-un grafic.

2. Concluzie despre modul de rezolvare a acestor sarcini și enunțul problemei, adică mesajul subiectului și scopul lecției.

- a) Este greu de rezolvat cu ajutorul selectiei daca este dat un interval mare.

- b) Metoda grafică nu oferă rezultate precise, necesită verificare și necesită mult timp.

- Prin urmare, trebuie să mai existe cel puțin o metodă, cea mai universală - să încercăm să o găsim. Deci, ce vom face astăzi în clasă? (Învățați să alegeți rădăcinile unei ecuații trigonometrice la un interval dat.)

- Exemplul 1 (elevul merge la tablă)

cos X= -0,5, unde xI [-].

Întrebare: De ce depinde răspunsul la această sarcină? (Din soluția generală a ecuației. Să scriem soluția în formă generală). Decizia este scrisă pe tablă

х = + 2? k, unde k R.

- Să scriem această soluție sub forma unui set:

- Ce părere aveți, pentru ce înregistrare a soluției este convenabil să alegeți rădăcini în interval? (de la a doua intrare). Dar aceasta este din nou o metodă de selecție. Ce trebuie să știm pentru a obține răspunsul corect? (Trebuie să cunoașteți valorile lui k).

(Să facem un model matematic pentru a găsi k).

deoarece kI Z, atunci k = 0, deci X= =	această inegalitate arată că nu există valori întregi ale lui k.

Concluzie: Pentru a selecta rădăcini dintr-un interval dat atunci când rezolvați o ecuație trigonometrică, trebuie să:

1. pentru a rezolva o ecuație de forma sin x = a, cos x = a este mai convenabil să scrieți rădăcinile ecuației ca două serii de rădăcini.
2. pentru a rezolva ecuații de forma tg x = a, ctg x = a notează formula generală pentru rădăcini.
3. întocmește un model matematic pentru fiecare soluție sub forma unei inegalități duble și află valoarea întreagă a parametrului k sau n.
4. înlocuiți aceste valori în formula rădăcină și calculați-le.

3. Ancorarea.

Rezolvați exemplele 2 și 3 din teme folosind algoritmul obținut. În același timp, doi elevi lucrează la tablă, urmat de verificarea lucrării.

În acest articol voi încerca să explic 2 moduri selectarea rădăcinilor în ecuația trigonometrică: folosind inegalitățile și folosind cercul trigonometric. Să mergem direct la un exemplu ilustrativ și să ne ocupăm de cazul.

A) Rezolvați ecuația sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
b) Aflați toate rădăcinile acestei ecuații aparținând intervalului [-7Pi / 2; -2Pi]

Să rezolvăm punctul a.

Folosim formula de reducere pentru sinus sin (Pi / 2 + x) = cos (x)

Sqrt (2) cos ^ 2x = cosx

Sqrt (2) cos ^ 2x - cosx = 0

Cosx (sqrt (2) cosx - 1) = 0

X1 = Pi / 2 + Pin, n ∈ Z

Sqrt (2) cosx - 1 = 0

Cosx = 1 / sqrt (2)

Cosx = sqrt (2) / 2

X2 = arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
x3 = -arccos (sqrt (2) / 2) + 2Pin, n ∈ Z

X2 = Pi / 4 + 2Pin, n ∈ Z
x3 = -Pi / 4 + 2Pin, n ∈ Z

Să rezolvăm punctul b.

1) Selectarea rădăcinilor folosind inegalități

Aici totul se face simplu, înlocuim rădăcinile obținute în intervalul dat [-7Pi / 2; -2Pi], găsiți valori întregi pentru n.

7Pi / 2 mai mic sau egal cu Pi / 2 + Pin mai mic sau egal cu -2Pi

Împărțiți totul în Pi deodată

7/2 este mai mic sau egal cu 1/2 + n este mai mic sau egal cu -2

7/2 - 1/2 mai mic sau egal cu n mai mic sau egal cu -2 - 1/2

4 mai mic sau egal cu n mai mic sau egal cu -5/2

Întregul n din acest interval este -4 și -3. Deci rădăcinile aparținând acestui interval vor fi Pi / 2 + Pi (-4) = -7Pi / 2, Pi / 2 + Pi (-3) = -5Pi / 2

În mod similar, mai facem două inegalități

7Pi / 2 mai mic sau egal cu Pi / 4 + 2Pin mai mic sau egal cu -2Pi
-15/8 mai mic sau egal cu n mai mic sau egal cu -9/8

Nu există un întreg n în acest interval

7Pi / 2 mai mic sau egal cu -Pi / 4 + 2Pin mai mic sau egal cu -2Pi
-13/8 mai mic sau egal cu n mai mic sau egal cu -7/8

Un număr întreg n în acest interval este -1. Deci rădăcina selectată pe acest interval este -Pi / 4 + 2Pi * (- 1) = -9Pi / 4.

Deci răspunsul la punctul b: -7Pi / 2, -5Pi / 2, -9Pi / 4

2) Selectarea rădăcinilor folosind un cerc trigonometric

Pentru a utiliza această metodă, trebuie să înțelegeți cum funcționează acest cerc. Voi încerca să explic într-un limbaj simplu cum înțeleg asta. Cred că în școlile la lecțiile de algebră acest subiect a fost explicat de multe ori prin cuvintele inteligente ale profesorului, formulări complexe din manuale. Personal, il inteleg ca pe un cerc ce poate fi parcurs de un numar infinit de ori, datorita faptului ca functiile sinus si cosinus sunt periodice.

Să mergem o dată în sens invers acelor de ceasornic

Să mergem de 2 ori în sens invers acelor de ceasornic

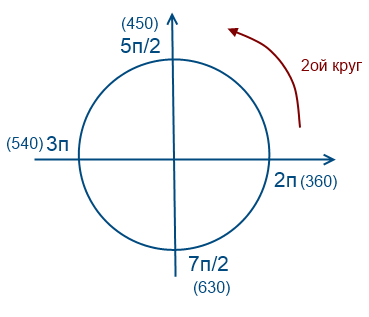
Să mergem în jur de 1 dată în sensul acelor de ceasornic (valorile vor fi negative)

Să revenim la întrebarea noastră, trebuie să selectăm rădăcinile în intervalul [-7Pi / 2; -2Pi]

Pentru a ajunge la numerele -7Pi / 2 și -2Pi, trebuie să ocoliți cercul în sens invers acelor de ceasornic de două ori. Pentru a găsi rădăcinile ecuației pe acest interval, este necesar să se estimeze și să se substituie.

Luați în considerare x = Pi / 2 + Pin. Care este valoarea aproximativă a lui n pentru ca valoarea lui x să fie undeva în acest interval? Înlocuind, să zicem -2, obținem Pi / 2 - 2Pi = -3Pi / 2, evident acest lucru nu este inclus în intervalul nostru, așa că luăm mai puțin de -3, Pi / 2 - 3Pi = -5Pi / 2, se potrivește, hai să încercăm din nou -4, Pi / 2 - 4Pi = -7Pi / 2 este de asemenea potrivit.

Raționând în mod similar pentru Pi / 4 + 2Pin și -Pi / 4 + 2Pin, găsim o altă rădăcină -9Pi / 4.

Comparația celor două metode.

Prima metodă (folosind inegalități) este mult mai fiabilă și mult mai ușor de înțeles, dar dacă vă ocupați cu adevărat serios de cercul trigonometric și de a doua metodă de selecție, atunci selectarea rădăcinilor va fi mult mai rapidă, puteți economisi aproximativ 15 minute pe examenul.

a) Rezolvați ecuația:.

b) Aflați toate rădăcinile acestei ecuații care aparțin segmentului.

Rezolvarea problemei

Această lecție are în vedere un exemplu de rezolvare a unei ecuații trigonometrice, care poate fi folosit ca exemplu pentru rezolvarea unor probleme de tip C1 în pregătirea examenului de matematică.

În primul rând, se determină domeniul de aplicare al funcției - toate valorile permise ale argumentului. Apoi, în timpul soluției, funcția sinus trigonometrică este convertită în cosinus folosind formula de reducere. În plus, toți termenii ecuației sunt transferați în partea stângă, unde factorul comun este scos din paranteze. Fiecare factor este setat egal cu zero, ceea ce vă permite să determinați rădăcinile ecuației. Apoi rădăcinile aparținând segmentului dat sunt determinate prin metoda spirelor. Pentru a face acest lucru, o buclă este marcată pe cercul unitar construit de la limita stângă a segmentului specificat la dreapta. În plus, rădăcinile găsite pe cercul unității sunt conectate prin segmente cu centrul său și sunt determinate punctele în care aceste segmente intersectează bucla. Aceste puncte de intersecție sunt răspunsul dorit la a doua parte a problemei.