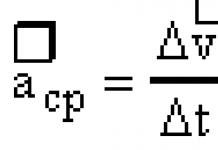Le të jetë x një pikë akull arbitrare në një lagje të një pike fikse x 0. diferenca x - x 0 zakonisht quhet rritje e ndryshores së pavarur (ose rritje e argumentit) në pikën x 0 dhe shënohet me Δx. Në këtë mënyrë,

Δx = x –x 0,

prej nga rrjedh se

Rritja e funksionit - ndryshimi midis dy vlerave të funksionit.

Lëreni funksionin në = f (x), e përcaktuar kur vlera e argumentit është e barabartë me X 0. Jepini argumentit një rritje D X, ᴛ.ᴇ. konsideroni vlerën e argumentit të barabartë x 0 + D X... Supozoni se kjo vlerë e argumentit është gjithashtu në objektin e këtij funksioni. Pastaj ndryshimi D y = f (x 0 + D X) – f (x 0)është e zakonshme të thirret funksioni increment. Rritja e funksionit f(x) në pikën xështë një funksion që zakonisht shënohet me Δ x f në ndryshoren e re Δ x përcaktuar si

Δ x f(Δ x) = f(x + Δ x) − f(x).

Gjeni shtimin e argumentit dhe shtimin e funksionit në pikën x 0, nëse

Shembulli 2. Gjeni shtimin e funksionit f (x) = x 2, nëse x = 1, ∆x = 0,1

Zgjidhje: f (x) = x 2, f (x + ∆x) = (x + ∆x) 2

Gjeni shtimin e funksionit ∆f = f (x + ∆x) - f (x) = (x + ∆x) 2 - x 2 = x 2 + 2x * ∆x + ∆x 2 - x 2 = 2x * ∆x + ∆x 2 /

Duke zëvendësuar vlerat x = 1 dhe ∆х = 0,1, marrim ∆f = 2 * 1 * 0,1 + (0,1) 2 = 0,2 + 0,01 = 0,21

Gjeni shtimin e argumentit dhe shtimin e funksionit në pikën x 0

2.f (x) = 2x 3.x 0 = 3 x = 2.4

3.f (x) = 2x 2 +2 x 0 = 1 x = 0,8

4.f (x) = 3x + 4 x 0 = 4 x = 3.8

Përkufizimi: Derivat funksioni në një pikë, është zakon që kufiri (nëse ai ekziston dhe është i fundëm) të thirret në rritje të raportit të funksionit në rritje me argumentin, me kusht që ky i fundit të priret në zero.

Emërtimet e mëposhtme të derivateve përdoren më së shpeshti:

Në këtë mënyrë,

Gjetja e derivatit zakonisht quhet diferencimi ... prezantuar përkufizimi i funksionit të diferencueshëm: Një funksion f që ka një derivat në çdo pikë të një intervali të caktuar zakonisht quhet i diferencueshëm në një interval të caktuar.

Le të përcaktohet një funksion në një lagje të një pike; U(x 0) mund të përfaqësohet si

f(x 0 + h) = f(x 0) + Ah + o(h)

nëse ekziston.

Përcaktimi i derivatit të një funksioni në një pikë.

Lëreni funksionin f (x) të përcaktuara në interval (a; b), dhe janë pikat e këtij intervali.

Përkufizimi... Funksioni derivativ f (x) në një pikë, është zakon që kufiri i raportit të rritjes së funksionit me argumentin të quhet rritje në. Është treguar.

Kur kufiri i fundit merr një vlerë përfundimtare specifike, atëherë ata flasin për ekzistencën derivati ​​përfundimtar në pikë... Nëse kufiri është i pafund, atëherë ata thonë këtë derivati ​​është i pafund në një pikë të caktuar... Nëse kufiri nuk ekziston, atëherë derivati ​​i funksionit nuk ekziston në këtë pikë.

Funksioni f (x) quhet i diferencueshëm në një pikë kur ka një derivat të fundëm në të.

Nëse funksioni f (x) i diferencueshëm në çdo pikë të një intervali (a; b), atëherë funksioni quhet i diferencueshëm në këtë interval. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, çdo pikë x jashtë ndërmjet (a; b) ne mund të lidhim vlerën e derivatit të funksionit në këtë pikë, pra kemi mundësinë të përcaktojmë një funksion të ri, i cili quhet derivat i funksionit. f (x) në interval (a; b).

Operacioni i gjetjes së derivatit zakonisht quhet diferencim.

1. rritja e argumentit dhe rritja e funksionit.

Le të jepet një funksion. Le të marrim dy vlera të argumentit: fillestar dhe i modifikuar, i cili zakonisht shënohet
, ku - quhet vlera me të cilën ndryshon argumenti kur kalon nga vlera e parë në të dytën duke rritur argumentin.

Vlerat e argumentit dhe korrespondojnë me vlerat specifike të funksionit: fillestar dhe i modifikuar
, vlera , me të cilin vlera e funksionit ndryshon kur argumenti ndryshon me një shumë, quhet nga rritja e funksionit.

2. koncepti i kufirit të një funksioni në një pikë.

Numri quhet kufiri i funksionit
kur priren të nëse për ndonjë numër
ka një numër të tillë
atë për të gjithë
duke kënaqur pabarazinë
, pabarazia
.

Përkufizimi i dytë: Një numër quhet kufiri i një funksioni me tendencë, nëse për ndonjë numër ka një fqinjësi të pikës të tillë që për ndonjë nga kjo fqinjësi. Shënohet
.

3. funksione pafundësisht të mëdha dhe infiniteminale në një pikë. Një funksion pafundësisht i vogël në një pikë është një funksion, kufiri i të cilit kur priret në një pikë të caktuar është zero. Një funksion pafundësisht i madh në një pikë është një funksion, kufiri i të cilit kur priret në një pikë të caktuar është i barabartë me pafundësinë.

4. teoremat kryesore mbi kufijtë dhe pasojat e tyre (pa vërtetim).

pasojë: faktori konstant mund të hiqet nga shenja kufitare:

Nëse sekuencat dhe konvergojnë dhe kufiri i sekuencës është jo zero, atëherë

pasojë: faktori konstant mund të nxirret jashtë shenjës kufitare.

11.nëse për ka kufij funksionesh
dhe
dhe kufiri i funksionit është jozero,

atëherë ekziston edhe një kufi i raportit të tyre, i barabartë me raportin e kufijve të funksioneve dhe:

.

12.nëse
, pastaj
, e kundërta është gjithashtu e vërtetë.

13. teorema mbi kufirin e sekuencës së ndërmjetme. Nëse sekuencat
konvergjente, dhe
dhe
pastaj

5. kufiri i funksionit në pafundësi.

Numri a quhet kufiri i një funksioni në pafundësi (pasi x tenton në pafundësi) nëse për çdo sekuencë që tenton në pafundësi
korrespondon një sekuencë vlerash që priren nga numri a.

6. g janë kufijtë e një sekuence numerike.

Numri a quhet kufiri i një sekuence numerike nëse për ndonjë numër pozitiv ekziston një numër natyror N i tillë që për të gjithë n> N qëndron pabarazia
.

Kjo përkufizohet simbolikisht si më poshtë:
i drejtë.

Fakti që numri aështë kufiri i sekuencës, i shënuar si më poshtë:

.

7. numri “e”. logaritmet natyrore.

Numri "E" përfaqëson kufirin e një sekuence numrash, n- anëtari i së cilës
, d.m.th.

.

Logaritmi natyror - logaritmi me bazë e. shënohen logaritmet natyrore
pa specifikuar bazën.

Numri
ju lejon të kaloni nga logaritmi dhjetor në atë natyror dhe mbrapa.

, quhet moduli i kalimit nga logaritmet natyrore në dhjetore.

8.kufij të shquar
,

.

Kufiri i parë i shquar:

pra në

nga teorema e kufirit të sekuencës së ndërmjetme

kufiri i dytë i shquar:

.

Për të vërtetuar ekzistencën e kufirit
përdorni lemën: për çdo numër real
dhe
pabarazia është e vërtetë
(2) (për
ose
pabarazia kthehet në barazi.)

Sekuenca (1) mund të shkruhet si më poshtë:

.

Tani merrni parasysh një sekuencë ndihmëse me një term të përbashkët
sigurohuni që të zvogëlohet dhe të kufizohet nga poshtë:
nëse
, atëherë sekuenca po zvogëlohet. Nëse
, atëherë sekuenca kufizohet nga poshtë. Le të tregojmë këtë:

për shkak të barazisë (2)

d.m.th.
ose
... Kjo do të thotë, sekuenca është në rënie, pasi sekuenca është e kufizuar nga poshtë. Nëse sekuenca është në rënie dhe e kufizuar nga poshtë, atëherë ajo ka një kufi. Pastaj

ka një kufi dhe sekuencë (1), pasi

dhe
.

L. Euler e emërtoi këtë kufi .

9. kufizime të njëanshme, boshllëk funksioni.

numri A është kufiri i majtë nëse sa vijon është e vërtetë për çdo sekuencë:.

numri A është kufiri i duhur nëse sa vijon është e vërtetë për çdo sekuencë:.

Nëse në pikën a që i përket fushës së përcaktimit të funksionit ose kufirit të tij, cenohet kushti i vazhdimësisë së funksionit, pastaj pika a quhet pikë ndërprerjeje ose ndërprerje e një funksioni.

12. shuma e anëtarëve të një progresion të pafundëm gjeometrik në rënie. Një progresion gjeometrik është një sekuencë në të cilën raporti midis anëtarëve të ardhshëm dhe të mëparshëm mbetet i pandryshuar, ky raport quhet emëruesi i progresionit. Shuma e të parës n anëtarët e një progresion gjeometrik shprehet me formulën
është e përshtatshme të përdoret kjo formulë për një progresion gjeometrik në rënie - një progresion në të cilin vlera absolute e emëruesit të tij është më e vogël se zero. - anëtari i parë; - emëruesi i progresionit; - numri i anëtarit të marrë të sekuencës. Shuma e një progresion të pafundmë në rënie është një numër të cilit shuma e anëtarëve të parë të një progresion në rënie i afrohet pafundësisht me një rritje të pakufizuar të numrit.
pastaj. Shuma e termave të një progresion gjeometrik pafundësisht në rënie është .

Përkufizimi 1

Nëse për çdo çift $ (x, y) $ vlerash të dy variablave të pavarur nga një rajon i caktuar lidhet një vlerë e caktuar prej $ z $, atëherë $ z $ thuhet se është një funksion i dy variablave $ (x, y) $. Shënimi: $ z = f (x, y) $.

Në lidhje me funksionin $ z = f (x, y) $, merrni parasysh konceptet e rritjes së përgjithshme (të plotë) dhe të pjesshme të një funksioni.

Le të jepet një funksion $ z = f (x, y) $ i dy ndryshoreve të pavarura $ (x, y) $.

Vërejtje 1

Meqenëse variablat $ (x, y) $ janë të pavarura, njëri prej tyre mund të ndryshojë, ndërsa tjetri mbetet konstant.

Le t'i japim variablit $ x $ një rritje prej $ \ Delta x $, duke mbajtur vlerën e ndryshores $ y $ të pandryshuar.

Atëherë funksioni $ z = f (x, y) $ do të marrë një rritje, e cila do të quhet rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me ndryshoren $ x $. Përcaktimi:

Në mënyrë të ngjashme, le t'i japim ndryshores $ y $ një rritje prej $ \ Delta y $, duke mbajtur të pandryshuar vlerën e ndryshores $ x $.

Atëherë funksioni $ z = f (x, y) $ do të marrë një rritje, e cila do të quhet rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me ndryshoren $ y $. Përcaktimi:

Nëse argumentit $ x $ i jepet rritja $ \ Delta x $, dhe argumentit $ y $ - rritja $ \ Delta y $, atëherë rritja e plotë e funksionit të dhënë $ z = f (x, y) $ është fituar. Përcaktimi:

Kështu, ne kemi:

$ \ Delta _ (x) z = f (x + \ Delta x, y) -f (x, y) $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ x $;

$ \ Delta _ (y) z = f (x, y + \ Delta y) -f (x, y) $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ y $;

$ \ Delta z = f (x + \ Delta x, y + \ Delta y) -f (x, y) $ - rritje e plotë e funksionit $ z = f (x, y) $.

Shembulli 1

Zgjidhja:

$ \ Delta _ (x) z = x + \ Delta x + y $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ x $;

$ \ Delta _ (y) z = x + y + \ Delta y $ është rritja e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ y $.

$ \ Delta z = x + \ Delta x + y + \ Delta y $ - rritje e plotë e funksionit $ z = f (x, y) $.

Shembulli 2

Llogaritni herësin dhe shtimin total të funksionit $ z = xy $ në pikën $ (1; 2) $ për $ \ Delta x = 0,1; \, \, \ Delta y = 0,1 $.

Zgjidhja:

Nga përkufizimi i rritjes private, gjejmë:

$ \ Delta _ (x) z = (x + \ Delta x) \ cdot y $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ x $

$ \ Delta _ (y) z = x \ cdot (y + \ Delta y) $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ y $;

Nga përkufizimi i rritjes së plotë, gjejmë:

$ \ Delta z = (x + \ Delta x) \ cdot (y + \ Delta y) $ - rritje e plotë e funksionit $ z = f (x, y) $.

Prandaj,

\ [\ Delta _ (x) z = (1 + 0,1) \ cdot 2 = 2,2 \] \ [\ Delta _ (y) z = 1 \ cdot (2 + 0,1) = 2,1 \] \ [\ Delta z = (1 + 0,1) \ cdot (2 + 0,1) = 1,1 \ cdot 2,1 = 2,31. \]

Vërejtje 2

Rritja totale e një funksioni të dhënë $ z = f (x, y) $ nuk është e barabartë me shumën e rritjeve të pjesshme të tij $ \ Delta _ (x) z $ dhe $ \ Delta _ (y) z $. Shënimi matematik: $ \ Delta z \ ne \ Delta _ (x) z + \ Delta _ (y) z $.

Shembulli 3

Kontrolloni vërejtjen e pohimit për funksionin

Zgjidhja:

$ \ Delta _ (x) z = x + \ Delta x + y $; $ \ Delta _ (y) z = x + y + \ Delta y $; $ \ Delta z = x + \ Delta x + y + \ Delta y $ (marrë në shembullin 1)

Gjeni shumën e rritjeve të pjesshme të funksionit të dhënë $ z = f (x, y) $

\ [\ Delta _ (x) z + \ Delta _ (y) z = x + \ Delta x + y + (x + y + \ Delta y) = 2 \ cdot (x + y) + \ Delta x + \ Delta y. \]

\ [\ Delta _ (x) z + \ Delta _ (y) z \ ne \ Delta z. \]

Përkufizimi 2

Nëse për çdo trefishtë $ (x, y, z) $ të vlerave të tre variablave të pavarur nga një rajon i caktuar lidhet një vlerë e caktuar prej $ w $, atëherë $ w $ thuhet se është një funksion i tre ndryshoreve $ ( x, y, z) $ në këtë zonë.

Shënimi: $ w = f (x, y, z) $.

Përkufizimi 3

Nëse për çdo koleksion $ (x, y, z, ..., t) $ të vlerave të variablave të pavarur nga një rajon i caktuar lidhet një vlerë e caktuar prej $ w $, atëherë $ w $ thuhet se është një funksion e variablave $ (x, y, z, ..., t) $ në këtë fushë.

Shënimi: $ w = f (x, y, z, ..., t) $.

Për një funksion prej tre ose më shumë ndryshoresh, në të njëjtën mënyrë si për një funksion të dy ndryshoreve, përcaktohen rritje të pjesshme për secilën prej variablave:

$ \ Delta _ (z) w = f (x, y, z + \ Delta z) -f (x, y, z) $ - rritje e pjesshme e funksionit $ w = f (x, y, z, .. ., t) $ nga $ z $;

$ \ Delta _ (t) w = f (x, y, z, ..., t + \ Delta t) -f (x, y, z, ..., t) $ - rritje e pjesshme e funksionit $ w = f (x, y, z, ..., t) $ nga $ t $.

Shembulli 4

Shkruani herësin dhe shtimin total të një funksioni

Zgjidhja:

Nga përkufizimi i rritjes private, gjejmë:

$ \ Delta _ (x) w = ((x + \ Delta x) + y) \ cdot z $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ x $

$ \ Delta _ (y) w = (x + (y + \ Delta y)) \ cdot z $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ y $;

$ \ Delta _ (z) w = (x + y) \ cdot (z + \ Delta z) $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ z $;

Nga përkufizimi i rritjes së plotë, gjejmë:

$ \ Delta w = ((x + \ Delta x) + (y + \ Delta y)) \ cdot (z + \ Delta z) $ - rritje e plotë e funksionit $ w = f (x, y, z) $ .

Shembulli 5

Llogaritni herësin dhe rritjen totale të funksionit $ w = xyz $ në pikën $ (1; 2; 1) $ për $ \ Delta x = 0,1; \, \, \ Delta y = 0,1; \, \, \ Delta z = 0,1 $.

Zgjidhja:

Nga përkufizimi i rritjes private, gjejmë:

$ \ Delta _ (x) w = (x + \ Delta x) \ cdot y \ cdot z $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ x $

$ \ Delta _ (y) w = x \ cdot (y + \ Delta y) \ cdot z $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ y $;

$ \ Delta _ (z) w = x \ cdot y \ cdot (z + \ Delta z) $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ z $;

Nga përkufizimi i rritjes së plotë, gjejmë:

$ \ Delta w = (x + \ Delta x) \ cdot (y + \ Delta y) \ cdot (z + \ Delta z) $ - rritje e plotë e funksionit $ w = f (x, y, z) $.

Prandaj,

\ [\ Delta _ (x) w = (1 + 0,1) \ cdot 2 \ cdot 1 = 2,2 \] \ [\ Delta _ (y) w = 1 \ cdot (2 + 0,1) \ cdot 1 = 2,1 \] \ [\ Delta _ (y) w = 1 \ cdot 2 \ cdot (1 + 0,1) = 2,2 \] \ [\ Delta z = (1 + 0,1) \ cdot (2 + 0,1) \ cdot (1 + 0,1) = 1,1 \ cdot 2,1 \ cdot 1,1 = 2,541. \]

Nga pikëpamja gjeometrike, rritja totale e funksionit $ z = f (x, y) $ (sipas përkufizimit, $ \ Delta z = f (x + \ Delta x, y + \ Delta y) -f (x , y) $) është e barabartë me rritjen e grafikut aplikoni funksionin $ z = f (x, y) $ kur kalon nga pika $ M (x, y) $ në pikën $ M_ (1) (x + \ Delta x , y + \ Delta y) $ (Fig. 1).

Foto 1.

në fizikën mjekësore dhe biologjike

LEKTURA Nr.1

FUNKSIONI DERIVATIV DHE DIFEENCIAL.

DERIVATE PRIVATE.

1. Koncepti i një derivati, kuptimi i tij mekanik dhe gjeometrik.

a ) Argumenti dhe rritja e funksionit.

Le të jepet funksioni y = f (x), ku x është vlera e argumentit nga domeni i funksionit. Nëse zgjedhim dy vlera të argumentit xo dhe x nga një interval i caktuar i domenit të funksionit, atëherë diferenca midis dy vlerave të argumentit quhet rritje e argumentit: x - xo = ∆x. .

Vlera e argumentit x mund të përcaktohet përmes x 0 dhe rritjes së tij: x = x o + ∆x.

Diferenca ndërmjet dy vlerave të funksionit quhet rritje e funksionit: ∆y = ∆f = f (x o + ∆x) - f (x o).

Rritja e argumentit dhe funksionit mund të paraqitet grafikisht (Fig. 1). Rritjet e argumenteve dhe rritjet e funksionit mund të jenë pozitive ose negative. Siç vijon nga Fig. 1 gjeometrikisht, rritja e argumentit ∆х përshkruhet nga rritja e abshisës, dhe rritja e funksionit ∆у përfaqësohet nga rritja e ordinatës. Llogaritja e rritjes së funksionit duhet të kryhet në rendin e mëposhtëm:

jepni argumentit një rritje ∆x dhe merrni vlerën - x + ∆x;

2) gjejmë vlerën e funksionit për vlerën e argumentit (x + ∆x) - f (x + ∆x);

3) gjejmë shtimin e funksionit ∆f = f (x + ∆x) - f (x).

Shembull: Përcaktoni rritjen e funksionit y = x 2 nëse argumenti ka ndryshuar nga x o = 1 në x = 3. Për pikën x o vlera e funksionit f (x o) = x² o; për pikën (x о + ∆х) vlera e funksionit f (x о + ∆х) = (x о + ∆х) 2 = x² о + 2х о ∆х + ∆х 2, prej nga ∆f = f (x о + ∆х) –f (х о) = (х о + ∆х) 2 –х² о = х² о + 2х о ∆х + ∆х 2 –х² о = 2х о ∆х + ∆х 2; ∆f = 2х о ∆х + ∆х 2; ∆х = 3–1 = 2; ∆f = 2 1 2 + 4 = 8.

b)Detyrat që çojnë në konceptin e një derivati. Përkufizimi i një derivati, kuptimi fizik i tij.

Koncepti i një argumenti dhe i rritjes së funksionit është i nevojshëm për të prezantuar konceptin e një derivati, i cili historikisht lindi nga nevoja për të përcaktuar shpejtësinë e proceseve të caktuara.

Konsideroni se si mund të përcaktoni shpejtësinë e një lëvizjeje drejtvizore. Lëreni trupin të lëvizë drejtvizor sipas ligjit: ∆Ѕ =  · ∆t. Për lëvizjen çift:  = ∆Ѕ / ∆t.

Për lëvizjen e ndryshueshme, vlera e ∆Ѕ / ∆t përcakton vlerën e av. , d.m.th. = ∆Ѕ / ∆t Por shpejtësia mesatare nuk bën të mundur pasqyrimin e veçorive të lëvizjes së trupit dhe të japë një ide të shpejtësisë së vërtetë në kohën t. Me një ulje të intervalit kohor, d.m.th. në ∆t → 0, shpejtësia mesatare tenton në kufirin e saj - shpejtësinë e menjëhershme:

 i menjëhershëm =
 Mër =
∆Ѕ / ∆t.

Shpejtësia e menjëhershme e një reaksioni kimik përcaktohet në të njëjtën mënyrë:

 i menjëhershëm =
 Mër =
∆х / ∆t,

ku x është sasia e substancës e formuar gjatë një reaksioni kimik gjatë kohës t. Detyra të ngjashme për përcaktimin e shpejtësisë së proceseve të ndryshme çuan në prezantimin e konceptit të derivatit të një funksioni në matematikë.

Le të jetë dhënë një funksion i vazhdueshëm f (x), i përcaktuar në intervalin] a, në [dhe shtimi i tij ∆f = f (x + ∆x) –f (x).
është funksion i ∆x dhe shpreh shpejtësinë mesatare të ndryshimit të funksionit.

Kufiri i raportit , kur ∆х → 0, me kusht që të ekzistojë ky kufi, quhet derivat i funksionit :

y "x =

.

Derivati ​​shënohet:
- (goditja kryesore x); f " (x) - (stroke eff nga x) ; y "- (dash); dy / dх – (de igrek po de iks); - (lojë me një pikë).

Bazuar në përkufizimin e derivatit, mund të themi se shpejtësia e menjëhershme e lëvizjes drejtvizore është derivati ​​kohor i shtegut:

 i menjëhershëm = S "t = f " (t).

Kështu, mund të konkludojmë se derivati ​​i funksionit në lidhje me argumentin x është shpejtësia e menjëhershme e ndryshimit të funksionit f (x):

y "x = f " (x) =  çastit.

Ky është kuptimi fizik i derivatit. Procesi i gjetjes së një derivati ​​quhet diferencim, kështu që shprehja "diferenconi një funksion" është e barabartë me shprehjen "gjeni derivatin e një funksioni".

v)Kuptimi gjeometrik i derivatit.

P
derivati ​​i funksionit y = f (x) ka një kuptim të thjeshtë gjeometrik të lidhur me konceptin e një tangjente në një vijë të lakuar në një pikë M. Për më tepër, tangjentja, d.m.th. një drejtëz shprehet analitikisht si y = kx = tanx, ku – këndi i prirjes së tangjentes (drejtëzës) ndaj boshtit X. Le të paraqesim një kurbë të vazhdueshme në funksion të y = f (x), të marrim një pikë M në kurbë dhe një pikë M 1 afër saj dhe japin një sekant nëpërmjet tyre. Pjerrësia e saj në sec = tan β = Nëse pika М 1 afrohet me M, atëherë rritja e argumentit ∆х do të priret në zero, dhe sekanti në β = α do të marrë pozicionin e tangjentes. Nga figura 2 rrjedh: tgα =
tgβ =
= y "x. Por tgα është e barabartë me pjerrësinë e tangjentes ndaj grafikut të funksionit:

k = tgα =
= y "x = f " (X). Pra, pjerrësia e tangjentes në grafikun e funksionit në një pikë të caktuar është e barabartë me vlerën e derivatit të saj në pikën e tangjences. Ky është kuptimi gjeometrik i derivatit.

G)Rregulla e përgjithshme për gjetjen e derivatit.

Bazuar në përkufizimin e një derivati, procesi i diferencimit të një funksioni mund të përfaqësohet si më poshtë:

f (x + ∆x) = f (x) + ∆f;

gjeni inkrementin e funksionit: ∆f = f (x + ∆x) - f (x);

Përcaktoni raportin e rritjes së funksionit me rritjen e argumentit:

;

Shembull: f (x) = x 2; f " (x) = ?.

Megjithatë, siç mund të shihet edhe nga ky shembull i thjeshtë, aplikimi i sekuencës së specifikuar gjatë marrjes së derivateve është një proces i mundimshëm dhe kompleks. Prandaj, për funksione të ndryshme prezantohen formula të përgjithshme për diferencim, të cilat janë paraqitur në formën e tabelës "Formulat bazë për funksionet diferencuese".

Përkufizimi 1

Nëse për çdo çift $ (x, y) $ vlerash të dy variablave të pavarur nga një rajon i caktuar lidhet një vlerë e caktuar prej $ z $, atëherë $ z $ thuhet se është një funksion i dy variablave $ (x, y) $. Shënimi: $ z = f (x, y) $.

Në lidhje me funksionin $ z = f (x, y) $, merrni parasysh konceptet e rritjes së përgjithshme (të plotë) dhe të pjesshme të një funksioni.

Le të jepet një funksion $ z = f (x, y) $ i dy ndryshoreve të pavarura $ (x, y) $.

Vërejtje 1

Meqenëse variablat $ (x, y) $ janë të pavarura, njëri prej tyre mund të ndryshojë, ndërsa tjetri mbetet konstant.

Le t'i japim variablit $ x $ një rritje prej $ \ Delta x $, duke mbajtur vlerën e ndryshores $ y $ të pandryshuar.

Atëherë funksioni $ z = f (x, y) $ do të marrë një rritje, e cila do të quhet rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me ndryshoren $ x $. Përcaktimi:

Në mënyrë të ngjashme, le t'i japim ndryshores $ y $ një rritje prej $ \ Delta y $, duke mbajtur të pandryshuar vlerën e ndryshores $ x $.

Atëherë funksioni $ z = f (x, y) $ do të marrë një rritje, e cila do të quhet rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me ndryshoren $ y $. Përcaktimi:

Nëse argumentit $ x $ i jepet rritja $ \ Delta x $, dhe argumentit $ y $ - rritja $ \ Delta y $, atëherë rritja e plotë e funksionit të dhënë $ z = f (x, y) $ është fituar. Përcaktimi:

Kështu, ne kemi:

$ \ Delta _ (x) z = f (x + \ Delta x, y) -f (x, y) $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ x $;

$ \ Delta _ (y) z = f (x, y + \ Delta y) -f (x, y) $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ y $;

$ \ Delta z = f (x + \ Delta x, y + \ Delta y) -f (x, y) $ - rritje e plotë e funksionit $ z = f (x, y) $.

Shembulli 1

Zgjidhja:

$ \ Delta _ (x) z = x + \ Delta x + y $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ x $;

$ \ Delta _ (y) z = x + y + \ Delta y $ është rritja e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ y $.

$ \ Delta z = x + \ Delta x + y + \ Delta y $ - rritje e plotë e funksionit $ z = f (x, y) $.

Shembulli 2

Llogaritni herësin dhe shtimin total të funksionit $ z = xy $ në pikën $ (1; 2) $ për $ \ Delta x = 0,1; \, \, \ Delta y = 0,1 $.

Zgjidhja:

Nga përkufizimi i rritjes private, gjejmë:

$ \ Delta _ (x) z = (x + \ Delta x) \ cdot y $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ x $

$ \ Delta _ (y) z = x \ cdot (y + \ Delta y) $ - rritje e pjesshme e funksionit $ z = f (x, y) $ në lidhje me $ y $;

Nga përkufizimi i rritjes së plotë, gjejmë:

$ \ Delta z = (x + \ Delta x) \ cdot (y + \ Delta y) $ - rritje e plotë e funksionit $ z = f (x, y) $.

Prandaj,

\ [\ Delta _ (x) z = (1 + 0,1) \ cdot 2 = 2,2 \] \ [\ Delta _ (y) z = 1 \ cdot (2 + 0,1) = 2,1 \] \ [\ Delta z = (1 + 0,1) \ cdot (2 + 0,1) = 1,1 \ cdot 2,1 = 2,31. \]

Vërejtje 2

Rritja totale e një funksioni të dhënë $ z = f (x, y) $ nuk është e barabartë me shumën e rritjeve të pjesshme të tij $ \ Delta _ (x) z $ dhe $ \ Delta _ (y) z $. Shënimi matematik: $ \ Delta z \ ne \ Delta _ (x) z + \ Delta _ (y) z $.

Shembulli 3

Kontrolloni vërejtjen e pohimit për funksionin

Zgjidhja:

$ \ Delta _ (x) z = x + \ Delta x + y $; $ \ Delta _ (y) z = x + y + \ Delta y $; $ \ Delta z = x + \ Delta x + y + \ Delta y $ (marrë në shembullin 1)

Gjeni shumën e rritjeve të pjesshme të funksionit të dhënë $ z = f (x, y) $

\ [\ Delta _ (x) z + \ Delta _ (y) z = x + \ Delta x + y + (x + y + \ Delta y) = 2 \ cdot (x + y) + \ Delta x + \ Delta y. \]

\ [\ Delta _ (x) z + \ Delta _ (y) z \ ne \ Delta z. \]

Përkufizimi 2

Nëse për çdo trefishtë $ (x, y, z) $ të vlerave të tre variablave të pavarur nga një rajon i caktuar lidhet një vlerë e caktuar prej $ w $, atëherë $ w $ thuhet se është një funksion i tre ndryshoreve $ ( x, y, z) $ në këtë zonë.

Shënimi: $ w = f (x, y, z) $.

Përkufizimi 3

Nëse për çdo koleksion $ (x, y, z, ..., t) $ të vlerave të variablave të pavarur nga një rajon i caktuar lidhet një vlerë e caktuar prej $ w $, atëherë $ w $ thuhet se është një funksion e variablave $ (x, y, z, ..., t) $ në këtë fushë.

Shënimi: $ w = f (x, y, z, ..., t) $.

Për një funksion prej tre ose më shumë ndryshoresh, në të njëjtën mënyrë si për një funksion të dy ndryshoreve, përcaktohen rritje të pjesshme për secilën prej variablave:

$ \ Delta _ (z) w = f (x, y, z + \ Delta z) -f (x, y, z) $ - rritje e pjesshme e funksionit $ w = f (x, y, z, .. ., t) $ nga $ z $;

$ \ Delta _ (t) w = f (x, y, z, ..., t + \ Delta t) -f (x, y, z, ..., t) $ - rritje e pjesshme e funksionit $ w = f (x, y, z, ..., t) $ nga $ t $.

Shembulli 4

Shkruani herësin dhe shtimin total të një funksioni

Zgjidhja:

Nga përkufizimi i rritjes private, gjejmë:

$ \ Delta _ (x) w = ((x + \ Delta x) + y) \ cdot z $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ x $

$ \ Delta _ (y) w = (x + (y + \ Delta y)) \ cdot z $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ y $;

$ \ Delta _ (z) w = (x + y) \ cdot (z + \ Delta z) $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ z $;

Nga përkufizimi i rritjes së plotë, gjejmë:

$ \ Delta w = ((x + \ Delta x) + (y + \ Delta y)) \ cdot (z + \ Delta z) $ - rritje e plotë e funksionit $ w = f (x, y, z) $ .

Shembulli 5

Llogaritni herësin dhe rritjen totale të funksionit $ w = xyz $ në pikën $ (1; 2; 1) $ për $ \ Delta x = 0,1; \, \, \ Delta y = 0,1; \, \, \ Delta z = 0,1 $.

Zgjidhja:

Nga përkufizimi i rritjes private, gjejmë:

$ \ Delta _ (x) w = (x + \ Delta x) \ cdot y \ cdot z $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ x $

$ \ Delta _ (y) w = x \ cdot (y + \ Delta y) \ cdot z $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ y $;

$ \ Delta _ (z) w = x \ cdot y \ cdot (z + \ Delta z) $ - rritje e pjesshme e funksionit $ w = f (x, y, z) $ në lidhje me $ z $;

Nga përkufizimi i rritjes së plotë, gjejmë:

$ \ Delta w = (x + \ Delta x) \ cdot (y + \ Delta y) \ cdot (z + \ Delta z) $ - rritje e plotë e funksionit $ w = f (x, y, z) $.

Prandaj,

\ [\ Delta _ (x) w = (1 + 0,1) \ cdot 2 \ cdot 1 = 2,2 \] \ [\ Delta _ (y) w = 1 \ cdot (2 + 0,1) \ cdot 1 = 2,1 \] \ [\ Delta _ (y) w = 1 \ cdot 2 \ cdot (1 + 0,1) = 2,2 \] \ [\ Delta z = (1 + 0,1) \ cdot (2 + 0,1) \ cdot (1 + 0,1) = 1,1 \ cdot 2,1 \ cdot 1,1 = 2,541. \]

Nga pikëpamja gjeometrike, rritja totale e funksionit $ z = f (x, y) $ (sipas përkufizimit, $ \ Delta z = f (x + \ Delta x, y + \ Delta y) -f (x , y) $) është e barabartë me rritjen e grafikut aplikoni funksionin $ z = f (x, y) $ kur kalon nga pika $ M (x, y) $ në pikën $ M_ (1) (x + \ Delta x , y + \ Delta y) $ (Fig. 1).

Foto 1.