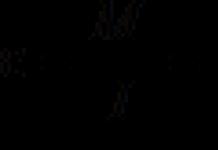Caractéristiques de la formation de concepts mathématiques de base chez les écoliers dans les conditions modernes. Concepts mathématiques Qu'est-ce qu'un concept mathématique

Le cours de mathématiques pour les classes 5 et 6 est une partie organique de l'ensemble mathématiques scolaires. Par conséquent, la principale exigence pour sa construction est la structuration du contenu sur une base idéologique unique, qui, d'une part, est une continuation et un développement des idées mises en œuvre dans l'enseignement des mathématiques en école primaire, et, d'autre part, sert à l'étude ultérieure des mathématiques au lycée.

Le développement de tous les contenus et lignes méthodologiques du cours de mathématiques primaires se poursuit : analyse numérique, algébrique, fonctionnelle, géométrique, logique, des données. Ils sont implémentés sur du matériel numérique, algébrique, géométrique.

DANS Dernièrement l'étude de la géométrie a été considérablement révisée. Le but de l'étude géométrie en 5e et 6e années, c'est la connaissance du monde qui nous entoure à travers le langage et les mathématiques. A l'aide de constructions et de mesures, l'élève identifie différents motifs géométriques, qu'il formule sous forme de proposition, d'hypothèse. L'aspect démonstratif de la géométrie est considéré d'un point de vue problématique : les étudiants sont inculqués à l'idée que de nombreux faits géométriques peuvent être découverts expérimentalement, mais que ces faits ne deviennent des vérités mathématiques que lorsqu'ils sont établis par des moyens acceptés en mathématiques.

Ainsi, le matériau géométrique de ce cours peut être caractérisé comme une géométrie d’activité visuelle. La formation est organisée comme un processus d'activité intellectuelle et pratique visant à développer des concepts spatiaux, des compétences visuelles, à élargir les horizons géométriques, au cours desquels les propriétés les plus importantes formes géométriques obtenu grâce à l’expérience et au bon sens.

La ligne de contenu « L'analyse des données ", qui combine trois directions : éléments statistiques mathématiques, combinatoire, théorie des probabilités. L’introduction de ce matériau a été dictée par la vie elle-même. Son étude vise à développer chez les écoliers à la fois une intuition probabiliste générale et des manières spécifiques d'évaluer les données. La tâche principale de ce lien est la formation d'un vocabulaire approprié, l'enseignement des techniques les plus simples pour collecter, présenter et analyser des informations, apprendre à résoudre des problèmes combinatoires en énumérant les options possibles, créer des idées élémentaires sur la fréquence et la probabilité. événements aléatoires.

Cependant, cette ligne n'est pas présente dans tous les manuels scolaires modernes de la 5e à la 6e année. Cette ligne est présentée de manière particulièrement détaillée et claire dans les manuels.

Algébrique Le matériel inclus dans le cours de mathématiques de la 5e à la 6e année constitue la base de l'étude systématique de l'algèbre au lycée. Les caractéristiques suivantes de l'étude de ce matériel algébrique peuvent être notées :

1. L'étude du matériel algébrique repose sur une base scientifique, en tenant compte des caractéristiques d'âge et des capacités des étudiants.

2. Formation concepts algébriques et le développement de compétences et d'aptitudes appropriées constituent un processus unique, construit sur un système détaillé d'exercices.

3. Le système d'exercices constitue un moyen fiable pour maîtriser le langage mathématique moderne, puisque ce langage est largement utilisé dans la formulation de diverses tâches. Par exemple, « Prouvez que cette inégalité est vraie : 29 2<1000».

4. L'amélioration des compétences informatiques est organiquement liée à l'étude du matériel algébrique.

Dans les classes 5 et 6, l'accent est mis sur le développement de la culture informatique, en particulier sur l'enseignement de techniques heuristiques pour estimer et évaluer les résultats des actions, en vérifiant leur plausibilité. Une attention accrue a été accordée aux techniques arithmétiques pour résoudre des problèmes écrits comme moyen d’enseigner le raisonnement, de choisir une stratégie de solution, d’analyser une situation, de comparer des données et, finalement, de développer la réflexion des élèves.

Les transformations identitaires d'expressions algébriques à variables étudiées à cette époque sont largement utilisées pour la propédeutique fonctionnelle. Une place importante dans le cours de mathématiques du secondaire est accordée au matériel à caractère fonctionnel. La définition d'une fonction est introduite en 7e année, et la propédeutique fonctionnelle commence en 5e année, où est considérée la notion de variable, une expression avec une variable, une formule qui précise les dépendances entre certaines quantités.

L'utilisation de la notation des lettres permet de poser la question de la construction des formules. Les relations entre les quantités sont également spécifiées sous forme de tableaux et de graphiques, et les enfants sont formés à la transition d'une forme de spécification d'une relation à une autre. Un travail systématique avec des dépendances spécifiques garantit que les enfants sont prêts à étudier les fonctions au lycée.

Méthodes . Le cours de mathématiques pour les classes 5 et 6 est construit de manière inductive. Le contenu du matériel pédagogique oblige à utiliser des méthodes qui contribuent à la formation d'activités à la fois productives et reproductrices.

En 5e et 6e années, les méthodes d'enseignement suivantes sont le plus souvent utilisées :

· Explicatif et illustratif. Toute une gamme de concepts mathématiques destinés aux niveaux 5 et 6 peuvent être introduits à l'aide de cette méthode. Avec son aide, il est possible d'étudier un matériel qui constitue une continuation et une extension logique du matériel principal. La même méthode peut être utilisée pour étudier des algorithmes spécifiques. L'information est également étudiée à l'aide de la méthode explicative et illustrative, qui peut être utilisée comme des connaissances toutes faites (formées à l'école primaire), mais recevant de nouvelles applications. Le but de l'étude de la matière à l'aide de la méthode explicative et illustrative est de développer la connaissance des règles, des lois, des algorithmes, etc. jusqu'au niveau de compétence.

· Méthodes de recherche partielle et de problèmes. Les concepts de base du cours doivent être étudiés à l'aide de méthodes garantissant le caractère créatif (productif) de l'activité des étudiants. Parmi ces méthodes, tout à fait applicables dans les classes 5 et 6, se trouve la recherche partielle. Cette méthode peut être utilisée pour étudier les notions suivantes : variable, inégalité vraie et fausse, etc.

Leçon . Les particularités de la matière mathématique de la 5e à la 6e année (presque chaque leçon nécessite l'apprentissage de nouveaux faits sur le sujet), les exigences du programme et le rythme d'étude de la matière ont conduit au fait que le type de leçon le plus courant dans ces classes est combiné.

Citons-en plus Certaines fonctionnalités enseigner les mathématiques de la 5e à la 6e année :

· Aux premières étapes de l'étude des mathématiques en 5e année, les élèves répètent les concepts qu'ils connaissent de la 1re à la 4e année, mais cette répétition s'effectue à un nouveau niveau, en utilisant la terminologie et les symboles mathématiques. Ceci afin de poser les bases d'un langage mathématique, les bases d'une culture mathématique.

· Au cours des classes de 5e et 6e années, lors de la présentation de l'arithmétique et des débuts de l'algèbre, ils ont souvent recours à des définitions géométriques utilisant une ligne ou un rayon de coordonnées, ce qui rend l'apprentissage plus visuel, et donc plus accessible et compréhensible pour les élèves. De la même manière, par exemple, la comparaison des fractions ordinaires et décimales est étudiée.

· L'une des caractéristiques de ce cours est une présentation linéaire-concentrique du matériel, selon laquelle les étudiants reviennent à plusieurs reprises sur toutes les questions fondamentales, s'élevant à un nouveau niveau dans chaque passage ultérieur.

Par exemple, lors de l'étude du sujet « Décimaux et pourcentages », il y a une transition de l'ensemble des nombres entiers non négatifs à l'ensemble des nombres rationnels non négatifs ; Dans le même temps, la formation repose sur des algorithmes d'actions avec des nombres naturels connus des étudiants, et les connaissances et compétences acquises précédemment sont constamment utilisées.

· La première difficulté rencontrée par les élèves de cinquième année est de travailler avec le texte explicatif du manuel. La raison en est la technique de lecture insuffisante de certains enfants, un vocabulaire restreint, ainsi que le fait que des textes aussi volumineux n'étaient pas trouvés dans les manuels scolaires du primaire.

Tout au long de la période d'études en 5e et 6e années, l'enseignant de mathématiques doit développer systématiquement chez les enfants la capacité de lire, de comprendre un texte et de travailler avec celui-ci. Ce travail constitue la base nécessaire à l'étude réussie des cours systématiques d'algèbre et de géométrie dans les niveaux suivants.

· L'apprentissage des mathématiques nécessite un effort mental actif. Il est très difficile de maintenir l'attention volontaire des élèves tout au long de la leçon. Une activité mentale intense, un grand nombre de calculs ou de transformations algébriques similaires et généralement routiniers fatiguent rapidement les écoliers. Il existe une manière universelle de maintenir le ton de travail des élèves : passer d’un type d’activité pédagogique à un autre. Mais vous pouvez aussi suivre le conseil de Blaise Pascal : « Le sujet des mathématiques est tellement sérieux qu’il est utile de profiter de chaque occasion pour le rendre un peu divertissant. » Ce conseil est particulièrement pertinent lors de l’enseignement des mathématiques de la 5e à la 6e année. Cependant, c'est aussi l'un des types de commutation.

2.4 Caractéristiques de la formation de concepts mathématiques dans les classes 5-6

Tout concept, y compris mathématique, est une abstraction de l'ensemble des objets spécifiques qu'il décrit. Le concept reflète les propriétés stables des objets et des phénomènes étudiés. Ces propriétés se répètent dans tous les objets unis par un concept. Mais chaque objet réel possède d’autres propriétés qui lui sont propres. La différence dans les propriétés non essentielles ne fait que mettre en évidence et souligner les propriétés essentielles.

Si, dans les classes élémentaires, l'apprentissage s'effectue principalement au niveau de la pensée visuelle et figurative, alors dans les classes 5 et 6, la pensée verbale et logique se développe plus profondément. Le contenu d'une telle pensée est constitué de concepts dont l'essence « n'est plus les signes externes, concrets et visuels des objets et de leurs relations, mais les propriétés internes les plus essentielles des objets et des phénomènes et les relations entre eux ».

Parmi les compétences que les mathématiques enseignent et que vous devez tous acquérir, la capacité de classer notions.

Le fait est que les mathématiques, comme beaucoup d'autres sciences, n'étudient pas des objets ou des phénomènes individuels, mais massif. Ainsi, lorsque vous étudiez des triangles, vous étudiez les propriétés de n’importe quel triangle, et il y en a un nombre infini. En général, la portée de tout concept mathématique est, en règle générale, infinie.

Afin de distinguer les objets des concepts mathématiques et d'étudier leurs propriétés, ces concepts sont généralement divisés en types et classes. En effet, en plus des propriétés générales, tout concept mathématique possède de nombreuses propriétés plus importantes qui ne sont pas inhérentes à tous les objets de ce concept, mais uniquement aux objets d'un certain type. Ainsi, les triangles rectangles, en plus des propriétés générales de tout triangle, possèdent de nombreuses propriétés très importantes pour la pratique, par exemple Théorème de Pythagore, relations entre angles et côtés, etc.

Au cours de l'étude séculaire des concepts mathématiques, au cours de leurs nombreuses applications dans la vie, dans d'autres sciences, certains types particuliers ont été identifiés de par leur portée, ayant les propriétés les plus intéressantes, qui sont le plus souvent rencontrées et utilisées dans la pratique. . Ainsi, il existe un nombre infini de quadrilatères différents, mais en pratique, en technologie, seuls certains types d'entre eux sont les plus utilisés : carrés, rectangles, parallélogrammes, losanges, trapèzes.

Diviser la portée d'un certain concept en parties est la classification de ce concept. Plus précisément, la classification s'entend comme la répartition des objets d'un concept en classes interdépendantes (espèces, types) selon les caractéristiques (propriétés) les plus essentielles. Le signe (propriété) par lequel s'effectue la classification (division) d'un concept en types (classes) est appelé base classements.

Une classification correctement construite d'un concept reflète les propriétés et les connexions les plus essentielles entre les objets du concept, aide à mieux naviguer dans l'ensemble de ces objets et permet d'établir les propriétés de ces objets qui sont les plus importantes pour l'application de ce concept dans d'autres sciences et dans la pratique quotidienne.

La classification d'un concept se fait selon un ou plusieurs des motifs les plus significatifs.

Ainsi, les triangles peuvent être classés selon la taille de leurs angles. Nous obtenons les types suivants : à angle aigu (tous les angles sont aigus), rectangulaire (un angle est droit, les autres sont aigus), à angle obtus (un angle est obtus, les autres sont aigus). Si nous prenons les relations entre les côtés comme base pour diviser les triangles, nous obtenons alors les types suivants : scalène, isocèle et régulier (équilatéral).

C'est plus difficile lorsqu'il faut classer un concept selon plusieurs critères. Ainsi, si les quadrilatères convexes sont classés selon le parallélisme de leurs côtés, alors essentiellement nous devons diviser tous les quadrilatères convexes simultanément selon deux critères : 1) une paire de côtés opposés est parallèle ou non ; 2) la deuxième paire de côtés opposés est parallèle ou non. En conséquence, nous obtenons trois types de quadrilatères convexes : 1) les quadrilatères à côtés non parallèles ; 2) quadrilatères avec une paire de côtés parallèles - trapèzes ; 3) les quadrilatères avec deux paires de côtés parallèles sont des parallélogrammes.

Assez souvent, un concept est classé par étapes : d'abord selon une base, puis certains types sont divisés en sous-espèces selon une autre base, etc. Un exemple est la classification des quadrangles. Dans un premier temps, ils sont divisés en fonction de la convexité. Ensuite, les quadrilatères convexes sont divisés sur la base du parallélisme des côtés opposés. À leur tour, les parallélogrammes sont divisés en fonction de la présence d'angles droits, etc.

Lors de la classification, certaines règles doivent être respectées. Indiquons les principaux.

Comme base de classification, on ne peut prendre qu'une caractéristique commune à tous les objets d'un concept donné. Ainsi, par exemple, il est impossible de prendre comme base pour la classification des expressions algébriques le signe de la disposition des termes en puissances d'une variable. Cette caractéristique n'est pas commune à toutes les expressions algébriques ; par exemple, elle n'a pas de sens pour les expressions fractionnaires ou les monômes. Seuls les polynômes possèdent cette fonctionnalité, les polynômes peuvent donc être classés selon le degré le plus élevé de la variable principale.
La base de la classification doit être les propriétés (caractéristiques) essentielles des concepts. Considérons à nouveau le concept d'expression algébrique. L'une des propriétés de ce concept est que les variables incluses dans une expression algébrique sont désignées par quelques lettres. Cette propriété est générale, mais pas essentielle, car la nature de l'expression ne dépend pas de la lettre avec laquelle une variable particulière est désignée. Ainsi, les expressions algébriques x+y Et a+b- c'est essentiellement la même expression. Par conséquent, vous ne devez pas classer les expressions en fonction de la désignation des variables par des lettres. C'est une autre affaire si, comme base pour la classification des expressions algébriques, on prend le signe du type d'actions par lesquelles les variables sont connectées, c'est-à-dire les actions qui sont effectuées sur les variables. Cette caractéristique générale est très importante et une classification selon cette caractéristique sera correcte et utile.
A chaque étape de classification, une seule base peut être utilisée. Il est impossible de classer simultanément un concept selon deux critères différents. Par exemple, il est impossible de classer les triangles à la fois par taille et par rapport entre les côtés, car nous obtiendrons ainsi des classes de triangles qui ont des éléments communs (par exemple, aigus et isocèles ou obtus et isocèles, etc. ). L'exigence de classification suivante n'est pas respectée ici : À la suite de la classification à chaque étape, les classes (types) résultantes ne doivent pas se croiser.
Dans le même temps la classification, quelle qu'en soit la base, doit être exhaustive et chaque objet du concept doit appartenir à une et une seule classe à la suite de la classification.

Par conséquent, la division de tous les entiers en positifs et négatifs est incorrecte, car l'entier zéro n'appartient à aucune des classes. Il faut le dire ainsi : les nombres entiers sont divisés en trois classes : le positif, le négatif et le nombre zéro.

Souvent, lors de la classification des concepts, seules certaines classes sont clairement identifiées, tandis que les autres ne sont qu'implicites. Ainsi, par exemple, lors de l'étude d'expressions algébriques, on distingue généralement uniquement ces types d'expressions : monômes, polynômes, expressions fractionnaires, irrationnelles. Mais ces types n’épuisent pas tous les types d’expressions algébriques, cette classification est donc incomplet.

Une classification complète et correcte des expressions algébriques peut être effectuée comme suit.

Au premier stade de classification des expressions algébriques, elles sont divisées en deux classes : rationnelles et irrationnelles. Lors de la deuxième étape, les expressions rationnelles sont divisées en nombres entiers et fractions. À la troisième étape, les expressions entières sont divisées en monômes, polynômes et expressions entières complexes.

Cette classification peut être représentée comme suit

Tâche 7

7.1. Pourquoi les nombres rationnels ne peuvent-ils pas être classés selon leur parité ?

7.2. Déterminez si la division du concept est correcte :

a) Les valeurs peuvent être égales ou inégales.

b) Les fonctions peuvent être croissantes ou décroissantes.

c) Les triangles isocèles peuvent être aigus, droits ou obtus.

d) Les rectangles sont des carrés et des losanges.

7.3. Divisez la notion de « figure géométrique » selon la propriété d'occuper une partie d'un plan et donnez des exemples de chaque type.

7.4. Construire des schémas de classification possibles pour les nombres rationnels.

7.5. Construire un schéma de classification pour les concepts suivants :

a) quadrilatère ;

b) deux angles.

7.6. Classez les concepts suivants :

a) triangle et cercle ;

b) angles dans un cercle ;

c) deux cercles ;

d) ligne droite et cercle ;

e) équations quadratiques ;

f) un système de deux équations du premier degré à deux inconnues.

travail d'études supérieures

1.1 Concepts mathématiques, leur contenu et leur portée, classification des concepts

Un concept est une forme de réflexion sur un ensemble holistique de propriétés essentielles et non essentielles d'un objet.

Les concepts mathématiques ont leurs propres caractéristiques : ils découlent souvent des besoins de la science et n'ont pas d'analogues dans le monde réel ; ils ont un haut degré d'abstraction. De ce fait, il est souhaitable de montrer aux étudiants l'émergence du concept étudié (soit à partir des besoins de la pratique, soit à partir des besoins de la science).

Chaque concept est caractérisé par son volume et son contenu. Contenu- de nombreuses caractéristiques essentielles du concept. Volume- un ensemble d'objets auxquels ce concept est applicable. Considérons le lien entre le volume et le contenu d'un concept. Si le contenu correspond à la réalité et ne comporte pas de caractéristiques contradictoires, alors le volume n'est pas un ensemble vide, ce qu'il est important de montrer aux étudiants lors de l'introduction du concept. Le contenu détermine entièrement le volume et vice versa. Cela signifie qu'un changement dans l'un entraîne un changement dans l'autre : si le contenu augmente, alors le volume diminue.

o doit être réalisé selon un seul critère ;

o les classes doivent être disjointes ;

o l'union de toutes les classes devrait donner l'ensemble complet ;

o la classification doit être continue (les classes doivent être les concepts d'espèce les plus proches par rapport au concept soumis à classification).

On distingue les types de classification suivants :

1. Selon une caractéristique modifiée. Les objets à classer peuvent avoir plusieurs caractéristiques, ils peuvent donc être classés de différentes manières.

Exemple. Le concept de « triangle ».

2. Dichotomique. Diviser la portée d'un concept en deux concepts spécifiques, l'un ayant une caractéristique donnée et l'autre non.

Soulignons les objectifs de la formation en classification :

1) développement de la pensée logique ;

2) en étudiant les différences entre les espèces, on se fait une idée plus précise du concept générique.

Les deux types de classification sont utilisés à l’école. En règle générale, d'abord dichotomique, puis sur une base modifiée.

Élever le sentiment de citoyenneté chez un enfant d'âge préscolaire

Le mot « patriote » est apparu pour la première fois lors de la Révolution française de 1789-1793. A cette époque, les combattants de la cause populaire, les défenseurs de la république, par opposition aux traîtres, aux traîtres à la patrie issus du camp monarchiste, se disaient patriotes...

Division des concepts

Afin d'opérer de manière significative avec les concepts et de les utiliser correctement dans la résolution de problèmes théoriques et pratiques, il est nécessaire d'être capable d'identifier deux caractéristiques logiques principales : la portée et le contenu du concept...

Division des concepts

La classification est la répartition des objets en groupes (classes), dans lesquels chaque classe a sa propre place permanente. La classification est un type de division du concept...

Recherche sur l'efficacité de l'utilisation des devoirs dans le processus d'éducation physique

L'activité indépendante est comprise comme un ensemble d'actions unies par un objectif commun et remplissant une fonction sociale spécifique (V.N. Shaulin, 1986). Dans notre cas, il s'agit d'activités d'éducation physique, c'est-à-dire d'activités...

Liens interdisciplinaires dans l’enseignement

Les connexions interdisciplinaires peuvent aider les écoliers à comprendre le monde qui les entoure, ses propriétés, les principaux phénomènes et processus qui s'y produisent et les modèles auxquels ils obéissent. Ainsi...

Méthodes et techniques d'enseignement d'une langue étrangère au niveau supérieur

Récemment, l’attrait des chercheurs nationaux et étrangers, comme les AA, est devenu très pertinent. Chtchoukine, I.P. Podlasy, M.A. Danilov, I.P. Pidkasisty, I.Ya. Lerner et al...

Organisation d'activités de projet d'étudiants utilisant les télécommunications

Le mot « projet » a été utilisé pour la première fois en 1908 par le chef du département pédagogique des écoles agricoles, D. Snezden, dans le domaine de l'enseignement agricole. Avec l'aide de projets, il a été proposé de lier le travail des écoles aux besoins de la production agricole...

Caractéristiques du travail d'orthophonie pour surmonter la dysgraphie agrammatique chez les élèves du secondaire

Pour la première fois, A. Kussmaul a signalé les troubles de la lecture et de l'écriture comme une pathologie indépendante de l'activité de la parole en 1877. Ensuite, de nombreux ouvrages sont apparus dans lesquels des descriptions d'enfants présentant divers troubles de la lecture et de l'écriture ont été données...

Caractéristiques de la formation de concepts mathématiques de la 5e à la 6e année

Définir un objet, c'est sélectionner parmi ses propriétés essentielles telles et telles que chacune d'elles est nécessaire, et toutes ensemble suffisantes pour distinguer cet objet des autres. Le résultat de cette action est enregistré dans la définition...

Dans la recherche pédagogique moderne liée aux problèmes d'amélioration du fonctionnement des systèmes pédagogiques, d'augmentation de l'efficacité du processus éducatif, l'un des aspects du plus grand intérêt...

Aspects psychologiques et pédagogiques de la résolution des problèmes de relations interpersonnelles chez les adolescents

Chaque époque est bonne à sa manière. Et en même temps, chaque âge a ses propres caractéristiques et difficultés. L'adolescence ne fait pas exception. L'adolescence est une certaine période de la vie entre l'enfance et l'âge adulte...

Travailler avec des enfants surdoués

28. Formes géométriques Triangle - Pentagone Les paires de concepts peuvent être prononcées à voix haute, présentées sous forme de cartes ou imprimées sur une feuille séparée. Les enfants peuvent répondre oralement ou par écrit. Tâche 4...

Problèmes modernes liés à l'éducation des enfants en famille et moyens de les résoudre

Dans le Petit Dictionnaire Encyclopédique, la notion de famille est interprétée comme « un petit groupe fondé sur le mariage ou la consanguinité, dont les membres sont liés par une vie commune, une assistance mutuelle, une responsabilité morale et juridique ». M.I. Demkov note...

Formation d'activités éducatives cognitives universelles basées sur l'individualisation et la différenciation de l'enseignement de la chimie dans un lycée de base

Comme toute institution sociale, une école polyvalente fait l’objet d’une modernisation permanente. À l'heure actuelle, la demande sociopolitique des écoles secondaires est de structurer le processus d'apprentissage de telle manière...

Etude expérimentale du sentiment de citoyenneté chez les enfants d'âge préscolaire

Un enseignant qui commence à aborder le problème du développement de la compétence civique a avant tout besoin de connaître la terminologie, les concepts clés de l'éducation civique et patriotique...

Cours 7. Concepts mathématiques

1. Groupes de concepts étudiés dans le cours initial de mathématiques. Caractéristiques des concepts mathématiques.

2. Portée et contenu du concept.

3. Relations entre les concepts.

4. Opérations avec des concepts : généralisation, limitation, définition et division du concept.

5. Règles nécessaires à la formulation de la définition des concepts par genre et différence spécifique.

6. Définitions contextuelles et ostensives. Description, comparaison.

Groupes de concepts étudiés dans le cours initial de mathématiques. Caractéristiques des concepts mathématiques.

Les concepts enseignés dans un cours d'introduction aux mathématiques sont généralement présentés en quatre groupes. D'abord les concepts liés aux nombres et aux opérations sur ceux-ci sont inclus : nombre, addition, somme, supérieur à, etc. Dans la seconde comprend des concepts algébriques : expression, égalité, équation, etc. troisième constituer des concepts géométriques : droite, segment, triangle, etc. Quatrième Le groupe est formé de concepts liés aux quantités et à leur mesure.

Comment étudier une telle abondance de concepts différents ?

Tout d'abord, vous devez avoir une idée du concept en tant que catégorie logique et des caractéristiques des concepts mathématiques.

Dans la logique des concepts envisagent comme forme de pensée, objets réfléchissants(objets ou phénomènes) dans leurs propriétés essentielles et générales. La forme linguistique du concept est mot ou groupe de mots.

Créer un concept sur un objet- cela signifie être capable de le distinguer d'autres objets qui lui sont similaires.

Les concepts mathématiques ont un certain nombre de caractéristiques. L’essentiel est que les objets mathématiques sur lesquels il faut formuler un concept n’existent pas dans la réalité. Les objets mathématiques sont créés par l'esprit humain. Ce sont des objets idéaux qui reflètent des objets ou des phénomènes réels. Par exemple, en géométrie, ils étudient la forme et la taille des objets sans tenir compte de leurs autres propriétés : couleur, masse, dureté, etc. Ils sont distraits de tout cela, abstraits. Par conséquent, en géométrie, au lieu du mot « objet », on dit « figure géométrique ».

Le résultat de l'abstraction sont des concepts mathématiques tels que « nombre » et « grandeur ».

Du tout les objets mathématiques n'existent que dans la pensée humaine et dans ces signes et symboles qui forment le langage mathématique.

A ce qui a été dit, nous pouvons ajouter que, étudier les formes spatiales et les relations quantitatives monde matériel, les mathématiques n'utilisent pas seulement divers techniques d'abstraction, mais l'abstraction elle-même agit comme un processus en plusieurs étapes. En mathématiques, ils considèrent non seulement les concepts apparus lors de l'étude d'objets réels, mais également les concepts apparus sur la base des premiers. Par exemple, le concept général de fonction comme correspondance est une généralisation des concepts de fonctions spécifiques, c'est-à-dire une abstraction des abstractions.

Afin de maîtriser les approches générales de l'étude des concepts dans le cours initial de mathématiques, l'enseignant a besoin de connaissances sur la portée et le contenu du concept, les relations entre les concepts et les types de définitions des concepts.

2. Portée et contenu du concept

Chaque objet mathématique possède certaines propriétés. Par exemple, un carré a quatre côtés, quatre angles droits et des diagonales égales. Vous pouvez spécifier ses autres propriétés.

Parmi propriétés de l'objet différencier significatif Et insignifiant.

Propriété considérée significatif pour un objet, s'il est inhérent à cet objet et sans lui il ne peut exister. Par exemple, pour un carré toutes les propriétés citées ci-dessus sont essentielles. La propriété « le côté AD est horizontal » n’est pas indispensable pour un carré ABCD. Si le carré pivote, le côté AD sera situé différemment (Fig. 26). Par conséquent, pour comprendre ce qu’est un objet mathématique donné, vous devez connaître ses propriétés essentielles.

Lorsque les gens parlent d'un concept mathématique, ils désignent généralement un ensemble d'objets désignés par un terme (un mot ou un groupe de mots). Ainsi, en parlant de carré, nous entendons toutes les figures géométriques qui sont des carrés. On pense que l’ensemble de tous les carrés constitue la portée du concept « carré ».

Tout concept est caractérisé par le mot, le volume et le contenu.

Portée du concept UN - c'est l'ensemble de tous les objets pouvant être appelés par un mot (terme) donné

Exemple. Soulignons le volume et le contenu du concept « rectangle ».

Portée du concept est un ensemble de rectangles différents, et dans son contenu inclut des propriétés des rectangles telles que « avoir quatre angles droits », « avoir des côtés opposés égaux », « avoir des diagonales égales », etc.

Il existe une relation entre la portée d'un concept et son contenu: Si le volume d’un concept augmente, alors son contenu diminue, et vice versa. Ainsi, par exemple, la portée du concept « carré » fait partie de la portée du concept « rectangle », et le contenu du concept « carré » contient plus de propriétés que le contenu du concept « rectangle » (« tous les côtés sont égales », « les diagonales sont perpendiculaires entre elles », etc. ).

Aucun concept ne peut être appris sans prendre conscience de sa relation avec d’autres concepts. Il est donc important de savoir dans quelles relations peuvent se trouver les concepts et de pouvoir établir ces liens.

Envoyer votre bon travail dans la base de connaissances est simple. Utilisez le formulaire ci-dessous

Les étudiants, étudiants diplômés, jeunes scientifiques qui utilisent la base de connaissances dans leurs études et leur travail vous seront très reconnaissants.

Agence fédérale pour l'éducation

Établissement d'enseignement public d'enseignement professionnel supérieur
Université humanitaire d'État de Viatka

Faculté de Mathématiques

Département d'analyse mathématique et de méthodes d'enseignement des mathématiques

Travaux finaux de qualification

Caractéristiques de la formation des mathématiquesconcepts en 5e et 6e années

Complété:

Étudiant de 5ème année de la Faculté de Mathématiques

Beltyukova Anastasia Sergueïevna

Conseiller scientifique:

Candidat en sciences pédagogiques, professeur agrégé, chef. Département d'analyse mathématique et MPM

M.V. Krutikhina

Critique:

Candidat en sciences pédagogiques, professeur agrégé du Département d'analyse mathématique et MPM ET .V Sitnikova

Admis en soutenance à la commission de certification de l'État

"___" __________2005 Tête. département M.V. Krutikhine

Introduction 3
Chapitre 1 Fondements des méthodes d'étude des concepts mathématiques 5

Chapitre 2 Caractéristiques psychologiques et pédagogiques de l'enseignement des mathématiques de la 5e à la 6e année 15

Chapitre 3 Enseignement expérimenté 36
Conclusion 44
Bibliographie 45

Introduction

Le concept est l'un des principaux éléments du contenu de toute matière académique, y compris les mathématiques.

L’un des premiers concepts mathématiques qu’un enfant rencontre à l’école est le concept de nombre. Si ce concept n’est pas maîtrisé, les élèves auront de sérieuses difficultés pour poursuivre leur apprentissage des mathématiques.

Dès le début, les étudiants découvrent des concepts lorsqu’ils étudient diverses disciplines mathématiques. Ainsi, lorsqu'on commence à étudier la géométrie, l'élève rencontre immédiatement les notions : point, droite, angle, puis avec tout un système de concepts associés aux types d'objets géométriques.

La tâche de l’enseignant est de garantir une compréhension complète des concepts. Cependant, dans la pratique scolaire, ce problème n'est pas résolu avec autant de succès que l'exigent les objectifs d'une école polyvalente.

« Le principal inconvénient de la maîtrise des concepts à l'école est le formalisme », explique le psychologue N.F. Talyzina. L'essence du formalisme est que les étudiants, tout en reproduisant correctement la définition d'un concept, c'est-à-dire en réalisant son contenu, ne savent pas comment l'utiliser pour résoudre des problèmes d'application de ce concept. La formation des concepts est donc un élément important. Acte à nal problème.

Objet d'étude : le processus de formation de concepts mathématiques dans les classes 5 et 6.

Cellule b travaux: élaborer des recommandations méthodologiques pour l'étude des concepts mathématiques de la 5e à la 6e année.

Objectifs du poste :

1. Étudier la littérature mathématique, méthodologique et pédagogique sur ce sujet.

2. Identifiez les principales manières de définir les concepts dans les manuels scolaires de la 5e à la 6e année.

3. Déterminer les caractéristiques de la formation des concepts mathématiques en 5e et 6e années.

Hypothèse de recherche : Si nous sommes en train de former des concepts mathématiques dans les classes 5-6, nous prenons en compte les caractéristiques suivantes :

· les concepts sont principalement définis par la construction, et souvent la formation d'une compréhension correcte du concept parmi les étudiants est obtenue à l'aide de descriptions explicatives ;

· les concepts sont introduits de manière concrète et inductive ;

· Tout au long du processus de formation du concept, une grande attention est accordée à la clarté, ce processus sera alors plus efficace.

Méthodes de recherche:

· étude de la littérature méthodologique et psychologique sur le sujet ;

· comparaison de différents manuels de mathématiques ;

· Enseignement expérimenté.

Chapitre 1
Fondamentaux des méthodes d'étude des concepts mathématiques

1.1 Concepts mathématiques, leur contenu et leur portée, classification des concepts

Un concept est une forme de réflexion sur un ensemble holistique de propriétés essentielles et non essentielles d'un objet.

Les concepts mathématiques ont leurs propres caractéristiques : ils découlent souvent des besoins de la science et n'ont pas d'analogues dans le monde réel ; ils ont un haut degré d'abstraction. De ce fait, il est souhaitable de montrer aux étudiants l'émergence du concept étudié (soit à partir des besoins de la pratique, soit à partir des besoins de la science).

Chaque concept est caractérisé par son volume et son contenu. Contenu - de nombreuses caractéristiques essentielles du concept. Volume - un ensemble d'objets auxquels ce concept est applicable. Considérons le lien entre le volume et le contenu d'un concept. Si le contenu correspond à la réalité et ne comporte pas de caractéristiques contradictoires, alors le volume n'est pas un ensemble vide, ce qu'il est important de montrer aux étudiants lors de l'introduction du concept. Le contenu détermine entièrement le volume et vice versa. Cela signifie qu'un changement dans l'un entraîne un changement dans l'autre : si le contenu augmente, alors le volume diminue.

Le contenu d'un concept s'identifie à sa définition, et sa portée se révèle à travers la classification. La classification est la division d'un ensemble en sous-ensembles qui satisfont aux exigences suivantes :

o doit être réalisé selon un seul critère ;

o les classes doivent être disjointes ;

o l'union de toutes les classes devrait donner l'ensemble complet ;

o la classification doit être continue (les classes doivent être les concepts d'espèce les plus proches par rapport au concept soumis à classification).

On distingue les types de classification suivants :

1. Selon une caractéristique modifiée. Les objets à classer peuvent avoir plusieurs caractéristiques, ils peuvent donc être classés de différentes manières.

Exemple. Le concept de « triangle ».

2. Dichotomique. Diviser la portée d'un concept en deux concepts spécifiques, l'un ayant une caractéristique donnée et l'autre non.

Exemple .

Soulignons les objectifs de la formation en classification :

1) développement de la pensée logique ;

2) en étudiant les différences entre les espèces, on se fait une idée plus précise du concept générique.

Les deux types de classification sont utilisés à l’école. En règle générale, d'abord dichotomique, puis sur une base modifiée.

1.2 Définition des concepts mathématiques, concepts primaires qui expliquent la description

Définir un objet - choisir parmi ses propriétés essentielles telles et telles que chacune d'elles soit nécessaire, et toutes ensemble suffisantes pour distinguer cet objet des autres. Le résultat de cette action est enregistré dans la définition.

Définition On considère une formulation qui réduit un nouveau concept à des concepts déjà connus du même domaine. Une telle réduction ne peut pas se poursuivre indéfiniment, c'est pourquoi la science a concepts primaires , qui ne sont pas définis explicitement, mais indirectement (par le biais d'axiomes). La liste des concepts primaires est ambiguë : par rapport aux sciences, il y a beaucoup plus de concepts primaires dans le cursus scolaire. La principale technique de clarification et d'introduction des concepts primaires est la compilation des généalogies.

Dans un cursus scolaire, il n’est pas toujours conseillé de donner aux concepts une définition stricte. Parfois, cela suffit pour se faire une bonne idée. Ceci est réalisé en utilisant ceinture nourrir descriptions - des phrases accessibles aux élèves qui évoquent en eux une image visuelle et les aident à comprendre le concept. Il n’est pas nécessaire ici de réduire le nouveau concept à ceux déjà étudiés. L'assimilation doit être portée à un niveau tel qu'à l'avenir, sans se souvenir de la description, l'étudiant puisse reconnaître l'objet lié à ce concept.

1.3 Façons de définir les concepts

Par structure logique les définitions sont divisées en conjonctives (les caractéristiques essentielles sont reliées par la conjonction « et ») et disjonctives (les caractéristiques essentielles sont reliées par la conjonction « ou »).

L'identification des caractéristiques essentielles enregistrées dans la définition et les connexions enregistrées entre elles est appelée analyse logique et mathématique de la définition .

Il existe une division des définitions en descriptives et constructives.

Descriptif - des définitions descriptives ou indirectes, généralement de la forme : « un objet est appelé... s'il a... ». De telles définitions ne découlent pas du fait de l'existence d'un objet donné, c'est pourquoi tous ces concepts nécessitent une preuve d'existence. Parmi elles, on distingue les méthodes suivantes de définition des concepts :

· À travers genre le plus proche et la différence entre les espèces. (Un losange est un parallélogramme dont les deux côtés adjacents sont égaux. Le concept générique est un parallélogramme, dont le concept défini se distingue par une différence spécifique).

· Définitions-accords- des définitions dans lesquelles les propriétés des concepts sont exprimées à l'aide d'égalités ou d'inégalités.

· Définitions axiomatiques. Dans la science elle-même, les mathématiques sont souvent utilisées, mais dans les cours scolaires, elles sont rarement utilisées pour des concepts intuitivement clairs. (L'aire d'une figure est une quantité dont la valeur numérique satisfait aux conditions : S(F)0 ; F 1 =F 2 S(F 1)=S(F 2) ; F=F 1 F 2, F 1 F 2 = S(F )=S(F 1)+S(F 2); S(E)=1.)

· Définitions via abstraction. Ils recourent à une telle définition d'un concept lorsqu'un autre est difficile ou impossible à mettre en œuvre (par exemple, un nombre naturel).

· Définition-négation- une définition qui fixe non pas la présence d'une propriété, mais son absence (par exemple, lignes parallèles).

Constructif (ou génétique) sont des définitions qui indiquent la méthode d'obtention d'un nouvel objet (par exemple, une sphère est une surface obtenue en faisant tourner un demi-cercle autour de son diamètre). Parmi ces définitions, on distingue parfois récursif- des définitions indiquant un certain élément de base d'une classe et une règle par laquelle de nouveaux objets de la même classe peuvent être obtenus (par exemple, la définition d'une progression).

1.4 Exigences méthodologiques pour la définition du concept

· Exigence scientifique.

· Exigence d'accessibilité.

· Exigence de commensurabilité (le volume du concept défini doit être égal au volume du concept définissant). La violation de cette exigence conduit à une définition soit très large, soit très étroite.

· La définition ne doit pas contenir de cercle vicieux.

· Les définitions doivent être claires, précises et ne pas contenir d'expressions métaphoriques.

· Minimum requis.

1.5 Introduction de concepts dans un cours de mathématiques scolaire

Lors de la formation de concepts, il est nécessaire d’organiser les activités des élèves pour maîtriser deux techniques logiques de base : subsumer un concept et tirer des conséquences du fait qu’un objet appartient à un concept.

Action englobant le concept a la structure suivante :

1) Sélection de toutes les propriétés enregistrées dans la définition.

2) Établir des liens logiques entre eux.

3) Vérifier si un objet a des propriétés sélectionnées et leurs connexions.

4) Obtenir une conclusion quant à l'appartenance d'un objet au champ d'application du concept.

Déduire des conséquences - c'est la sélection des caractéristiques essentielles d'un objet appartenant à un concept donné.

Il y a trois manières dans la méthodologie introduction aux concepts :

1) Concrètement inductif :

o Prise en compte de divers objets appartenant ou non au périmètre du concept.

o Identification des caractéristiques essentielles d'un concept basée sur la comparaison d'objets.

o Introduction du terme, formulation de la définition.

2) Abstrait-déductif :

o Introduction de la définition par l'enseignant.

o Prise en compte de cas particuliers et individuels.

o Formation de la capacité à subsumer un objet sous un concept et à en tirer des conséquences primaires.

En introduisant un concept de la première manière, les élèves comprennent mieux les motivations de l'introduction, apprennent à construire des définitions et comprennent l'importance de chaque mot qu'il contient. Lors de l'introduction d'un concept de la deuxième manière, on gagne beaucoup de temps, ce qui n'est pas non plus sans importance.

3) Combiné . Utilisé pour des concepts de calcul plus avancés. Sur la base d'un petit nombre d'exemples précis, une définition du concept est donnée. Ensuite, en résolvant des problèmes dans lesquels des caractéristiques sans importance varient et en comparant ce concept avec des exemples spécifiques, la formation du concept se poursuit.

1.6 Principales étapes de l'apprentissage d'une notion à l'école

Dans la littérature, il existe trois étapes principales de l'apprentissage des concepts à l'école :

1. Quand présentation du concept l'une des trois méthodes décrites ci-dessus est utilisée. Au cours de cette étape, vous devez considérer les éléments suivants :

· Tout d'abord, il est nécessaire de fournir une motivation pour introduire ce concept.

· Lors de la construction d'un système de tâches pour englober un concept, assurez-vous de la portée la plus complète du concept.

· Il est important de montrer que la portée d'un concept n'est pas un ensemble vide.

· Révéler le contenu du concept, travailler sur les fonctionnalités essentielles, mettre en avant celles qui ne sont pas essentielles.

· En plus de connaître la définition, il est souhaitable que les élèves aient une compréhension visuelle du concept.

· Maîtriser la terminologie et le symbolisme.

Le résultat de cette étape est la formulation d'une définition dont l'assimilation constitue le contenu de l'étape suivante. Maîtriser la définition d'un concept signifie maîtriser les actions de reconnaissance d'objets appartenant au concept, déduire les conséquences de l'appartenance d'un objet au concept, construire des objets liés à la portée du concept.

2. Au stade maîtriser la définition Le travail se poursuit sur la mémorisation de la définition. Ceci peut être réalisé en utilisant les techniques suivantes :

· Écrire les définitions dans un cahier.

· Prononcer, souligner ou une sorte de numérotation des propriétés essentielles.

· Utilisation de contre-exemples pour respecter les règles de commensurabilité.

· Sélection des mots manquants dans la définition, recherche de mots supplémentaires.

· Apprendre à donner des exemples et des contre-exemples.

· Apprendre à appliquer la définition dans les situations les plus simples, mais tout à fait typiques, puisque la répétition répétée de la définition en dehors de la résolution de problèmes est inefficace.

· Signaler la possibilité de définitions différentes, prouver leur équivalence, mais en choisir une seule pour la mémorisation.

· Apprendre à construire une définition, utiliser pour cela la compilation de généalogies, en expliquant la structure logique ; présenter les règles de construction d’une définition.

· Donnez des paires de concepts similaires en comparaison et en contraste.

Ainsi, chaque propriété essentielle du concept utilisé dans la définition à ce stade devient un objet d'étude particulier.

3.Prochaine étape - consolidation . Un concept peut être considéré comme formé si les élèves le reconnaissent immédiatement dans le problème sans aucun tri dans ses caractéristiques, c'est-à-dire que le processus d'intégration du concept est écourté. Ceci peut être réalisé des manières suivantes :

· Application de la définition à des situations plus complexes.

· Inclusion d'un nouveau concept dans des connexions logiques, des relations avec d'autres concepts (par exemple, comparaison de généalogies, classifications).

· Il est conseillé de montrer que la définition n'est pas donnée pour elle-même, mais pour qu'elle « fonctionne » lors de la résolution de problèmes et de la construction d'une nouvelle théorie.

Chapitre 2
Caractéristiques psychologiques et pédagogiques de l'enseignement des mathématiques de la 5e à la 6e année

2.1 Caractéristiques de l'activité cognitive

Perception. Un écolier de la 5e à la 6e année a un niveau suffisant de développement de la perception. Il possède un niveau élevé d'acuité visuelle, d'audition et d'orientation par rapport à la forme et à la couleur d'un objet.

Le processus d’apprentissage impose de nouvelles exigences à la perception de l’élève. Dans le processus de perception de l’information éducative, le caractère aléatoire et le sens des activités des élèves sont nécessaires. Premièrement, l'enfant est attiré par l'objet lui-même et, tout d'abord, par ses signes extérieurs lumineux. Mais les enfants sont déjà capables de se concentrer et d'examiner attentivement toutes les caractéristiques d'un objet, en mettant en évidence les éléments principaux et essentiels qu'il contient. Cette caractéristique se manifeste dans le processus d'activités éducatives. Ils peuvent analyser des groupes de figures, organiser des objets selon diverses caractéristiques et classer des figures selon une ou deux propriétés de ces figures.

Les écoliers de cet âge commencent à observer comme une activité particulière et développent l'observation comme un trait de caractère.

Le processus de formation de concepts est un processus graduel, dans les premières étapes duquel la perception sensorielle d'un objet joue un rôle important.

Mémoire. Un écolier de la 5e à la 6e année est capable de contrôler sa mémorisation volontaire. La capacité de mémoriser (mémoriser) augmente lentement mais progressivement.

À cet âge, la mémoire se restructure, passant de la prédominance de la mémorisation mécanique à la prédominance de la mémorisation sémantique. Dans le même temps, la mémoire sémantique elle-même est reconstruite. Elle acquiert un caractère indirect et la pensée y est nécessairement incluse. Il est donc nécessaire d’apprendre aux élèves à raisonner correctement afin que le processus de mémorisation repose sur la compréhension de la matière proposée.

Parallèlement à la forme, le contenu de la mémorisation change également. La mémorisation de matériel abstrait devient plus accessible.

Attention. Le processus de maîtrise des connaissances, des capacités et des compétences nécessite une maîtrise de soi constante et efficace des étudiants, ce qui n'est possible que si un niveau d'attention volontaire suffisamment élevé est formé.

Un écolier de la 5e à la 6e année est tout à fait capable de gérer son attention. Il se concentre bien sur les activités qui lui tiennent à cœur. Il est donc nécessaire de maintenir l’intérêt de l’élève pour l’apprentissage des mathématiques. Dans ce cas, il convient de s'appuyer sur des moyens auxiliaires (objets, images, tableaux).

A l'école pendant les cours, l'attention a besoin du soutien de l'enseignant.

Imagination. Au cours des activités d'apprentissage, l'étudiant reçoit de nombreuses informations descriptives. Cela l'oblige à recréer constamment des images, sans lesquelles il est impossible de comprendre et d'assimiler le matériel pédagogique, c'est-à-dire Dès le début de leur éducation, la recréation de l'imagination des élèves de la 5e à la 6e année est incluse dans des activités ciblées qui contribuent à leur développement mental.

À mesure qu’un enfant développe la capacité de contrôler son activité mentale, l’imagination devient un processus de plus en plus contrôlé.

Pour les écoliers de la 5e à la 6e année, l'imagination peut se transformer en une activité interne indépendante. Ils peuvent interpréter des problèmes mentaux avec des signes mathématiques dans leur esprit, opérer avec les significations et les significations du langage, reliant deux fonctions mentales supérieures : l'imagination et la pensée.

Toutes les caractéristiques ci-dessus constituent la base du développement du processus d'imagination créatrice, dans lequel les connaissances particulières des étudiants jouent un rôle important. Ces connaissances constituent la base du développement de l’imagination créatrice au cours des périodes ultérieures de la vie de l’élève.

Pensée. La pensée théorique et la capacité d'établir le maximum de connexions sémantiques dans le monde qui nous entoure commencent à devenir de plus en plus importantes. L'étudiant est psychologiquement immergé dans la réalité du monde objectif, des systèmes figuratifs et de signes. La matière étudiée à l'école devient pour lui une condition pour construire et tester ses hypothèses.

De la 5e à la 6e année, l'élève développe une pensée formelle. Un écolier de cet âge peut déjà raisonner sans se relier à une situation précise.

Les scientifiques ont étudié la question des capacités mentales des écoliers de la 5e à la 6e année. À la suite de la recherche, il a été révélé que les capacités mentales de l’enfant sont plus larges qu’on ne le pensait auparavant et que lorsque les conditions appropriées sont créées, c’est-à-dire Avec une organisation méthodologique spéciale de formation, un élève de la 5e à la 6e année peut apprendre du matériel mathématique abstrait.

Comme le montre ce qui précède, les processus mentaux sont caractérisés par des caractéristiques liées à l'âge, dont la connaissance et la prise en compte sont nécessaires pour organiser un apprentissage réussi et le développement mental des élèves.

2.2 Aspects psychologiques de la formation des concepts

Tournons-nous vers la littérature psychologique et découvrons les principales dispositions du concept de formation des concepts scientifiques.

Le manuel parle de l'impossibilité de transmettre le concept sous une forme toute faite. Un enfant ne peut le recevoir qu'à la suite de sa propre activité, visant non pas les mots, mais les objets dont nous voulons former en lui le concept.

La formation de concepts est le processus de formation non seulement d'un modèle particulier du monde, mais également d'un certain système d'actions. Les actions et les opérations constituent le mécanisme psychologique des concepts. Sans eux, le concept ne peut ni être appris ni appliqué à l’avenir pour résoudre des problèmes. De ce fait, les caractéristiques des concepts formés ne peuvent être comprises sans se référer aux actions dont ils sont le produit. Et il est nécessaire de former les types d'actions suivants utilisés lors de l'étude des concepts :

· L'action de reconnaissance est utilisée lorsqu'un concept est appris à reconnaître des objets appartenant à une classe donnée. Cette action peut être utilisée dans la formation de concepts à structure logique conjonctive et disjonctive.

· Tirer des conclusions.

· Comparaison.

· Classification.

· Actions liées à l'établissement de relations hiérarchiques au sein d'un système de concepts, et autres.

Le rôle de la définition d'un concept dans le processus de son assimilation est également considéré. La définition est une base indicative pour évaluer les objets avec lesquels l'apprenant interagit. Ainsi, ayant reçu la définition d'un angle, l'étudiant peut désormais analyser divers objets du point de vue de la présence ou de l'absence de signes d'un angle en eux. Un tel travail réel crée une image des objets de ce cours dans la tête de l’élève. Ainsi, obtenir une définition est seulement premier pas sur la voie de la compréhension du concept.

Deuxième étape - inclusion de la définition d'un concept dans les actions des élèves qu'ils effectuent avec les objets correspondants et à l'aide desquelles ils construisent dans leur tête un concept sur ces objets.

Troisième étape est d'apprendre aux écoliers à se concentrer sur le contenu de la définition lorsqu'ils effectuent diverses actions avec des objets. Si cela n'est pas garanti, alors dans certains cas, les élèves s'appuieront sur les propriétés qu'ils ont eux-mêmes identifiées dans les objets, dans d'autres cas, les enfants ne pourront utiliser qu'une partie des propriétés spécifiées ; troisièmement, ils peuvent ajouter leurs propres définitions à ces définitions.

Conditions garantissant la maîtrise du processus d’acquisition du concept ème

1. La présence d’une action adéquate : elle doit viser des propriétés essentielles.

2. Connaissance de la composition de l'action utilisée. Par exemple, l'action de reconnaissance comprend : a) la mise à jour du système de propriétés nécessaires et suffisantes du concept ; b) vérifier chacun d'eux dans les objets proposés ; c) évaluation des résultats obtenus.

3. Représentation de tous les éléments de l'action sous une forme externe et matérielle.

4. Formation étape par étape de l'action introduite.

5. La présence d'un contrôle opérationnel lors de la maîtrise de nouvelles formes d'action.

N.F. Talyzina s'attarde en détail sur la formation étape par étape des concepts. Après avoir réalisé 5 à 8 tâches avec des objets ou des modèles réels, les élèves mémorisent à la fois les caractéristiques du concept et la règle d'action sans aucune mémorisation. Ensuite, l'action est traduite sous forme de discours externe, lorsque les tâches sont données par écrit et que les signes de concepts, de règles et de règlements sont nommés ou écrits de mémoire par les élèves.

Dans le cas où une action est effectuée facilement et correctement sous la forme vocale externe, elle peut être traduite sous la forme interne. La tâche est donnée sous forme écrite et les élèves reproduisent les signes, les vérifient et comparent en silence les résultats obtenus avec la règle. Tout d'abord, l'exactitude de chaque opération et la réponse finale sont vérifiées. Progressivement, le contrôle s'effectue uniquement sur le résultat final si nécessaire.

Si l'action est réalisée correctement, elle est alors transférée au stade mental : l'élève lui-même exécute et contrôle l'action. Le contrôle de la part de l'étudiant n'est assuré que sur le produit final des actions. L'étudiant reçoit de l'aide en cas de difficultés ou d'incertitudes quant à l'exactitude du résultat. Le processus d’exécution est désormais caché, l’action est devenue complètement mentale.

Ainsi, l’action se transforme progressivement en forme. La transformation en termes de généralité est assurée par une sélection particulière de tâches

Une transformation ultérieure de l'action est obtenue en répétant des tâches similaires. Il est conseillé de le faire uniquement dans les dernières étapes. A toutes les autres étapes, seul le nombre de tâches est indiqué qui assure l'assimilation de l'action sous une forme donnée.

Exigences relatives au contenu et à la forme des missions

1. Lors de la création de tâches, vous devez vous concentrer sur les nouvelles actions en cours de formation.

2. La deuxième exigence des tâches est que la forme corresponde au stade d'assimilation. Par exemple, au début, les objets avec lesquels les étudiants travaillent doivent être accessibles pour une véritable transformation.

3. Le nombre de tâches dépend de l'objectif et de la complexité de l'activité en cours de formation.

4. Lors de la sélection des tâches, il faut tenir compte du fait que la transformation des actions se produit non seulement dans la forme, mais aussi en termes de généralisation, d'automatisation, etc.

De nombreuses expériences ont été réalisées lorsque les conditions spécifiées étaient réalisées. Dans tous les cas, dit N. F. Talyzina, les concepts ont été formés non seulement avec un contenu donné, mais également avec des indicateurs élevés pour les caractéristiques suivantes :

· le caractère raisonnable des actions des sujets ;

· conscience de l'assimilation;

· la confiance des élèves dans leurs connaissances et leurs actions ;

· manque de lien avec les propriétés sensorielles des objets ;

· généralité des concepts et des actions ;

· force des concepts et des actions formés.

Ainsi, l'enfant développe progressivement une certaine image des objets d'une classe donnée. Le concept ne peut vraiment pas être donné sous une forme toute faite, il ne peut être construit que par l'étudiant lui-même en réalisant un certain système d'actions avec des objets. L'enseignant aide l'élève à former cette image avec un contenu en avance sur les propriétés essentielles des objets d'une classe donnée, et pose un point de vue socialement développé sur les objets avec lesquels l'élève travaille. Un concept est le produit d’actions réalisées par un élève avec des objets d’une classe donnée.

2.3 Quelques caractéristiques pédagogiques de l'enseignement des mathématiques en 5e et 6e années

L'idée directrice du concept moderne de l'enseignement scolaire est l'idée d'humanisation, qui place l'élève avec ses intérêts et ses capacités au centre du processus d'apprentissage, nécessitant la prise en compte des caractéristiques de sa personnalité. Les principales orientations de l'enseignement mathématique sont de renforcer le son culturel général et d'accroître son importance pour la formation de la personnalité d'une personne en pleine croissance. Les idées principales qui sous-tendent le cours de mathématiques de 5e à 6e années sont une orientation culturelle générale du contenu, le développement intellectuel des élèves utilisant les mathématiques sur du matériel qui répond aux intérêts et aux capacités des enfants de 10 à 12 ans.

Le cours de mathématiques pour les classes 5 et 6 est une partie importante de l'éducation mathématique et du développement des écoliers. À ce stade, fondamentalement, l'apprentissage à compter sur un ensemble de nombres rationnels se termine, le concept de variable est formé et les premières connaissances sont données sur les techniques de résolution d'équations linéaires, l'apprentissage de la résolution de problèmes verbaux se poursuit, les compétences en constructions géométriques et les mesures sont améliorées et enrichies. Une attention particulière est accordée au développement de la capacité de raisonner, de faire des preuves simples et de justifier les actions accomplies. Parallèlement, les bases sont posées pour l'étude de cours systématiques de stéréométrie, de physique, de chimie et d'autres matières connexes.

Le cours de mathématiques pour les niveaux 5 et 6 fait partie intégrante de toutes les mathématiques scolaires. Par conséquent, la principale exigence pour sa construction est la structuration du contenu sur une base idéologique unique, qui, d'une part, est une continuation et un développement des idées mises en œuvre dans l'enseignement des mathématiques à l'école primaire et, d'autre part, sert à l'étude ultérieure des mathématiques au lycée.

Le développement de tous les contenus et lignes méthodologiques du cours de mathématiques primaires se poursuit : analyse numérique, algébrique, fonctionnelle, géométrique, logique, des données. Ils sont implémentés sur du matériel numérique, algébrique, géométrique.

Récemment, l'étude de la géométrie a été considérablement révisée. Le but de l'étude géométrie en 5e et 6e années, c'est la connaissance du monde qui nous entoure à travers le langage et les mathématiques. A l'aide de constructions et de mesures, l'élève identifie différents motifs géométriques, qu'il formule sous forme de proposition, d'hypothèse. L'aspect démonstratif de la géométrie est considéré d'un point de vue problématique : les étudiants sont inculqués à l'idée que de nombreux faits géométriques peuvent être découverts expérimentalement, mais que ces faits ne deviennent des vérités mathématiques que lorsqu'ils sont établis par des moyens acceptés en mathématiques.

Ainsi, le matériau géométrique de ce cours peut être caractérisé comme une géométrie d’activité visuelle. La formation est organisée comme un processus d'activité intellectuelle et pratique visant à développer des concepts spatiaux, des compétences visuelles, à élargir les horizons géométriques, au cours desquels les propriétés les plus importantes des figures géométriques sont obtenues par l'expérience et le bon sens.

La ligne de contenu « L'analyse des données ", qui combine trois domaines : éléments de statistique mathématique, combinatoire, théorie des probabilités. L’introduction de ce matériau a été dictée par la vie elle-même. Son étude vise à développer chez les écoliers à la fois une intuition probabiliste générale et des manières spécifiques d'évaluer les données. La tâche principale de ce lien est la formation d'un vocabulaire approprié, l'enseignement des techniques les plus simples pour collecter, présenter et analyser des informations, apprendre à résoudre des problèmes combinatoires en énumérant les options possibles, en créant des idées élémentaires sur la fréquence et la probabilité d'événements aléatoires.

Cependant, cette ligne n'est pas présente dans tous les manuels scolaires modernes de la 5e à la 6e année. Cette ligne est présentée de manière particulièrement détaillée et claire dans les manuels.

Algébrique Le matériel inclus dans le cours de mathématiques de la 5e à la 6e année constitue la base de l'étude systématique de l'algèbre au lycée. Les caractéristiques suivantes de l'étude de ce matériel algébrique peuvent être notées :

1. L'étude du matériel algébrique repose sur une base scientifique, en tenant compte des caractéristiques d'âge et des capacités des étudiants.

2. La formation de concepts algébriques et le développement des compétences correspondantes constituent un processus unique, construit sur un système détaillé d'exercices.

3. Le système d'exercices constitue un moyen fiable pour maîtriser le langage mathématique moderne, puisque ce langage est largement utilisé dans la formulation de diverses tâches. Par exemple, « Prouvez que cette inégalité est vraie : 29 2<1000».

4. L'amélioration des compétences informatiques est organiquement liée à l'étude du matériel algébrique.

L'utilisation de la notation des lettres permet de poser la question de la construction des formules. Les relations entre les quantités sont également spécifiées sous forme de tableaux et de graphiques, et les enfants sont formés à la transition d'une forme de spécification d'une relation à une autre. Un travail systématique avec des dépendances spécifiques garantit que les enfants sont prêts à étudier les fonctions au lycée.

Méthodes . Le cours de mathématiques pour les classes 5 et 6 est construit de manière inductive. Le contenu du matériel pédagogique oblige à utiliser des méthodes qui contribuent à la formation d'activités à la fois productives et reproductrices.

En 5e et 6e années, les méthodes d'enseignement suivantes sont le plus souvent utilisées :

Leçon . Les caractéristiques de la matière mathématique de la 5e à la 6e année (presque chaque leçon nécessite l'apprentissage de nouveaux faits sur le sujet), les exigences du programme et le rythme d'étude de la matière ont conduit au fait que le type de leçon le plus courant en ces classes sont combinées.

Citons-en plus Certaines fonctionnalités enseigner les mathématiques de la 5e à la 6e année :

· Aux premières étapes de l'étude des mathématiques en 5e année, les élèves répètent les concepts qu'ils connaissent de la 1re à la 4e année, mais cette répétition s'effectue à un nouveau niveau, en utilisant la terminologie et les symboles mathématiques. Ceci afin de poser les bases d'un langage mathématique, les bases d'une culture mathématique.

· Au cours des classes de 5e et 6e années, lors de la présentation de l'arithmétique et des débuts de l'algèbre, ils ont souvent recours à des définitions géométriques utilisant une ligne ou un rayon de coordonnées, ce qui rend l'apprentissage plus visuel, et donc plus accessible et compréhensible pour les élèves. De la même manière, par exemple, la comparaison des fractions ordinaires et décimales est étudiée.

· L'une des caractéristiques de ce cours est une présentation linéaire-concentrique du matériel, selon laquelle les étudiants reviennent à plusieurs reprises sur toutes les questions fondamentales, s'élevant à un nouveau niveau dans chaque passage ultérieur.

Par exemple, lors de l'étude du sujet « Décimaux et pourcentages », il y a une transition de l'ensemble des nombres entiers non négatifs à l'ensemble des nombres rationnels non négatifs ; Dans le même temps, la formation repose sur des algorithmes d'actions avec des nombres naturels connus des étudiants, et les connaissances et compétences acquises précédemment sont constamment utilisées.

· La première difficulté rencontrée par les élèves de cinquième année est de travailler avec le texte explicatif du manuel. La raison en est la technique de lecture insuffisante de certains enfants, un vocabulaire restreint, ainsi que le fait que des textes aussi volumineux n'étaient pas trouvés dans les manuels scolaires du primaire.

Tout au long de la période d'études en 5e et 6e années, l'enseignant de mathématiques doit développer systématiquement chez les enfants la capacité de lire, de comprendre un texte et de travailler avec celui-ci. Ce travail constitue la base nécessaire à l'étude réussie des cours systématiques d'algèbre et de géométrie dans les niveaux suivants.

2.4 Caractéristiques de la formation de concepts mathématiques dans les classes 5-6

Toutes les notions étudiées au primaire sont ensuite repensées à un niveau théorique supérieur (variable, équation, figure, etc.) ou approfondies et généralisées (la notion de nombre, les algorithmes des opérations arithmétiques, les lois des opérations arithmétiques, etc.).

Il n'est pas toujours possible ni même nécessaire de former des définitions intentionnellement : 1) le sexe est indiqué ; 2) sont indiquées les caractéristiques qui distinguent cette espèce (le concept étant défini) des autres espèces du genre le plus proche. Les étudiants apprennent sur une base visuelle et intuitive à comprendre la signification des caractéristiques essentielles et non essentielles afin de révéler l'essence du concept défini, c'est-à-dire qu'il suffit de se forger la bonne idée. Dans un cours de mathématiques destiné aux niveaux 5 et 6, ceci est souvent réalisé en utilisant ceinture je Yu soupe aux choux X descriptions - des phrases accessibles aux élèves qui évoquent en eux une image visuelle et les aident à comprendre le concept. Il n’est pas nécessaire ici de réduire le nouveau concept à ceux déjà étudiés. L'assimilation doit être portée à un niveau tel qu'à l'avenir, sans se souvenir de la description, l'étudiant puisse reconnaître l'objet lié à ce concept. Exemple, descriptions explicatives de polygone, polyèdre, distance, symétries, nombre naturel, etc.

La plupart des enfants de 5e année perçoivent le texte explicatif du manuel, la formulation des définitions et des règles, comme étant assez homogènes - il leur est difficile de trouver un concept définissable et déterminant, une indication des propriétés mathématiques d'un objet mathématique. C'est ce qui explique en grande partie les difficultés de mémorisation et de reproduction correcte des principes théoriques et des règles d'action : tous les mots semblent d'égale importance à l'étudiant (ou d'égale importance ?), et donc la mémorisation se fait purement mécaniquement, et la perte ou le remplacement passe inaperçu pour lui. .

L'essentiel lorsque l'on travaille avec des définitions en 5e et 6e années est de montrer aux élèves la différence entre les définitions et les autres phrases mises en gras dans le manuel ; leur apprendre à analyser la construction des définitions ; utiliser la méthode inductive pour former des définitions de concepts de base.

Si les élèves de la 5e à la 6e année acquièrent les compétences nécessaires pour travailler avec des définitions, comprennent un raisonnement logique simple et distinguent les structures logiques de diverses phrases mathématiques, ils seront alors en mesure d'étudier le cours de mathématiques du secondaire de manière plus consciente.

Les définitions sont considérées dans leur forme la plus simple à travers le genre et l'espèce. La formation du concept de preuve est basée sur des idées réelles sur le besoin de justification et le caractère persuasif du raisonnement. Cette étape initiale est progressivement remplacée par des idées sur une preuve adéquate aux mathématiques.

Après avoir analysé les manuels scolaires de la 5e à la 6e année, nous constatons qu'il n'y a pas de définitions axiomatiques, les concepts géométriques sont principalement définis par la construction, les concepts algébriques reçoivent principalement des définitions-accords, des descriptions explicatives.

Donnons un pourcentage comparatif des définitions données dans les manuels. Il y a 53% de définitions-accords, 20% - descriptions explicatives, 27% - définitions constructives, et dans les définitions-accords - 33%, descriptions explicatives - 32%, définitions constructives - 35%. Les différences s'expliquent par le grand nombre de concepts géométriques introduits.

Les concepts à ce stade de l’apprentissage doivent être introduits de manière concrète et inductive, en accordant une grande attention à la motivation de l’introduction. Pour maîtriser les concepts à cet âge, les psychologues recommandent de confier 10 à 12 tâches.

Regardons des exemples spécifiques.

Coin 2

Dans chacune des images, retrouvez et nommez les rayons ainsi que leurs origines. Qu'est-ce qu'une « poutre » ? Un rayon a-t-il un début ?

Vous savez ce qu'est un polygone (Fig. 8). Quels éléments d'un polygone pouvez-vous nommer ? (Côtés, sommets). Il s'avère que le polygone comporte d'autres éléments. Aujourd'hui, nous devons les étudier. Faites attention à la figure 4, vous voyez deux rayons avec une origine commune, ils forment ensemble une seule figure. Et afin de ne pas le diviser en parties, les anciens donnaient à cette figure un nom spécial - "angle".

Comment obtient-on une figure appelée angle ?

1. Prenez un point arbitraire (dans notre cas c'est le point O) ;

2. Deux faisceaux sont dessinés à partir de ce point (OA, OB).

Ainsi, angle Ils appellent une figure formée de deux rayons émanant d'un point (les enfants peuvent formuler eux-mêmes la définition !). Les rayons formant un angle sont appelés côtés de l’angle, et le point d’où ils émergent est appelé sommet de l’angle.

Dans notre figure, les côtés de l'angle sont les rayons OA et OB, et son sommet est le point O. Cet angle est noté comme suit :<АОВ. При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначать и одной буквой (название его вершины): <О.

Exercice 1 : Dans chacune des images (Fig. 1-Fig. 7), sélectionnez les angles et nommez-les correctement.

Tâche 2 : Choisissez le symbole correct pour les angles suivants.

UN)
B)
DANS)
G)
D)<С

Tâche 3 : Écrivez les symboles des angles suivants dans votre cahier. Et dessinez-les.

Tâche 4 : Dessinez des angles arbitraires :
Voyons comment les points d'un plan peuvent être localisés par rapport à un angle donné.

La figure montre l'angle F.

Les points C, D se trouvent à l’intérieur de l’angle F.

Les points X, Y se trouvent à l'extérieur de l'angle F.

Les points M, K sont des côtés de l'angle F.

Tâche 5 : Tracez l'angle O et tracez les points suivants :

A) A, B, C - coin intérieur O ;

B) D, F, E, K - sur les côtés de l'angle O ;

B) M, P, S, T - coin extérieur O.

Tâche 6 : Dessinez l'angle MOD et dessinez le rayon OT à l'intérieur. Nommez et étiquetez les angles dans lesquels ce rayon divise l'angle MOD.

Tâche 7 : Dessinez 4 rayons : OA, OB, OS, OD. Notez les noms des six angles dont les côtés sont ces rayons.

Plus grand diviseur commun.

Exercice 1 : Est-il vrai que:

A) 5 - diviseur 45 ; B) 16 - diviseur 8 ; Q) 17 est-il un diviseur de 172 ?

Tâche 2 : Nommez tous les diviseurs de nombres :

A) 6 ; B) 18 ; B) 125 ; D)19.

Tâche 3 : Choisissez le plus grand nombre :

A) 1, 5, 3, 8, 12, 4 ; B) 15, 30, 45, 90.

Tâche 4 : En combien de piles égales 36 noix peuvent-elles être divisées ?

Ensuite, l’enseignant pose des questions comme celles-ci (les élèves doivent se rappeler ce que sont un « nombre naturel » et un « diviseur de nombre naturel ») :

Quel nombre est appelé diviseur de cet nombre naturel ?

Le Père Noël dispose de 48 bonbons « Hirondelle » et de 36 bonbons « Cheburashka » ; il doit réaliser le plus grand nombre de cadeaux identiques pour les enfants en utilisant tous les bonbons.

Que devrait-il faire? Aujourd'hui, vous apprendrez comment aider rapidement le Père Noël.

1. Diviseurs 6 : 1, 2, 3, 6 - nombres naturels.

Diviseurs 18 : 1, 2, 3, 6, 18 - nombres naturels

2. Diviseurs 15 : 1, 3, 5, 15 - nombres naturels

Diviseurs 30: 1, 3, 5, 15, 2, 6, 10, 30 - nombres naturels

3. Diviseurs 40: 1, 2, 4, 5, 8, 10, 20, 40 sont des nombres naturels.

Diviseurs 18: 1, 2, 3, 6, 18 sont des nombres naturels.

Comme vous pouvez le constater, dans tous les cas, les diviseurs communs de deux nombres naturels sont identifiés, et le plus grand nombre naturel est sélectionné parmi ces diviseurs communs.

Revenons aider le Père Noël. En quel nombre égal de cadeaux 48 bonbons « hirondelle » peuvent-ils être divisés ? Pour répondre à cette question, vous devez écrire tous les diviseurs du nombre 48.

48: 1, 2, 3, 4, 6, 9, 12, 24, 48.

En quel nombre égal de cadeaux peut-on diviser 36 bonbons Cheburashka ? Pour répondre à cette question, vous devez écrire tous les diviseurs du nombre 36.

36: 1, 2, 3, 4, 6, 9, 12, 18, 36.

Mais le Père Noël doit faire des cadeaux absolument identiques, il doit donc choisir les diviseurs communs des nombres 48 et 36.

Facteurs communs de 48 et 36: 1, 2, 3. 6, 12.

En choisissant le plus grand nombre naturel parmi les diviseurs communs des nombres 48 et 36, le Père Noël composera le plus grand nombre de cadeaux identiques pour les enfants. Ce numéro sera le numéro 12.

Cela signifie que vous pouvez faire 12 cadeaux pour le Père Noël, dont chacun contiendra 4 bonbons « Hirondelle » (48:12 = 4) et 3 bonbons « Cheburashka » (36:12 = 3).

Ainsi, le plus grand nombre naturel pouvant être divisé sans reste est un Et b , appelé le plus grand diviseur commun de ces nombres .

Exercice 1. Trouvez tous les diviseurs communs des nombres :

A) 18 et 60 ; B) 72, 98 et 120 ; B) 35 et 88.

Tâche 2. Écrivez les diviseurs communs des nombres un Et b et trouvez leur plus grand diviseur commun si :

A) Diviseurs UN: 1, 2, 3, 4, 6, 9, 12, 18, 36

Diviseurs b : 1, 2. 3, 5, 6, 9, 10, 15, 18, 30. 45, 90

B) Diviseurs UN: 1, 2, 3. 6, 18

Diviseurs b : 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.

Tâche 3 : Trouver la factorisation première du plus grand diviseur commun des nombres un Et b , Si:

UN) UN =2·2·3·3 et b =2·3·3·5;

B) une = 5·5·7·7·7 et b = 3·5·7·7.

Tâche 4 : Trouvez le plus grand diviseur commun des nombres :

A) 12 et 18 ; B) 50 et 175.

Tâche 5 : Les gars à la fête du Nouvel An ont reçu les mêmes cadeaux. Tous les cadeaux contenaient ensemble 123 oranges et 82 pommes. Combien d’enfants étaient présents au sapin de Noël ?

chapitre 3
Enseignement expérimenté

Sur la base théorique présentée dans les chapitres précédents, une leçon a été élaborée et enseignée en 5e année de l'école secondaire Talitskaya du district de Falensky. Ce qui suit est un résumé de cette leçon.

Classe: 5.

Nombre de leçons par section: 26

Sujet de la leçon :"Actions. Fractions ordinaires.

Type de cours : leçon d'apprentissage de nouveau matériel.

Numéro de cours dans la section"Fractions ordinaires": 5

Objectifs:

Éducatif:

· créer les conditions permettant aux élèves de maîtriser les notions de fraction, de fraction commune, de numérateur et de dénominateur ;

· apprendre à utiliser les fractions pour résoudre divers problèmes.

Éducatif:

· développement de l'intérêt cognitif et d'un discours mathématique compétent ;

· développement de la pensée logique.

Éducatif:

· éducation à la discipline;

· éducation à la précision.

Équipement: une aide visuelle en forme de pomme coupée, des fiches avec une tâche (à distribuer avant le cours).

Littérature:.

Plan de cours:

1. Étape organisationnelle.

2. Actualisation des connaissances.

3. Étape d'apprentissage du nouveau matériel :

1) Introduction de la notion de part, moitié, tiers, trimestre.

2) Maîtriser la notion de partage.

3) Introduction de la notion de fraction.

4) Maîtriser la notion de fractions.

4. L'étape de consolidation des acquis.

5. Étape des devoirs

6. Résumer la leçon

Pendant les cours :

Tableau/cahier

1 .

Bonjour! Asseyez-vous les gars, s'il vous plaît ! Aujourd’hui, nous allons étudier les nombres spéciaux appelés fractions ordinaires.

"Date de"

Travail en classe.

Tout d’abord, rappelons-nous ce qu’est un nombre naturel ? A quoi servent les nombres naturels ? Droite.

Les nombres naturels sont utilisés pour compter les objets.

1) Imaginez que vous avez 5 pommes. Et vous devez les répartir également entre cinq amis. Combien de pommes chaque personne aura-t-elle ? Droite.

Et si maman achetait une pastèque et la coupait en 6 parts égales : pour les grands-parents, papa, deux enfants et elle-même, alors ces parts égales s'appelleront actions .

Puisque la pastèque était divisée en 6 parts, chacun recevait une « part de pastèque » ou « pastèque ».

Maintenant, veuillez dessiner dans votre cahier un segment AB de 5 cm de long.

Quelle proportion du segment AB sera un segment de 1 cm de long ?

Laissez chacun de vous avoir une pomme. Comment agirez-vous si je vous demande de couper la moitié d’une pomme ?

Celui qui divise la pomme en deux parties aura raison, car une part s'appelle une moitié,

- un tiers, et - un quart.

Par exemple, une demi-heure équivaut à 30 minutes, un quart à 15 minutes et un tiers à 20 minutes.

2) La pomme a été coupée en 8 tranches et 3 tranches ont été mangées. Combien reste-t-il d’actions ? Ces 5 lobes représentent la "pomme"

Encore un exemple. Et dans ce cas, combien d’actions reste-t-il ?

Faites maintenant attention au dessin. Le rectangle dessus est ombré, et quelle partie du rectangle n'est pas ombrée ?

Enregistrements du formulaire : appelé fractions ordinaires .

La partie supérieure de la fraction s’appelle le numérateur et la partie inférieure s’appelle le dénominateur. Revenons au dessin d'une pomme. Quel est le numérateur et quel est le dénominateur de cette fraction ?

Documents similaires

L'essence de la formation du concept, son schéma général et ses caractéristiques, les étapes de mise en œuvre et les voies possibles. Classification des concepts et sa méthodologie pour les disciplines mathématiques. La définition comme étape finale de la formation d'un concept, de ses variétés et de ses caractéristiques.
résumé, ajouté le 24/04/2009

Étapes de formation des concepts mathématiques lors de l'étude des mathématiques à l'école. Erreurs typiques que commettent les étudiants lors de la définition des concepts. Méthodes de travail sur les définitions mathématiques, étapes de leur étude. Techniques pédagogiques pour introduire des concepts.
résumé, ajouté le 07/03/2010

« Concept » dans la littérature psychologique, pédagogique, philosophique, pédagogique et méthodologique. Types et définitions de concepts mathématiques en mathématiques élémentaires. Le rôle et les fonctions de la classification dans la formation des concepts. Système de formation de concepts mathématiques.
thèse, ajoutée le 23/11/2008

Caractéristiques psychologiques et pédagogiques des élèves de la 5e à la 6e année, spécificités de la formation de concepts mathématiques en eux. Caractéristiques psychologiques de l'apprentissage des fractions. Analyse comparative des approches méthodologiques de l'étude du thème « Fractions », leurs avantages et inconvénients.
thèse, ajoutée le 22/07/2011

Fondements psychologiques et pédagogiques de la formation des concepts scientifiques. L'essence et les sources de l'apprentissage vitagène. Méthodes et techniques pour identifier et mettre à jour l’expérience vitale des étudiants. Formation de concepts scientifiques comme problème pédagogique. Types de concepts scientifiques.
thèse, ajoutée le 13/12/2009

article, ajouté le 15.09.2009

Caractéristiques de l'étude des mathématiques à l'école primaire selon la norme éducative de l'État fédéral pour l'enseignement primaire général. Le contenu des cours. Analyse des concepts mathématiques de base. L'essence d'une approche individuelle en didactique.
travail de cours, ajouté le 29/09/2016

Fondements psychologiques et pédagogiques du développement des élèves doués dans le processus d'enseignement des mathématiques. Caractéristiques méthodologiques de l'enseignement des mathématiques de la 5e à la 6e année, visant le développement des enfants surdoués. Mise en œuvre de ces objectifs dans les activités parascolaires.
thèse, ajoutée le 19/04/2011

Le problème de la compréhension des messages texte dans la recherche psycholinguistique et psychopédagogique. Idées modernes sur le texte dans les méthodes d'enseignement scolaire. Caractéristiques du vocabulaire des collégiens. Psychologie du processus de formation des concepts.
travail de cours, ajouté le 18/08/2011

Formation de concepts de fonctions trigonométriques inverses, ainsi que développement de méthodes pour enseigner ce sujet dans les écoles et les classes avec une étude approfondie des mathématiques. Utilisation des technologies de l'information dans l'étude des fonctions trigonométriques inverses.

			Tableau/cahier
1 .	Bonjour! Asseyez-vous les gars, s'il vous plaît ! Aujourd’hui, nous allons étudier les nombres spéciaux appelés fractions ordinaires.		"Date de" Travail en classe.
	Tout d’abord, rappelons-nous ce qu’est un nombre naturel ? A quoi servent les nombres naturels ? Droite.	Les nombres naturels sont utilisés pour compter les objets.
		1) Imaginez que vous avez 5 pommes. Et vous devez les répartir également entre cinq amis. Combien de pommes chaque personne aura-t-elle ? Droite. Et si maman achetait une pastèque et la coupait en 6 parts égales : pour les grands-parents, papa, deux enfants et elle-même, alors ces parts égales s'appelleront actions . Puisque la pastèque était divisée en 6 parts, chacun recevait une « part de pastèque » ou « pastèque ». Maintenant, veuillez dessiner dans votre cahier un segment AB de 5 cm de long. Quelle proportion du segment AB sera un segment de 1 cm de long ? Laissez chacun de vous avoir une pomme. Comment agirez-vous si je vous demande de couper la moitié d’une pomme ? Celui qui divise la pomme en deux parties aura raison, car une part s'appelle une moitié, - un tiers, et - un quart. Par exemple, une demi-heure équivaut à 30 minutes, un quart à 15 minutes et un tiers à 20 minutes. 2) La pomme a été coupée en 8 tranches et 3 tranches ont été mangées. Combien reste-t-il d’actions ? Ces 5 lobes représentent la "pomme" Encore un exemple. Et dans ce cas, combien d’actions reste-t-il ? Faites maintenant attention au dessin. Le rectangle dessus est ombré, et quelle partie du rectangle n'est pas ombrée ? Enregistrements du formulaire : appelé fractions ordinaires . La partie supérieure de la fraction s’appelle le numérateur et la partie inférieure s’appelle le dénominateur. Revenons au dessin d'une pomme. Quel est le numérateur et quel est le dénominateur de cette fraction ?

Mon secret

2.4 Caractéristiques de la formation de concepts mathématiques dans les classes 5-6

1.1 Concepts mathématiques, leur contenu et leur portée, classification des concepts

Envoyer votre bon travail dans la base de connaissances est simple. Utilisez le formulaire ci-dessous

Introduction

Chapitre 1 Fondamentaux des méthodes d'étude des concepts mathématiques

1.1 Concepts mathématiques, leur contenu et leur portée, classification des concepts

Un concept est une forme de réflexion sur un ensemble holistique de propriétés essentielles et non essentielles d'un objet.

Le contenu d'un concept s'identifie à sa définition, et sa portée se révèle à travers la classification. La classification est la division d'un ensemble en sous-ensembles qui satisfont aux exigences suivantes :

o doit être réalisé selon un seul critère ;

o les classes doivent être disjointes ;

o l'union de toutes les classes devrait donner l'ensemble complet ;

o la classification doit être continue (les classes doivent être les concepts d'espèce les plus proches par rapport au concept soumis à classification).

On distingue les types de classification suivants :

1. Selon une caractéristique modifiée. Les objets à classer peuvent avoir plusieurs caractéristiques, ils peuvent donc être classés de différentes manières.

Exemple. Le concept de « triangle ».

2. Dichotomique. Diviser la portée d'un concept en deux concepts spécifiques, l'un ayant une caractéristique donnée et l'autre non.

Exemple .

Soulignons les objectifs de la formation en classification :

1) développement de la pensée logique ;

2) en étudiant les différences entre les espèces, on se fait une idée plus précise du concept générique.

1.2 Définition des concepts mathématiques, concepts primaires qui expliquent la description

Définir un objet - choisir parmi ses propriétés essentielles telles et telles que chacune d'elles soit nécessaire, et toutes ensemble suffisantes pour distinguer cet objet des autres. Le résultat de cette action est enregistré dans la définition.

1.3 Façons de définir les concepts

Par structure logique les définitions sont divisées en conjonctives (les caractéristiques essentielles sont reliées par la conjonction « et ») et disjonctives (les caractéristiques essentielles sont reliées par la conjonction « ou »).

L'identification des caractéristiques essentielles enregistrées dans la définition et les connexions enregistrées entre elles est appelée analyse logique et mathématique de la définition .

Il existe une division des définitions en descriptives et constructives.

· À travers genre le plus proche et la différence entre les espèces. (Un losange est un parallélogramme dont les deux côtés adjacents sont égaux. Le concept générique est un parallélogramme, dont le concept défini se distingue par une différence spécifique).

· Définitions-accords- des définitions dans lesquelles les propriétés des concepts sont exprimées à l'aide d'égalités ou d'inégalités.

· Définitions via abstraction. Ils recourent à une telle définition d'un concept lorsqu'un autre est difficile ou impossible à mettre en œuvre (par exemple, un nombre naturel).

· Définition-négation- une définition qui fixe non pas la présence d'une propriété, mais son absence (par exemple, lignes parallèles).

1.4 Exigences méthodologiques pour la définition du concept

· Exigence scientifique.

· Exigence d'accessibilité.

· Exigence de commensurabilité (le volume du concept défini doit être égal au volume du concept définissant). La violation de cette exigence conduit à une définition soit très large, soit très étroite.

· La définition ne doit pas contenir de cercle vicieux.

· Les définitions doivent être claires, précises et ne pas contenir d'expressions métaphoriques.

· Minimum requis.

1.5 Introduction de concepts dans un cours de mathématiques scolaire

Lors de la formation de concepts, il est nécessaire d’organiser les activités des élèves pour maîtriser deux techniques logiques de base : subsumer un concept et tirer des conséquences du fait qu’un objet appartient à un concept.

Action englobant le concept a la structure suivante :

1) Sélection de toutes les propriétés enregistrées dans la définition.

2) Établir des liens logiques entre eux.

3) Vérifier si un objet a des propriétés sélectionnées et leurs connexions.

4) Obtenir une conclusion quant à l'appartenance d'un objet au champ d'application du concept.

Déduire des conséquences - c'est la sélection des caractéristiques essentielles d'un objet appartenant à un concept donné.

Il y a trois manières dans la méthodologie introduction aux concepts :

1) Concrètement inductif :

o Prise en compte de divers objets appartenant ou non au périmètre du concept.

o Identification des caractéristiques essentielles d'un concept basée sur la comparaison d'objets.

o Introduction du terme, formulation de la définition.

2) Abstrait-déductif :

o Introduction de la définition par l'enseignant.

o Prise en compte de cas particuliers et individuels.

o Formation de la capacité à subsumer un objet sous un concept et à en tirer des conséquences primaires.

1.6 Principales étapes de l'apprentissage d'une notion à l'école

Dans la littérature, il existe trois étapes principales de l'apprentissage des concepts à l'école :

1. Quand présentation du concept l'une des trois méthodes décrites ci-dessus est utilisée. Au cours de cette étape, vous devez considérer les éléments suivants :

· Tout d'abord, il est nécessaire de fournir une motivation pour introduire ce concept.

· Lors de la construction d'un système de tâches pour englober un concept, assurez-vous de la portée la plus complète du concept.

· Il est important de montrer que la portée d'un concept n'est pas un ensemble vide.

· Révéler le contenu du concept, travailler sur les fonctionnalités essentielles, mettre en avant celles qui ne sont pas essentielles.

· En plus de connaître la définition, il est souhaitable que les élèves aient une compréhension visuelle du concept.

· Maîtriser la terminologie et le symbolisme.

2. Au stade maîtriser la définition Le travail se poursuit sur la mémorisation de la définition. Ceci peut être réalisé en utilisant les techniques suivantes :

· Écrire les définitions dans un cahier.

· Prononcer, souligner ou une sorte de numérotation des propriétés essentielles.

· Utilisation de contre-exemples pour respecter les règles de commensurabilité.

· Sélection des mots manquants dans la définition, recherche de mots supplémentaires.

· Apprendre à donner des exemples et des contre-exemples.

· Apprendre à appliquer la définition dans les situations les plus simples, mais tout à fait typiques, puisque la répétition répétée de la définition en dehors de la résolution de problèmes est inefficace.

· Signaler la possibilité de définitions différentes, prouver leur équivalence, mais en choisir une seule pour la mémorisation.

· Apprendre à construire une définition, utiliser pour cela la compilation de généalogies, en expliquant la structure logique ; présenter les règles de construction d’une définition.

· Donnez des paires de concepts similaires en comparaison et en contraste.

Ainsi, chaque propriété essentielle du concept utilisé dans la définition à ce stade devient un objet d'étude particulier.

· Application de la définition à des situations plus complexes.

· Inclusion d'un nouveau concept dans des connexions logiques, des relations avec d'autres concepts (par exemple, comparaison de généalogies, classifications).

· Il est conseillé de montrer que la définition n'est pas donnée pour elle-même, mais pour qu'elle « fonctionne » lors de la résolution de problèmes et de la construction d'une nouvelle théorie.

Chapitre 2 Caractéristiques psychologiques et pédagogiques de l'enseignement des mathématiques de la 5e à la 6e année

2.1 Caractéristiques de l'activité cognitive

Chapitre 1
Fondamentaux des méthodes d'étude des concepts mathématiques

Chapitre 2
Caractéristiques psychologiques et pédagogiques de l'enseignement des mathématiques de la 5e à la 6e année