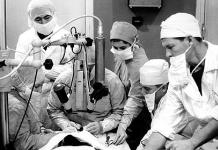
Lors de la fabrication ou de la transformation de pièces en bois, il est dans certains cas nécessaire de déterminer où se trouve leur centre géométrique. Si la pièce a une forme carrée ou rectangulaire, ce n'est pas difficile à faire. Il suffit de relier les coins opposés avec des diagonales qui se couperont exactement au centre de notre figure.
Pour les produits ayant la forme d’un cercle, cette solution ne fonctionnera pas, puisqu’ils n’ont pas de coins, et donc pas de diagonales. Dans ce cas, une autre approche est nécessaire, basée sur des principes différents.

Et ils existent, et sous de nombreuses variantes. Certains d'entre eux sont assez complexes et nécessitent plusieurs outils, d'autres sont faciles à mettre en œuvre et ne nécessitent pas tout un ensemble d'appareils.
Nous allons maintenant examiner l'un des plus des moyens simples Trouver le centre du cercle en utilisant uniquement une règle et un crayon ordinaires.

La séquence de recherche du centre du cercle :

1. Tout d’abord, nous devons nous rappeler qu’une corde est une ligne droite reliant deux points d’un cercle et ne passant pas par le centre du cercle. Ce n'est pas du tout difficile à reproduire : il suffit de placer une règle n'importe où sur le cercle pour qu'elle coupe le cercle en deux endroits, et de tracer une ligne droite avec un crayon. Le segment à l’intérieur du cercle sera la corde.
En principe, vous pouvez vous en sortir avec un seul accord, mais pour augmenter la précision de l'établissement du centre du cercle, nous en dessinerons au moins quelques-uns, voire mieux - 3, 4 ou 5 accords de longueurs différentes. Cela nous permettra de niveler les erreurs dans nos constructions et de faire face avec plus de précision à la tâche.

2. Ensuite, en utilisant la même règle, nous trouvons les milieux des accords que nous avons reproduits. Par exemple, si longueur totale une corde mesure 28 cm, alors son centre sera en un point situé à 14 cm en ligne droite de l'intersection de la corde avec le cercle.
Après avoir ainsi déterminé les centres de toutes les cordes, nous traçons des lignes perpendiculaires à travers elles, en utilisant, par exemple, triangle rectangle.

3. Si nous continuons maintenant ces lignes droites perpendiculairement aux cordes en direction du centre du cercle, alors elles se couperont approximativement en un point, qui sera le centre souhaité du cercle.

4. Après avoir établi l'emplacement du centre de notre cercle particulier, nous pouvons utiliser ce fait à diverses fins. Ainsi, si vous placez la jambe d'un compas de menuisier à cet endroit, vous pouvez tracer un cercle idéal, puis découper un cercle à l'aide de l'outil de coupe approprié et du point central du cercle que nous avons déterminé.

Objectifs:

consolider les notions de « cercle » et de « cercle » chez les élèves ; en dériver la notion de « rayon de cercle » ; apprendre à construire des cercles d'un rayon donné ; développer la capacité de raisonner et d’analyser.

UUD personnelle :
formulaire attitude positive aux cours de mathématiques ;
intérêt pour les activités de recherche sur le sujet;

Tâches méta-sujets

UUD réglementaire :
accepter et sauvegarder la tâche d'apprentissage ;
en collaboration avec l'enseignant et la classe, trouver plusieurs solutions ;

UUD cognitive :
formulation et solution de problèmes :
identifier et formuler le problème de manière indépendante ;
enseignement général:
trouver les informations nécessaires dans le manuel ;
construire un cercle d'un rayon donné à l'aide d'un compas ;
casse-tête:
former la notion de « rayon » ;
effectuer une classification, une comparaison ;
formuler des conclusions de manière indépendante ;

UUD de communication :
participer activement au travail d'équipe, en utilisant des moyens verbaux ;
argumenter votre point de vue ;

Compétences en matière :
identifier caractéristiques essentielles la notion de « rayon de cercle » ;
construire des cercles avec des rayons différents ;
reconnaître les rayons dans un dessin.

Pendant les cours

Motivation pour les activités d'apprentissage

- Vérifions si tout le monde est prêt pour le cours ?

« Entrée émotionnelle dans la leçon » :

Souriez comme le soleil.

Froncer les sourcils comme des nuages

Pleure comme la pluie

Soyez surpris comme si vous voyiez un arc-en-ciel

Maintenant, répétez après moi

Jeu "Écho Amical"

2.Mise à jour des connaissances

Comptage verbal

a) 60-40 36+12 10+20 58-12 90-50 31+13

Démêlez le motif. Continuez le rang.

Réponse : 20, 48,30,46,40,44 50,42

b) Résoudre le problème :

1. Le premier jour, le magasin a vendu 42 kg de fruits et le deuxième jour, 2 kg de plus. Combien de kilos ont été vendus le deuxième jour ?

Ce qu'il faut changer pour que le problème puisse être résolu en 2 étapes.

Balles - 16 pièces.

Cordes à sauter – 28 pcs.

Trouvez une solution à ce problème.

28-16 28+16

Changez la question pour que le problème soit résolu par soustraction.

3. Mise en scène tâche éducative

1. Nommez les formes géométriques

Boule ovale à circonférence de cercle

Quel chiffre est l'intrus ?

Quel est le point commun entre ces chiffres ? (Cercle, cercle, balle ont même forme)

Quelle est la différence?

2.B

Quels points appartiennent au cercle ? Quels points se trouvent en dehors du cercle ?

Que signifie le point O ? (au centre du cercle)

Quel est le nom du segment OB ?

Combien de rayons peut-on tracer dans un cercle ?

Quel segment n'est pas un rayon ? Pourquoi?

Que peut-on conclure ?

Conclusion : tous les rayons ont la même longueur .

3. Combien de cercles y a-t-il sur l’image ?

En quoi les cercles sont-ils différents ? (taille)

Qu'est-ce qui détermine la taille d'un cercle ?

Que peut-on conclure ?

Conclusion : plus le cercle est grand, plus son rayon est grand.

Déterminez le sujet de la leçon.

Sujet: Construire un cercle d'un rayon donné à l'aide d'un compas.

Quelles tâches pouvons-nous nous fixer pour cette leçon ?

4. Travailler sur le sujet

a) Construire un cercle.

Ce qu'il faut savoir pour dessiner un cercle taille donnée?

Tracez un cercle d'un rayon de 3 cm.

b) Préparation à les activités du projet

1) Regardez la photo

De quelles formes se compose un papillon ? Des cercles de même rayon ?

2) Travaillez en binôme.

Rétablir l'ordre des étapes du projet.

Présentation ou démonstration de projet

Concept (faire un croquis)

Construire des chiffres pour mettre en œuvre le plan

Considérez quel rayon les formes devraient avoir

c) Travailler sur le projet.

Travailler en groupe selon l'algorithme compilé

§ 1 Cercle. Concepts de base

En mathématiques, il existe des phrases qui expliquent la signification d’un nom ou d’une expression particulière. De telles phrases sont appelées définitions.

Définissons la notion de cercle. Un cercle est une figure géométrique constituée de tous les points du plan situés sur distance donnéeà partir de ce point.

Ce point, appelons-le point O, est appelé le centre du cercle.

Le segment reliant le centre à n’importe quel point du cercle est appelé rayon du cercle. Il existe de nombreux segments de ce type qui peuvent être dessinés, par exemple OA, OB, OS. Ils auront tous la même longueur.

Un segment reliant deux points d’un cercle s’appelle une corde. MN est la corde du cercle.

La corde passant par le centre du cercle s’appelle le diamètre. AB est le diamètre du cercle. Le diamètre est constitué de deux rayons, ce qui signifie que la longueur du diamètre est le double du rayon. Le centre d'un cercle est le milieu de n'importe quel diamètre.

Deux points quelconques sur un cercle le divisent en deux parties. Ces parties sont appelées arcs de cercle.

ANB et AMB sont des arcs de cercle.

La partie du plan délimitée par un cercle s’appelle un cercle.

Pour représenter un cercle dans un dessin, une boussole est utilisée. Le cercle peut également être tracé au sol. Pour ce faire, utilisez simplement une corde. Fixez une extrémité de la corde à un piquet enfoncé dans le sol et tracez un cercle avec l'autre extrémité.

§ 2 Constructions avec compas et règle

En géométrie, de nombreuses constructions peuvent être réalisées en utilisant uniquement un compas et une règle sans divisions d'échelle.

En utilisant uniquement une règle, vous pouvez tracer une ligne droite arbitraire, ainsi qu'une ligne droite arbitraire passant par un point donné, ou une ligne droite passant par deux points donnés.

Une boussole permet de tracer un cercle de rayon arbitraire, ainsi qu'un cercle dont le centre est en un point donné et le rayon est égal à un segment donné.

Séparément, chacun de ces outils permet de réaliser les constructions les plus simples, mais avec l'aide de ces deux outils on peut déjà réaliser des opérations plus complexes, par exemple,

résoudre des problèmes de construction tels que

Construire un angle égal à celui donné,

Construire un triangle avec les côtés donnés,

Divisez le segment en deux

Par un point donné tracez une ligne perpendiculaire à la ligne donnée, etc.

Considérons le problème.

Tâche : Sur un rayon donné, depuis son début, tracez un segment égal à celui donné.

Étant donné un rayon OS et un segment AB. Il faut construire un segment OD égal au segment AB.

A l'aide d'un compas, on construit un cercle de rayon, égal à la longueur segment AB, avec le centre au point O. Ce cercle coupera le rayon OS donné à un moment donné D. Le segment OD est le segment requis.

Liste de la littérature utilisée :

1. Géométrie. 7e à 9e années : manuel. pour l'enseignement général organisations / L.S. Atanasyan, V.F. Butouzov, S.B. Kadomtsev et al. - M. : Education, 2013. - 383 p. : ill.
2. Gavrilova N.F. Développements de cours en géométrie 7e année. - M. : « VAKO », 2004. - 288 p. - (Pour aider le professeur de l'école).
3. Belitskaïa O.V. Géométrie. 7e année. Partie 1. Essais. – Saratov : Lycée, 2014. – 64 p.

Une phrase qui explique la signification d'une expression ou d'un nom particulier est appelée définition. Nous avons déjà rencontré des définitions, par exemple avec la définition d'un angle, d'angles adjacents, d'un triangle isocèle, etc. Donnons une définition d'un autre figure géométrique- des cercles.

Définition

Ce point est appelé centre du cercle, et le segment reliant le centre à n'importe quel point du cercle est rayon du cercle(Fig. 77). De la définition d'un cercle, il résulte que tous les rayons ont la même longueur.

Riz. 77

Un segment reliant deux points d'un cercle s'appelle sa corde. Une corde passant par le centre d'un cercle s'appelle son diamètre.

Sur la figure 78, les segments AB et EF sont les cordes du cercle, le segment CD est le diamètre du cercle. Évidemment, le diamètre d’un cercle est le double de son rayon. Le centre d'un cercle est le milieu de n'importe quel diamètre.

Riz. 78

Deux points quelconques sur un cercle le divisent en deux parties. Chacune de ces parties est appelée un arc de cercle. Sur la figure 79, ALB et AMB sont des arcs délimités par les points A et B.

Riz. 79

Pour représenter un cercle dans un dessin, utilisez boussole(Fig. 80).

Riz. 80

Pour tracer un cercle au sol, vous pouvez utiliser une corde (Fig. 81).

Riz. 81

La partie du plan délimitée par un cercle est appelée cercle (Fig. 82).

Riz. 82

Constructions avec compas et règle

Nous avons déjà traité des constructions géométriques : nous avons tracé des lignes droites, tracé des segments égaux aux données, dessiné des angles, des triangles et d'autres figures. En même temps, nous avons utilisé une règle à échelle, un compas, un rapporteur et une équerre à dessin.

Il s'avère que de nombreuses constructions peuvent être réalisées en utilisant uniquement un compas et une règle sans divisions d'échelle. Par conséquent, en géométrie, on distingue particulièrement les tâches de construction qui peuvent être résolues en utilisant uniquement ces deux outils.

Que peux-tu faire avec eux? Il est clair que la règle permet de tracer une ligne droite arbitraire, ainsi que de construire une ligne droite passant par deux points donnés. À l'aide d'une boussole, vous pouvez tracer un cercle de rayon arbitraire, ainsi qu'un cercle dont le centre est en un point donné et le rayon est égal à un segment donné. En effectuant ces opérations simples, nous pouvons résoudre de nombreux problèmes de construction intéressants :

construire un angle égal à celui donné ;
passant par un point donné, tracez une ligne perpendiculaire à la ligne donnée ;
diviser ce segment en deux et d'autres tâches.

Commençons par une tâche simple.

Tâche

Sur un rayon donné, depuis son début, tracez un segment égal à celui donné.

Solution

Représentons les chiffres donnés dans l'énoncé du problème : rayon OS et segment AB (Fig. 83, a). Ensuite, à l'aide d'un compas, on construit un cercle de rayon AB de centre O (Fig. 83, b). Ce cercle coupera le rayon OS en un point D. Le segment OD est celui requis.

Riz. 83

Exemples de problèmes de construction

Construire un angle égal à un angle donné

Tâche

Soustrayez un angle d'un rayon donné égal à un angle donné.

Solution

Cet angle avec le sommet A et le rayon OM sont représentés sur la figure 84. Il faut construire un angle égal à l'angle A, pour qu'un de ses côtés coïncide avec le rayon OM.

Riz. 84

Traçons un cercle de rayon arbitraire dont le centre est au sommet A de l'angle donné. Ce cercle coupe les côtés de l'angle aux points B et C (Fig. 85, a). Puis on trace un cercle de même rayon dont le centre est à l'origine de ce rayon OM. Il coupe le faisceau au point D (Fig. 85, b). Après cela, nous construirons un cercle de centre D dont le rayon est égal à BC. Les cercles de centres O et D se coupent en deux points. Notons l'un de ces points par la lettre E. Montrons que l'angle MOE est celui recherché.

Riz. 85

Considérons les triangles ABC et ODE. Les segments AB et AC sont les rayons d'un cercle de centre A, et les segments OD et OE sont les rayons d'un cercle de centre O (voir Fig. 85, b). Puisque par construction ces cercles ont des rayons égaux, alors AB = OD, AC = OE. Également par construction BC = DE.

Donc Δ ABC = Δ ODE sur trois côtés. Par conséquent, ∠DOE = ∠BAC, c'est-à-dire que l'angle construit MOE est égal à l'angle A donné.

La même construction peut être réalisée au sol si vous utilisez une corde à la place d’un compas.

Construire une bissectrice d'angle

Tâche

Construire la bissectrice de l’angle donné.

Solution

Cet angle BAC est représenté sur la figure 86. Traçons un cercle de rayon arbitraire dont le centre est le sommet A. Il coupera les côtés de l'angle aux points B et C.

Riz. 86

Ensuite, nous dessinons deux cercles de même rayon BC avec des centres aux points B et C (seules des parties de ces cercles sont représentées sur la figure). Ils se croiseront en deux points, dont au moins un se trouve à l’intérieur du coin. Notons-le par la lettre E. Montrons que le rayon AE est la bissectrice de l'angle donné BAC.

Considérons les triangles ACE et ABE. Ils sont égaux sur trois côtés. En fait, AE - côté commun; AC et AB sont égaux aux rayons d'un même cercle ; CE = BE par construction.

De l'égalité des triangles ACE et ABE il résulte que ∠CAE = ∠BAE, c'est-à-dire que le rayon AE est la bissectrice de l'angle donné BAC.

Commentaire

Est-il possible de diviser un angle donné en deux angles égaux à l’aide d’un compas et d’une règle ? Il est clair que c'est possible - pour ce faire, vous devez tracer la bissectrice de cet angle.

Cet angle peut également être divisé en quatre angles égaux. Pour ce faire, vous devez le diviser en deux, puis diviser à nouveau chaque moitié en deux.

Est-il possible de diviser un angle donné en trois angles égaux à l’aide d’un compas et d’une règle ? Cette tâche, appelée problèmes de trisection d'angle, a attiré l'attention des mathématiciens depuis de nombreux siècles. Ce n'est qu'au XIXe siècle qu'il a été prouvé qu'une telle construction était impossible sous un angle arbitraire.

Construction de lignes perpendiculaires

Tâche

Étant donné une ligne droite et un point dessus. Construire une droite passant par un point donné et perpendiculaire à une droite donnée.

Solution

Une droite donnée a et un point donné M appartenant à cette droite sont représentés sur la figure 87.

Riz. 87

Sur les rayons de la droite a, issus du point M, on trace des segments égaux MA et MB. Ensuite, nous construisons deux cercles de centres A et B de rayon AB. Ils se croisent en deux points : P et Q.

Traçons une droite passant par le point M et l'un de ces points, par exemple la droite MR (voir Fig. 87), et prouvons que cette droite est celle désirée, c'est-à-dire qu'elle est perpendiculaire à la droite donnée a .

En fait, puisque la médiane PM du triangle isocèle RAB est aussi la hauteur, alors PM ⊥ a.

Construire le milieu d'un segment

Tâche

Construisez le milieu de ce segment.

Solution

Soit AB le segment donné. Construisons deux cercles de centres A et B de rayon AB. Ils se coupent aux points P et Q. Traçons une droite PQ. Le point O de l'intersection de cette droite avec le segment AB est le milieu souhaité du segment AB.

En fait, les triangles APQ et BPQ sont égaux sur trois côtés, donc ∠1 =∠2 (Fig. 89).

Riz. 89

Par conséquent, le segment PO est la bissectrice du triangle isocèle ARB, et donc la médiane, c'est-à-dire que le point O est le milieu du segment AB.

Tâches

143. Lesquels des segments représentés sur la figure 90 sont : a) les cordes du cercle ; b) les diamètres d'un cercle ; c) les rayons du cercle ?

Riz. 90

144. Les segments AB et CD sont les diamètres d'un cercle. Montrer que : a) les accords BD et AC sont égaux ; b) les accords AD et BC sont égaux ; c) ∠MAUVAIS = ∠BCD.

145. Le segment MK est le diamètre d'un cercle de centre O, et MR et RK sont des cordes égales de ce cercle. Trouvez ∠POM.

146. Les segments AB et CD sont les diamètres d'un cercle de centre O. Trouvez le périmètre du triangle AOD si l'on sait que CB = 13 cm, AB = 16 cm.

147. Sur un cercle de centre O, les points A et B sont marqués de telle sorte que l'angle AOB soit un angle droit. Le segment BC est le diamètre d'un cercle. Montrer que les accords AB et AC sont égaux.

148. Deux points A et B sont donnés sur une droite. Sur la continuation du rayon BA A, disposer un segment BC de telle sorte que BC = 2AB.

149. Étant donné une droite a, un point B qui ne s'y trouve pas et un segment PQ. Construisez le point M sur la droite a de telle sorte que BM = PQ. Un problème a-t-il toujours une solution ?

150. Étant donné un cercle, un point A qui ne s'y trouve pas et un segment PQ. Construisez un point M sur le cercle tel que AM = PQ. Un problème a-t-il toujours une solution ?

151. Étant donné un angle aigu BAC et un rayon XY. Construisez l’angle YXZ de telle sorte que ∠YXZ = 2∠BAC.

152. Daniel angle obtus AOB. Construisez le rayon OX de telle sorte que les angles HOA et HOB soient des angles obtus égaux.

153. Étant donné une droite a et un point M qui ne s'y trouve pas. Construire une droite passant par le point M et perpendiculaire à la droite a.

Solution

Construisons un cercle avec un centre en un point donné M, coupant une ligne donnée a en deux points, que nous désignons par les lettres A et B (Fig. 91). Ensuite nous construirons deux cercles de centres A et B passant par le point M. Ces cercles se coupent au point M et en un autre point, que nous désignerons par la lettre N. Traçons une droite MN et prouvons que cette droite est la droite souhaitée un, c’est-à-dire qu’il est perpendiculaire à la droite a.

Riz. 91

En fait, les triangles AMN et BMN sont égaux sur trois côtés, donc ∠1 = ∠2. Il s'ensuit que le segment MC (C est le point d'intersection des droites a et MN) est la bissectrice du triangle isocèle AMB, et donc sa hauteur. Ainsi, MN ⊥ AB, c'est-à-dire MN ⊥ a.

154. Étant donné un triangle ABC. Construire : a) bissectrice AK ; b) VM médiane ; c) hauteur CH du triangle. 155. À l'aide d'un compas et d'une règle, construisez un angle égal à : a) 45° ; b) 22°30".

Réponses aux problèmes

152. Instruction. Tout d’abord, construisons la bissectrice de l’angle AOB.