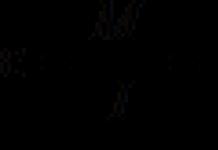Intégrale définie comme limite de la somme intégrale

ne peut exister (c'est-à-dire avoir une certaine valeur finale) que si les conditions sont remplies

Si au moins une de ces conditions n’est pas respectée, la définition perd son sens. En effet, dans le cas d'un segment infini, par exemple [ un; ) il ne peut pas être divisé en P. parties de longueur finie
, qui tendrait par ailleurs vers zéro avec une augmentation du nombre de segments. Dans le cas d'illimité à un moment donné Avec[un; b] l'exigence de sélection arbitraire de points n'est pas respectée sur segments partiels – ne peut pas être sélectionné =Avec, puisque la valeur de la fonction à ce stade n'est pas définie. Cependant, même dans ces cas, il est possible de généraliser le concept d’intégrale définie en introduisant un autre passage à la limite. Les intégrales sur des intervalles infinis et sur des fonctions discontinues (illimitées) sont appelées pas le vôtre.

Définition.

Laissez la fonction
est défini sur l'intervalle [ un; ) et est intégrable sur tout intervalle fini [ un; b], c'est à dire. existe
pour tout le monde b > un. Limite de type
appelé intégrale impropre premier type (ou une intégrale impropre sur un intervalle infini) et désignent
.

Ainsi, par définition,
=
.

Si la limite à droite existe et est finie, alors l'intégrale impropre
appelé convergent . Si cette limite est infinie, ou n'existe pas du tout, alors on dit que l'intégrale impropre diverge .

De même, on peut introduire la notion d’intégrale impropre de la fonction
le long de l'intervalle (– ; b]:

=
.

Et l'intégrale impropre de la fonction
sur l'intervalle (– ; +) est défini comme la somme des intégrales introduites ci-dessus :

=
+
,

Où UN– point arbitraire. Cette intégrale converge si les deux termes convergent, et diverge si au moins un des termes diverge.

D'un point de vue géométrique, l'intégrale
,
, détermine la valeur numérique de l'aire d'un trapèze curviligne infini délimité au dessus par le graphique de la fonction
, gauche – tout droit
, d’en bas – par l’axe OX. La convergence de l'intégrale signifie l'existence d'une aire finie d'un tel trapèze et son égalité à la limite de l'aire d'un trapèze curviligne à paroi droite mobile
.

Au cas d’une intégrale à limite infinie, on peut généraliser Formule de Newton-Leibniz:

=
= F( + ) – F( un),

où F( + ) =
. Si cette limite existe, alors l’intégrale converge, sinon elle diverge.

Nous avons envisagé une généralisation du concept d'intégrale définie au cas d'un intervalle infini.

Considérons maintenant une généralisation pour le cas d'une fonction illimitée.

Définition

Laissez la fonction
est défini sur l'intervalle [ un; b), est illimité dans certains voisinages du point b, et est continu sur n'importe quel intervalle
, où >0 (et donc intégrable sur cet intervalle, c'est-à-dire
existe). Limite de type
appelé intégrale impropre du deuxième type (ou une intégrale impropre d'une fonction illimitée) et est noté
.

Ainsi, l’intégrale impropre de l’illimité au point b les fonctions existent par définition

=
.

Si la limite à droite existe et est finie, alors l'intégrale s'appelle convergent. S’il n’y a pas de limite finie, alors l’intégrale impropre est appelée divergent.

De même, on peut définir l'intégrale impropre de la fonction
ayant une discontinuité infinie au point UN:

=
.

Si la fonction
a un espace infini au point intérieur Avec
, alors l'intégrale impropre est définie comme suit

=
+
=
+
.

Cette intégrale converge si les deux termes convergent, et diverge si au moins un terme diverge.

D'un point de vue géométrique, l'intégrale impropre d'une fonction illimitée caractérise également l'aire d'un trapèze courbe illimité :

Puisqu'une intégrale impropre est dérivée du passage à la limite d'une intégrale définie, toutes les propriétés d'une intégrale définie peuvent être transférées (avec des raffinements appropriés) à des intégrales impropres du premier et du deuxième type.

Dans de nombreux problèmes qui conduisent à des intégrales impropres, il n'est pas nécessaire de savoir à quoi cette intégrale est égale, il suffit simplement de vérifier sa convergence ou sa divergence. Pour cela, ils utilisent signes de convergence. Signes de convergence d'intégrales impropres :

1) Signe de comparaison.

Que ce soit pour tout le monde X

. Puis si
converge, puis converge
, et

. Si
diverge, puis diverge et
.

2) Si converge
, puis converge et
(la dernière intégrale dans ce cas s'appelle absolument convergent).

Les signes de convergence et de divergence des intégrales impropres de fonctions illimitées sont similaires à ceux formulés ci-dessus.

Exemples de résolution de problèmes.

Exemple 1.

UN)
; b)
; V)

G)
; d)
.

Solution.

a) Par définition on a :

.

b) De même

Cette intégrale converge donc et est égale à .

c) Par définition
=
+
, et UN– nombre arbitraire. Mettons dans notre cas
, alors on obtient :

Cette intégrale converge.

Cela signifie que cette intégrale diverge.

e) Considérons
. Pour trouver la primitive de l'intégrande, il faut appliquer la méthode de l'intégration par parties. On obtient alors :

Puisque ni l'un ni l'autre
, ni
n'existe pas, alors n'existe pas et

Cette intégrale diverge donc.

Exemple 2.

Étudier la convergence de l’intégrale en fonction de la P..

Solution.

À
nous avons:

Si
, Que
Et . L’intégrale diverge donc.

Si
, Que
, UN
, Alors

= ,

L’intégrale converge donc.

Si
, Que

par conséquent, l’intégrale diverge.

Ainsi,

Exemple 3.

Calculer l'intégrale impropre ou établir sa divergence :

UN)
; b)
; V)
.

Solution.

a) Intégrale
est une intégrale impropre de la seconde espèce, puisque l'intégrande
pas limité à un moment donné

. Alors, par définition,

.

L'intégrale converge et est égale à .

b) Considérez
. Ici aussi, l'intégrande n'est pas limité au point
. Cette intégrale est donc impropre de seconde espèce et, par définition,

L’intégrale diverge donc.

c) Considérez
. Intégrande
souffre d'un écart infini en deux points :
Et
, dont le premier appartient à l'intervalle d'intégration
. Par conséquent, cette intégrale est une intégrale impropre de la seconde espèce. Alors, par définition

=

=

.

L’intégrale converge donc et est égale à
.

Intégrales impropres du premier type. Essentiellement, il s'agit de la même intégrale définie, mais dans les cas où les intégrales ont des limites d'intégration supérieures ou inférieures infinies, ou les deux limites d'intégration sont infinies.

Intégrales impropres du deuxième type. Essentiellement, il s'agit de la même intégrale définie, mais dans les cas où l'intégrale est extraite de fonctions illimitées, l'intégrande en un nombre fini de points n'a pas de segment fini d'intégration, se tournant vers l'infini.

En comparaison. Lors de l'introduction du concept d'intégrale définie, il a été supposé que la fonction F(X) est continue sur l'intervalle [ un, b], et le segment d'intégration est fini, c'est-à-dire qu'il est limité par des nombres et non par l'infini. Certaines tâches conduisent à la nécessité d'abandonner ces restrictions. C'est ainsi qu'apparaissent les intégrales impropres.

Signification géométrique de l'intégrale impropre Cela s'avère tout simplement. Dans le cas où le graphique d'une fonction oui = F(X) est au dessus de l'axe Bœuf, l'intégrale définie exprime l'aire d'un trapèze curviligne délimité par une courbe oui = F(X) , axe des x et ordonnées X = un , X = b. À son tour, l'intégrale impropre exprime l'aire d'un trapèze curviligne illimité (infini) enfermé entre les lignes oui = F(X) (dans l'image ci-dessous - rouge), X = un et l'axe des abscisses.

Les intégrales impropres sont définies de la même manière pour d'autres intervalles infinis :

L'aire d'un trapèze courbe infini peut être un nombre fini, auquel cas l'intégrale impropre est dite convergente. L'aire peut aussi être infinie, et dans ce cas l'intégrale impropre est appelée divergente.

Utiliser la limite d'une intégrale au lieu de l'intégrale impropre elle-même. Afin d'évaluer l'intégrale impropre, vous devez utiliser la limite de l'intégrale définie. Si cette limite existe et est finie (non égale à l'infini), alors l'intégrale impropre est appelée convergente, et sinon, divergente. La tendance d'une variable sous le signe limite dépend du fait qu'il s'agit d'une intégrale impropre du premier type ou du deuxième type. Découvrons-le maintenant.

Intégrales impropres du premier type - avec des limites infinies et leur convergence

Intégrales incorrectes avec limite supérieure infinie

Ainsi, l’écriture d’une intégrale impropre diffère de l’intégrale définie habituelle en ce sens que la limite supérieure d’intégration est infinie.

Définition. Une intégrale impropre avec une limite supérieure infinie d'intégration d'une fonction continue F(X) dans l'intervalle de un avant ∞ la limite de l'intégrale de cette fonction avec la limite supérieure d'intégration est appelée b et la limite inférieure d'intégration un à condition que la limite supérieure d'intégration croisse sans limite, c'est à dire.

.

Si cette limite existe et est égale à un nombre plutôt qu’à l’infini, alors une intégrale impropre est dite convergente, et le nombre auquel la limite est égale est pris comme valeur. Sinon une intégrale impropre est appelée divergente et aucun sens ne lui est attribué.

Exemple 1. Calculer l'intégrale impropre(s'il converge).

Solution. Sur la base de la définition de l’intégrale impropre, nous trouvons

Puisque la limite existe et est égale à 1, alors ceci l'intégrale impropre converge et est égal à 1.

Dans l'exemple suivant, l'intégrande est presque le même que dans l'exemple 1, seul le degré x n'est pas deux, mais la lettre alpha, et la tâche consiste à étudier l'intégrale impropre pour la convergence. C'est-à-dire que la question reste sans réponse : à quelles valeurs d'alpha cette intégrale impropre converge-t-elle, et à quelles valeurs diverge-t-elle ?

Exemple 2. Examiner l'intégrale impropre pour la convergence(la limite inférieure d'intégration est supérieure à zéro).

Solution. Supposons d'abord que, puis

Dans l’expression résultante, on passe à la limite en :

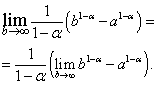
Il est facile de voir que la limite du côté droit existe et est égale à zéro quand, c'est-à-dire, et n'existe pas quand, c'est-à-dire.

Dans le premier cas, c'est-à-dire quand . Si donc et n'existe pas.

La conclusion de notre étude est la suivante : l'intégrale impropre convergeà et divergeà .

Application de la formule de Newton-Leibniz au type d'intégrale impropre étudiée , vous pouvez en déduire la formule suivante, qui lui est très similaire :

.

Il s'agit d'une formule de Newton-Leibniz généralisée.

Exemple 3. Calculer l'intégrale impropre(s'il converge).

La limite de cette intégrale existe :

La deuxième intégrale, constituant la somme exprimant l'intégrale d'origine :

La limite de cette intégrale existe aussi :

.

On retrouve la somme de deux intégrales, qui est aussi la valeur de l'intégrale impropre originale avec deux limites infinies :

Intégrales impropres du deuxième type - à partir de fonctions illimitées et de leur convergence

Laissez la fonction F(X) donné sur le segment de un avant b et il est illimité là-dessus. Supposons que la fonction tende vers l'infini au point b , alors qu'en tous les autres points du segment, il est continu.

Définition. Une intégrale impropre d'une fonction F(X) sur le segment de un avant b la limite de l'intégrale de cette fonction avec la limite supérieure d'intégration est appelée c , si en s'efforçant c À b la fonction augmente sans limite, et au point X = b fonction non définie, c'est à dire.

.

Si cette limite existe, alors l'intégrale impropre de seconde espèce est dite convergente, sinon elle est dite divergente.

En utilisant la formule de Newton-Leibniz, nous dérivons.

Considérons deux types d'intervalles impropres :

• 1. Intégrales impropres de la première espèce avec des limites d'intégration infinies ;
• 2. Intégrales impropres de la seconde espèce à partir de fonctions à discontinuités infinies.

Intégrales impropres du premier type avec des limites d'intégration infinies

Définition : Les intégrales de la forme : sont appelées intégrales impropres de première espèce à limites infinies, qui sont définies à l'aide des limites :

Définition Les intégrales impropres sont dites convergentes s'il existe des limites finies par lesquelles ces intégrales sont définies.

Les intégrales impropres sont dites divergentes si ces limites n'existent pas ou sont infinies.

En effet, soit la fonction f(x) définie et continue pour toute valeur x = in à partir d'un segment semi-infini de fonctions que nous avons :

Elle converge vers 1. Alors, selon le théorème 1, l'intégrale impropre de la plus petite fonction : converge également et sa valeur est inférieure à 1.

Théorème 2. Si pour les fonctions positives pour lesquelles l'inégalité 0?g(x)?f(x) est vraie, pour tout x ? et, l'intégrale impropre de la plus petite fonction diverge, alors l'intégrale impropre de la plus grande fonction diverge également.

Exemple. Étudiez la convergence de l’intégrale :

Solution. Comparons l'intégrande avec la fonction. Pour des signes positifs sur l'intervalle. Les intégrales impropres du deuxième type sont définies différemment, selon la localisation des points de discontinuité sur l'intervalle [ un; b].

1) Supposons que la fonction F(X) a une discontinuité infinie en un point interne du domaine d'intégration ( cÎ( un; b)) Aux autres points du segment [ un; b] la fonction est supposée continue.

Alors, si les limites et existent et sont finies, alors on dit que l'intégrale converge et est égale à

. (8.22)
2) Soit le seul point de discontinuité de la fonction F(X) coïncide avec le point UN

. (8.23)
3) Soit le seul point de discontinuité de la fonction F(X) coïncide avec le point b. Alors, si la limite existe et est finie, alors l’intégrale est dite converger et est égale à

. (8.24)
On suppose partout que e > 0 et d > 0.

Problème 8.12. Calculez l’intégrale impropre.

Solution. X= 2. Par conséquent,

Problème 8.13. Calculez l’intégrale impropre.

Solution. L'intégrande a une discontinuité du deuxième type au point X= 0 (dans la région d'intégration). Ainsi,

La première limite existe et est finie, mais la deuxième limite est égale à l'infini (at). Cette intégrale diverge donc.

Chapitre 9. Fonctions de plusieurs variables

§9.1. Définition n-Espace euclidien dimensionnel Rn.

Avant de passer à l’étude des fonctions de nombreuses variables, il est utile d’introduire le concept n-espace dimensionnel pour tout n = 1, 2, 3,… .

2 points xn-l'espace dimensionnel (vecteur) est une collection ordonnée n nombres réels.

Le numéro est appelé jeème coordonnée du vecteur.

2 Distance entre deux points n-espace dimensionnel et est déterminé par la formule :

Distance d'un point à un autre X appelé module du vecteur X et est désigné . De la formule (9.1) il résulte que .

DANS n-espace dimensionnel, la notion de produit scalaire est naturellement introduite :

Angle entre les vecteurs X Et oui peut être déterminé par la formule :

Comme auparavant, les vecteurs X Et oui sont perpendiculaires si et seulement si leur produit scalaire est nul.

2Ensemble de tous les points n-espace dimensionnel dans lequel la distance est définie selon la formule (9.1) et le produit scalaire est appelé n-espace vectoriel euclidien dimensionnel et est noté .

Quand n= 1 l'espace coïncide avec la ligne, dans le cas n= 2 – avec un avion, et dans le cas n= 3 – avec espace.

2 Soit et . L’ensemble de tous les points tels que , est appelé n-balle mesurée avec le centre au point X ou e-quartier du point X dans l'espace et est noté .

Sous forme de coordonnées, cette définition ressemble à ceci :

Dans le cas d'une ligne directe, c'est-à-dire à n= 1, le voisinage du point est un intervalle centré au point du rayon e. Dans le cas d'un avion, c'est-à-dire à n= 2, le voisinage du point est un cercle ouvert dont le centre est au point du rayon e. Dans le cas de l'espace, c'est-à-dire à n= 3 le voisinage du point est une boule ouverte centrée au point du rayon e.

§9.2. Le domaine de définition d'une fonction de plusieurs variables. Continuité

2 Fonction n variables est une règle (loi) selon laquelle chaque ensemble constitué de n variables tirées d'une certaine zone Dn-espace dimensionnel, est attribué à un seul nombre z. Dans le cas le plus simple.

2 Une fonction de 2 variables est une règle (loi) selon laquelle chaque point M(X; oui), appartenant à une zone D avion xOy, correspond au nombre singulier z.

De nombreux points dans l'espace avec des coordonnées forment une certaine surface (Fig. 9.1), s'élevant au-dessus de la zone D(signification géométrique d'une fonction de deux variables).

2 Zone D, pour lequel la correspondance ci-dessus est construite, est appelé le domaine de définition de la fonction.

Problème 9.1. Trouver le domaine d'une fonction

Solution. Le domaine de définition requis est un ensemble de points sur le plan xOy, satisfaisant le système d’inégalités. Inégalités et changent de signe à l'opposé (respectivement) lorsque les droites suivantes se croisent : X = oui Et X = 0, oui= 0. Ces lignes divisent le plan xOy pour 6 régions. De manière cohérente, en substituant des points arbitraires de chaque domaine dans le système, nous sommes convaincus que l'union des domaines (1) et (3) est le domaine de définition de la fonction d'origine. En plus c'est direct X = oui, à l'exception du point (0 ; 0), est inclus dans le domaine de définition, et les droites X= 0, et oui= 0 – non inclus (Fig. 9.2).

2 La fermeture d'une région est un ensemble de points dans l'espace, dont tout voisinage de chacun contient des points de la région D.

Laissez, par exemple, D– une zone ouverte (la bordure n'est pas incluse) dans l'avion xOy. Alors la fermeture de la région sera obtenue si à la région D attacher sa bordure g .

2 Laisser entrer dans une zone D avion xOy la fonction est donnée, et soit un point de fermeture de la région D(). Nombre UN est appelée la limite de la fonction au point M 0 si pour n'importe quel nombre e> 0 il y a un tel nombre δ > 0, qui pour tous les points autres que le point M 0 et à moins d'une distance de celui-ci δ , l'inégalité est satisfaite.

2 Une fonction est dite continue en un point si elle est définie en ce point () et que l'égalité est vérifiée.

§9.3. Lignes de niveau d'une fonction de deux variables

2 lignes dans un avion xOy, donné par les équations , où AVEC– une constante arbitraire, appelée lignes de niveau de fonction.

Les lignes de niveau sont les lignes d'intersection d'une surface, d'une fonction donnée et d'un plan. z = C, parallèle au plan xOy. À l'aide de lignes de niveau, vous pouvez étudier la forme de la surface spécifiée par la fonction.

Exemple 9.2. Trouvez les lignes de niveau et déterminez la forme de la surface donnée par l'équation.

Les équations des lignes de niveau dans ce cas ont la forme . En C< 0 уравнение дает пустое множество решений (следовательно, вся поверхность расположена выше плоскости xOy). À C= 0 un seul point satisfait l'équation de la ligne de niveau X = 0, oui= 0 (avec avion xOy la surface ne se coupe qu'à l'origine des coordonnées). À C> Les lignes de niveau 0 sont des ellipses, avec des demi-axes et . Lignes de niveau correspondant à différentes valeurs AVEC, montré sur la fig. 9.3. La surface définie par l'équation est appelée un paraboloïde elliptique (Fig. 9.4).

§9.4. Dérivées partielles du premier ordre

Laisser entrer dans une zone D avion xOy la fonction est donnée et correspond à un certain point dans la région D.

X

, (9.2)

2 Dérivée partielle d'une fonction en un point par rapport à une variable oui(noté par ou ) appelé

, (9.3)
si cette limite existe et est finie.

2 Fonction dérivée partielle n variables à un point par variable x je appelé

, (9.4)
si cette limite existe et est finie.

Comme le montrent les formules (9.2) – (9.4), les dérivées partielles sont déterminées de la même manière que la dérivée d'une fonction d'une variable a été déterminée. Lors du calcul de la limite, une seule des variables reçoit un incrément ; les variables restantes ne reçoivent pas d'incréments et restent constantes. Par conséquent, les dérivées partielles peuvent être calculées en utilisant les mêmes règles que les dérivées ordinaires, en traitant toutes les variables libres (sauf celle par laquelle la différenciation est effectuée) comme des constantes.

Problème 9.3. Trouver les dérivées partielles d'une fonction

Solution. .

Problème 9.4. Trouver les dérivées partielles d'une fonction.

Solution. Lors de la différenciation d'une fonction donnée par rapport à une variable X nous utilisons la règle pour différencier une fonction puissance et pour trouver la dérivée partielle par rapport à une variable oui– la règle de différenciation de la fonction exponentielle :

Problème 9.5. Calculez les dérivées partielles de la fonction en ce point.

Solution. En appliquant la règle de différenciation d'une fonction complexe, on trouve les dérivées partielles

Substitution des coordonnées du point en dérivées partielles M, on a

§9.5. Dégradé d'une fonction de plusieurs variables.
Dérivée directionnelle

2 Le gradient d'une fonction en un point est un vecteur composé des dérivées partielles d'une fonction donnée calculées en un point donné :

2 La dérivée d'une fonction en un point dans la direction du vecteur est la projection du vecteur gradient de cette fonction calculé en ce point M 0 , dans cette direction

En calculant la projection d'un vecteur sur un vecteur selon la formule (2.6), on obtient

. (9.7)
Remarquant que là où un– l'angle que fait le vecteur avec l'axe BŒUF, on obtient une autre formule pour calculer la dérivée par rapport à la direction du vecteur

Problème 9.6. Trouver le gradient d'une fonction en un point M 0 (4 ; 2) et la dérivée par rapport à la direction du vecteur

Solution. Trouvons les dérivées partielles

Calculons les valeurs des dérivées partielles au point M 0:

Dégradé d'une fonction en un point M 0 sera trouvé en utilisant la formule (9.5) :

Problème 9.7.À ce point M 0 (0 ; 1) calculer la dérivée de la fonction dans la direction de la bissectrice du deuxième angle de coordonnées.

Solution. Trouvons les dérivées partielles de la fonction :

Calculons les valeurs des dérivées partielles et le gradient de la fonction au point M 0:

Dérivée d'une fonction en un point M 0 dans la direction de la bissectrice du deuxième angle de coordonnées (cette direction est avec l'axe BŒUF coin un= 135°) peut être trouvé à l'aide de la formule (9.8) :

§9.6. Différentielle d'une fonction de plusieurs variables
et son application aux calculs approximatifs

1 Si en un point une fonction a des dérivées partielles continues et , alors son incrément total lors du déplacement du point M 0 en un point peut être représenté comme :

, (9.9)
où à , .

2 L'expression est appelée différentielle totale de la fonction en ce point.

De la formule (9.9), il s'ensuit que la différentielle de la fonction est la partie linéaire principale de l'incrément total de la fonction. Pour un D suffisamment petit X et D oui l'expression est nettement inférieure au différentiel et peut être négligée. On arrive ainsi à la formule approximative suivante :

. (9.10)
Commentaire. La formule (9.10) peut être utilisée pour calculer approximativement les valeurs des fonctions uniquement à des points suffisamment proches du point . Plus la valeur est petite, plus la valeur trouvée à l'aide de la formule (9.9) est précise.

Exemple 9.8. Calculez approximativement en utilisant le différentiel.

Considérons la fonction. Besoin de calculer la valeur z 1 de cette fonction au point ( X 1 ; oui 1) = (0,09 ; 6,95). Utilisons la formule approchée (9.9), en choisissant le point (0 ; 7) comme point. Puis D X = X 1 – X 0 = 0,09 – 0 = 0,09, D oui =oui 1 – oui 0 = 6,95 – 7 = – 0,05.

Ainsi,

§9.7. Dérivées partielles d'ordre supérieur

Laisser entrer dans la région D on donne une fonction qui a des dérivées partielles continues et dans ce domaine. Ainsi, dans la zone D nous avons obtenu deux nouvelles fonctions continues de deux variables et . Si à un moment donné dans la région D fonctions et ont des dérivées partielles à la fois par rapport à la variable X, et par changement oui, alors ces dérivées sont appelées dérivées du second ordre de la fonction. Ils sont désignés comme suit :

1 Si à un moment donné dans la zone D la fonction a des dérivées mixtes continues et , alors au point ces dérivées sont égales : . D, les conditions suivantes doivent être remplies : D = 32 – 9 = 23.

Puisque le discriminant est supérieur à zéro, alors au point M la fonction a un extremum. A savoir un minimum local, puisque UN Et AVEC Au dessus de zéro. Où

Appelé Intégrale incorrecte De la fonctionF(X) avec une limite supérieure infinie. Si cette limite existe et est finie, alors l'intégrale impropre est appelée Convergent. Mais s'il n'existe pas ou est égal
± ¥, alors cette intégrale impropre est appelée Divergent.

Si F(X) ≥ 0 pour tous X ≥ UN, Que U l'intégrale impropre (6.1) a une signification géométrique évidente, qui découle de la signification géométrique (4.3) de l'intégrale définie ordinaire. En effet, d'après la Fig. 5.14

(6.2)

(6.3)

Ici S¥ - zone infiniment étendue dans la direction de l'axe Oh trapèze curviligne (Fig. 5.15). Malgré son étendue infinie, elle peut aussi s’avérer limitée. Mais cela peut arriver, selon la Fig. 5.15, uniquement dans le cas où Oui = F(X) → 0 à X → ¥ . Et même alors, si la fonction Oui = F(X) → 0 à X → ¥ assez rapide.

Exemple 1. Rechercher une zone S¥ , montré sur la fig. 5.16.

,
depuis ln B → ¥ à B → ¥ .

Donc, S¥ = ¥. Et ce malgré le fait que la fonction lorsque X → ¥ . Une intégrale impropre, ce qui signifie qu’elle diverge.

Exemple 2. Rechercher une zone S¥ , montré sur la fig. 5.17.

Ici S¥ = 1. Autrement dit, une zone infiniment étendue s’est avérée finie. Cela s'est produit parce que la fonction d'intégrande à X → ¥ assez rapide (au moins beaucoup plus rapide que l'intégrande de l'exemple précédent). Une intégrale impropre (un nombre), ce qui signifie qu'elle converge.

Exemple 3 . Découvrez si l’intégrale impropre converge ou diverge.

Solution . Calculons cette intégrale :

N'existe pas. Ceci est évident si l'on rappelle le comportement du graphe de la fonction Oui= = Péché X(sinusoïdes) à X → ¥ . Il n’existe donc pas, ce qui signifie qu’il diverge. Cependant, il ne pourrait en être autrement, car la fonction intégrale cos X ne tend pas vers zéro lorsque X →¥ .

Notez que lors du calcul d'intégrales de type impropres, ainsi que lors du calcul d'intégrales définies ordinaires, vous pouvez immédiatement appliquer la formule de Newton-Leibniz :

Ici

Vraiment:

Si la valeur F(¥ ) existe et est fini, alors selon la formule de Newton-Leibniz (6.4) l'intégrale impropre converge également.

Note. De manière tout à fait analogue aux intégrales à limite supérieure infinie, on peut considérer des intégrales impropres à limite inférieure infinie et même avec les deux limites d'intégration infinies. Autrement dit, les intégrales de la forme

Pour les calculer, vous pouvez également utiliser la formule de Newton-Leibniz.

Exemple 4.

Donc, (nombre), c'est-à-dire que cette intégrale converge. Sa valeur π est égale à l'aire S¥ la figure infiniment étendue dans les deux directions représentée sur la Fig. 5.18.

A noter que le fait même de convergence-divergence d'intégrales impropres avec des limites d'intégration infinies ne doit pas être établi par calcul direct de ces intégrales. Cette question peut souvent être résolue beaucoup plus simplement en comparant cette intégrale impropre à une autre intégrale pour laquelle la convergence-divergence a déjà été établie.

Supposons, par exemple, qu’il existe des inégalités pour tout le monde. F(X) £ g(X), Où Oui = F(X) ET Oui = g(X) - Deux fonctions continues et non négatives (Fig. 5.19). Il est alors évident que

À partir de l’inégalité (6.6) et de la Fig. 5.19 suit évidemment ce qu'on appelle Test de comparaison pour les intégrales impropres:

1) Si (nombre) converge, alors (nombre) - converge, et B 2) Si - diverge, alors - diverge. 3) Si - diverge donc - on ne peut rien dire de cette intégrale. 4) Si (nombre) - converge, alors - rien ne peut être dit sur cette intégrale.

En tant que fonction g(X) , avec lequel cette fonction est comparée sur l'intervalle F(X), la fonction est souvent utilisée et l'intégrale est utilisée comme intégrale de comparaison, en tenant compte du fait que lorsque UN > 0 et toute fonction α est une fonction positive et continue, et que

Exemple 5.

Solution. Il est évident que pour tous X Î }