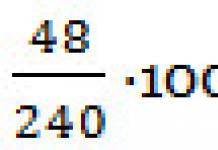La transformation d'une équation quadratique complète en une équation incomplète ressemble à ceci (pour le cas \(b=0\)) :

Pour les cas où \(c=0\) ou lorsque les deux coefficients sont égaux à zéro, tout est similaire.

Attention, il n'est pas question que \(a\) soit égal à zéro ; il ne peut pas être égal à zéro, puisque dans ce cas il se transformera en :

Résolution d'équations quadratiques incomplètes

Tout d'abord, vous devez comprendre qu'une équation quadratique incomplète est toujours une , et peut donc être résolue de la même manière qu'une équation quadratique ordinaire (via ). Pour ce faire, on ajoute simplement la composante manquante de l'équation avec un coefficient nul.

Exemple : Trouver les racines de l'équation \(3x^2-27=0\)
Solution :

		Nous avons une équation quadratique incomplète de coefficient \(b=0\). Autrement dit, nous pouvons écrire l’équation comme suit :
\(3x^2+0\cdot x-27=0\)		En fait, c’est la même équation qu’au début, mais elle peut maintenant être résolue comme une équation quadratique ordinaire. Nous écrivons d’abord les coefficients.
\(a=3;\) \(b=0;\) \(c=-27;\)		Calculons le discriminant en utilisant la formule \(D=b^2-4ac\)
\(D=0^2-4\cdot3\cdot(-27)=\) \(=0+324=324\)		Trouvons les racines de l'équation à l'aide des formules \(x_(1)=\)\(\frac(-b+\sqrt(D))(2a)\) et \(x_(2)=\)\(\frac(-b-\sqrt(D) )(2a)\)
\(x_(1)=\) \(\frac(-0+\sqrt(324))(2\cdot3)\)\(=\)\(\frac(18)(6)\) \(=3\) \(x_(2)=\) \(\frac(-0-\sqrt(324))(2\cdot3)\)\(=\)\(\frac(-18)(6)\) \(=-3\)		Écrivez la réponse

Répondre : \(x_(1)=3\); \(x_(2)=-3\)

Exemple : Trouver les racines de l'équation \(-x^2+x=0\)
Solution :

		Encore une équation quadratique incomplète, mais maintenant nulle le coefficient est égal\(c\). Nous écrivons l'équation comme complète.

L'utilisation d'équations est répandue dans nos vies. Ils sont utilisés dans de nombreux calculs, construction de structures et même dans le sport. L’homme utilisait des équations dans l’Antiquité et depuis lors, leur utilisation n’a fait que croître. Le discriminant permet de résoudre n'importe quelle équation quadratique à l'aide d'une formule générale, qui a la forme suivante :

La formule discriminante dépend du degré du polynôme. La formule ci-dessus convient pour résoudre des équations quadratiques de la forme suivante :

Le discriminant a les propriétés suivantes que vous devez connaître :

* « D » vaut 0 lorsque le polynôme a plusieurs racines (racines égales) ;

* « D » est un polynôme symétrique par rapport aux racines du polynôme et est donc un polynôme dans ses coefficients ; de plus, les coefficients de ce polynôme sont des entiers quelle que soit l'extension dans laquelle sont prises les racines.

Disons que l'on nous donne une équation quadratique de la forme suivante :

1 équation

D'après la formule on a :

Puisque \, l’équation a 2 racines. Définissons-les :

Où puis-je résoudre une équation à l’aide d’un solveur discriminant en ligne ?

Vous pouvez résoudre l’équation sur notre site https://site. Le solveur en ligne gratuit vous permettra de résoudre des équations en ligne de toute complexité en quelques secondes. Tout ce que vous avez à faire est simplement de saisir vos données dans le solveur. Vous pouvez également regarder les instructions vidéo et découvrir comment résoudre l'équation sur notre site Web. Et si vous avez des questions, vous pouvez les poser dans notre groupe VKontakte http://vk.com/pocketteacher. Rejoignez notre groupe, nous sommes toujours heureux de vous aider.

Résoudre des équations à l'aide de la méthode "lancer"

Considérons l'équation quadratique

hache 2 + bx + c = 0, où est a ? 0.

En multipliant les deux côtés par a, on obtient l'équation

une 2 x 2 + abx + ac = 0.

Soit ax = y, d'où x = y/a ; alors nous arrivons à l'équation

y 2 + par + ac = 0,

est équivalent à cela. Nous trouvons ses racines pour 1 et 2 en utilisant le théorème de Vieta.

On obtient finalement x 1 = y 1 /a et x 1 = y 2 /a. Avec cette méthode, le coefficient a est multiplié par le terme libre, comme s'il lui était « jeté », c'est pourquoi on l'appelle la méthode « jeter ». Cette méthode est utilisée lorsque les racines de l'équation peuvent être facilement trouvées à l'aide du théorème de Vieta et, surtout, lorsque le discriminant est un carré exact.

* Exemple.

Résolvons l'équation 2x 2 - 11x + 15 = 0.

Solution. "Jetons" le coefficient 2 au terme libre, et nous obtenons ainsi l'équation

y 2 - 11 ans + 30 = 0.

D'après le théorème de Vieta

oui 1 = 5 x 1 = 5/2 x 1 = 2,5

oui 2 = 6 x 2 = 6/2 x 2 = 3.

Réponse : 2,5 ; 3.

Propriétés des coefficients d'une équation quadratique

UN. Soit l'équation quadratique ax 2 + bx + c = 0, où a ? 0.

1) Si a+ b + c = 0 (c'est-à-dire que la somme des coefficients est nulle), alors x 1 = 1,

Preuve. Divisons les deux côtés de l'équation par a ? 0, on obtient l'équation quadratique réduite

x 2 + b/a * x + c/a = 0.

D'après le théorème de Vieta

x 1 + x 2 = - b/a,

x 1 x 2 = 1* c/a.

Par condition, a - b + c = 0, d'où b = a + c. Ainsi,

x 1 + x 2 = - une + b/une= -1 - c/une,

x 1 x 2 = - 1* (- c/a),

ceux. x 1 = -1 et x 2 = c/a, ce que nous devions prouver.

• * Exemples.
• 1) Résolvez l'équation 345x 2 - 137x - 208 = 0.

Solution. Puisque a + b + c = 0 (345 - 137 - 208 = 0), alors

x 1 = 1, x 2 = c/a = -208/345.

Réponse 1; -208/345.

2) Résolvez l'équation 132x 2 - 247x + 115 = 0.

Solution. Puisque a + b + c = 0 (132 - 247 + 115 = 0), alors

x 1 = 1, x 2 = c/a = 115/132.

Réponse 1; 115/132.

B. Si le deuxième coefficient b = 2k est un nombre pair, alors la formule racine

* Exemple.

Résolvons l'équation 3x2 - 14x + 16 = 0.

Solution. On a : a = 3, b = - 14, c = 16, k = - 7 ;

Yakupova M.I. 1

Smirnova Yu.V. 1

1 Budget municipal établissement d'enseignement moyenne école polyvalente № 11

Le texte de l'ouvrage est affiché sans images ni formules.
Version complète le travail est disponible dans l'onglet "Fichiers de travail" au format PDF

Histoire équations du second degré

Babylone

La nécessité de résoudre des équations non seulement du premier degré, mais aussi du second dans les temps anciens était due à la nécessité de résoudre des problèmes liés à la recherche de zones. terrains, avec le développement de l’astronomie et des mathématiques elles-mêmes. Les équations quadratiques ont pu être résolues vers 2000 avant JC. e. Babyloniens. Les règles de résolution de ces équations, énoncées dans les textes babyloniens, coïncident essentiellement avec les règles modernes, mais dans ces textes il n'y a pas de concept de nombre négatif et méthodes générales résoudre des équations quadratiques.

La Grèce ancienne

La résolution d'équations quadratiques a également été réalisée dans La Grèce ancienne des scientifiques tels que Diophante, Euclide et Héron. Diophantus Diophantus d'Alexandrie est un mathématicien grec ancien qui a probablement vécu au 3ème siècle après JC. L'œuvre principale de Diophante est « l'Arithmétique » en 13 livres. Euclide. Euclide est un mathématicien grec ancien, l'auteur du premier traité théorique de mathématiques qui nous soit parvenu, Héron. Héron - mathématicien et ingénieur grec apparu pour la première fois en Grèce au 1er siècle après JC. donne une manière purement algébrique de résoudre une équation quadratique

Inde

Les problèmes liés aux équations quadratiques se retrouvent déjà dans le traité d'astronomie « Aryabhattiam », compilé en 499 par le mathématicien et astronome indien Aryabhatta. Un autre scientifique indien, Brahmagupta (VIIe siècle), décrit règle générale solutions d'équations quadratiques réduites à une seule forme canonique : ax2 + bx = c, a> 0. (1) Dans l'équation (1) les coefficients peuvent être négatifs. La règle de Brahmagupta est essentiellement la même que la nôtre. Les concours publics visant à résoudre des problèmes difficiles étaient courants en Inde. L'un des vieux livres indiens dit ce qui suit à propos de telles compétitions : « De même que le soleil éclipse les étoiles avec son éclat, ainsi homme instruitéclipsera la gloire de assemblées populaires, proposer et résoudre des problèmes algébriques. Les problèmes étaient souvent présentés sous forme poétique.

C’est l’un des problèmes du célèbre mathématicien indien du XIIe siècle. Bhaskars.

"Un troupeau de singes fringants

Et douze au bord des vignes, après avoir mangé à cœur joie, se sont amusés

Ils ont commencé à sauter, à se suspendre

La huitième partie d'entre eux au carré

Combien y avait-il de singes ?

Je m'amusais dans la clairière

Dis-moi, dans ce pack ?

La solution de Bhaskara indique que l'auteur savait que les racines des équations quadratiques sont à deux valeurs. Bhaskar écrit l'équation correspondant au problème sous la forme x2 - 64x = - 768 et, afin de compléter le côté gauche de cette équation en un carré, ajoute 322 aux deux côtés, obtenant alors : x2 - b4x + 322 = -768 + 1024 , (x - 32)2 = 256, x - 32= ±16, x1 = 16, x2 = 48.

Équations quadratiques dans Europe XVII siècle

Les formules de résolution d'équations quadratiques inspirées d'Al-Khorezmi en Europe ont été présentées pour la première fois dans le Livre de l'Abacus, écrit en 1202 par le mathématicien italien Leonardo Fibonacci. Cet ouvrage volumineux, qui reflète l'influence des mathématiques, tant des pays d'Islam que de la Grèce antique, se distingue par son exhaustivité et la clarté de sa présentation. L'auteur a développé indépendamment de nouveaux exemples algébriques résoudre des problèmes et a été le premier en Europe à introduire des nombres négatifs. Son livre a contribué à la diffusion des connaissances algébriques non seulement en Italie, mais aussi en Allemagne, en France et dans d'autres pays européens. De nombreux problèmes du Livre de l'Abacus ont été utilisés dans presque tous les manuels européens des XVIe et XVIIe siècles. et en partie XVIII. La dérivation de la formule pour résoudre une équation quadratique sous forme générale est disponible chez Viète, mais Viète ne reconnaissait que les racines positives. Les mathématiciens italiens Tartaglia, Cardano, Bombelli furent parmi les premiers au XVIe siècle. En plus des racines positives, les racines négatives sont également prises en compte. Seulement au 17ème siècle. Grâce aux travaux de Girard, Descartes, Newton et autres façon des scientifiques la résolution d'équations quadratiques prend une forme moderne.

Définition d'une équation quadratique

Une équation de la forme ax 2 + bx + c = 0, où a, b, c sont des nombres, est dite quadratique.

Coefficients d'équation quadratique

Les nombres a, b, c sont les coefficients de l'équation quadratique. a est le premier coefficient (avant x²), a ≠ 0 ; b est le deuxième coefficient (avant x) ; c est le terme libre (sans x).

Laquelle de ces équations n’est pas quadratique ??

1. 4x² + 4x + 1 = 0;2. 5x-7 = 0;3. - x² - 5x - 1 = 0;4. 2/x² + 3x + 4 = 0;5. ¼ x² - 6x + 1 = 0;6. 2x² = 0 ;

7. 4x² + 1 = 0;8. x² - 1/x = 0;9. 2x² -x = 0;10. x² -16 = 0;11. 7x² + 5x = 0;12. -8x²= 0;13. 5x³ +6x -8= 0.

Types d'équations quadratiques

Nom	Forme générale de l'équation	Caractéristique (quels sont les coefficients)	Exemples d'équations
	hache 2 + bx + c = 0	a, b, c - nombres autres que 0	1/3x 2 + 5x - 1 = 0
Incomplet
			x2 - 1/5x = 0
Donné	x 2 + bx + c = 0		x2 - 3x + 5 = 0

Réduit est une équation quadratique dans laquelle le coefficient principal est égal à un. Une telle équation peut être obtenue en divisant l'expression entière par le coefficient dominant un:

X 2 + px + q =0, p = b/a, q = c/a

Une équation quadratique est dite complète si tous ses coefficients sont différents de zéro.

Une équation quadratique est dite incomplète dans laquelle au moins un des coefficients, à l'exception du premier (soit le deuxième coefficient, soit le terme libre), égal à zéro.

Méthodes de résolution d'équations quadratiques

Méthode I Formule générale de calcul des racines

Pour trouver les racines d'une équation quadratique hache 2 + b + c = 0 En général, vous devez utiliser l'algorithme ci-dessous :

Calculer la valeur du discriminant d'une équation quadratique : voici son expression D= b 2 - 4ac

Dérivation de la formule :

Note: Il est évident que la formule d'une racine de multiplicité 2 est un cas particulier de la formule générale, obtenue en y substituant l'égalité D=0, et la conclusion sur l'absence de racines réelles en D0, et (displaystyle (sqrt ( -1))=i) = je.

La méthode présentée est universelle, mais elle est loin d'être la seule. La résolution d’une seule équation peut être abordée de différentes manières, les préférences dépendant généralement du solveur. De plus, souvent à cette fin, certaines méthodes s'avèrent beaucoup plus élégantes, simples et moins laborieuses que la méthode standard.

IIème méthode. Racines d'une équation quadratique à coefficient pair b Méthode III. Résolution d'équations quadratiques incomplètes

Méthode IV. Utilisation de rapports partiels de coefficients

Il existe des cas particuliers d'équations quadratiques dans lesquelles les coefficients sont en relation les uns avec les autres, ce qui les rend beaucoup plus faciles à résoudre.

Racines d'une équation quadratique dans laquelle la somme du coefficient dominant et du terme libre est égale au deuxième coefficient

Si dans une équation quadratique hache 2 + bx + c = 0 la somme du premier coefficient et du terme libre est égale au deuxième coefficient : a+b=c, alors ses racines sont -1 et le nombre opposé au rapport du terme libre au coefficient dominant ( -Californie).

Par conséquent, avant de résoudre une équation quadratique, vous devez vérifier la possibilité de lui appliquer ce théorème : comparer la somme du coefficient principal et du terme libre avec le deuxième coefficient.

Racines d'une équation quadratique dont la somme de tous les coefficients est nulle

Si dans une équation quadratique la somme de tous ses coefficients est nulle, alors les racines d'une telle équation sont 1 et le rapport du terme libre au coefficient dominant ( Californie).

Par conséquent, avant de résoudre une équation à l'aide de méthodes standards, vous devez vérifier l'applicabilité de ce théorème : additionnez tous les coefficients de cette équation et voyez si cette somme n'est pas égale à zéro.

Méthode V. Factorisation d'un trinôme quadratique en facteurs linéaires

Si le trinôme est de la forme (style d'affichage hache ^ (2) + bx + c (anot = 0)) hache 2 + bx + c(une ≠ 0) peut en quelque sorte être représenté comme un produit de facteurs linéaires (displaystyle (kx+m)(lx+n)=0)(kx + m)(lx + n), alors nous pouvons trouver les racines de l'équation hache 2 + bx + c = 0- ils seront -m/k et n/l, en effet, après tout (displaystyle (kx+m)(lx+n)=0Longleftrightarrow kx+m=0cup lx+n=0)(kx + m)(lx + n) = 0 kx + mUlx + n, et après avoir résolu le problème indiqué équations linéaires, nous obtenons ce qui précède. A noter que le trinôme quadratique ne se décompose pas toujours en facteurs linéaires à coefficients réels : cela est possible si l'équation correspondante a des racines réelles.

Considérons quelques cas particuliers

Utilisation de la formule de la somme au carré (différence)

Si le trinôme quadratique a la forme (displaystyle (ax)^(2)+2abx+b^(2))ax 2 + 2abx + b 2 , alors en lui appliquant la formule ci-dessus, nous pouvons le factoriser en facteurs linéaires et , donc, trouvez des racines :

(hache) 2 + 2abx + b 2 = (hache + b) 2

Isoler le carré complet de la somme (différence)

La formule ci-dessus est également utilisée en utilisant une méthode appelée « sélection du carré complet de la somme (différence) ». Par rapport à l’équation quadratique ci-dessus avec la notation introduite précédemment, cela signifie ce qui suit :

Note: Si vous remarquez, cette formule coïncide avec celle proposée dans la section « Racines de l'équation quadratique réduite », qui, à son tour, peut être obtenue à partir de la formule générale (1) en substituant l'égalité a=1. Ce fait n'est pas qu'une coïncidence : en utilisant la méthode décrite, bien qu'avec quelques raisonnements supplémentaires, il est possible de déduire formule générale, et prouver également les propriétés du discriminant.

Méthode VI. Utilisation du théorème de Vieta direct et inverse

Le théorème direct de Vieta (voir ci-dessous dans la section du même nom) et son théorème inverse permettent de résoudre oralement les équations quadratiques ci-dessus, sans recourir à des calculs assez fastidieux utilisant la formule (1).

Selon inverse du théorème, chaque paire de nombres (nombre) (displaystyle x_(1),x_(2))x 1, x 2 étant une solution du système d'équations ci-dessous sont les racines de l'équation

Dans le cas général, c'est-à-dire pour une équation quadratique non réduite ax 2 + bx + c = 0

x 1 + x 2 = -b/a, x 1 * x 2 = c/a

Un théorème direct vous aidera à trouver des nombres qui satisfont oralement à ces équations. Avec son aide, vous pouvez déterminer les signes des racines sans connaître les racines elles-mêmes. Pour ce faire, vous devez suivre la règle :

1) si le terme libre est négatif, alors les racines ont des signes différents, et la plus grande en valeur absolue des racines a un signe opposé au signe du deuxième coefficient de l'équation ;

2) si le terme libre est positif, alors les deux racines ont le même signe, et c'est le signe opposé au signe du deuxième coefficient.

Méthode VII. Méthode de transfert

La méthode dite de « transfert » permet de réduire la solution d'équations non réduites et irréductibles à la forme d'équations réduites à coefficients entiers en les divisant par le coefficient dominant à la solution d'équations réduites à coefficients entiers. C'est le suivant :

Ensuite, l'équation est résolue oralement de la manière décrite ci-dessus, puis ils reviennent à la variable d'origine et trouvent les racines des équations (displaystyle y_(1)=ax_(1)) oui 1 =hache 1 Et oui 2 =hache 2 .(style d'affichage y_(2)=ax_(2))

Signification géométrique

Le graphique d'une fonction quadratique est une parabole. Les solutions (racines) d'une équation quadratique sont les abscisses des points d'intersection de la parabole avec l'axe des abscisses. Si la parabole décrite fonction quadratique, ne coupe pas l'axe des x, l'équation n'a pas de vraies racines. Si une parabole coupe l'axe des x en un point (au sommet de la parabole), l'équation a une racine réelle (on dit aussi que l'équation a deux racines coïncidantes). Si la parabole coupe l'axe des x en deux points, l'équation a deux racines réelles (voir l'image de droite.)

Si coefficient (style d'affichage a) un positif, les branches de la parabole sont dirigées vers le haut et vice versa. Si le coefficient (style d'affichage b) bpositif (si positif (style d'affichage a) un, si négatif, vice versa), alors le sommet de la parabole se situe dans le demi-plan gauche et vice versa.

Application des équations quadratiques dans la vie

L'équation quadratique est largement utilisée. Il est utilisé dans de nombreux calculs, structures, sports, et aussi autour de nous.

Considérons et donnons quelques exemples d'application de l'équation quadratique.

Sport. Sauts en hauteur : lors de l'élan du sauteur, des calculs liés à la parabole sont utilisés pour obtenir l'impact le plus net possible sur la barre d'envol et le vol en hauteur.

De plus, des calculs similaires sont nécessaires pour le lancer. La portée de vol d'un objet dépend de l'équation quadratique.

Astronomie. La trajectoire des planètes peut être trouvée à l’aide d’une équation quadratique.

Vol d'avion. Le décollage d’un avion est l’élément principal du vol. Nous prenons ici le calcul de la faible résistance et de l'accélération du décollage.

Les équations quadratiques sont également utilisées dans diverses disciplines économiques, dans des programmes de traitement de graphiques audio, vidéo, vectoriels et raster.

Conclusion

À la suite des travaux effectués, il s'est avéré que les équations quadratiques ont attiré les scientifiques les temps anciens, ils les ont déjà rencontrés en résolvant certains problèmes et ont essayé de les résoudre. Considérant différentes manières En résolvant des équations quadratiques, je suis arrivé à la conclusion qu'elles ne sont pas toutes simples. À mon avis, le plus la meilleure façon résoudre des équations quadratiques, c'est résoudre par des formules. Les formules sont faciles à retenir, cette méthode est universelle. L'hypothèse selon laquelle les équations sont largement utilisées dans la vie et en mathématiques a été confirmée. Après avoir étudié le sujet, j'ai beaucoup appris faits intéressants sur les équations quadratiques, leur utilisation, leur application, leurs types, leurs solutions. Et je serai heureux de continuer à les étudier. J'espère que cela m'aidera à réussir mes examens.

Liste de la littérature utilisée

Matériaux du chantier :

Wikipédia

Cours ouvert.rf

Manuel de mathématiques élémentaires Vygodsky M. Ya.

5x (x - 4) = 0

5 x = 0 ou x - 4 = 0

x = ± √ 25/4

Après avoir appris à résoudre des équations du premier degré, bien sûr, vous souhaitez travailler avec d'autres, en particulier avec des équations du deuxième degré, autrement appelées quadratiques.

Les équations quadratiques sont des équations comme ax² + bx + c = 0, où la variable est x, les nombres sont a, b, c, où a n'est pas égal à zéro.

Si dans une équation quadratique l'un ou l'autre coefficient (c ou b) est égal à zéro, alors cette équation sera classée comme une équation quadratique incomplète.

Comment résoudre une équation quadratique incomplète si les élèves n’ont jusqu’à présent pu résoudre que des équations du premier degré ? Considérez des équations quadratiques incomplètes différents types et des moyens simples de les résoudre.

a) Si le coefficient c est égal à 0 et que le coefficient b n'est pas égal à zéro, alors ax ² + bx + 0 = 0 se réduit à une équation de la forme ax ² + bx = 0.

Pour résoudre une telle équation, il faut connaître la formule de résolution d'une équation quadratique incomplète, qui consiste à factoriser le côté gauche de celle-ci et à utiliser plus tard la condition que le produit soit égal à zéro.

Par exemple, 5x² - 20x = 0. On factorise le côté gauche de l'équation, tout en effectuant l'opération mathématique habituelle : sortir le facteur commun des parenthèses

5x (x - 4) = 0

Nous utilisons la condition selon laquelle les produits sont égaux à zéro.

5 x = 0 ou x - 4 = 0

La réponse sera : la première racine est 0 ; la deuxième racine est 4.

b) Si b = 0, et que le terme libre n'est pas égal à zéro, alors l'équation ax ² + 0x + c = 0 se réduit à une équation de la forme ax ² + c = 0. Les équations sont résolues de deux manières : a) en factorisant le polynôme de l'équation du côté gauche ; b) utiliser les propriétés de l'arithmétique racine carrée. Une telle équation peut être résolue en utilisant l'une des méthodes, par exemple :

x = ± √ 25/4

x = ± 5/2. La réponse sera : la première racine est 5/2 ; la deuxième racine est égale à - 5/2.

c) Si b est égal à 0 et c est égal à 0, alors ax ² + 0 + 0 = 0 se réduit à une équation de la forme ax ² = 0. Dans une telle équation x sera égal à 0.

Comme vous pouvez le constater, les équations quadratiques incomplètes ne peuvent avoir plus de deux racines.