Problème numéro 1
La logique est simple : nous allons agir comme avant, malgré le fait que maintenant les fonctions trigonométriques ont un argument plus complexe !
Si on résolvait une équation de la forme :
Ensuite, nous écririons la réponse suivante :
Ou (depuis)
Mais maintenant, nous avons l'expression suivante dans notre rôle :
Ensuite, vous pouvez écrire :
Notre objectif avec vous est de rendre la gauche debout simplement, sans aucune "impureté" !
Éliminons-les progressivement !
Tout d'abord, nous enlevons le dénominateur à : pour cela nous multiplions notre égalité par :
Maintenant, débarrassons-nous en en divisant les deux parties :
Débarrassons-nous maintenant des huit :
L'expression résultante peut être écrite comme 2 séries de solutions (par analogie avec une équation quadratique, où nous ajoutons ou soustrayons le discriminant)
Nous devons trouver la plus grande racine négative ! Il est clair qu'il faut faire le tri.
Considérons d'abord la première série :
Il est clair que si nous prenons, alors nous obtiendrons des nombres positifs, et ils ne nous intéressent pas.
Vous devez donc le prendre en négatif. Laisser.
Lorsque la racine est déjà :
Et nous devons trouver le plus grand négatif !! Cela signifie que cela n'a plus de sens d'aller dans le sens négatif. Et la plus grande racine négative pour cette série sera.
Regardons maintenant la deuxième série :
Et encore nous substituons :, puis :
Pas intéressé!
Alors ça n'a plus de sens d'augmenter ! Nous allons réduire ! Soit donc :
Convient !
Laisser. Puis
Alors - la plus grande racine négative !
Réponse:
Problème numéro 2
Encore une fois, nous résolvons, quel que soit l'argument cosinus complexe :
Exprimons maintenant à gauche à nouveau :
On multiplie les deux côtés par
Nous divisons les deux côtés en
Il ne reste plus qu'à le déplacer vers la droite, en changeant son signe du moins au plus.
Nous avons à nouveau 2 séries de racines, l'une avec et l'autre avec.
Nous devons trouver la plus grande racine négative. Considérons la première série :
Il est clair que nous recevrons la première racine négative à, elle sera égale et sera la plus grande racine négative de 1 série.
Pour la deuxième série
La première racine négative sera également obtenue à et sera égale à. Puisque, alors est la plus grande racine négative de l'équation.
Réponse: .
Problème numéro 3
Résoudre quel que soit l'argument tangent complexe.
Cela semble n'être rien de compliqué, non?
Comme précédemment, nous exprimons sur le côté gauche :
Et bien c'est super, il n'y a qu'une seule série de racines ici ! Trouvez à nouveau le plus grand négatif.
Il est clair qu'il s'avère si nous mettons. Et cette racine est égale.
Réponse:
Essayez maintenant de résoudre vous-même les problèmes suivants.
Devoirs ou 3 tâches pour une solution autonome.
- Équation de décisions-shi-te.
- Équation de décisions-shi-te.
Dans les ot-ve-those na-pi-shi-te, la plus petite racine de po-li-tel. - Équation de décisions-shi-te.
Dans les ot-ve-those na-pi-shi-te, la plus petite racine de po-li-tel.
Prêt? Vérification. Je ne décrirai pas en détail l'ensemble de l'algorithme de solution, il me semble qu'on lui a déjà prêté suffisamment d'attention ci-dessus.
Eh bien, est-ce que tout est correct ? Oh, ces méchants sinus, il y a toujours des problèmes avec eux !
Eh bien, vous pouvez maintenant résoudre les équations trigonométriques les plus simples !
Vérifiez les solutions et les réponses :
Problème numéro 1
exprimons
La plus petite racine positive est obtenue si l'on pose, puisque, alors
Réponse:
Problème numéro 2
La plus petite racine positive est obtenue quand.
Ce sera égal.
Réponse: .
Problème numéro 3
Quand on arrive, quand on arrive.
Réponse: .
Ces connaissances vous aideront à résoudre bon nombre des problèmes auxquels vous serez confrontés lors de l'examen.
Si vous postulez pour une note de « 5 », il vous suffit d'aller lire l'article pour niveau moyen, qui sera consacrée à la résolution d'équations trigonométriques plus complexes (tâche C1).
NIVEAU MOYEN
Dans cet article, je vais décrire résoudre des équations trigonométriques d'un type plus complexe et comment sélectionner leurs racines. Ici, je vais m'appuyer sur les sujets suivants :
- Équations trigonométriques pour le niveau d'entrée (voir ci-dessus).
Des équations trigonométriques plus complexes sont à la base de problèmes plus complexes. En eux, il est nécessaire à la fois de résoudre l'équation elle-même sous sa forme générale et de trouver les racines de cette équation appartenant à un certain intervalle spécifié.
La résolution d'équations trigonométriques se résume à deux sous-tâches :
- Solution d'équation
- Sélection de racines
Il convient de noter que ce dernier n'est pas toujours requis, mais une sélection est néanmoins requise dans la plupart des exemples. Et si ce n'est pas nécessaire, alors vous pouvez plutôt sympathiser - cela signifie que l'équation est assez compliquée en soi.
Mon expérience dans l'analyse des tâches C1 montre qu'elles sont généralement divisées en ces catégories.
Quatre catégories de tâches de complexité accrue (anciennement C1)
- Équations qui se réduisent à la factorisation.
- Équations se réduisant à la forme.
- Équations résolues par changement variable.
- Équations nécessitant une sélection supplémentaire de racines en raison de l'irrationalité ou du dénominateur.
Pour faire simple : si vous rencontrez l'un des trois premiers types d'équations alors considérez-vous chanceux. Pour eux, en règle générale, vous devez également ramasser des racines appartenant à un certain intervalle.
Si vous rencontrez une équation de type 4, alors vous êtes moins chanceux: vous devez la bricoler un peu plus longtemps et de plus près, mais bien souvent, cela ne nécessite pas de sélection supplémentaire de racines. Néanmoins, j'analyserai ce type d'équations dans le prochain article, et celui-ci sera consacré à la résolution d'équations des trois premiers types.
Équations de factorisation
La chose la plus importante à retenir pour résoudre des équations de ce type est
Comme le montre la pratique, en règle générale, cette connaissance est suffisante. Regardons quelques exemples :
Exemple 1. Équation de réduction en factorisation à l'aide de formules de réduction et de sinus à double angle
- Équation res-shi-te
- Nay-di-te toutes les racines de cette équation
Ici, comme promis, les formules de casting fonctionnent :
Alors mon équation ressemblera à ceci:
Alors mon équation prendra la forme suivante :
Un étudiant myope pourrait dire : et maintenant je vais raccourcir les deux parties, obtenir l'équation la plus simple et profiter de la vie ! Et il se trompera amèrement !
| RAPPELEZ-VOUS : NE JAMAIS RÉDUIRE LES DEUX PARTIES DE L'ÉQUATION TRIGONOMÉTRIQUE PAR UNE FONCTION CONTENANT UN INCONNU ! ALORS VOUS PERDEZ DES RACINES ! |
Donc que fais-tu? Oui, tout est simple, déplacez tout dans un sens et sortez le facteur commun :
Eh bien, nous le prenons en compte dans les facteurs, hourra ! Maintenant, nous décidons :
La première équation a des racines :
Et le deuxième:
Ceci termine la première partie du problème. Maintenant, nous devons sélectionner les racines :
L'écart est comme ceci :
Ou il peut aussi s'écrire comme ceci :
Eh bien, prenons les racines :
Tout d'abord, travaillons avec la première série (et c'est plus facile, que dire !)
Puisque notre intervalle est entièrement négatif, il n'est pas nécessaire d'en prendre des non-négatifs, ils donneront tout de même des racines non-négatives.
Prenons, alors - un peu trop, ne convient pas.
Laissez, alors - n'a pas frappé à nouveau.
Encore une tentative - alors - il y a, frappez ! Première racine trouvée !
Je tire à nouveau : puis - je frappe encore !
Bon, encore une fois :: - c'est déjà un vol.
Donc à partir de la première série 2 racines appartiennent à l'intervalle :.
Nous travaillons avec la deuxième série (nous construisons à un degré selon la règle):
Sous-dépasser !
Sous-dépasser à nouveau !
Encore une fois sous-dépassé !
J'ai compris!
Voyage en avion!
Ainsi, les racines suivantes appartiennent à mon span :
C'est par cet algorithme que nous résoudrons tous les autres exemples. Pratiquons ensemble avec un autre exemple.
Exemple 2. Une équation qui se réduit à la factorisation à l'aide de formules de réduction
- Résous l'équation
Solution:
Encore les fameuses formules de casting :
Encore une fois, n'essayez pas de réduire !
La première équation a des racines :
Et le deuxième:
Maintenant, recherchez à nouveau les racines.
Je vais commencer par la deuxième série, je sais déjà tout de l'exemple précédent ! Regardez et assurez-vous que les racines appartenant à l'écart sont les suivantes :
Maintenant le premier épisode et c'est plus simple :
Si - convient
Si - est également bon
Si - déjà un vol.
Les racines seront alors les suivantes :
Travail indépendant. 3 équations.
Eh bien, la technique est-elle claire pour vous? Résoudre des équations trigonométriques ne semble plus si difficile ? Ensuite, résolvez rapidement vous-même les problèmes suivants, puis vous et moi résoudrons d'autres exemples :
- Résous l'équation
Non, ce sont toutes les racines de cette équation, attachées à l'intervalle. - Équation res-shi-te
Indiquer les racines de l'équation - Équation res-shi-te
Nay-di-ce sont toutes les racines de cette équation-non-niy, attaché-sur-le-zha-shi-pro-me-zhut-ku.
Équation 1.
Et encore la formule de casting :
Première série de racines :
Deuxième série de racines :
Sélection de départ pour l'écart
Réponse: , .
Équation 2. Vérification du travail indépendant.
Un regroupement assez délicat en facteurs (j'utiliserai la formule du sinus à double angle) :
alors ou
C'est une solution générale. Maintenant, nous devons sélectionner les racines. L'ennui, c'est qu'on ne peut pas dire la valeur exacte de l'angle dont le cosinus est égal à un quart. Par conséquent, je ne peux pas simplement me débarrasser de l'arccosinus - c'est vraiment dommage !
Ce que je peux faire, c'est comprendre quoi et comment, alors.
Faisons un tableau : intervalle :
Eh bien, après de douloureuses recherches, nous sommes arrivés à la conclusion décevante que notre équation a une racine à l'intervalle indiqué : \ displaystyle arccos \ frac (1) (4) -5 \ pi
Équation 3. Vérification du travail indépendant.
Une équation effrayante. Cependant, il peut être résolu tout simplement en appliquant la formule du double angle sinus :
Réduire de 2 :
Regroupons le premier terme avec le deuxième et le troisième avec le quatrième et retirons les facteurs communs :
Il est clair que la première équation n'a pas de racines, et considérons maintenant la seconde :
En général, j'allais m'attarder sur la solution de telles équations un peu plus tard, mais comme cela s'est produit, alors il n'y a rien à faire, il faut résoudre ...
Équations de la forme :
Cette équation est résolue en divisant les deux parties par :
Ainsi, notre équation a une seule série de racines :
Il faut trouver ceux d'entre eux qui appartiennent à l'intervalle :.
Construisons à nouveau une table, comme je l'ai fait plus tôt :
Réponse: .
Équations qui se réduisent à la forme :
Eh bien, il est maintenant temps de passer au deuxième lot d'équations, d'autant plus que j'ai déjà expliqué en quoi consiste la solution d'équations trigonométriques d'un nouveau type. Mais il ne sera pas superflu de répéter qu'une équation de la forme
Il est résolu en divisant les deux parties par le cosinus :
- Équation res-shi-te
Indiquez les racines de l'équation-not-nia, when-over-lying-from-cutting. - Équation res-shi-te
Indiquez les racines de l'équation-not-nia, when-over-le-zha-shi-pro-me-zhut-ku.
Exemple 1.
Le premier est très simple. Déplacez-vous vers la droite et appliquez la formule du cosinus double angle :
Ah ! Équation de la forme :. Je divise les deux parties en
Nous procédons au tamisage des racines :
Écart:
Réponse:
Exemple 2.
Tout est aussi assez trivial : développons les crochets à droite :
Identité trigonométrique de base :
Sinus à double angle :
On obtient finalement :
Perte de racine : écart.
Réponse: .
Eh bien, comment aimez-vous la technique, n'est-ce pas trop compliqué? J'espère que non. On peut tout de suite faire une réserve : sous leur forme pure, les équations, qui se réduisent immédiatement à une équation de la tangente, sont assez rares. Typiquement, cette transition (division par cosinus) n'est qu'une partie d'un problème plus complexe. Voici un exemple pour vous entraîner :
- Équation res-shi-te
- Nay-di-ce sont toutes les racines de cette équation-pas-nia, attachée-sur-le-zha-shi-ku.
Allons vérifier:
L'équation est résolue immédiatement, il suffit de diviser les deux parties en :
Abandon de la racine :
Réponse: .
D'une manière ou d'une autre, nous n'avons pas encore rencontré d'équations du type de celles que nous venons d'analyser. Cependant, il est trop tôt pour arrondir : il y a encore une « couche » d'équations que nous n'avons pas analysée. Alors:
Résoudre des équations trigonométriques en changeant une variable
Tout est transparent ici : on regarde de près l'équation, on la simplifie au maximum, on fait une substitution, on résout, on fait une substitution inverse ! En mots, tout est très facile. Voyons en action :
Exemple.
- Résous l'équation:.
- Nay-di-ce sont toutes les racines de cette équation-pas-nia, attachée-sur-le-zha-shi-ku.
Eh bien, ici, le remplacement lui-même demande à être entre nos mains !
Ensuite, notre équation se transformera en ceci:
La première équation a des racines :
Et le second est celui-ci :
Maintenant, nous allons trouver les racines appartenant à l'intervalle
Réponse: .
Reprenons ensemble un exemple un peu plus complexe :
- Équation res-shi-te
- Indiquez les racines de l'équation donnée-non-niy, when-over-le-za-shi-n-e-zhut-ku.
Ici le remplacement n'est pas immédiatement visible, de plus, il n'est pas très évident. Réfléchissons d'abord : que pouvons-nous faire ?
Par exemple, on peut imaginer
Et en même temps
Alors mon équation prendra la forme :
Maintenant attention, concentrez-vous :
Divisons les deux côtés de l'équation par :
Soudain, toi et moi avons une équation quadratique pour ! Faisons un remplacement, alors nous obtenons:
L'équation a les racines suivantes :
Mauvaise deuxième série de racines, mais on n'y peut rien ! Nous sélectionnons les racines dans l'intervalle.
Nous devons également considérer que
Depuis et puis
Réponse:
Pour consolider, avant de résoudre les problèmes vous-même, voici un autre exercice pour vous :
- Équation res-shi-te
- Nay-di-ce sont toutes les racines de cette équation-non-niy, attaché-sur-le-zha-shi-pro-me-zhut-ku.
Ici, il faut garder les yeux ouverts : nous avons maintenant des dénominateurs qui peuvent être nuls ! Il faut donc être particulièrement attentif aux racines !
Tout d'abord, je dois transformer l'équation afin que je puisse faire une substitution appropriée. Je ne vois rien de mieux pour le moment que de réécrire la tangente en termes de sinus et de cosinus :
Je vais maintenant passer du cosinus au sinus par identité trigonométrique de base :
Et enfin, je ramènerai le tout à un dénominateur commun :
Je peux maintenant passer à l'équation :
Mais à (c'est-à-dire à).
Tout est maintenant prêt pour le remplacement :
Alors soit
Cependant, veuillez noter que si, alors en même temps !
Qui souffre de ça ? Le problème avec la tangente, c'est qu'elle est indéfinie lorsque le cosinus est nul (division par zéro).
Ainsi, les racines de l'équation sont les suivantes :
Maintenant, nous passons au crible les racines dans l'intervalle :
| - s'adapte | |
| - Force brute |
Ainsi, notre équation a une racine unique dans l'intervalle, et elle est égale à.
Vous voyez : l'apparition du dénominateur (ainsi que la tangente, entraîne certaines difficultés avec les racines ! Ici, il faut être plus prudent !).
Eh bien, vous et moi avons presque terminé l'analyse des équations trigonométriques, il en reste très peu - pour résoudre indépendamment deux problèmes. Les voici.
- Résous l'équation
Nay-di-ce sont toutes les racines de cette équation-pas-nia, attachée-sur-le-zha-shi-ku. - Équation res-shi-te
Indiquez les racines de cette équation, attachées à la coupe.
Décidé? Pas très difficile ? Allons vérifier:
- Nous travaillons selon les formules de réduction :
Substituer dans l'équation :
Réécrivons tout en termes de cosinus, pour qu'il soit plus pratique de faire le remplacement :
Maintenant, il est facile de faire le remplacement :
Il est clair qu'il s'agit d'une racine étrangère, puisque l'équation n'a pas de solutions. Puis:
Nous recherchons les racines dont nous avons besoin dans l'intervalle
Réponse: .
Ici le remplacement est immédiatement visible :Alors soit
- convient ! - convient ! - convient ! - convient ! - parcelle! - beaucoup aussi ! Réponse:
Eh bien, maintenant c'est ça ! Mais la résolution des équations trigonométriques ne s'arrête pas là, nous nous retrouvons avec les cas les plus difficiles : lorsqu'il y a de l'irrationalité dans les équations ou toutes sortes de « dénominateurs complexes ». Nous verrons comment résoudre de telles tâches dans l'article pour le niveau avancé.
NIVEAU AVANCÉ
En plus des équations trigonométriques discutées dans les deux articles précédents, nous considérerons une autre classe d'équations qui nécessitent une analyse encore plus minutieuse. Ces exemples trigonométriques contiennent soit de l'irrationalité, soit un dénominateur, ce qui les rend plus difficiles à analyser.... Cependant, vous pouvez très bien rencontrer ces équations dans la partie C de la copie d'examen. Cependant, il y a une doublure argentée: pour de telles équations, en règle générale, la question de savoir laquelle de ses racines appartient à un intervalle donné n'est pas soulevée. Ne tournons pas autour du pot, mais juste des exemples trigonométriques.
Exemple 1.
Résolvez l'équation et trouvez les racines qui appartiennent au segment.
Solution:
Nous avons un dénominateur qui ne doit pas être nul ! Alors résoudre cette équation revient à résoudre le système
Résolvons chacune des équations :
Et maintenant le deuxième :
Voyons maintenant la série :
Il est clair que l'option ne nous convient pas, puisque dans ce cas le dénominateur est mis à zéro (voir la formule pour les racines de la deuxième équation)
Si, cependant, tout est en ordre, et le dénominateur n'est pas zéro ! Alors les racines de l'équation sont les suivantes :,.
Maintenant, nous sélectionnons les racines appartenant à l'intervalle.
| - ne correspond pas | - s'adapte | |
| - s'adapte | - s'adapte | |
| Force brute | Force brute |
Alors les racines sont les suivantes :
Vous voyez, même l'apparition d'un petit bruit sous la forme d'un dénominateur a affecté de manière significative la solution de l'équation : nous avons laissé tomber une série de racines qui mettent le dénominateur à zéro. La situation peut être encore plus difficile si vous tombez sur des exemples trigonométriques qui ont de l'irrationalité.
Exemple 2.
Résous l'équation:
Solution:
Bon, au moins il n'y a pas besoin de sélectionner les racines et c'est tant mieux ! Résolvons d'abord l'équation, indépendamment de l'irrationalité :
Est-ce tout? Non, hélas, ce serait trop facile ! Il faut se rappeler que seuls les nombres non négatifs peuvent être sous la racine. Puis:
La solution de cette inégalité :
Reste maintenant à savoir si certaines des racines de la première équation se sont accidentellement retrouvées là où l'inégalité n'est pas satisfaite.
Pour ce faire, vous pouvez à nouveau utiliser le tableau :
| : , mais | Pas! | |
| Oui! | ||
| Oui! |
Ainsi, l'une des racines « est tombée » de moi ! Il s'avère que si vous le mettez. Alors la réponse peut s'écrire comme suit :
Réponse:
Vous voyez, la racine demande encore plus d'attention ! Pour compliquer les choses : permettez-moi maintenant d'avoir une fonction trigonométrique sous la racine.
Exemple 3.
Comme précédemment : nous allons d'abord résoudre chacun séparément, puis nous réfléchirons à ce que nous avons fait.
Maintenant la deuxième équation :
Maintenant, le plus difficile est de savoir si des valeurs négatives sous la racine arithmétique sont obtenues si nous y substituons les racines de la première équation :
Le nombre doit être compris en radians. Puisque les radians correspondent aux degrés, les radians correspondent aux degrés. C'est le coin du deuxième quart-temps. Quel est le signe du cosinus du deuxième quart ? Moins. Et le sinus ? Un plus. Alors que dire de l'expression :
C'est moins que zéro !
Cela signifie que ce n'est pas la racine de l'équation.
C'est maintenant au tour.
Comparons ce nombre à zéro.
La cotangente est une fonction décroissante sur 1 quart (plus l'argument est petit, plus la cotangente est grande). les radians sont approximativement des degrés. Dans le même temps
depuis, alors, et donc
,
Réponse: .
Cela pourrait-il être encore plus difficile ? Je vous en prie! Ce sera plus difficile si la fonction trigonométrique est toujours sous la racine et que la deuxième partie de l'équation est à nouveau la fonction trigonométrique.
Plus il y a d'exemples trigonométriques, mieux c'est, voir plus loin :
Exemple 4.
La racine ne convient pas en raison du cosinus limité
Maintenant le deuxième :
En même temps, par définition de la racine :
Nous devons nous souvenir du cercle unité : à savoir, ces quarts où le sinus est inférieur à zéro. De quels quartiers s'agit-il ? Troisième et quatrième. Ensuite, nous nous intéresserons aux solutions de la première équation qui se situent dans le troisième ou le quatrième trimestre.
La première série produit des racines à l'intersection des troisième et quatrième quartiers. La deuxième série, qui lui est diamétralement opposée, donne naissance à des racines situées à la frontière des premier et deuxième quartiers. Par conséquent, cette série ne nous convient pas.
Réponse: ,
Et encore exemples trigonométriques avec « irrationalité difficile »... Non seulement nous avons à nouveau la fonction trigonométrique sous la racine, mais maintenant elle est aussi au dénominateur !
Exemple 5.
Eh bien, rien ne peut être fait - nous agissons comme avant.
Travaillons maintenant avec le dénominateur :
Je ne veux pas résoudre l'inégalité trigonométrique, et donc je vais agir avec ruse : je vais prendre et substituer ma série de racines dans l'inégalité :
Si - pair, alors on a :
depuis, alors tous les angles de vue se situent dans le quatrième quart. Et encore la question sacrée : quel est le signe du sinus au quatrième quart ? Négatif. Alors l'inégalité
Si c'est étrange, alors :
Dans quel quartier se trouve le coin ? C'est le coin du deuxième quart-temps. Ensuite, tous les coins sont à nouveau les coins du deuxième quart. Le sinus y est positif. Juste ce qu'il vous faut ! Ainsi, la série :
Convient !
Traitez la deuxième série de racines de la même manière :
Nous substituons dans notre inégalité :
Si - pair, alors
Coins du premier quart. Le sinus y est positif, donc la série convient. Maintenant, si - impair, alors :
convient aussi !
Eh bien, maintenant nous écrivons la réponse!
Réponse:
Eh bien, c'était peut-être le cas le plus chronophage. Maintenant, je vous propose des problèmes pour votre propre solution.
Entraînement
- Résoudre et trouver toutes les racines de l'équation qui appartiennent au segment.
Solutions:
Première équation :
ou
Racine ODZ :Deuxième équation :
Sélection des racines qui appartiennent à l'espace
Réponse:
Ou
ou
Mais
Envisager:. Si - pair, alors
- ne correspond pas!
Si - impair, : - convient !
Cela signifie que notre équation a la série de racines suivante :
ou
Sélection des racines dans l'intervalle :
| - ne correspond pas | - s'adapte | |
| - s'adapte | - parcelle | |
| - s'adapte | parcelle |
Réponse: , .
Ou
Depuis, quand la tangente n'est pas définie. On jette tout de suite cette série de racines !
Deuxième partie:
Dans le même temps, selon ODZ, il est nécessaire que
On vérifie les racines trouvées dans la première équation :
Si le signe est :
Coins du premier quart où la tangente est positive. Ne convient pas !
Si le signe est :
Quatrième quart d'angle. Là, la tangente est négative. Convient. Nous écrivons la réponse :
Réponse: , .
Nous avons couvert ensemble des exemples trigonométriques complexes dans cet article, mais vous devez résoudre les équations vous-même.
FORMULES SOMMAIRE ET DE BASE
Une équation trigonométrique est une équation dans laquelle l'inconnue est strictement sous le signe de la fonction trigonométrique.
Il existe deux manières de résoudre les équations trigonométriques :
La première consiste à utiliser des formules.
La deuxième façon passe par le cercle trigonométrique.
Vous permet de mesurer des angles, de trouver leurs sinus, cosinus, etc.
Préparation au niveau profil de l'examen d'état unifié en mathématiques. Du matériel utile sur la trigonométrie, de grandes conférences vidéo théoriques, des analyses vidéo de problèmes et une sélection de travaux des années passées.
Matériaux utiles
Sélections vidéo et cours en ligne
Formules trigonométriques
Illustration géométrique des formules trigonométriques
Fonctions d'arc. Équations trigonométriques les plus simples
Équations trigonométriques
- La théorie nécessaire pour résoudre les problèmes.
- a) Résoudre l'équation $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $.
b) Trouver toutes les racines de cette équation qui appartiennent à l'intervalle $\left [-\dfrac (7\pi)(2); -\dfrac (3\pi)(2)\droit] $. - a) Résoudre l'équation $\dfrac (6) (\cos ^ 2 x) - \dfrac (7) (\cos x) + 1 = 0 $.
b) Trouvez toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [-3 \ pi; - \ pi \ droite] $. - Résolvez l'équation $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $.
- a) Résous l'équation $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $.
b) Trouvez toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [- \ pi; \dfrac (5\pi)(2)\droit] $. - a) Résoudre l'équation $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $.
- Résoudre l'équation $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $.
- Résoudre l'équation $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $.
b) Trouver toutes les racines de cette équation qui appartiennent à l'intervalle $\left [-\dfrac (5\pi)(2); - \ pi \ à droite) $.- a) Résoudre l'équation $ \ cos 2x = \ sin \ left (\ dfrac (3 \ pi) (2) - x \ right) $.
b) Trouver toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [\ dfrac (3 \ pi) (2); \dfrac (5\pi)(2)\droit] $. - a) Résoudre l'équation $ 2 \ sin ^ 2 \ left (\ dfrac (3 \ pi) (2) + x \ right) = \ sqrt3 \ cos x $.
b) Trouver toutes les racines de cette équation qui appartiennent à l'intervalle $\left [-\dfrac (7\pi)(2); -2 \ pi \ droite] $.
Analyse vidéo des tâches
b) Trouvez toutes les racines de cette équation qui appartiennent au segment $ \ left [\ sqrt (3); \ sqrt (20) \ right] $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $\left [-\dfrac (9\pi)(2); -3 \ pi \ droit] $.
b) Trouvez toutes les racines de cette équation qui appartiennent au segment $ \ left [- \ sqrt (3); \ sqrt (30) \ right] $.
a) Résoudre l'équation $ \ cos 2x = 1 - \ cos \ left (\ dfrac (\ pi) (2) - x \ right) $.
b) Trouver toutes les racines de cette équation qui appartiennent à l'intervalle $\left [-\dfrac (5\pi)(2); - \ pi \ à droite) $.
a) Résoudre l'équation $ \ cos ^ 2 (\ pi - x) - \ sin \ left (x + \ dfrac (3 \ pi) (2) \ right) = 0 $.
b) Trouver toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [\ dfrac (5 \ pi) (2); 4 \ pi \ droit] $.
b) Trouvez toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [\ log_5 2; \ log_5 20 \ droit] $.
a) Résoudre l'équation $ 8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) = 9 $.
b) Trouver toutes les racines de cette équation qui appartiennent à l'intervalle $\left [-\dfrac (5\pi)(2); - \ pi \ droite] $.
a) Résoudre l'équation $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $.
b) Trouvez toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [\ pi; \dfrac (5\pi)(2)\droit] $.
a) Résoudre l'équation $ \ gauche (\ dfrac (1) (49) \ droite) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $.
b) Trouver toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [\ dfrac (3 \ pi) (2); 3 \ pi \ droit] $.
a) Résoudre l'équation $ \ sin x + \ left (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ right) \ left (\ cos \ dfrac (x) (2) + \ sin \ dfrac (x) (2) \ right) = 0 $.
b) Trouvez toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [\ pi; \dfrac (5\pi)(2)\droit] $.
a) Résoudre l'équation $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $.
b) Trouvez toutes les racines de cette équation qui appartiennent à l'intervalle $ \ left [-4 \ pi; -\dfrac (5\pi)(2)\droit] $.
Une sélection de missions des années précédentes
- a) Résoudre l'équation $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $\left [-\dfrac (9\pi)(2); -3 \ pi \ droit] $. (USE-2018. Première vague) - a) Résoudre l'équation $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $.
b) Trouvez toutes les racines de cette équation qui appartiennent au segment $ \ left [- \ sqrt (3); \ sqrt (30) \ right] $. (USE-2018. Early wave, jour de réserve) - a) Résoudre l'équation $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) = \ cos x $.
b) Trouvez toutes les racines de cette équation qui appartiennent au segment $ \ left [-2 \ pi; -\dfrac(\pi)(2)\droit] $. (USE-2018. Vague principale) - a) Résoudre l'équation $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ left (x + \ dfrac (\ pi) (6) \ right) $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $\left [3\pi; \dfrac (9\pi)(2)\droit] $. (USE-2018. Vague principale) - a) Résoudre l'équation $ \ sin x + 2 \ sin \ left (2x + \ dfrac (\ pi) (6) \ right) = \ sqrt3 \ sin 2x + 1 $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $\left [-\dfrac (7\pi)(2); -2 \ pi \ droite] $. (USE-2018. Vague principale) - a) Résoudre l'équation $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) $.
b) Trouvez toutes les racines de cette équation qui appartiennent au segment $ \ left [-4 \ pi; -\dfrac (5\pi)(2)\droit] $. (USE-2018. Vague principale) - a) Résoudre l'équation $ 2 \ sin \ left (2x + \ dfrac (\ pi) (3) \ right) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $.
- a) Résoudre l'équation $ 2 \ sqrt3 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) - \ cos 2x = 3 \ cos x - 1 $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $ \ left [2 \ pi; \dfrac (7\pi)(2)\droit] $. (USE-2018. Vague principale) - a) Résoudre l'équation $ 2 \ sin \ left (2x + \ dfrac (\ pi) (6) \ right) - \ cos x = \ sqrt3 \ sin 2x - 1 $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $\left [\dfrac (5\pi)(2); 4 \ pi \ droit] $. (USE-2018. Vague principale) - a) Résoudre l'équation $ \ sqrt2 \ sin \ left (\ dfrac (\ pi) (4) + x \ right) + \ cos 2x = \ sin x - 1 $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $ \ left [\ dfrac (7 \ pi) (2); 5 \ pi \ droit] $. (USE-2018. Vague principale) - a) Résoudre l'équation $ \ sqrt2 \ sin \ left (2x + \ dfrac (\ pi) (4) \ right) + \ sqrt2 \ cos x = \ sin 2x - 1 $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $\left [-\dfrac (5\pi)(2); - \ pi \ droite] $. (USE-2018. Vague principale) - a) Résoudre l'équation $ 2 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) + \ cos 2x = \ sqrt3 \ cos x + 1 $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $ \ left [-3 \ pi; -\dfrac (3\pi)(2)\droit] $. (USE-2018. Vague principale)
b) Trouvez toutes les racines de cette équation qui appartiennent au segment $ \ left [\ pi; \dfrac (5\pi)(2)\droit] $. (USE-2018. Vague principale)- a) Résoudre l'équation $ 2 \ sin \ left (x + \ dfrac (\ pi) (4) \ right) + \ cos 2x = \ sqrt2 \ cos x + 1 $.
b) Trouvez toutes les racines de cette équation qui appartiennent au segment $ \ left [\ pi; \dfrac (5\pi)(2)\droit] $. (USE-2018. Vague principale, jour de réserve) - a) Résoudre l'équation $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $\left [-\dfrac (7\pi)(2); -2 \ pi \ droite] $. (USE-2018. Vague principale, jour de réserve) - a) Résoudre l'équation $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $\left [-\dfrac (9\pi)(2); -3 \ pi \ droit] $. (USE-2018. Vague principale, jour de réserve) - a) Résoudre l'équation $ 2 \ sqrt2 \ sin \ left (x + \ dfrac (\ pi) (3) \ right) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $.
b) Trouver toutes les racines de cette équation qui appartiennent au segment $ \ left [-3 \ pi; -\dfrac (3\pi)(2)\droit] $. (USE-2018. Vague principale, jour de réserve) - a) Résoudre l'équation $ x - 3 \ sqrt (x - 1) + 1 = 0 $.
b) Trouvez toutes les racines de cette équation qui appartiennent au segment $ \ left [\ sqrt (3); \ sqrt (20) \ right] $. (USE-2018. Vague principale, jour de réserve) - a) Résoudre l'équation $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [-\dfrac(\pi)(2);\\pi\right]$. (USE-2017, vague principale, jour de réserve) - a) Résoudre l'équation $ \ log_3 (x ^ 2 - 2x) = 1 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [\ log_2 0 (,) 2; \ \ log_2 5 \ right] $. (USE-2017, vague principale, jour de réserve) - a) Résoudre l'équation $ \ log_3 (x ^ 2 - 24x) = 4 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [\ log_2 0 (,) 1; \ 12 \ sqrt (5) \ right] $. (USE-2017, vague principale, jour de réserve) - a) Résoudre l'équation $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [2\pi;\\dfrac (7\pi)(2)\right]$. (USE-2017, vague principale) - a) Résoudre l'équation $ \ log_8 \ left (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ right) = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [\dfrac (3\pi)(2);\3\pi\right]$. (USE-2017, vague principale) - a) Résoudre l'équation $ \ log_4 \ left (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ right) = x $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [\dfrac (5\pi)(2);\4\pi\right]$. (USE-2017, vague principale) - a) Résoudre l'équation $ 2 \ log_2 ^ 2 \ left (\ sin x \ right) - 5 \ log_2 \ left (\ sin x \ right) - 3 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [- 3\pi;\-\dfrac (3\pi)(2)\right] $. (USE-2017, vague principale) - a) Résoudre l'équation $ 81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [- 4\pi;\-\dfrac (5\pi)(2)\right] $. (USE-2017, vague principale) - a) Résoudre l'équation $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [\ log_5 2; \ \ log_5 20 \ right] $. (USE-2017, première vague) - a) Résoudre l'équation $ 2 \ log ^ 2_9 x - 3 \ log_9 x + 1 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [\ sqrt (10); \ \ sqrt (99) \ right] $. (USE-2016, vague principale, jour de réserve) - a) Résoudre l'équation $ 6 \ log ^ 2_8 x - 5 \ log_8 x + 1 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [2; \ 2 (,) 5 \ right] $. (USE-2016, vague principale, jour de réserve) - a) Résoudre l'équation $ \ sin 2x = 2 \ sin x + \ sin \ left (x + \ dfrac (3 \ pi) (2) \ right) + 1 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [-4\pi;\-\dfrac (5\pi)(2)\right]$. (USE-2016, vague principale, jour de réserve) - a) Résoudre l'équation $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ left (\ dfrac (3 \ pi) (2) - x \ right) $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [\dfrac (3\pi)(2);\3\pi\right]$. (USE-2016, vague principale) - a) Résoudre l'équation $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [-2\pi;\-\dfrac(\pi)(2)\right]$. (USE-2016, vague principale) - a) Résoudre l'équation $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [\ log_2 5; \ \ log_2 11 \ right] $. (USE-2016, première vague) - a) Résoudre l'équation $ \ cos 2x + \ cos ^ 2 \ left (\ dfrac (3 \ pi) (2) - x \ right) = 0,25 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [-4\pi;\-\dfrac (5\pi)(2)\right]$. (USE-2016, première vague) - a) Résoudre l'équation $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [-3\pi;\-\dfrac (3\pi)(2)\right]$. (USE-2016, première vague) - a) Résoudre l'équation $ \ dfrac (\ sin2x) (\ sin \ left (\ dfrac (7 \ pi) (2) - x \ right)) = \ sqrt (2) $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left $. (USE-2015, vague principale) - a) Résoudre l'équation $ 4 \ sin ^ 2 x = \ mathrm (tg) x $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [- \ pi; \ 0 \ right] $. (USE-2015, vague principale) - a) Résoudre l'équation $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [\pi;\\dfrac (5\pi)(2)\right]$. (USE-2015, vague principale) - a) Résoudre l'équation $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [-3\pi;\-\dfrac (3\pi)(2)\right]$. (USE-2015, vague principale) - a) Résoudre l'équation $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [\pi;\\dfrac (5\pi)(2)\right]$. (USE-2015, première vague) - a) Résoudre l'équation $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $\left [2\pi;\\dfrac (7\pi)(2)\right]$. (USE-2015, première vague) - a) Résoudre l'équation $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $.
b) Indiquer les racines de cette équation qui appartiennent au segment $\left [\dfrac (5\pi)(2); \ 4 \ pi \ à droite] $. (USE-2014, vague principale) - a) Résoudre l'équation $ 2 \ sqrt (3) \ cos ^ 2 \ left (\ dfrac (3 \ pi) (2) + x \ right) - \ sin 2x = 0 $.
b) Indiquer les racines de cette équation qui appartiennent au segment $\left [\dfrac (3\pi)(2); \ 3 \ pi \ right] $. (USE-2014, vague principale) - a) Résoudre l'équation $ \ cos 2x + \ sqrt (2) \ sin \ left (\ dfrac (\ pi) (2) + x \ right) + 1 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ right] $. (USE-2014, vague principale) - a) Résoudre l'équation $ - \ sqrt (2) \ sin \ left (- \ dfrac (5 \ pi) (2) + x \ right) \ cdot \ sin x = \ cos x $.
b) Indiquer les racines de cette équation qui appartiennent au segment $\left [\dfrac (9\pi)(2); \ 6 \ pi \ à droite] $. (USE-2014, première vague) - a) Résoudre l'équation $ \ sin 2x = \ sin \ left (\ dfrac (\ pi) (2) + x \ right) $.
b) Indiquer les racines de cette équation qui appartiennent au segment $\left [-\dfrac (7\pi)(2); \ - \ dfrac (5 \ pi) (2) \ right] $. (USE-2013, vague principale) - a) Résoudre l'équation $ 6 \ sin ^ 2 x + 5 \ sin \ left (\ dfrac (\ pi) (2) - x \ right) - 2 = 0 $.
b) Indiquez les racines de cette équation qui appartiennent au segment $ \ left [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ right] $. (USE-2012, deuxième vague)
Le but de la leçon :
une) consolider la capacité à résoudre les équations trigonométriques les plus simples;
b) apprendre à choisir les racines des équations trigonométriques à partir d'un intervalle donné
Pendant les cours.
1. Actualisation des connaissances.
a) Vérification des devoirs : la classe a reçu un devoir d'anticipation - pour résoudre l'équation et trouver un moyen de sélectionner des racines à partir d'un intervalle donné.
1) car X= -0,5, où xI [-]. Réponse:.
2) le péché X=, où xI. Réponse: ; ...
3) cos 2 X= -, où I. Réponse:
Les élèves notent la solution au tableau, quelqu'un utilisant un graphique, quelqu'un utilisant une méthode de sélection.
A cette époque la classe fonctionne à l'oral.
Trouvez le sens de l'expression :
a) tg - sin + cos + sin. Réponse 1.
b) 2arccos 0 + 3 arccos 1. Réponse: ?
c) arcsin + arcsin. Réponse:.
d) 5 arctan (-) - arcco (-). Réponse:-.
- Vérifions tes devoirs, ouvrons tes cahiers de devoirs.
Certains d'entre vous ont trouvé une solution par une méthode d'ajustement, et d'autres par un graphique.
2. Conclusion sur la façon de résoudre ces tâches et l'énoncé du problème, c'est-à-dire le message du sujet et le but de la leçon.
- a) Il est difficile à résoudre à l'aide d'une sélection si un grand intervalle est donné.
- b) La méthode graphique ne donne pas des résultats précis, nécessite une vérification et prend beaucoup de temps.
- Par conséquent, il doit y avoir au moins une autre méthode, la plus universelle - essayons de la trouver. Alors, qu'allons-nous faire en classe aujourd'hui? (Apprenez à choisir les racines d'une équation trigonométrique à un intervalle donné.)
- Exemple 1 (L'élève va au tableau)
car X= -0,5, où xI [-].
Question : De quoi dépend la réponse à cette tâche ? (À partir de la solution générale de l'équation. Écrivons la solution sous forme générale). La décision est écrite au tableau
= + 2?k, où k R.
- Écrivons cette solution sous la forme d'un ensemble :

- Qu'en pensez-vous, pour quel enregistrement de la solution est-il pratique de choisir des racines dans l'intervalle ? (à partir de la deuxième entrée). Mais c'est encore une méthode de sélection. Que devons-nous savoir pour obtenir la bonne réponse ? (Vous devez connaître les valeurs de k).
(Faisons un modèle mathématique pour trouver k).
puisque kI Z, alors k = 0, d'où X= = |
cette inégalité montre qu'il n'y a pas de valeurs entières de k. |
Conclusion: Pour sélectionner les racines d'un intervalle donné lors de la résolution d'une équation trigonométrique, vous devez :
- pour résoudre une équation de la forme péché x = un, cos x = un il est plus commode d'écrire les racines de l'équation sous la forme de deux séries de racines.
- pour résoudre des équations de la forme tg x = un, ctg x = unécris la formule générale des racines.
- établir un modèle mathématique pour chaque solution sous la forme d'une double inégalité et trouver la valeur entière du paramètre k ou n.
- substituez ces valeurs dans la formule racine et calculez-les.
Résoudre les exemples 2 et 3 des devoirs en utilisant l'algorithme obtenu. En parallèle, deux élèves travaillent au tableau, puis vérifient le travail.
Dans cet article, je vais essayer d'expliquer 2 façons sélection de racines dans l'équation trigonométrique: en utilisant les inégalités et en utilisant le cercle trigonométrique. Passons directement à un exemple illustratif et traitons le cas.
A) Résoudre l'équation sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
b) Trouver toutes les racines de cette équation appartenant à l'intervalle [-7Pi/2 ; -2Pi]
Résolvons le point a.
On utilise la formule de réduction pour le sinus sin (Pi/2 + x) = cos (x)
Sqrt (2) cos ^ 2x = cosx
Sqrt (2) cos ^ 2x - cosx = 0
Cosx (sqrt (2) cosx - 1) = 0
X1 = Pi / 2 + Broche, n Z
Sqrt (2) cosx - 1 = 0
Cosx = 1 / carré (2)
Cosx = carré (2) / 2
X2 = arccos (sqrt (2) / 2) + 2Pin, n Z
x3 = -arccos (sqrt (2) / 2) + 2Pin, n Z
X2 = Pi / 4 + 2Pin, n Z
x3 = -Pi / 4 + 2Pin, n Z
Résolvons le point b.
1) Sélection de racines à l'aide d'inégalités
Ici tout se fait simplement, on substitue les racines obtenues dans l'intervalle donné [-7Pi/2; -2Pi], trouvez des valeurs entières pour n.
7Pi / 2 inférieur ou égal à Pi / 2 + Pin inférieur ou égal à -2Pi
Divisez tout en Pi à la fois
7/2 est inférieur ou égal à 1/2 + n est inférieur ou égal à -2
7/2 - 1/2 inférieur ou égal à n inférieur ou égal à -2 - 1/2
4 inférieur ou égal à n inférieur ou égal à -5/2
L'entier n dans cette plage est -4 et -3. Donc les racines appartenant à cet intervalle seront Pi/2 + Pi (-4) = -7Pi/2, Pi/2 + Pi (-3) = -5Pi/2
De même, nous faisons deux autres inégalités
7Pi / 2 inférieur ou égal à Pi / 4 + 2Pin inférieur ou égal à -2Pi
-15/8 inférieur ou égal à n inférieur ou égal à -9/8
Il n'y a pas d'entier n dans cet intervalle
7Pi / 2 inférieur ou égal à -Pi / 4 + 2Pin inférieur ou égal à -2Pi
-13/8 inférieur ou égal à n inférieur ou égal à -7/8
Un entier n dans cet intervalle est -1. La racine sélectionnée sur cet intervalle est donc -Pi / 4 + 2Pi * (- 1) = -9Pi / 4.
Donc la réponse au point b : -7Pi/2, -5Pi/2, -9Pi/4
2) Sélection des racines à l'aide d'un cercle trigonométrique
Pour utiliser cette méthode, vous devez comprendre comment fonctionne ce cercle. Je vais essayer d'expliquer dans un langage simple comment je comprends cela. Je pense que dans les écoles d'algèbre, ce sujet a été expliqué à plusieurs reprises par les mots intelligents du professeur, des formulations complexes dans les manuels. Personnellement, je comprends cela comme un cercle qui peut être parcouru un nombre infini de fois, du fait que les fonctions sinus et cosinus sont périodiques.
Allons dans le sens antihoraire une fois
Faisons le tour 2 fois dans le sens antihoraire
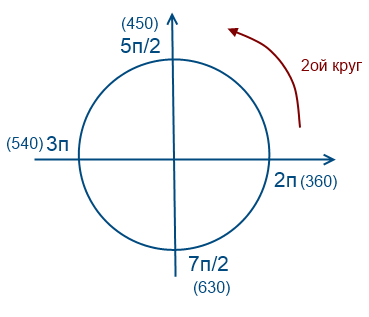
Faisons le tour 1 fois dans le sens des aiguilles d'une montre (les valeurs seront négatives)

Revenons à notre question, nous devons sélectionner des racines dans l'intervalle [-7Pi/2; -2Pi]
Pour arriver aux nombres -7Pi/2 et -2Pi, vous devez faire deux fois le tour du cercle dans le sens inverse des aiguilles d'une montre. Afin de trouver les racines de l'équation sur cet intervalle, il est nécessaire d'estimer et de substituer.
Considérons x = Pi / 2 + Pin. Quelle est la valeur approximative de n pour que la valeur de x se situe quelque part dans cet intervalle ? En substituant, disons -2, nous obtenons Pi/2 - 2Pi = -3Pi/2, évidemment ce n'est pas inclus dans notre intervalle, donc nous prenons moins de -3, Pi/2 - 3Pi = -5Pi/2, ça rentre, essayons à nouveau -4, Pi/2 - 4Pi = -7Pi/2 convient également.
En raisonnant de la même manière pour Pi/4 + 2Pin et -Pi/4 + 2Pin, on trouve une autre racine -9Pi/4.

Comparaison des deux méthodes.
La première méthode (utilisant les inégalités) est beaucoup plus fiable et beaucoup plus facile à comprendre, mais si vous traitez vraiment sérieusement le cercle trigonométrique et la deuxième méthode de sélection, alors la sélection des racines sera beaucoup plus rapide, vous pouvez gagner environ 15 minutes sur l'examen.
a) Résous l'équation :.
b) Trouve toutes les racines de cette équation qui appartiennent au segment.
La solution du problème

Cette leçon considère un exemple de résolution d'équation trigonométrique, qui peut être utilisé comme exemple pour résoudre des problèmes de type C1 en préparation à l'examen de mathématiques.
Tout d'abord, la portée de la fonction est déterminée - toutes les valeurs autorisées de l'argument. Ensuite, pendant la résolution, la fonction sinus trigonométrique est convertie en cosinus à l'aide de la formule de réduction. De plus, tous les termes de l'équation sont transférés sur son côté gauche, où le facteur commun est retiré des parenthèses. Chaque facteur est égal à zéro, ce qui vous permet de déterminer les racines de l'équation. Ensuite, les racines appartenant au segment donné sont déterminées par la méthode des tours. Pour ce faire, une boucle est marquée sur le cercle unité construit de la limite gauche du segment spécifié vers la droite. De plus, les racines trouvées sur le cercle unité sont reliées par des segments avec son centre et les points auxquels ces segments coupent la boucle sont déterminés. Ces points d'intersection sont la réponse souhaitée à la deuxième partie du problème.

































