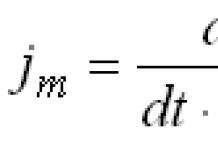Détermination des lignes qui se croisent dans l'espace. La position relative de deux lignes dans l'espace. Preuve du test de ligne oblique. Comment trouver le point d'intersection des lignes spatiales

Conférence: Lignes sécantes, parallèles et croisées ; perpendiculaire des lignes

Lignes d'intersection

S'il y a plusieurs lignes droites sur un plan, alors tôt ou tard elles se couperont arbitrairement, ou à angle droit, ou seront parallèles. Examinons chaque cas.

Les lignes qui ont au moins un point d'intersection peuvent être appelées sécantes.

Vous vous demandez peut-être pourquoi au moins une ligne droite ne peut pas couper une autre ligne droite deux ou trois fois. Tu as raison! Mais les lignes droites peuvent complètement coïncider les unes avec les autres. Dans ce cas, il y aura une infinité de points communs.

Parallélisme

Parallèle Vous pouvez nommer ces lignes qui ne se croiseront jamais, même à l'infini.

Autrement dit, les parallèles sont ceux qui n’ont pas un seul point commun. Veuillez noter que cette définition n'est vrai que si les lignes sont dans le même plan, mais si elles n'ont pas de points communs, étant dans des plans différents, alors elles sont considérées comme sécantes.

Exemples de lignes parallèles dans la vie : deux bords opposés d'un écran de moniteur, des lignes dans des cahiers, ainsi que de nombreuses autres parties d'objets ayant une forme carrée, rectangulaire et autre.

Quand ils veulent montrer par écrit qu'une ligne droite parallèlement à la seconde, puis utilisez la notation suivante a||b. Cette entrée indique que la ligne a est parallèle à la ligne b.

Lors de l'étude de ce sujet, il est important de comprendre une autre affirmation : passant par un certain point du plan qui n'appartient pas à une ligne donnée, on peut tracer une seule ligne parallèle. Mais attention, encore une fois la correction est dans l'avion. Si l'on considère espace tridimensionnel, alors il est possible de tracer un nombre infini de lignes droites qui ne se couperont pas, mais se couperont.

La déclaration décrite ci-dessus s'appelle axiome des droites parallèles.

Perpendicularité

Les lignes directes ne peuvent être appelées que si perpendiculaire, s'ils se coupent selon un angle égal à 90 degrés.

Dans l’espace, passant par un certain point sur une ligne, un nombre infini de lignes perpendiculaires peuvent être tracées. Cependant, si nous parlons d'un plan, vous pouvez tracer une seule ligne perpendiculaire passant par un point sur une ligne.

Lignes droites croisées. Sécante

Si certaines lignes se coupent en un certain point selon un angle arbitraire, elles peuvent être appelées métissage.

Toutes les lignes qui se croisent ont des angles verticaux et adjacents.

Si les angles formés par deux droites sécantes ont un côté en commun, alors ils sont dits adjacents :

Les angles adjacents totalisent 180 degrés.

Si deux droites dans l’espace ont un point commun, alors on dit que ces deux droites se coupent. Dans la figure suivante, les lignes a et b se coupent au point A. Les lignes a et c ne se coupent pas.

Deux lignes droites n'ont qu'un seul point commun ou n'ont aucun point commun.

Lignes parallèles

Deux droites dans l’espace sont dites parallèles si elles se trouvent dans le même plan et ne se coupent pas. Pour désigner des lignes parallèles, utilisez une icône spéciale - ||.

La notation a||b signifie que la ligne a est parallèle à la ligne b. Dans la figure présentée ci-dessus, les droites a et c sont parallèles.

Théorème des lignes parallèles

Par tout point de l'espace qui ne se trouve pas sur une ligne donnée, passe une ligne parallèle à celle donnée et, de plus, une seule.

Les lignes des passages piétons

Deux droites situées dans le même plan peuvent se croiser ou être parallèles. Mais dans l’espace, deux droites n’appartiennent pas nécessairement à ce plan. Ils peuvent être situés dans deux plans différents.

Il est évident que les lignes situées dans des plans différents ne se coupent pas et ne sont pas des lignes parallèles. Deux droites qui ne se trouvent pas dans le même plan sont appelées traverser des lignes droites.

La figure suivante montre deux droites sécantes a et b, situées dans des plans différents.

Test et théorème sur les lignes asymétriques

Si l'une des deux lignes se trouve dans un certain plan et que l'autre ligne coupe ce plan en un point qui ne se trouve pas sur la première ligne, alors ces lignes se coupent.

Théorème sur les lignes asymétriques: par chacune de deux lignes sécantes passe un plan parallèle à l'autre ligne, et de plus un seul.

Ainsi, nous avons considéré tous les cas possibles de positions relatives des lignes dans l'espace. Il n'y en a que trois.

1. Les lignes se croisent. (C'est-à-dire qu'ils n'ont qu'un seul point commun.)

2. Les droites sont parallèles. (C'est-à-dire qu'ils n'ont pas de points communs et se trouvent dans le même plan.)

3. Les lignes droites se croisent. (C'est-à-dire qu'ils sont situés dans des plans différents.)

Pas même une minute ne s'était écoulée avant que je crée un nouveau dossier Verdov et que je poursuive un sujet aussi fascinant. Vous devez capturer des moments d'ambiance de travail, il n'y aura donc pas d'introduction lyrique. Il y aura une fessée prosaïque =)

Deux espaces droits peuvent :

1) se croiser ;

2) se croisent au point ;

3) être parallèle ;

4) correspondre.

Le cas n°1 est fondamentalement différent des autres cas. Deux droites se coupent si elles ne se trouvent pas dans le même plan. Levez un bras et étendez l’autre bras vers l’avant – voici un exemple de lignes croisées. Aux points n° 2 à 4, les lignes droites doivent se trouver dans un seul avion.

Comment connaître les positions relatives des lignes dans l'espace ?

Considérons deux espaces directs :

- droit, donné par le point et un vecteur de direction ;
– une droite définie par un point et un vecteur directeur.

Pour une meilleure compréhension, faisons un dessin schématique :

Le dessin montre des lignes droites sécantes à titre d'exemple.

Comment gérer ces lignes droites ?

Puisque les points sont connus, il est facile de trouver le vecteur.

Si droit croiser, alors les vecteurs pas coplanaire(voir leçon Dépendance linéaire (non) des vecteurs. Base des vecteurs), et, par conséquent, le déterminant composé de leurs coordonnées est non nul. Ou, ce qui revient en fait au même, il sera non nul : .

Dans les cas n°2 à 4, notre structure « tombe » dans un seul plan, tandis que les vecteurs coplanaire, et le produit mixte de vecteurs linéairement dépendants est égal à zéro : .

Développons davantage l'algorithme. Faisons comme si Par conséquent, les lignes se coupent, sont parallèles ou coïncident.

Si les vecteurs directeurs colinéaire, alors les lignes sont soit parallèles, soit coïncidentes. Pour le clou final, je propose la technique suivante : prendre n'importe quel point sur une droite et substituer ses coordonnées dans l'équation de la deuxième droite ; si les coordonnées « correspondent », alors les lignes coïncident ; si elles « ne correspondent pas », alors les lignes sont parallèles.

L'algorithme est simple, mais exemples pratiquesça ne fera toujours pas de mal :

Exemple 11

Découvrez la position relative de deux lignes

Solution: comme dans de nombreux problèmes de géométrie, il convient de formuler la solution point par point :

1) On sort les points et les vecteurs directeurs des équations :

2) Trouvez le vecteur :

Ainsi, les vecteurs sont coplanaires, ce qui signifie que les lignes se trouvent dans le même plan et peuvent se croiser, être parallèles ou coïncider.

4) Vérifions la colinéarité des vecteurs directeurs.

Créons un système à partir des coordonnées correspondantes de ces vecteurs :

Depuis tout le mondeéquations, il s'ensuit que, par conséquent, le système est cohérent, les coordonnées correspondantes des vecteurs sont proportionnelles et les vecteurs sont colinéaires.

Conclusion : les droites sont parallèles ou coïncident.

5) Découvrez si les lignes ont des points communs. Prenons un point appartenant à la première droite et substituons ses coordonnées dans les équations de la droite :

Ainsi, les droites n’ont pas de points communs et elles n’ont d’autre choix que d’être parallèles.

Répondre:

Exemple intéressant Pour décision indépendante:

Exemple 12

Découvrez les positions relatives des lignes

Ceci est un exemple à résoudre par vous-même. Veuillez noter que la deuxième ligne a la lettre comme paramètre. Logique. Dans le cas général, il s’agit de deux lignes différentes, chaque ligne possède donc son propre paramètre.

Et encore une fois je vous conseille de ne pas sauter les exemples, les tâches que je propose sont loin d'être aléatoires ;-)

Problèmes avec une ligne dans l'espace

Dans la dernière partie de la leçon, j'essaierai de considérer quantité maximale divers problèmes avec les lignes spatiales. Dans ce cas, l'ordre original de l'histoire sera observé : nous examinerons d'abord les problèmes de lignes qui se croisent, puis de lignes qui se croisent, et à la fin nous parlerons de lignes parallèles dans l'espace. Cependant, je dois dire que certaines tâches de cette leçon peuvent être formulées pour plusieurs cas de localisation de lignes à la fois, et à cet égard, la division de la section en paragraphes est quelque peu arbitraire. Il y en a plus exemples simples, il y en a plus exemples complexes, et j'espère que chacun trouvera ce dont il a besoin.

Les lignes des passages piétons

Permettez-moi de vous rappeler que les lignes droites se coupent s'il n'y a pas de plan dans lequel elles se trouvent toutes les deux. En réfléchissant à la pratique, un problème de monstre m'est venu à l'esprit, et maintenant je suis heureux de présenter à votre attention un dragon à quatre têtes :

Exemple 13

Étant donné des lignes droites. Requis:

a) prouver que les lignes se coupent ;

b) trouver les équations d'une droite passant par un point perpendiculaire aux droites données ;

c) composer les équations d'une droite qui contient perpendiculaire commune les lignes des passages piétons;

d) trouver la distance entre les lignes.

Solution: Celui qui marche maîtrisera la route :

a) Montrons que les droites se coupent. Trouvons les points et les vecteurs directeurs de ces droites :

Trouvons le vecteur :

Calculons produit mixte de vecteurs:

Ainsi, les vecteurs pas coplanaire, ce qui signifie que les lignes se croisent, ce qui restait à prouver.

Tout le monde a probablement remarqué depuis longtemps que pour franchir les lignes, l'algorithme de vérification est le plus court.

b) Trouver les équations de la droite qui passe par le point et qui est perpendiculaire aux droites. Faisons un dessin schématique :

Pour changer, j'ai posté un direct DERRIÈRE tout droit, regardez comme c'est un peu effacé aux points de croisement. Croisement? Oui, en général, la droite « de » sera croisée avec les droites originelles. Même si ce moment ne nous intéresse pas, il suffit de construire une ligne perpendiculaire et c’est tout.

Que sait-on du « de » direct ? Le point qui lui appartient est connu. Il n'y a pas assez de vecteur de guidage.

Selon la condition, la droite doit être perpendiculaire aux droites, ce qui signifie que son vecteur directeur sera orthogonal aux vecteurs directeurs. Déjà familier depuis l’exemple n°9, trouvons le produit vectoriel :

Composons les équations de la droite « de » à l’aide d’un point et d’un vecteur directeur :

Prêt. En principe, vous pouvez changer les signes dans les dénominateurs et écrire la réponse sous la forme , mais ce n'est pas nécessaire.

Pour vérifier, vous devez remplacer les coordonnées du point dans les équations de droite résultantes, puis utiliser produit scalaire de vecteurs assurez-vous que le vecteur est bien orthogonal aux vecteurs directeurs « pe un » et « pe deux ».

Comment trouver les équations d’une droite contenant une perpendiculaire commune ?

c) Ce problème sera plus difficile. Je recommande aux nuls de sauter ce point, je ne veux pas refroidir votre sincère sympathie pour la géométrie analytique =) D'ailleurs, il vaudrait peut-être mieux que les lecteurs plus préparés s'attendent aussi, le fait est qu'en termes de complexité l'exemple devrait être placé en dernier lieu dans l'article, mais selon la logique de présentation, il devrait être situé ici.

Vous devez donc trouver les équations d’une droite qui contient la perpendiculaire commune des droites obliques.

- il s'agit d'un segment reliant ces droites et perpendiculaire à ces droites :

Voici notre beau mec : - perpendiculaire commune aux lignes qui se croisent. Il est le seul. Il n’y en a pas d’autre comme ça. Nous devons créer des équations pour la droite qui contient ce segment.

Que sait-on du « euh » direct ? Son vecteur directeur est connu, trouvé dans le paragraphe précédent. Mais malheureusement, nous ne connaissons aucun point appartenant à la droite « em », ni les extrémités de la perpendiculaire – les points . Où cette ligne perpendiculaire coupe-t-elle les deux lignes originales ? En Afrique, en Antarctique ? D'après l'examen initial et l'analyse de l'état, il n'est pas du tout clair comment résoudre le problème... Mais il y a mouvement délicat, associé à l'utilisation d'équations paramétriques en ligne droite.

Nous formulerons la décision point par point :

1) Réécrivons les équations de la première ligne sous forme paramétrique :

Considérons le point. Nous ne connaissons pas les coordonnées. MAIS. Si un point appartient à une droite donnée, alors ses coordonnées correspondent à , notons-le par . Ensuite les coordonnées du point s’écriront sous la forme :

La vie s'améliore, une inconnue ne signifie toujours pas trois inconnues.

2) Le même outrage doit être commis sur le deuxième point. Réécrivons les équations de la deuxième ligne sous forme paramétrique :

Si un point appartient à une droite donnée, alors avec une signification très précise ses coordonnées doivent satisfaire les équations paramétriques :

Ou:

3) Le vecteur, comme le vecteur trouvé précédemment, sera le vecteur directeur de la droite. Comment construire un vecteur à partir de deux points a été discuté depuis des temps immémoriaux en classe Vecteurs pour les nuls. Maintenant, la différence est que les coordonnées des vecteurs sont écrites avec des valeurs de paramètres inconnues. Et alors? Personne n'interdit de soustraire les coordonnées correspondantes du début du vecteur des coordonnées de la fin du vecteur.

Il y a deux points : .

Trouver le vecteur :

4) Puisque les vecteurs directeurs sont colinéaires, un vecteur est exprimé linéairement à travers l'autre avec un certain coefficient de proportionnalité « lambda » :

Ou coordonnée par coordonnée :

Il s'est avéré que c'était le plus ordinaire système d'équations linéairesà trois inconnues, ce qui est normalement résoluble, par exemple, La méthode de Cramer. Mais ici, il est possible de s'en sortir avec peu de pertes ; à partir de la troisième équation, nous exprimerons « lambda » et le substituerons dans la première et la deuxième équations :

Ainsi: , et nous n’avons pas besoin de « lambda ». Le fait que les valeurs des paramètres se soient avérées identiques est purement un accident.

5) Le ciel s'éclaircit complètement, remplaçons les valeurs trouvées à nos points:

Le vecteur direction n’est pas particulièrement nécessaire puisque son homologue a déjà été trouvé.

C'est toujours intéressant de vérifier après un long voyage.

:

Les égalités correctes sont obtenues.

Remplaçons les coordonnées du point dans les équations :

Les égalités correctes sont obtenues.

6) Accord final : créons les équations d'une droite en utilisant un point (vous pouvez le prendre) et un vecteur direction :

En principe, vous pouvez sélectionner un « bon » point avec des coordonnées intactes, mais c’est cosmétique.

Comment trouver la distance entre des lignes qui se croisent ?

d) Nous avons coupé la quatrième tête du dragon.

Première méthode. Pas même une méthode, mais un petit cas particulier. La distance entre les lignes qui se croisent est égale à la longueur de leur perpendiculaire commune : .

Points extrêmes de la perpendiculaire commune trouvé dans le paragraphe précédent, et la tâche est élémentaire :

Deuxième méthode. En pratique, le plus souvent les extrémités de la perpendiculaire commune sont inconnues, c'est pourquoi une approche différente est utilisée. Par deux lignes droites qui se croisent, nous pouvons tracer plans parallèles, et la distance entre ces plans est égale à la distance entre ces droites. En particulier, une perpendiculaire commune dépasse entre ces plans.

Au cours de la géométrie analytique, à partir des considérations ci-dessus, une formule est dérivée pour trouver la distance entre les lignes droites qui se croisent :
(au lieu de nos points « euh un, deux », vous pouvez prendre des points de lignes arbitraires).

Produit mixte de vecteurs déjà trouvé au point "a": .

Produit vectoriel de vecteurs trouvé au paragraphe "être": , calculons sa longueur :

Ainsi:

Affichons fièrement les trophées sur une seule rangée :

Répondre:
UN) , ce qui signifie que les droites se coupent, ce qui devait être prouvé ;
b) ;
V) ;
G)

Que pouvez-vous dire d’autre sur le franchissement des lignes ? Il y a un angle défini entre eux. Mais nous considérerons la formule de l'angle universel dans le paragraphe suivant :

Les espaces droits qui se croisent se trouvent nécessairement dans le même plan :

La première pensée est de s’appuyer de toutes ses forces sur le point d’intersection. Et j'ai immédiatement pensé, pourquoi se priver les bonnes envies?! Maîtrisons-la tout de suite !

Comment trouver le point d’intersection des lignes spatiales ?

Exemple 14

Trouver le point d'intersection des lignes

Solution: Réécrivons les équations des droites sous forme paramétrique :

Cette tâche a été discutée en détail dans l'exemple n° 7 de cette leçon (voir. Équations d'une droite dans l'espace). Et d'ailleurs, j'ai repris les lignes droites elles-mêmes de l'exemple n°12. Je ne mentirai pas, je suis trop paresseux pour en inventer de nouvelles.

La solution est standard et a déjà été rencontrée lorsque nous essayions de comprendre les équations de la perpendiculaire commune des lignes sécantes.

Le point d'intersection des droites appartient à la droite, donc ses coordonnées satisfont aux équations paramétriques de cette droite, et leur correspond une valeur de paramètre très spécifique:

Mais ce même point appartient aussi à la deuxième ligne, donc :

Nous assimilons les équations correspondantes et effectuons des simplifications :

Reçu système de troiséquations linéaires à deux inconnues. Si les droites se croisent (ce qui est prouvé dans l'exemple n°12), alors le système est nécessairement cohérent et a une solution unique. Cela peut être résolu Méthode gaussienne, mais nous ne pécherons pas avec un tel fétichisme de la maternelle, nous ferons plus simple : à partir de la première équation, nous exprimons « te zéro » et le substituons dans les deuxième et troisième équations :

Les deux dernières équations se sont révélées être essentiellement les mêmes, et il en résulte que . Alors:

Remplaçons la valeur trouvée du paramètre dans les équations :

Répondre:

Pour vérifier, on substitue la valeur trouvée du paramètre dans les équations :
Les mêmes coordonnées ont été obtenues et devaient être vérifiées. Les lecteurs méticuleux peuvent substituer les coordonnées du point dans les équations canoniques originales des lignes.

D'ailleurs, il était possible de faire l'inverse : trouver le point via « es zéro » et le vérifier via « te zéro ».

Une superstition mathématique bien connue dit : là où l'on discute de l'intersection de droites, il y a toujours une odeur de perpendiculaires.

Comment construire une ligne d’espace perpendiculaire à une ligne donnée ?

(les lignes se croisent)

Exemple 15

a) Écrivez les équations d'une droite passant par un point perpendiculaire à la droite (les lignes se croisent).

b) Trouvez la distance entre le point et la ligne.

Note : clause « les lignes se croisent » – significatif. À travers le point
vous pouvez tracer un nombre infini de lignes perpendiculaires qui couperont la droite « el ». La seule solution se produit dans le cas où une droite perpendiculaire à un point donné est tracée deux donné par une droite (voir exemple n°13, point « b »).

UN) Solution: On note la droite inconnue par . Faisons un dessin schématique :

Que sait-on de la ligne droite ? Selon la condition, un point est attribué. Afin de composer les équations d’une droite, il est nécessaire de trouver le vecteur direction. Le vecteur est tout à fait approprié en tant que tel vecteur, nous allons donc nous en occuper. Plus précisément, prenons l'extrémité inconnue du vecteur par la peau du cou.

1) Retirons son vecteur directeur des équations de la droite « el », et réécrivons les équations elles-mêmes sous forme paramétrique :

Beaucoup ont deviné que pour la troisième fois au cours de la leçon, le magicien sortirait un cygne blanc de son chapeau. Considérons un point dont les coordonnées sont inconnues. Puisque le point est , ses coordonnées satisfont aux équations paramétriques de la droite « el » et elles correspondent à une valeur de paramètre spécifique :

Ou en une seule ligne :

2) Selon la condition, les droites doivent être perpendiculaires, donc leurs vecteurs directeurs sont orthogonaux. Et si les vecteurs sont orthogonaux, alors leur produit scalaire est égal à zéro :

Ce qui s'est passé? Le plus simple équation linéaire avec une inconnue :

3) La valeur du paramètre est connue, trouvons le point :

Et le vecteur direction :
.

4) Composons les équations d’une droite à l’aide d’un point et d’un vecteur directeur :

Les dénominateurs de la proportion se sont avérés fractionnaires, et c'est exactement le cas lorsqu'il convient de se débarrasser des fractions. Je vais juste les multiplier par -2 :

Répondre:

Note : une fin plus rigoureuse à la solution est formalisée ainsi : composons les équations d’une droite à l’aide d’un point et d’un vecteur directeur. En effet, si un vecteur est le vecteur directeur d'une droite, alors le vecteur colinéaire, naturellement, sera aussi le vecteur directeur de cette droite.

La vérification comprend deux étapes :

1) vérifier l'orthogonalité des vecteurs directeurs des lignes ;

2) on substitue les coordonnées du point dans les équations de chaque droite, elles doivent « s'adapter » à la fois là et là.

On a beaucoup parlé d'actions typiques, alors j'ai vérifié sur un brouillon.

Au fait, j'ai oublié un autre point : construire un point « zyu » symétrique au point « en » par rapport à la droite « el ». Cependant, il existe un bon « analogue plat », que l'on peut trouver dans l'article Les problèmes les plus simples avec une ligne droite dans un avion. Ici, la seule différence résidera dans la coordonnée « Z » supplémentaire.

Comment trouver la distance d’un point à une ligne dans l’espace ?

b) Solution: Trouvons la distance d'un point à une ligne.

Première méthode. Cette distance est exactement égale à la longueur de la perpendiculaire : . La solution est évidente : si les points sont connus , Que:

Deuxième méthode. DANS problèmes pratiques la base de la perpendiculaire est souvent un secret scellé, il est donc plus rationnel d'utiliser une formule toute faite.

La distance d'un point à une ligne est exprimée par la formule :
, où est le vecteur directeur de la droite « el », et – gratuit un point appartenant à une ligne donnée.