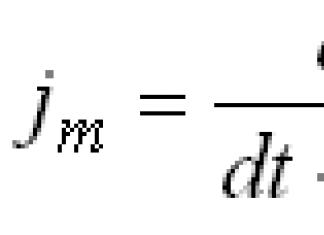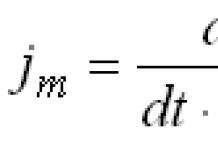« Leçon Tangente à un cercle » - Montrer que la droite AC est tangente à un cercle donné. Problème 1. Étant donné : env.(O;OM), MR – tangente, angle KMR=45?. Calculez la longueur de BC si OD = 3 cm. Leçon générale. Tracez une tangente au cercle donné. Thème : « cercle ». Solution : Résolution de problèmes. Travaux pratiques. Prenez des notes et des notes.

« Tangente à un cercle » - Propriété d'une tangente. Soit d la distance du centre O à la droite KM. Les segments AK et AM sont appelés segments tangents tirés de A. Tangente à un cercle. Alors. Une tangente à un cercle est perpendiculaire au rayon tracé jusqu'au point de tangence. Preuve. Montrons que si AK et AM sont des segments tangents, alors AK = AM, ?OAK = ? OAM.

"Circonférence et cercle" - Calculez. Trouvez la circonférence. Trouvez le rayon du cercle. Trouvez l'aire de la figure ombrée. Cercle. Secteur circulaire. Trace un cercle de centre K et de rayon 2 cm et complète l'énoncé. Travail indépendant. Circonférence. Cercle. Aire d'un cercle. Calculez la longueur de l'équateur. Un jeu.

« Équation d'un cercle » - Construisez un cercle dans votre cahier, donné par des équations: Centre du cercle O(0;0), (x – 0)2 + (y – 0)2 = R 2, x2 + y2 = R 2 ? équation d'un cercle de centre à l'origine. . O (0;0) – centre, R = 4, alors x2 + y2 = 42 ; x2 + y2 = 16. Trouvez les coordonnées du centre et le rayon si AB est le diamètre du cercle donné.

« Longueur du cercle 6e année » - Devise de la leçon : Histoire des nombres ?. Le diamètre de la roue de la locomotive diesel est de 180 cm. Lambert a trouvé pour ? les vingt-sept premières fractions appropriées. Cours de mathématiques en 6e année Professeur de mathématiques : Nikonorova Lyubov Arkadyevna. Plan de cours. Concours "Mosaïque de Présentations". Mais vous pouvez trouver une séquence infinie de fractions appropriées.

Cette œuvre Un cycliste a quitté le point A d'un itinéraire circulaire, et 30 minutes plus tard un motocycliste l'a suivi. En 10 minutes (Check) sur le sujet (Macroéconomie et administration publique), a été fabriqué sur commande par des spécialistes de notre entreprise et a passé avec succès sa défense. Travaux - Un cycliste a quitté le point A d'une piste circulaire, et 30 minutes plus tard un motocycliste l'a suivi. En 10 minutes, le sujet Macroéconomie et administration publique reflète son sujet et la composante logique de sa divulgation, l'essence de la question étudiée est révélée, les principales dispositions et idées directrices de ce sujet sont mises en évidence.
Travaux - Un cycliste a quitté le point A d'une piste circulaire, et 30 minutes plus tard un motocycliste l'a suivi. Après 10 minutes, contient : des tableaux, des dessins, les dernières sources littéraires, l'année de soumission et de défense de l'œuvre - 2017. Dans l'œuvre Un cycliste a quitté le point A du parcours circulaire, et 30 minutes plus tard un motocycliste l'a suivi. Après 10 minutes (Macroéconomie et administration publique), la pertinence du sujet de recherche est révélée, le degré de développement du problème est reflété, sur la base d'une évaluation et d'une analyse approfondies des connaissances scientifiques et littérature méthodologique, dans les travaux sur le thème de la macroéconomie et de l'administration publique, l'objet d'analyse et ses enjeux sont pris en compte de manière globale, tant du côté théorique que pratique, le but et les tâches spécifiques du sujet considéré sont formulés, il existe une logique de présentation du matériel et de sa séquence.

Du point A d'une piste circulaire d'une longueur de 75 km, deux voitures sont parties simultanément dans la même direction. La vitesse de la première voiture est de 89 km/h, celle de la deuxième voiture est de 59 km/h. Combien de minutes après le départ la première voiture aura-t-elle exactement un tour d'avance sur la seconde ?

La solution du problème

Cette leçon montre comment utiliser une formule physique pour déterminer le moment où Mouvement uniforme: , créez une proportion pour déterminer le moment où une voiture en dépassera une autre en cercle. Lors de la résolution d'un problème, une séquence claire d'actions à résoudre est indiquée tâches similaires: nous introduisons une désignation spécifique pour ce que nous voulons trouver, notons le temps qu'il faut à une et à la deuxième voiture pour parcourir un certain nombre de tours, en tenant compte du fait que ce temps est la même valeur - nous assimilons les égalités résultantes. La solution consiste à trouver la quantité inconnue dans une équation linéaire. Pour obtenir les résultats, il ne faut pas oublier de substituer le nombre de tours obtenus dans la formule de détermination du temps.

La solution à ce problème est recommandée aux élèves de 7e année lorsqu'ils étudient le thème « Langage mathématique ». Modèle mathématique" ( Équation linéaire avec une variable"). Lors de la préparation à l'OGE, la leçon est recommandée lors de la répétition du thème « Langage mathématique ». Modèle mathématique".

«Professeur d'école primaire» - Thème. Analyse du travail de la formation scolaire des enseignants classes primaires. Développer itinéraires individuels, favorisant la croissance professionnelle des enseignants. Renforcement de la base pédagogique et matérielle. Activités organisationnelles et pédagogiques. Poursuivre la recherche de nouvelles technologies, formes et méthodes d'enseignement et d'éducation. Domaines de travail école primaire.

« Jeunesse et élections » - Développement de la conscience politique et juridique chez les jeunes : Jeunesse et élections. Développement de la conscience politique et juridique dans les écoles et les établissements secondaires spécialisés : Un ensemble de mesures pour attirer les jeunes aux élections. Pourquoi ne votons-nous pas ? Développement de la conscience politique et juridique dans les établissements d'enseignement préscolaire :

« Guerre d'Afghanistan 1979-1989 » - Les dirigeants soviétiques portent au pouvoir un nouveau président, Babrak Karmal. Résultats de la guerre. Guerre soviéto-afghane 1979-1989 Le 15 février 1989, le dernier troupes soviétiques. Raison de la guerre. Après le retrait armée soviétique Depuis le territoire afghan, le régime pro-soviétique du président Najibullah a duré encore 3 ans et, après avoir perdu le soutien de la Russie, a été renversé en avril 1992 par les commandants moudjahidines.

"Signes de divisibilité des nombres naturels" - Pertinence. L'épreuve de Pascal. Un signe que les nombres sont divisibles par 6. Un signe que les nombres sont divisibles par 8. Un signe que les nombres sont divisibles par 27. Un signe que les nombres sont divisibles par 19. Un signe que les nombres sont divisibles par 13. Identifiez les signes de divisibilité. Comment apprendre à calculer rapidement et correctement. Test de divisibilité des nombres par 25. Test de divisibilité des nombres par 23.

« Théorie de Butlerov » - Les conditions préalables à la création de la théorie étaient : Isomérie-. L'importance de la théorie des structures matière organique. La science de la structure spatiale des molécules - stéréochimie. Le rôle de la création de théories structure chimique substances. Apprenez les principes de base de la théorie de la structure chimique de A. M. Butlerov. Poste de base théorie moderne structure des composés.

"Concours de mathématiques pour les écoliers" - Termes mathématiques. Partie d'une droite reliant deux points. Connaissances des étudiants. Concours de mathématiciens joyeux. Tâche. Un rayon divisant un angle en deux. Les angles sont bons. Intervalle de temps. Concours. La plus belle. Vitesse. Rayon. Se préparer pour l'hiver. Libellule sauteuse. Chiffre. Jouer avec le public. Somme des angles d'un triangle.

Il y a un total de 23 687 présentations dans le sujet

Sections: Mathématiques

L'article traite de problèmes pour aider les élèves : développer des compétences dans la résolution de problèmes de mots en préparation à l'examen d'État unifié, lors de l'apprentissage de la résolution de problèmes pour créer un modèle mathématique de situations réelles dans tous les parallèles de l'école primaire et secondaire. Il présente des tâches : sur le mouvement en cercle ; trouver la longueur d’un objet en mouvement ; pour trouver la vitesse moyenne.

I. Problèmes impliquant le mouvement en cercle.

Les problèmes de mouvement circulaire se sont révélés difficiles pour de nombreux écoliers. Ils sont résolus presque de la même manière que les problèmes de mouvement ordinaires. Ils utilisent également la formule. Mais il y a un point auquel nous aimerions prêter attention.

Tache 1. Un cycliste a quitté le point A de la piste circulaire et 30 minutes plus tard, un motocycliste l'a suivi. 10 minutes après le départ, il a rattrapé le cycliste pour la première fois, et 30 minutes plus tard, il l'a rattrapé pour la deuxième fois. Trouvez la vitesse du motocycliste si la longueur du parcours est de 30 km. Donnez votre réponse en km/h.

Solution. Les vitesses des participants seront prises en compte X km/h et y km/h. Pour la première fois, un motocycliste a dépassé un cycliste 10 minutes plus tard, soit une heure après le départ. Jusqu'à présent, le cycliste était sur la route depuis 40 minutes, soit des heures. Les participants au mouvement parcouraient les mêmes distances, c'est-à-dire y = x. Entrons les données dans le tableau.

Tableau 1

Le motocycliste a ensuite doublé le cycliste une seconde fois. Cela s'est produit 30 minutes plus tard, soit une heure après le premier dépassement. Jusqu’où ont-ils voyagé ? Un motocycliste a dépassé un cycliste. Cela signifie qu'il a bouclé un tour de plus. C'est le moment

auquel vous devez faire attention. Un tour correspond à la longueur de la piste, soit 30 km. Créons une autre table.

Tableau 2

On obtient la deuxième équation : y - x = 30. On a un système d'équations : Dans la réponse, nous indiquons la vitesse du motocycliste.

Réponse : 80 km/h.

Tâches (indépendamment).

I.1.1. Un cycliste a quitté le point « A » du parcours circulaire et, 40 minutes plus tard, un motocycliste l'a suivi. 10 minutes après le départ, il a rattrapé le cycliste pour la première fois, et 36 minutes plus tard, il l'a rattrapé pour la deuxième fois. Trouvez la vitesse du motocycliste si la longueur du parcours est de 36 km. Donnez votre réponse en km/h.

I.1. 2. Un cycliste a quitté le point « A » du parcours circulaire et, 30 minutes plus tard, un motocycliste l'a suivi. 8 minutes après le départ, il a rattrapé le cycliste pour la première fois, et 12 minutes plus tard, il l'a rattrapé pour la deuxième fois. Trouvez la vitesse du motocycliste si la longueur du parcours est de 15 km. Donnez votre réponse en km/h.

I.1. 3. Un cycliste a quitté le point « A » du parcours circulaire et, 50 minutes plus tard, un motocycliste l'a suivi. Dix minutes après le départ, il a rattrapé le cycliste pour la première fois, puis 18 minutes plus tard, il l'a rattrapé pour la deuxième fois. Trouvez la vitesse du motocycliste si la longueur du parcours est de 15 km. Donnez votre réponse en km/h.

Deux motocyclistes partent simultanément dans la même direction à partir de deux points diamétralement opposés sur une piste circulaire dont la longueur est de 20 km. Combien de minutes faudra-t-il aux motocyclistes pour se rencontrer pour la première fois si la vitesse de l'un d'eux est supérieure de 15 km/h à celle de l'autre ?

Solution.

Image 1

Avec un départ simultané, le motocycliste parti de « A » a parcouru un demi-tour de plus que celui parti de « B ». Soit 10 km. Lorsque deux motocyclistes se déplacent dans la même direction, la vitesse de déplacement v = -. Selon les conditions du problème, v = 15 km/h = km/min = km/min – vitesse de dépose. On retrouve le temps après lequel les motards se rejoignent pour la première fois.

10 : = 40 (minutes).

Répondre: 40 minutes.

Tâches (indépendamment).

I.2.1. Deux motocyclistes partent simultanément dans la même direction depuis deux points diamétralement opposés sur une piste circulaire dont la longueur est de 27 km. Combien de minutes faudra-t-il aux motocyclistes pour se rencontrer pour la première fois si la vitesse de l'un d'eux est supérieure de 27 km/h à celle de l'autre ?

I.2.2. Deux motocyclistes partent simultanément dans la même direction depuis deux points diamétralement opposés sur une piste circulaire dont la longueur est de 6 km. Combien de minutes faudra-t-il aux motocyclistes pour se rencontrer pour la première fois si la vitesse de l'un d'eux est supérieure de 9 km/h à celle de l'autre ?

A partir d'un point sur une piste circulaire d'une longueur de 8 km, deux voitures ont démarré simultanément dans la même direction. La vitesse de la première voiture est de 89 km/h et 16 minutes après le départ, elle avait un tour d'avance sur la deuxième voiture. Trouvez la vitesse de la deuxième voiture. Donnez votre réponse en km/h.

Solution.

x km/h est la vitesse de la deuxième voiture.

(89 – x) km/h – vitesse de déplacement.

8 km est la longueur du parcours circulaire.

L'équation.

(89 – x) = 8,

89 – x = 2 15,

Répondre: 59 km/h.

Tâches (indépendamment).

I.3.1. A partir d'un point sur une piste circulaire d'une longueur de 12 km, deux voitures ont démarré simultanément dans la même direction. La vitesse de la première voiture est de 103 km/h et 48 minutes après le départ, elle avait un tour d'avance sur la deuxième voiture. Trouvez la vitesse de la deuxième voiture. Donnez votre réponse en km/h.

I.3.2. A partir d'un point sur une piste circulaire d'une longueur de 6 km, deux voitures ont démarré simultanément dans la même direction. La vitesse de la première voiture est de 114 km/h, et 9 minutes après le départ, elle avait un tour d'avance sur la deuxième voiture. Trouvez la vitesse de la deuxième voiture. Donnez votre réponse en km/h.

I.3.3. A partir d'un point sur une piste circulaire d'une longueur de 20 km, deux voitures ont démarré simultanément dans la même direction. La vitesse de la première voiture est de 105 km/h et 48 minutes après le départ, elle avait un tour d'avance sur la deuxième voiture. Trouvez la vitesse de la deuxième voiture. Donnez votre réponse en km/h.

I.3.4. A partir d'un point sur une piste circulaire d'une longueur de 9 km, deux voitures ont démarré simultanément dans la même direction. La vitesse de la première voiture est de 93 km/h, et 15 minutes après le départ, elle avait un tour d'avance sur la deuxième voiture. Trouvez la vitesse de la deuxième voiture. Donnez votre réponse en km/h.

L'horloge avec aiguilles indique 8 heures 00 minutes. Dans combien de minutes l’aiguille des minutes s’alignera-t-elle avec l’aiguille des heures pour la quatrième fois ?

Solution. Nous supposons que nous ne résolvons pas le problème expérimentalement.

En une heure, l’aiguille des minutes parcourt un cercle et l’aiguille des heures parcourt un cercle. Laissez leurs vitesses être de 1 (tours par heure) et Début - à 8h00. Trouvons le temps qu'il faut à l'aiguille des minutes pour rattraper l'aiguille des heures pour la première fois.

L'aiguille des minutes se déplacera plus loin, nous obtenons donc l'équation

Cela signifie que pour la première fois, les flèches s'aligneront sur

Laissez les flèches s'aligner une deuxième fois après le temps z. L'aiguille des minutes parcourra une distance de 1·z et l'aiguille des heures parcourra un cercle supplémentaire. Écrivons l'équation :

Après l'avoir résolu, nous obtenons cela.

Ainsi, à travers les flèches, ils s'aligneront pour la deuxième fois, après l'autre - pour la troisième fois, et après l'autre - pour la quatrième fois.

Par conséquent, si le départ était à 8h00, alors pour la quatrième fois les aiguilles s'aligneront

4h = 60 * 4 min = 240 min.

Réponse : 240 minutes.

Tâches (indépendamment).

I.4.1.L'horloge à aiguilles indique 4 heures 45 minutes. Dans combien de minutes l’aiguille des minutes s’alignera-t-elle avec l’aiguille des heures pour la septième fois ?

I.4.2. L'horloge à aiguilles indique exactement 2 heures. Dans combien de minutes l’aiguille des minutes s’alignera-t-elle avec l’aiguille des heures pour la dixième fois ?

I.4.3. L'horloge à aiguilles indique 8 heures 20 minutes. Dans combien de minutes l’aiguille des minutes s’alignera-t-elle avec l’aiguille des heures pour la quatrième fois ? quatrième

II. Problèmes pour trouver la longueur d'un objet en mouvement.

Un train, se déplaçant uniformément à une vitesse de 80 km/h, dépasse un poteau routier en 36 s. Trouvez la longueur du train en mètres.

Solution. Puisque la vitesse du train est indiquée en heures, nous convertirons les secondes en heures.

1) 36 secondes =

2) trouver la longueur du train en kilomètres.

80·

Réponse : 800 m.

Tâches (indépendamment).

II.2 Un train, circulant uniformément à une vitesse de 60 km/h, dépasse un poteau routier en 69 s. Trouvez la longueur du train en mètres. Réponse : 1150m.

II.3. Un train se déplaçant uniformément à une vitesse de 60 km/h traverse une ceinture forestière de 200 m de long en 1 min 21 s. Trouvez la longueur du train en mètres. Réponse : 1150m.

III. Problèmes de vitesse moyenne.

Lors d'un examen de mathématiques, vous pourriez rencontrer un problème pour trouver la vitesse moyenne. Il faut rappeler que la vitesse moyenne n'est pas égale à la moyenne arithmétique des vitesses. La vitesse moyenne est trouvée à l'aide d'une formule spéciale :

S'il y avait deux sections du chemin, alors .

La distance entre les deux villages est de 18 km. Un cycliste voyageait d'un village à l'autre pendant 2 heures et revenait par la même route pendant 3 heures. Quelle est la vitesse moyenne du cycliste sur tout le parcours ?

Solution:

2 heures + 3 heures = 5 heures - consacrées à l'ensemble du mouvement,

.

Le touriste a marché à une vitesse de 4 km/h, puis exactement en même temps à une vitesse de 5 km/h. Quelle est la vitesse moyenne du touriste sur tout le parcours ?

Laissez le touriste marcher à une vitesse de 4 km/h et à une vitesse de 5 km/h. Puis en 2t heures, il a parcouru 4t + 5t = 9t (km). La vitesse moyenne d'un touriste est = 4,5 (km/h).

Réponse : 4,5 km/h.

On constate que la vitesse moyenne du touriste s'est avérée égale à la moyenne arithmétique des deux vitesses données. Vous pouvez vérifier que si le temps de trajet sur deux tronçons de l'itinéraire est le même, alors la vitesse moyenne de déplacement est égale à la moyenne arithmétique des deux vitesses données. Pour ce faire, résolvons le même problème sous sa forme générale.

Le touriste marchait à une vitesse de km/h, puis exactement en même temps à une vitesse de km/h. Quelle est la vitesse moyenne du touriste sur tout le parcours ?

Laissez le touriste marcher à une vitesse de km/h et à une vitesse de km/h. Puis en 2t heures il a parcouru t + t = t (km). La vitesse moyenne d'un touriste est

= (km/h).

La voiture a parcouru une certaine distance en montée à une vitesse de 42 km/h et en descente à une vitesse de 56 km/h.

.

La vitesse moyenne de déplacement est de 2 s : (km/h).

Réponse : 48 km/h.

La voiture a parcouru une certaine distance en montée à une vitesse de km/h et en descente de la montagne à une vitesse de km/h.

Quelle est la vitesse moyenne de la voiture sur tout le parcours ?

Soit la longueur de la section de chemin égale à s km. Ensuite, la voiture a parcouru 2 s km dans les deux sens, passant tout le trajet .

La vitesse moyenne de déplacement est de 2 s : (km/h).

Réponse : km/h.

Considérons un problème dans lequel la vitesse moyenne est donnée et l'une des vitesses doit être déterminée. L’application de l’équation sera nécessaire.

Le cycliste montait une pente à une vitesse de 10 km/h et descendait la montagne à une autre vitesse constante. Selon ses calculs, la vitesse moyenne était de 12 km/h.

.

III.2. La moitié du temps passé sur la route, la voiture roulait à une vitesse de 60 km/h, et la seconde moitié du temps à une vitesse de 46 km/h. Trouvez la vitesse moyenne de la voiture tout au long du trajet.

III.3. Sur le chemin d'un village à un autre, la voiture a marché un certain temps à une vitesse de 60 km/h, puis exactement le même temps à une vitesse de 40 km/h, puis exactement le même temps à une vitesse égale à la vitesse moyenne sur les deux premiers tronçons du parcours. Quelle est la vitesse moyenne de déplacement sur l’ensemble du trajet d’un village à l’autre ?

III.4. Un cycliste se rend de chez lui au travail vitesse moyenne 10 km/h, et retour à une vitesse moyenne de 15 km/h, puisque la route descend légèrement. Trouvez la vitesse moyenne du cycliste depuis la maison jusqu'au travail et retour.

III.5. Une voiture s'est rendue du point A au point B à vide à une vitesse constante et est revenue par la même route avec une charge à une vitesse de 60 km/h. A quelle vitesse roulait-il à vide si la vitesse moyenne était de 70 km/h ?

III.6. La voiture a roulé pendant les 100 premiers kilomètres à une vitesse de 50 km/h, pendant les 120 kilomètres suivants à une vitesse de 90 km/h, puis pendant 120 km à une vitesse de 100 km/h. Trouvez la vitesse moyenne de la voiture tout au long du trajet.

III.7. La voiture a parcouru les 100 premiers kilomètres à une vitesse de 50 km/h, les 140 kilomètres suivants à une vitesse de 80 km/h, puis 150 km à une vitesse de 120 km/h. Trouvez la vitesse moyenne de la voiture tout au long du trajet.

III.8. La voiture a roulé pendant les 150 premiers kilomètres à une vitesse de 50 km/h, pendant les 130 kilomètres suivants à une vitesse de 60 km/h, puis sur 120 km à une vitesse de 80 km/h. Trouvez la vitesse moyenne de la voiture tout au long du trajet.

III. 9. La voiture a parcouru les 140 premiers kilomètres à une vitesse de 70 km/h, les 120 kilomètres suivants à une vitesse de 80 km/h, puis 180 km à une vitesse de 120 km/h. Trouvez la vitesse moyenne de la voiture tout au long du trajet.