პრობლემა ნომერი 1
ლოგიკა მარტივია: ჩვენ ვიმოქმედებთ ისე, როგორც ადრე, მიუხედავად იმისა, რომ ახლა ტრიგონომეტრიულ ფუნქციებს უფრო რთული არგუმენტი აქვთ!
თუ გადავჭრით ფორმის განტოლებას:
შემდეგ ჩვენ დავწერთ შემდეგ პასუხს:
ან (მას შემდეგ)
მაგრამ ახლა ჩვენ გვაქვს შემდეგი გამოთქმა ჩვენს როლში:
მაშინ შეგიძლია დაწერო:
ჩვენი მიზანი თქვენთან ერთად არის, რომ მარცხენა სადგამი იყოს უბრალოდ, ყოველგვარი "მინარევების" გარეშე!
ნელ-ნელა მოვიშოროთ ისინი!
პირველ რიგში, ჩვენ ვხსნით მნიშვნელს: ამისათვის ვამრავლებთ ჩვენს ტოლობას:
ახლა მოვიშოროთ იგი ორივე ნაწილის დაყოფით:
ახლა მოდი, მოვიშოროთ რვა:
შედეგად მიღებული გამონათქვამი შეიძლება დაიწეროს ამონახსნების 2 სერიის სახით (ანალოგიით კვადრატული განტოლებით, სადაც ვამატებთ ან ვაკლებთ დისკრიმინანტს)
ჩვენ უნდა ვიპოვოთ ყველაზე დიდი უარყოფითი ფესვი! გასაგებია, რომ საჭიროა დალაგება.
ჯერ განვიხილოთ პირველი სერია:
გასაგებია, რომ თუ ავიღებთ, შედეგად მივიღებთ დადებით ციფრებს და ისინი არ გვაინტერესებს.
ასე რომ თქვენ უნდა მიიღოთ ის უარყოფითი. დაე.
როდესაც ფესვი უკვე არის:
და ჩვენ უნდა ვიპოვოთ ყველაზე დიდი უარყოფითი !! ეს ნიშნავს, რომ უარყოფითი მიმართულებით წასვლას აზრი აღარ აქვს. და ამ სერიის ყველაზე დიდი უარყოფითი ფესვი იქნება.
ახლა გადავხედოთ მეორე სერიას:
და ისევ ვცვლით:, შემდეგ:
Არ არის დაინტერესებული!
მერე გაზრდას აზრი აღარ აქვს! ჩვენ შევამცირებთ! მოდით, მაშინ:
ჯდება!
დაე. მერე
მაშინ - ყველაზე დიდი უარყოფითი ფესვი!
პასუხი:
პრობლემა ნომერი 2
ჩვენ კვლავ ვხსნით რთული კოსინუსების არგუმენტის მიუხედავად:
ახლა ისევ მარცხნივ გამოვხატავთ:
ვამრავლებთ ორივე მხარეს
ორივე მხარეს ვყოფთ
რჩება მხოლოდ მისი გადატანა მარჯვნივ, მისი ნიშნის შეცვლა მინუსიდან პლუსზე.
ჩვენ ისევ გვაქვს ფესვების 2 სერია, ერთი და მეორე.
ჩვენ უნდა ვიპოვოთ ყველაზე დიდი უარყოფითი ფესვი. განვიხილოთ პირველი სერია:
გასაგებია, რომ ჩვენ მივიღებთ პირველ უარყოფით ფესვს, ის ტოლი იქნება და იქნება ყველაზე დიდი უარყოფითი ფესვი 1 სერიაში.
მეორე სერიისთვის
პირველი უარყოფითი ფესვი ასევე მიიღება და ტოლი იქნება. ვინაიდან, მაშინ არის განტოლების ყველაზე დიდი უარყოფითი ფესვი.
პასუხი: .
პრობლემა ნომერი 3
ამოხსენით რთული ტანგენტის არგუმენტის მიუხედავად.
როგორც ჩანს, ეს არაფერია რთული, არა?
როგორც ადრე, ჩვენ გამოვხატავთ მარცხენა მხარეს:
კარგია, აქ ფესვების მხოლოდ ერთი სერიაა! კვლავ იპოვეთ ყველაზე დიდი უარყოფითი.
გასაგებია, რომ გამოდის, თუ დავაყენებთ. და ეს ფესვი ტოლია.
პასუხი:
ახლა შეეცადეთ თავად მოაგვაროთ შემდეგი პრობლემები.
საშინაო დავალება ან 3 დავალება დამოუკიდებელი გადაწყვეტისთვის.
- გადაწყვეტილებები-ში-ტე განტოლება.
- გადაწყვეტილებები-ში-ტე განტოლება.
ოტ-ვე-იმ ნა-პი-ში-ტეში, ყველაზე პატარა პო-ლი-ტელ-ფესვი. - გადაწყვეტილებები-ში-ტე განტოლება.
ოტ-ვე-იმ ნა-პი-ში-ტეში, ყველაზე პატარა პო-ლი-ტელ-ფესვი.
მზადაა? შემოწმება. მე დეტალურად არ აღვწერ გადაწყვეტის მთელ ალგორითმს, მეჩვენება, რომ მას ზემოთ უკვე დაეთმო საკმარისი ყურადღება.
ისე, ყველაფერი სწორია? ოჰ, ეს საზიზღარი სინუსები, მათთან ყოველთვის არის რაღაც პრობლემები!
ახლა თქვენ შეგიძლიათ ამოხსნათ უმარტივესი ტრიგონომეტრიული განტოლებები!
შეამოწმეთ გადაწყვეტილებები და პასუხები:
პრობლემა ნომერი 1
მოდით გამოვხატოთ
უმცირესი დადებითი ფესვი მიიღება თუ დავაყენებთ, მას შემდეგ
პასუხი:
პრობლემა ნომერი 2
ყველაზე პატარა დადებითი ფესვი მიიღება როცა.
თანაბარი იქნება.
პასუხი: .
პრობლემა ნომერი 3
როცა მივიღებთ, როცა მივიღებთ.
პასუხი: .
ეს ცოდნა დაგეხმარებათ გადაჭრათ ბევრი პრობლემა, რომელიც გამოცდაზე შეგხვდებათ.
თუ თქვენ განაცხადებთ "5" კლასზე, მაშინ უბრალოდ უნდა წახვიდეთ სტატიის კითხვაზე საშუალო დონე,რომელიც დაეთმობა უფრო რთული ტრიგონომეტრიული განტოლებების ამოხსნას (ამოცანა C1).
საშუალო დონე
ამ სტატიაში მე აღვწერ უფრო რთული ტიპის ტრიგონომეტრიული განტოლებების ამოხსნადა როგორ შევარჩიოთ მათი ფესვები. აქ მე ვაფუძნებ შემდეგ თემებს:
- ტრიგონომეტრიული განტოლებები საწყისი დონისთვის (იხ. ზემოთ).
უფრო რთული ტრიგონომეტრიული განტოლებები უფრო რთული ამოცანების საფუძველია. მათში საჭიროა როგორც თავად განტოლების გადაჭრა ზოგადი ფორმით, ასევე ამ განტოლების ფესვების პოვნა, რომელიც მიეკუთვნება გარკვეულ განსაზღვრულ ინტერვალს.
ტრიგონომეტრიული განტოლებების ამოხსნა ორ ქვეამოცანამდე მოდის:
- განტოლების ამოხსნა
- ფესვების შერჩევა
უნდა აღინიშნოს, რომ ეს უკანასკნელი ყოველთვის არ არის საჭირო, მაგრამ მაინც შერჩევაა საჭირო მაგალითების უმეტესობაში. და თუ ეს არ არის საჭირო, მაშინ შეგიძლიათ საკმაოდ თანაუგრძნოთ - ეს ნიშნავს, რომ განტოლება თავისთავად საკმაოდ რთულია.
ჩემი გამოცდილება C1 ამოცანების ანალიზში აჩვენებს, რომ ისინი ჩვეულებრივ იყოფა ამ კატეგორიებად.
გაზრდილი სირთულის ამოცანების ოთხი კატეგორია (ყოფილი C1)
- განტოლებები, რომლებიც მცირდება ფაქტორიზაციამდე.
- ფორმამდე შემცირებული განტოლებები.
- ცვლადი ცვლილებით ამოხსნილი განტოლებები.
- განტოლებები, რომლებიც საჭიროებენ ფესვების დამატებით შერჩევას ირაციონალურობის ან მნიშვნელის გამო.
მარტივად რომ ვთქვათ: თუ შეგხვდებათ პირველი სამი ტიპის განტოლებიდან ერთ-ერთიმაშინ ჩათვალე თავი იღბლიანი. მათთვის, როგორც წესი, თქვენ დამატებით უნდა აიღოთ ფესვები, რომლებიც მიეკუთვნება გარკვეულ ინტერვალს.
თუ მე-4 ტიპის განტოლებას წააწყდებით, მაშინ ნაკლებად გაგიმართლათ: საჭიროა ცოტა ხანს და უფრო მჭიდროდ შეაერთოთ იგი, მაგრამ საკმაოდ ხშირად ეს არ საჭიროებს მასში ფესვების დამატებით შერჩევას. მიუხედავად ამისა, ამ ტიპის განტოლებებს გავაანალიზებ შემდეგ სტატიაში და ეს პირველი სამი ტიპის განტოლებების ამოხსნას დაეთმობა.
ფაქტორინგის განტოლებები
ყველაზე მნიშვნელოვანი, რაც უნდა გვახსოვდეს ამ ტიპის განტოლებების ამოსახსნელად არის
როგორც პრაქტიკა გვიჩვენებს, როგორც წესი, ეს ცოდნა საკმარისია. მოდით შევხედოთ რამდენიმე მაგალითს:
მაგალითი 1. განტოლება რედუცირება ფაქტორიზაციამდე შემცირების ფორმულების და ორკუთხა სინუსის გამოყენებით
- Res-shi-te განტოლება
- Nay-di-te ამ განტოლების ყველა ფესვი
აქ, როგორც დავპირდი, კასტინგის ფორმულები მუშაობს:
მაშინ ჩემი განტოლება ასე გამოიყურება:
მაშინ ჩემი განტოლება მიიღებს შემდეგ ფორმას:
შორსმჭვრეტელმა სტუდენტმა შეიძლება თქვას: ახლა კი ორივე ნაწილს დავამოკლებ, უმარტივეს განტოლებას მივიღებ და ცხოვრებით დავტკბები! და ეს მწარედ შეცდება!
| გახსოვდეთ: არასოდეს შეამციროთ ტრიგონომეტრიული განტოლების ორივე ნაწილი უცნობის შემცველი ფუნქციით! ასე რომ თქვენ დაკარგავთ ფესვებს! |
Ასე რომ, რას აკეთებ? დიახ, ყველაფერი მარტივია, გადაიტანეთ ყველაფერი ერთი მიმართულებით და ამოიღეთ საერთო ფაქტორი:
კარგად, ჩვენ მას ფაქტორებად ვაქცევთ, ჩქარა! ახლა ჩვენ გადავწყვიტეთ:
პირველ განტოლებას აქვს ფესვები:
და მეორე:
ამით სრულდება პრობლემის პირველი ნაწილი. ახლა ჩვენ უნდა ავირჩიოთ ფესვები:
უფსკრული ასეთია:
ან შეიძლება ასეც დაიწეროს:
აბა, ავიღოთ ფესვები:
პირველ რიგში, მოდით ვიმუშაოთ პირველ სერიასთან (და ეს უფრო ადვილია, რა შეგვიძლია ვთქვათ!)
ვინაიდან ჩვენი ინტერვალი მთლიანად ნეგატიურია, არ არის საჭირო არაუარყოფითიების აღება, ისინი მაინც იძლევიან არაუარყოფით ფესვებს.
ავიღოთ, მერე - ცოტა მეტისმეტად, არ ჯდება.
დაე, მაშინ - აღარ მოხვდა.
კიდევ ერთი მცდელობა - მაშინ - არის, დაარტყი! ნაპოვნია პირველი ფესვი!
ისევ ვესროლე: მერე - ისევ დავარტყი!
აბა, კიდევ ერთხელ:: - ეს უკვე რეისია.
ასე რომ, პირველი სერიიდან 2 ფესვი ეკუთვნის ინტერვალს:.
ჩვენ ვმუშაობთ მეორე სერიით (ვაშენებთ ხარისხში წესის მიხედვით):
Undershoot!
ხელახლა სროლა!
ისევ დაქვეითება!
Გავიგე!
Ფრენა!
ამრიგად, შემდეგი ფესვები ეკუთვნის ჩემს სპანს:
სწორედ ამ ალგორითმით მოვაგვარებთ ყველა სხვა მაგალითს. ვივარჯიშოთ ერთად კიდევ ერთი მაგალითით.
მაგალითი 2. განტოლება, რომელიც მცირდება ფაქტორიზაციამდე შემცირების ფორმულების გამოყენებით
- ამოხსენით განტოლება
გამოსავალი:
ისევ ყბადაღებული კასტინგის ფორმულები:
კიდევ ერთხელ, ნუ ეცდებით შემცირებას!
პირველ განტოლებას აქვს ფესვები:
და მეორე:
ახლა ისევ მოძებნეთ ფესვები.
დავიწყებ მეორე სერიით, წინა მაგალითიდან უკვე ვიცი ამის შესახებ ყველაფერი! შეხედეთ და დარწმუნდით, რომ უფსკრულის ფესვები შემდეგია:
ახლა პირველი ეპიზოდი და უფრო მარტივია:
თუ - ჯდება
თუ - ასევე კარგია
თუ - უკვე რეისი.
შემდეგ ფესვები იქნება შემდეგი:
დამოუკიდებელი მუშაობა. 3 განტოლება.
ისე, ტექნიკა გასაგებია თქვენთვის? ტრიგონომეტრიული განტოლებების ამოხსნა ასე რთული აღარ ჩანს? შემდეგ სწრაფად მოაგვარეთ შემდეგი პრობლემები და შემდეგ მე და თქვენ მოვაგვარებთ სხვა მაგალითებს:
- ამოხსენით განტოლება
ნაი-დი-ეს არის ამ განტოლების ყველა ფესვი, რომელიც ერთვის ინტერვალს. - Res-shi-te განტოლება
მიუთითეთ განტოლების ფესვები - Res-shi-te განტოლება
ნაი-დი-ეს არის ამ განტოლების ყველა ფესვი-არა-ნი, მიმაგრებული-ზე-ლე-ჟა-ში-პრო-მე-ჟუტ-კუ.
განტოლება 1.
და ისევ ჩამოსხმის ფორმულა:
ფესვების პირველი სერია:
ფესვების მეორე სერია:
დაწყებული შერჩევა უფსკრულისთვის
პასუხი: ,.
განტოლება 2. დამოუკიდებელი მუშაობის შემოწმება.
საკმაოდ რთული დაჯგუფება ფაქტორებად (გამოვიყენებ ორმაგი კუთხის სინუს ფორმულას):
მაშინ ან
ეს არის ზოგადი გამოსავალი. ახლა ჩვენ უნდა ავირჩიოთ ფესვები. უბედურება ის არის, რომ ჩვენ ვერ ვიტყვით კუთხის ზუსტ მნიშვნელობას, რომლის კოსინუსი უდრის მეოთხედს. მაშასადამე, მე არ შემიძლია უბრალოდ არკოზინის მოშორება - ეს ისეთი სირცხვილია!
რა შემიძლია გავაკეთო არის იმის გარკვევა, თუ როგორ, მაშინ.
მოდით გავაკეთოთ ცხრილი: ინტერვალი:
ისე, მტკივნეული ძიების შედეგად მივედით იმედგაცრუებულ დასკვნამდე, რომ ჩვენს განტოლებას აქვს ერთი ფესვი მითითებულ ინტერვალზე: \ displaystyle arccos \ frac (1) (4) -5 \ pi
განტოლება 3. დამოუკიდებელი მუშაობის შემოწმება.
საშინელი განტოლება. თუმცა, მისი მოგვარება საკმაოდ მარტივად შეიძლება ორმაგი კუთხის სინუს ფორმულის გამოყენებით:
2-ით შემცირება:
დავაჯგუფოთ პირველი ტერმინი მეორესთან, მესამე კი მეოთხესთან და ამოვიღოთ საერთო ფაქტორები:
ნათელია, რომ პირველ განტოლებას არ აქვს ფესვები და ახლა განვიხილოთ მეორე:
ზოგადად, ცოტა მოგვიანებით ვაპირებდი ასეთი განტოლებების ამოხსნაზე შეჩერებას, მაგრამ რადგან ის აღმოჩნდა, მაშინ არაფერია გასაკეთებელი, საჭიროა ამოხსნა ...
ფორმის განტოლებები:
ეს განტოლება წყდება ორივე ნაწილის გაყოფით:
ამრიგად, ჩვენს განტოლებას აქვს ფესვების ერთი სერია:
აუცილებელია იპოვოთ ისინი, რომლებიც მიეკუთვნება ინტერვალს:.
მოდი ისევ ავაშენოთ მაგიდა, როგორც ადრე გავაკეთე:
პასუხი:.
განტოლებები, რომლებიც მცირდება ფორმამდე:
კარგი, ახლა დროა გადავიდეთ განტოლებათა მეორე პარტიაზე, მით უმეტეს, რომ მე უკვე ვთქვი, რისგან შედგება ახალი ტიპის ტრიგონომეტრიული განტოლებების ამონახსნი. მაგრამ ზედმეტი არ იქნება ამ ფორმის განტოლების გამეორება
ის წყდება ორივე ნაწილის კოსინუსზე გაყოფით:
- Res-shi-te განტოლება
მიუთითეთ განტოლების ფესვები-არა-ნია, როდესაც-ზედ-დაწოლა-გან-ჭრის. - Res-shi-te განტოლება
მიუთითეთ განტოლების ფესვები-არა-ნია, როცა-ზე-ლე-ჟა-ში-პრო-მე-ჟუტ-კუ.
მაგალითი 1.
პირველი ძალიან მარტივია. გადადით მარჯვნივ და გამოიყენეთ ორმაგი კუთხის კოსინუსის ფორმულა:
აჰა! ფორმის განტოლება:. ორივე ნაწილად ვყოფ
ვაკეთებთ ფესვების გაცრას:
უფსკრული:
პასუხი:
მაგალითი 2.
ყველაფერი ასევე საკმაოდ ტრივიალურია: მოდით გავაფართოვოთ ფრჩხილები მარჯვნივ:
ძირითადი ტრიგონომეტრიული იდენტურობა:
ორმაგი კუთხის სინუსი:
საბოლოოდ მივიღებთ:
Root dropout: უფსკრული.
პასუხი:.
აბა, როგორ მოგწონთ ტექნიკა, არ არის ძალიან რთული? იმედი მაქვს არა. ჩვენ შეგვიძლია დაუყოვნებლივ გავაკეთოთ დათქმა: მათი სუფთა სახით, განტოლებები, რომლებიც დაუყოვნებლივ მცირდება ტანგენტის განტოლებამდე, საკმაოდ იშვიათია. როგორც წესი, ეს გადასვლა (გაყოფა კოსინუსებით) უფრო რთული პრობლემის მხოლოდ ნაწილია. აქ არის მაგალითი, რომ ივარჯიშოთ:
- Res-shi-te განტოლება
- ნაი-დი-ეს არის ამ განტოლების ყველა ფესვი-არა-ნია, მიმაგრებული-ზე-ლე-ჟა-ში-კუ.
მოდით შევამოწმოთ:
განტოლება წყდება მაშინვე, საკმარისია ორივე ნაწილი გავყოთ:
root მიტოვება:
პასუხი:.
ასეა თუ ისე, ჩვენ ჯერ არ შეგვხვედრია ისეთი განტოლებები, როგორიც ახლახან გავაანალიზეთ. თუმცა, ჩვენთვის ჯერ ნაადრევია დამრგვალება: არის განტოლების კიდევ ერთი „ფენა“, რომელიც ჩვენ არ გავაანალიზეთ. Ისე:
ტრიგონომეტრიული განტოლებების ამოხსნა ცვლადის შეცვლით
აქ ყველაფერი გამჭვირვალეა: ჩვენ კარგად ვუყურებთ განტოლებას, ვამარტივებთ მას მაქსიმალურად, ვაკეთებთ ჩანაცვლებას, ვხსნით, ვაკეთებთ საპირისპირო ჩანაცვლებას! სიტყვებით, ყველაფერი ძალიან მარტივია. ვნახოთ მოქმედებაში:
მაგალითი.
- ამოხსენით განტოლება:.
- ნაი-დი-ეს არის ამ განტოლების ყველა ფესვი-არა-ნია, მიმაგრებული-ზე-ლე-ჟა-ში-კუ.
ისე, აქ ჩანაცვლება თავად ითხოვს ჩვენს ხელში იყოს!
მაშინ ჩვენი განტოლება გადაიქცევა შემდეგში:
პირველ განტოლებას აქვს ფესვები:
და მეორე ეს არის:
ახლა ჩვენ ვიპოვით ინტერვალის კუთვნილ ფესვებს
პასუხი:.
მოდით ერთად გადავხედოთ ოდნავ უფრო რთულ მაგალითს:
- Res-shi-te განტოლება
- მიუთითეთ მოცემული განტოლების ფესვები-non-niy, when-over-le-za-shi-n-e-zhut-ku.
აქ ჩანაცვლება დაუყოვნებლივ არ ჩანს, უფრო მეტიც, ეს არც ისე აშკარაა. ჯერ ვიფიქროთ: რა ვქნათ?
მაგალითად, შეგვიძლია წარმოვიდგინოთ
და ამავე დროს
მაშინ ჩემი განტოლება მიიღებს ფორმას:
ახლა ყურადღება, ფოკუსირება:
მოდით გავყოთ განტოლების ორივე მხარე:
უცებ მე და შენ მივიღეთ კვადრატული განტოლება! მოდით გავაკეთოთ ჩანაცვლება, შემდეგ მივიღებთ:
განტოლებას აქვს შემდეგი ფესვები:
საზიზღარი მეორე სერია ფესვები, მაგრამ ეს არ შეიძლება დაეხმარა! ჩვენ ვირჩევთ ფესვებს ინტერვალში.
ჩვენც ეს უნდა გავითვალისწინოთ
მას შემდეგ და მერე
პასუხი:
კონსოლიდაციისთვის, სანამ პრობლემებს თავად მოაგვარებთ, აქ არის კიდევ ერთი სავარჯიშო თქვენთვის:
- Res-shi-te განტოლება
- ნაი-დი-ეს არის ამ განტოლების ყველა ფესვი-არა-ნი, მიმაგრებული-ზე-ლე-ჟა-ში-პრო-მე-ჟუტ-კუ.
აქ თქვენ უნდა გაახილოთ თვალები: ახლა ჩვენ გვაქვს მნიშვნელები, რომლებიც შეიძლება იყოს ნული! ამიტომ, თქვენ განსაკუთრებით ფრთხილად უნდა იყოთ ფესვების მიმართ!
უპირველეს ყოვლისა, მე მჭირდება განტოლების გარდაქმნა, რათა შევძლო შესაბამისი ჩანაცვლება. ახლა ვერაფერზე უკეთესს ვერ მოვიფიქრებ, ვიდრე ტანგენტის გადაწერა სინუსსა და კოსინუსში:
ახლა მე გადავალ კოსინუსიდან სინუსზე ძირითადი ტრიგონომეტრიული იდენტობის მიხედვით:
და ბოლოს, მე მივიყვან ყველაფერს საერთო მნიშვნელთან:
ახლა შემიძლია გადავიდე განტოლებაზე:
მაგრამ at (ეს არის, at).
ახლა ყველაფერი მზად არის ჩანაცვლებისთვის:
მერე ან
თუმცა, გთხოვთ გაითვალისწინოთ, რომ თუ, მაშინ ამავე დროს!
ვინ იტანჯება ამით? ტანგენტის პრობლემა, ის განუსაზღვრელია, როდესაც კოსინუსი არის ნულოვანი (გაყოფა ნულზე).
ამრიგად, განტოლების ფესვები შემდეგია:
ახლა ჩვენ ამოვიცრათ ფესვები ინტერვალში:
| - შეესაბამება | |
| - უხეში ძალა |
ამრიგად, ჩვენს განტოლებას აქვს ერთი ფესვი ინტერვალში და ის ტოლია.
ხედავთ: მნიშვნელის გამოჩენა (ისევე როგორც ტანგენსი, იწვევს გარკვეულ სირთულეებს ფესვებთან! აქ უფრო ფრთხილად უნდა იყოთ!).
ისე, მე და შენ თითქმის დავასრულეთ ტრიგონომეტრიული განტოლებების ანალიზი, ძალიან ცოტა დარჩა - ორი ამოცანის დამოუკიდებლად გადაჭრა. აი ისინი.
- ამოხსენით განტოლება
ნაი-დი-ეს არის ამ განტოლების ყველა ფესვი-არა-ნია, მიმაგრებული-ზე-ლე-ჟა-ში-კუ. - Res-shi-te განტოლება
მიუთითეთ ამ განტოლების ფესვები, მიმაგრებული ჭრილზე.
გადაწყვიტა? არ არის ძალიან რთული? მოდით შევამოწმოთ:
- ჩვენ ვმუშაობთ შემცირების ფორმულების მიხედვით:
ჩაანაცვლეთ განტოლებაში:
მოდით გადავიწეროთ ყველაფერი კოსინუსების მიხედვით, რათა უფრო მოსახერხებელი იყოს ჩანაცვლება:
ახლა ადვილია ჩანაცვლება:
ნათელია, რომ ეს არის ზედმეტი ფესვი, რადგან განტოლებას არ აქვს ამონახსნები. შემდეგ:
ჩვენ ვეძებთ ფესვებს, რომლებიც გვჭირდება ინტერვალში
პასუხი:.
აქ ჩანაცვლება დაუყოვნებლივ ჩანს:მერე ან
- შეესაბამება! - შეესაბამება! - შეესაბამება! - შეესაბამება! -ბევრი! - ძალიან ბევრი! პასუხი:
აბა, ახლა ეს არის! მაგრამ ტრიგონომეტრიული განტოლებების ამოხსნა ამით არ მთავრდება, ჩვენ გვრჩება ურთულესი შემთხვევები: როცა განტოლებებში ირაციონალურობაა ან ყველანაირი „კომპლექსური მნიშვნელი“. ჩვენ განვიხილავთ, თუ როგორ უნდა მოვაგვაროთ ასეთი ამოცანები სტატიაში მოწინავე დონისთვის.
გაფართოებული დონე
წინა ორ სტატიაში განხილული ტრიგონომეტრიული განტოლებების გარდა, განვიხილავთ განტოლებების სხვა კლასს, რომელიც მოითხოვს კიდევ უფრო ფრთხილად ანალიზს. ეს ტრიგონომეტრიული მაგალითები შეიცავს ან ირაციონალურობას ან მნიშვნელს, რაც ართულებს მათ ანალიზს.... თუმცა, თქვენ შეიძლება შეხვდეთ ამ განტოლებებს საგამოცდო ნაშრომის C ნაწილში. თუმცა, არსებობს ვერცხლის ხაზი: ასეთი განტოლებისთვის, როგორც წესი, არ დგება საკითხი, თუ რომელი ფესვი ეკუთვნის მოცემულ ინტერვალს. მოდი, არ ვიაროთ ბუჩქის გარშემო, არამედ მხოლოდ ტრიგონომეტრიული მაგალითები.
მაგალითი 1.
ამოხსენით განტოლება და იპოვეთ ფესვები, რომლებიც მიეკუთვნება სეგმენტს.
გამოსავალი:
ჩვენ გვაქვს მნიშვნელი, რომელიც არ უნდა იყოს ნული! მაშინ ამ განტოლების ამოხსნა იგივეა, რაც სისტემის ამოხსნა
მოდით ამოხსნათ თითოეული განტოლება:
და ახლა მეორე:
ახლა გადავხედოთ სერიას:
გასაგებია, რომ ვარიანტი არ ჯდება, რადგან ამ შემთხვევაში მნიშვნელი ნულოვანია (იხ. მეორე განტოლების ფესვების ფორმულა)
თუ, თუმცა, მაშინ ყველაფერი რიგზეა და მნიშვნელი არ არის ნული! მაშინ განტოლების ფესვები ასეთია:,.
ახლა ჩვენ ვირჩევთ ინტერვალის კუთვნილ ფესვებს.
| - არ ერგება | - შეესაბამება | |
| - შეესაბამება | - შეესაბამება | |
| უხეში ძალა | უხეში ძალა |
შემდეგ ფესვები შემდეგია:
ხედავთ, მნიშვნელის სახით მცირე ხმაურის გამოჩენაც კი მნიშვნელოვნად იმოქმედა განტოლების ამოხსნაზე: ჩვენ ჩამოვყარეთ ფესვების სერია, რომლებიც ნულს აკლებენ მნიშვნელს. სიტუაცია შეიძლება კიდევ უფრო რთული იყოს, თუ შეხვდებით ტრიგონომეტრიულ მაგალითებს, რომლებსაც აქვთ ირაციონალურობა.
მაგალითი 2.
ამოხსენით განტოლება:
გამოსავალი:
ისე, მაინც არ არის საჭირო ფესვების შერჩევა და ეს კარგია! ჯერ განტოლება გადავწყვიტოთ, ირაციონალურობის მიუხედავად:
Სულ ეს არის? არა, სამწუხაროდ, ეს ძალიან ადვილი იქნებოდა! უნდა გვახსოვდეს, რომ ფესვის ქვეშ შეიძლება იყოს მხოლოდ არაუარყოფითი რიცხვები. შემდეგ:
ამ უთანასწორობის გამოსავალი:
ახლა რჩება იმის გარკვევა, შემთხვევით მოხვდა თუ არა პირველი განტოლების ზოგიერთი ფესვი იქ, სადაც უტოლობა არ არის დაკმაყოფილებული.
ამისათვის შეგიძლიათ კვლავ გამოიყენოთ ცხრილი:
| : , მაგრამ | არა! | |
| დიახ! | ||
| დიახ! |
ამგვარად, ერთ-ერთი ფესვი ჩემგან „გავარდა“! თუ დააყენებ თურმე. მაშინ პასუხი შეიძლება დაიწეროს შემდეგნაირად:
პასუხი:
ხედავთ, ფესვი კიდევ უფრო მეტ ყურადღებას მოითხოვს! საქმეების გასართულებლად: ახლა ნება მომეცით მქონდეს ტრიგონომეტრიული ფუნქცია ფესვის ქვეშ.
მაგალითი 3.
როგორც ადრე: ჯერ თითოეულს ცალ-ცალკე მოვაგვარებთ და მერე ვიფიქრებთ რა გავაკეთეთ.
ახლა მეორე განტოლება:
ახლა ყველაზე რთულია იმის გარკვევა, მიიღება თუ არა უარყოფითი მნიშვნელობები არითმეტიკული ფესვის ქვეშ, თუ ჩვენ შევცვლით ფესვებს იქ პირველი განტოლებიდან:
რიცხვი უნდა გავიგოთ, როგორც რადიანები. ვინაიდან რადიანები დაახლოებით გრადუსია, რადიანები დაახლოებით გრადუსია. ეს მეორე მეოთხედის კუთხეა. რა არის მეორე მეოთხედის კოსინუსის ნიშანი? მინუს. და სინუსი? Პლუსი. რა შეიძლება ითქვას გამონათქვამზე:
ნულზე ნაკლებია!
ეს ნიშნავს, რომ ეს არ არის განტოლების ფესვი.
ახლა ჯერი დადგა.
შევადაროთ ეს რიცხვი ნულს.
კოტანგენსი არის ფუნქცია, რომელიც მცირდება 1 მეოთხედში (რაც უფრო მცირეა არგუმენტი, მით უფრო დიდია კოტანგენსი). რადიანები დაახლოებით გრადუსია. Ამავე დროს
მას შემდეგ და აქედან გამომდინარე
,
პასუხი:.
შეიძლება კიდევ უფრო რთული იყოს? Არაფრის! უფრო რთული იქნება, თუ ტრიგონომეტრიული ფუნქცია ჯერ კიდევ ფესვის ქვეშ იქნება, ხოლო განტოლების მეორე ნაწილი ისევ ტრიგონომეტრიული ფუნქციაა.
რაც უფრო მეტი ტრიგონომეტრიული მაგალითია მით უკეთესი, იხილეთ შემდგომი:
მაგალითი 4.
ფესვი არ არის შესაფერისი შეზღუდული კოსინუსის გამო
ახლა მეორე:
ამავდროულად, ფესვის განმარტებით:
უნდა გვახსოვდეს ერთეული წრე: კერძოდ, ის მეოთხედები, სადაც სინუსი ნულზე ნაკლებია. რა კვარტლები არიან? მესამე და მეოთხე. შემდეგ ჩვენ დავინტერესდებით პირველი განტოლების ის ამონახსნები, რომლებიც დევს მესამე ან მეოთხე კვარტალში.
პირველი სერია აწარმოებს ფესვებს მესამე და მეოთხე მეოთხედის გადაკვეთაზე. მეორე სერია, რომელიც მის დიამეტრულად საპირისპიროა, წარმოშობს პირველი და მეორე მეოთხედის საზღვარზე დაყრილ ფესვებს. ამიტომ ეს სერია არ გვიწყობს.
პასუხი:,
Და ისევ ტრიგონომეტრიული მაგალითები "რთული ირაციონალურობით"... არა მხოლოდ ტრიგონომეტრიული ფუნქცია გვაქვს ისევ ფესვის ქვეშ, არამედ ახლა ის ასევე არის მნიშვნელში!
მაგალითი 5.
ისე, არაფრის გაკეთება არ შეიძლება - ჩვენ ისე ვიქცევით, როგორც ადრე.
ახლა ჩვენ ვმუშაობთ მნიშვნელთან:
მე არ მსურს ტრიგონომეტრიული უტოლობის ამოხსნა და ამიტომ ვიქცევი ეშმაკურად: ავიღებ და ჩავანაცვლებ ჩემს ფესვთა სერიას უტოლობაში:
თუ - კი, მაშინ გვაქვს:
ვინაიდან, მაშინ ხედვის ყველა კუთხე მეოთხე მეოთხედშია. და ისევ წმინდა კითხვა: რა არის სინუსის ნიშანი მეოთხე მეოთხედში? უარყოფითი. შემდეგ უთანასწორობა
თუ უცნაურია, მაშინ:
რომელ კვარტალში დევს კუთხე? ეს მეორე მეოთხედის კუთხეა. შემდეგ ყველა კუთხე ისევ მეორე მეოთხედის კუთხეა. სინუსი იქ დადებითია. მხოლოდ ის, რაც გჭირდებათ! აქედან გამომდინარე, სერია:
ჯდება!
გაუმკლავდეთ ფესვების მეორე სერიას ანალოგიურად:
ჩვენ ვცვლით ჩვენს უთანასწორობას:
თუ - თუნდაც, მაშინ
პირველი მეოთხედი კუთხეები. სინუსი იქ დადებითია, ამიტომ სერია შესაფერისია. ახლა თუ - კენტი, მაშინ:
ასევე შეესაბამება!
აბა, ახლა ჩვენ ვწერთ პასუხს!
პასუხი:
ისე, ეს ალბათ ყველაზე შრომატევადი შემთხვევა იყო. ახლა მე გთავაზობთ პრობლემებს საკუთარი გადაწყვეტისთვის.
Ვარჯიში
- ამოხსენით და იპოვეთ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს.
გადაწყვეტილებები:
პირველი განტოლება:
ან
ODZ ფესვი:მეორე განტოლება:
ფესვების შერჩევა, რომლებიც მიეკუთვნება უფსკრული
პასუხი:
ან
ან
მაგრამ
განიხილეთ:. თუ - თუნდაც, მაშინ
- არ ერგება!
თუ - კენტი,: - შეესაბამება!
ეს ნიშნავს, რომ ჩვენს განტოლებას აქვს ფესვების შემდეგი სერია:
ან
ფესვების შერჩევა ინტერვალში:
| - არ ერგება | - შეესაბამება | |
| - შეესაბამება | -ბევრი | |
| - შეესაბამება | ბევრი |
პასუხი: ,.
ან
მას შემდეგ, რაც ტანგენსი არ არის განსაზღვრული. ფესვების ამ სერიას სასწრაფოდ ვუგდებთ!
Მეორე ნაწილი:
ამავდროულად, ODZ-ის მიხედვით, საჭიროა, რომ
ჩვენ ვამოწმებთ პირველ განტოლებაში ნაპოვნი ფესვებს:
თუ ნიშანია:
პირველი მეოთხედი კუთხეები, სადაც ტანგენსი დადებითია. არ ჯდება!
თუ ნიშანია:
მეოთხე მეოთხედი კუთხე. იქ ტანგენსი უარყოფითია. ჯდება. ჩვენ ვწერთ პასუხს:
პასუხი: ,.
ჩვენ ამ სტატიაში ერთად განვიხილეთ რთული ტრიგონომეტრიული მაგალითები, მაგრამ თქვენ თავად უნდა ამოხსნათ განტოლებები.
შემაჯამებელი და ძირითადი ფორმულები
ტრიგონომეტრიული განტოლება არის განტოლება, რომელშიც უცნობი არის მკაცრად ტრიგონომეტრიული ფუნქციის ნიშნის ქვეშ.
ტრიგონომეტრიული განტოლებების ამოხსნის ორი გზა არსებობს:
პირველი გზა არის ფორმულების გამოყენება.
მეორე გზა გადის ტრიგონომეტრიულ წრეში.
საშუალებას გაძლევთ გაზომოთ კუთხეები, იპოვოთ მათი სინუსები, კოსინუსები და სხვა.
მათემატიკაში ერთიანი სახელმწიფო გამოცდის პროფილის საფეხურისთვის მომზადება. სასარგებლო მასალები ტრიგონომეტრიაზე, დიდი თეორიული ვიდეო ლექციები, პრობლემების ვიდეო ანალიზი და გასული წლების დავალებების შერჩევა.
სასარგებლო მასალები
ვიდეოს შერჩევა და ონლაინ კურსები
ტრიგონომეტრიული ფორმულები
ტრიგონომეტრიული ფორმულების გეომეტრიული ილუსტრაცია
Arc ფუნქციები. უმარტივესი ტრიგონომეტრიული განტოლებები
ტრიგონომეტრიული განტოლებები
- აუცილებელი თეორია პრობლემების გადასაჭრელად.
- ა) ამოხსენით განტოლება $ 7 \ cos ^ 2 x - \ cos x - 8 = 0 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის ინტერვალს $ \ მარცხენა [- \ dfrac (7 \ pi) (2); - \ dfrac (3 \ pi) (2) \ მარჯვნივ] $. - ა) ამოხსენით განტოლება $ \ dfrac (6) (\ cos ^ 2 x) - \ dfrac (7) (\ cos x) + 1 = 0 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ მარცხენა [-3 \ pi-ს ინტერვალს; - \ pi \ მარჯვნივ] $. - ამოხსენით განტოლება $ \ sin \ sqrt (16 - x ^ 2) = \ dfrac12 $.
- ა) ამოხსენით განტოლება $ 2 \ cos 2x - 12 \ cos x + 7 = 0 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ left [- \ pi; \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. - ა) ამოხსენით განტოლება $ \ dfrac (5) (\ mathrm (tg) ^ 2 x) - \ dfrac (19) (\ sin x) + 17 = 0 $.
- ამოხსენით განტოლება $ \ dfrac (2 \ cos ^ 3 x + 3 \ cos ^ 2 x + \ cos x) (\ sqrt (\ mathrm (ctg) x)) = 0 $.
- ამოხსენით განტოლება $ \ dfrac (\ mathrm (tg) ^ 3x - \ mathrm (tg) x) (\ sqrt (- \ sin x)) = 0 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის ინტერვალს $ \ მარცხენა [- \ dfrac (5 \ pi) (2); - \ pi \ მარჯვნივ) $.- ა) ამოხსენით განტოლება $ \ cos 2x = \ sin \ მარცხენა (\ dfrac (3 \ pi) (2) - x \ მარჯვენა) $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ მარცხენა [\ dfrac (3 \ pi) (2) ინტერვალს; \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. - ა) ამოხსენით განტოლება $ 2 \ sin ^ 2 \ მარცხენა (\ dfrac (3 \ pi) (2) + x \ მარჯვენა) = \ sqrt3 \ cos x $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ left [- \ dfrac (7 \ pi) (2) ინტერვალს; -2 \ pi \ მარჯვნივ] $.
დავალებების ვიდეო ანალიზი
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ sqrt (3); \ sqrt (20) \ მარჯვნივ] $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ dfrac (9 \ pi) (2); -3 \ pi \ მარჯვნივ] $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ sqrt (3); \ sqrt (30) \ მარჯვნივ] $.
ა) ამოხსენით განტოლება $ \ cos 2x = 1 - \ cos \ მარცხენა (\ dfrac (\ pi) (2) - x \ მარჯვნივ) $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის ინტერვალს $ \ მარცხენა [- \ dfrac (5 \ pi) (2); - \ pi \ მარჯვნივ) $.
ა) ამოხსენით განტოლება $ \ cos ^ 2 (\ pi - x) - \ sin \ მარცხენა (x + \ dfrac (3 \ pi) (2) \ მარჯვნივ) = 0 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ left [\ dfrac (5 \ pi) (2) ინტერვალს; 4 \ pi \ მარჯვნივ] $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ მარცხენა [\ log_5 2 ინტერვალს; \ log_5 20 \ მარჯვნივ] $.
ა) ამოხსენით განტოლება $ 8 \ sin ^ 2 x + 2 \ sqrt (3) \ cos \ მარცხენა (\ dfrac (3 \ pi) (2) - x \ მარჯვენა) = 9 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის ინტერვალს $ \ მარცხენა [- \ dfrac (5 \ pi) (2); - \ pi \ მარჯვნივ] $.
ა) ამოხსენით განტოლება $ 2 \ log_3 ^ 2 (2 \ cos x) - 5 \ log_3 (2 \ cos x) + 2 = 0 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ left [\ pi ინტერვალს; \ dfrac (5 \ pi) (2) \ მარჯვნივ] $.
ა) ამოხსენით განტოლება $ \ მარცხენა (\ dfrac (1) (49) \ მარჯვნივ) ^ (\ sin x) = 7 ^ (2 \ sin 2x) $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ მარცხენა [\ dfrac (3 \ pi) (2) ინტერვალს; 3 \ pi \ მარჯვნივ] $.
ა) ამოხსენით განტოლება $ \ sin x + \ მარცხენა (\ cos \ dfrac (x) (2) - \ sin \ dfrac (x) (2) \ მარჯვენა) \ მარცხენა (\ cos \ dfrac (x) (2) + \ sin \ dfrac (x) (2) \ მარჯვნივ) = 0 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ left [\ pi ინტერვალს; \ dfrac (5 \ pi) (2) \ მარჯვნივ] $.
ა) ამოხსენით განტოლება $ \ log_4 (\ sin x + \ sin 2x + 16) = 2 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ მარცხენა [-4 \ pi-ს ინტერვალს; - \ dfrac (5 \ pi) (2) \ მარჯვნივ] $.
გასული წლების დავალებების შერჩევა
- ა) ამოხსენით განტოლება $ \ dfrac (\ sin x) (\ sin ^ 2 \ dfrac (x) (2)) = 4 \ cos ^ 2 \ dfrac (x) (2) $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ dfrac (9 \ pi) (2); -3 \ pi \ მარჯვნივ] $. (გამოყენება-2018. ადრეული ტალღა) - ა) ამოხსენით განტოლება $ \ sqrt (x ^ 3 - 4x ^ 2 - 10x + 29) = 3 - x $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ sqrt (3); \ sqrt (30) \ მარჯვნივ] $. (გამოყენება-2018. ადრეული ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ 2 \ sin ^ 2 x + \ sqrt2 \ sin \ მარცხენა (x + \ dfrac (\ pi) (4) \ მარჯვენა) = \ cos x $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [-2 \ pi; - \ dfrac (\ pi) (2) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ sqrt6 \ sin ^ 2 x + \ cos x = 2 \ sin \ მარცხენა (x + \ dfrac (\ pi) (6) \ მარჯვნივ) $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [3 \ pi; \ dfrac (9 \ pi) (2) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ sin x + 2 \ sin \ მარცხენა (2x + \ dfrac (\ pi) (6) \ მარჯვნივ) = \ sqrt3 \ sin 2x + 1 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ dfrac (7 \ pi) (2); -2 \ pi \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ cos ^ 2 x + \ sin x = \ sqrt2 \ sin \ მარცხენა (x + \ dfrac (\ pi) (4) \ მარჯვნივ) $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის $ \ მარცხენა [-4 \ pi; - \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 2 \ sin \ მარცხენა (2x + \ dfrac (\ pi) (3) \ მარჯვნივ) - \ sqrt (3) \ sin x = \ sin 2x + \ sqrt3 $.
- ა) ამოხსენით განტოლება $ 2 \ sqrt3 \ sin \ მარცხენა (x + \ dfrac (\ pi) (3) \ მარჯვენა) - \ cos 2x = 3 \ cos x - 1 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [2 \ pi; \ dfrac (7 \ pi) (2) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 2 \ sin \ მარცხენა (2x + \ dfrac (\ pi) (6) \ მარჯვნივ) - \ cos x = \ sqrt3 \ sin 2x - 1 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ dfrac (5 \ pi) (2); 4 \ pi \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ sqrt2 \ sin \ მარცხენა (\ dfrac (\ pi) (4) + x \ მარჯვენა) + \ cos 2x = \ sin x - 1 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ dfrac (7 \ pi) (2); 5 \ pi \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ sqrt2 \ sin \ მარცხენა (2x + \ dfrac (\ pi) (4) \ მარჯვნივ) + \ sqrt2 \ cos x = \ sin 2x - 1 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ dfrac (5 \ pi) (2); - \ pi \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 2 \ sin \ მარცხენა (x + \ dfrac (\ pi) (3) \ მარჯვნივ) + \ cos 2x = \ sqrt3 \ cos x + 1 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [-3 \ pi; - \ dfrac (3 \ pi) (2) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა)
ბ) იპოვნეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ pi; \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა)- ა) ამოხსენით განტოლება $ 2 \ sin \ მარცხენა (x + \ dfrac (\ pi) (4) \ მარჯვნივ) + \ cos 2x = \ sqrt2 \ cos x + 1 $.
ბ) იპოვნეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ pi; \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ 2 \ cos x - \ sqrt3 \ sin ^ 2 x = 2 \ cos ^ 3 x $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ dfrac (7 \ pi) (2); -2 \ pi \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ 2 \ cos x + \ sin ^ 2 x = 2 \ cos ^ 3 x $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ dfrac (9 \ pi) (2); -3 \ pi \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ 2 \ sqrt2 \ sin \ მარცხენა (x + \ dfrac (\ pi) (3) \ მარჯვნივ) + 2 \ cos ^ 2 x = 2 + \ sqrt6 \ cos x $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [-3 \ pi; - \ dfrac (3 \ pi) (2) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ x - 3 \ sqrt (x - 1) + 1 = 0 $.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ sqrt (3); \ sqrt (20) \ მარჯვნივ] $. (გამოყენება-2018. მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ 2x \ cos x - 8 \ cos x + x - 4 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ dfrac (\ pi) (2); \ \ pi \ მარჯვნივ] $. (USE-2017, მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ \ log_3 (x ^ 2 - 2x) = 1 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ log_2 0 (,) 2; \ \ log_2 5 \ მარჯვნივ] $. (USE-2017, მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ \ log_3 (x ^ 2 - 24x) = 4 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ log_2 0 (,) 1; \ 12 \ sqrt (5) \ მარჯვნივ] $. (USE-2017, მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ 0 (,) 4 ^ (\ sin x) + 2 (,) 5 ^ (\ sin x) = 2 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [2 \ pi; \ \ dfrac (7 \ pi) (2) \ მარჯვნივ] $. (USE-2017, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ log_8 \ მარცხენა (7 \ sqrt (3) \ sin x - \ cos 2x - 10 \ მარჯვნივ) = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ dfrac (3 \ pi) (2); \ 3 \ pi \ მარჯვნივ] $. (USE-2017, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ log_4 \ მარცხენა (2 ^ (2x) - \ sqrt (3) \ cos x - 6 \ sin ^ 2 x \ მარჯვნივ) = x $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ dfrac (5 \ pi) (2); \ 4 \ pi \ მარჯვნივ] $. (USE-2017, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 2 \ log_2 ^ 2 \ მარცხენა (\ sin x \ მარჯვენა) - 5 \ log_2 \ მარცხენა (\ sin x \ მარჯვნივ) - 3 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [- 3 \ pi; \ - \ dfrac (3 \ pi) (2) \ მარჯვნივ] $. (USE-2017, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 81 ^ (\ cos x) - 12 \ cdot 9 ^ (\ cos x) + 27 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [- 4 \ pi; \ - \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (USE-2017, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 8 ^ x - 9 \ cdot 2 ^ (x + 1) + 2 ^ (5 - x) = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ log_5 2; \ \ log_5 20 \ მარჯვნივ] $. (USE-2017, ადრეული ტალღა) - ა) ამოხსენით განტოლება $ 2 \ log ^ 2_9 x - 3 \ log_9 x + 1 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ sqrt (10); \ \ sqrt (99) \ მარჯვნივ] $. (USE-2016, მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ 6 \ log ^ 2_8 x - 5 \ log_8 x + 1 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [2; \ 2 (,) 5 \ მარჯვნივ] $. (USE-2016, მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ \ sin 2x = 2 \ sin x + \ sin \ მარცხენა (x + \ dfrac (3 \ pi) (2) \ მარჯვნივ) + 1 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (USE-2016, მთავარი ტალღა, სარეზერვო დღე) - ა) ამოხსენით განტოლება $ 2 \ cos ^ 2 x + 1 = 2 \ sqrt (2) \ cos \ მარცხენა (\ dfrac (3 \ pi) (2) - x \ მარჯვნივ) $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ dfrac (3 \ pi) (2); \ 3 \ pi \ მარჯვნივ] $. (USE-2016, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 2 \ log ^ 2_2 (2 \ cos x) - 9 \ log_2 (2 \ cos x) + 4 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [-2 \ pi; \ - \ dfrac (\ pi) (2) \ მარჯვნივ] $. (USE-2016, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 8 ^ x - 7 \ cdot 4 ^ x - 2 ^ (x + 4) + 112 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ log_2 5; \ \ log_2 11 \ მარჯვნივ] $. (USE-2016, ადრეული ტალღა) - ა) ამოხსენით განტოლება $ \ cos 2x + \ cos ^ 2 \ მარცხენა (\ dfrac (3 \ pi) (2) - x \ მარჯვენა) = 0,25 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [-4 \ pi; \ - \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (USE-2016, ადრეული ტალღა) - ა) ამოხსენით განტოლება $ \ dfrac (13 \ sin ^ 2 x - 5 \ sin x) (13 \ cos x + 12) = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ მარჯვნივ] $. (USE-2016, ადრეული ტალღა) - ა) ამოხსენით განტოლება $ \ dfrac (\ sin2x) (\ sin \ მარცხენა (\ dfrac (7 \ pi) (2) - x \ მარჯვენა)) = \ sqrt (2) $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის $ \ მარცხენა $ სეგმენტს. (USE-2015, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 4 \ sin ^ 2 x = \ mathrm (tg) x $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ pi; \ 0 \ მარჯვნივ] $. (USE-2015, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 3 \ cos 2x - 5 \ sin x + 1 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ pi; \ \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (USE-2015, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ cos 2x - 5 \ sqrt (2) \ cos x - 5 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ მარჯვნივ] $. (USE-2015, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ sin 2x + \ sqrt (2) \ sin x = 2 \ cos x + \ sqrt (2) $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ pi; \ \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (USE-2015, ადრეული ტალღა) - ა) ამოხსენით განტოლება $ 2 \ cos ^ 3 x - \ cos ^ 2 x + 2 \ cos x - 1 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [2 \ pi; \ \ dfrac (7 \ pi) (2) \ მარჯვნივ] $. (USE-2015, ადრეული ტალღა) - ა) ამოხსენით განტოლება $ \ mathrm (tg) ^ 2 x + (1 + \ sqrt (3)) \ mathrm (tg) x + \ sqrt (3) = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ dfrac (5 \ pi) (2); \ 4 \ pi \ მარჯვნივ] $. (USE-2014, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 2 \ sqrt (3) \ cos ^ 2 \ მარცხენა (\ dfrac (3 \ pi) (2) + x \ მარჯვენა) - \ sin 2x = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ dfrac (3 \ pi) (2); \ 3 \ pi \ მარჯვნივ] $. (USE-2014, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ \ cos 2x + \ sqrt (2) \ sin \ მარცხენა (\ dfrac (\ pi) (2) + x \ მარჯვენა) + 1 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [-3 \ pi; \ - \ dfrac (3 \ pi) (2) \ მარჯვნივ] $. (USE-2014, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ - \ sqrt (2) \ sin \ მარცხენა (- \ dfrac (5 \ pi) (2) + x \ მარჯვენა) \ cdot \ sin x = \ cos x $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [\ dfrac (9 \ pi) (2); \ 6 \ pi \ მარჯვნივ] $. (USE-2014, ადრეული ტალღა) - ა) ამოხსენით განტოლება $ \ sin 2x = \ sin \ მარცხენა (\ dfrac (\ pi) (2) + x \ მარჯვენა) $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [- \ dfrac (7 \ pi) (2); \ - \ dfrac (5 \ pi) (2) \ მარჯვნივ] $. (USE-2013, მთავარი ტალღა) - ა) ამოხსენით განტოლება $ 6 \ sin ^ 2 x + 5 \ sin \ მარცხენა (\ dfrac (\ pi) (2) - x \ მარჯვენა) - 2 = 0 $.
ბ) მიუთითეთ ამ განტოლების ფესვები, რომლებიც ეკუთვნის სეგმენტს $ \ მარცხენა [-5 \ pi; \ - \ dfrac (7 \ pi) (2) \ მარჯვნივ] $. (USE-2012, მეორე ტალღა)
გაკვეთილის მიზანი:
ა) უმარტივესი ტრიგონომეტრიული განტოლებების ამოხსნის უნარის კონსოლიდაცია;
ბ) ასწავლეთ ტრიგონომეტრიული განტოლებების ფესვების არჩევა მოცემული ინტერვალიდან
გაკვეთილების დროს.
1. ცოდნის აქტუალიზაცია.
ა) საშინაო დავალების შემოწმება: კლასს მიეცა წინასწარი საშინაო დავალება - ამოხსნას განტოლება და მოძებნოს გზა მოცემული ინტერვალიდან ფესვების ამორჩევისთვის.
1) cos x= -0.5, სადაც xI [-]. პასუხი:.
2) ცოდვა x=, სადაც xI. პასუხი: ; ...
3) co 2 x= -, სადაც хI. პასუხი:
მოსწავლეები წერენ ამოხსნას დაფაზე, ვინმე იყენებს გრაფიკს, ვიღაც იყენებს შერჩევის მეთოდს.
ამ დროს კლასი მუშაობს ზეპირად.
იპოვნეთ გამოთქმის მნიშვნელობა:
ა) ტგ - ცოდვა + cos + ცოდვა. პასუხი: 1.
ბ) 2 arccos 0 + 3 arccos 1. პასუხი:?
გ) arcsin + arcsin. პასუხი:.
დ) 5 arctan (-) - arccos (-). პასუხი: -.
- შევამოწმოთ საშინაო დავალება, გახსენით საშინაო დავალების რვეულები.
ზოგიერთმა თქვენგანმა იპოვა გამოსავალი fit მეთოდით, ზოგმა კი გრაფიკით.
2. დასკვნა ამ ამოცანების ამოხსნის შესახებ და პრობლემის ფორმულირება, ანუ თემის მესიჯი და გაკვეთილის მიზანი.
- ა) ძნელია ამოხსნა შერჩევის დახმარებით, თუ დიდი ინტერვალია მოცემული.
- ბ) გრაფიკული მეთოდი არ იძლევა ზუსტ შედეგებს, მოითხოვს გადამოწმებას და დიდ დროს მოითხოვს.
- მაშასადამე, კიდევ ერთი მეთოდი მაინც უნდა იყოს, ყველაზე უნივერსალური - ვცადოთ მისი პოვნა. მაშ, რას ვაპირებთ დღეს კლასში? (ისწავლეთ ტრიგონომეტრიული განტოლების ფესვების არჩევა მოცემულ ინტერვალზე.)
- მაგალითი 1 (მოსწავლე მიდის დაფაზე)
cos x= -0.5, სადაც xI [-].
კითხვა: რაზეა დამოკიდებული ამ ამოცანის პასუხი? (განტოლების ზოგადი ამონახსნებიდან. ამოხსნა დავწეროთ ზოგადი ფორმით). გადაწყვეტილება იწერება დაფაზე
х = + 2? k, სადაც k R.
- ჩავწეროთ ეს გამოსავალი კომპლექტის სახით:

- როგორ ფიქრობთ, ხსნარის რომელი ჩანაწერისთვის არის მოსახერხებელი ფესვების არჩევა ინტერვალში? (მეორე ჩანაწერიდან). მაგრამ ეს ისევ შერჩევის მეთოდია. რა უნდა ვიცოდეთ სწორი პასუხის მისაღებად? (თქვენ უნდა იცოდეთ k-ის მნიშვნელობები).
(მოდით გავაკეთოთ მათემატიკური მოდელი კ-ის საპოვნელად).
ვინაიდან kI Z, მაშინ k = 0, აქედან გამომდინარე X= = |
ეს უტოლობა გვიჩვენებს, რომ არ არსებობს k-ის მთელი მნიშვნელობები. |
დასკვნა:ტრიგონომეტრიული განტოლების ამოხსნისას მოცემული ინტერვალიდან ფესვების ასარჩევად საჭიროა:
- ფორმის განტოლების ამოხსნა sin x = a, cos x = aუფრო მოსახერხებელია განტოლების ფესვების დაწერა ფესვების ორი რიგის სახით.
- ფორმის განტოლებების ამოხსნა tg x = a, ctg x = aჩამოწერეთ ფესვების ზოგადი ფორმულა.
- შეადგინეთ მათემატიკური მოდელი თითოეული ამოხსნისთვის ორმაგი უტოლობის სახით და იპოვეთ k ან n პარამეტრის მთელი რიცხვი.
- ჩაანაცვლეთ ეს მნიშვნელობები ფესვის ფორმულაში და გამოთვალეთ ისინი.
ამოიღეთ მაგალითები 2 და 3 საშინაო დავალებიდან მიღებული ალგორითმის გამოყენებით. პარალელურად ორი მოსწავლე მუშაობს დაფაზე, რასაც მოჰყვება ნამუშევრის შემოწმება.
ამ სტატიაში შევეცდები აგიხსნათ 2 გზა ფესვების შერჩევა ტრიგონომეტრიულ განტოლებაში: უტოლობების გამოყენებით და ტრიგონომეტრიული წრის გამოყენებით. პირდაპირ საილუსტრაციო მაგალითზე გადავიდეთ და საქმეს მივხედოთ.
ა) ამოხსენით განტოლება sqrt (2) cos ^ 2x = sin (Pi / 2 + x)
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც მიეკუთვნება [-7Pi / 2; -2Pi]
ამოხსნათ წერტილი a.
ჩვენ ვიყენებთ შემცირების ფორმულას სინუს სინუსისთვის (Pi / 2 + x) = cos (x)
Sqrt (2) cos ^ 2x = cosx
Sqrt (2) cos ^ 2x - cosx = 0
Cosx (sqrt (2) cosx - 1) = 0
X1 = Pi / 2 + Pin, n ∈ Z
Sqrt (2) cosx - 1 = 0
Cosx = 1 / sqrt (2)
Cosx = sqrt (2) / 2
X2 = arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
x3 = -arccos (sqrt (2) / 2) + 2Pin, n ∈ Z
X2 = Pi / 4 + 2Pin, n ∈ Z
x3 = -Pi / 4 + 2Pin, n ∈ Z
გადავწყვიტოთ ბ წერტილი.
1) ფესვების შერჩევა უტოლობების გამოყენებით
აქ ყველაფერი კეთდება უბრალოდ, ჩვენ ვცვლით მიღებულ ფესვებს მოცემულ ინტერვალში [-7Pi / 2; -2Pi], იპოვნეთ n-ის მთელი მნიშვნელობები.
7Pi / 2 ნაკლები ან ტოლი Pi / 2 + Pin ნაკლები ან ტოლი -2Pi
დაყავით ყველაფერი Pi-ზე ერთდროულად
7/2 ნაკლებია ან ტოლია 1/2-ზე + n არის -2-ზე ნაკლები ან ტოლი
7/2 - 1/2 ნაკლები ან ტოლი n-ზე ნაკლები ან ტოლი -2 - 1/2
4-ით ნაკლები ან ტოლი n-ზე ნაკლები ან ტოლი -5/2-ის
მთელი n ამ დიაპაზონში არის -4 და -3. ამრიგად, ამ ინტერვალის კუთვნილი ფესვები იქნება Pi / 2 + Pi (-4) = -7Pi / 2, Pi / 2 + Pi (-3) = -5Pi / 2
ანალოგიურად, ჩვენ ვაკეთებთ კიდევ ორ უტოლობას
7Pi / 2 ნაკლები ან ტოლი Pi / 4 + 2Pin ნაკლები ან ტოლი -2Pi
-15/8 ნაკლები ან ტოლი n-ზე ნაკლები ან ტოლი -9/8
ამ ინტერვალში არ არის მთელი რიცხვი n
7Pi / 2 ნაკლები ან ტოლი -Pi / 4 + 2Pin ნაკლები ან ტოლი -2Pi
-13/8 ნაკლები ან ტოლი n-ზე ნაკლები ან ტოლი -7/8
ერთი მთელი რიცხვი n ამ დიაპაზონში არის -1. ასე რომ, არჩეული ფესვი ამ ინტერვალზე არის -Pi / 4 + 2Pi * (- 1) = -9Pi / 4.
ასე რომ, პასუხი ბ პუნქტში: -7Pi / 2, -5Pi / 2, -9Pi / 4
2) ფესვების შერჩევა ტრიგონომეტრიული წრის გამოყენებით
ამ მეთოდის გამოსაყენებლად, თქვენ უნდა გესმოდეთ, როგორ მუშაობს ეს წრე. შევეცდები მარტივი ენით ავხსნა, როგორ მესმის ეს. ვფიქრობ, სკოლებში ალგებრის გაკვეთილებზე ეს თემა ბევრჯერ აიხსნება მასწავლებლის ჭკვიანური სიტყვებით, სახელმძღვანელოებში რთული ფორმულირებებით. პირადად მე მესმის ეს, როგორც წრე, რომლის გავლა შესაძლებელია უსასრულოდ რამდენჯერმე, იმის გამო, რომ სინუს და კოსინუს ფუნქციები პერიოდულია.
მოდით წავიდეთ საათის ისრის საწინააღმდეგოდ ერთხელ
მოდით ვიაროთ 2-ჯერ საათის ისრის საწინააღმდეგოდ
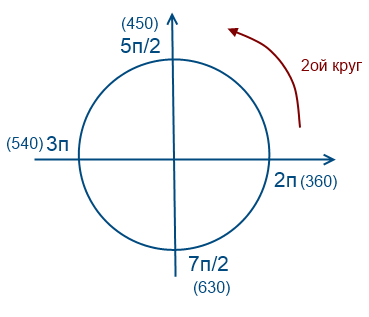
მოდით ვიაროთ 1 ჯერ საათის ისრის მიმართულებით (მნიშვნელობები უარყოფითი იქნება)

დავუბრუნდეთ ჩვენს კითხვას, ჩვენ უნდა ავირჩიოთ ფესვები ინტერვალში [-7Pi / 2; -2Pi]
-7Pi / 2 და -2Pi ნომრებზე მისასვლელად, თქვენ უნდა გაიაროთ წრე საათის ისრის საწინააღმდეგოდ ორჯერ. იმისათვის, რომ ვიპოვოთ განტოლების ფესვები ამ ინტერვალზე, საჭიროა შეფასება და ჩანაცვლება.
განვიხილოთ x = Pi / 2 + Pin. რა არის n-ის მიახლოებითი მნიშვნელობა იმისთვის, რომ x-ის მნიშვნელობა იყოს სადღაც ამ ინტერვალში? ჩანაცვლებით, ვთქვათ -2, მივიღებთ Pi / 2 - 2Pi = -3Pi / 2, ცხადია, ეს არ შედის ჩვენს ინტერვალში, ამიტომ ვიღებთ -3-ზე ნაკლებს, Pi / 2 - 3Pi = -5Pi / 2, ჯდება, მოდით კიდევ ერთხელ ვცადოთ -4, Pi / 2 - 4Pi = -7Pi / 2 ასევე შესაფერისია.
ანალოგიურად მსჯელობისას Pi / 4 + 2Pin და -Pi / 4 + 2Pin, ჩვენ ვპოულობთ სხვა ფესვს -9Pi / 4.

ორი მეთოდის შედარება.
პირველი მეთოდი (უტოლობების გამოყენება) ბევრად უფრო საიმედო და ბევრად უფრო ადვილი გასაგებია, მაგრამ თუ ნამდვილად სერიოზულად გაუმკლავდებით ტრიგონომეტრიულ წრეს და მეორე შერჩევის მეთოდს, მაშინ ფესვების შერჩევა ბევრად უფრო სწრაფი იქნება, შეგიძლიათ დაზოგოთ დაახლოებით 15 წუთი. გამოცდა.
ა) ამოხსენით განტოლება:.
ბ) იპოვეთ ამ განტოლების ყველა ფესვი, რომელიც ეკუთვნის სეგმენტს.
პრობლემის გადაწყვეტა

ეს გაკვეთილი განიხილავს ტრიგონომეტრიული განტოლების ამოხსნის მაგალითს, რომელიც შეიძლება გამოყენებულ იქნას როგორც მაგალითი C1 ტიპის ამოცანების გადასაჭრელად მათემატიკაში გამოცდისთვის მოსამზადებლად.
უპირველეს ყოვლისა, განისაზღვრება ფუნქციის ფარგლები - არგუმენტის ყველა დაშვებული მნიშვნელობა. შემდეგ, ამოხსნის დროს, ტრიგონომეტრიული სინუს ფუნქცია გარდაიქმნება კოსინუსში შემცირების ფორმულის გამოყენებით. გარდა ამისა, განტოლების ყველა პირობა გადადის მის მარცხენა მხარეს, სადაც საერთო ფაქტორი ამოღებულია ფრჩხილებიდან. თითოეული ფაქტორი დაყენებულია ნულის ტოლი, რაც საშუალებას გაძლევთ განსაზღვროთ განტოლების ფესვები. შემდეგ მონაცვლეობის მეთოდით განისაზღვრება მოცემული სეგმენტის კუთვნილი ფესვები. ამისათვის აგებულ ერთეულ წრეზე აღინიშნება მარყუჟი მითითებული სეგმენტის მარცხენა საზღვრიდან მარჯვნივ. გარდა ამისა, ერთეულ წრეზე ნაპოვნი ფესვები დაკავშირებულია სეგმენტებით მის ცენტრთან და განისაზღვრება წერტილები, რომლებზეც ეს სეგმენტები კვეთენ მარყუჟს. ეს გადაკვეთის წერტილები არის პრობლემის მეორე ნაწილის სასურველი პასუხი.

































