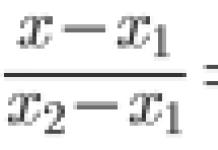Antidarinis ir neapibrėžtas integralas – Žinių hipermarketas. Antiderivative Antiderivative sprendimo radimas

Pamoka ir pristatymas tema: "Antiderivatinė funkcija. Funkcijos grafikas"

Papildomos medžiagos
Mieli vartotojai, nepamirškite palikti savo komentarų, atsiliepimų, pageidavimų! Visa medžiaga buvo patikrinta antivirusine programa.

Mokymo priemonės ir simuliatoriai Integral internetinėje parduotuvėje 11 klasei
Algebriniai parametrų uždaviniai, 9–11 kl
„Interaktyvios užduotys apie kūrimą erdvėje 10 ir 11 klasėms“

Antiderivatinė funkcija. Įvadas

Vaikinai, jūs žinote, kaip rasti funkcijų išvestinius naudojant įvairias formules ir taisykles. Šiandien mes išnagrinėsime atvirkštinę išvestinės apskaičiavimo operaciją. Išvestinės sąvoka dažnai vartojama Tikras gyvenimas. Leiskite jums priminti: išvestinė yra funkcijos kitimo greitis konkrečiame taške. Procesai, susiję su judėjimu ir greičiu, yra gerai aprašyti šiais terminais.

Pažvelkime į šią problemą: „Tiesia linija judančio objekto greitis apibūdinamas formule $V=gt$. Jis reikalingas judėjimo dėsniui atkurti.
Sprendimas.
Gerai žinome formulę: $S"=v(t)$, kur S yra judėjimo dėsnis.
Mūsų užduotis yra surasti funkciją $S=S(t)$, kurios išvestinė yra lygi $gt$. Atidžiai pažiūrėję galite atspėti, kad $S(t)=\frac(g*t^2)(2)$.
Patikrinkime šios problemos sprendimo teisingumą: $S"(t)=(\frac(g*t^2)(2))"=\frac(g)(2)*2t=g*t$.
Žinodami funkcijos išvestinę, radome pačią funkciją, tai yra, atlikome atvirkštinę operaciją.
Tačiau verta atkreipti dėmesį į šią akimirką. Mūsų problemos sprendimas reikalauja paaiškinimo, jei prie rastos funkcijos pridėsime bet kurį skaičių (konstantą), tada išvestinės reikšmė nepasikeis: $S(t)=\frac(g*t^2)(2)+; c,c=const$.
$S"(t)=(\frac(g*t^2)(2))"+c"=g*t+0=g*t$.

Vaikinai, atkreipkite dėmesį: mūsų problema turi begalę sprendimų!
Jei problema nenurodo pradinės ar kitos sąlygos, nepamirškite prie sprendimo pridėti konstantos. Pavyzdžiui, mūsų užduotis gali nurodyti mūsų kūno padėtį pačioje judesio pradžioje. Tada nesunku apskaičiuoti konstantą, į gautą lygtį pakeitus nulį, gauname konstantos reikšmę.

Kaip vadinasi ši operacija?
Atvirkštinė diferenciacijos operacija vadinama integracija.
Funkcijos radimas iš duotosios išvestinės – integracija.
Pati funkcija bus vadinama antiderivative, tai yra vaizdas, iš kurio buvo gauta funkcijos išvestinė.
Įprasta rašyti antidarinį Didžioji raidė$y=F"(x)=f(x)$.

Apibrėžimas. Funkcija $y=F(x)$ vadinama funkcijos $у=f(x)$ antiišvestine intervale X, jei bet kuriai $хϵХ$ galioja lygybė $F'(x)=f(x)$ .

Padarykime antidarinių lentelę už įvairių funkcijų. Jis turėtų būti atspausdintas kaip priminimas ir įsimintinas.

Mūsų lentelėje nebuvo nurodytos pradinės sąlygos. Tai reiškia, kad prie kiekvienos išraiškos dešinėje lentelės pusėje reikia pridėti konstantą. Šią taisyklę paaiškinsime vėliau.

Antidarinių radimo taisyklės

Užsirašykime keletą taisyklių, kurios padės mums rasti antidarinius. Jie visi panašūs į diferenciacijos taisykles.

1 taisyklė. Sumos antidarinė lygi antidarinių sumai. $F(x+y)=F(x)+F(y)$.

Pavyzdys.
Raskite funkcijos $y=4x^3+cos(x)$ antidarinį.
Sprendimas.
Sumos antiderivatinė yra lygi antidarinių sumai, tada turime rasti kiekvienos pateiktos funkcijos antidarinį.
$f(x)=4x^3$ => $F(x)=x^4$.
$f(x)=cos(x)$ => $F(x)=sin(x)$.
Tada pradinės funkcijos antidarinė bus: $y=x^4+sin(x)$ arba bet kuri formos $y=x^4+sin(x)+C$ funkcija.

2 taisyklė. Jei $F(x)$ yra $f(x)$ antidarinė, tai $k*F(x)$ yra funkcijos $k*f(x)$ antidarinė.(Koeficientą nesunkiai galime paimti kaip funkciją).

Pavyzdys.
Raskite funkcijų antidarinius:
a) $y=8sin(x)$.
b) $y=-\frac(2)(3)cos(x)$.
c) $y=(3x)^2+4x+5$.
Sprendimas.
a) $sin(x)$ antidarinys yra atėmus $cos(x)$. Tada pradinės funkcijos antiderivatinė bus tokia: $y=-8cos(x)$.

B) $cos(x)$ antidarinys yra $sin(x)$. Tada pradinės funkcijos antiderivatinė bus tokia: $y=-\frac(2)(3)sin(x)$.

C) $x^2$ antidarinys yra $\frac(x^3)(3)$. X antidarinys yra $\frac(x^2)(2)$. 1 antidarinys yra x. Tada pradinės funkcijos antidarinė bus tokia: $y=3*\frac(x^3)(3)+4*\frac(x^2)(2)+5*x=x^3+2x ^2+5x$ .

3 taisyklė. Jei $у=F(x)$ yra funkcijos $y=f(x)$ priešišvestinė, tai funkcijos $y=f(kx+m)$ antidarinė yra funkcija $y=\frac(1 )(k)* F(kx+m)$.

Pavyzdys.
Raskite šių funkcijų antidarinius:
a) $y=cos(7x)$.
b) $y=sin(\frac(x)(2))$.
c) $y=(-2x+3)^3$.
d) $y=e^(\frac(2x+1)(5))$.
Sprendimas.
a) $cos(x)$ antidarinys yra $sin(x)$. Tada funkcijos $y=cos(7x)$ antidarinė bus funkcija $y=\frac(1)(7)*sin(7x)=\frac(sin(7x))(7)$.

B) $sin(x)$ antidarinys yra atėmus $cos(x)$. Tada funkcijos $y=sin(\frac(x)(2))$ antidarinė bus funkcija $y=-\frac(1)(\frac(1)(2))cos(\frac(x) )(2) )=-2cos(\frac(x)(2))$.

C) $x^3$ antidarinys yra $\frac(x^4)(4)$, tada pradinės funkcijos $y=-\frac(1)(2)*\frac(((-) 2x+3) )^4)(4)=-\frac(((-2x+3))^4)(8)$.

D) Šiek tiek supaprastinkite išraišką iki laipsnio $\frac(2x+1)(5)=\frac(2)(5)x+\frac(1)(5)$.
Eksponentinės funkcijos antiderivatinė yra pati eksponentinė funkcija. Pradinės funkcijos antidarinė bus $y=\frac(1)(\frac(2)(5))e^(\frac(2)(5)x+\frac(1)(5))=\frac (5)(2)*e^(\frac(2x+1)(5))$.

Teorema. Jei $y=F(x)$ yra funkcijos $y=f(x)$ intervalo X antidarinė, tai funkcija $y=f(x)$ turi be galo daug antidarinių, ir visos jos turi forma $y=F( x)+С$.

Jei visuose aukščiau aptartuose pavyzdžiuose reikėjo rasti visų antidarinių rinkinį, tada visur reikia pridėti konstantą C.
Funkcijos $y=cos(7x)$ visi antidariniai turi tokią formą: $y=\frac(sin(7x))(7)+C$.
Funkcijos $y=(-2x+3)^3$ visi antidariniai turi tokią formą: $y=-\frac(((-2x+3))^4)(8)+C$.

Pavyzdys.
Autorius duotas įstatymas kūno greičio pokyčiai laikui bėgant $v=-3sin(4t)$ raskite judėjimo dėsnį $S=S(t)$, jei pradiniu laiko momentu kūno koordinatė buvo lygi 1,75.
Sprendimas.
Kadangi $v=S’(t)$, turime rasti tam tikro greičio antidarinį.
$S=-3*\frac(1)(4)(-cos(4t))+C=\frac(3)(4)cos(4t)+C$.
Šioje užduotyje pateikiama papildoma sąlyga – pradinis laiko momentas. Tai reiškia, kad $t=0$.
$S(0)=\frac(3)(4)cos(4*0)+C=\frac(7)(4)$.
$\frac(3)(4)cos(0)+C=\frac(7)(4)$.
$\frac(3)(4)*1+C=\frac(7)(4)$.
$C=1$.
Tada judėjimo dėsnis aprašomas formule: $S=\frac(3)(4)cos(4t)+1$.

Problemos, kurias reikia spręsti savarankiškai

1. Raskite funkcijų antidarinius:
a) $y=-10sin(x)$.
b) $y=\frac(5)(6)cos(x)$.
c) $y=(4x)^5+(3x)^2+5x$.
2. Raskite šių funkcijų antidarinius:
a) $y=cos(\frac(3)(4)x)$.
b) $y=sin(8x)$.
c) $y=((7x+4))^4$.
d) $y=e^(\frac(3x+1)(6))$.
3. Pagal pateiktą kūno greičio kitimo per laiką dėsnį $v=4cos(6t)$, raskite judėjimo dėsnį $S=S(t)$, jei pradiniu laiko momentu kūnas turėjo koordinatė lygi 2.

Kiekvienam matematiniam veiksmui yra atvirkštinis veiksmas. Diferencijavimo veiksmui (funkcijų išvestinių radimui) yra ir atvirkštinis veiksmas – integracija. Integruojant funkcija randama (atkuriama) iš jos duotosios išvestinės arba diferencialo. Rasta funkcija vadinama antiderivatinis.

Apibrėžimas. Diferencijuojama funkcija F(x) vadinamas funkcijos antidariniu f(x) tam tikru intervalu, jei visiems X iš šio intervalo galioja ši lygybė: F′(x)=f (x).

Pavyzdžiai. Raskite funkcijų antidarinius: 1) f (x)=2x; 2) f (x) = 3 cos3x.

1) Kadangi (x²)′=2x, tai pagal apibrėžimą funkcija F (x)=x² bus funkcijos f (x)=2x antidarinė.

2) (sin3x)′=3cos3x. Jei pažymėsime f (x)=3cos3x ir F (x)=sin3x, tada pagal antidarinės apibrėžimą turime: F'(x)=f (x), todėl F (x)=sin3x yra antidarinys, kai f (x)=3cos3x.

Atkreipkite dėmesį, kad (sin3x +5 )′= 3cos3x, ir (sin3x -8,2 )′= 3cos3x, ... bendra forma galime rašyti: (sin3x +C)′= 3cos3x, Kur SU- tam tikra pastovi vertė. Šie pavyzdžiai rodo integracijos veiksmo dviprasmiškumą, priešingai nei diferenciacijos veiksmas, kai bet kuri diferencijuojama funkcija turi vieną išvestinę.

Apibrėžimas. Jei funkcija F(x) yra funkcijos antidarinys f(x) tam tikru intervalu, tada visų šios funkcijos antidarinių rinkinys turi tokią formą:

F(x)+C, kur C yra bet koks realusis skaičius.

Visų nagrinėjamo intervalo funkcijos f (x) antidarinių F (x)+C aibė vadinama neapibrėžtuoju integralu ir žymima simboliu ∫ (integralus ženklas). Užsirašyti: ∫f (x) dx=F (x)+C.

Išraiška ∫f(x)dx skaitykite: „integralas ef nuo x iki de x“.

f(x)dx- integrantinė išraiška,

f(x)- integravimo funkcija,

X yra integracijos kintamasis.

F(x)- funkcijos antidarinys f(x),

SU- tam tikra pastovi vertė.

Dabar nagrinėjamus pavyzdžius galima parašyti taip:

1) ∫ 2хdx=x²+C. 2) ∫ 3cos3xdx=sin3x+C.

Ką reiškia d ženklas?

d- diferencialinis ženklas – turi dvejopą paskirtį: pirma, šis ženklas atskiria integrandą nuo integravimo kintamojo; antra, viskas, kas yra po šio ženklo, pagal numatytuosius nustatymus yra diferencijuojama ir padauginama iš integrando.

Pavyzdžiai. Raskite integralus: 3) ∫ 2pxdx; 4) ∫ 2pxdp.

3) Po diferencialo piktograma d išlaidas XX, A R

∫ 2хрdx=рх²+С. Palyginkite su pavyzdžiu 1).

Patikrinkime. F′(x)=(px²+C)′=p·(x²)′+C′=p·2x=2px=f (x).

4) Po diferencialo piktograma d išlaidas R. Tai reiškia, kad integracijos kintamasis R, ir daugiklis X turėtų būti laikoma tam tikra pastovia verte.

∫ 2хрдр=р²х+С. Palyginkite su pavyzdžiais 1) Ir 3).

Patikrinkime. F′(p)=(p²x+C)′=x·(p²)′+C′=x·2p=2px=f (p).

Matėme, kad darinys turi daugybę panaudojimo būdų: išvestinė yra judėjimo greitis (arba, apskritai, bet kokio proceso greitis); išvestinė yra nuolydis funkcijos grafiko liestinė; naudodami išvestinę funkciją galite ištirti monotoniškumą ir ekstremalumą; išvestinė padeda išspręsti optimizavimo problemas.

Tačiau realiame gyvenime turime išspręsti ir atvirkštines problemas: pavyzdžiui, kartu su greičio nustatymo pagal žinomą judėjimo dėsnį problema susiduriame ir su judėjimo dėsnio pagal žinomą greitį atkūrimo problema. Panagrinėkime vieną iš šių problemų.

1 pavyzdys. Juda tiesia linija materialus taškas, jo judėjimo greitis momentu t pateikiamas formule u = tg. Raskite judėjimo dėsnį.

Sprendimas. Tegu s = s(t) yra norimas judėjimo dėsnis. Yra žinoma, kad s"(t) = u"(t). Tai reiškia, kad norint išspręsti problemą reikia pasirinkti funkcija s = s(t), kurios išvestinė lygi tg. Tai nesunku atspėti

Iš karto atkreipkime dėmesį, kad pavyzdys išspręstas teisingai, bet nepilnai. Mes nustatėme, kad iš tikrųjų problema turi be galo daug sprendimų: bet kokia formos funkcija savavališka konstanta gali būti judėjimo dėsnis, nes

Kad užduotis būtų konkretesnė, reikėjo pataisyti pradinę situaciją: nurodyti judančio taško koordinatę tam tikru laiko momentu, pavyzdžiui, t=0. Jei, tarkime, s(0) = s 0, tai iš lygybės gauname s(0) = 0 + C, t.y. S 0 = C. Dabar judėjimo dėsnis yra vienareikšmiškai apibrėžtas:
Matematikoje abipusiai atvirkštiniai veiksmai suteikiami skirtingais pavadinimais ir sugalvojami specialūs žymėjimai: pavyzdžiui, kvadratas (x 2) ir ištraukimas. kvadratinė šaknis sinusas (sinх) ir arcsine(arcsin x) ir kt. Duotos funkcijos išvestinės radimo procesas vadinamas diferenciacija, o atvirkštine operacija, t.y. funkcijos radimo iš duotosios išvestinės procesas – integracija.
Pats terminas „išvestinė“ gali būti pateisinamas „kasdieniais terminais“: funkcija y - f(x) „gimsta“ nauja funkcija y"= f"(x) Funkcija y = f(x) veikia kaip "tėvas", bet matematikai, žinoma, nevadina jos "tėvu" ar "gamintojas", jie sako, kad taip yra. funkcija y"=f"(x), pirminis vaizdas arba, trumpai tariant, antidarinys.

1 apibrėžimas. Funkcija y = F(x) vadinama funkcijos y = f(x) antiderivatine duotame intervale X, jei visiems x iš X galioja lygybė F"(x)=f(x).

Praktikoje intervalas X paprastai nenurodomas, o numanomas (kaip natūrali funkcijos apibrėžimo sritis).

Štai keletas pavyzdžių:

1) Funkcija y = x 2 yra funkcijos y = 2x priešišvestinė, nes visiems x lygybė (x 2)" = 2x yra teisinga.
2) funkcija y - x 3 yra funkcijos y-3x 2 priešišvestinė, nes visiems x lygybė (x 3)" = 3x 2 yra teisinga.
3) Funkcija y-sinх yra funkcijos y = cosx priešišvestinė, nes visiems x lygybė (sinx)" = cosx yra teisinga.
4) Funkcija yra intervalo funkcijos antiderivinė, nes visiems x > 0 lygybė yra teisinga
Apskritai, žinant darinių radimo formules, nesunku sudaryti antidarinių radimo formulių lentelę.

Tikimės, kad supratote, kaip sudaryta ši lentelė: funkcijos išvestinė, kuri įrašyta antrame stulpelyje, yra lygi funkcijai, parašyta atitinkamoje pirmojo stulpelio eilutėje (patikrinkite, nepatingėkite, tai labai naudinga). Pavyzdžiui, funkcijai y = x 5 antidarinė, kaip jūs nustatysite, yra funkcija (žr. ketvirtą lentelės eilutę).

Pastabos: 1. Toliau įrodysime teoremą, kad jei y = F(x) yra funkcijos y = f(x) antidarinė, tai funkcija y = f(x) turi be galo daug antidarinių ir jie visi turi formą y = F(x ) + C. Todėl teisingiau būtų pridėti terminą C visur antrame lentelės stulpelyje, kur C yra savavališkas realusis skaičius.
2. Trumpumo dėlei kartais vietoj frazės „funkcija y = F(x) yra funkcijos y = f(x) antidarinė“, sakoma, kad F(x) yra f(x) antidarinė. .

2. Antidarinių radimo taisyklės

Ieškant antidarinių, taip pat ieškant išvestinių, naudojamos ne tik formulės (jos nurodytos lentelėje 196 p.), bet ir kai kurios taisyklės. Jos yra tiesiogiai susijusios su atitinkamomis išvestinių finansinių priemonių apskaičiavimo taisyklėmis.

Žinome, kad sumos išvestinė yra lygi jos išvestinių sumai. Ši taisyklė sukuria atitinkamą taisyklę antiderivatams rasti.

1 taisyklė. Sumos antidarinė lygi antidarinių sumai.

Atkreipiame jūsų dėmesį į šiokį tokį „lengvumą“. Tiesą sakant, reikėtų suformuluoti teoremą: jei funkcijos y = f(x) ir y = g(x) turi antidarinius intervale X, atitinkamai y-F(x) ir y-G(x), tada funkcijų y suma = f(x)+g(x) turi antidarinį intervale X, o ši antidarinė yra funkcija y = F(x)+G(x). Tačiau dažniausiai formuluojant taisykles (o ne teoremas) jos paliekamos tik raktinius žodžius- tai leidžia patogiau taikyti taisyklę praktikoje

2 pavyzdys. Raskite funkcijos y = 2x + cos x antidarinį.

Sprendimas. 2x antidarinys yra x"; cox antidarinys yra sin x. Tai reiškia, kad funkcijos y = 2x + cos x antidarinė bus funkcija y = x 2 + sin x (ir apskritai bet kuri formos funkcija Y = x 1 + sinx + C) .
Žinome, kad pastovųjį veiksnį galima išimti iš išvestinės ženklo. Ši taisyklė sukuria atitinkamą taisyklę antiderivatams rasti.

2 taisyklė. Iš antidarinio ženklo galima išimti pastovų faktorių.

3 pavyzdys.

Sprendimas. a) Sin x antidarinys yra -soz x; Tai reiškia, kad funkcijai y = 5 sin x antidarinė funkcija bus funkcija y = -5 cos x.

b) cos x antidarinys yra sin x; Tai reiškia, kad funkcijos antidarinys yra funkcija
c) x 3 antidarinys yra x antidarinys, funkcijos y = 1 antidarinys yra funkcija y = x. Naudodami pirmąją ir antrąją antidarinių radimo taisykles, nustatome, kad funkcijos y = 12x 3 + 8x-1 antidarinys yra funkcija
komentuoti. Kaip žinoma, sandaugos išvestinė nėra lygi išvestinių sandaugai (produkto diferencijavimo taisyklė yra sudėtingesnė), o dalinio išvestinė nelygi išvestinių sandaugai. Todėl nėra taisyklių, kaip rasti produkto antidarinį arba dviejų funkcijų koeficiento antidarinį. Būk atsargus!
Išsiaiškinkime kitą antidarinių radimo taisyklę. Žinome, kad funkcijos y = f(kx+m) išvestinė apskaičiuojama pagal formulę

Ši taisyklė sukuria atitinkamą taisyklę antiderivatams rasti.
3 taisyklė. Jei y = F(x) yra funkcijos y = f(x) antidarinė, tai funkcijos y=f(kx+m) antidarinė yra funkcija

Iš tikrųjų,

Tai reiškia, kad tai funkcijos y = f(kx+m) antidarinė.
Trečiosios taisyklės prasmė yra tokia. Jei žinote, kad funkcijos y = f(x) antidarinė yra funkcija y = F(x), ir jums reikia rasti funkcijos y = f(kx+m) antiišvestinę, tada elkitės taip: imkite ta pati funkcija F, bet vietoj argumento x pakeiskite išraiška kx+m; be to, nepamirškite prieš funkcijos ženklą parašyti „pataisos koeficientas“.
4 pavyzdys. Raskite nurodytų funkcijų antidarinius:

Sprendimas, a) Sin x antidarinys yra -soz x; Tai reiškia, kad funkcijai y = sin2x antidarinė bus funkcija
b) cos x antidarinys yra sin x; Tai reiškia, kad funkcijos antidarinys yra funkcija

c) x 7 antidarinė reiškia, kad funkcijai y = (4-5x) 7 antidarinė bus funkcija

3. Neapibrėžtas integralas

Aukščiau jau pažymėjome, kad uždavinys rasti tam tikros funkcijos y = f(x) antidarinį turi daugiau nei vieną sprendimą. Pakalbėkime apie šią problemą išsamiau.

Įrodymas. 1. Tegul y = F(x) yra funkcijos y = f(x) antiišvestinė intervale X. Tai reiškia, kad visiems x iš X galioja lygybė x"(x) = f(x). Raskite bet kurios formos y = F(x)+C išvestinę:
(F(x) +C) = F"(x) +C = f(x) +0 = f(x).

Taigi, (F(x)+C) = f(x). Tai reiškia, kad y = F(x) + C yra funkcijos y = f(x) antidarinė.
Taigi, mes įrodėme, kad jei funkcija y = f(x) turi antidarinį y=F(x), tai funkcija (f = f(x) turi be galo daug antidarinių, pavyzdžiui, bet kuri y = formos funkcija F(x) +C yra antidarinys.
2. Dabar įrodykime, kad nurodytas funkcijų tipas išsemia visą antidarinių rinkinį.

Tegul y=F 1 (x) ir y=F(x) yra dvi funkcijos Y = f(x) antidarinės intervale X. Tai reiškia, kad visiems x iš intervalo X galioja šie ryšiai: F^ ( x) = f (X); F"(x) = f(x).

Panagrinėkime funkciją y = F 1 (x) -.F(x) ir raskime jos išvestinę: (F, (x) -F(x))" = F[(x)-F(x) = f(x) ) – f(x) = 0.
Yra žinoma, kad jei funkcijos išvestinė intervale X yra identiškai lygi nuliui, tai funkcija yra pastovi intervale X (žr. 3 teoremą iš § 35). Tai reiškia, kad F 1 (x) - F (x) = C, t.y. Fx) = F(x)+C.

Teorema įrodyta.

5 pavyzdys. Duotas greičio kitimo su laiku dėsnis: v = -5sin2t. Raskite judėjimo dėsnį s = s(t), jei žinoma, kad momentu t=0 taško koordinatė buvo lygi skaičiui 1,5 (t. y. s(t) = 1,5).

Sprendimas. Kadangi greitis yra koordinatės, kaip laiko funkcijos, išvestinė, pirmiausia reikia rasti greičio antidarinį, t.y. funkcijos v = -5sin2t antidarinys. Vienas iš tokių antidarinių yra funkcija, o visų antidarinių rinkinys turi tokią formą:

Norėdami rasti konkrečią konstantos C reikšmę, naudojame pradines sąlygas, pagal kurias s(0) = 1,5. Į formulę (1) pakeitę reikšmes t=0, S = 1,5, gauname:

Pakeitę rastą C reikšmę į (1) formulę, gauname mus dominantį judėjimo dėsnį:

2 apibrėžimas. Jei funkcija y = f(x) intervale X turi antidarinį y = F(x), tai visų antidarinių aibė, t.y. y = F(x) + C formos funkcijų aibė vadinama funkcijos y = f(x) neapibrėžtuoju integralu ir žymima taip:

(skaitykite: " neapibrėžtas integralas ef iš x de x").
Kitoje pastraipoje išsiaiškinsime, kas yra paslėpta prasmė nurodytas žymėjimas.
Remdamiesi šiame skyriuje pateikta antidarinių lentele, sudarysime pagrindinių neapibrėžtų integralų lentelę:

Remdamiesi aukščiau pateiktomis trimis taisyklėmis, kaip rasti antidarinius, galime suformuluoti atitinkamas integravimo taisykles.

1 taisyklė. Funkcijų sumos integralas yra lygus šių funkcijų integralų sumai:

2 taisyklė. Iš integralo ženklo galima išimti pastovų koeficientą:

3 taisyklė. Jeigu

6 pavyzdys. Raskite neapibrėžtus integralus:

Sprendimas, a) Naudodami pirmą ir antrą integravimo taisykles gauname:

Dabar naudokime 3 ir 4 integravimo formules:

Rezultate gauname:

b) Naudodami trečiąją integravimo taisyklę ir 8 formulę, gauname:

c) Norėdami tiesiogiai rasti duotąjį integralą, neturime nei atitinkamos formulės, nei atitinkamos taisyklės. Tokiais atvejais iš anksto vykdomas tapatybės transformacijos išraiška, esanti po integraliu ženklu.

Pasinaudokime trigonometrinė formulė Laipsnio sumažinimas:

Tada iš eilės randame:

A.G. Mordkovičiaus algebra 10 klasė

Kalendorinis teminis planavimas matematikoje, vaizdo įrašą matematika internetu, Matematika mokykloje

Yra trys pagrindinės taisyklės, kaip rasti antiderivatines funkcijas. Jos labai panašios į atitinkamas diferenciacijos taisykles.

1 taisyklė

Jei F yra kokios nors funkcijos f antidarinys, o G yra kokios nors funkcijos g antidarinys, tai F + G bus f + g antidarinys.

Pagal antidarinio apibrėžimą F’ = f. G' = g. Ir kadangi šios sąlygos yra įvykdytos, pagal funkcijų sumos išvestinės apskaičiavimo taisyklę turėsime:

(F + G)’ = F’ + G’ = f + g.

2 taisyklė

Jei F yra kokios nors funkcijos f antidarinys, o k yra kokia nors konstanta. Tada k*F yra funkcijos k*f antidarinė. Ši taisyklė išplaukia iš sudėtingos funkcijos išvestinės apskaičiavimo taisyklės.

Turime: (k*F)’ = k*F’ = k*f.

3 taisyklė

Jei F(x) yra tam tikra funkcijos f(x) antidarinė, o k ir b yra tam tikros konstantos, o k nėra lygus nuliui, tada (1/k)*F*(k*x+b) bus funkcijos f (k*x+b) antidarinys.

Ši taisyklė išplaukia iš sudėtingos funkcijos išvestinės apskaičiavimo taisyklės:

((1/k)*F*(k*x+b))’ = (1/k)*F’(k*x+b)*k = f(k*x+b).

Pažvelkime į keletą šių taisyklių taikymo pavyzdžių:

1 pavyzdys. Rasti bendra forma funkcijos f(x) = x^3 +1/x^2 antidariniai. Funkcijos x^3 viena iš antidarinių bus funkcija (x^4)/4, o funkcijai 1/x^2 viena iš antidarinių bus funkcija -1/x. Naudodami pirmą taisyklę, turime:

F(x) = x^4/4 - 1/x +C.

2 pavyzdys. Raskime funkcijos f(x) = 5*cos(x) antidarinių bendrąją formą. Funkcijos cos(x) viena iš antidarinių bus funkcija sin(x). Jei dabar naudosime antrąją taisyklę, turėsime:

F(x) = 5*sin(x).

3 pavyzdys. Raskite vieną iš funkcijos y = sin(3*x-2) antidarinių. Funkcijos sin(x) viena iš antidarinių bus funkcija -cos(x). Jei dabar naudosime trečiąją taisyklę, gautume antidarinio išraišką:

F(x) = (-1/3)*cos(3*x-2)

4 pavyzdys. Raskite funkcijos f(x) = 1/(7-3*x)^5 antidarinį

Funkcijos 1/x^5 antidarinė bus funkcija (-1/(4*x^4)). Dabar, naudodamiesi trečiąja taisykle, gauname.

Pamokos santrauka apie algebrą ir bazinę analizę 11 klasės mokiniams švietimo įstaigos

Tema: „Antidarinių radimo taisyklės“

Pamokos tikslas:

Švietimas: įvesti taisykles, kaip rasti antidarinius naudojant jų lentelės reikšmes ir naudoti jas sprendžiant problemas.

Užduotys:

pateikti integravimo operacijos apibrėžimą;

supažindinti mokinius su antidarinių lentele;

supažindinti mokinius su integracijos taisyklėmis;

mokyti mokinius sprendžiant uždavinius naudotis antidarinių lentele ir integravimo taisyklėmis.

Vystomasis: prisidėti prie mokinių gebėjimo analizuoti, lyginti duomenis ir daryti išvadas ugdymo.

Švietimas: prisidėti prie kolektyvo formavimo ir savarankiškas darbas, ugdyti gebėjimą tiksliai ir kompetentingai atlikti matematinius žymėjimus.

Mokymo metodai: indukcinis-reprodukcinis, dedukcinis-reprodukcinis

tyvi.

Pamokos tipas: naujų žinių įsisavinimas.

Reikalavimai ZUN:

Mokiniai turėtų žinoti:

- integravimo operacijos apibrėžimas;

Antidarinių lentelė;

mokiniai turi sugebėti:

Sprendžiant problemas taikyti antidarinių lentelę;

Išspręskite problemas, kuriose būtina rasti antidarinius.

Įranga: kompiuteris, ekranas, multimedijos projektorius, pristatymas.

Literatūra:

1. A.G. Mordkovich ir kt. „Algebra ir analizės pradžia. Užduočių knygelė 10-11 klasei" M.: Mnemosyne, 2001.

2. Sh.A. Alimovas „Algebra ir analizės pradžia. 10-11 klasė. Vadovėlis" M.: Edukacija, 2004. - 384 p.

3. Matematikos mokymo metodai ir technologija. M.: Bustard, 2005. – 416 p.

Pamokos struktūra:

aš. Laiko organizavimas(2 minutės.)

II. Žinių atnaujinimas (7 min.)

III. Naujos medžiagos mokymasis (15 min.)

VI. Išmoktos medžiagos sutvirtinimas (17 min.)

V. Sumavimas ir D/Z (4 min.)

Per užsiėmimus

aš . Laiko organizavimas

Mokinių pasisveikinimas, neatvykimų ir patalpos pasirengimo pamokai tikrinimas.

II . Žinių atnaujinimas

Rašymas lentoje (sąsiuviniuose)

Data.

Klasės darbas

Antidarinių radimo taisyklės.

Mokytojas: Šios dienos pamokos tema: „Antidarinių radimo taisyklės“ (1 skaidrė). Bet prieš pradedant mokytis nauja tema Prisiminkime aptrauktą medžiagą.

Prie lentos kviečiami du mokiniai, kiekvienam duodama individuali užduotis (jei mokinys atliko užduotį be klaidų, gauna pažymį „5“).

Užduočių kortelės

№ 1

y = 6x – 2x 3 .

f ( x )=3 x 2 +4 x –1 taške x =3.

№ 2

2) Raskite funkcijos išvestinės reikšmęf ( x )=5 x 2 +5 x – 5 taške x =1.

Sprendimas

Kortelė Nr.1

1) Raskite didėjančios ir mažėjančios funkcijos intervalusy = 6x – 2x 3 .

; Tebūnie, tada tikrai; X 1 Ir X 2 stacionarūs taškai;

2. Stacionarūs taškai padalina koordinačių tiesę į tris intervalus. Tuose intervaluose, kur funkcijos išvestinė yra teigiama, pati funkcija didėja, o kur neigiama – mažėja.

- + -

adresu -1 1

Vadinasi adresu mažėja ties X (- ;-1) (1; ) ir didėja kartu suX (-1;1).

2) f ( x )=3 x 2 +4 x –1 ; ; .

Kortelė Nr.2

1) Raskite funkcijos ekstremalinius taškus .

1. Raskime stacionarius taškus, tam rasime šios funkcijos išvestinę, tada prilyginsime nuliui ir išspręsime gautą lygtį, kurios šaknys bus stacionarūs taškai.

; Leiskite , Taigi, todėl , ir .

2. Stacionarūs taškai padalina koordinačių tiesę į keturis intervalus. Tie taškai, per kuriuos funkcijos išvestinė keičia ženklą, yra ekstremumo taškai.

+ - - +

adresu -3 0 3

Reiškia - ekstremalūs taškai ir yra maksimalus taškas ir - minimalus taškas.

2) f ( x )=5 x 2 +5 x – 5; ; .

Kol prie lentos pakviesti mokiniai sprendžia pavyzdžius, likusiai klasės daliai užduodami teoriniai klausimai. Klausimų metu mokytojas stebi, ar mokiniai atliko užduotį, ar ne.

Mokytojas: Taigi atsakykime į keletą klausimų. Prisiminkime, kokia funkcija vadinama antidariniu? (2 skaidrė)

Studentas: Funkcija F ( x ) vadinamas funkcijos antidariniuf ( x ) tam tikru intervalu, jei visiemsx iš šio tarpo .

(2 skaidrė).

Mokytojas: Teisingai. Kaip vadinamas funkcijos išvestinės paieškos procesas? (3 skaidrė)

Studentas: Diferencijavimas.

Mokiniui atsakius, teisingas atsakymas dubliuojamas skaidrėje (3 skaidrė).

Mokytojas: Kaip parodyti tą funkcijąF ( x ) yra funkcijos antidarinysf ( x ) ? (4 skaidrė).

Studentas: Raskite funkcijos išvestinęF ( x ) .

Mokiniui atsakius, teisingas atsakymas dubliuojamas skaidrėje (4 skaidrė).

Mokytojas: gerai. Tada pasakykite man, ar funkcija yraF ( x )=3 x 2 +11 x funkcijos antidarinysf ( x )=6x+10? (5 skaidrė)

Studentas: Ne, nes funkcijos išvestinėF ( x )=3 x 2 +11 x lygus 6x+11, bet ne 6x+10 .

Mokiniui atsakius, teisingas atsakymas dubliuojamas skaidrėje (5 skaidrė).

Mokytojas: Kiek antidarinių galima rasti tam tikrai funkcijai?f ( x ) ? Pagrįskite savo atsakymą. (6 skaidrė)

Studentas: Be galo daug, nes Prie gautos funkcijos visada pridedame konstantą, kuri gali būti bet koks realusis skaičius.

Mokiniui atsakius, teisingas atsakymas dubliuojamas skaidrėje (6 skaidrė).

Mokytojas: Teisingai. Dabar kartu patikrinkime mokinių, dirbančių lentoje, sprendimus.

Mokiniai patikrina sprendimą kartu su mokytoju.

III . Naujos medžiagos mokymasis

Mokytojas: Atvirkštinė operacija, kai reikia rasti tam tikros funkcijos antidarinį, vadinama integracija (iš lotyniško žodžiointegrare - atkurti). Kai kurių funkcijų antidarinių lentelę galima sudaryti naudojant išvestinių lentelę. Pavyzdžiui, žinant tai, mes gauname , iš ko išplaukia, kad visos antidarinės funkcijos yra parašyti formoje, Kur C – savavališka konstanta.

Rašymas lentoje (sąsiuviniuose)

mes gauname,

iš kur išplaukia, kad visos antidarinės funkcijos yra parašyti formoje, Kur C – savavališka konstanta.

Mokytojas: Atsiverskite savo vadovėlius į 290 puslapį. Čia yra antidarinių lentelė. Jis taip pat pateikiamas skaidrėje. (7 skaidrė)

Mokytojas: Integravimo taisykles galima gauti naudojant diferencijavimo taisykles. Apsvarstykite šias integravimo taisykles: tegulF ( x ) Ir G ( x ) – atitinkamų funkcijų antidariniaif ( x ) Ir g ( x ) tam tikru intervalu. Tada: